1 Introduction

Although the level of completeness of hydrological time series is meant to be increasing (Dixon 2010), handling missing data in hydrology still remains to be a challenge. Gaps in water-related datasets not only constrain the analysis and interpretation of historical riverflow variation but may also have a deleterious influence on hydrological models and the associated predictions (Harvey et al. 2012). Indeed, Gill et al. (2007) claimed that ignoring missing values before modelling is more detrimental for data-based models, such as those based on learning algorithms, than for physically-based approaches (Zhang and Post 2018).

In early 2010’s, Harvey et al. (2012) argued that “there are currently no widely-accepted standard techniques for data infilling, either in the UK or internationally”. More recently, Gao et al. (2018) provided a similar assessment of the state-of-art in the field of handling missing data in hydrology and wrote that “Imputation in hydrology has very often been done in an ad hoc manner, lacking a clear theoretical basis”. Though there are attempts to develop robust gap-filling approaches (e.g. Dembélé et al. 2019; Hamzah et al. 2021; Khampuengson and Wang 2023), commonly, various statistical methods are adopted to reconstruct missing parts of a hydrograph (e.g. McCuen 2003). In hydrological sciences, however, hydrograph data reveal certain specifics – a high flow is characterized by a rising limb, a crest, and a slowly-declining recession limb (e.g. Reddy 2005). Therefore, adopting a given statistical method should not be carried out ad hoc, but it needs to account for shape of a hydrograph and/or its specific variability.

Though gap filling using hydrological models was found to have a negligible impact on the determination of trend in riverflow (Zhang and Post 2018), such an approach may provide valuable information when water level predictions are issued. Indeed, to build a lumped model based on time series methods, such as for instance vector autoregression (Niedzielski 2007; Niedzielski and Miziński 2017), continuous time series is required. As mentioned above, hydrological data reveal the specific shape, and therefore flexible non-linear approaches, such as autoregressive integrated moving average (ARIMA) or autoregressive conditional heteroscedastic (ARCH) ones (Gao et al. 2018), are needed. It has been found that the application of ARIMA models in the process of filling gaps in streamflow time series is justified, with limitation on the number of missing data (Lopes Martins et al. 2023). Furthermore, the ARIMA approach is not computationally-demanding (Ren et al. 2022), which makes it applicable in hydrological applications that require rapid data processing.

The ARIMA models, however, when used to simulate or predict variation of hydrological data within a no-data gap, may occasionally reveal instability driven by integrating a spike-rich reconstructed part produced by combining predictions with forthcoming data (Fig. 1). Instability of ARIMA models and the deterioration of their performance has been reported by Li et al. (2023) who claim that there is scarcity of research in this topic. Also, the instability in question has been reported in the hydrological context by Gui et al. (2021) who argue that the ARIMA approach belongs to a set of a few mathematical models which reveal unsatisfactory skills in simulating streamflow. Herein, we propose a new method and its Python implementation to address the problem of instability of ARIMA models used for data gap infilling in hydrology. The structure of the paper is the following: first we describe our gap-filling methodology, named hereinafter as LinAR (Section 2), second we present datasets used for validation (Section 3), third we show the results on the accuracy of our interpolation method (Section 4), fourth we discuss our findings with similar studies (Section 5), and finally we conclude the article (Section 6).

Fig. 1
figure 1

Example of unrealistic instability of water level reconstructions (triangles) based on the ARIMA model fitted to data (black circles) or data+predictions (black circles + black triangles): a predictions imputed in the 15-step no-data gap (triangles with white filling) along with single real data occurring after the gap (circle with white filling), b data+predictions+data (black symbols) from (a) are modelled and used to produce forecasts for filling the 20-step no-data gap (triangles with white filling) along with next single real data occurring after the gap (circle with white filling), c data+predictions+data+predictions+data (black symbols) from (b) are modelled and utilized to produce forecasts for filling the 10-step no-data gap (triangles with white filling) along with next single real data occurring after the gap (circle with white filling), d data+predictions+data+predictions+data+prediction+data (black symbols) from (c) are modelled and used to produce forecasts for filling the 25-step no-data gap (triangles with white filling) along with next single real data occurring after the gap (circle with white filling)

Full size image

2 Rationale and Methods

The primary objective of this study is to introduce the LinAR approach, which combines the ARI-based imputation with linear interpolation. By doing so, the proposed method aims to address the issue of unrealistic jumps in the hydrological time series resulting from the use of the ARIMA model and imitate short-term hydrological variability in the available data.

As explained in Fig. 1 and its caption, the use of the ARIMA model for interpolating missing hydrological data may lead to unrealistic jumps between last reconstructed values in a no-data gap and first real record. Such jumps do not occur if simple linear interpolation is employed, as in the papers by Niedzielski and Miziński (2017) and Kulanuwat et al. (2021). However, such a simplistic approach introduces artificial trend-like intervals, particularly when gaps are long, potentially causing constraints in data-based lumped modelling (i.e. fitting time series models to partially linear data is not recommended). In addition, Musial et al. (2011) argue that linear interpolation has a limited potential in offering reliable estimates as it reveals tendency to underestimate real observations, since the imputation is limited by bounds associated with true data before/after the no-data gap. Lepot et al. (2017) add that overestimation is also possible while applying linear interpolation.

On the contrary, Gnauck (2004) claims that the linear approach performs better than the nonlinear interpolation methods in filling gaps in water quality time series. The latter finding justifies our approach, in which simple linear interpolation is used to reconstruct a general tendency and the integrated autoregressive (ARI, i.e. ARIMA without a moving average part) model (also linear in its stochastic structure) is used to reproduce some portion of irregular variability between bounds, as postulated by Musial et al. (2011). Hence, herein we propose the combination of the ARI-based imputation with linear interpolation, both avoiding the aforementioned jumps and imitating (in short term) hydrological variability of the available data. The Python implementation of LinAR is freely available in our GitHub repository (https://github.com/MichalHalicki4/LinAR-interpolation).

The LinAR approach begins with the computation of autoregressive-based predictions with a lead time equal to the number of missing data points within a given no-data gap. Next, we employ linear interpolation between the last available measurement before the gap and the first measurement after the gap. Additionally, linear interpolation is applied between the last available measurement before the gap and the last autoregressive prediction. The scaling factor is then determined using the differences between the linearly interpolated values and the corresponding ARI-based predictions within the entire no-data gap (Fig. 2).

Fig. 2
figure 2

Graphical explanation of the LinAR gap imputation approach that combines ARI-prediction (gray circles) and linear interpolation (crosses)

Full size image

The ARI model corresponds to autoregressive (AR) model, after m-time differencing input time series \(x_t\) in order to produce residuals \(y_t\). Firstly, each \(x_t\) is differenced to produce residuals \(\nabla x_t = x_t - x_{t-1}\). To check stationarity, we propose to use two tests jointly, i.e. the augmented Dickey-Fuller (ADF) test for stationarity is applied to dataset and the F-test for the equality of two variances is applied to two equal-size parts of dataset (first and second half of dataset when sample size is even, and first and second half of dataset without middle value when sample size is odd). Such a two-test approach passes data with relatively constant variance, even if the ADF test fails to detect non-stationarity. If \(\nabla x_t\) is stationary, no further differencing is needed, and therefore \(\nabla x_t\) is assumed to be residuals \(y_t\) prepared for further processing. If \(\nabla x_t\) is non-stationary, \(\nabla x_t\) is again differenced to produce \(\nabla ^2 x_t = \nabla (\nabla x_t) = \nabla (x_t-x_{t-1}) = x_t - 2x_{t-1} + x_{t-2}\). If \(\nabla ^2 x_t\) passes the two-test stationarity verification it becomes the residual time series \(y_t\). In our work, we assume the significance level of 0.05.

The zero-mean autoregressive AR stochastic process \(Y_t\), where \(y_t\) represents its trajectory, is mathematically described by the equation:

$$\begin{aligned} Y_t = \sum _{i = 1}^{p} a_i Y_{t-i} + Z_t, \end{aligned}$$
(1)

where \(a_i\) denotes the autoregressive coefficients, p represents the order of autoregression, and \(Z_t\) signifies white noise. To produce a forecast of \(x_t\), the prognosis of \(y_t\) is attached to residuals, and such an extended residual signal is integrated m times.

Second, linear interpolation between the last available measurement before n-step no-data gap and the first measurement after this gap is applied. Each k-th imputed value within the gap is calculated using the following expression:

$$\begin{aligned} \tilde{x}(k) = k \frac{(x_{after gap}-x_{before gap})}{n+1} + x_{before gap}, \end{aligned}$$
(2)

where \(x_{after gap}\), \(x_{before gap}\) are bounds, and \(1 \le k \le n\).

Third, linear interpolation between the last available measurement before n-step no-data gap and the last ARI-based prediction into step n is utilized. Each k-th value within the gap is computed along the lines of Eq. 2 as:

$$\begin{aligned} \tilde{p}(k) = k \frac{(p_{lastingap}-x_{before gap})}{n} + x_{before gap}, \end{aligned}$$
(3)

where \(p_{lastingap}\) is the last forecasted (into n-th step) value, and \(1 \le k \le n-1\).

Fourth, both linear expressions \(\tilde{x}\) and \(\tilde{p}\) are used to produce a scaling factor, the objective of which is to correct the imputation based on ARI model. Namely, the difference:

$$\begin{aligned} \alpha (k) = \tilde{x}(k) - \tilde{p}(k) \end{aligned}$$
(4)

is added to every ARI-based prediction for k steps ahead, selected from a prognosis with maximum lead time of n steps and issued for the entire no-data gap (gray circles in Fig. 2 are moved up and become black squares).

3 Data

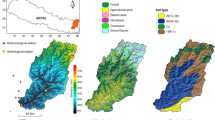
The imputation approach described in this paper is tested on 28 hourly water level time series, collected within the Odra/Oder River basin (SW Poland) at hydrological gauges of the Institute for Meteorology and Water Management – State Research Institute (IMGW-PIB). Spatial distribution of these gauges is presented in Fig. 3. The data span the time interval from 01/01/2016 to 31/12/2021.

Fig. 3
figure 3

Location of hydrological gauges selected for the study

Full size image

The Odra/Oder River has its headwaters in Czechia. It flows northward to Poland, where it drains a considerable area of Polish territory, being the second largest river in the country. The Odra/Oder River in its middle reach becomes a transboundary river between Poland and Germany. Gauges maintained by IMGW-PIB are vertically referenced to Kronsztadt’86 vertical datum. Hence, water levels processed in this paper are values in centimetres above local zeros, the absolute heights of which are expressed in Kronsztadt’86.

Every water level time series studied in this paper contains no-data gaps (from 2 in Bardo to 318 in Ścinawa). The gaps reveal different lengths, ranging from 1 in many gauges to 2928 in Nowa Sól. Table 1 juxtaposes main characteristics of missing data in the above-mentioned time series.

Table 1 Juxtaposition of gauges located along the Odra/Oder River from which data are processed in this paper. Characteristics of no-data gaps are also provided
Full size table

Since reference data are needed for validation, the above-mentioned true gaps are not used to evaluate the performance of the LinAR method. To assess our approach, artificial gaps are produced so that the removed measurements are used as ground truth to compare with the interpolated values. Namely, at each hourly step selected from the studied time interval 2016–2021, we (1) artificially delete one measurement, compute interpolation and carry out the comparison, (2) artificially remove two measurements, compute interpolation of two missing data and conduct the comparison, (3) we continue the process above-described in (1) and (2) until our artificially-produced no-data gap has length of 72 steps. Literally, for each gauge we consider approx. 3,744,000 interpolations based on LinAR (52,000 hourly steps \(\times\) 72). The same procedure is repeated for purely linear interpolation. To have long enough time series to fit an ARI model (we assume 5 days) and to ensure enough data for validation (72 h), we produce buffers (from 72 h before the true no-data gap to 5 days after the gap) within which we do not interpolate. Figure 4 presents how gauge data and their interpolated equivalents correspond and how they are juxtaposed in each iteration to calculate root mean square error (RMSE).

Fig. 4
figure 4

Example sketch explaining the validation approach: a true water level data measured at a gauge; b interpolated water level when artificial no-data gaps are of length 1 (window width W\(_1\)) and interpolation step is of length 1 (lead time L\(_1\)), in this example \(RMSE(1,1) = \frac{1}{7}\sum _{i=1}^{7}(red_{t_{i-1}} - black_{t_{i-1}})^2\); c interpolated water level when artificial no-data gaps are of length 2 (window width W\(_2\)) and interpolation steps are of length 1 and 2 (lead time L\(_1\) and L\(_2\)), in this example \(RMSE(2,1) = \frac{1}{6}\sum _{i=1}^{6}(pink_{t_{i-1}} - black_{t_{i-1}})^2\) and \(RMSE(2,2) = \frac{1}{6}\sum _{i=1}^{6}(blue_{t_{i}} - black_{t_{i}})^2\); d interpolated water level when artificial no-data gaps are of length 3 (window width W\(_3\)) and interpolation steps are of length 1, 2 and 3 (lead time L\(_1\), L\(_2\) and L\(_3\)), in this example \(RMSE(3,1) = \frac{1}{5}\sum _{i=1}^{5}(yellow_{t_{i-1}} - black_{t_{i-1}})^2\), \(RMSE(3,2) = \frac{1}{5}\sum _{i=1}^{5}(orange_{t_{i}} - black_{t_{i}})^2\) and \(RMSE(3,3) = \frac{1}{5}\sum _{i=1}^{5}(green_{t_{i+1}} - black_{t_{i+1}})^2\)

Full size image

4 Results

Although we study 28 hydrological time series, our scrutiny begins with four specific cases (Fig. 5) that allow the reader to follow complete findings juxtaposed in Table 2 and Appendix. Black contour separates interpolations for which the LinAR method performs better than the purely linear approach.

The most expected result has a graphical representation as in Fig. 5a for gauge 2 (Biała Góra, Odra, river width at gauge of 200 m, gauge within lowland). On average, in a no-data gaps of widths up to 16 (W = \(1,2,\ldots ,16\)), all LinAR interpolations with lengths up to 15 (L = \(1, 2, \ldots , 15\)) are characterised by a smaller RMSE than RMSE for the linear method. However, the improvement is up to 3% of RMSE. For longer no-data gaps the linear approach is superior over the LinAR one.

Table 2 Accuracy of LinAR and purely linear (LIN) interpolation
Full size table

A different picture is shown in Fig. 5b that corresponds to gauge 6 (Ścinawa, Odra, river width at gauge of 70 m, gauge within lowland). The improvement (LinAR in respect to purely linear) is noticed for all no-data gaps (W = \(1,2,\ldots ,72\)), however, only for first steps within these gaps (L = \(1, 2, \ldots , 7\)). In this case, the improvement can exceed 15%.

An unequivocal case is presented in Fig. 5c where improvement is noticed predominantly for very small number of steps (L), independently on widths of no-data gaps (W). Again, for some combinations of L and W the improvement exceeds 15%.

If our tests incorrectly pass non-stationary cases, artificial periodicities occur as presented in Fig. 5d. Such highly departing values are unique, but considerable in their absolute values, therefore they meaningfully increase the overall RMSE. Fortunately, such situations are mainly reported for long no-data gaps.

It is apparent from Fig. 5 that the LinAR approach can be recommended for short no-data gaps. It is in agreement with properties of autoregressive predictions which are irregular for several steps into the future and for longer lead times converge to a theoretical mean of the autoregressive process (zero for the zero-mean model).

Fig. 5
figure 5

Examples of percentage differences between linear and LinAR interpolation errors (RMSE) as a function of width of no-data gap (W) and interpolation length (L): Odra river at Biała Góra (a), Odra river at Ścinawa (b), Nysa Kłodzka at Skorogoszcz (c), Stobrawa at Karłowice (d). Positive values indicate better performance of the LinAR approach, while negative numbers correspond to an opposite case

Full size image

It is apparent from Table 2 that the application of the LinAR approach leads to better results in first dozen of steps (for details, see “improved windows" column). Also, the scatter plots of “improved windows" and “improved values" against river width show that our approach is suitable for rivers of considerable size rather than for small channels (Fig. 6). It is likely that the dependence of the LinAR performance on river width is driven by less abrupt streamflow variability in wider channels. For instance, Hwang et al. (2020) claim that “[...] the river width affects flow rate significantly.”. Autoregressive processes are linear and stationary time series models, and thus they have only limited potential in describing non-stationary and non-linear data (Karthikeyan and Nagesh Kumar 2013).

Fig. 6
figure 6

Scatter plot of interpolation improvement statistics, i.e. improved windows (a) and improved values (b), against river width. For explanation of improvement statistics see Table 2

Full size image

When averaging RMSE differences – such as those presented in Fig. 5, but for each gauge – over interpolation length (L), mean RMSE differences can be expressed as a function of width of no-data gap (Fig. 7). When gauges are ordered according to local river width, it is apparent that the LinAR approach can be recommended for sites where river is wide, and the performance is limited to a dozen of steps.

Fig. 7
figure 7

Comparison of performance of LinAR approach in respect to purely linear interpolation method. Gauges in y-axis are sorted by river width and placed in the descending order from the top of figure

Full size image

In order to estimate the recommended width of no-data gap (\(\hat{W}\)) for which the LinAR method is superior over the purely linear approach, we make use of convex combination of improved windows in the following way:

$$\begin{aligned} \hat{W} = \sum _{g=1}^{28} W_g i_g, \end{aligned}$$
(5)

where g is the index of a given gauge (Table 1), \(W_g\) is the value known in Table 2 as the improved windows, and \(i_g\) is the ratio of percentage average improvement to sum of percentage average improvement values (Table 2). When \(W_g\) and \(i_g\) values from Table 2 are imputed into Eq. 5, the estimate \(\hat{W}\) is of 12. It means that – based on the aforementioned assumptions – our approach is recommended for gaps of lengths up to 12 steps.

When we consider no-data gaps of length up to 12, we may clearly notice that percentage of improved values is meaningful (reaching even 85%), as juxtaposed in Table 3. This statistics is particularly high for gauges where river width is considerable. In addition, percentage difference in RMSE can attain as much as 10% on average (gauge 6). In contrast, there is no improvement or there exists deterioration of water level interpolation accuracy for narrow river sections (up to \(-\)2.5%).

Table 3 Accuracy of LinAR and purely linear (LIN) interpolation for windows \(\le\) 12
Full size table

Although the statistics that describe the percentage improvement of interpolation accuracy are promising, the differences in RMSE, which is a measure of water level interpolation error in metres, are very low (Tables 2 and 3). It means that the significance of improvement may be questioned. According to Kalarus et al. (2010), to say if a given mean prediction error is smaller than the other it is necessary to use error bars of mean prediction error. Therefore, to evaluate the significance of the improvement (LinAR in respect to purely linear interpolation), RMSE error bars are used following the paper by Niedzielski and Kosek (2008).

Figure 8 presents situations (combinations of W and L) in which LinAR is significantly different from linear interpolation (for selected cases already shown in Fig. 5). One of the features of the LinAR approach is that it is identical to linear interpolation at the last interpolation point (see Fig. 2), therefore if W = L the RMSE error bar is always greater than RMSE difference (which in this case is equal to 0). It is apparent from Fig. 8 that for most (W,L) pairs the difference is statistically significant. Also, when we consider all scrutinized gauges and take an average over L (Fig. 9) the above-mentioned significance occurs more frequently than insignificance, predominantly for wide river sections under study.

Fig. 8
figure 8

Significance of accuracy difference as a function of width of no-data gap (W) and interpolation length (L) at the selected gauges: Odra river at Biała Góra (a), Odra river at Ścinawa (b), Nysa Kłodzka at Skorogoszcz (c), Stobrawa at Karłowice (d). The significance determination was based on RMSE error bars, computed following Niedzielski and Kosek (2008)

Full size image
Fig. 9
figure 9

Significance of accuracy differences as a function of W, averaged over L. Gauges in y-axis are sorted by river width and placed in the descending order from the top of figure

Full size image

5 Discussion

Our LinAR approach was found to provide unequivocal results, i.e. it works better for short gaps (up to 12 steps) and for rivers of considerable size, however it fails to improve purely linear interpolation in opposite cases. Such an unequivocal picture can also be found in a few papers that compare linear interpolation with various ARIMA-based interpolation approaches. In this context, our study presents a partly contradictory view on the opinion of Gnauck (2004) who argues that the linear interpolation is usually better than the non-linear one in environmental studies. Based on our experiments, similar conclusion can be drawn, however, only for long gaps and small streams. In addition, Ponkina et al. (2021) claim that the ARMA model, compared to simple linear interpolation of soil temperature and soil moisture data, was significantly better.

Our estimate (maximum length of gaps = 12) is in agreement with findings presented by Lopes Martins et al. (2023) who argued that the ARIMA method can be utilized for filling riverflow data gaps with lengths up to 15 steps. Such a number is explained by high autocorrelation, typical for ARIMA models, which is responsible for predictability (Tigabu et al. 2018). It should be noted that although the agreement between lengths of no-data gaps is considerable (12 vs. 15 steps), the sampling intervals were different, i.e. daily data (Lopes Martins et al. 2023) and hourly data (this study). In case of the ARIMA application, autocorrelation at a given lag (number of steps) does not directly depend on how long the step size is. For aggregated time series (e.g. daily averages), we can expect smaller hydrograph variability, better predictability and therefore good LinAR performance. Also, the superior ARIMA performance for gaps up to 12 steps has been shown in a problem of filling gaps in soil temperature and soil moisture data (Ponkina et al. 2021). Indeed, when gaps are classified into intervals (1–12, 13–24, 25–50 h), the best results correspond to the first class. More general observation has been made by Ren et al. (2022) who claim that the relative error of ARIMA interpolation increases along with length of no-data gap.

According to Ren et al. (2022), ARIMA models do not perform well when reconstructing abruptly changing water-related time series. This is in agreement with a general theory of ARIMA-based forecasting (Cholette 1982). Our scrutiny shows that the 12-step LinAR interpolation works on rivers of considerable size and is not recommended for small (and often mountainous) rivers. The riverflow fluctuations are usually higher and more abrupt on the latter streams, as confirmed for the study area by Sen and Niedzielski (2010), which forms a constraint in ARIMA-based modelling.

Discussion should also be developed on cases when our LinAR approach occasionally fails for long no-data gaps (see Fig. 5d). Ren et al. (2022) argue that the ARIMA approach used for no-data gap filling in hydrology produces outliers of large positive/negative errors for gap of lengths 48 and 72 hourly steps. Herein, our maximum interpolation window is of 72 steps (hours) and, as presented in Fig. 5d and explained in Section 4, for long no-data gaps the LinAR interpolation departs from reference data. Such an effect is interpreted in the light of occasional non-stationarity (if statistical tests incorrectly pass such signals to LinAR interpolation).

Recently, Khampuengson and Wang (2023) presented a new method for gap infilling in hydrologic time series and compared it with five other interpolation techniques. The linear approach was found to perform best at gauges where riverflow did not reveal strong periodic patterns. Our time series are free of harmonic changes, and with LinAR we are able to perform even better.

Some national providers of hydrological data may publish raw measurements, and in such cases the LinAR approach may serve as one of potential methods for gap infilling. Although it is more complex than pure linear interpolation, it is computationally efficient and can be performed on a standard PC. For example, on a laptop with an Intel Core i7-7700HQ processor (2.80 GHz) and 16 GB RAM, a six-year hourly time series with 10% missing data (56,209 data points and 5621 gaps) is interpolated in about 13.7 s (average of 100 simulations).

6 Conclusions

We developed the LinAR approach (combination of linear interpolation and integrated autoregressive model) for interpolating riverflow data, checking its performance for no-data gaps ranging from 1 to 72 hourly steps. We analysed 28 water level gauges at which hourly water level data were collected between 2016 and 2021 (over 52,000 hourly steps for each gauge). In the iterative manner, we artificially removed known measurement data to enable a reliable validation of the LinAR method. This resulted in determining RMSE values of interpolation for each length of no-data gap (\(1,2,\ldots ,72\)), also considering LinAR-based predictions of various lengths (from 1 to gap size). All in all, we scrutinized over 100 million assessments (\(\approx 28 \times 52 000 \times 72\)).

Taking into account our findings and discussing them with recent papers on the ARIMA-based interpolation in hydrology, the LinAR approach may be considered useful when filling short (up to 12 hourly steps) no-data gaps in water level time series collected at rivers of considerable size. Although the superior performance of the LinAR method over purely linear interpolation has been expressed as percentage improvement (up to 10%), differences between absolute errors were very small. However, using statistical inference approaches (e.g. Niedzielski and Kosek 2008; Kalarus et al. 2010; Ren et al. 2022), they were found to be significantly more accurate than the purely linear interpolation method.

Although the LinAR method reveals a considerable potential in gap infilling in hydrological time series, it also has some limitations. First, though the LinAR implementation includes statistical tests for stationarity, they may occasionally fail, passing non-stationary signal to further analysis. This can lead to unrealistic interpolated values, especially for long no-data gaps. Thus, we recommend to use LinAR for filling short gaps. Second, if a hydrograph is highly irregular the LinAR approach may lead to unsatisfactory interpolation, because the autoregressive model reveals mediocre skills when modelling highly variable stochastic signals (usually for small rivers). Third, the absolute RMSE improvement (LinAR vs. linear interpolation) is small (but statistically significant), which may be evaluated by practitioners to have negligible effect on refining the entire process of gap imputation.

The main takeaway from the study is that the proposed LinAR approach can improve the linear interpolation of missing data in hydrology. Although LinAR uses a stochastic model, it is computationally efficient, and therefore can be utilized in practical or operational no-data gap infilling. The limitations of the approach can be mitigated by carrying further studies in: (1) better detection of non-stationarities, (2) employing various stochastic methods (other than ARI) in combination with linear interpolation.