Could probability be out of proportion? Self-explanation and example-based practice help students with lower proportional reasoning skills learn probability

Abstract

Proportional reasoning failures seem to constitute most errors in probabilistic reasoning, yet there is little empirical evidence about its role for attaining probabilistic knowledge and how to effectively intervene with students who have less proportional reasoning skills. We examined the contributions of students' proportional reasoning skill and example-based practice when learning about probabilities from a reformed seventh grade curriculum. Teachers in their regular classrooms were randomly assigned to instruct with a reformed textbook (control) or a version revised to incorporate correct and incorrect example problems with prompts to explain (treatment). Students' prior knowledge in proportional reasoning skill separately predicted probabilistic knowledge at posttest, regardless of their prior knowledge in probability or minority status. Overall, students in the treatment condition improved more in their probabilistic knowledge, if they started with less proportional reasoning skills. Our findings suggest that example-based practice is beneficial for students with less prior knowledge of proportions, likely a key concept for developing probabilistic knowledge.

Despite an increase in statistics content and attempts to reform statistics instruction (Garfield & Ben‐Zvi, 2007), probabilistic reasoning remains one of the most challenging reasoning abilities for young and adult learners (Bryant & Nunes, 2012; Piaget & Inhelder, 1975), and probability instruction is often unsuccessful at improving this reasoning (Garfield & Ben-Zvi, 2007). In an attempt to ameliorate these issues, educational psychologists and health scientists (Bryant & Nunes, 2012; Fischbein & Gazit, 1984; Gigerenzer et al., 2009) as well as mathematics disciplinary panels (National Council of Teachers of Mathematics, 2000) have attempted to understand the mechanisms by which probabilistic reasoning develops in order to improve probability instruction.

One possibility is that probabilistic knowledge may be partially built on a prior understanding of proportional reasoning—the mathematical ability to reason about relationships and to make comparisons between quantities and values (Fischbein & Gazit, 1984; Nunes et al., 2014; Piaget & Inhelder, 1975). Numerous studies with varying methodologies have documented this connection (Bramwell et al., 2006; Hoffrage & Gigerenzer, 1998; Labarge et al., 2003; Prinz et al., 2015; Zhu & Gigerenzer, 2006) through paradigms that measure performance on probability problems while manipulating the proportional reasoning demands (e.g. high vs. low). Also, large scale and experimental studies have documented numerous probabilistic reasoning errors as stemming from proportional reasoning failures (Lemke et al., 2004; Falk & Wilkening, 1998). Taken together, these studies provide important insights into the connection between probabilistic reasoning and proportional reasoning as it relates to performance (e.g. one test without an intervention), but to the authors’ knowledge, no studies examined this link as it relates to learning (e.g. pretest-intervention-posttest; Bryant & Nunes, 2012).

The literature from the science of learning suggests many cognitive principles that may be useful for teaching about probabilities (Booth et al., 2017; Dunlosky et al., 2013; Pan & Rickard, 2018; Pashler et al., 2007; Rittle-Johnson et al., 2001). One avenue with particular promise for reforming everyday classroom practice is to embed the principles of using different variants of worked-examples, such as worked out examples with self-explanation prompts, partially-completed worked-examples, and incorrect examples into textbooks (Booth et al., 2013). Despite this wealth of knowledge about learning principles, there seems to be a dearth in the successful implementations of instructional recommendations stemming from the science of learning into everyday classrooms (Booth et al., 2015b; for notable exceptions see Booth et al., 2015c; Butler et al., 2014; Stark, 2004; van Loon-Hillen et al., 2012). This has resulted in some arguing that educational research is the hardest discipline of all (Berliner, 2002), with others recommending more work is needed in order to effectively translate the principles from the science of learning in everyday classrooms (Daniel, 2012; Kornell et al., 2012; Mayer, 2012).

Thus, in the present study, we examine whether proportional reasoning is involved in the process of learning about probabilities in everyday classrooms through a reformed textbook about probabilities, modified to interleave variants of worked-out examples. We expect that prior knowledge of proportions will be an important component for learning about probabilities and that, overall, variants of worked-examples will amplify learning for all students. Next, we review the literature on proportional and probabilistic reasoning, followed by a review of the literature on worked-out examples, self-explanation prompts, and incorrect examples. Lastly, we provide specific detail on the present study, our hypotheses and their implications for understanding the mechanisms underlying the link between proportional and probabilistic reasoning.

Proportional and probabilistic reasoning

From a conceptual standpoint, the connections between proportional reasoning and probabilistic reasoning have been theorized under two accounts: one in which the conceptual schema of probabilities is separate from that of proportions and another where both schemata (probabilities and proportions) stem from the same root (Fischbein & Gazit, 1984). If the former is true, then knowledge about proportions should not have greater impacts on probabilistic reasoning, than knowledge about probability, itself. Whereas, if the latter is true then either schema may contribute to the development of probabilistic reasoning (Piaget & Inhelder, 1975). While the theories on conceptual representations remain unsettled, from a mathematical perspective, proportional reasoning is required to quantify the concept of probability because probabilities represent a quantity based on a proportion (Bryant & Nunes, 2012; Falk et al., 2012). However, young children and adults regularly fail to account for proportions (Boyer & Levine, 2015), especially when asked to solve probability problems represented with rational numbers (Bryant & Nunes, 2012; Falk et al., 2012; Gigerenzer et al., 2009). This could be occurring because probabilistic reasoning is a cognitively complex task, requiring: (a) understanding of randomness, (b) analyzing the sample space, (c) quantifying probabilities proportionally, and (d) understanding and using correlations (Bryant & Nunes, 2012). Evidence suggests that people struggle with each (Fischbein & Gazit, 1984; Gilovich et al., 1985; Martignon & Krauss, 2009; Van Dooren et al., 2003; Wason, 1968), due to a variety of factors (e.g. “the representativeness heuristic”; Kahneman & Tversky, 1972). In the present study, we focus on proportional reasoning as an integral part of components (b), (c) and (d), where successes or failures for children solving problems involving probabilities largely seem to depend on whether children attend to the proportional (i.e., the intensive) nature of probabilities (see Bryant & Nunes, 2012 for examples on how proportional reasoning is required for b, c, and d).

Consistent with this hypothesis, K-12 students who do not convert numerical information in probability problems into proportions, or make proportional comparisons, are less likely to solve those probability problems correctly (Lemke et al., 2004; Falk & Wilkening, 1998). Further, middle school students who have received more instruction on proportional reasoning were better equipped to learn probabilities (Fischbein & Gazit, 1984). In addition, a considerable number of studies have documented that children and adults are better at solving probability problems when proportional reasoning demands are reduced (Bramwell et al., 2006; Hoffrage & Gigerenzer, 1998; Labarge et al., 2003; Prinz et al., 2015; Zhu & Gigerenzer, 2006). Thus, some of the most common mistakes in probabilistic reasoning appear to stem from failures to use proportional reasoning (Piaget & Inhelder, 1975). For instance, Zhu and Gigerenzer (2006) asked fourth, fifth, sixth-graders, and adults the following problem:

Pingping goes to a small village to ask for directions. In this village, the probability that the person he meets will lie is 10%. If a person lies, the probability that he/she has a red nose is 80%. If a person doesn’t lie, the probability that he/she also has a red nose is 10%. Imagine that Pingping meets someone in the village with a red nose. What is the probability that the person will lie? (p. 3)

In order to find the final probability, the demands on proportional reasoning gradually increase as the problem becomes more complex by requiring students to account for proportions within proportions (Fig. 1). In one way of solving this, the student has to account for six proportions in total to reach the final answer (see solution steps in Fig. 1). There are eight people (or 8%; Step 4) who lie and have a red nose and nine people (or 9%; Step 5) who do not lie and have a red nose. This results in 17 people out of 100 (or 17%; Step 6) who have a red nose. Out of the 17 people, eight out 17, or 47% (Step 7), have a red nose and will lie, which is the answer to this problem. Not a single student could solve this problem and almost half (47%) of the adults failed.

Fig. 1

An illustration of the Pingping problem (Zhu & Gigerenzer, 2006) as a worked out example

A possible explanation for these results around proportions within proportions and the percentage symbols (denoting probabilities) which are likely creating conditions that increase cognitive load for novice students with lower background knowledge who have a frail proportional reasoning schema. The percentage symbol for one number (representing a probability), requires reasoners to map that number to a proportion of two numbers. When the same proportion is represented as frequencies (e.g., 10% vs. 1 out of 10) the two numbers underlying the ratio are made explicit. Thus, the mapping of one number (representing a proportion) to two numbers in the underlying ratio is not necessary. Zhu and Gigerenzer (2006) repeated the procedure of the problem shown above, but replaced percentages (rational numbers) with frequencies, thus reducing the proportional reasoning demands, as below:

Pingping goes to a small village to ask for directions. In this village, 10 out of every 100 people will lie. Of the 10 people who lie, 8 have a red nose. Of the remaining 90 people who don’t lie, 9 also have a red nose. Imagine that Pingping meets a group of people in the village with red noses. How many of these people will lie? ____ out of ____. (p. 3)

This led 19% of fourth graders, 39% of fifth graders, and 54% of sixth graders and 76% of adults to correctly solve the problem (Zhu & Gigerenzer, 2006). Similarly, in medical fields, professionals who were tested on interpreting diagnostic reports from positive screener results, such as inferring the probability of breast cancer (Hoffrage & Gigerenzer, 1998), dementia (Labarge et al., 2003), or Down syndrome (Bramwell et al., 2006) were much more accurate when diagnostic reports were presented in frequencies instead of percentages. Thus, it is possible that the additional mapping required to reason with the percentage symbols, which represent the proportion of the two numbers makes this probability problem more difficult for reasoners who with a frail proportional reasoning schema required to reason with probabilities.

Taken together, these findings point towards prior proportional knowledge as one key component for understanding probabilities. Thus, understanding how children’s proportional reasoning influences performance on probability problems may provide important insights into the development of probabilistic reasoning, and potentially illuminate how individual differences in children’s prior knowledge in proportional reasoning might influence their ability to learn about probabilities (Bryant & Nunes, 2012). Yet, the complexity and interplay between proportions and probabilities presents another important challenge–how do we teach students about probabilistic reasoning?

Worked example variants for teaching mathematics concepts

In their basic form, worked examples consist of a problem, solution steps, and the final solution (Renkl & Atkinson, 2003). Worked out examples within researcher controlled settings have been shown to improve knowledge of many content areas in mathematics, including algebra (Booth et al., 2013; Sweller & Cooper, 1985), geometry (Paas & Van Merriënboer, 1994), and probability (Catrambone, 1998; Große & Renkl, 2007). Having students study worked examples is thought to be a beneficial instructional approach because they reduce cognitive demands, freeing up computational resources for conceptual learning and building domain specific schemas (Sweller & Cooper, 1985). According Sweller and Cooper’s seminal work (1985), worked examples reduce cognitive load by reducing processes involved in searching for a solution to a problem state. As such, the effect of worked examples seems to dissipate for learners with higher domain knowledge as they become experts, known as the expertise reversal effect (Kalyuga, 2007). Instead, worked examples appear most useful for learning concepts that have high element interactivity and place a greater cognitive load on the student as is typically the case with novel concepts (Chen et al., 2016).

For example, the symbol for “mother” in sign language can be learned independently from the symbol for “father.” These symbols have low interactivity. However, in the case of our example with Pingping, the understanding of the percentage symbol (%) and that it represents the proportion of the whole, namely, 10% is a tenth out of a whole (commonly thought of as 10 out of 100). This interacts with how the learner represents the likelihood of meeting someone who lies, which requires knowledge of the relationships between the symbols, 10% and their representations (e.g. 10 out of 100), which likely has high interactivity for novices (a worked example for this prompt is shown in Fig. 1). With the Pingping problem, the intrinsic cognitive load and interactivity between proportional and probabilistic reasoning assumedly increases as students have to reason about proportions within proportions, to know the representation of 80% of 10% of people with a red nose who also lie is 8% of the whole (e.g. 8 out of 100, because 80% of 10% can be the same as 8 out of 10). But students have to also account for the other proportions in the problem (see Fig. 1) which has the potential for further increasing the cognitive load and interactivity between proportional knowledge and the students’ ability to calculate the final probability. The worked example could serve to offload cognitive demands of holding multiple representations in mind and relegate those resources towards the connections between the proportional representations and the procedural steps necessary to find the final probability. This cognitive offload and shift of focus on structural features is thought to be key for supporting students in knowledge building and schema formation (Renkl, 2014). We hope this exemplifies why it is thought that mastery of the concept (e.g. proportions, rational numbers), decreases interactivity and reduces cognitive load, subsequently waning the effect of worked examples (Chen et al., 2016).

Over three decades of research on worked examples suggest multiple ways to successfully augment worked examples to increase learning benefits; we integrate three of these strategies: self-explanation prompts, incorrect examples, and fading out worked examples.

Self-explanation prompts

First, self-explanation prompts—that is, prompts that encourage students to explain the principles or rationale of the provided solutions—serve to engage students with the material in meaningful ways that also promote monitoring of their developing knowledge (Atkinson et al., 2003). For instance, with the Pingping example a student could be asked, “why is it necessary to divide 0.8/0.17 to find the final answer?” As such self-explanations appear to serve students in generating new knowledge and filling gaps in their own knowledge and/or integrating their own prior knowledge by revising and tuning their mental models (Renkl & Atkinson, 2003; Roy & Chi, 2005). The greatest learning gains from self-explanation stem from students who engage in deep meaningful questions in contrast to students who generate superficial explanations or re-read the questions (Chi et al., 1989; Fergusson-Hessler & de Jong, 1990; Renkl, 1997). As such, self-explanations are theorized to be a critical mechanism through which worked examples focus reasoners’ processing on structural features of problems, and in turn, support their ability to abstract general rules, understand domain specific principles, and create conceptual schemas (Chi et al., 1989).

Incorrect worked examples

Second, addressing student misconceptions by using a combination of correct and incorrect examples can yield improved learning (Booth et al., 2015c; Große & Renkl, 2007; Ohlsson, 1996; Siegler, 2002), perhaps because they force students to confront their misconceptions and let go of incorrect strategies, after realizing why they are wrong (Ohlsson, 1996; Siegler, 2002). For instance, in the Pingping problem, a misconception students harbor is that they may compare 8% (people who have a red nose and lie) over 100% (the whole sample) and neglect that they should be considering a proportion (subsample) of all people who have a red nose (Zhu & Gigerenzer, 2006). If reasoners realize this error, it may lead them to abstract the correct solution procedure from correct worked examples and create a new schema or revise their existing schema by integrating their knowledge, and correcting or filling in gaps in their knowledge (Booth et al., 2015c).

Fading worked examples

Third, fading out worked examples may benefit students by providing an appropriate challenge as they begin to master procedures and/or concepts (for a review see, Renkl & Atkinson, 2003). This cognitive technique is thought to aid students to move from studying examples to solving problems on their own and seems to work best when the last solution steps were omitted from the worked out examples (Renkl, 2002). In the example with Pingping, a faded worked example may only include Step 1 and 2, but the student would have to solve the remaining steps on their own. The fading technique can have additive effects when paired with self-explanation prompts that identify the underlying principles to be learned (Atkinson et al., 2003).

The moderating role of prior knowledge on worked example variants

There is convincing evidence, however, that students’ prior knowledge interacts with learning from worked examples (Atkinson et al., 2000; Booth et al., 2015a). Students with lower prior knowledge benefit the most from studying worked examples (Kalyuga et al., 2001a, 2001b) and even the worked example variants seem to have a greater benefit for struggling students, as lower prior knowledge students tend to spontaneously self-explain less than students with higher prior knowledge (Renkl et al., 1998). Unfortunately, students with less prior knowledge also need the most supports, and self-explanation prompts, thus, seem to serve as an effective strategy to guide poorer learners to reason about meaningful concepts during their knowledge construction and schema building (Chi et al., 1994).

Further, students with low prior knowledge are perhaps more likely to harbor misconceptions in need of correction through incorrect examples (Barbieri & Booth, 2016). A potential drawback of using common misconceptions as example solutions to problems is that they may lead to object instantiation of wrongful solutions and confirmation of incorrect biases (Begolli & Richland, 2016). One way to overcome this is to provide scaffolds, such as highlight incorrect examples as incorrect and provide feedback or engage students in self-explanations on why the solution is incorrect (Booth et al., 2015c).

An important aspect of the expertise-reversal effect is that as knowledge builds interactivity decreases and the use of worked examples begins to dissipate (Kalyuga & Renkl, 2010). Thus, to continue to support students with less prior knowledge as they build more knowledge, it is important to fade out one or more procedural steps from the worked examples, which could serve as an important transitional strategy for preparing students to solve problems without supports.

One indicator of prior knowledge and academic achievement more broadly that could play a significant role in our study is students’ racial/ethnic backgrounds where minorities traditional underperform in mathematics (Fryer Jr & Levitt, 2004). To better account for student differences, in the current study we classified students according to racial and ethnic populations underrepresented in mathematics: Underrepresented minority (URM) students (African American, Hispanic, and bi-racial) or non-URM (White and Asian) as there is ample evidence of gaps between these populations (Fryer Jr & Levitt, 2004; Hanushek & Woessmann, 2012).

Taken together, the literature points towards the idea that worked examples for students with frail proportional knowledge, providing a worked example could help them offload their cognitive demands because those students would have a harder time holding in mind multiple proportions as well as consider which are the correct procedural steps to take. Some have suggested this process becomes instrumental for allocating those cognitive resources on structural features of problems, which in turn supports reasoners in abstracting general and domain specific rules and in schema generation (Renkl, 2014). For this reason, worked examples included in this study were strategically designed to include prompts that challenged students to think about core ideas and common misconceptions as they relate to probability and proportion concepts. In sum, in order to maximize the potential effect of worked examples on student learning, we utilize a combination of self-explanations, incorrect examples, and fading worked examples.

Despite promising results from over thirty years of research, worked examples have not made serious forays into educational textbooks and curricula (Booth et al., 2015a). This is likely due, at least in part, to the lack of evidence stemming from work conducted in real classrooms with practical implications for teachers (for notable exceptions and examples see Begolli et al., 2018; Begolli & Richland, 2017; Booth et al., 2015b, 2017; Kapur & Bielaczyc, 2011; Klahr & Li, 2005; Stark, 2004). Further, learning principles have not always produced benefits and it is not always clear how they should be implemented in everyday classroom settings (Daniel, 2012; Kornell et al., 2012; Mayer, 2012). Full translation of these variants of the worked example principle to classroom practice requires more rigorous testing to understanding whether these strategies are beneficial in classroom settings, whether they benefit all students, or just some of the students in the classroom and under which conditions. In the case of the worked example effect, recent studies by Booth and colleagues (Booth et al., 2015b, 2015c) show that using correct and incorrect worked examples with self-explanation prompts benefit students within everyday mathematics classroom, and may be particularly constructive for helping students overcome misconceptions.¹

The present study

In the present study, we draw from a laboratory-tested cognitive science principle—variants of worked examples in order to test whether worked examples can help to teach students about probabilistic reasoning in real world mathematics classrooms. Based on previous literature, proportional reasoning may be a prerequisite schema for attaining robust probabilistic knowledge. The learning principle of worked examples and it’s variants may provide a fruitful avenue for improving proportional and probabilistic reasoning, yet, as outlined above, the effectiveness of worked examples seems to depend on students’ prior knowledge. If a proportional reasoning schema is integral for learning about probabilities, then prior knowledge of proportions may also interact with their learning of probabilistic reasoning. Thus, worked examples may be particularly beneficial for improving students’ knowledge of proportions, which might, in turn, influence students’ knowledge of probabilities.

In the current study, we integrated a combination of self-explanation prompts, partially worked-out examples, and correct and incorrect examples in a reformed seventh grade mathematics curriculum: Connected Mathematics Project 2, within the unit on probabilities (What Do You Expect?; (Lappan et al., 2006). We examined the following research questions:

H1a

Learning with a CMP textbook that embeds incorrect and correct worked examples, partially worked out examples, and self-explanation prompts (treatment condition) will lead to greater knowledge in probability compared to learning with the original CMP textbook (control condition).

H1b

The learning benefits of probabilities from the treatment CMP textbook over the original CMP textbook will be greater for students with lower proportional reasoning than for students with higher proportional reasoning.

H2a

We predict that proportional reasoning knowledge will improve more for students in the treatment condition than in the control condition.

H2b

Proportional reasoning pretest knowledge will significantly predict probabilistic reasoning scores at posttest even when taking into account probabilistic reasoning at pretest (H2b).

In regards to H1a, numerous laboratory studies have demonstrated the positive effects of various worked example variations on learning, yet evidence from traditional classrooms is still accumulating (Begolli & Richland, 2017), especially for incorrect worked examples (Booth et al., 2015a). Recent studies have found benefits in algebra, however, to the authors’ knowledge, there are no classroom studies within the domain of probabilities in which researcher involvement is minimal. Thus, the current study would provide an important data point on the success of translating worked example research to everyday classroom settings. Based on the expertise-reversal effect (Kalyuga, 2007) and work suggesting proportional reasoning is necessary for solving probability problems (Bryant & Nunes, 2012), there is a high possibility that worked examples provide the most benefit to students with less prior knowledge of proportions. Yet, we expect an ordinal interaction (Widaman et al., 2012) considering we do not expect students with less prior knowledge to outperform students with higher prior knowledge or for students with higher prior knowledge to regress in their learning. Taken together, confirmation of H1b and/or H2b would provide another data point to support the theoretical accounts that the schemata for proportional reasoning and probabilities stem from the same root (Piaget & Inhelder, 1975) or that knowledge for solving probability problems partly operates through learners’ knowledge of proportional reasoning. A confirmation of H2b and not H2a, would suggest that our treatment was successful in teaching students how to use their proportional reasoning skill (i.e. prerequisite skill) in the context of probability problem solving–but not successful at improving proportional reasoning, overall. Thus, it is likely that worked examples may help students fill gaps in their proportional reasoning knowledge necessary for solving problems about probabilities.

Method

Participants

Seventh grade students (typical age in the United States is 12–13-years old; no age data collected; N = 220; Girls = 48%; Underrepresented Minority = 38%) from 10 classrooms (5 teachers) participated in this study. All students were in regular (non-honors or remedial) classrooms in an inner-ring suburban (i.e. neighborhoods very close to a large city center) school district in the Midwestern region of the United States. The study received research ethics committee approval from the Institutional Review Board (IRB) at Temple University, which reviewed it as exempt because it fell under the normal educational practices and settings category. All data were de-identified prior to sharing it with the research team. The authors declare that there were no conflicts of interest.

Classrooms were randomly assigned to either the control or treatment condition; for teachers who had more than one classroom, we ensured that at least one of their classes was assigned to the treatment condition (Table 1). Five classrooms of students completed control assignments (N = 117; Girls = 37%; Underrepresented Minority = 33%) and five classrooms of students completed treatment assignments (N = 103; Girls = 57%; Underrepresented Minority = 40%).

Table 1 Condition assignment by teacher

Intervention materials

Original textbook (control)

Materials from Pearson’s Connected Mathematics Project (CMP; Lappan et al., 2006) were adapted for the purposes of this study. We utilized the What Do You Expect textbook, which focuses on probabilities and expected value and is made up of four sections. The first section—Evaluating Games of Chance—focused on review of experimental and theoretical probabilities, equally likely events, fair/unfair games, and strategies for determining theoretical probabilities through problems that ask students to predict outcomes that involve spinners, choosing marbles from buckets, and rolling dice. The second section—Analyzing Situations Using an Area Model-focused on helping students use an area model to examine probabilities of two stage events, such as spinning two spinners, etc. The third section–Expected Value–focused on helping students compare experimental probabilities and theoretical probabilities (from area models) of a probabilistic situation (e.g. shooting free throws). The fourth and last section—Binomial Outcomes—focused on helping students examine binomial probabilities in contexts such as guessing on a four item true/false quiz through the use of lists or trees. Each of the four sections was broken into three lesson segments: a Launch (connecting prior knowledge and presenting a challenge for students), Explore (prompts for student individual problem solving and discussion), and Summarize (teacher led discussion and reflection on student learning) segment. This is followed by a problem-solving segment typically assigned for homework, but teachers also use some of these problems during their lessons. The student book provides approximately 180 practice problems, but the teacher’s manual for the textbook indicates 70 particular problems that should definitely be assigned; the teachers are trained to assign at least those core 70 problems. The problem-solving segment was revised in the treatment textbook, described next.

Revised example-based textbook (treatment)

Worked examples and self-explanation prompts were incorporated into each of the problem-solving segments of the original What Do You Expect textbook, leaving the lesson segments identical. Three types of worked examples were incorporated: (a) correct worked examples (7-items), (b) partially completed worked examples (10-items), and (c) incorrect worked examples (5-items; Please see Fig. 2 for a comparison between the three types of problems as well as a control version of the problem and Appendix 1 for a description of each problem). Self-explanation prompts accompanied all (a) and (c) items, and two (b) items (14 self-explanation items total), and students were expected to only complete the remaining partially completed examples (8-items). As mentioned above, teachers were trained to assign the 70 core practice problems in the textbook, but in the revised book 22 of those practice problems were replaced with one of the three worked examples types. A list of item changes and targets addressed is included in Appendix 1. Thus, treatment and control classrooms saw the same problems and worked with the same number of items (see Fig. 2 for sample items). Apart from these modifications, the problem-solving segments were identical in both textbooks.

Fig. 2

Sample items from the control condition and worked-example items in the treatment condition. Items adapted from actual textbook. In this example, all worked examples include a self-explanation prompt. *The spinner figure for problem 6 shown in the treatment condition was also included for problem 6 of the control condition, but removed in our example to save space

Procedure

All students completed an identical pretest before and posttest after the conclusion of the What Do You Expect? unit (~ 4-weeks later) and teachers completed our fidelity measure. The classrooms in the control group used unaltered CMP textbooks, while the treatment classrooms used the revised textbooks. Teachers received no training and taught the content with the unaltered CMP lessons and assigned the problem-solving items as they typically would, either as in-class practice or homework. The conditions varied on whether they used the control or treatment version of the items when solving practice problems.

Mathematics measures

The pre and posttests were identical and had twenty-five items which measured students’ knowledge of probabilistic reasoning (16-items) and proportional reasoning (9-items; see Fig. 3 and Appendix 2 for sample of items). The probabilistic reasoning items were generated using the content taught in the What Do You Expect? unit (see Fig. 3 and Appendix 2 for sample items). Four probabilistic reasoning items were dropped due to a wording error resulting in a total of 16-items. The proportional reasoning items were modified from measures used in the existing literature (e.g. Billings, 2001; Noelting, 1980; Post et al., 1988). These items were further reduced to create a Probabilistic Reasoning Composite Score (KR20 = 0.55 & 0.79 for pretest and posttest, respectively) and a Proportional Reasoning Composite Score (KR20 = 0.67 & 0.55 for pretest and posttest, respectively; with acceptable KR20’s > 0.50; see Traub (1994); see Appendix 2 for samples of retained items). We use the KR20 to test item consistency as this is a special case of Cronbach’s alpha, but preferred as measure of reliability when items have a dichotomous (binary; correct or incorrect) outcome with varying levels of difficulty (Cronbach, 1951; Kuder & Richardson, 1937; Richardson & Kuder, 1937 1939). We excluded problematic items and created composite scores for Probabilistic Reasoning and Proportional Reasoning based on the results of exploratory factor analysis of all items, as described next.

Fig. 3

Sample assessment items used to measure probabilistic reasoning (top) and proportional reasoning skill (bottom)

Factor analyses

Note that both measures were newly developed and administered to participants with minimal to moderate prior knowledge of the content assessed. In order to obtain further psychometric evidence, we conducted two rounds of exploratory factor analyses (EFA) on item scores to examine the dimensionality of the probabilistic and proportional reasoning measures, respectively. This allowed us to: (1) uncover the latent dimensions—probabilistic reasoning and proportional reasoning skills—underlying the corresponding items, and (2) examine which items have the strongest (as opposed to weakest) association on its designated factor (DiStefano et al., 2009). Considering our hypotheses focused on the relationship between prior knowledge of proportional and probabilistic knowledge after the intervention, we conducted the EFA on the Proportional Reasoning items at Time 1 and on Probabilistic Reasoning items at Time 2, only. Prior to the beginning of the study, participants had already had teacher-administered lessons on proportional reasoning and thus were expected to have some prior knowledge of proportions. However, they had not received any instruction on probabilities and we predicted that the probabilistic reasoning scores at pretest were therefore not as ideal to use for uncovering the factor structure of the scale due to concerns of violating normality. Considering the purpose of factor analyses, we decided to use proportional reasoning scores at pretest and probabilistic reasoning scores at posttest to examine the factor structure of the corresponding scales using an exploratory factor analysis approach² and generate factor scores. Indeed, students’ knowledge of probabilities was much more frail compared to their proportional reasoning skills at pretest, which was supported by pretest data of these two measures (M_PretestPbR = 20% vs. M_PretestPR = 45%; see Table 2).

Table 2 Descriptive statistics for treatment and control conditions showing weighted sum scores of remaining items for proportional reasoning and probability scores

A principal-factor method was used to analyze the correlation matrix. The factor loadings were computed using the squared multiple correlations as estimates of the communality. We used a minimal Eigenvalue of 1.5 and the scree plot for the factor retention criterion; direct Oblimin factor rotation would be applied if more than one factor was retained. We retained all items whose standardized factor loadings were ≥ 0.3, which is a common loading cutoff for similar studies in terms of conducting factor analysis (as oppose to principal component analysis), a young student sample, and the sample size (Peterson, 2000). The first round of EFAs included all original items and the second round included only the retained items based on the criteria listed above. Items loading below 0.30 on a factor were excluded from both pretest and posttest to ensure measure consistency (see Table 3 for factor loadings and items retained; 10 items for Probabilistic Reasoning at Time 2 and 8 items for Proportional Reasoning at Time 1 were retained). We followed up the EFAs with KMO test to examine whether the items that remain in the model were adequate and suited for the EFA. KMO test results of 0.64–0.72 indicated acceptable to good factorial simplicity (Kaiser, 1974).

Table 3 Exploratory factor analysis loadings showing the original and retained items (≥ 0.3) and weights for probabilistic reasoning at posttest and for proportional reasoning at pretest

Creating composite scores

Our measure items had different loadings, indicating different degrees to which they are associated with the latent factor, e.g., Probabilistic Reasoning. In other words, the items bared largely on varied “weights” as indicators of Probabilistic Reasoning. To reflect the differential associations between items and its underlying factor or the different weights, we created weighted sum score for each measure using the standardized factor loadings estimated by the EFA as recommended by DiStefano et al. (2009), rather than simply summing up all items (i.e., assigning an equal weight of 1 to all items), such that correctly answering a heavier-weighted item (e.g., 0.7415) would contribute more to the measure score than correctly answering a low-weighted item (e.g., 0.3005). Using the standardized factor loadings suggested in the second round of the EFA, which excluded that items that were loaded on the latent factor by < 0.300 in the first round, we created weighted sums for the PR and PbR scores.

Fidelity measures

Fidelity was assessed through a survey which was given to all five teachers and three teachers who had more than one class at the end of the study returned the survey, but two teachers, both of whom taught a single class each (one control and one treatment), did not return the surveys (see Appendix 3 for survey questions). While this is not an ideal situation, one of our main concerns were to avoid spillover effects (e.g. accidentally using intervention items in a control classroom), which could have occurred for teachers who taught multiple classes. Those three teachers confirmed no spillover of materials. This was not an issue for teachers who taught a single class. The following summarizes survey answers of those three teachers, which were unanimous. All teachers reported: (a) to have utilized all sections of the revised textbook; (b) they did not do anything differently in control and treatment classrooms, apart from using a different textbook; (c) they assigned students in both conditions to solve the same problems as graded homework; (d) students completed these problems; (e) teachers and students discussed those problems in class; and (f) students in the treatment classroom completed all assigned example-based problems. Overall, teachers using the treatment textbook reported positive feelings about the revised practice problems and welcomed similar revisions to other CMP textbooks. For example, one teacher reported “students were able to show how to create the area models for the path/cave game because of the worked examples….” A different teacher said “I liked that there were examples in the ACE problems.” A third teacher stated “it was interesting to see how they [students] did on their tests” and “examples helped.”

Results

Preliminary analyses

Analyses were conducted using Stata MP 14.2, and an alpha level of 0.05. We first obtained descriptive statistics, bivariate correlations, and independent t-tests by treatment on our mathematic measures.

We conducted ordinary least squares (OLS) regressions to examine the treatment effect on Probabilistic Reasoning at posttest accounting for Probabilistic Reasoning at pretest, Proportional Reasoning at pretest, and underrepresented minority (URM) status. We include URM status as a control variable due to significant literature showing achievement gaps for minority students (e.g., Fryer Jr & Levitt, 2004; Hanushek & Woessmann, 2012).

When examining Probabilistic Reasoning at posttest, we took an exploratory approach for arriving at a final regression model with the constraints to: (a) include all the predictors and (b) controls involved in answering all of our research questions, and (c) align with previous theoretical accounts regarding our student populations. In turn, this would also render a model that is parsimonious by removing predictors which do not contribute in explaining variance in the model. The model analytic approach is detailed in Appendix 4.

All regression models were checked for violations of assumptions for linear regressions, such as, linearity, normality, independence, multicollinearity, and homogeneity of residual variances. We screened for outliers and leverages. There were no violations of OLS regression assumptions. In addition, our study design included 10 classrooms, thus, we checked for dependency within classrooms. We obtained the intra-class correlation of the dependent variables, Probabilistic Reasoning posttest (ICC = 0.04, 95%CI [0.004, 0.241]), and Proportional Reasoning posttest (ICC = 0.05, 95%CI [0.009, 0.218], accordingly we adopted a cluster sandwich estimator for all of the regression models (see Table 4) to adjust for clustering effects within classrooms. Specifically, this estimator produced accounted for within-class clustering of the dependent variables and adjusted the underestimated standard errors caused by the minor clustering within classrooms (Rogers, 1994).

Table 4 Multiple regression models of posttest probabilistic reasoning scores

Summary statistics

The two groups were generally comparable before the treatment at the p > 0.15 level, with no significant differences between the treatment and control groups in terms of (1) underrepresented minority (χ² = 0.741, p = 0.389), (2) pretest Probabilistic Reasoning (t₍₂₁₉₎ = 1.35, p = 0.179, d = 0.18), or (3) pretest Proportional Reasoning (t₍₂₁₉₎ = 1.04, p = 0.300, d = 0.14).

We observed significant but moderate bivariate correlations between each continuous predictor and the outcome variable, posttest Probabilistic Reasoning factor scores (Table 5): higher scores on the Probabilistic Reasoning and the Proportional Reasoning pretest measures were associated with higher scores on the Probabilistic Reasoning posttest. The two pretest scores were also positively and moderately correlated (Table 5). Non-URM students outperformed URM students on both Probabilistic Reasoning (t_{pretestPbR(214)} = 6.93, p < 0.001, d = 0.97; t_{posttestPbR(205)} = 6.14, p < 0.001, d = 0.88) and Proportional Reasoning measures (t_{pretestPR(205)} = 5.63, p < 0.001, d = 0.79; t_{posttestPR(205)} = 3.38, p < 0.001, d = 0.49).

Table 5 Descriptive statistics and bivariate correlations between continuous variables

Hypotheses testing

As mentioned in the analytic approach section, to examine the effects of treatment on Probabilistic Reasoning, we analyzed a series of four regression models (the results of all models are summarized in Table 6). We report and discuss the final model (Model 4) in the following.

Table 6 Series of multiple regressions of probabilistic reasoning (PbR) scores at posttest

The regression of posttest Probabilistic Reasoning weighted sum score was significant³ (F [5, 9] = 60.58, p < 0.001, adjusted MSE = 1.34), and a total of 29.4% of variance was explained by the predictors. Among all predictors, the treatment, pretest Probabilistic Reasoning, pretest Proportional Reasoning, URM status, and the interaction between treatment and pretest Proportional Reasoning significantly predicted posttest Probabilistic Reasoning scores.

As can be seen in Table 6, and in support of H1a, the students who used the worked example revised textbook improved significantly more in Probabilistic Reasoning scores than students who used the standard CMP textbook, confirmed by a significant treatment predictor (b_Treatment = 0.85, SE = 0.31, t = 2.78, p = 0.021).

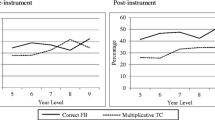
In support of H1b, the significant interaction between treatment and pretest Proportional Reasoning scores (b_{Treatment x PR Pretest} = − 0.34, SE = 0.15, t = − 2.34, p = 0.044) had a small negative influence on posttest Probabilistic Reasoning scores, indicating that the treatment participants with poorer pretest Proportional Reasoning scores actually benefited more from the treatment, which resulted in higher scores in Probabilistic Reasoning at posttest compared to the treatment participants with higher pretest Proportional Reasoning scores (Fig. 4). As expected, non-URM students outperformed URM students in posttest Probabilistic Reasoning (b_URM = – 0.76, SE = 0.24, t = – 3.22, p = 0.010).

Fig. 4

Plot of model 4 showing the interaction between treatment and control on probabilistic reasoning scores at posttest based on prior proportional reasoning knowledge at pretest with 95% confidence interval bars

Finally, to answer H2a, whether students who used the revised textbook improved more in Proportional Reasoning than students who use the original textbook, we utilized Model 4, but replaced Probabilistic Reasoning at posttest with Proportional Reasoning at posttest and did not include Probabilistic Reasoning at pretest as a covariate. Overall, the results of Model 4 (with PR score as a dependent variable) run contrary to H2a. Thus, the regression of Proportional Reasoning at posttest on Proportional Reasoning at pretest (b_{PR Pretest} = 0.28, SE = 0.14, t = 1.98, p = 0.079), treatment (b_Treatment = 0.30, SE = 0.37, t = 0.83, p = 0.428), pretest-treatment interaction (b_{Treatment x PR Pretest} < 0.01, SE = 0.17, t < 0.01, p = 0.999), and URM status (b_URM = − 0.24, SE = 0.14, t = − 1.66, p = 0.131) showed that none of the predictors had a significant coefficient, despite the model explaining significant variance as a whole (F [4, 9] = 17.04, p < 0.001, adjusted MSE = 0.826, R² = 17%). The regression results suggest that PR scores for students in the treatment condition did not improve significantly more from pretest to posttest than the PR scores of students in the control condition.

Discussion

After over three decades of cognitive science research, learning principles have been challenging to incorporate in educational curricula with widespread adoption and sustained implementation (Daniel, 2012; Dunlosky & Rawson, 2012; Kornell et al., 2012; Mayer, 2012). Our data suggest that the use of worked example variants may be a successful avenue for translational research to reform mathematics curricula, potentially with highest benefits for lower performing students. While Model 4 suggests that all students benefitted from the treatment (H1a), this result seems to be largely driven by students who had lower prior knowledge scores in proportional reasoning, not probabilistic reasoning, and who benefited the most from our treatment (H1b). These results suggest an ordinal interaction as the students with higher prior knowledge did not seem to regress in their learning nor did students with lower prior knowledge outperform students with higher prior knowledge.

At the same time, for about four decades, scientists have pointed towards proportional reasoning as a key concept for understanding probabilities (Fischbein & Gazit, 1984; Garfield & Ben‐Zvi, 2007; Gigerenzer et al., 2009; Piaget & Inhelder, 1975). However, their claims remained largely constrained to performance (e.g. tested only once without prior interventions), not learning (Bryant & Nunes, 2012). To our knowledge, this is the first study to provide evidence that prior proportional knowledge is germane for learning about probabilities, not just performance, which supports the theoretical accounts that proportional and probabilistic reasoning schemata stem from the same root. Two of our data points support this claim. First, proportional reasoning knowledge at pretest (H2b) was a significant predictor of probabilistic reasoning improvement, even when controlling for prior knowledge of probability for the control group. Second, students with less prior knowledge of proportions (H1b) were the ones who also had the most to gain from our treatment. Thus, prior knowledge of proportional reasoning predicted learning for the control group and students with less prior knowledge of proportions benefited from the treatment either by filling in knowledge gaps in proportional reasoning or by providing examples that allowed them to abstract strategies for solving probability problems. Interestingly, the effect of URM status seems stronger than that of prior knowledge, suggesting URM students begin and end with lower performance, overall. Yet, we did not find an interaction between treatment and URM status, perhaps because URM status may be associated with more general mathematics skills, not proportional reasoning, specifically. This provides another data point to support that proportional reasoning could be our most germane measure for predicting the development of probabilistic reasoning. On the other hand, all students improved in proportional reasoning, but the improvements did not differ by treatment (H2a), suggesting the treatment may have mainly targeted abstract rules and procedures related to solving probability problems.

Taken together, our results suggest that proportional reasoning may be crucial for understanding probabilities and the worked example intervention helped lower prior knowledge students gain a better understanding of probability concepts. A caveat to this is that it is unclear whether these learning principles affected students only through the use of the revised textbook or due to these principles prompting teachers to have richer discussions with their students, or a combination of the two. While the teacher self-reports on our fidelity measures suggest no spillover effects and positive feelings about the treatment textbook, there were no direct researcher observations, thus, the findings should be interpreted with caution. Overall, these findings have a significant import for several lines of research, including cognitive research on learning principles, mathematical cognition, and probability instruction, discussed next.

Implications for cognitive principles

The results support prior findings that students with less prior knowledge benefit more from worked examples (Chen et al., 2015, 2016; Kalyuga et al., 2001a, 2001b). Students with less prior knowledge did not outperform students with higher knowledge nor did the students with higher knowledge regress in their learning, supporting our expectations of an ordinal interaction also found in the literature on worked examples. This aligns with most studies in natural classroom contexts, albeit in Algebra, utilizing worked-example worksheets (Booth et al., 2015b) or worked examples embedded within a computerized tutor (Booth et al., 2013), which found that low-performing students benefit the most from the combination of correct and incorrect worked examples, as well as from incorrect examples alone (Barbieri & Booth, 2016). Though Große and Renkl (2007) previously found evidence that correct and incorrect examples were most helpful for students with higher prior knowledge, this only occurred when errors were not highlighted, meaning that success in their study required students to locate the errors within the problems, a necessarily difficult task which may overburden cognitive resources for students who might have made similar errors themselves. Students with less proportional reasoning knowledge have the potential to experience increased the level of interactivity when attempting to understand and solve probability problems, because these students have to hold in mind and manipulate both proportional and probabilistic reasoning concepts simultaneously and/or how these concepts work together without an appropriate schema to support these processes. In the present study, all incorrect examples were clearly highlighted, thus, according to CL Theory (e.g. Sweller & Chandler, 1991) the students with less prior knowledge may benefit because they did not have to engage the in search processes to identify what is and is not correct before considering and explaining why the examples were wrong. Instead, students could allocate those cognitive resources to towards filling in gaps, revising, or creating more robust schemas. Overall, worked examples with self-explanation prompts, incorrect examples, and faded solution steps may serve to reduce the interactivity level for these students in numerous ways, such as potentially offloading students’ thinking resources on how these concepts fit together and/or automatizing proportional reasoning concepts, which seems especially helpful for helping students with less prior knowledge focus their attention on building schemas about solving probabilities.

The instructional implementation of cognitive principles in classroom settings, such as worked examples, has not always been straightforward, with many principles not always translating seamlessly into classroom routines (Daniel, 2012; Dunlosky & Rawson, 2012; Kornell et al., 2012; Mayer, 2012). The current study provides an important data point supporting the practice of having students explain correct and incorrect worked examples as a fruitful avenue that may be especially beneficial for leveling the playing field for lower performing students. At the same time, we recognize that in translating a combination of learning principles into a textbook in order to maximize student learning, we are not able to examine the effects of each principle individually. Future studies would be needed to disentangle the impact of any specific factor.

Implications for mathematics cognition

Important insights on the role of proportional reasoning comes from evidence on the developmental trajectory of rational number understanding (Siegler & Lortie-Forgues, 2014; Vamvakoussi & Vosniadou, 2012). Rational numbers, often used to represent probabilities, are counterintuitive due to students’ overextensions of procedural operations of whole numbers to rational number operations (DeWolf & Vosniadou, 2013; Vamvakoussi & Vosniadou, 2012). For example, a significant proportion of fifth and sixth grade students chose 0.274 to be larger than 0.83 (Rittle-Johnson et al., 2001), suggesting a whole number bias.

While we do not use a standardized assessment of probabilities, our findings suggest that prior knowledge of proportional reasoning reveals deeper insights into students’ potential for learning about probabilistic reasoning, than prior knowledge of the concept of probability itself. Another possibility is that students with lower prior knowledge had more room for improvement than students with higher prior knowledge, thus, explaining the interaction between treatment and prior knowledge. However, if this was the case, then the effect of the interaction with prior probability knowledge (e.g. the concepts taught in the lesson) should be equivalent or greater than the interaction with prior proportional reasoning knowledge, but this was not the case. If probabilities represent an entirely novel concept for seventh graders, it may also be the case that our proportional reasoning measure served as a proxy for students’ general math knowledge. Yet, URM status may have also played a similar function in capturing general knowledge as reflected by strong negative effects on overall learning of probabilities. Unlike with the case of prior knowledge of proportions, URM status did not interact with treatment. While this provides another possible control for general ability and a data point in support of proportional reasoning as our most predictive measure of probabilistic reasoning, future work should control for students’ general math ability and/or EFs to better understand these connections and further isolate the effects of each factor.

Our results also contribute to a broader literature of recent studies in mathematical cognition suggesting proportional reasoning is crucial for more complex mathematical concepts, such as algebra understanding (Booth & Newton, 2012; DeWolf et al., 2015). While the National Mathematics Advisory Panel (National Mathematics Advisory Panel, 2008) emphasized that fractions are foundational for algebra, empirical evidence making direct connections between the two concepts is fairly recent (Booth & Newton, 2012). A similar case could be made for the relationship between proportional reasoning and probabilities (Bryant & Nunes, 2012). Yet, for algebra, we understand that fraction magnitude (Booth et al., 2014) or the relational nature of fractions and decimal magnitude (DeWolf et al., 2015) contribute to algebra understanding, but no such specificity exists for the relationship between proportional and probabilistic reasoning.

On a conceptual level, Fischbein and Gazit (1984) suggested two possible accounts that link probabilistic and proportional reasoning: one for which the conceptual schema of probabilities is separate from that of proportional reasoning and another where the two schemata share the same root. Our data align with the latter explanation, considering that improvements were highest for low proportional reasoning students and proportional reasoning provided greater insight about student learning than prior probability knowledge. The support for these interpretations would have been stronger, if there was evidence that students in the treatment condition improved in their proportional reasoning knowledge from pretest to posttest more than the students in the control group, but this was not the case. Both groups improved in this aspect. This may have happened because most of the textbook problems that we changed (18 out of 22) related directly to probabilistic reasoning and only four problems involved proportional reasoning, explicitly (see Appendix 1).

Implications for improving instruction

In the current U.S. curriculum standards, proportions and probabilities are not explicitly connected in the seventh grade aims, and the link is only mentioned once in the Statistics and Probability aim of the current U.S. Common Core State Standards in Mathematics (Common Core State Standards Initiative, 2010). This could be partly due to the lack of evidence pinning down proportional reasoning as key for learning about probabilities. Our findings provide one data point indicating that explicit connections between proportions and probabilities may lead students to develop a deeper understanding of probabilities. It is possible that balancing the amount of probability instruction with proportional reasoning instruction may be more successful than teaching only about probabilities. But, it remains unclear how this should be done (see Nunes et al., 2014). Our results suggest that incorporating correct and incorrect examples about probabilities with prompts for self-explanations, and partially worked out examples helps. It is also possible that these learning principles operated by prompting teachers to lead more meaningful discussions in their classrooms, which in turn lead to better student outcomes. This is in line with reformed mathematics educators who have promoted problem solving to espouse a more constructivist approach to learning who emphasize scaffolding as key for knowledge building. Our data and teachers suggest student learning improved and teachers state in their surveys that the revised textbook provided a platform for struggling students to construct their knowledge. For instance, one teacher mentioned “I liked worked examples because it gave students that were struggling a good starting point. The worked examples helped me determine how students were understanding concepts.” Another teacher reported “the worked examples helped with investigations 3 [Expected Value] and 4 [Binomial Outcomes] when teaching expected value. This topic was difficult for students and having the examples to use in class when reviewing homework and for use at home was helpful, when traditionally CMP does not include examples.” Future work should delineate the contribution of each factor within our manipulation in order to understand the impact of each principle (i.e. confronting students’ misconceptions, prompting students to self-explain, to finish partially-completed examples) or whether these principles are operating by prompting richer teacher-student interaction, or both.

Traditional curricula in the U.S. have introduced proportional reasoning by linking it with notions of sharing with fractions, but not ratio explicitly. However, this may take away from a more robust concept of rational numbers, which is also at the core of probabilistic reasoning (Nunes et al., 2014). For instance, Nunes and colleagues (2014) demonstrated that instruction about ratios (together with logical multiplication and classification training) improved sixth graders’ knowledge about sample space—a critical component of probabilistic reasoning. However, the active control group did not receive training on probabilities, making it unclear whether a curriculum combining probability and proportions is more beneficial than just receiving traditional probability instruction alone. These are important first steps for developing curricula, and it would be important to understand which mathematical components (i.e. part/part; part/whole, decimal, or percentages) or misconceptions within proportional reasoning have a stronger influence for learning the concept of probability and for discovering the ideal teaching sequence of these components.

In sum, our results show that probabilistic reasoning is contingent on students’ prior knowledge of proportional reasoning and that correct and incorrect worked examples may be particularly helpful for students with less prior knowledge of proportions. Worked examples provide a fruitful cognitive tool for enhancing learning, and especially for lower performing students in everyday classrooms in a relatively inexpensive and unobtrusive manner, without hindering higher performers (e.g., by reforming existing textbooks to include worked examples). Future work examining the concept of probabilities and statistical literacy in general should include separate measures of proportional reasoning in order to gain deeper insight into the conceptual factors that influence probabilistic reasoning and better inform the design of probability curricula.

Appendices

Appendix 1

Description of all changes made to CMP textbook (Self-Explanation abbreviated as SE)

Page	Type of example	ACE	Target
10a	Correct w/ SE	Application	Understanding the statement "the events are equally likely."
10b	Incomplete w/o SE	Application	Explaining why events are not equally likely
15a	Incomplete w/ SE	Application	Listing all possible outcomes and understanding why the same outcome could be listed more than once
15b	Incorrect w/ SE	Application	Writing a ratio—student switches numerator and denominator
16	Correct w/ SE	Application	Determining number of outcomes based on different combinations of numbers, determining probability because on number of outcomes
18	Incorrect w/ SE	Connections	Incorrectly writing a fraction based in the two parts rather than the part and the whole
31	Incomplete w/ SE	Application	Interpreting area model. Comparing area model to tree diagram
33	Correct w/ SE	Application	Compare area model to drawing. Comparing area model to equation
38	Incomplete w/o SE	Connections	Using a grid to write a probability in fraction form
40	Incomplete w/o SE	Connections	Determine probability by using an area model
49	Correct w/ SE	Application	Explaining why an area model correctly represents a given probability situation
50a	Incorrect w/ SE	Application	Comparing ratios with different number of outcomes
50b	Incomplete w/o SE	Application	Use probability to complete free-throw problem
52	Correct w/ SE	Application	Understanding how to determine average outcome based on two different possible outcomes
53	Incomplete w/o SE	Application	Understanding how to determine whether to accept or reject a deal based on probability
54	Incomplete w/o SE	Connections	Using an area model to determine probability
64	Correct w/ SE	Application	Comparing tree diagram to probability
65	Correct w/ SE	Application	Understanding how to determine whether to accept of reject a deal based on probability
66	Incomplete w/o SE	Application	Determining all possible combinations
67	Incorrect w/ SE	Application	Interpreting meaning of "at least"
68	Incomplete w/o SE	Application	Determine probability given diagram
71	Incorrect w/ SE	Connections	Interpreting tree diagram

Appendix 2

Sample items from pretest and posttest

Use the tree diagram to answer #1:

Look at each spinner. Could it be spinner X? Circle Yes or No.

Martha randomly chooses one book from each shelf. There are 2 blue books, 1 red book, and 1 yellow book on the top shelf, and there are 3 blue books and 2 yellow books on the bottom shelf.

Does each area model represent the situation above? Circle Yes or No.

If Martha randomly chooses 1 book from each shelf 100 times:

• a. How many times do you expect her to choose a red book from the top shelf and a yellow book from the bottom shelf?

• b. How many times do you expect her to choose a blue book from the top shelf and a blue book from the bottom shelf?

If you decrease the number of times a coin is tossed, what happens to the total number of outcomes?

If you toss four coins at the same time, is the probability of getting four heads the same as or different from the probability of getting four heads when you toss one coin four times in a row? Explain your reasoning.

Is each statement correct? Circle Yes or No.

(a)	A 9 year old boy is 1.3 m tall, so he will be 2.6 m tall when he is 18	Yes	No
(b)	A photo whose size is 3 ½ inches by 5 inches can be enlarged so that it is 8 ½ inches by 11 inches	Yes	No
(c)	A recipe for 3 cupcakes calls for 4 tsp of sugar, so baking 4 cupcakes will require 5 1/3 tsp sugar	Yes	No
(d)	Jen’s pencil is 4 large buttons long, and Sam’s pencil is 6 large buttons long. If paper clips were used to measure instead, Jen’s pencil is 6 paper clips long, so Sam’s pencil must be 4 paper clips long	Yes	No
(e)	Melissa paid $0.86 for 0.43 of a pound of wheat flour. For 0.50 of a pound, she would have to pay $1.00	Yes	No

Appendix 3

Seventh Grade CMP2: “What Do You Expect” Study

Teacher Survey

Thank you so much for your participation in our study this year! We are very excited to see how the study went and will be happy to share results with you after we analyze your students’ tests. Please complete both sides of this survey and return to NAME REDACTED by email or on paper.

Appendix 4

We began the model building with the simplest model, Model 1, which included only the treatment as a predictor without any controls. Then in Model 2, we added covariates to account for the effect of prior knowledge in probabilistic and proportional reasoning, and URM status, thus, Model 2 allowed us to examine the effect of treatment above and beyond these controls that affect our main outcome as well as it included the variables necessary to answer H2b, and H1. In Model 3, we added treatment-covariate interactions, which allowed us to examine the differences-in-differences effect necessary to answer H1b. Finally, in Model 4, we removed interactions that were non-significant, but kept URM based on previous theoretical accounts. This final model, Model 4, allowed us to arrive at the most parsimonious model of Probabilistic Reasoning at posttest which included all of the predictors necessary (treatment [H1a], prior knowledge of proportions [H2b], the interaction between treatment and prior knowledge of proportions [H1b]) to answer all of our research questions and account for covariates that are theoretically implicated in Probabilistic Reasoning (prior knowledge of probabilities and URM status; see Table 4 for the series of regression models). The other two interactions (treatment-pretest Probabilistic Reasoning, and treatment-URM) were not found to significantly predict posttest Probabilistic Reasoning scores (see Table 6 for regression coefficients) and were thus not included in Model 4.

To answer H2a, we utilize the final, most parsimonious model, Model 4, but replace our measure of Probabilistic Reasoning at posttest as a criterion (i.e. dependent variable) with our measure of Proportional Reasoning knowledge at posttest and also do not include Probabilistic Reasoning at pretest as a covariate since students’ probability knowledge was not necessary to answer H2a. Thus, in this modified Model 4, we conducted a regression of Proportional Reasoning at posttest on Proportional Reasoning at pretest, treatment, the PR pretest-treatment interaction, and URM.