1 Article Highlights

  • Plurigaussian simulation can produce suitable structures at the meso- and micro-scale for cementitious materials.

  • Uncertainty at the macro-scale is accounted for through the multi-level approach

  • The effect of the pore-space geometry and aggregate distribution on the diffusion response is simulated

2 Introduction

The prediction of solute transport in cementitious materials is important for a wide range of applications including reinforcing bar corrosion, carbonation and self-healing. Typically, models developed for such applications are deterministic, and effective diffusion coefficients for the material are obtained through back-analysis of experimental data or through the use of empirical relationships (Papadakis 2000). However, it is well known that concrete transport properties are subject to a significant variability due to the inherent heterogeneity of concrete (Neville 2011; Conciatori et al. 2014, 2015). In addition, the prediction of solute transport and therefore the service life of concrete structures are highly dependent on the effective diffusion parameters (Conciatori et al. 2015).

An alternative to using empirical relationships or fitting experimental data is to simulate transport at lower scales and either employ this directly in a multi-scale modelling framework, or combine this with a suitable up-scaling technique to feed into a macro-scale model. For the former, a number of approaches have been developed including FE2 (Feyel and Chaboche 2000; Rocha et al. 2021), equation-free modelling (EFM) (Kevrekidis et al. 2003) and the heterogeneous multi-scale method (HMM) (Weinan and Bjorn 2003). In the FE2 approach, the lower-scale transport problem and macro-scale problem are solved in a nested manner. Whilst this has the advantage of avoiding the need for constitutive equations, this comes at an increased computational cost that can be prohibitive (Lange et al. 2021). Recently, a number of researchers addressed this issue through techniques such as model reduction, GPU programming, and replacement of lower-scale solutions with machine learning-based surrogate models (Fritzen and Hodapp 2016; Raschi et al. 2021; Rocha et al. 2021). HMM and EFM are similar approaches that employ a macro-scale model with large time steps, in which the primary variables evolve through the solution of a micro-scale model over smaller time steps (Tretiak et al. 2022). In such models, the need for macroscopic constitutive equations is avoided, and in some cases (e.g. EFM) the macro-scale finite element equations also are not required (Tretiak et al. 2022). As with the FE2 approach, the main disadvantage is the computational cost (Vassaux et al. 2019). In alternative approaches, steady-state transport simulations at the lower scales are used to calculate effective transport properties for the homogenous macro-scale model. Such effective properties can be calculated through a numerical homogenisation procedure (Pollmann et al. 2021), fitting of an analytical equation such as Fick’s or Darcy’s law for diffusion and permeability coefficients, respectively (Gostick et al. 2016), or through machine learning techniques (Wu et al. 2019). In the case of machine learning, the effective properties can be estimated directly from images of the structure of the medium, avoiding the need for the lower-scale simulations. Such an approach was taken by Wu et al. (2019), who employed convolutional neural networks (CNNs) trained using images of porous media and effective coefficients predicted from numerical simulations. The authors found that the CNN performed better than a known empirical equation. For the simulation of transport at the lower scales, among the most common approaches are pore network models (PNM) (Gostick et al. 2016; Babaei et al. 2021), finite element models (FEM) (Xu et al. 2020; Sun et al. 2022) and lattice Boltzmann methods (LBM) (Yang and Wang 2018; Patel et al. 2021).

In order to simulate multi-scale solute transport in concrete, a representation of both micro- and meso-structure is required. Whilst such representations can be obtained from images, it can be advantageous to generate such structures virtually (Holla et al. 2021). For cementitious materials, the most commonly employed approach to obtaining a virtual micro-structure is to use a cement hydration model such as HYMOSTRUC3D (van Breugel 1995; Koenders 1997) or CEMHYD3D (Bentz 2005). Patel et al. (2018a) combined both HYMOSTRUC3D and CEMHYD3D with a LBM to simulate the effects of calcium leaching on cement paste micro-structure. The authors found that the rate of leaching for both models was similar for a water-to-cement ratio of 0.25, but that the rate was faster for HYMOSTRUC3D-generated micro-structures for water-to-cement ratios of 0.4–0.5. The contrast in the results was thought to be due to differences in the predicted depercolation of capillary pores that arose as a direct result of differences in model assumptions (i.e. CEMHYD3D employs a voxel-based approach as opposed to the vector-based approach employed in HYMOSTRUC3D). Cruz et al. (2016) used machine learning, trained on the results of Bullard's (2007) cellular automation hydration model, to generate cement paste micro-structures. The authors found that the machine learning model was able to generate micro-structures that compared favourably to those produced by the hydration model and at a fraction of the computational cost. A random macro-meso-pores method (RGMMP) was proposed by Hussain et al. (2015) for the representation of the pore structure of building materials. The model is based on stochastic growth theory and assumes that macro-pores are connected through meso-pores. The authors combined the RGMMP with a LBM for predicting the effective diffusivity of a range of building materials and found good agreement with experimental data.

Aggregate placing methods (Thilakarathna et al. 2020) are usually employed for generating concrete meso-structures, comprising a mortar matrix and large aggregate particles. In such methods, aggregate particles are placed randomly within the volume starting with the largest, with constraints concerning the minimum distance to existing particles being enforced (Thilakarathna et al. 2020). A review of approaches for the generation of concrete meso-structures is provided by Thilakarathna et al. (2020). A key challenge in such models is the representation of the complex shapes exhibited by aggregate particles, with a number of models idealising their shape as spherical or ellipsoidal (Zheng et al. 2009; Li et al. 2016). In order to generate more realistic concrete meso-structures, a number of techniques for capturing the complex shape of aggregate particles have been proposed (Qian et al. 2016; Zhang et al. 2018; Holla et al. 2021). In the Anm model, developed by Qian et al. (2016), aggregate particle shapes are represented using spherical harmonic functions. The model was used to represent both large aggregate particles, embedded in a mortar matrix, and fine aggregate particles, embedded in a cement paste matrix. In Lu and Garboczi (2014), meso-structures generated with the Anm model were combined with an algorithm that produces tetrahedral finite element meshes for use in numerical analyses. Zhang et al. (2018) generated polyhedral-shaped aggregate particles by first creating a 3D Voronoi tessellation of the domain, before employing a shrinking algorithm to generate the aggregate phase. An open-source toolbox, written in Python, for the generation of concrete meso-structures was presented by Holla et al. (2021). In their model, polyhedral-shaped aggregate particles are generated by reduction of a cuboid to an angular ellipsoid shape through slicing operations, whilst concave depressions are represented using Gaussian surfaces. The ability of the model to generate realistic meso-structures was demonstrated both qualitatively through an image comparison and quantitatively through the comparison of the predicted elastic properties (calculated using a numerical homogenisation tool) to experimental values.

A less explored method of structural generation at the micro- or meso-scale is that of plurigaussian simulation (PGS), first introduced by Galli et al. (1994) and developed further in following years (Le Loc’h and Galli, 1997; Dowd et al. 2003; Armstrong et al. 2014) for geological applications. The approach is primarily applied in this domain as the generated fields match well with discrete geological structures observed in the field. The method is derived from truncated Gaussian simulation where a Gaussian distribution is truncated sequentially to represent different geological facies in a nested fashion (Matheron et al. 1987; Beucher and Renard 2016). PGS is not limited to sequential relationships between facies. More complex connectivity patterns, between the distinct components in the resulting field, can be generated through a prescribed lithotype rule. The lithotype is a representation of the spatial relationship between facies (Doligez et al. 2011) and can be used to determine the connectivity and relative proportions they exhibit. The method is most commonly applied in attaining field-scale representations of ore deposits (Betzhold and Roth 2000; Yunsel and Ersoy 2011; Renard and Beucher 2012; Talebi et al. 2013; Maleki and Emery 2014; Mery et al. 2017) and petroleum reservoirs (Chautru et al. 2015; Beucher and Renard 2016; Zagayevskiy and Deutsch 2016; Martinius et al. 2017; Madani et al. 2018), but has also been used at much smaller scales such as in the generation of the micro-structure of solid oxide cells (SOCs). Abdallah et al. (2016) applied the truncated plurigaussian model in a set of 3D simulations of three-phase anode layers. The authors found good agreement in the covariance, granulometry, and visual representation between 2D SEM images and the simulated results, with the ease, efficiency and versatility of the method being highlighted. Moussaoui et al. (2018) also replicated SOC micro-structure and focused on validating the resulting fields through comparison with effective gas diffusivities and effective charge conductivities, as well as on analysing the morphology of the fields. Furthermore, the authors discussed the effects of non-stationary random fields in replicating a graded electrode. They explored different correlation lengths in the underlying fields and introduced localised roughness into the system. The method was shown to be flexible in depicting more complex microstructural architectures and matched well with the experimental phase effective diffusivities. Other applications at this scale that have been considered are: rock mineralogical composition (Méndez-Venegas and Díaz-Viera 2013), partially miscible liquids confined in nanopores (Gommes 2013), and food micro-structure (Bron and Jeulin 2011).

In this study, PGS is coupled with a finite-element (FE) model for chemical transport in concrete using a multi-level modelling approach. Structural representations of pores and aggregate in mortar are generated at the micro- and meso-scale, respectively, using the plurigaussian method, and are employed in a FE model to calculate the effective diffusion coefficients of the two-phase medium at both scales. From these results, a range of effective diffusion coefficients at the macro-scale are calculated and used to simulate an example problem concerning the diffusion of chloride ions through a saturated concrete specimen. By using this stochastic approach, variability can be inferred at the macro-scale when using a homogenised model due to the variation in diffusion coefficients obtained at the different scales.

Section 2 presents the theory of the plurigaussian model, solute transport model and multi-level upscaling approach. Section 3 describes the finite element framework of the chemical transport model and explains how the field is implemented. Section 4 gives details of how PGS is used to represent the specific micro- and meso-structures considered in this paper. Section 5 presents an example problem of multi-level chemical transport using structures generated through PGS, including an experimental validation, and Sect. 6 highlights the main conclusions of the study.

3 Theoretical Basis

3.1 Plurigaussian Model

Let \(\left\{ {Z_{1} ,Z_{2} } \right\}\) be a set of two independent random fields in \({\mathbb{R}}^{2}\) whose covariance kernels can be of Gaussian or Matérn forms and define a random field \({\varvec{Z}}\) where

$${\varvec{Z}}\left( {\text{x}} \right) = \left( {Z_{1} \left( {\text{x}} \right),Z_{2} \left( {\text{x}} \right)} \right),\,\, \forall {\text{x}} \in {\mathbb{R}}^{2} .$$
(1)

Let \(L = \left\{ {D_{1} , \ldots ,D_{n} } \right\}\) be a partition of \({\mathbb{R}}^{2}\) into \(n\) disjoint subdomains, such that the plurigaussian random field \({\varvec{P}}\) with \(n\) distinct facies is defined as:

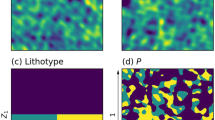
$$\left( {\text{x}} \right) = i {\text{ if}} \;{\text{and}}\; {\text{only}}\;{\text{if}}\;Z\left( {\text{x}} \right) \in D_{i} ,\forall {\text{x}} \in \mathbb{R}^{2}$$
(2)

The set \(L\) is the selected lithotype rule and can be used to assign different facies for representation in terms of the micro- or meso-structure. Figure 1 shows an example realisation of the phasal structures that can be generated. \(Z_{1}\) and \(Z_{2}\) are two Gaussian random fields (Fig. 1a, b, respectively) generated using the Fourier integral method (Pardo-Igúzquiza and Chica-Olmo 1993; Müller et al. 2022), and the lithotype (Fig. 1c) consists of three quadrilateral facies. Due to the construction of the lithotype, there is a connectivity between all facies, meaning that \({\mathbf{P}}\) will have connectivity between the same facies. Conversely, taking disjoint facies will result in disjoint facies in \({\mathbf{P}}\). Similarly, the choice of quadrilaterals is not unique.

Fig. 1
figure 1

Schematic of plurigaussian simulation where a, b are Gaussian random fields, c is the lithotype consisting of facies D1, D2, and D3, and d the resulting simulated field

Full size image

At both the micro- and meso-scales, the structure of a multi-phase system can be controlled through careful choice of subdomains in the lithotype rule \(L\). Similarly, the underlying covariance kernel of the fields \({Z}_{1},{Z}_{2}\) can be used as a way of controlling the roughness of the resulting field: if the kernel is smooth such as the Gaussian kernel, then the resulting field structure will reflect this. See Sect. 4 for a discussion on the effects of varying the lithotype rule subdomains on the resulting field, as well as on the choices made at both scales.

3.2 Solute Transport Model

In the present work, the reactive transport model described in Freeman et al. (2019) is employed. Solute transport is governed by the mass balance equation that, with boundary conditions, reads:

$$\frac{{\partial \left( {\eta S_{l} \rho_{l} c_{i} } \right)}}{\partial t} + \nabla \cdot {\mathbf{J}}_{{\varvec{i}}} = \eta \rho_{p} \frac{{\partial \left( {S_{p} } \right)}}{\partial t}, \forall {\mathbf{x}} \in {\Omega }$$
(3a)
$${\mathbf{J}}_{{\varvec{i}}} \cdot {\mathbf{n}} - \gamma \left( {c_{i} { } - c_{env} } \right) = 0, \forall {\mathbf{x}} \in {\Gamma }_{c}$$
(3b)
$$c_{i} { } = c_{b} , \forall {\mathbf{x}} \in {\Gamma }_{d}$$
(3c)

where \({\Omega }\) is the problem domain, \(\eta\) is the porosity of the medium, \(S_{l}\) is the degree of saturation of the pores, \(\rho_{l}\) and \(\rho_{p}\) are the liquid and sorbed material densities, respectively, \(c_{i}\) is the solute concentration for a species \(i\), \({\mathbf{J}}_{{\varvec{i}}}\) is the diffusive flux and \(S_{p}\) is the degree of saturation of sorbed material. The Cauchy-type boundary condition (3b) represents the transfer of mass between the specimen and the environment where \({\mathbf{n}}\) is the outward facing unit normal, \(\gamma\) is a mass transfer coefficient, \(c_{env}\) is the solute concentration in the environment and \({\Gamma }_{c} \subset {\Gamma }\) (where \({\Gamma }\) is the domain boundary) is the part of the boundary to which Cauchy-type boundary conditions are applied. Finally, the Dirichlet boundary condition (3c) fixes the solute concentration at \(c_{b}\) on \({\Gamma }_{d} \subset {\Gamma }\).

The diffusive flux is given by the Poisson–Nernst–Planck equations that can be written as (Baroghel-Bouny et al. 2011):

$${\mathbf{J}}_{{\varvec{i}}}=-\eta {S}_{l}{\rho }_{l}{D}_{i}\left(\nabla {c}_{i}+\frac{{z}_{i}F}{RT}\nabla \psi \right)$$
(4a)
$$\varepsilon \nabla ^{2} \cdot \psi + F\left( {\mathop \sum \limits_{{i = 1}}^{{ns}} z_{i} c_{i} + \rho } \right) = 0$$
(4b)

where \({D}_{i}\) is the coefficient of molecular diffusion, \({z}_{i}\) is the charge of an ion, \(F\) is Faraday’s constant, \(R\) is the ideal gas constant, \(T\) is the temperature and \(\psi\) is the electric potential. Equation (4b) describes the electric potential, where \(\varepsilon\) is the dielectric permittivity of the medium, \(\rho\) is the charge density and \(ns\) is the number of solutes. Noting that both \(\varepsilon\) and \(\rho\) are negligible, (4b) reduces to the charge neutrality condition (Lasaga 1979), which, noting that the pore solution is initially charge neutral, is ensured through the no-electric-current condition (Lasaga 1979; Song et al. 2014), leading to a diffusive flux given by:

$${\mathbf{J}}_{{\varvec{i}}}=-\eta {S}_{l}{\rho }_{l}{D}_{i}\left(\nabla {c}_{i}+{z}_{i}{c}_{i}\frac{\sum_{i=1}^{ns}{z}_{i}{D}_{i}\nabla {c}_{i}}{\sum_{i=1}^{ns}{z}_{i}^{2}{D}_{i}{c}_{i}}\right)$$
(5)

Finally, the chemical reaction considered is of the sorption of chemical ions onto the cementitious matrix and is simulated using a kinetic Freundlich-type isotherm that reads (Baroghel-Bouny et al. 2011):

$$\frac{\partial {S}_{p}}{\partial t}=\frac{\left({S}_{p}-\mu {c}_{i}^{\lambda }\right)}{\tau }$$
(6)

in which \(\mu\) is the binding capacity, \(\lambda\) is a rate parameter and \(\tau\) is a characteristic time. It is noted that molar concentrations are employed in the calculation of the reaction rates.

3.3 Multi-level Upscaling

In this study, transport properties—in this case diffusion coefficients—are up-scaled from the micro-scale, assumed to comprise mortar matrix and saturated pores, through the meso-scale comprising the homogenous porous mortar matrix and large aggregate phase and finally to the macro-scale that considers the concrete as a homogenous medium. This process is illustrated in Fig. 2.

Fig. 2
figure 2

Schematic of multi-level upscaling of transport properties

Full size image

The OpenPNM approach is used to calculate the effective diffusion coefficients of the two-phase medium (Gostick et al. 2016), whereby steady-state diffusion is simulated, and then, the effective diffusion coefficient is computed as:

$${D}^{eff}=\frac{{J}_{i}^{xr}L}{A\Delta c}$$
(7)

where \({J}_{i}^{xr}\) is the flux in the x direction on the right-hand boundary, \(L\) is the domain length, \(A\) is the cross-sectional area and \(\Delta c\) is the concentration gradient applied to the domain. Given the effective diffusion coefficients, the formation factor can also be calculated, \({F}_{m}={D}^{r}/{D}^{eff}\), and tortuosity, \({T}_{t}=\eta {D}^{r}/{D}^{eff}\), where \({D}^{r}=1\) is a relative diffusion coefficient.

The effective diffusion coefficient at the macro-scale (\({D}_{mas}\)) is calculated by multiplying the free water diffusion coefficient, \({D}_{fw}\), by the effective coefficients at both the micro- (\({D}_{mic}^{eff}\)) and meso- (\({D}_{mes}^{eff}\)) scales:

$${D}_{mas}={D}_{fw}{D}_{mic}^{eff}{D}_{mes}^{eff}$$
(8)

4 Numerical Implementation

4.1 Finite Element Framework

The governing equations for solute transport are discretised using the finite element method. The weak form of the governing equations reads:

$$\int_{\Omega } {{\mathbf{W}}\left( {\frac{{\partial \left( {\eta S_{l} \rho _{l} c_{i} } \right)}}{{\partial t}} - \eta \rho _{p} \frac{{\partial \left( {S_{p} } \right)}}{{\partial t}}} \right)d\Omega } - \int_{\Omega } {\nabla {\mathbf{W}} \cdot \left( { - \eta S_{l} \rho _{l} D_{i} \left( {\nabla c_{i} + z_{i} c_{i} \frac{{\sum\nolimits_{{i = 1}}^{{ns}} {z_{i} } D_{i} \nabla c_{i} }}{{\sum\nolimits_{{i = 1}}^{{ns}} {z_{i}^{2} } D_{i} c_{i} }}} \right)} \right)d\Omega } + \int_{{\Gamma _{c} }} {{\mathbf{W}}\left( {\gamma \left( {c_{i} ~ - c_{{env}} } \right)} \right)d\Gamma _{c} = 0}$$
(9)

The Galerkin-weighted residual method is employed such that the weight functions (\(\mathbf{W}\)) are equal to the shape functions (\(\mathbf{N}\)), with the primary variables being the solute concentrations. The resulting system of equations reads:

$$\mathbf{C}{\partial }_{t}\left({\overline{\mathbf{c}} }_{i}\right)+\mathbf{K}{\overline{\mathbf{c}} }_{i}=\mathbf{F}$$
(10)

in which the primary variable is interpolated from the nodal values in the usual manner (i.e. \({c}_{i}=\mathbf{N}{\overline{\mathbf{c}} }_{{\varvec{i}}}\)).

The global matrices read:

$$\mathbf{C}=\sum_{nel}\left({\int }_{{{\varvec{\Omega}}}_{{\varvec{e}}}}{{\varvec{N}}}^{T}\left(\eta {S}_{l}{\rho }_{l}\right){\varvec{N}}d{\Omega }_{e}\right)$$
(11)
$$\mathbf{K}=\sum_{nel}\left({\int }_{{{\varvec{\Omega}}}_{{\varvec{e}}}}\nabla {{\varvec{N}}}^{T}\left(\eta {S}_{l}{\rho }_{l}{D}_{i}\right)\nabla {\varvec{N}}d{\Omega }_{e}\right)$$
(12)
$$\mathbf{F}=\sum_{nel}\left({\int }_{{{\varvec{\Omega}}}_{{\varvec{e}}}}\nabla {{\varvec{N}}}^{T}\left(-\eta {S}_{l}{\rho }_{l}{D}_{i}\left({z}_{i}{c}_{i}\frac{\sum_{i=1}^{ns}{z}_{i}{D}_{i}\nabla {c}_{i}}{\sum_{i=1}^{ns}{z}_{i}^{2}{D}_{i}{c}_{i}}\right)\right)d{\Omega }_{e}-{\int }_{{\Gamma }_{c,e}}\mathbf{W}\left(\gamma \left({c}_{i} -{c}_{env}\right)\right)d{\Gamma }_{c,e}\right)$$
(13)

An implicit Euler backward difference scheme is used for the temporal discretisation:

$$\frac{1}{\Delta t}\mathbf{C}\left({\overline{{\varvec{c}}} }_{i}^{t+1}-{\overline{{\varvec{c}}} }_{i}^{t}\right)+\mathbf{K}{\overline{{\varvec{c}}} }_{i}^{t+1}=\mathbf{F}$$
(14)

The nonlinear equations are solved with a standard Newton–Raphson procedure, which gives the following iterative update of the solution:

$$\delta {\overline{{\varvec{c}}} }_{i,k+1}^{t+1}={\left[\frac{\partial {{\varvec{\xi}}}^{t+1}}{\partial {\overline{{\varvec{c}}} }_{i,k}}\right]}^{-1}\left(-{\varvec{\xi}}\right)$$
(15)

where \({\varvec{\xi}}\) is the approximation error that is given by:

$${\varvec{\xi}}=\mathbf{C}\left({\overline{{\varvec{c}}} }_{i}^{t+1}-{\overline{{\varvec{c}}} }_{i}^{t}\right)+\Delta t\mathbf{K}{\overline{{\varvec{c}}} }_{i}^{t+1}-\Delta t\mathbf{F}$$
(16)

and the iterative updates are terminated once the norm of the error meets a defined convergence tolerance of 0.001%.

The numerical simulations at the micro- and meso-scales employ a pixel-based finite element method, such that the discretisation of the finite element mesh matches the resolution of the micro- and meso-structure images, and the material properties assigned to a given element are based on the phase in which the element is found. An example of this at the micro-structure level is shown in Fig. 3, where the red elements represent the pore space and the blue elements the mortar matrix.

Fig. 3
figure 3

Pixel-based finite element mesh of two-phase material

Full size image

4.2 Field

A plurigaussian simulation tool was written in Python to generate fields of varying structure. First, the lithotype rule must be defined in terms of facies shape, position and phase, and then, the lithotype is constructed by combining the defined facies. Two random fields are then generated based on the supplied covariance kernel, where here we can choose between Gaussian and Matérn kernels. The initial random fields are generated using the Python package gstools (Müller et al. 2022), and for a given domain, a simple pixelwise evaluation is carried out to determine the phase of each point in the simulation domain adhering to the field-based mapping. The final discrete fields are then recorded on a pixel-wise basis to be read by the FE model on execution. Here, the correlation lengths of the two underlying fields are chosen to be the same in both cases. Whilst it is possible to introduce a localised roughness effect by using differing lengths, a similar effect can be achieved by using the Matérn covariance kernel.

5 Plurigaussian Field Representation

5.1 Effect of Lithotype Facies

The resulting structure of the generated plurigaussian field \({\varvec{P}}\) will depend on the lithotype facies chosen, as well as the covariance functions of the random fields \({Z}_{1},{Z}_{2}\) used in the generation process. Thus, the probability density function of \({Z}_{1},{Z}_{2}\) will determine the likelihood of reaching certain areas in the lithotype. In the following example, we consider a binary lithotype rule with fields \({Z}_{1},{Z}_{2}\) having a Gaussian covariance kernel. Figure 4c shows a lithotype with a central circular facie to illustrate how such a facie would capture most of the possible combinations of the two Gaussian fields. The black dots depict the positions of the lithotype that are mapped by fields (a) and (b). As both (a) and (b) are based on a Gaussian distribution, their combination can be thought of as a multivariate normal distribution, and as such, we attain a concentration of points near the centre of the lithotype rule. Clearly, a change of shape or size in facies located near the centre of the lithotype will have a larger effect on the structure of \({\varvec{P}}\). We can see this in Fig. 5, where three different facies are taken at the centre and corner of the lithotype. Table 1 shows the relative areas of the facies and structure in \({\varvec{P}}\) relative to the domain area. Thus, we can choose a combination of facies based on the connectivity and sparsity of the structure we are looking to represent. Multiple disjointed shapes in \({\varvec{P}}\) can be generated using a lithotype with disjoint facies away from its centre. For the opposite case of a generated field with well-connected phases, a single facie that spans the centre of the lithotype is employed.

Fig. 4
figure 4

Gaussian random fields (a), (b), and their mapping positions show in binary lithotype (c)

Full size image
Fig. 5
figure 5

Central facies and resulting plurigaussian field below (a), and the equivalent plurigaussian field for shifted lithotype facies (b)

Full size image
Table 1 Comparison of relative phase areas for different lithotype facies shapes and their position
Full size table

5.2 Example of Mortar Micro-Structure Lithotypes

It is worth noting here that in the following, the choice of lithotype facies shape and position is not unique, and other combinations exist that would give similar results. A number of examples are given below of how different lithotype rules can be used to achieve a desired structure.

To develop representative plurigaussian fields of the typical micro-structure found in cement paste, backscattered electron scanning electron microscope (SEM-BSE) images from Lyu et al. (2019) (reproduced in Fig. 6) were used to match the relative size of the pore network. The average generated micro-scale porosity was 0.261 with a range of 0.053, which is within the range of the porosity observed in Lyu et al. (2019), which was found to be 0.117–0.294 for a w/c ratio of 0.4. In addition to this, the pore size range was comparable (≤ 9.47 µm for w/c ratio of 0.3 (Lyu et al. 2019), compared with ≤ 6.67 µm in the generated micro-structures).

Fig. 6
figure 6

BSE images of cement paste with a water-to-cement ratio of 0.4 of size 0.19 mm × 0.14 mm for a original BSE image, b binary image. (Reused with permission after Lyu et al. (2019))

Full size image

Much of the connectivity of the network relies on having three spatial dimensions, but here it is assumed that there is some degree of planar connectivity to allow for diffusion across the domain. It has been shown that a porosity above a percolation threshold of 0.2 will lead to good predictions of diffusivity when considering samples of w/c rations in the range of 0.3–0.5 (Patel et al. 2018b). As such, the generated porosity and level of connectivity present at the micro-scale are sufficient in leading to suitable predictions in diffusivity. The correlation length and covariance kernel of both \({Z}_{1},{Z}_{2}\), as well as the lithotype rule, were used together to match the micro-structure. It was found that a Gaussian kernel resulted in a field with a smooth idealised network, whilst a Matérn kernel produced a field with the structural irregularities seen in the scans (see Fig. 7 for a comparison).

Fig. 7
figure 7

Comparison between micro-scale structure generated with fields of Gaussian kernels (a) and Matérn kernels (b)

Full size image

Similarly, the correlation length of \({Z}_{1},{Z}_{2}\) allowed for control over the relative length of connecting channels and the size of the pores which they connect. Finally, an ellipse with large eccentricity was found to be an appropriate lithotype facie, and as can be seen in Fig. 8c along with the Matérn fields (a),(b) and resulting plurigaussian field (e). Figure 8d also shows the mapping from (a), (b) to (c). It is worth noting that in this case, the choice of lithotype shape is practically equivalent to segmenting the random field \({Z}_{1}\).

Fig. 8
figure 8

a, b Random Matérn fields, c lithotype rule, d mapping distribution, e resulting plurigaussian field representing mortar micro-structure

Full size image

In a mortar paste, it is known that high levels of porosity do not translate to high levels of permeability due to the likelihood of low connectivity in the pore structure (Bindiganavile et al. 2018). In addition, connected porosity obtained from SEM images has been shown to be lower than the total porosity (Song et al. 2019). The generated micro-structures exhibit this behaviour, with several disconnected regions being observed in Fig. 8e.

5.3 Example of Concrete Meso-Structure Lithotypes

A similar process can be performed in representing the meso-structure. Images were taken of fractured concrete samples (Fig. 9), where the sample and aggregate size influenced the choice of model parameters.

Fig. 9
figure 9

Example image of concrete meso-structure

Full size image

As the sample aggregate pieces were relatively polygonal in shape, a convex hull transform was applied to the final field to ensure the plurigaussian field would have a similar structure. Applying a convex closure to the shapes generated through PGS (Fig. 10e) results in the smallest convex shape, which contains the original shape. The Gaussian covariance kernel was chosen to give smoother output. Taking disjoint facies in the lithotype resulted in disjoint structures in the plurigaussian field, so here four disjoint quadrilaterals facies were chosen, positioned away from the centre of the lithotype. This leads to less frequent mapping to the facies based on the probability density functions of the Gaussian fields, which further lead to more disjoint structures in the plurigaussian field. Finally, the correlation length of \({Z}_{1},{Z}_{2}\) gave the control over the size of the aggregate pieces, which can be seen in Fig. 10f.

Fig. 10
figure 10

a, b Gaussian random fields, c lithotype rule, d mapping distribution, e resulting plurigaussian field, f plurigaussian field after convex hull transformation

Full size image

The average generated meso-scale aggregate content was 0.4147, which compares well with aggregate content in Selvarajoo et al. (2020), which was 0.4108. In addition to this, the aggregate size range was comparable (≤ 10.00 mm (Selvarajoo et al. 2020), compared with ≤ 10.63 mm in the generated meso-structures).

6 Example Problem

6.1 Multi-Scale Solute Transport Simulations

To demonstrate the performance of the model, we consider an example problem concerning the diffusion of chloride ions through a saturated concrete specimen presented in Oh and Jang (2007). To this end, a series of virtual micro- and meso-structures were generated to calculate the effective diffusion coefficients. The effective diffusion coefficient of the concrete at the macro-scale varies as a result of the statistical variability of the micro- and meso-structures. As such, uncertainty in its value is accounted for, and the numerical simulations produce an envelope of predicted chloride profiles.

6.1.1 Micro-Scale

The first step is the simulation of diffusion at the micro-scale, which was accomplished by generating nine virtual micro-structures of size 100 × 100 μm using the lithotypes shown in Fig. 8 (see Fig. 11), with an average porosity of 0.264 (Patel et al 2018b). The simulation considered steady-state diffusion, with the left-hand and right-hand boundaries being fixed at concentrations of 1 and 0, respectively, whilst at the top and bottom boundaries a zero flux condition was applied. It was assumed that the pore space was saturated and that the mortar matrix was impermeable. The finite element mesh employed matched the resolution of the micro-structure images and contained 62,500 elements of size 0.4 μm. To simulate for the assumed impermeability of the mortar matrix, the physical domain was restricted to the pore space (i.e. elements representing the mortar matrix were removed). The results of the simulations can be seen in Fig. 12, and the calculated effective diffusion coefficients, formation factors and tortuosities are given in Table 2. It can be seen from Fig. 12 that in some cases large sections of the pore space are not connected across the domain and therefore do not contribute to the transport of solutes. For the case with the lowest porosity, it was found that there was no connected pore space that crossed the domain and as such the effective diffusion coefficient for the domain was zero (and effective formation factor and tortuosity infinity). This suggests that the percolation threshold is around 23% porosity, which is in good agreement with the results of Patel et al. (2018b). In addition, the relative diffusivity predicted at the micro-scale compares well with the results of Ma et al. (2014) (reported in Patel et al. 2018b). (The average calculated value was 0.02194, whilst the results of Ma et al. (2014) are in the range 0.0194–0.0265.)

Fig. 11
figure 11

Generated micro-structures

Full size image
Fig. 12
figure 12

Steady-state concentration profiles at micro-scale

Full size image
Table 2 Micro-scale results
Full size table

It can be seen that there is large variance between the properties of the nine samples. Modelling in 3D would increase how statistically representative the simulations are of the diffusive processes and would decrease the observed variance (Marafini et al. 2020). It is noted that whilst the micro-scale domain constitutes a representative elementary volume (REV) when considering the porosity (see Appendix), it does not necessary for other quantities of interest (such as diffusivity). As such, the micro-scale domain size could be enlarged to be more representative of the pore-structure characteristics.

6.1.2 Meso-Scale

For the meso-scale simulations, nine virtual meso-structures of size 75 × 75 mm were generated using the lithotypes shown in Fig. 10 (see Fig. 13), with an average aggregate content of 0.411 (Qian et al. 2016; Holla et al. 2021). Again, the simulation considered steady-state diffusion, with the left-hand and right-hand boundaries being fixed at concentrations of 1 and 0, respectively. It was assumed that the aggregate particles were impermeable. The finite element mesh employed contained 62,500 elements of size 0.3 mm. The results of the simulations can be seen in Fig. 14, whilst the calculated effective diffusion coefficients, formation factors and tortuosities are given in Table 3. It can be seen that the transport through the domain is non-uniform due to the presence of the aggregate, with regions of slower transport being found behind large or clusters of aggregate particles.

Fig. 13
figure 13

Generated meso-structures

Full size image
Fig. 14
figure 14

Steady-state concentration profiles at the meso-scale

Full size image
Table 3 Meso-Scale results
Full size table

As with the micro-scale results, there is a large variance between the properties of the 9 samples. It is again noted that this could be decreased through both modelling in 3D (Marafini et al. 2020) and, potentially, through increasing the domain size (though the meso-scale domain does constitute an REV when considering aggregate content, see Appendix).

6.2 Statistical Analysis of Effective Diffusion Coefficients

In order to quantify the uncertainty associated with the calculated effective diffusion coefficients, at both the micro- and meso-scales, a statistical analysis was undertaken. The diffusion coefficients were assumed to follow a normal distribution. The mean values of the diffusion coefficients at the micro- and meso-scales (\({\overline{D} }_{mi}\) and \({\overline{D} }_{me}\), calculated as the average of the effective diffusion coefficients found in Tables 2 and 3, respectively), the corresponding standard deviations (\({s}\)) and mean normalised standard deviations can be seen in Table 4, and a plot of the probability density functions is given in Fig. 15. The figure shows that the effective diffusion coefficient is higher at the meso-scale than at the micro-scale and that there is less uncertainty in its value when considering the mean normalised standard deviation. It can be noted that in the results, the second sample at the micro-scale was neglected due to the fact that the porosity is below the percolation threshold, as indicated by the zero value for the effective diffusion coefficient.

Table 4 Statistical parameters
Full size table
Fig. 15
figure 15

Distribution of diffusion coefficients at micro- and meso-scales

Full size image

Using this underlying distribution, the confidence level that the mean effective diffusion coefficient of the population at each scale (\({\overline{D} }_{mi}^{p}\) and \({\overline{D} }_{me}^{p}\)) lies within the range of calculated effective diffusion coefficients can be calculated. The confidence interval (\(CI\)) is calculated based on the following formula:

$$CI=\overline{x}\pm t\frac{s}{\sqrt{n} }=\overline{x }\pm tSE$$
(17)

where \(\overline{x }\), \(s\) and \(n\) indicate the sample mean, sample standard deviation and sample size, respectively, and \(SE\) is the standard error. Finally, \(t\) is the t-score that has been used in place of the z-score to correct for the sample size (Campbell 2021). Using Eq. (17), the t-scores for the range of effective diffusion coefficients at the micro- and meso-scales (Tables 2 and 3, respectively) can be calculated. Once the t-scores are obtained, the corresponding confidence level can be found from a t-table (Campbell 2021). For the micro-scale, the lowest diffusion coefficient was found to be 3.12 \(SE\) s from the mean, whilst the highest was 5.54 \(SE\) s away, giving a range of \({\overline{D} }_{mi}-3.12SE\le {\overline{D} }_{mi}^{p}\le {\overline{D} }_{mi} +5.54SE\), which gives 99.52% certainty that the mean effective diffusion coefficient of the population lies in this range. For the meso-scale, the lowest diffusion coefficient was found to be 4.43 \(SE\) s from the mean, whilst the highest was 4.38 \(SE\) s away, giving a range of \({\overline{D} }_{me}-4.43SE\le {\overline{D} }_{me}^{p}\le {\overline{D} }_{me}+4.38SE\), which gives 99.73% certainty that the mean effective diffusion coefficient of the population lies in this range. In addition to quantifying the confidence that the population mean lies within the range of calculated effective diffusion coefficients, the distribution can also be used to calculate what the range of values need to be for a given confidence level. An example of this for a 95% confidence level, along with a summary of the current confidence levels and range of values, is given in Table 5.

Table 5 Diffusion coefficient ranges at each scale and confidence level
Full size table

6.3 Experimental Validation of Macro-scale Reactive Transport

The example considered here is that presented in Oh and Jang (2007) which concerns the diffusion of chlorides in a concrete specimen. In the experiments, concrete cylinders (100(h) × 200(d) mm) were cured for 28 days in water, before being immersed in a 3.5% chloride solution for 15 weeks, after which concentration profiles were measured. The surfaces of the specimen were sealed, with the exception of one face, ensuring one-dimensional transport of chlorides.

For the numerical simulations, the range of diffusion coefficients is accounted for through the consideration of the bounding values, obtained as the product of the extreme values at each scale with the free-water diffusion coefficient. It is noted that the median of the range compares well with the approximate experimental value for ordinary Portland cements reported in Oh and Jang (2007) (2.01 × 10–11 m2/s compared with ~ 2.00 × 10–11 m2/s). Following mesh and time step convergence studies, a finite element mesh containing 42 elements with a maximum size of 3 mm and a time step size of 36 s was employed. The parameters used in the simulations are given in Table 6. The porosity was calculated as the average from the micro- and meso-structures, whilst the diffusion coefficient range accounts for the statistical variability. A comparison between the numerical predictions and the experiment results is given in Fig. 16 where ‘Exp–C1’ and ‘Exp–C5’ denote the experimental profiles that correspond to cement types Cem-I and Cem-V, respectively. It can be seen that there is a good agreement between the simulations and the experimental data, with the latter being mostly contained within the envelope of numerical predictions. It may also be seen that the width of the envelope of numerical predictions is non-uniform, with a wider range (and therefore uncertainty) present at higher depths.

Table 6 Model parameters
Full size table
Fig. 16
figure 16

Comparison between numerical envelope and experimental results of Oh and Jang (2007)

Full size image

7 Concluding Remarks

A new coupling of plurigaussian simulation for micro- and meso-structure representation with multi-scale modelling of particulate materials has been presented, and its application to the finite element simulation of chloride diffusion in a concrete specimen. The method carries out a geometric evaluation of the effective diffusion coefficients at the micro- and meso-scales and passes these up to the macro-scale. In doing so, a level of statistical variability is introduced into the macro-scale simulations, accounting for the uncertainty associated with the properties of cementitious materials. In addition, such an approach avoids the need to use either empirical formulas, or experimental calibration, to estimate the effective diffusion coefficients at the macro-scale. The approach instead relies only on statistical parameters describing the micro- and meso-structures of the material.

Plurigaussian simulation has been shown to be a suitable method in random structural generation for pore networks and aggregate distributions, highlighting the ability of this computationally inexpensive and tractable method to represent highly complex structures in a stochastic manner. At both the micro- and meso-scales, the correlation length and covariance kernel of the two input fields were shown to be significant in altering the resulting plurigaussian field. Similarly, the lithotype rule and facies were influential in the outcome, since these are directly coupled with the probability density function of both input fields. The shapes of the facies affect the resulting field in terms of the roughness of the structure, but this has not been explored systematically in the present work. A binary system produced realistic representations of the observed structure at both scales for the particulate materials considered in this study. It is worth noting that the current generative model can account for an arbitrary number of lithotype facies and is therefore applicable to a wide range of composite materials and physical phenomena.

The performance of the model was demonstrated through the simulation of a chloride diffusion test. The results showed that the model was able to accurately reproduce the experimental behaviour and showed the validity of a multi-level upscaling approach as an alternative to more computationally expensive methods such as FE2. Whilst in the present study the model is implemented in 2D, the approach can be readily extended to 3D. Even though there was agreement between the experimental and numerical results in this 2D idealisation, this extension would further improve the statistical representation of the generated structures at all scales and reduce the REV size.