1 Introduction

Understanding the complex response of materials at different scales can give insight into their overall behaviour, where often the micro-level dynamics have a large influence on the macro-level response. This is true for many mechanical or transport-based processes, which are often dependent on the geometry of the discrete structures seen at each level. One such process is thermal diffusion, where the thermal conductivity is a key consideration when employing materials in the built environment. For example, insulative properties of materials can significantly influence comfort and heating costs for individuals in surrounding areas. Similarly, it has been shown that the associated damage mechanisms of these heterogeneous materials originates from thermal-related micro- and meso-scale behaviour (Evans 1978), highlighting the need for accurate prediction at all scales of observation of effective material properties.

In the first instance, research focussed on the behaviour of heterogeneous solids through variational principles, such that upper and lower bounds could be computed for the effective material properties (Rosen and Hashin 1970; Hashin 1983; Gibiansky and Torquato 1997). An alternative approach was then taken, deriving closed-form expressions for said properties based on a solution of inclusions within an infinite medium (Noor and Shah 1993), but often relied on idealisation of the material geometry and system response. The use of asymptotic methods has been considered for determining the constitutive components of periodic microstructures (Auriault 1983). Originally being used to solve differential equations with periodic boundary conditions, the approach utilises an asymptotic expansion of a given unknown field such as temperature or displacement, and truncates the higher-order terms to give homogenised properties. Due to the significant advancement of computational resources, many approaches have been developed for numerical homogenisation (Ghosh and Liu 1995; Jiang et al. 2002), often using the finite element method (FEM) in conjunction with multi-level simulation (Özdemir et al. 2008; Rocha et al. 2021; Ricketts et al. 2023c). Macro-level models are fed information about the solution -calculated at various scales- such that the need for highly empirical relations is negated, and is seen in methods such as FE2 (Feyel and Chaboche 2000) and equation free modelling (Bindal et al. 2006; Tretiak et al. 2022). Typically, these are computationally expensive, as a boundary value problem (BVP) is solved at the micro-scale for each integration point in the macro-level domain. It is worth noting that methods have been developed to reduce this cost, such as neural network based surrogate models (Lefik et al. 2009; Ghavamian and Simone 2019; Rocha et al. 2020), and model order reduction techniques (Chaturantabut and Sorensen 2010; Kerfriden et al. 2011; Goury et al. 2016; Ghavamian et al. 2017).

The unifying factor in all the considered approaches is that a description of the micro-scale geometry is necessary in terms of a representative volume element, over which the homogenisation process is conducted. Generally, this is simplified in terms of the geometry, and is often not representative of the true complex microstructural geometry, which is known to impact the resulting effective properties. Whilst experimentally obtained scans -e.g. from micro-X-ray computed tomography- could be used as the BVP domain, these are often expensive to analyse in terms of time and computing resources (Le Houx et al. 2023). It would be advantageous to be able to generate these virtually at low computational cost. Many methods exist for generating virtual cementitious materials, such as the use of CEMHYD3D (Bentz 2006), aggregate placing methods (Zhang et al. 2018; Thilakarathna et al. 2020; Holla et al. 2021), machine learning alternatives (Cruz et al. 2016), with the most commonly used being HYMOSTRUC3D (van Breugel 1995; Patel et al. 2018a).

Plurigaussian simulation (PGS) is a lesser explored stochastic method for microstructural generation. It was first introduced by Galli et al. (1994), and developed further in the following years (Loc’h and Galli 1997; Dowd et al. 2003; Armstrong et al. 2014) for geological applications. The method is based on the truncation of Gaussian random fields (Matheron et al. 1987; Beucher and Renard 2016), but unlike the sequential relationship that the resulting field has between its phases, PGS can produce more complex connectivity between its phases in a non-sequential manner. This is determined by a prescribed lithotype rule, which controls the distinct geometry and proportions of the generated field, as well as the spatial relationship between facies (Doligez et al. 2011). The method commonly applied in representing field scale structures such as ore deposits or geologic formations (Betzhold and Roth 2000; Yunsel and Ersoy 2011; Renard and Beucher 2012; Talebi et al. 2013; Maleki and Emery 2014; Mery et al. 2017; Teles et al. 2023) and petroleum reservoirs (Chautru et al. 2015; Beucher and Renard 2016; Zagayevskiy and Deutsch 2016; Martinius et al. 2017; Madani et al. 2018), but has also been used at much smaller scales such as in the generation of the micro-structure of solid oxide cells (Abdallah et al. 2016), porous media (Méndez-Venegas and Díaz-Viera 2013), mineral microstructures (Teichmann et al. 2021), as well as concrete at various scales for the calculation of effective diffusion coefficients through a multi-level approach (Ricketts et al. 2023c).

In many asymptotic or computational homogenisation approaches, the micro-scale representative volume elements are assumed periodic. Thus, in this study, the PGS framework is extended to allow for the generation of periodic structures, being denoted as P-PGS. The highly flexible approach allows for the generation of many complex discrete geometries with minimal computational cost. A series of pore-scale representations of cement paste are generated based on experimental observations (Khan 2002; Liu et al. 2020; Stolarska and Strzałkowski 2020), and their effective thermal conductivities are calculated for dry and saturated pore conditions. Finally, these are compared against experimental values to assess the generated microstructures in being representative of the pore-scale geometry. Taking a numerical approach for material characterisation allows for a much wider description of the material to be attained much more quickly than the equivalent experimental process. The use of P-PGS enables the quantification of material properties based on a more closely fitting geometric representation than current solutions offer, such as pore network modelling (Van Marcke et al. 2010; Yang et al. 2019).

Here, the simulations are conducted in 2D, but it is noted that there is an intrinsic difference between 2D analyses and the 3D reality of pore-scale transport processes, being inherently three dimensional. Despite the potential for discrepancy in qualitative information, 2D representations have been employed as a step towards more complex 3D investigations, where this methodological choice is rooted in the current scope of the research. As will be seen in Sect. 4, the results correlate well with experimental data for thermal conductivity under both dry and saturated conditions, validating the robustness and relevance of the 2D approach within its acknowledged limitations. Whilst 3D analyses hold the promise of yielding quantitatively differing results, the approach is conceptually equivalent in 2D, and provides a basis for understanding transport phenomena at the pore-scale.

The layout for the remainder of the paper is as follows: Sect. 2 presents the theory of the PGS model, its extension to P-PGS, and the numerical homogenisation regime that is employed; Sect. 3 gives the numerical formulation of the finite element solution for heat transport through Poisson’s equation, as well as numerical details of the field generation; Sect. 4 presents the determination of the effective thermal conductivity for cement paste; and Sect. 5 highlights the main conclusions of the study.

2 Theoretical Basis

In the following, the PGS theory and the chosen numerical homogenisation scheme are given. The applied numerical approach will allow the effective thermal conductivity of cement paste to be calculated under steady state conditions. It is worth noting that this can also be done for the transient case, as well as for other material properties, but these will not be considered here. The method is versatile, suitable for thermal properties across various materials, and will be presented with this generality in mind. Similarly, the formulation relating to PGS and its periodic extension will be presented in \({\mathbb{R}}^{2}\). Whilst the method is not limited by dimensionality -being equally as applicable in \({\mathbb{R}}^{3}\), for instance- the cases that will be considered in later sections are in \({\mathbb{R}}^{2}\), hence, the formulation will be given in this space for consistency.

2.1 Periodic Plurigaussian Simulation

Let \(\left\{{Z}_{1},{Z}_{2}\right\}\) be a set of two independent random fields in \({\mathbb{R}}^{2}\), such that the random field \(\mathbf {Z}\) is defined as

$$\mathbf{Z}\left( \varvec{x} \right) = \left( {Z_{1} \left( \varvec{x} \right),Z_{2} \left( \varvec{x} \right)} \right), \forall \varvec{x} \in {\mathbb{R}}^{2}$$
(1)

Then, let \(L=\left\{{D}_{1},\dots ,{D}_{n}\right\}\) be a partition of \({\mathbb{R}}^{2}\) into \(n\) disjoint subdomains, such that the resulting random field \(\mathbf {P}\) with at most \(n\) distinct facies is defined as

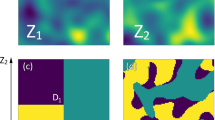
$$\mathbf{P}\left( \varvec{x} \right) = i \Leftrightarrow \mathbf{Z}\left( \varvec{x}{ }\right) \in D_{i} , \forall \varvec{x} \in {\mathbb{R}}^{2}$$
(2)

where \(i\) is the phase of \({D}_{i}\). The set \(L\) is the lithotype rule, and determines the number phases that could be present in the resulting field \(\mathbf{P}\), where each phase is related to a facie \({D}_{i}\). Figure 1d presents an example realisation of that is generated through PGS, where the random fields have a Gaussian kernel (a, b), and \(L\) consists of 3 quadrilateral facies (c).

Fig. 1
figure 1

Schematic of plurigaussian simulation where a, b are gaussian random fields, c is the lithotype rule consisting of 3 facies, and d is the resulting simulated field \(\mathbf{P}\)

Full size image

The covariance structure of the random fields \({Z}_{1},{Z}_{2}\) influences the general form of \(\mathbf{P}\), where here the smoothness of (a, b) result in a smooth field (d). Using a rougher covariance structure, such as the Matérn kernel, will result in a rougher realisation of \(\mathbf{P}\) (Ricketts et al. 2023c). The lithotype also allows control of the connectivity between phases in \(\mathbf{P}\). If two facies are not connected in \(L\), then the same will be true in \(\mathbf{P}\). This allows for complex structures to be represented based on careful choices of \(L\).

Similarly, to the use of non-stationary random fields in generating a non-stationary field of \(\mathbf{P}\), the extension to P-PGS relies on the generated fields \({Z}_{1},{Z}_{2}\) being periodic. For both \({Z}_{1}\) and \({Z}_{2}\), their values on opposing boundaries will be equal, such that they map to the same position in \(L\). If the generated random fields are now assumed periodic, denoted as \(\overline{{Z }_{1}}\), \(\overline{{Z }_{2}}\), the convolutional nature of the method ensures that the periodicity of \(\overline{{Z }_{1}}\), \(\overline{{Z }_{2}}\) enforces periodicity in \(\mathbf{P}\). This is illustrated in Fig. 2, where (a) depicts a more complex lithotype rule, (b) gives the resulting field \(\mathbf{P}\), and (c) illustrates a tiled version of \(\mathbf{P}\) to shows its periodicity.

Fig. 2
figure 2

An example of P-PGS where a is the lithotype rule, b is the resulting periodic field \(\mathbf{P}\), and c is a tiled illustration of \(\mathbf{P}\) to highlight its periodicity

Full size image

The extension to P-PGS was inspired by numerical homogenisation techniques. In many cases, the calculation of effective material properties is done numerically over domains which mimic the structures found at different levels of the material. Often, the microstructure of composite materials is assumed periodic in numerical homogenisation approaches (Andreassen and Andreasen 2014), hence, extending to P-PGS allows for greater flexibility in the usage of the generated structures, making it highly appropriate for multi-level material representation.

2.1.1 Random Field Generation

Random fields are a key component of PGS, where the covariance kernel of the input fields will dictate the characteristics of the resulting discrete field (Ricketts et al. 2023c). Gaussian random fields are a common choice due to their smooth behaviour making them suitable at representing many spatially varying parameters. Various methods exist to generate such fields, with the choice often being dictated by the computational efficiency of the method. Covariance matrix decomposition (CMD) is commonly adopted due to its simplicity and accuracy, in which a random field \(\mathbf{Z}\) can be computed as \(\mathbf{Z} = {\mathbf{LN}}\), where \(\mathbf{N}\) is a vector sampled from a standard normal distribution, \(\mathbf{L}\) is the decomposition matrix satisfying \({\mathbf{LL}}^{T} = A\), and \(A\) is the correlation matrix for all locations (Li et al. 2019). Cholesky- or eigen-decomposition is often used in the computation of \(\mathbf{L}\), and the choice of autocorrelation function to form \(A\) determines the covariance kernel of the resulting fields. Whilst this method is simple to employ, it suffers greatly in computational expense when considering larger problems (Tang et al. 2020). Alternatives such as the SPDE approach, Karhunen-Loève expansion, or spectral methods offer cheaper alternatives (Müller et al. 2022; Ricketts et al. 2023b). See Ricketts et al. (2023a) for a summary of methods as well as their computational complexity.

The approach for generating periodic random fields is less trivial. Recently, CMD has been employed using a modified squared exponential kernel, enforcing periodicity at opposing boundaries (González Acosta et al. 2023). The periodicity of the autocorrelation function matched the domain width, enforcing the same resulting field values at opposing boundaries. Due to the application, only horizontal periodicity was necessary, but this could be readily extended to all opposing boundaries. In this paper, an approach derived from Hu and Tonder (1992) is employed in generating periodic self-affine surfaces (Yastrebov et al. 2017). The method is based on filtering in the Fourier space of random noise such that a fractal surface is generated, and depending on the cut off frequencies in the Fourier space, the generated surfaces can be made Gaussian in nature. The advantages of having smooth Gaussian fields has already been highlighted, but this approach of variable roughness through the choice of cut-off frequencies allows for roughness to be introduced into the plurigaussian simulation method, leading to more flexibility in representing discrete rough geometries. For further details on the approach, see Yastrebov et al. (2015).

2.2 Numerical Homogenisation

Generally, numerical homogenisation approaches are used to conduct multi-scale analyses where the material response is computed by solving a boundary value problem (BVP) on a representative volume of the microstructure. This can be done for multiple scales, for example, macro- and micro-scales. The first step in this approach is to define a microstructural representative volume element (RVE) that represents the characteristics of the material in terms of its physical geometry. The RVE is used as the domain of the micro-scale BVP, and allows for the calculation of macroscopic quantities through a domain averaging scheme. Here, the RVE is generated through the appropriate use of P-PGS. In the following, the formulation of the thermal problem at both the macro and micro-scale -denoted with \(M\) and \(m\) respectively- as well as the scheme for micro to macro transition will be given.

The approach taken follows the work of Özdemir et al. (2008), where the principles of numerical homogenisation are extended to thermal problems based on the work of Kouznetsova et al. (2001) for stress analyses. The time dependency of heat storage is neglected at the micro-scale, such that steady-state thermal equilibrium is achieved as

$$\nabla_{m} \cdot \mathbf{q}_{{\text{m}}} \left( \varvec{x} \right) = 0$$
(3)

where \(\mathbf{q}_m\left(\varvec{x}\right)\) is the microscopic heat flux vector. The solution of (3) over the volume \(V\) of the RVE domain requires proper boundary conditions in terms of a prescribed temperature of heat flux normal to the boundary \(\Gamma\). At the macro-level, heat balance takes the form of

$$\left( {{\rho c}_{v} } \right)_{M} \dot{\theta }_{M} + \nabla_{M} \cdot \mathbf{q}_{{\text{M}}} = 0$$
(4)

where \({\left(\uprho {{\text{c}}}_{v}\right)}_{M}\) is the heat capacity, \(\theta\) is the temperature where the \(\dot{\theta }\) indicates the time derivative, and \(\mathbf{q}_{{\text{M}}}\) is the macroscopic flux. Again, this balance equation requires macro-level boundary conditions and additional initial conditions for its solution. In this study, numerical homogenisation is used to obtain the macroscopic flux from the solution over the micro-scale RVE. This is done such that the macroscopic effective thermal conductivity can be evaluated. As suggested by Eq. (3), the heat storage is neglected at the micro-scale. The same assumption is made at the macro-level, such that the steady-state solution can be computed. If a multi-level transient simulation was conducted, then this could be upscaled from the micro-level such that the heat capacity is preserved.

Using a multi-scale approach, the microscopic temperature profile \({\theta }_{m}\left({\varvec{x}}\right)\) for a position vector \({\varvec{x}}\) can be decomposed without loss of generality into a spatially linear mean field at the macro-level, and a fluctuation field \({\theta }_{f}\left({\varvec{x}}\right)\), where

$$\theta_{m} \left( \varvec{x} \right) = \theta_{m}^{k} + \nabla_{M} \theta_{M} \cdot \left( {\varvec{x} - \varvec{x}^{k} } \right) + \theta_{f} \left( \varvec{x} \right)$$
(5)

where \({\theta }_{m}^{k}\) is the temperature at an arbitrary point \({{\varvec{x}}}^{k}\) within the RVE (Özdemir et al. 2008). This can be seen as a perturbation of a mean macroscopic field that has fluctuations at the micro-scale due to material property variations in the RVE, in this case being the conductivity.

Heat conduction is driven by the temperature gradient that develops in the domain due to the applied boundary conditions. Thus, temperature gradients should be preserved in the transition between scales. As the temperature field is additively split into its micro and macro contributions as in Eq. (5), the volume averaged micro-scale temperature gradient can be written as

$$\frac{1}{V}\int\limits_{V} {\nabla_{{\text{m}}} \theta_{{\text{m}}} {\text{d}}V = \nabla_{{\text{M}}} \theta_{{\text{M}}} + \frac{1}{V}\int\limits_{\Gamma } {\theta_{f} \varvec{n}{\text{d}}\Gamma } }$$
(6)

where the Gauss divergence theorem is applied to the volume integral involving the fluctuation field to convert it to an integral over \(\Gamma\), the domain boundary, and \({\nabla }_{{\text{M}}}{\theta }_{{\text{M}}}\) is the gradient reflecting the thermal effects of macroscopic heat flow transferred through the boundary conditions to the RVE. The introduction of a scale transition to enforce the macroscopic temperature gradient to equal the volume average of its microscopic counterpart leads to the constraint

$$\int\limits_{\Gamma } {\theta_{{\text{f}}} \varvec{n}{\text{d}}\Gamma } = 0$$
(7)

and is satisfied by RVE boundary conditions to be defined.

The scale transition constraint (7) can be explicitly written as

$$\int\limits_{{\Gamma^{L} }} {\left\{ {\theta_{{\text{f}}}^{L} - \theta_{{\text{f}}}^{R} } \right\}\varvec{n}^{L} {\text{d}}\Gamma + \int\limits_{{\Gamma^{B} }} {\left\{ {\theta_{{\text{f}}}^{B} - \theta_{{\text{f}}}^{T} } \right\}\varvec{n}^{B} {\text{d}}\Gamma = 0} }$$
(8)

where \(L, R, B, T,\) represent the left, right, bottom and top boundaries of the microscopic RVE.

For Eqs. (7) and (8) to be true, the fluctuation field \({\theta }_{{\text{f}}}\) must equal zero. Thus, the fluctuation field is neglected from Eq. (5), and the macro and microscopic quantities can be formulated as

$$\theta_{{\text{m}}}^{R} - \theta_{{\text{m}}}^{L} = \nabla_{{\text{M}}} \theta_{{\text{M}}} \cdot \left( {\varvec{x}^{R} - \varvec{x}^{L} } \right)$$
(9)

and

$$\theta_{{\text{m}}}^{T} - \theta_{{\text{m}}}^{B} = \nabla_{{\text{M}}} \theta_{{\text{M}}} \cdot \left( {\varvec{x}^{T} - \varvec{x}^{B} } \right)$$
(10)

These relate to periodic boundary conditions which naturally enforce anti-periodic normal flux at the boundary due to the heat balance equation. It is noted that the use of periodic boundary conditions is purely mathematically motivated and does not imply geometric restrictions on the micro-scale domain. Their application has been seen to give better predictions when applied as opposed to uniform boundary conditions (Hazanov and Huet 1994; Hori and Nemat-Nasser 1999; Bouaoune et al. 2016; Tian et al. 2019).

The micro–macro scale transition can be achieved by first considering the second law of thermodynamics, which then leads to Fourier’s inequality

$$- \frac{1}{\theta }\nabla \theta \cdot \mathbf{q} \ge 0$$
(11)

being the entropy change due to heat conduction. Eliminating \(\theta\) from the denominator and enforcing consistent entropy change at both the macro- and micro-level results in

$$\frac{1}{V}\mathop \smallint \limits_{V} \nabla_{{\text{m}}} \theta_{{\text{m}}} \cdot \mathbf{q}_{{\text{m}}} {\text{d}}V = \nabla_{{\text{M}}} \theta_{{\text{M}}} \cdot \mathbf{q}_{{\text{M}}}$$
(12)

implying that the change in entropy due to heat conduction at the macro-level should be consistent with that at the micro-level. Thus, from Eqs. (6) and (7), the micro and macro flux fields can be associated through

$$\frac{1}{V}\mathop \smallint \limits_{V} \mathbf{q}_{{\text{m}}} {\text{d}}V = \mathbf{q}_{{\text{M}}}$$
(13)

showing that the volume averaged micro-scale heat flux is equivalent to the macroscopic heat flux.

3 Numerical Formulation

In the following, the numerical approach to solving the thermal problem at the micro-scale is presented, as well as details relating to the implementation of the P-PGS framework.

3.1 Finite Element Framework: Thermal Diffusion

As previously stated, numerical homogenisation is employed to calculate the effective thermal properties at the pore-scale of cement paste, specifically to attain the effective thermal conductivity of the medium. This is done through solving a BVP with appropriate boundary conditions and constitutive components over the RVE using the FEM. Before the solution process begins, the microstructures generated through P-PGS are read in as an image, and used to define material sub-domains that can be assigned distinct material properties, in this case being the different thermal conductivities of the medium.

The transfer of heat at the micro-scale is governed by nothing more than a description of diffusion governed by Poisson’s equation. There are many approaches to solving this, but here the standard variational form of the steady-state Poisson’s equation is employed and solved in FEniCS over the RVE (Logg et al. 2012). Periodic boundary conditions akin to those given in Eqs. (9) and (10) are enforced through the function space definition, such that the periodic fluctuation at the micro-scale is solved for directly. Following this, the solution can be averaged over the domain as in Eq. (13) to directly give the effective thermal conductivity of the medium at the macroscale.

The problem is given as

$$\begin{gathered} - \nabla \cdot \left( {k\left( {\nabla \theta_{M} + \nabla \theta_{m} } \right)} \right) = {\text{in}}\;\Omega \hfill \\ \theta_{{\text{m}}}^{R} - \theta_{{\text{m}}}^{L} = \nabla_{{\text{M}}} \theta_{{\text{M}}} \cdot \left( {\varvec{x}^{R} - \varvec{x}^{L} } \right){\text{on }}\Gamma_{LR} = \Gamma_{L} \cup \Gamma_{R} \hfill \\ \theta_{{\text{m}}}^{T} - \theta_{{\text{m}}}^{B} = \nabla_{{\text{M}}} \theta_{{\text{M}}} \cdot \left( {\varvec{x}^{T} - \varvec{x}^{B} } \right){\text{ on }}\Gamma_{TB} = \Gamma_{T} \cup \Gamma_{B} \hfill \\ \end{gathered}$$
(14)

where \(\Omega \in {\mathbb{R}}^{2}\) is the problem domain whose boundary \(\partial \Omega\) has periodic boundary conditions enforced between opposing boundaries, \(k\) is the thermal conductivity, and \(\theta_{m}\) is the periodic fluctuation in \(\Omega\). To compute the effective thermal conductivity \(k\), Fourier’s law \(k \cdot \nabla \theta_{{\text{M}}} = \mathbf{q}_{{\text{M}}}\) is employed, where \(\mathbf{q}_{{\text{M}}}\) is the macroscopic flux computed by taking the volume-average of the microscopic flux see Eq. 13 and \(\nabla \theta_{{\text{M}}}\) is the prescribed macroscopic temperature gradient as in Eq. (14).

The domain is discretised into linear Lagrangian triangular elements in a uniform grid, and can be posed as: find \({\theta }_{m}\in {H}^{1}\left(\Omega \right)\) such that

$$\mathop \smallint \limits_{\Omega } \nabla \hat{\theta }_{m} k \cdot \left( {\nabla \theta_{M} + \nabla \theta_{m} } \right){\text{d}}\Omega = \mathop \smallint \limits_{\Omega } \hat{\theta }_{m} f{\text{d}}\Omega , \, \forall \hat{\theta }_{m} \in H^{1} \left( \Omega \right)$$
(15)

where \({\widehat{\theta }}_{m}\) are the test functions. This is an ill-posed problem, so an additional constraint of zero-average of the fluctional field \({\theta }_{m}\) is applied through additional Lagrange multipliers \(\lambda\). The problem is then: find \(\left( {\theta_{m} ,\lambda } \right) \in H^{1} \left( \Omega \right) \times {\mathbb{R}}^{2}\) such that

$$\mathop \smallint \limits_{\Omega } \nabla \hat{\theta }_{m} k \cdot \left( {\nabla \theta_{M} + \nabla \theta_{m} } \right){\text{d}}\Omega + \mathop \smallint \limits_{\Omega } \lambda \cdot \hat{\theta }_{m} {\text{d}}\Omega + \mathop \smallint \limits_{\Omega } \hat{\lambda } \cdot \theta_{m} {\text{d}}\Omega = \mathop \smallint \limits_{\Omega } \hat{\theta }_{m} f{\text{d}}\Omega$$
(16)

\(\forall \left( {\hat{\theta }_{m} ,\hat{\lambda }} \right) \in H^{1} \left( \Omega \right) \times {\mathbb{R}}^{2}\). This can then be solved numerically by employing the Galerkin weighted residual approach for spatial discretisation. The conductivity tensor is employed in the weak form to represent the differing thermal conductivities of the sub-domains present in the generated microstructures. The domain is discretised such that each pixel contains two linear Lagrangian elements. A schematic to describe the overall process from is presented in Fig. 3, illustration the collection of material microstructural information, its representation using P-PGS, and the numerical homogenisation that occurs to compute the effective thermal conductivity.

Fig. 3
figure 3

Schematic of the process for computing the effective thermal conductivity of a given material (part of which is reused with permission after Lyu et al. 2019)

Full size image

It is noted that the contribution of convective heat transport is neglected in the boundary value problem. As the finite element method is flexible, other physical processes such as convection can be accounted for by including additional terms in the governing equations, and subsequent integrals in the weak form.

3.2 Field Generation

The PGS framework that was mentioned in Ricketts et al. (2023a, b, c) was extended to include the generation of periodic Gaussian random fields. A lithotype rule must first be defined, composed of facies of a given shape. In two dimensions, two periodic Gaussian random fields are generated to convolutionally map each position in the simulation domain to the lithotype rule to determined its phase. This pixel-wise evaluation is saved as an image to be read by the finite element model upon execution. For more details on the effects of lithotype facies, see Ricketts et al. (2023a, b, c).

4 Example Problem: Effective Thermal Properties of Mortar Paste

To assess the applicability of P-PGS in representing material microstructures, the effective thermal conductivity of cement paste was calculated based on the presented numerical homogenisation regime. Experimental measurements from the literature were collected to compare with the calculated values. Specifically data presented by Stolarska and Strzałkowski (2020) of the thermal parameters of mortars based on different water content (W/C) ratios and cement types, namely CEM I 42.5R, CEM II A-S 52.5N and CEM III A 42.5N are considered. Three samples at W/C ratios of 0.5, 0.55, and 0.6 were made for three different cement types with dimensions 25 × 25 × 6 cm. For each of the 9 samples, the thermal conductivity, volume-specific heat and thermal difussivity were analysed under different levels of saturation. Measurements from three consistent points on each sample were taken, such that all samples were measured a total of 9 times, with the mean value of each of the material properties for each sample being reported. The porosity was also evaluated through mercury intrusion porosimetry on two subsamples of each of the 9 samples, with dimensions 0.7 × 0.7 × 2 cm. Table 1 shows a summary of the measured results in terms of their total porosity and average thermal conductivity for each sample. These will be used directly to compare with the calculated equivalents.

Table 1 Summary of measured values of total porosity and average thermal conductivity (after Stolarska and Strzałkowski 2020)
Full size table

Whilst direct comparison of effective properties is possible, the geometric structure of the samples was not reported, making it challenging to represent through P-PGS. Due to this, the generated microstructures were based upon backscattered electron scanning electron microscope (SEM-BSE) images reported in Lyu et al. (2019) and seen in Fig. 4, where (a) is the raw image and (b) is the binarised equivalent.

Fig. 4
figure 4

BSE images of size 190  × 140 \(\upmu\)m for cement paste with a W/C ratio of 0.35 for a original image and b binary image. (reused with permission after Lyu et al. 2019)

Full size image

The covariance structure of the random fields as well as the lithotype rule used in P-PGS were chosen such that the porosity of the resulting fields matched well with the reported measurements in Table 1, as well as adhering to the geometry seen in Fig. 4. The selected lithotype appears as an off-centre and rotated ellipse, as illustrated in Fig. 5a. Ricketts et al. (2023a, b, c) observed that a central ellipse was an appropriate choice for generating cement paste pore-structures. In this case, the microstructures are less interconnected, and iterative testing suggested that shifting the ellipse from the lithotype's centre encouraged more disconnected structures in the final field. The domain size was chosen to be 100  × 100 \(\upmu\)m, where a sample realisation can be seen in Fig. 5b.

Fig. 5
figure 5

Illustration of a the employed lithotype, b generated pore-structure, and c is the tiled version to highlight the periodicity

Full size image

The periodicity is also highlighted in Fig. 5c, showing the connectivity between opposing boundaries. The low connectivity of the pore-structures is a result of the low porosities seen in Table 1. It has been shown that a porosity of 20% is a sufficient percolation threshold for good predictions of diffusivity in samples of W/C 0.3–0.5 (Patel et al. 2018b). This assumes a certain level of connectivity to allow for percolation, and as the generated porosities are below this threshold, it is fair to assume that they will be made up of larger disconnected pore structures. This is further suggetsed by Fig. 5b. To assess whether the generated microstructures are RVEs, the RVE size was calculated using the open-source image analysis python package PoreSpy (Gostick et al. 2019), where the domain will constitute an RVE once the quatity being analysed changes negligably with increasing domain size. As seen in Fig. 6 for a given generated structure, the porosity converges to a stable value, suggesting that the domain size used is suffient in representing the overall behaviour of the microstructure. It is worth noting that whilst the domain represents an RVE for porsitiy at this scale, this may not be true for other quantities of interest, but this was not determined.

Fig. 6
figure 6

RVE analysis of a generated pore-structure at 100  × 100 \(\upmu\)m highlighting convergence and that the RVE size is suitable

Full size image

In total, 250 microstructures of size 100  × 100 \(\upmu\)m were generated based on the reasoning above. For additional verification of the generated microstructures, their maximal pore-size was calculated and compared with experimental results. The calculation is based on assigning each pixel to be the value of the largest circle that overlaps it inside the pore, and was evaluated using PoreSpy (Gostick et al. 2019). This has been reported in the literature as \(\le \hspace{0.17em}\)9.47 \(\upmu\)m for W/C ratio of 0.3 (Lyu et al. 2019). Due to the stochasticity of the microstructural generation, around 10% of the resulting fields lay outside of the experimental range and were neglected. Similarly, the resulting volume fractions of the microstructures can vary. Those outside of the experimental porosity range of Table 1 (14–18%) were filtered out, leaving 152 images (see Fig. 7 for more examples). It is noted that even with further trial and error through changing the lithotype and input field parameters, the random nature of the approach means that it is often the case that some generated fields will be unsuitable. With such a constrained lithotype as in Fig. 5c, this is inevitable.

Fig. 7
figure 7

Samples of generated periodic pore-scale microstructures

Full size image

The diffusion of heat through the medium was simulated using the approach presented in Sect. 3.1, where material conductivities for the paste and pore phases were taken from the literature. The thermal conductivity of cement paste has been reported in the range of 2.48  \(\to \hspace{0.17em}\)3.43 W/mK for a porosity of 22.9 \(\to \hspace{0.17em}\)24.10% (Khan 2002). Similarly, the thermal conductivity of air filled pores and water filled pores has been reported as 0.026 and 0.607 W/mK respectively (Liu et al. 2020). The pore-space conductivities are taken directly as model input parameters depending on whether air or water filled pore conditions are being simulated. Here, the porosity of the generated microstructures is lower than porosity of the samples used to back calculate the reported thermal conductivity associated with the cement paste (Khan 2002), where the authors used Campbell-Allen and Thorne’s approach (Campbell-Allen and Thorne 1963). Similarly, it is assumed that the conductivity does not change between cement type, where in reality this could be the case. The material parameters of each phase used in the model are given in Table 2.

Table 2 Material parameters
Full size table

Figures 8 and 9 show the microscopic solution \({\theta }_{m}\) over \(\Omega\) for a given generated microstructure under the assumption of air and water filled pores respectively.

Fig. 8
figure 8

Microscopic solution of the microscale boundary value problem over a the cement paste and b the pore-space under air filled conditions

Full size image
Fig. 9
figure 9

Microscopic solution of the microscale boundary value problem over a the cement paste and b the pore-space under water filled conditions

Full size image

Table 3 shows the comparison between the experimental and numerical results of the effective thermal conductivities for both air and water filled conditions in terms of the mean, maximum and minimum thermal conductivities of all samples.

Table 3 Comparison of the experimental and calculated thermal conductivity for both air and water filled conditions
Full size table

It can be seen that the calculated mean values match well with the experimental observations for both conditions, suggesting that the generated microstructures are representative of these materials in terms of their geometry. A greater range of calculated thermal conductivities is seen numerically when compared with the experimental observations. Clearly, the evaluation of many more samples of varied porosities and pore structures will widen the range in which the calculated conductivities will lie. This enlarged range is most pronounced in the case of air filled pores, as seen in Fig. 10, due to the much larger ratio between the conductivity of the paste and pore phases.

Fig. 10
figure 10

Histograms of the calculated thermal conductivities

Full size image

The structure of the pores -as well as the overall porosity- will have a greater effect on the diffusive process, leading to more variability in the calculated effective properties as is seen in Table 3. Similarly, the maximum and minimum experimental values given in Table 3 are in fact the maximum and minimum of the mean samples values that were reported in Stolarska and Strzałkowski (2020). As the authors did not report the variability in the measurements of each sample, it is likely that the true maximum and minimum would differ from the given values.

5 Concluding Remarks

An extension of the plurigaussian simulation method has been presented, such that the generated structures are periodic in nature. The use of periodic random fields ensures periodicity in the resulting structures, a characteristic that is particularly important when calculating effective material properties. Heat diffusion was simulated at the pore-scale of cement paste, and numerical homogenisation employed to calculate its effective thermal conductivity. This was done to assess how representative the generated microstructures are of the pore-scale geometry. Strong agreement was obtained between the numerical and experimental observations, suggesting that P-PGS is appropriate for generating complex material microstructures. Using such an approach mitigates the reliance on empirical formulas and experimental calibration, reducing the cost and time associated with material testing or design. This computationally inexpensive method can generate complex structures in a stochastic manner, and is appropriate for material representation at all scales.

When considering a given material at different scales, numerous phases could be present. The presented approach is not limited to two phase materials as seen here, both in the microstructure or heat diffusion stage for computational homogenisation. P-PGS allows for an arbitrary number of phases to be represented by choosing a lithotype rule that contains information about all phases present in the material at a given scale, making it suitable for a wide range of material microstructures. The difficulty lies in choosing an appropriate lithotype as a given microstructure can be generated through many morphologically equivalent lithotypes. Investigation into this matter is on-going. The approach is also extendable to 3-D, where the calculated effective properties would be more sensitive to the complex pore geometries. Similarly, other processes could be modelled such as electrical diffusion and its associated properties, as well as transient solutions at differing scales.

Many approaches to numerical homogenisation or simulation over RVE BVPs employ idealised representations of the material geometry. Whilst for many cases this can be appropriate, the use of discrete geometrically consistent representations can lead to more accurate estimations of effective material properties and is something that P-PGS can provide.