1 Introduction

Now that the new activity of the 24th solar cycle has begun, it is a good time to discuss features of the whole solar minimum 23/24 (the minimum between cycles 23 and 24), which is a broadly investigated period because of its very peculiar nature (see, e.g., McComas et al. 2008; Smith and Balogh 2008; Gibson et al. 2011; Lee et al. 2011; Dikpati 2011). Fortunately, measurements of solar activity and solar wind parameters are today very effectively performed by a large number of world-wide operating ground-based observatories and space probes. The values of solar activity indices in the relatively long-lasting minimum 23/24 are appreciably different compared with previous solar minima. The Sun was extremely quiet and had almost no sunspots on its surface (e.g., Smith 2011). This unusually long and deep solar minimum has also been detected in a variety of other solar cycle indices, such as solar radio flux and total solar irradiance (e.g., Fröhlich 2009; Domingo et al. 2009). Simultaneously, the observations at the Wilcox Solar Observatory (WSO) reveal that the solar magnetic field is reduced across the whole surface of the Sun (Lee et al. 2011), and the polar fields are about half as strong as those observed during the previous minimum period (Hoeksema 2009). The mean value of the strength B of the interplanetary magnetic field (IMF) in the period of 2007 – 2009 was at a record-low level (≈ 2.5 nT) compared with previous minimum epochs (≈ 4 nT in 1985 – 1987 and ≈ 3.4 nT in 1995 – 1997). The reason for the decrease in IMF in this minimum 23/24 is still under discussion: it may be either due to less input from interplanetary coronal mass ejections (ICMEs; Owens et al. 2008) or a weaker input from the solar polar magnetic flux (Cliver and Ling 2011). Alternatively, Zhao and Fisk (2011) argued that the magnetic flux was the same in the two past minima, but the field strength was lower in this minimum 23/24 because it filled a larger area as a consequence of narrower streamer stalks. The consequences of these weaker solar magnetic fields were visible in changes of the solar wind plasma flow through the interplanetary medium. Observations near the Earth orbit during the end-phase of solar cycle 23 demonstrated that the IMF strength and solar wind density were about 30 % lower than in the minimum 22/23, and the momentum flux was about 38 % lower (Lee et al. 2011), whereas the solar wind speed remained unchanged compared with the previous solar minimum (Lee et al. 2009). At the same time, the Ulysses (Balogh et al. 1992; Bame et al. 1992) out-of-ecliptic observations show comparable changes throughout the heliosphere, namely a reduction in the radial magnetic field by about 64 %, of the dynamic pressure by about 22 %, and of the thermal pressure by about 25 % (Smith and Balogh 2008; McComas et al. 2008).

Generally, active regions on the Sun’s surface exhibit the latitudinal drift of the sunspot-generating zone in the course of the 11-year cycle (Carrington 1858), which leads to the butterfly diagram (Maunder 1904). It has been proposed that the extension of the meridional circulation and its speed determines the length of the solar cycle (Dikpati and Charbonneau 1999). Dikpati (2011) reported that the meridional circulation pattern behaved distinctly different during solar cycles 22 and 23. In particular, the Sun’s surface plasma flow was poleward all the way up to the pole and seemed to consist of one large flow cell that persisted during the major part of solar cycle 23. During solar cycle 22, however, the poleward surface flow ended at around 60∘ latitude, beyond which it became equator-ward and consisted of a two-cell flow pattern. Dikpati (2011) furthermore noted that the highest average flow speed at the surface was the same during solar cycles 22 and 23. Altrock (2010) showed that emission of active regions in the peculiar solar cycle 24 began in the same way as in previous cycles, although at a 40 % slower rate.

A comparison of observations from the first three orbits of Ulysses demonstrated that the 3-D structure of the solar wind varies dramatically during the solar cycle (see McComas et al. 2006). These authors suggested that this difference might be a regular feature of the full ≈ 22-year Hale cycle in considering the polarity changes of solar magnetic fields. Lario and Roelof (2007) reported that the long-lived and well-defined ≈ 26-day recurring intensity enhancement is observed in the minimum epoch of solar activity when A>0 (the north pole had positive polarity) during the first (1992 – 1994) southern excursion of Ulysses. In contrast to this, during the third (2005 – 2007) southern excursion of Ulysses, which also took place in low-activity conditions but when A<0, observations showed a more variable structure in the solar wind stream. Dunzlaff et al. (2008) suggested that this might be caused by the difference in the coronal hole structures between cycles 22 (1986 – 1996) and 23 (1996 – 2008); an extended, stable coronal hole structure was present during cycle 22, but not in cycle 23. The polar coronal hole disappeared during the declining phase of cycle 23 (Kirk et al. 2009) and a part of the coronal hole structure existed in the equatorial region (Abramenko et al. 2010).

The most probable source of the differences between solar cycles 22 and 23 is the dynamics of the Sun’s interior, which influences the generation and evolution of the Sun’s global magnetic fields through the dynamo process. Consequently, the modulation of Galactic cosmic rays (GCR) in solar cycles 22 and 23 has recently been explained by the differences in the evolution pattern of coronal holes connected with the dynamo-generated large-scale magnetic fields (Dikpati 2011). On the other hand, Zhao and Fisk (2011) reported that in the recent minimum 23/24 the fundamental physical process that accelerates the solar wind is unchanged and the global model for the behavior of the IMF remains valid.

The GCR intensity modulation in the minimum 23/24 is also a broadly investigated subject because of its very unusual character (e.g., Heber et al. 2009; McDonald, Webber, and Reames 2010; Schwadron et al. 2010). Recently, Paouris et al. (2012) studied the GCR modulation in the minimum 23/24 in relation to solar activity indices and heliospheric parameters, such as the sunspot number, the interplanetary magnetic field, the CME index, and the tilt angle of the heliospheric current sheet.

It is well-known that the diffusion coefficient K of GCR particles depends, among other parameters, on the magnitude B of the IMF as K∝1/B. Therefore, the unusually weak IMF in the minimum 23/24 should lead to a relatively high parallel diffusion coefficient, which naturally causes higher GCR intensities, which were observed by neutron monitors (e.g., Moraal and Stoker 2010) and space probes (e.g., Mewaldt et al. 2010) as well.

During solar minima, transient disturbances in the interplanetary space are infrequent and the regular IMF is well established. Therefore, it is relatively easy to distinguish the quasi-periodic variations caused by the Sun’s rotation. For the observer on the Earth the recurrence period of these variations (the synodic period) is about 27 – 28 days considering the differential rotation of the Sun near the equatorial regions.

The 27-day GCR intensity variations are generally caused by the (heliographic) longitudinal asymmetry of the electro-magnetic conditions in the heliosphere during one solar rotation. The variations are caused by the inhomogeneous distribution of active regions on the Sun’s surface and depend on the lifetime of this asymmetry in the interplanetary space (Dorman 1961). This topic, first announced by Forbush (1938), has been discussed extensively (for a review, see e.g., Richardson 2004).

Generally, higher harmonics of the 27-day GCR intensity variations (e.g., 14 and 9 days) are related to the simultaneous existence of several active longitudes (Alania and Shatashvili 1974). Particularly, the period of ≈ 14 days mainly originates from two groups of active regions that are roughly 180∘ apart in longitude. This second harmonics was studied in detail, e.g., by Mursula and Zieger (1996). Recently, Sabbah and Kudela (2011) presented the power spectra of GCR time series in the period range of T<27 days from measurements of neutron monitors and muon telescopes and discussed the connections between the higher harmonics, particularly the third harmonic (≈ 9 days), and the power spectra of the geomagnetic activity and interplanetary parameters.

In the recent minimum 23/24, the peculiarities in the 27-day recurring variations were clearly manifested in a variety of cosmic ray counts detected by neutron monitors (e.g., Alania, Modzelewska, and Wawrzynczak 2010) and space probes (e.g., Leske et al. 2011). The magnitude of the 27-day solar wind speed variations remains almost at the same level as in the previous minimum 22/23 (1995 – 1997), but the range of observed solar wind speed is more extended with the significant second (≈ 14 days) and third (≈ 9 days) harmonics (Modzelewska and Alania 2012). Recently, Modzelewska and Alania (2012) and Gil, Modzelewska, and Alania (2012) suggested that the peculiarities in the amplitude of the 27-day GCR intensity variations and their dependence on the Sun’s global magnetic field may be due to the large-scale structures of the solar wind speed and the IMF with their stable longitudinal asymmetries.

In this paper we will study the properties of the first (≈ 27 days), second (≈ 14 days), and third (≈ 9 days) harmonics of the 27-day GCR intensity variations,of the solar wind velocity in more detail, and also investigate IMF components in the minimum 23/24. Moreover, we study their synodic quasi-periodicity as it is connected to the Sun’s rotation and the powers of these quasi-periodic variations. Based on spectral and wavelet analysis methods, we investigate the temporal variations of the synodic periodicity in the selected solar wind parameters. By combining these with the analysis of GCR intensity variations, possible evidence for the onset of the new 24th solar cycle will be proposed.

2 Experimental Data

In the activity minimum, sunspots generally exist both in the lower latitudes that belong to the old cycle and in the middle latitudes that belong to the new cycle. Therefore, it is interesting to know how different latitudinal locations of the longitudinal asymmetry in sunspot distributions and the solar wind properties affect the quasi-periodic variations of the GCR intensity generated by the Sun’s differential rotation. For this purpose we studied the synodic periodicity (period T) connected to the Sun’s rotation and its power P in the GCR intensity and selected the corelated solar wind parameters with spectral and wavelet analysis methods.

To reveal the synodic period T in the GCR intensity connected to the Sun’s rotation, we analyzed the data obtained by the Kiel neutron monitor [ http://www.nmdb.eu ]. The solar wind velocity V and B x and the B y components of the IMF were taken from the OMNIWEB database [ http://omniweb.gsfc.nasa.gov/ow.html ]. These data cover the period of 2007 – 2009, corresponding to the 2367 – 2406 Bartel rotation (BR) periods.

To study the temporal evolution of the 27-day GCR intensity variations and similar quasi-periodic variations in other parameters, we divided the interval of 2007 – 2009 (2367 – 2406 BR periods) into three periods, I: BR 2367 – 2388, II: BR 2389 – 2395, and III: BR 2396 – 2406. This division is motivated by different character of the quasi-periodic variations of the GCR intensity; the 27-day GCR intensity variations are stable in period I, vanish in period II, and in period III they showed longer periods (T≈34 days). We then studied the temporal evolution of the first (≈ 27 days), second (≈ 14 days), and third (≈ 9 days) harmonics of the synodic periodicity (related to the Sun’s rotation) in the GCR intensity and solar wind parameters during the minimum 23/24 (2007 – 2009). Long-term changes in the GCR intensity variations caused by the solar rotation in the period 1953 – 1994 were studied in, e.g., Basilevskaya et al. (1995).

We derived the period T in the analyzed time series using the power spectrum density. This method decomposes the time series into components with different frequency (ω) or period (T) (e.g., Otnes and Enochson 1972; Press et al. 2002):

$$ \psi(\omega) = \int_{ - \infty }^{\infty } R(t) \mathrm{e}^{ - \mathrm{i}\omega t}\,\mathrm{d}t, \quad \omega = 2\pi f = \frac{2\pi}{T}, $$
(1)

where R(t) is the auto-correlation function. In a discrete case we have

$$ \psi(\omega) = \Delta t\sum_{r = - N}^{N} W \cdot R(r) \mathrm{e}^{ - \mathrm{i}\omega r\Delta t}, $$
(2)

where \(R(r) = \frac{1}{N - r}\sum_{i = 1}^{N - r} x_{i} x_{i + r}\) is the auto-correlation function and W is the window function (we used Parzen’s window function). The power P of each period/frequency was calculated as P=|ψ(ω)|2 Hz−1. To improve the statistical reliability, the frequency components were calculated based on the time series consisting of ten BR periods (270 days). The temporal changes of the recognized synodic periodicity were examined by removing and adding one BR period in the analyzed time series. To show the quasi-periodic character of the analyzed data, we fitted the time series with Fourier series truncated at order m with the least-squares method (e.g., Gubbins 2004):

$$ f(t) \approx a_{0} + \sum_{j = 1}^{m} \bigl(a_{j} \cos(j \cdot\omega t) + b_{j}\sin(j \cdot\omega t)\bigr),\quad m < \frac{N}{2}, $$
(3)

where

$$ a_{0} = \frac{1}{N}\sum_{i = 1}^{N} Y_{i},\qquad a_{j} = \frac{2}{N}\sum _{i = 1}^{N} Y_{i}\cos(j \cdot X_{i}),\qquad b_{j} = \frac{2}{N}\sum _{i = 1}^{N} Y_{i}\sin(j \cdot X_{i}). $$
(4)

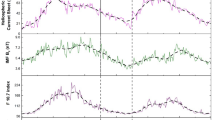
In the top panel of Figure 1a we show the temporal variations of daily GCR intensity measured by the Kiel neutron monitor, and the approximations by the sum of the first (27 days), second (14 days), and third (9 days) harmonics according to Equations (3) and (4). Similar plots are provided for the solar wind velocity V (Figure 1b) and B x (Figure 1c) and the B y (Figure 1d) components of the IMF. We did not consider contributions from the B z component in the magnitude \(B = \sqrt{B_{x}^{2} + B_{y}^{2} + B_{z}^{2}}\) of the IMF because of its low values. Indeed, for the considered period of 2007 – 2009 (2367 – 2406 BR), the average values are \(B_{z}^{2}=0.52~\mbox{nT}^{2}\), \(B_{x}^{2}=3.39~\mbox{nT}^{2}\), and \(B_{y}^{2}=3.64~\mbox{nT}^{2}\). Consequently, the contributions from the B z component are less than 10 % of those from the B x and B y components. Figures 1a – 1d clearly show the recurring variations of ≈ 27-day period in cosmic ray counts detected by neutron monitors and in the solar wind parameters.

Figure 1a
figure 1

Top panel: Temporal evolution of the daily GCR intensity in the recent solar minimum 23/24 measured by the Kiel neutron monitor (red dots connected by solid lines) and the approximation represented by the sum of the first (27 days), second (14 days), and third (9 days) harmonics (green dotted lines). Middle panel: Periods of GCR variations connected with the Sun’s rotation; the first harmonic (T≈27 days, red circles), the second harmonic (T≈14 days, green crosses), and the third harmonic (T≈9 days, blue squares). Bottom panel: Power P of the recognized periodicity; the first harmonic (red circles), the second harmonic (green crosses), and the third harmonic (blue squares). The vertical lines designate the boundaries of period I (BR 2367 – 2388), period II (BR 2389 – 2395), and period III (BR 2396 – 2406).

Full size image
Figure 1b
figure 2

The same as Figure 1a but for the solar wind velocity V.

Full size image
Figure 1c
figure 3

The same as Figure 1a but for the B x component of the IMF.

Full size image
Figure 1d
figure 4

The same as Figure 1a but for the B y component of the IMF.

Full size image

The middle panels of Figures 1b – 1d show that the synodic period T seen in the solar wind speed and components of the IMF is ≈ 26 – 27 days and is stable in the analyzed three periods. The solar wind parameters we used were obtained by the spacecraft located at the Lagrangian point L 1 and only reflect the wind conditions limited in the equatorial region of the heliosphere extending only up to ± 7∘ latitudes. Therefore, it is not possible to derive the direct relationship between the solar wind parameters at higher latitudes and the observed values around the equatorial region. On the other hand, the GCR intensity variations measured by neutron monitors reflect the conditions both in the limited local surroundings of the equatorial region and in the global 3-D heliosphere that also covers higher latitude regions.

Because of very peculiar behavior of the observed periodicity in the GCR intensity in periods II and III, we carried out more precise analyses with the time resolution of one day instead of 1 BR. For this we handled daily data series as follows: i) First of all, we used a power spectral analysis for the data series {x 1,x 2,…,x n }; to obtain reliable results the length of the data series was taken to be 270 days (consisting of 10 BR periods), as mentioned above. The period T of the component and its power P were computed with a 95 % confidence level. ii) Then we calculated the same parameters for the next series of data {x 2,x 3,…,x n+1}, i.e., we omitted the data of the beginning day and added one extra day to the time series, and period T and power P were calculated. This process was repeated, and we obtained T and P with a time resolution of one day.

We found that the synodic period T of the GCR intensity (middle panel in Figure 1a) remains almost constant, ≈ 26 – 27 days, which agrees well with similar changes in the solar wind velocity V and B x and the B y components of the IMF for period I. In period II the stability of the synodic periodicity is weakened; one can see a reduction in the power of the synodic periodicity. Finally, in the last part of period II and in period III, we observe a gradual increase in the period T from 26 – 27 days up to 33 – 36 days. These findings demonstrate that i) the 27-day GCR intensity variations take place in the 3-D space of the heliosphere, and ii) the sources of these variations must include contributions from active regions located at higher latitudes, which rotate slower than the equatorial region because of the differential rotation of the Sun.

The higher harmonics, namely the second (≈ 14 days) and third (≈ 9 days) harmonics of the synodic periodicity, are almost constant for all parameters during the entire investigated period. This means that the sources of these harmonics have stable (heliographic) longitudinal and latitudinal distributions. The bottom panels of Figures 1a –1d present the temporal evolution of powers P for the first (P 27), second (P 14), and third (P 9) harmonics of the 27-day GCR intensity variations, the solar wind velocity, and the components of the IMF. To illustrate this, we consider period I (BR 2367 – 2388). One can see the very large power of the quasi-periodic variations connected to the Sun’s rotation with different delay times. Namely, the maximum in power of the 27-day solar wind velocity variations (P 27(V)) is observed ≈ 3 – 4 BRs before that of the GCR intensity (P 27(GCR)). The maximum in power of the IMF components (P 27(B x ) and P 27(B y )) precedes that of the GCR intensity by ≈ 1 BR.

To consider whether the quasi-periodic changes in the solar wind velocity V and in the IMF components B x and B y are the causes of the similar GCR intensity variations (with different delay times), we computed the time delay, which maximizes the correlation coefficient r between the power of the 27-day GCR intensity variations (P 27(GCR)) and the same power of all analyzed parameters (P 27(V), P 27(B x ), and P 27(B y )). To study precisely the delay time among these parameters, we fixed the temporal changes of the GCR intensity and shifted all other parameters with respect to the GCR by delay times in units of BR. Table 1 shows the results; the highest correlation coefficients r are between GCR and V (r=0.92±0.05) with the delay time of 3 – 4 BR, between GCR and B x component of the IMF (r=0.94±0.04) with the delay time of ≈ 0 BR, and between GCR and B y component of the IMF (r=0.75±0.08) with the delay time of ≈ 1 BR.

Table 1 The correlation coefficients as a function of the delay time in BR between the powers of the 27-day GCR intensity variations (P 27(GCR)) and those of the solar wind velocity (P 27(V)) and the B x and B y components of the IMF (P 27(B x ), P 27(B y )).
Full size table

To study the temporal changes of the periodicity in GCR connected with the Sun’s rotation, we adopted the wavelet time-frequency spectrum technique. The wavelet technique is described in detail by Torrence and Compo (1998). We used the wavelet software available at the website [ http://paos.colorado.edu/research/wavelets/software.html ]. In our calculation we used the Morlet-wavelet mother function. In Figures 2a – 2c we present the wavelet analysis of the GCR intensity measured by the Kiel neutron monitor for periods I, II, and III. The results confirm that the 27-day GCR intensity variations were stable in period I (Figure 2a), disappeared in period II (Figure 2b), and in period III there was feeble indication of longer periods ≈ 32 – 35 days (Figure 2c).

Figure 2a
figure 5

Wavelet analysis of the GCR intensity measured by the Kiel neutron monitor for period I (BR 2367 – 2388).

Full size image
Figure 2b
figure 6

Wavelet analysis of the GCR intensity measured by the Kiel neutron monitor for period II (BR 2389 – 2395).

Full size image
Figure 2c
figure 7

Wavelet analysis of the GCR intensity measured by the Kiel neutron monitor for period III (BR 2396 – 2406).

Full size image

3 Theoretical Modeling

The main goal of this section is to compare theoretical predictions obtained from the numerical solutions to the transport equation with the experimental data of the GCR intensity measured by neutron monitors. We model the period of 2007 – 2008 corresponding to BR numbers 2367 – 2388 (period I considered in the previous section). This choice may be justified with the stable 27-day GCR intensity variations and similar quasi-periodic changes of the solar wind parameters and the IMF.

To investigate theoretically the 27-day GCR variations we used the steady-state, 3-D transport equation formulated by Parker (1965),

$$ \nabla_{i} \cdot\bigl( K_{ij}^{\mathrm{S}} \cdot \nabla_{j}f \bigr) - ( v_{\mathrm{d},i} + V_{i} ) \cdot \nabla_{j}f + \frac{1}{3}(\nabla_{i} \cdot V_{i})\frac{\partial f}{\partial \ln R} = 0 , $$
(5)

where f and R are the distribution function and the rigidity of cosmic ray particles, V i is the solar wind speed, v d,i is the drift velocity, and \(K_{ij}^{\mathrm{S}}\) is the symmetric part of the anisotropic diffusion tensor K ij . The drift velocity is modeled as \(\langle v_{\mathrm{d}, i}\rangle = \partial K_{_{ij}}^{\mathrm{A}} / \partial x_{j} \) (Jokipii, Levy, and Hubbard 1977), where \(K_{ij}^{\mathrm{A}}\) is the anti-symmetric part of the anisotropic diffusion tensor \((K_{ij} = K_{ij}^{\mathrm{S}} + K_{ij}^{\mathrm{A}})\) of the GCR particles.

We extended the model of our previous papers (Alania, Modzelewska, and Wawrzynczak 2010, 2011) and considered the Sun’s differential rotation as a simple kinematic indicator of the dynamo-generated solar magnetic field and the IMF. In this approach, the Sun’s differential rotation is expressed by the angular velocity Ω, which depends on the latitude as (Gibson, 1977)

$${\Omega}(\theta) = 1 - 0.3\cos^{2}\theta. $$

Based on the analysis of observed data of the GCR intensity, we ascribe its 27-day periodicity to the similar quasi-periodic changes (due to longitudinal asymmetry) of the solar wind velocity and the IMF. In our model we included in situ measurements of the solar wind velocity, and the corresponding components of the IMF were obtained by solving a system of Maxwell equations. The measured in situ radial speed was approximated by the first three terms of the Fourier series according to Equations (3) and (4) (Figure 3):

(6)

where φ is the heliographic longitude. Using Equation (6) for in situ measurements of the solar wind velocity, we solve the system of Maxwell equations,

figure a

where V is the solar wind velocity and B is the IMF. A complete description of our methodology of solving Maxwell equations with variable solar wind speed and implementating the solutions into Parker’s transport equation was presented in our previous papers (Alania, Modzelewska, and Wawrzynczak 2010, 2011).

Figure 3
figure 8

Temporal changes of the solar wind speed (points with error bars) in 2007 – 2008 corresponding to BR 2367 – 2388 (period I) The fitting with a Fourier series with three terms is shown superimposed (green dotted lines).

Full size image

Observations of solar wind parameters in the last minimum epoch of significantly low solar activity imply that the estimated parallel diffusion coefficient for the cosmic ray transport was considerably greater (e.g., Moraal and Stoker 2010; Mewaldt et al. 2010). Therefore, to obtain a better agreement between the theoretical model of the 27-day GCR intensity variations with the observed data for the last minimum epoch of solar activity (2007 – 2008), we increased the parallel diffusion coefficient by 40 % (κ ∥≈1.4×1023 cm2 s−1).

Recently it was demonstrated (Alania, Modzelewska, and Wawrzynczak 2011) that the modulation parameter ζ, which is proportional to the product of the solar wind velocity V and the strength B of the regular IMF (ζ∼VB), showed a remarkable negative correlation with the expected 27-day GCR intensity wave near solar minimum conditions. This is a hidden effect of the electric field in the cosmic ray transport, in general, for the convection-diffusion propagation of GCRs (Parker 1965; Gleeson and Axford 1967), and is also responsible for recurring changes of the GCR intensity. Therefore, it is natural to examine this relationship between the product VB and the GCR intensity based on the observational data and the theoretical model during the whole recent solar minimum 23/24.

In Figures 4a and 4b we present the changes of both the observed (Kiel neutron monitor, Figure 4a) and expected (Figure 4b) GCR intensity (dashed line) and the product VB (solid line) during an average solar rotation for the minimum 23/24 in 2007 – 2008. The results of theoretical modeling for the 27-day GCR intensity variations with differential rotation of the Sun agree well with the data of the Kiel neutron monitor. A remarkable negative correlation is also found between the product of VB and the 27-day GCR intensity wave, both in the theoretical model and in the observed data in 2007 – 2008. We confirm that an important role of the modulation effect, determined specifically by the product of the solar wind velocity V and the magnitude B of the IMF, is clearly manifested in the 27-day GCR intensity wave throughout the recent solar minimum 23/24.

Figure 4a
figure 9

Changes during one solar rotation in 2007 – 2008 corresponding to BR 2367 – 2388 (period I) of the observed GCR intensity at the Earth orbit (green dashed curve with crosses) and the product VB (blue solid curve with pluses).

Full size image
Figure 4b
figure 10

Same as Figure 4a but for the GCR intensity of effective rigidity ≈ 10 GV at the Earth orbit (green dashed curve) and the product VB (blue solid curve) expected from the model.

Full size image

Additionally, we separately investigated the correlation between the 27-day GCR intensity wave and the solar wind velocity V or the magnitude B of the IMF. One can see (Figures 5a and 5b) a very high negative correlation between the solar wind speed and the GCR intensity, both observationally (−78 %) and theoretically (−75 %). Between the IMF B and the GCR intensity (Figures 6a and 6b) this correlation is weaker (11 % observationally, −56 % theoretically). According to the theory of GCR modulation (Parker 1965; Gleeson and Axford 1967), the relationship between the product VB and the 27-day GCR intensity wave variations has an evident physical origin; this is a hidden effect of the electric field in the cosmic ray transport, as described above. Since V and B act together in this process, separating this effect into solely the solar wind speed V or the IMF B is impossible.

Figure 5a
figure 11

Same as Figure 4a but for the observed GCR intensity (green crosses) and the solar wind speed V (red pluses).

Full size image
Figure 5b
figure 12

Same as Figure 4b but for the GCR intensity of effective rigidity ≈10 GV at the Earth orbit (green dashed curve) and the solar wind speed V (red solid curve) expected from the model.

Full size image
Figure 6a
figure 13

Same as Figure 4a but for the observed GCR intensity at the Earth orbit (green crosses) and the magnitude B of the IMF (purple pluses).

Full size image
Figure 6b
figure 14

Same as Figure 4b but for the GCR intensity of effective rigidity ≈ 10 GV at the Earth orbit (green dashed curve) and the magnitude B of the IMF (purple dotted curve) expected from the model.

Full size image

4 Conclusions

  1. i)

    The quasi-periodic changes of the solar wind speed and IMF components related to the Sun’s rotation show a stable ≈ 26 – 27 day periodicity, which agrees well with the similar changes of the GCR intensity for period I (2007 – 2008, BR 2367 – 2388). However, there is some exception in the period of 2009, when the GCR intensity showed a gradual increase in the period from 26 – 27 days up to 33 – 36 days. We assign it to the formation nature of the 27-day GCR intensity variations, i.e., it takes place not only in the limited local surroundings of the equatorial region, but in the global 3-D space of the heliosphere, including higher latitude regions. The observations of solar wind parameters reflect only changes in the limited local surroundings in the equatorial region.

  2. ii)

    Results of theoretical modeling for the 27-day GCR variations with differential rotation of the Sun agree well with the observed data of the Kiel neutron monitor. We confirm that an important role of the modulation effect, determined specifically by the product (VB) of the solar wind velocity V and magnitude B of IMF, is clearly manifested in the 27-day GCR intensity wave in the recent solar minimum 23/24.