Introduction

In kinetic analysis of complex catalytic reactions, a task inherent to chemical reaction engineering, it is often important to determine the values of kinetic and thermodynamic parameters in a reliable way. Reaction kinetic data are used extensively in reactor design [1, 2]. While even simple power law expressions can sometimes be used in simulation of industrial reactors [3], such an approach has a limited insight into the reaction mechanism and can be applied only in a limited range of reaction conditions [4]. More complex reaction mechanisms, such as those usually referred to as Langmuir–Hinshelwood or Eley–Rideal [1] mechanisms assume quasi-equilibria of adsorption/desorption steps and certain rate determining steps. The Langmuir–Hinshelwood approach based typically on one or just few most abundant surface intermediates has clear limitations, even if it is useful for chemical reaction engineering and reactor modelling. An alternative approach is to consider in a more comprehensive way the elementary reactions on surfaces [5, 6], which exhibit either nonuniformity of active sites or lateral interactions of adsorbed species [7]. The theory of complex reactions developed by Horiuti and Temkin [8, 9] did not assume any rate determining step allowing derivation of rate equations for multistep reaction mechanisms, at least following linear sequences on ideal surfaces, i.e. reaction mechanisms with only linear steps [1]. Development of kinetic models for complex heterogeneous reactions and subsequent computer assisted modelling [10, 11] requires formulation of a hypothesis for the reaction mechanism, derivation of the rate equations and finally numerical data fitting along with identification of kinetic parameters. Obviously the statistical analysis of parameters [12] should include an analysis of how physically reasonable are the regressed parameters. Moreover, already in Refs. [10, 11] it was suggested that theoretically sound values of pre-exponential factors, activation energies, adsorption enthalpy and entropy, distribution functions for the number of actives sites with different heats of adsorption, Polanyi parameters for elementary steps, etc., should be introduced as an input to computer subroutines. A more refined methodology coined microkinetic modelling [4, 13,14,15,16], has become a widespread approach to incorporate the essential features of surface chemistry. For relatively simple cases, such as ammonia synthesis, based on the surface science data it is possible to describe the experimental observations without any fitting of the parameters.

Unfortunately, not all reaction intermediates as well as for example lateral interactions between them are accessible to experimental measurements or theoretical predictions [4]. Besides the often unknown effects of the coadsorbed species, application of model instead of real surfaces in density functional theory (DFT) calculations or an assumption of rapid diffusion in the adsorbed layer, also dynamic changes in the catalytically active phase during the reaction can lead to limitations in not only design of catalytic materials [4], but in reliable description of kinetic data as well. While microkinetic modelling per se aids in understanding the reaction mechanisms, it does not eliminate the need for numerical data fitting and statistical analysis of kinetic parameters. The reason is that kinetic and thermodynamic parameters of elementary surface reactions are estimated with a certain degree of precision and the calculated values of reaction rates or concentrations do not necessarily match theoretical predictions. For example, current DFT calculations of adsorption energies and activation energies can have ca. 20 kJ/mol uncertainties [17]

Microkinetic modelling can be used for catalyst design and explanation of reaction mechanisms, predicting the kinetic trends, however, a more rigorous reactor design should be based on an adequate description of experimental observations. An option of incorporating microkinetic analysis is to specify all variables except few using this approach and then apply nonlinear regression to estimate the unspecified parameters [18].

A standard tool in kinetic analysis is parameter estimation by nonlinear regression [12], which requires representative initial values resulting hopefully in parameter values with physical and statistical significance. One of the problems in kinetic analysis of heterogeneous catalytic reactions is that for either simplified models based on the Langmuir adsorption isotherms and most abundant surface intermediates, or for mechanisms based on the theory of complex reactions, the rate expressions contain kinetic and thermodynamic parameters both in the numerators and denominators. This leads to strong correlation between the parameters even if the experimental data are of high quality. Severe correlations between the parameters make them not reliable, also not allowing extrapolation beyond the experimental domain. In particular, there are often correlations between the activation energy and the frequency factors. The intrinsic parameter correlation problem in such kinetic models requires a sophisticated statistical approach, which will be addressed in the current work.

The Bayesian parameter estimation approach, contrary to conventional parameter estimation, addresses the probability of the values of parameters constructing posteriori distributions of the estimated parameter values. A more detailed account of the basic principles of the Bayesian statistics applied to kinetic modelling of chemical reactions is available in literature [17, 19, 20]. The approach is well-known in chemical kinetics as a tool of discrimination of kinetic models and identification of kinetic parameters [19].

While the Bayesian statistics can be used not only for parameter estimation, but also for the design of experiments [20], the current work is limited to statistical evaluation of parameters obtained by nonlinear regression using the Markov Chain Monte Carlo (MCMC) algorithm [21]. This method, incorporated in the modelling and optimization software ModEst [22], allows an evaluation of the reliability of the model parameters by treating all the uncertainties in the data and in the modelling as statistical distributions [23].

Hydrogenation of toluene to methylcyclohexane over nickel catalysts in gas [24] and liquid phases [25] was selected as an example. In the former case, the data were generated on a Ni/Al2O3 catalyst in a differential reactor operating at constant temperature between 150 and 200 °C and at atmospheric pressure, but varying systematically hydrogen and toluene partial pressures. For the liquid phase hydrogenation, performed in a shaker operating under high vibration frequency, the experimental data covered the temperature range between 160 and 200 °C and the pressure of hydrogen between 0.2 and 5 MPa. The models despite reflecting the same reaction are of different type allowing thus elucidation of the Bayesian approach to different kinetics.

Gas phase hydrogenation

Both gas and liquid phase hydrogenation of monoaromatics are very selective giving only the cyclic compound as a product. The reaction product of toluene hydrogenation is methylcyclohexane.

(1)

Mechanistic aspects of gas-phase toluene hydrogenation have been addressed in numerous publications [26,27,28,29]. For the purpose of this work, the same mechanistic Langmuir–Hinshelwood type model based on simultaneous competitive quasi-equilibrium adsorption of hydrogen and toluene on the catalyst surface as proposed in the original paper [24] will be used. Adsorption of hydrogen is considered to be dissociative, while adsorption of toluene is non-dissociative. Hydrogenation of toluene leads to methylcyclohexane, which was assumed to desorb rapidly from the surface.

The general form of the rate equation is [24]

$$r = \frac{{kK_{T} K_{H}^{Y/2} P_{T} P_{H}^{Y/2} }}{{(1 + K_{T} P_{T} + K_{H}^{1/2} P_{H}^{1/2} )^{Y + 1} }}$$
(2)

Here r is the reaction rate, k the reaction rate parameter and KT and KH are the respective adsorption equilibrium parameters for toluene and hydrogen, and PT and PH are the partial pressures of toluene and hydrogen. Y denotes the number of hydrogen atoms added simultaneously to adsorbed toluene molecule. Equation (2) can be rearranged to have less correlated parameters

$$r = \frac{{k^{\prime}_{1} P_{T} P_{H}^{Y/2} }}{{(1 + K_{T} P_{T} + K_{H}^{1/2} P_{H}^{1/2} )^{Y + 1} }}$$
(3)

Here k’ is the lumped parameter \(k^{\prime} = kK_{T} K_{H}^{Y/2}\). In order to improve the estimation statistics of temperature dependent parameters the reference temperature Tref is introduced [1]

$$k{^{\prime}}={k{^{\prime}}}_{ref}{e}^{\frac{{-E}_{a }z}{R}}$$
(4)

Here Ea is the activation energy of the hydrogenation reaction, while ΔHT and ΔHH are the adsorption enthalpies of toluene and hydrogen on the catalyst surface and z is

$$z=\left(\frac{1}{T}-\frac{1}{{T}_{ref}}\right)$$
(5)

This means that \({k{^{\prime}}}_{ref}\) is the rate constant at the reference temperature.

Estimation of parameters by nonlinear regression was done by ModEst modelling and parameter estimation software [22] using the Levenberg−Marquardt algorithm. Experimental data from a laboratory scale tubular reactor were used. Because of conversion levels, the differential reactor model was used. Reaction rates were determined directly from the experimental data. The goodness of the fit is reflected by the degree of explanation (R2), defined as the ratio of the squared difference in the experimental and the estimated values of reaction rates, and the square of the differences between the experimental and the mean of the estimated rates. The parameter estimation was done for the whole data sets at all partial pressures of reactants simultaneously by solving Eq. 3 for different parameter values. The residual sum of squares was used as the objective function in the parameter estimation.

The results presented in Table 1 and Fig. 1 clearly illustrate capability of the model to describe the experimental concentration dependencies in an excellent way. The errors of the parameters (Table 1) are, however, large implying that although the fit per se is adequate confirming the capability of the model to capture the reaction kinetics, there is still uncertainly about the statistical reliability of the parameters.

Table 1 Parameter values for the kinetic model represented by Eq. (3) for gas- phase hydrogenation of toluene [24] (Tmean = 171 °C)
Full size table
Fig. 1
figure 1

Comparison between experimental [24] and calculated (Eq. 3) values of rates (mol/kg/s) given as black dots for hydrogenation of toluene over a nickel catalyst. Degree of explanation R2 = 99%. Red dots represent simulations with parameters fixed after MCMC analysis (see explanation in the text)

Full size image

The Markov Chain Monte-Carlo analysis of the correlation between the parameters represented by the contour plots (Fig. 2) illustrates that some parameters exhibit a strong mutual correlation which is visible as elongated ovals (e.g. KT and , or KH and ).

Fig. 2
figure 2

Contour plots for all parameter combinations, 95% confidence regions with Monte Carlo simulated points

Full size image

The parameter was let floating during the statistical data fitting. From the mechanistic viewpoint its value of 1.93 is very close to two, which indicates an addition of a pair of hydrogen atoms or an adsorbed molecule. Setting = 2 the degree of explanation after the data fitting can be marginally improved to 99.2% also somewhat diminishing the errors (Table 2).

Table 2 Parameter values for the kinetic model represented by Eq. 3 for gas-phase hydrogenation of toluene [24] (Tmean = 171 °C) with \(\gamma = 2\)
Full size table

At the same time despite the estimated large errors for the rate constant and adsorption coefficient for dihydrogen, the MCMC analysis confirms that the parameters have well defined maxima (Fig. 3). It was thus interesting to compare the results of the data fitting using the simplex- Levenberg–Marquardt approach with the simulation when all parameters are fixed to their optimal values according to the MCMC analysis. Such comparison is presented in Fig. 1 illustrating just a small difference in the calculated rates. It should be noted that the interpretation of the parameter \(k_{ref}^{^{\prime}}\) (Fig. 3) might be too optimistic as the 2D posterior graphs (Fig. 2) show a sharp upper bound.

Fig. 3
figure 3

MCMC analysis of parameters (Table 2) determined by nonlinear regression. Y-axes correspond to posterior distributions for the parameters reflecting their probability while the parameters are shown in x axes. The most probable values of parameters are at maxima

Full size image

Liquid-phase hydrogenation

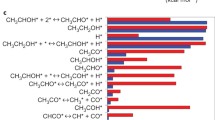
The liquid-phase hydrogenation of toluene will be considered as another example. The reaction kinetics was extensively investigated previously [25, 28, 30,31,32,33]. Taking into account kinetic regularities different from the gas-phase hydrogenation as well as thermodynamic considerations, the following scheme for hydrogenation of toluene (relevant for other aromatic compound) was proposed.

(6)

Here T is toluene, M is methylcyclohexane, Y is methylcyclohexene, TH2 and TH4 are intermediate complexes, step 3′ is rapid because hydrogenation of cycloalkenes is much faster than aromatic compounds and step 4 is at quasi-equilibrium. A similar approach has been was applied more lately for hydrogenation of substituted alkylbenzenes [34,35,36,37,38].

Derivation of the kinetic equation for this reaction system using the steady-state approximation is provided in the original publications [25, 31]. The same equation can be also derived from an expression for the four-step sequence is given in [39] considering irreversibility of step 3,

$$r = \frac{{\omega_{ + 1} \omega_{ + 2} \omega_{ + 3} \omega_{ + 4} }}{D}C_{cat}$$
(7)
$$\begin{gathered} D = \omega_{{ + 2}} \omega_{{ + 3}} \omega_{{ + 4}} + \, \omega_{{ - 1}} \omega_{{ + 3}} \omega_{{ + 4}} + \omega_{{ - 1}} \omega_{{ - 2}} \omega_{{ + 4}} + \omega_{{ + 1}} \omega_{{ + 2}} \omega_{{ + 3}} + \, \omega_{{ - 4}} \omega_{{ + 2}} \omega_{{ + 3}} + \hfill \\ \omega_{{ - 4}} \omega_{{ - 1}} \omega_{{ + 3}} + \omega_{{ - 4}} \omega_{{ - 1}} \omega_{{ - 2}} + \omega_{{ + 4}} \omega_{{ + 1}} \omega_{{ + 2}} + \, \omega_{{ + 3}} \omega_{{ + 4}} \omega_{{ + 1}} + \, \omega_{{ - 2}} \omega_{{ + 4}} \omega_{{ + 1}} \hfill \\ \end{gathered}$$
(8)

Here \(\omega_{i}\) are frequencies of steps [9]. Step 4 is at quasi-equilibrium, therefore the rates are rapid in both directions. Further simplifications of Eq. 7 by dividing the numerator and the denominator by \(\omega_{{ + 4}}\), neglecting subsequently the terms \(\omega_{{ + 1}} \omega_{{ + 2}} \omega_{{ + 3}} /\omega_{{ + 4}}\) and \(\omega_{{ - 3}} \omega_{{ + 1}} \omega_{{ + 2}} /\omega_{{ + 4}}\) and using the mole fractions of the liquid-phase components and the pressure of hydrogen instead of hydrogen concentrations in the liquid phase, result in the expression

$$r = \frac{{k^{\prime}_{ + 1} P_{{H_{2} }} k^{\prime}_{ + 2} P_{{H_{2} }} k_{ + 3} }}{{(k^{\prime}_{ + 2} P_{{H_{2} }} k_{ + 3} + \, k_{ - 1} k_{ + 3} + k_{{ - 1}} k_{{ - 2}} )\left(1 + \frac{{1 - N_{T} }}{{K_{{4}} N_{T} }}\right) + k^{\prime}_{ + 1} P_{{H_{2} }} k^{\prime}_{ + 2} P_{{H_{2} }} + k_{{ + 3}} k^{\prime}_{ + 1} P_{{H_{2} }} + \, k_{{ - 2}} k^{\prime}_{ + 1} P_{{H_{2} }} }}C_{cat}$$
(9)

Here \(K_{{4}} = k_{ + 4} /k_{ - 4}\); \(N_{T}\) is the mole fraction of the reactant with the initial value \(N_{T}^{o}\), and \(k^{\prime}_{ + 1} ;k^{\prime}_{ + 2}\) are modified rate constants reflecting the utilization of hydrogen pressure rather than hydrogen concentration in the liquid phase.

Equation (9) explains the observed kinetic regularities, such as the reaction order in hydrogen exceeding unity at low hydrogen partial pressures and zero orders in toluene and hydrogen at high pressures. This equation can be further rearranged resulting in the expression, which was used for parameter estimation

$$- \frac{{dN_{{}} }}{{(\frac{m}{n}dt)}} = \frac{{k^{\prime}_{ + 1} P_{{H_{2} }} k^{\prime}_{ + 2} P_{{H_{2} }} k_{ + 3} }}{{(k^{\prime}_{ + 2} P_{{H_{2} }} k_{ + 3} + \, k_{ - 1} k_{ + 3} + k_{{ - 1}} k_{{ - 2}} )\left(1 + \frac{{1 - N_{A} }}{{K_{{4}} N_{A} }}\right) + k^{\prime}_{ + 1} P_{{H_{2} }} k^{\prime}_{ + 2} P_{{H_{2} }} + k_{{ + 3}} k^{\prime}_{ + 1} P_{{H_{2} }} + \, k_{{ - 2}} k^{\prime}_{ + 1} P_{{H_{2} }} }}$$
(10)

While in Ref. [25] data fitting was done after linearization of Eq. (10), in the current study estimation of parameters by nonlinear regression was done using the same procedure as applied for the gas-phase hydrogenation for the whole set of experimental data generated at different temperatures and pressures. The results of calculations shown in Fig. 4 correspond to the goodness of the fit of 95.4%. The calculated values of parameters are shown in Table 3.

Fig. 4
figure 4

Comparison between experimental [25] and calculated values of mole fractions (Eq. 10) for hydrogenation of toluene over a nickel catalyst: a mole fractions as a function of modified time (m/n*t, where m in gram, n—in moles, t in h); b the parity plot between experimental and calculated values of mole fractions. Black dots correspond to simplex-Levenberg–Marquardt parameters obtained by numerical data fitting. Red dots—simulations with parameters fixed after MCMC analysis

Full size image
Table 3 Values of kinetic parameters for the model represented by Eq. (10) for the liquid-phase phase hydrogenation of toluene [25] on a nickel catalyst. First iteration
Full size table

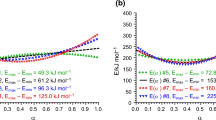
Similar to the gas-phase hydrogenation kinetics (Table 1) the errors of some parameters are (Table 3) rather large, therefore the Markov Chain Monte-Carlo (MCMC) analysis of the correlation between the parameters is needed to explore potential correlations between the parameters. The results displayed in Fig. 5 show apparent correlations for few parameters (e.g. k2 vs Ea2). MCMC analysis (Fig. 6) illustrates that some parameters have poor maxima while the others are much better identified.

Fig. 5
figure 5

Contour plots for all kinetic parameter combinations for hydrogenation of toluene over a nickel catalyst [25], 95% confidence regions with Monte Carlo simulated points

Full size image
Fig. 6
figure 6

MCMC analysis of parameters (Table 2) determined by nonlinear regression. First iteration

Full size image

For several parameters (e.g. \(k^{\prime}_{1}\), \(k^{\prime}_{2}\) or \(k_{ - 1}\) with very large errors of parameters exceeding 100%) the MCMC analysis illustrates that the values of parameters regressed during numerical data fitting do not exhibit too broad maxima, while other parameters (\(K_{{H_{2} }}\) and especially \(E_{a, - 2}\)) were not properly identified. The value of the activation energy for the second step in the forward direction is also probably too high.

As in the previous case of the gas-phase toluene hydrogenation, an interpretation of the values of constants should be done in combination with the 2D contour plots. Otherwise, a decrease in 1D plot can be just an artefact because 2D graphs show for example that a certain parameter hits an upper bound, set during numerical data fitting.

Considering that the stability of the aromatic ring is broken in the addition of the first hydrogen molecule (or pair of hydrogen atoms) it can be assumed that the activation barrier during the second addition is much lower in both directions. On the contrary, the activation energy for the third step cannot be neglected, because this step corresponding to the isomerization in the adsorbed layer of complex explains the zero order in both reactants (i.e. toluene and hydrogen) at high hydrogen pressures. With this assumption (\(E_{a,2} < < E_{a,1};\; E_{a, - 2} < < E_{a,1}\)) the goodness of the fit can be slightly improved giving the degree of explanation of 95.7%. The calculated values of parameters are shown in Table 4.

Table 4 Values of kinetic parameters for the model represented by Eq. (10) for the liquid-phase phase hydrogenation of toluene [25] over nickel. Second iteration assuming that \(E_{a,2} < < E_{a,1} ;E_{a, - 2} < < E_{a,1}\))
Full size table

As can be seen from Table 4 at least three parameters have very large errors. Interestingly enough the MCMC analysis (Fig. 7) gives a possibility first to elucidate the optimum values of these parameters and then to freeze them in the subsequent parameter estimation.

Fig. 7
figure 7

MCMC analysis of parameters (Table 4) with high errors

Full size image

The quality of the fit with the parameters in Fig. 7 fixed to the optimum values does not influence the degree of explanation making, the values, of constants more statistically reliable (Table 5) with a minimal correlation between parameters (Table 6). The run with all parameters fixed at the maxima of the posteriori distribution (Fig. 4) illustrates just a minor difference between the data fitting with simplex—Levenberg–Marquardt parameters and the simulation with the fixed MCMC optimal parameters.

Table 5 Values of kinetic parameters for the model represented by Eq. (10) for the liquid-phase phase hydrogenation of toluene [25] over nickel
Full size table
Table 6 The correlation matrix of the kinetic parameters (10) for the liquid-phase phase hydrogenation of toluene [25] over nickel
Full size table

Conclusions

Quite often in analysis of kinetic parameters by numerical data fitting the errors of parameters are becoming very large. Moreover, the structure of kinetic models often applied in heterogeneous catalysis inevitably leads to correlation between parameters present in both the numerator and th denominator. The Bayesian parameter estimation approach, which addresses the probabilities of the parameter values, was applied in the current work to the elucidate kinetics of the gas- and liquid phase hydrogenation of toluene on nickel catalysts. The Markov Chain Monte Carlo analysis was applied to parameters obtained by numerical data fitting allowing to determine the most probable values even for those parameters which exhibit large errors. The strategy utilized in the current study was to fix the values of such parameters at the optima and then repeat make the parameter estimation. For the investigated cases of toluene hydrogenation the overall description was the same while other parameters were even better identified.

The non-identification of a parameter should not be viewed, however, as a serious shortcoming of a particular numerical data fitting. For example, when the model simulations are not going to be extrapolated beyond the experimental conditions of the experiments, the value of such an unidentified parameter simply does not impact the simulations. Such a parameter value can be still restricted in the domain revealed by MCMC. Moreover, even if the unidentified parameters do have an impact on the model values in some extrapolated experimental conditions at either laboratory or industrial conditions, that still provides a hint on the domain of conditions where additional experiments should be conducted.

The approach used in this work can be suggested for the elucidation of kinetic parameters for complex heterogeneous catalytic reactions when the model structure leads to strong correlations between parameters.