Quantum teleportation through noisy channels with multi-qubit GHZ states

Abstract

We investigate two-party quantum teleportation through noisy channels for multi-qubit Greenberger–Horne–Zeilinger (GHZ) states and find which state loses less quantum information in the process. The dynamics of states is described by the master equation with the noisy channels that lead to the quantum channels to be mixed states. We analytically solve the Lindblad equation for $n$-qubit GHZ states $n\in \{4,5,6\}$ where Lindblad operators correspond to the Pauli matrices and describe the decoherence of states. Using the average fidelity, we show that 3GHZ state is more robust than $n$GHZ state under most noisy channels. However, $n$GHZ state preserves same quantum information with respect to Einstein–Podolsky–Rosen and 3GHZ states where the noise is in $x$ direction in which the fidelity remains unchanged. We explicitly show that Jung et al.’s conjecture (Phys Rev A 78:012312, 2008), namely “average fidelity with same-axis noisy channels is in general larger than average fidelity with different-axes noisy channels,” is not valid for 3GHZ and 4GHZ states.

Appendix

Here, we present quantum teleportation process through ($L_{2,x},L_{3,y},L_{4,z}$) noisy channel for 3GHZ state, which is not studied in Ref. [26]. For this case, the density matrix after $\delta t$ reads

$$\begin{aligned} \varepsilon (\rho _{3\mathrm{GHZ}})\Big |_{t=\delta t} = \frac{1}{2}{\left( \begin{array}{llllllll} 1 -2 \kappa \delta t &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1-4 \kappa \delta t \\ 0 &{} 0 &{} 0 &{} 0&{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} \kappa \delta t &{} 0 &{} 0 &{} -\kappa \delta t &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \kappa \delta t &{} \kappa \delta t &{} 0&{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \kappa \delta t &{} \kappa \delta t &{} 0&{} 0 &{} 0 \\ 0 &{} 0 &{} -\kappa \delta t &{} 0 &{} 0 &{} \kappa \delta t &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{} 0 \\ 1 -4 \kappa \delta t &{} 0 &{} 0 &{} 0 &{} 0 &{}0 &{} 0 &{} 1 -2 \kappa \delta t \end{array} \right) .} \end{aligned}$$

(61)

So, we examine the following ansatz

$$\begin{aligned} \varepsilon (\rho _{3\mathrm{GHZ}}) = \left( \begin{array}{llllllll} a &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} d \\ 0 &{} b&{} 0 &{} 0 &{} 0 &{} 0 &{} e &{} 0 \\ 0 &{} 0 &{} c &{} 0 &{} 0 &{} f &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} c &{} g &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} g &{} c &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} f &{} 0&{} 0 &{} c &{} 0 &{} 0 \\ 0 &{} e &{} 0 &{} 0&{} 0 &{} 0 &{} b &{} 0 \\ d &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0&{} a \end{array} \right) , \end{aligned}$$

(62)

which results in two sets of coupled equations

$$\begin{aligned} \left\{ \begin{array}{l} \dot{a}(t) = 2k\Big (c(t)-a(t)\Big ),\\ \dot{b}(t) = 2k\Big (c(t)-b(t)\Big ),\\ \dot{c}(t) = k\Big (a(t)+b(t)-2c(t)\Big ), \end{array}\right. \end{aligned}$$

(63)

and

$$\begin{aligned} \left\{ \begin{array}{l} \dot{d}(t) = k\Big (g(t)-4d(t)-f(t)\Big ),\\ \dot{e}(t) = k\Big (f(t)-4e(t)-g(t)\Big ),\\ \dot{f}(t) = k\Big (e(t)-d(t)-4f(t)\Big ),\\ \dot{g}(t) = k\Big (d(t)-e(t)-4g(t)\Big ), \end{array}\right. \end{aligned}$$

(64)

subject to $a(0)=d(0)=1/2$ and $b(0)=c(0)=e(0)=f(0)=g(0)=0$. The solutions are

$$\begin{aligned} \left\{ \begin{array}{l} a(t) =e^{2 \kappa t}d(t)=\frac{1}{8}\Big ( 1 + 2 e^{-2 \kappa t} + e^{-4 \kappa t}\Big ),\\ b(t) =-e^{2 \kappa t}e(t)=\frac{1}{8}\Big ( 1 -2 e^{-2 \kappa t} + e^{-4 \kappa t} \Big ),\\ c(t) =e^{2 \kappa t}g(t)=-e^{2 \kappa t}f(t)=\frac{1}{8}\Big ( 1 - e^{-4 \kappa t}\Big ). \end{array}\right. \end{aligned}$$

(65)

Using the unitary gate matrix which can be read off from Fig. 2 of Ref. [26], the fidelity, $F(\theta , \phi )$, and the average fidelity, $\overline{F}$, are given by

$$\begin{aligned} F(\theta , \phi ) = \frac{1}{2} \left[ 1 + e^{-2 \kappa t}\left( \cos ^2 \theta + \sin ^2 \theta \sin ^2 \phi \right) + e^{-4 \kappa t} \sin ^2 \theta \cos ^2 \phi \right] , \end{aligned}$$

(66)

and

$$\begin{aligned} \overline{F} = \frac{1}{6} \left( 3 + 2e^{-2 \kappa t}+ e^{-4 \kappa t} \right) . \end{aligned}$$

(67)

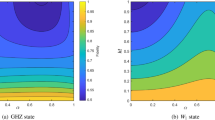
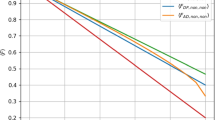
In Fig. 7, we depicted the average fidelity for 3GHZ state through various noises where the results for the same-axis and isotropic noises are given in Ref. [26]. Therefore, the average fidelity for ($L_{2,x},L_{3,y},L_{4,z}$) noise explicitly contradicts the conjecture proposed by Jung et al. [26].

Fig. 7

The plot of time dependence of average fidelity through noisy channels for 3GHZ state