Skip to main content
SpringerLink
Log in

Symmetric quantum fully homomorphic encryption with perfect security

  • Published:
Quantum Information Processing Aims and scope Submit manuscript

Abstract

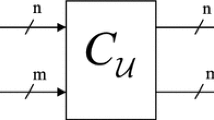
Suppose some data have been encrypted, can you compute with the data without decrypting them? This problem has been studied as homomorphic encryption and blind computing. We consider this problem in the context of quantum information processing, and present the definitions of quantum homomorphic encryption (QHE) and quantum fully homomorphic encryption (QFHE). Then, based on quantum one-time pad (QOTP), we construct a symmetric QFHE scheme, where the evaluate algorithm depends on the secret key. This scheme permits any unitary transformation on any \(n\)-qubit state that has been encrypted. Compared with classical homomorphic encryption, the QFHE scheme has perfect security. Finally, we also construct a QOTP-based symmetric QHE scheme, where the evaluate algorithm is independent of the secret key.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Rivest, R.L., Adleman, L., Dertouzos, M.L.: On data banks and privacy homomorphisms. Found. Secur. Comput. 4(11), 169 (1978)

    MathSciNet  Google Scholar 

  2. Feigenbaum, J.: Encrypting problem instances. Advances in cryptology. In: Proceedings of Crypto’85, p. 477. Springer, Berlin (1985)

  3. Abadi, M., Feigenbaum, J., Kilian, J.: On hiding information from an oracle. J. Comput. Syst. Sci. 39(1), 21 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  4. Brickell, E., Yacobi, Y.: On privacy homomorphisms. Advances in cryptology. In: Proceedings of Eurocrypt’87, p. 117. Springer, Berlin (1987)

  5. Gentry, C.: A fully homomorphic encryption scheme. PhD thesis, Stanford University (2009)

  6. Gentry, C.: Computing arbitrary functions of encrypted data. Commun. ACM 53(3), 97 (2010)

    Article  Google Scholar 

  7. Castelluccia, C., Chan, A.C., Mykletun, E., Tsudik, G.: Efficient and provably secure aggregation of encrypted data in wireless sensor networks. ACM Trans. Sens. Netw. 5(3), 20 (2009)

    Article  Google Scholar 

  8. Hessler, A., Kakumaru, T., Perrey, H., Westhoff, D.: Data obfuscation with network coding. Comput. Commun. 35(1), 48–61 (2012)

    Article  Google Scholar 

  9. Armknecht, F., Augot, D., Perret, L., Sadeghi, A.R.: On constructing homomorphic encryption schemes from coding theory. In: Chen, L.Q. (ed.) Cryptography and Coding. Springer, Berlin (2011)

    Google Scholar 

  10. Bennett, C.H., Brassard, G.: Quantum cryptography: public key distribution and coin tossing. In: Proceedings of IEEE International Conference on Computers, Systems, and Signal Processing, p. 175. IEEE, New York (1984)

  11. Ekert, A.K.: Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661 (1991)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  12. Tamaki, K., Koashi, M., Imoto, N.: Unconditionally secure key distribution based on two nonorthogonal states. Phys. Rev. Lett 90, 167904 (2003)

    Article  ADS  Google Scholar 

  13. Childs, A.M.: Secure assisted quantum computation. Quantum Inf. Comput. 5, 456 (2005)

    MATH  MathSciNet  Google Scholar 

  14. Arrighi, P., Salvail, L.: Blind quantum computation. Int. J. Quantum Inf. 4, 883 (2006)

    Article  MATH  Google Scholar 

  15. Aharonov, D., Ben-Or, M., Eban, E.: Interactive proofs for quantum computations. In: Proceeding of Innovation in Computer Science, p. 453. Tsinghua University Press, Beijing (2010)

  16. Broadbent, A.J., Fitzsimons, F., Kashefi, E.: Universal blind quantum computation. In: Proceedings of the 50th Annual IEEE Symposium on Foundations of Computer Science, p. 517. IEEE Computer Society, Los Alamitos (2009)

  17. Sueki, T., Koshiba, T., Morimae, T.: Ancilla-Driven Universal Blind Quantum Computation. Available via http://arxiv.org/abs/1210.7450

  18. Barz, S., Kashefi, E., Broadbent, A., Fitzsimons, J.F., Zeilinger, A., Walther, P.: Demonstration of blind quantum computing. Science 335, 303 (2012)

    Article  MathSciNet  ADS  Google Scholar 

  19. Vedral, V.: Moving beyond trust in quantum computing. Science 335(6066), 294 (2012)

    Article  MathSciNet  ADS  Google Scholar 

  20. Morimae, T., Fujii, K.: Blind topological measurement-based quantum computation. Nat. Commun. 3, 1036 (2012)

    Article  ADS  Google Scholar 

  21. Morimae, T.: Continuous-variable blind quantum computation. Phys. Rev. Lett. 109, 230502 (2012)

    Article  ADS  Google Scholar 

  22. Morimae, T., Dunjko, V., Kashefi, E.: Ground state blind quantum computation on AKLT state. Available via http://arxiv.org/abs/1009.3486

  23. Fitzsimons, J.F., Kashefi, E.: Unconditionally verifiable blind computation. Available via http://arxiv.org/abs/1203.5217

  24. Rohde, P.P., Fitzsimons, J.F., Gilchrist, A.: Quantum walks with encrypted data. Phys. Rev. Lett. 109(15), 150501 (2012)

    Article  ADS  Google Scholar 

  25. Giovannetti, V., Lloyd, S., Maccone, L.: Quantum private queries. Phys. Rev. Lett. 100(23), 230502 (2008)

    Article  MathSciNet  ADS  Google Scholar 

  26. Tseng, H.Y., Lin, J., Hwang, T.: New quantum private comparison protocol using EPR pairs. Quantum Inf. Process. 11(2), 373–384 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  27. Lin, S., Sun, Y., Liu, X.F., Yao, Z.Q.: Quantum private comparison protocol with d-dimensional Bell states. Quantum Inf. Process. 12(1), 559–568 (2013)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  28. Guo, F.Z., Gao, F., Qin, S.J., Zhang, J., Wen, Q.Y.: Quantum private comparison protocol based on entanglement swapping of d-level Bell states. Quantum Inf. Process. 12(3), 1–10 (2013)

    MathSciNet  Google Scholar 

  29. Li, Y.B., Qin, S.J., Yuan, Z., Huang, W., Sun, Y.: Quantum private comparison against decoherence noise. Quantum Inf. Process. 12(6), 2191–2205 (2013)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  30. Liu, B., Gao, F., Jia, H.Y., Huang, W., Zhang, W.W., Wen, Q.Y.: Efficient quantum private comparison employing single photons and collective detection. Quantum Inf. Process. 12(2), 887–897 (2013)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  31. Boykin, P.O., Roychowdhury, V.: Optimal encryption of quantum bits. Phys. Rev. A 67(4), 042317 (2003)

    Article  ADS  Google Scholar 

  32. Ambainis, A., Mosca, M., Tapp, A., Wolf, R.: Private quantum channels. In: Proceedings of the 41st IEEE Annual Symposium on Foundations of Computer Science, p. 547. IEEE Computer Society, Los Alamitos (2000)

  33. Nielsen, M., Chuang, I.: Quantum Computation and Quantum Information. Cambridge University Press, Cambridge (2000)

    MATH  Google Scholar 

  34. Liang, M., Yang, L.: Universal quantum circuit of near-trivial transformations. Sci. China-Phys. Mech. Astron. 54(10), 1819–1827 (2011)

    Article  MathSciNet  ADS  Google Scholar 

  35. Dupuis, F., Nielsen, J.B., Salvail, L.: Secure two-party quantum evaluation of unitaries against specious adversaries. Advances in cryptology. In: Proceedings of Crypto 2010, pp. 685–706. Springer, Berlin (2010)

  36. Dupuis, F., Nielsen, J.B., Salvail, L.: Actively secure two-party evaluation of any quantum operation. Advances in cryptology. In: Proceedings of Crypto 2012, pp. 794–811. Springer, Berlin (2012)

  37. Ambainis, A., Smith, A.: Small pseudo-random families of matrices: derandomizing approximate quantum encryption. In: Jansen, K., Khanna, S., Rolim, J.D.P., Ron, D. (eds.) Approximation, Randomization, and Combinatorial Optimization. Springer, Berlin (2004)

    Google Scholar 

  38. Liang, M., Yang, L.: Public-key encryption and authentication of quantum information. Sci. China-Phys. Mech. Astron. 55, 1618 (2012)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Data Communication Science and Technology Research Institute, Beijing, 100191, China

    Min Liang

Authors
  1. Min Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Min Liang.

Appendix

Appendix

This section lists some commutation rules about the operators \(X,Y,Z,H, CNOT, R_z(\theta ),R_y(\theta )\). Here, \(j,k,l,m\) are single-bit numbers.

$$\begin{aligned}&Z^kX^j=(-1)^{j\cdot k}X^jZ^k, \\&R_z(\theta )X^j=X^jR_z((-1)^j\theta ),\forall \theta \in [0,2\pi ),\\&R_y(\theta )X^j=X^jR_y((-1)^j\theta ),\forall \theta \in [0,2\pi ),\\&R_y(\theta )Z^k=Z^kR_y((-1)^k\theta ),\forall \theta \in [0,2\pi ),\\&R_y(\theta )H^j=H^jR_y((-1)^j\theta ),\forall \theta \in [0,2\pi ),\\&CNOT(X^j \otimes I)=(X^j \otimes X^j)CNOT, \\&CNOT(Z^k \otimes I)=(Z^k \otimes I)CNOT, \\&CNOT(I \otimes X^l)=(I \otimes X^l)CNOT, \\&CNOT(I \otimes Z^m)=(Z^m \otimes Z^m)CNOT. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Cite this article

Liang, M. Symmetric quantum fully homomorphic encryption with perfect security. Quantum Inf Process 12, 3675–3687 (2013). https://doi.org/10.1007/s11128-013-0626-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11128-013-0626-5

Keywords

Search

Navigation