Production analysis with asymmetric noise

Abstract

Symmetric noise is the prevailing assumption in production analysis, but it is often violated in practice. Not only does asymmetric noise cause least-squares models to be inefficient, it can hide important features of the data which may be useful to the firm/policymaker. Here, we outline how to introduce asymmetric noise into a production or cost framework as well as develop a model to introduce inefficiency into said models. We derive closed-form solutions for the convolution of the noise and inefficiency distributions, the log-likelihood function, and inefficiency, as well as show how to introduce determinants of heteroskedasticity, efficiency and skewness to allow for heterogenous results. We perform a Monte Carlo study and profile analysis to examine the finite sample performance of the proposed estimators. We outline R and Stata packages that we have developed and apply to three empirical applications to show how our methods lead to improved fit, explain features of the data hidden by assuming symmetry, and how our approach is still able to estimate efficiency scores when the least-squares model exhibits the well-known “wrong skewness” problem in production analysis. The proposed models are useful for modeling risk linked to the outcome variable by allowing error asymmetry with or without inefficiency.

1 Introduction

The usage of symmetric noise in econometric models engraves the assumption that a circumstance, choice, or behavior of an economic agent is ruled by the normal law where positive and negative deviations from the “trend” have the same effect on the outcome variable of an individual firm. There is substantial evidence across a wide array of fields to suggest that in practice, symmetry is not always a reasonable assumption (e.g., Genton 2004).

Asset Pricing: The probability distribution of asset returns is often skewed (Adcock 2007). When the distribution is asymmetric, the mean and variance are not sufficient statistics for investors to make optimal asset allocation decisions and ordinary least-squares (OLS) estimation is inefficient. Hence, authors have looked to methods that exploit the asymmetric nature of the data. For example, Adcock (20052010) employ multivariate skewed distributions to study the sensitivity of asset returns to return on the market portfolio. These methods extend the mean-variance methods for portfolio selection to mean-variance-skewness which can lead to improvements in performance.

Risk Management: A popular measure of an investment prospect is Value at Risk (VaR), which measures the risk of loss for investments. It is obtained by focusing on the the bottom tail of the returns distribution. For simplicity and convenience, it is often naively assumed that the distribution is symmetric. Assuming symmetry can vastly understestimate the risk being taken on by the investor. Exploiting the asymmetric nature of the data can lead to gains. For example, Goh et al. (2012) are able to outperform mean-variance approaches using half-space statistical information when asset returns are asymmetric.

Banking: Asymmetric shocks can severely impact banks. For example, managers may take on excess risk as a consequence of a principal agent problem. These low probability events emerge as large negative shocks. On the other side, deposits across large banks and savings institutions or within a single bank are highly positively skewed (Aubuchon and Wheelock 2010). In practice, the direction of the asymmetry may not be clear a priori.

Supply Shocks: Ball and Mankiw (1995) study the effects of supply shocks on inflation (i.e., shifts in the short-run Philips curve) based on relative price changes and frictions in nominal price adjustments. Price rigidities typically occur because of a sluggish price adjustment and costs associated with adjusting nominal prices. Firms typically adjust to large shocks, but not to small shocks and thus these large shocks have a disproportional impact on prices. The authors argue in favor of disproportionate effects of supply shocks on inflation and find that the inflation-skewness relationship is stronger than the inflation-variance relationship.

Interest Rate Parity: Louis et al. (1999) account for transaction costs in testing interest rate parity (IRP). They consider the relevant no-arbitrage conditions that in equilibrium are bounded in one direction. They argue that the assumption of symmetric noise in an IRP equation would result in inconsistency and therefore consider skewed composite errors (convolution of symmetric noise and one-sided error term) using stochastic frontier analysis. With this approach, they find that arbitrage margins are sometimes violated and hence there are possible arbitrage opportunities.

Educational Outcomes: There is a large literature estimating production functions using educational data (e.g., de Witte and López-Torres 2017, de Witte et al. 2010, Johnes et al. 2017, Ruggiero 1996, Thanassoulis et al. 201620172018, Thanssoulis 1999). Random shocks occur in education and some of these can be unpleasant or terrible events such as bullying, bereavement, unfair treatment, or an external event such as a school shooting. In practice, it is common to model these “shocks” as inputs in an educational production function (Ponzo 2013). Alternatively, we can allow for these large negative impacts on educational outcomes (Gershenson and Tekin 2018) to be treated as shocks. We no longer need to attribute such observations as outliers, because asymmetric noise distributions can potentially account for these unfortunate events.

Weather: Asymmetry in weather shocks also plays a role in production. Floodings, droughts, tornadoes and earthquakes are thought of as low probability events, but can result in huge damages. In agriculture, adverse events play an important role as they jeopardize the harvest. For example, Qi et al. (2015) use climactic variables as inputs in a stochastic production frontier of Wisconsin dairy farms. Modeling these events via asymmetric shocks may help determine potential losses which may prove useful for crop insurance premiums (Shaik 2013).

Measurement Error: Finally, one source of asymmetry could be measurement error. Consider the case where the output variable is measured with a one-sided error in a production function (or in a stochastic production frontier). This would produce the same type of behavior that we are attempting to model. For example, Millimet and Parmeter (2022) argue that one-sided measurement error is common for outcome variables used in political science as variables such as casualities are reported via governments which may have an incentive to skew their values.

1.1 Modeling asymmetry in production

If such asymmetries in preferences and behavior are not accounted for, we may estimate the wrong model that eventually leads to incorrect policy prescriptions. For example, the normality of the crop yield has long been rejected and was shown to be skewed, and ignoring this lead to overprediction of field crop yields (Day 1965). Profits can be driven by asymmetric capacities (Mao et al. 2019).

The main goal of this paper is to model production uncertainty by allowing for asymmetric noise in production analysis. The modeling of asymmetric noise is extremely rare in production economics.¹ We propose a set of models that introduce asymmetric noise in estimation of a production relationship in situations where a researcher believes that the production units may operate with or without efficiency.

1.2 Inefficiency

In empirical applications, firms or individuals are often assumed to operate with 100% efficiency. In neoclassical economics, firms and economic agents can exhibit inefficiency by being below their production possibilities. The conceptualization and formulation of inefficiency in production can be traced back to Koopmans (1951) and Afriat (1972).

In their seminal econometric papers, Aigner et al. (1977) and Meeusen and van den Broeck (1977) formulated stochastic frontier (SF) models, where inefficiency followed a half-normal and exponential distribution, respectively. Many extensions of these models exist and include other distributions for the unobserved inefficiency component. These include assuming the distribution of inefficiency to be truncated normal (Stevenson 1980), truncated normal with determinants (Kumbhakar et al. 1991), jointly estimated technical and allocative efficiency (Kumbhakar and Tsionas 2005), generalized exponential distribution of inefficiency (Papadopoulos 2021), semiparametric smooth coefficient framework (Yao et al. 2019), dealing with endogeneity (Amsler et al. 2016, Lai and Kumbhakar 2018, Lien et al. 2018) and modeled where noise can follow any (symmetric) law (Florens et al. 2020). Greene (2008) and Stead et al. (2019) discuss methodological advances in stochastic frontier modeling and especially distributional specifications. While in academic papers the convolution of the noise and inefficiency distributions are overwhelming skewed (Li 1996), each of these models assumes that the noise is term is symmetrically (overwhelmingly normally) distributed (Horrace and Parmeter 2018, Wheat et al. 2019).²

Here we will propose a SF model whereby the skewness of the composite error (convolution of noise and inefficiency) may have either sign. We formulate a composite error that is skew-normal for the noise and has a one-sided distribution for the inefficiency component. We are able to derive closed-form solutions for the convolution of the two distributions as well as the log-likelihood function and its gradients. Further, we derive closed-form solutions for the inefficiency estimates as well as discuss how to incorporate determinants of heteroskedasticity, efficiency and skewness to allow for heterogenous effects.

It turns out, with our approach, if we take the stance that “wrong skewness” is an empirical issue (e.g., Simar and Wilson 2009), we are still able to estimate efficiency scores when least-squares residuals are of the “wrong skewness” (Cho and Schmidt 2020, Olson et al. 1980).³ In this case, the SF model is inconsistent with the data and it is assumed that there is no inefficiency.

1.3 Finite sample performance

Obviously, all of our parameters are identified by the parametric assumptions on the model and the maximum likelihood principle, however, in practice, it can sometimes be difficult to estimate parameters via standard maximum likelihood techniques. This seems especially true when we have two forms of asymmetry and the sign of one of those is potentially unknown. To understand how our estimators perform in various scenarios and with various sample sizes, we conduct a Monte Carlo study and profile analysis. We obtain reliable estimates of the variance parameters in all scenarios and reliable estimates of our skewness parameter for sample sizes at or above above 200. In short, our study suggests that our estimators possess desirable finite sample properties.

1.4 Empirical performance

In order to see how asymmetric noise distributions perform in practice, we provide three empirical applications. The first application looks at risk behavior of U.S. Banks. We re-examine the cost function in Restrepo-Tobón and Kumbhakar (2014) both with and without assuming symmetric noise. Our metrics suggest that the SF model with skewed noise best fits the data. We further discover that the most risky banks (as determined by the standard deviation of return on assets) are more likely to be hit by negative shocks that have large negative effects on total costs.

In our second example, we look at an educational production function. Here we take the data collected by Gershenson and Tekin (2018) to see the impact the “Beltway Sniper” had on public school student math test scores in Virginia. As in the previous example, our SF model with asymmetric noise best fits the data. Here we find that skewness of the noise distribution is negative and is getting closer to 0 as a school is further away from a sniper attack. In other words, for those schools that are close to at least one sniper attack scene, they have a larger probability to exhibit poor academic performance.

In these first two examples, we demonstrate the performance of the proposed models applied to cost and production functions, respectively. We conclude that the model that takes the skewness of the noise distribution into account is superior to the model with symmetric noise. In both applications, we find that the most flexible model that allows (i) skewed noise where (ii) the parameters of its distribution vary across observations as well as (iii) inefficiency with observation-specific determinants performs best and provides the richest scope for interpretation. We expect that these methods will prove fruitful in uncovering previously ignored/misplaced information.

In our final example, we take data from the NBER-CES Manufacturing Industry Database (Bartelsman and Gray 1996) and examine the efficiency scores of 4-digit textile industries. For each year (1958–2011), we run separate cross-sectional regressions and report both the estimated skewness parameter and average efficiency score for each year. While most skewness estimates are near zero, many estimates are significantly above or below zero. In those years where the model has the “wrong skewness”, the conventional SF model predicts no inefficiency. This is found to be the case in about half of the cases. For our SF model, for those years, the average estimated efficiency scores are below unity.

1.5 Roadmap

The remainder of the paper is organized as follows: Section 2 summarizes the skew-normal distribution. Section 3 proposes to allow for skew-normal noise in a production or cost function as well as extends the model to allow for inefficiency. This section further examines the finite sample performance of our estimators and how to implement the procedures in both R and Stata with packages that we have created. Section 4 provides our empirical examples and the fifth section concludes. The appendices include our full set of derivations (Appendix A), extensions to truncated normal inefficiency (Appendix B), the results of the simulation study and profiling analysis (Appendix C) as well as R code to help replicate our empirical and simulation results (Appendix E).

2 Skew-normal distribution

In what follows, we employ a skew-normal (SN) noise distribution. While other distributions may be feasible or more general, we chose this skewed distribution for at least five reasons. First, it is a well studied skewed distribution with known properties and inferential aspects. Second, the standard model with normally distributed noise is a special case of the SN. Third, we are able to derive closed form solutions for many objects of interest. Fourth, it can be skewed in either direction and only requires one additional parameter to estimate.⁴ Finally, our analysis can be the basis for extensions to more complicated skew-elliptical distributions (Azzalini and Capitanio 2013, Genton 2004).

Formally, the SN distribution generalizes the normal distribution by allowing for non-zero skewness. The probability density function of the extended SN distribution with the skewness parameters α₀ and α₁, the location parameter $\xi \in {\mathbb{R}}$, and the variance ${\sigma }_{\omega }^{2}\, >\, 0$ is given by

$$g(\omega ;\xi ,{\sigma }_{\omega }^{2},{\alpha }_{0},{\alpha }_{1})=\frac{\phi \left(\frac{\omega -\xi }{{\sigma }_{\omega }}\right)\Phi \left({\alpha }_{0}+{\alpha }_{1}\left(\frac{\omega -\xi }{{\sigma }_{\omega }}\right)\right)}{\Phi \left(\frac{{\alpha }_{0}}{\sqrt{1+{\alpha }_{1}^{2}}}\right)},$$

where ϕ(⋅) and Φ(⋅) are the density and distribution functions of a standard normal distribution, respectively. We say that ω is skew-normally distributed: ω ~ SN(ξ, σ², α₀, α₁).

Azzalini (1985) proposes to set α₀ = 0 so the skewness is determined by a single parameter (α ≡ α₁).⁵ The density becomes

$$h(\omega ;\xi ,{\sigma }_{\omega }^{2},\alpha )=\frac{2}{{\sigma }_{\omega }}\phi \left(\frac{\omega -\xi }{{\sigma }_{\omega }}\right)\Phi \left(\alpha \frac{\omega -\xi }{{\sigma }_{\omega }}\right),$$

(1)

where the expected value of ω ~ SN(ξ, σ², α) is

$$E(\omega )=\xi +{\sigma }_{\omega }\sqrt{\frac{2}{\pi }}\frac{\alpha }{\sqrt{1+{\alpha }^{2}}}.$$

For the case where $E\left(\omega \right)=0$, the density in (1) can be concentrated in terms of ξ and can be written as

$$h\left(\omega ;\xi =0,{\sigma }_{\omega }^{2},\alpha \right)=\frac{2}{{\sigma }_{\omega }}\phi \left({\omega }_{rs}\right)\Phi \left(\alpha {\omega }_{rs}\right),$$

(2)

where the rescaled and shifted ω is given by

$${\omega }_{rs}=\frac{\omega }{{\sigma }_{\omega }}+\sqrt{\frac{2}{\pi }}\frac{\alpha }{\sqrt{1+{\alpha }^{2}}}.$$

The shape of the density is determined by the parameter α. The upper and lower panels of Fig. 1 show densities of a SN random variable for σ_ω = 0.1 and σ_ω = 5. The two plots differ only by the scale of the axes. Here we choose only to show negative values of the skewness parameter (α < 0). For positive values of α, the density is flipped symmetrically around 0. As the absolute value of α increases, the skewness of the distribution is increasing. For α = ∞, the skew normal distribution becomes the truncated normal (Horrace 2005a, b). Figure 1 suggests that the distribution is very skewed (i.e., approaches the truncated normal distribution) for an absolute value of α around 10.⁶

Fig. 1

pdf of the skew-normal random variable

3 Production model

In this section, we describe how to introduce an asymmetric noise distribution into a production framework. We then derive the results for this noise distribution in a stochastic frontier framework. More specifically, we derive closed form solutions for the convolution of the noise and inefficiency distributions, the log-likelihood function, and inefficiency, as well show how to introduce determinants of heteroskedasticity, efficiency and skewness to allow for heterogenous results. Finally, we discuss finite sample performance via a Monte Carlo and profile analysis as well as mention R and Stata packages that we have developed and will distribute so that our results may be replicated and for authors to use for their own studies.

Our production function can be written as

$$y=f({{{\boldsymbol{x}}}};{{{\boldsymbol{\beta }}}})+v,$$

(3)

where the outcome variable y is the logarithm of output for a stochastic production function (or the logarithm of cost for a stochastic cost function). $f\left({{{\boldsymbol{x}}}};{{{\boldsymbol{\beta }}}}\right)$ is a log-linear (in parameters) production or cost function with input row vector x (a constant, logarithms of the input variables and possibly other observed covariates that include environment variables that are not primary inputs, but nonetheless affect the outcome variable) and the finite parameter vector β (Sun et al. 2011).

We assume that the noise v is SN distributed with zero expectation, E(v) = 0,

$$v \sim SN\left(-{\sigma }_{v}\sqrt{\frac{2}{\pi }}\frac{\alpha }{\sqrt{1+{\alpha }^{2}}},{\sigma }_{v}^{2},\alpha \right)$$

with a probability density function (pdf) adopted from equation (2)

$${f}_{v}(v)=\frac{2}{{\sigma }_{v}}\phi \left(\frac{v}{{\sigma }_{v}}+\sqrt{\frac{2}{\pi }}\frac{\alpha }{\sqrt{1+{\alpha }^{2}}}\right)\Phi \left(\alpha \left[\frac{v}{{\sigma }_{v}}+\sqrt{\frac{2}{\pi }}\frac{\alpha }{\sqrt{1+{\alpha }^{2}}}\right]\right).$$

The log-likelihood function for a log-linear (in parameters) conditional expectation production (or cost) function with SN noise is given as

$$\begin{array}{l}\ln 2-\ln {\sigma }_{v}+\ln \left[\phi \left(\frac{y-f({{{\boldsymbol{x}}}};{{{\boldsymbol{\beta }}}})}{{\sigma }_{v}}+\sqrt{\frac{2}{\pi }}\frac{\alpha }{\sqrt{1+{\alpha }^{2}}}\right)\right]\\ \qquad\,+\,\ln \left[\Phi \left(\alpha \frac{y-f({{{\boldsymbol{x}}}};{{{\boldsymbol{\beta }}}})}{{\sigma }_{v}}+\sqrt{\frac{2}{\pi }}\frac{{\alpha }^{2}}{\sqrt{1+{\alpha }^{2}}}\right)\right]\end{array}$$

(4)

and the parameters can be estimated via maximum-likelihood (ML). Note that while least-squares estimation here is unbiased as it is equivalent to the quasi-maximum likelihood estimator under the assumption of normally distributed errors, it is no longer efficient (Yao and Zhao 2013).

Here we note the relationship of what we have just presented to the model originally proposed by Aigner et al. (1977), where the error term v in (3) is composed of a symmetric component that is normally distributed with a variance ς² and a non-negative technical inefficiency component that is half-normally distributed with variance τ². Replacing α in (4) by τ/ς and σ_v by $\sqrt{{\tau }^{2}+{\varsigma }^{2}}$ yields the likelihood function for the model proposed by Aigner et al. (1977) (see equation (13.2) in Domínguez-Molina et al. 2004 as well as the discussion in Badunenko and Kumbhakar 2016). In other words, the popular SF model can be seen as a special case of the model considered in (3). The inferential aspects of this special case were studied in Badunenko et al. (2012).

With the exception of Li (1996), SF models employ asymmetric compound noise. However, those models assume that the asymmetry that is present in the composite error term is due to existing technical inefficiencies. We propose a set of models where we split the asymmetry/skewness into components attributable to uncertainty (skewed noise) and technical inefficiency (non-negative error part). We show that they can be separated. In what follows, we present a more general model, where inefficiency exists and the noise can be skewed.

3.1 Production model with inefficiency

In the presence of inefficiency, (3) becomes

$$y=f({{{\boldsymbol{x}}}};{{{\boldsymbol{\beta }}}})+v-{\mathsf{p}}u=f({{{\boldsymbol{x}}}};{{{\boldsymbol{\beta }}}})+\epsilon ,$$

(5)

where, analogous to before, the outcome variable y is the logarithm of output for a stochastic production frontier model or the logarithm of cost for a stochastic cost frontier model, x is the row vector of a constant, logarithms of the input variables and possibly other observed covariates that include environment variables that are not primary inputs but nonetheless affect the outcome variable. To present this in a general setting, we introduce the known value p, which signifies either a production or cost function:

$${\mathsf{p}}=\left\{\begin{array}{ll}1\quad &\,{{\mbox{for a stochastic production frontier model}}}\,\\ -1\quad &\,{{\mbox{for a stochastic cost frontier model}}}\,.\end{array}\right.$$

We assume that the noise v is SN distributed with a zero expectation, E(v) = 0,

$$v \sim SN\left(-{\sigma }_{v}\sqrt{\frac{2}{\pi }}\frac{\alpha }{\sqrt{1+{\alpha }^{2}}},{\sigma }_{v}^{2},\alpha \right)$$

with a pdf adopted from equation (2)

$${f}_{v}(v)=\frac{2}{{\sigma }_{v}}\phi \left(\frac{v}{{\sigma }_{v}}+\sqrt{\frac{2}{\pi }}\frac{\alpha }{\sqrt{1+{\alpha }^{2}}}\right)\Phi \left(\alpha \left[\frac{v}{{\sigma }_{v}}+\sqrt{\frac{2}{\pi }}\frac{\alpha }{\sqrt{1+{\alpha }^{2}}}\right]\right).$$

We assume that the inefficiency term is exponentially distributed (Jradi et al. 2021), so its density is given by

$${f}_{u}(u)=\lambda \exp (-\lambda u),$$

where $\lambda =\frac{1}{{\sigma }_{u}}$.⁷ Denoting ${\xi }_{v}=-{\sigma }_{v}\sqrt{\frac{2}{\pi }}\frac{\alpha }{\sqrt{1+{\alpha }^{2}}}$ and noting from equation (5) that ϵ = v − pu, and v − ξ_v = ϵ + pu − ξ_v = ϵ_r + pu, where ϵ_r = ϵ − ξ_v, the joint density of u and ϵ is given by

$$\begin{array}{rcl}f(\epsilon ,u)&=&\underbrace{\frac{2}{{\sigma }_{v}\frac{1}{\sqrt{2\pi }}\exp \left[-\frac{1}{2}{\left(\frac{{\epsilon }_{r}+{{\rm{p}}}u}{{\sigma }_{v}}\right)}^{2}\right]\Phi \left(\alpha \frac{{\epsilon }_{r}+{\rm{p}}u}{{\sigma }_{v}}\right)}}_{\begin{array}{c}{f}_{v}(v)\end{array}}\underbrace{\lambda \exp \left(-\lambda u\right)}_{\begin{array}{c}{f}_{u}(u)\end{array}}\\ &=&\frac{2\lambda }{{\sigma }_{v}}\frac{1}{\sqrt{2\pi }}\Phi \left(\alpha \frac{{\epsilon }_{r}+{\rm{p}}u}{{\sigma }_{v}}\right)\exp \left[-\frac{1}{2}\left\{{\left(\frac{{\epsilon }_{r}+{\rm{p}}u}{{\sigma }_{v}}\right)}^{2}+2\lambda u\right\}\right].\end{array}$$

(6)

3.1.1 Convolution of the skew normal and exponential distributions

The marginal density of ϵ is obtained by integrating u out of f(ϵ, u), noting that u ≥ 0 (i.e., $f(\epsilon )=\int\nolimits_{0}^{\infty }f(\epsilon ,u)du$). To do so, we first rewrite equation (6) as

$$f(\epsilon ,u)=\frac{2\lambda }{{\sigma }_{v}}\exp \left({\mathsf{p}}{\epsilon }_{r}\lambda +\frac{{\lambda }^{2}{\sigma }_{v}^{2}}{2}\right)\phi \left(\frac{u+{\mathsf{p}}{\epsilon }_{r}+\lambda {\sigma }_{v}^{2}}{{\sigma }_{v}}\right)\Phi \left(\alpha \frac{{\epsilon }_{r}+{\mathsf{p}}u}{{\sigma }_{v}}\right).$$

Then,

$$\begin{array}{rcl}f(\epsilon )&=&\int\nolimits_{0}^{\infty }f(\epsilon ,u)du\\ &=&\int\nolimits_{0}^{\infty }\frac{2\lambda }{{\sigma }_{v}}\exp \left({\mathrm{p}}{\epsilon }_{r}\lambda +\frac{{\lambda }^{2}{\sigma }_{v}^{2}}{2}\right)\phi \left(\frac{u\,+\,{\mathrm{p}}{\epsilon }_{r}\,+\,\lambda {\sigma }_{v}^{2}}{{\sigma }_{v}}\right)\Phi \left(\alpha \frac{{\epsilon }_{r}\,+\,{\mathrm{p}}u}{{\sigma }_{v}}\right)du\\ &=&\frac{2\lambda }{{\sigma }_{v}}\exp \left({\mathrm{p}}{\epsilon }_{r}\lambda +\frac{{\lambda }^{2}{\sigma }_{v}^{2}}{2}\right)\int\nolimits_{0}^{\infty }\phi \left(\frac{u\,+\,{\mathrm{p}}{\epsilon }_{r}\,+\,\lambda {\sigma }_{v}^{2}}{{\sigma }_{v}}\right)\Phi \left(\alpha \frac{{\epsilon }_{r}\,+\,{\mathrm{p}}u}{{\sigma }_{v}}\right)du.\end{array}$$

The integral

$$\int\nolimits_{0}^{\infty }\phi \left(\frac{u+{\mathrm{p}}{\epsilon }_{r}+\lambda {\sigma }_{v}^{2}}{{\sigma }_{v}}\right)\Phi \left(\alpha \frac{{\epsilon }_{r}+{\mathrm{p}}u}{{\sigma }_{v}}\right)du$$

(7)

can be obtained in a closed form using Owen’s T-function (see Owen 19561980). The details of the derivation are given in Appendix A. Denote the solution to (7) as ${{{\mathcal{A}}}}$:

$$\begin{array}{rcl}{{{\mathcal{A}}}}&=&-T\left({u}_{1},\frac{{a}_{2}}{{u}_{1}}\right)-T\left({a}_{2},\frac{{u}_{1}}{{a}_{2}}\right)+T\left({u}_{1},b+\frac{a}{{u}_{1}}\right)\\ &&+T\left({a}_{2},b+\frac{{u}_{1}(1+{b}^{2})}{a}\right)+\Phi \left({a}_{2}\right)\Phi \left(-{u}_{1}\right),\end{array}$$

(8)

where a = − αpλσ_v, b = αp, ${a}_{2}=a/\sqrt{1+{b}^{2}},{u}_{1}={\mathrm{p}}{\epsilon }_{r}/{\sigma }_{v}+\lambda {\sigma }_{v}$ and

$$T(h,a)=\frac{1}{2\pi }\int\nolimits_{0}^{a}\frac{\exp \left[-0.5{h}^{2}\left(1+{t}^{2}\right)\right]}{1+{t}^{2}}dt.$$

Then the marginal density can be given in closed form as

$$f(\epsilon )=2\lambda \exp \left({\mathsf{p}}{\epsilon }_{r}\lambda +\frac{{\lambda }^{2}{\sigma }_{v}^{2}}{2}\right){{{\mathcal{A}}}},$$

(9)

where examples of this probability density function for a few choices of the three parameters σ_v, α and σ_u are shown in Fig. 2.

Fig. 2

pdf of the convolution of skew-normal and exponential random variables, ϵ = v − pu, where p = −1

Given the above information, the log-likelihood based on (9) is

$$\ln \left(2\lambda \right)+{\mathsf{p}}{\epsilon }_{r}\lambda +\frac{{\lambda }^{2}{\sigma }_{v}^{2}}{2}+\ln {{{\mathcal{A}}}}.$$

(10)

The full derivation, as well as the gradients of this log-likelihood function, which are useful for programming purposes, can be found in Appendix A.

3.1.2 Efficiency estimation

To obtain observation-specific estimates of inefficiency (u), we follow Jondrow et al. (1982) and first obtain the conditional distribution of u given ϵ:

$$\begin{array}{ll}f(u| \epsilon )\,=\,\frac{f(u,\epsilon )}{f(\epsilon )}\\ \quad\qquad\,=\,\frac{\frac{2\lambda }{{\sigma }_{v}}\exp \left({\mathrm{p}}{\epsilon }_{r}\lambda \,+\,\frac{{\lambda }^{2}{\sigma }_{v}^{2}}{2}\right)\phi \left(\frac{u\,+\,{\mathrm{p}}{\epsilon }_{r}\,+\,\lambda {\sigma }_{v}^{2}}{{\sigma }_{v}}\right)\Phi \left(\alpha \frac{{\epsilon }_{r}\,+\,{\mathrm{p}}u}{{\sigma }_{v}}\right)}{2\lambda \exp \left({\mathrm{p}}{\epsilon }_{r}\lambda \,+\,\frac{{\lambda }^{2}{\sigma }_{v}^{2}}{2}\right){{{\mathcal{A}}}}}\\ \,\quad\qquad\,=\,\frac{\frac{1}{{\sigma }_{v}}\phi \left(\frac{u\,+\,{\mathsf{p}}{\epsilon }_{r}\,+\,\lambda {\sigma }_{v}^{2}}{{\sigma }_{v}}\right)\Phi \left(\alpha \frac{{\epsilon }_{r}\,+\,{\mathrm{p}}u}{{\sigma }_{v}}\right)}{{{{\mathcal{A}}}}}.\end{array}$$

(11)

We then obtain the point estimator for u (observation-specific) by finding the mean value of the conditional distribution in (11),

$$E(u| \epsilon )=\int\nolimits_{0}^{+\infty }\frac{u\times \frac{1}{{\sigma }_{v}}\phi \left(\frac{u\,+\,{\mathsf{p}}{\epsilon }_{r}\,+\,\lambda {\sigma }_{v}^{2}}{{\sigma }_{v}}\right)\Phi \left(\alpha \frac{{\epsilon }_{r}\,+\,{\mathsf{p}}u}{{\sigma }_{v}}\right)}{{{{\mathcal{A}}}}}du.$$

(12)

It can be shown (see Appendix A) that the integral in (12) has a closed form solution,

$$E(u| \epsilon )=-{\sf{p}}{\epsilon }_{r}-\lambda {\sigma }_{v}^{2}+\frac{{\sigma }_{v}}{{{{\mathcal{A}}}}}\times \left[\begin{array}{l}\frac{b}{\sqrt{1+{b}^{2}}}\phi \left(\frac{a}{\sqrt{1+{b}^{2}}}\right)\\ \times \Phi \left(-{u}_{1}\sqrt{1+{b}^{2}}-\frac{ab}{\sqrt{1+{b}^{2}}}\right)\\ +\phi \left({u}_{1}\right)\Phi \left(a+b{u}_{1}\right)\end{array}\right],$$

(13)

where ${\mathcal{A}}$ is defined in (8) and a, b, and u₁ are defined immediately after. The estimates of efficiency can be obtained by exponentiating the negation of the quantity in (13).

3.1.3 Comparison to existing approaches

There are at least three differences between existing models and those proposed here. First, we consider a skew-normal exponential model. Wei et al. (2021a) use a half-normal distribution instead of an exponential distribution. Our own simulations along with the discussion in Papadopoulos and Parmeter (2021) and Papadopoulos (2022) suggest possible major identification issues in the skew-normal half-normal setting (and no issue with a skew-normal exponential setting). An identification problem can occur because a skew-normal distribution can be obtained via the convolution of a half-normal and a normal distribution and we apriori do not know the sign of the noise skewness. Papadopoulos (2022) shows a similar result when looking at combining an asymmetric Laplace with exponential inefficiency (even with a correctly specified model). His solution, assuming availability, is to include determinants of inefficiency. We will discuss this possibility in the next section.

Second, we derive the results in closed form, this precludes non-convergence due to approximations and adds precision to the estimates of the frontier and efficiencies. Speed of estimation is also gained which is helpful for the multistart procedure we discuss later.

Third, we introduce determinants of all error components along with skewness. While this has been studied for both variance and inefficiency, none of the aforementioned papers do so with respect to the skewness parameter.

There has also been some work on incorporating copulas into efficiency analysis (Bonanno et al. 2017 and Wei et al. 2021b). From a statistical point of view, this appears to be a generalization of our approach. Conceptually, however, we are not quite sure why we would want to introduce this dependence between the error term and inefficiency. That being said, if it did exist, these estimators would be preferable. However, if it does not exist (our prior) our model would exploit this effect and would be more efficient. We leave the comparison of these methods to future research.

3.1.4 Determinants of heteroskedasticity, efficiency, and skewness

It is feasible to modify our approach to allow for determinants of all parameters of error components (Kumbhakar et al. 1991, Lien et al. 2018). In other words, assuming data are available, we can model each component (variance, inefficiency and skewness) with both a deterministic and a stochastic component. We can attempt to explain the performance of firms based on exogenous variables within the firm’s production environment.⁸ Examples of naturally occurring environment variables include, but are not limited to, human capital levels of managers, input and output quality measures, market share and/or climactic variables.

The noise term can be made heteroskedastic by allowing the variance to depend upon a set of exogenous environment variables (z_v). To ensure that the variance is positive, we adopt the following specification

$$\ln {\sigma }_{v}^{2}={{{{\boldsymbol{z}}}}}_{v}{{{{\boldsymbol{\gamma }}}}}_{v},$$

(14)

where the parameter vector γ_v may include an intercept term. Since noise in a production relationship can be viewed as production risk, the typically employed determinant of noise variance is the size of the unit of observation (e.g., total assets in banking).

Similarly, the variance of inefficiency, and hence the inefficiency itself, can be modeled to depend upon a set of exogenous environment variables (z_u). Again, to ensure that the variance is positive, we adopt the specification

$$\ln {\sigma }_{u}^{2}={{{{\boldsymbol{z}}}}}_{u}{{{{\boldsymbol{\gamma }}}}}_{u},$$

(15)

where the parameter vector γ_u may include an intercept term.

The first two approaches exist in the literature (Caudill et al. 1995), and here we suggest they analogously be extended for the skewness parameter to allow for heterogenous effects. Our skewness parameter can be made observation specific via

$$\alpha ={{{{\boldsymbol{z}}}}}_{s}{{{{\boldsymbol{\gamma }}}}}_{s},$$

(16)

where again, the parameter vector γ_s may include an intercept term. Allowing for heterogeneity in skewness may be particularly useful as we may be able to determine that some firms are more susceptible to negative shocks than others. Note that this formulation allows for the skewness to take either sign and heterogeneity (as we will see later in our empirical applications) allows for both signs within a given dataset.

3.2 Finite sample performance

The parameters of (3) and (5) are obtained using maximum likelihood estimation (MLE) based on (4) and (10), respectively. The theoretical properties of MLE are well-known and all our parameters are identified by the parametric assumptions on the model. However, it can sometimes be difficult to obtain reliable estimates for some datasets in practice. The finite sample properties of the MLE estimator for (4) for different parameter constellations has been studied by Azzalini and Capitanio (1999) and Badunenko et al. (2012). If one considers (5) to be a generic statistical model with two skewed distributions, Badunenko and Kumbhakar (2016) studied the finite sample properties of a special case of this model.

For completeness, we have performed a small Monte Carlo study and profile analysis (Ritter and Bates 1996). Tables with estimated bias and MSE as well as likelihood profiles are available in Appendix C. The plots of the medians of the likelihood ratio statistics show the effect the sample size has on the finite sample performance of the estimator. As expected, the parameters are more precisely estimated with larger samples. We find some evidence that α may be difficult to estimate precisely for sample sizes below 200. Further, some profiles suggest the possibility of local maxima for α (Azzalini and Capitanio 2013, Chapter 3). To avoid this issue in practice, we suggest using a multistart procedure for optimization when using Broyden-Fletcher-Goldfarb-Shanno (BFGS) or Newton-Raphson (NR) methods.⁹ The variance parameters in both (3) and (5) are precisely estimated in all scenarios.

Out of curiosity, we also wanted to see how estimates fared versus those which assume symmetry. To study this, for each production function, we generate the noise from either a Skew Normal (Appendix D.1) or a Normal distribution (Appendix D.2). The results are primarily as expected. This holds true for the parameters of the model and the efficiency scores (Appendix D). The traditional model wins out when the true distribution is symmetric and our approach tends to dominate when the noise is asymmetric. The R code for this can be found in Appendix E.5.

Overall, our Monte Carlo studies suggests that our estimators possess desirable finite sample properties.

3.3 Stata and R packages

All the analysis above can be performed using packages we have created in R (the snreg R package) and Stata statistical softwares. The R package and the Stata command can be obtained from the authors’ websites. Both softwares are accompanied by help and example files. In both softwares the names of the commands are snreg and snsf. Different from the selm command from the R package sn, the snreg command allows for determinants of heteroskedasticity as in (14) and skewness as in (16). Appendix E presents R code to help replicate our empirical results, which we discuss next.

4 Empirical illustration

In this section, we demonstrate the usefulness of our proposed methodology in three separate applications. We will look at both cost and production functions with symmetric and asymmetric noise. We will further introduce inefficiency of production units into our models. Finally, we will highlight our most flexible model that allows asymmetric noise and inefficiency, as well as determinants of (i) heteroskedasticity, (ii) inefficiency, and (iii) skewness.

We will showcase such comparisons by modeling risk in the U.S. banking industry, the effect of extreme adverse events on educational outcomes, and finally, annual data from the U.S. textile sector.

4.1 U.S. Banks

For our first application, we use a random subset of the firms employed in Restrepo-Tobón and Kumbhakar (2014). We chose a random sample of 500 banks observed in 2007 and whose total assets were between the 10th and 90th percentiles of the total assets distribution, and whose total costs were between the 10th and 90th percentiles of the total costs distribution. The code to obtain our random sample is shown in Appendix E.2.1.¹⁰

Our goal is to estimate and compare the following models: (N0) symmetric noise with no inefficiency, (SN0) asymmetric noise with no inefficiency, (SF0) symmetric noise with inefficiency, (SF1) asymmetric noise with inefficiency and (SF2) asymmetric noise with inefficiency and determinants. These models go from the most restrictive to the most general. If the noise is asymmetric, inefficiency exists and our determinants are significant, we expect SF2 to perform best. However, if none of those events are true, N0 represents the most efficient model.

4.1.1 Translog cost function

We assume a full translog specification of the technology where 2 outputs are produced by 3 inputs. To ensure the necessary condition that the cost function is homogeneous of degree 1, we divide the total costs and prices of the first two inputs by the price of the third input.¹¹ More formally, our translog cost function is given as

$$\begin{array}{ll}\ln (TC/{W}_{3})\,=\,{\beta }_{0}+{\beta }_{1}\ln ({Y}_{1})+{\beta }_{2}\ln ({Y}_{2})+{\beta }_{3}\ln ({W}_{1}/{W}_{3})+{\beta }_{4}\ln ({W}_{2}/{W}_{3})\\ \qquad\qquad\qquad\,\,+\,0.5{\beta }_{5}\ln {({Y}_{1})}^{2}+0.5{\beta }_{6}\ln {({Y}_{2})}^{2}+0.5{\beta }_{7}\ln {({W}_{1}/{W}_{3})}^{2}\\ \qquad\qquad\qquad\,\,+\,0.5{\beta }_{8}\ln {({W}_{2}/{W}_{3})}^{2}+{\beta }_{9}\ln ({Y}_{1})\ln ({Y}_{2})+{\beta }_{10}\ln ({Y}_{1})\ln ({W}_{1}/{W}_{3})\\ \qquad\qquad\qquad\,\,+\,{\beta }_{11}\ln ({Y}_{1})\ln ({W}_{2}/{W}_{3})+{\beta }_{12}\ln ({Y}_{2})\ln ({W}_{1}/{W}_{3})\\ \qquad\qquad\qquad\,\,+\,{\beta }_{13}\ln ({Y}_{2})\ln ({W}_{2}/{W}_{3})+{\beta }_{14}\ln ({W}_{1}/{W}_{3})\ln ({W}_{2}/{W}_{3})+\epsilon \end{array}$$

where TC represents total costs of the bank, Y₁ and Y₂ are their outputs (total securities of the bank and total loans, respectively) and W₁, W₂ and W₃ are their inputs (cost of fixed assets, cost of labor and cost of borrowed funds, respectively).¹² Each of the β represent parameters to be estimated and the form of ϵ will depend upon the model chosen.

Table 1 presents the results of our translog cost function for each of the above specifications. Recall that Model N0 is the traditional cost function where the noise is homoskedastic and symmetric, i.e., v_i ~ N(0, σ_v) in (3).¹³ Model SN0 allows the noise to be SN, where the skewness parameter α is the same for all observations. Model SF0 is the standard SF model where noise is normally distributed with a constant variance and inefficiency is exponentially distributed. Model SF1 extends model SF0 by allowing noise to be SN.

Table 1 Dependent variable $\ln (TC/{W}_{3})$

Following the above discussion, we suggest a model where risk influences total costs of production through the noise. More specifically, for each bank, the shape/skewness of the distribution of the noise¹⁴ depends upon the risk level of that bank. Thus, risk affects the total costs of a bank, not directly, but rather through the expected shock that a bank experiences due to being risky. Therefore, model SF2 allows the skewness parameter to be bank-specific as in (16). Here we employ a commonly used risk measure in the banking literature (Koetter et al. 2012), standard deviation of return on assets (sdroa).¹⁵ It can be viewed as the variability in returns.

Model SF2 also adds explanatory variables for heteroskedasticity and inefficiency (Equations (14) and (15), respectively). For the variance, we look at the total assets (TA) of the bank and for inefficiency, we use a scope variable, which is the Hirschman-Herfindahl index across five loan categories (i.e., how focused a bank is in terms of loans).¹⁶

4.1.2 Results

Our most basic comparison is between the first two models: N0 and SN0 (symmetric and asymmetric noise without inefficiency, respectively). The estimated skewness coefficient is 1.38, which is significant at conventional levels. The noise distribution is close to the pink density shown in Fig. 1, mirrored around 0. The N0 model is rejected by the LR test in favor of the SN0 model (p-value of the LR test is 0.0036). Although OLS is unbiased, it is no longer efficient in the presence of asymmetric noise.

We now move to introducing inefficiency into our cost function.¹⁷ Table 1 shows that the symmetric SF model SF0 exhibits better fit than SN0 with the same number of parameters. We should be careful here however as SF0 and SN0 are non-nested and hence the LR-test is not necessarily informative. When we allow both skewed noise and inefficiency (model SF1), the LR test clearly rejects SN0 in favor of SF1 (p-value of the LR test is 6.13e-05)¹⁸ and also for SF1 in favor of SF0 (p-value of the LR test is 0.0078). However, note that SF1 restricts the shapes of the noise and inefficiency distributions to be the same for all banks. The most flexible model, SF2, best fits the data among all those considered in Table 1. The LR test gives preference to SF2 over SF1 (the p-value of the LR test is 7.57e-05).¹⁹

Figure 3 shows the kernel estimated density of the predicted skewness ($\hat{\alpha }(z)$) for our preferred model, SF2. The probability mass of a negatively skewed distribution with a zero mean implies that the majority of banks are expected to have a slight negative shock to their operations. Another property of this distribution is that the left tail is thicker than the right. In other words, large positive shocks are more frequent than large negative shocks.

Fig. 3

Kernel estimated densities of skewness (Model SF2). The vertical dash-dotted line is 0. The solid vertical line is the mean

Figure 4 plots the predicted skewness against a skewness determinant. There are only a few very risky banks (i.e., sdroa is very large). At low risk levels, the skewness is quite low (approximately − 4 for sdroa). A shock of a low risk bank comes from a very skewed distribution and therefore such a bank is likely to be hit by a negative shock that has a detrimental effect on total costs. At the mean level of sdroa (0.32), the estimated skewness is − 2.5, the value of the estimated skewness in SF1 (where skewness is assumed constant). The skewness remains negative until sdroa reaches 0.95, which is the 96th percentile of the sdroa distribution. For the 4 percent (of the most) risky banks in our sample, the skewness is positive, implying a thicker right tail of the noise distribution.

Fig. 4

The estimate of skewness (fitted values) plotted against the determinant (Model SF2). The rug plot on each axis essentially shows a one-dimensional heatmap

It is worth noting that in SF2, the inefficiency determinant scope, is statistically significant. The negative coefficient means that as scope increases, bank inefficiency is decreasing. Further, the determinant of heteroskedasticity (total assets) is also statistically significant. The negative coefficient here suggests that the variance decreases with the size of total assets. Finally, Fig. 5 shows estimated densities of efficiency scores from all of our SF models. There are no marked differences in the distributions.

Fig. 5

Kernel estimated densities of efficiencies. Vertical lines are respective means

4.2 Beltway sniper

Here we investigate the effects of the 2002 “Beltway Sniper” mass shootings on student achievement in Virginia’s public elementary schools (Gershenson and Tekin 2018). Traumatic events, especially those which are ‘close to home’, can have serious impacts on student outcomes. However, different from past research (Ponzo 2013), we attempt to model these low probability events in the noise distribution.²⁰

We follow Levin (1974) and Hanushek (1979) and consider an educational production function as a process of converting inputs (i.e., school resources) into outputs (i.e., student achievement). We go a step further and account for inefficiency in educational production as it has been argued that estimating educational production functions accounting for inefficiency is a proper approach for examining educational outcomes (Ruggiero 20062019, Thanassoulis et al. 20162018).

4.2.1 Educational production function

Our (school level) educational production function is given as

$$\begin{array}{rcl}\ln (math)&=&{\beta }_{0}+{\beta }_{1}\ln (ratio)+{\beta }_{2}\ln (fte)+0.5{\beta }_{3}\ln {(ratio)}^{2}\\ &&+0.5{\beta }_{4}\ln {(fte)}^{2}+{\beta }_{5}\ln (ratio)\ln (fte)\\ &&+{\beta }_{6}\ln (black)+{\beta }_{7}\ln (hispanic)+\epsilon ,\end{array}$$

where the βs represent parameters to be estimated and the composition of ϵ follows the same models in the previous sub-section. math is our output variable measured in logs (school-level proficiency in the Standards of Learning standardized test given each spring in Virginia public schools). Our input variables are student-teacher ratios (ratio), full-time equivalent teachers (fte), percent Black (black), and percent Hispanic (hispanic).

Similar to before, we estimate five different models (N0, SN0, SF0, SF1, and SF2). In this context, “production inefficiency” represents student underachievement. We will use total enrollment (enroll) as a measure of size, percent free lunch (frp), and closeness (closeness) to a sniper attack as determinants of our noise components.²¹closeness is the primary determinant of interest and measures the distance (in miles) the school is from the closest sniper attack.

4.2.2 Results

Table 2 provides the regression results for our familiar set of models. Note that in the previous sub-section we analyzed a cost function (i.e., p = −1) and the smaller outcome variable was preferable. Here, we analyzing a production function (i.e., p = 1) and larger outcome values are preferable (i.e., higher levels of proficiency). The results here represent 5th grade students in the year 2003 (same academic year as the attacks).

Table 2 Dependent variable is log of percent proficient of the Math test

It is clear that the SN0 model fits the data far better than N0 (the LR statistic is 136.53 while the critical value of the ${\chi }_{1}^{2}$ at the 1% level of significance is 6.63), and thus there is a good reason to believe the skewness of the noise term is not 0. Based on the LR test, including inefficiency (SF0) provides a better fit than simply allowing for asymmetric noise (the LR statistic is 40.97). When we consider the model that contains both inefficiency and skewness, restricting the shape of the noise distribution for all schools to be the same (model SF1), the constant skewness parameter is not statistically insignificant. The likelihood increased by only 0.4, which is not enough to conclude that SF1 is preferred to SF0. Note that when we do not account for possible skewness in the noise, we overestimate the effect of the proportion of Black or Hispanic students on educational outcome.

The most flexible model (SF2) allows the skewness parameter to vary depending on how close the school is from a shooting scene. We find a significant increase in the log-likelihood (the LR statistic of the LR test between SF2 and SF1 is 118.4 whereas the critical value of the ${\chi }_{3}^{2}$ at the 1% level of significance is 11.34). As for the determinants of the error components, we find that as the proportion of pupils who are eligible for free or reduced-price lunch is increasing, underachievement is increasing. The skewness of the noise distribution is increasing as a school is further away from a sniper attack (as shown in Fig. 6).²² The noise for those schools that are close to at least one sniper attack scene, have large negative skewness, implying that the left tail is much thicker than the right tail. In other words, as risk is increasing, schools have a larger probability to exhibit poor, rather than good test results. Figure 7 shows that negative skewness is a feature of the noise distribution for all public schools in our sample.

Fig. 6

The estimate of skewness (fitted values) plotted against the respective determinant. The rug plot on each axis essentially shows a one-dimensional heatmap

Fig. 7

Kernel estimated density of skewness. The vertical dashed-dotted line is 0. The solid vertical line is the mean

4.3 NBER data: textile industries

Our final application uses data from the well studied (Bonanno et al. 2017) NBER-CES Manufacturing Industry Database (Bartelsman and Gray 1996). For each available year (1958–2011), we focus on the textile industry (SIC 4-digit industry: 2200–2399) because these particular samples are known to exhibit the “wrong skewness” of OLS residuals (Hafner et al. 2018).

We estimate SF models where noise is either assumed to normal or SN and the distribution of the inefficiency term is assumed to be exponentially distributed. In the case of a SN distribution, we omit determinants and therefore have a constant skewness parameter for each year. In each setting, we use a translog production function where the output (total value added) is produced by capital (total real capital stock), labor (total employment) and materials (total cost of materials).

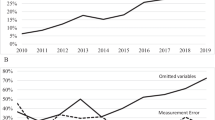
Figure 8 plots the estimated skewness parameter for each year. The blue circles represent coefficients that are statistically insignificant, while the red triangles represent statistically significant estimates of α. We do not observe uniformity of coefficient magnitudes; they range from roughly −2.5 to approximately 6. Although we see both signs for skewness, most estimates are close to 0. With regards to the magnitude, there is no clustering, trend, or situation where the estimates appear to be persistent over time. The skewness coefficient can be negative in 1 year and positive the year after. Finally, there appears to be no clustering or trend with respect to significance of the estimated coefficients.

Fig. 8

The estimated skewness coefficient by year

Figure 9 dissects Fig. 8 to differentiate between years where the skewness of the OLS residuals are negative (‘correct’ skewness) or positive (‘wrong’ skewness). In years where the SN-Exp model results in a large positive significant skewness parameter, the skewness of OLS residuals is ‘wrong’. Where the skewness of OLS residuals is ‘correct’, the skewness parameter is only rarely significant.

Fig. 9

The estimated skewness coefficient by year

Finally, Fig. 10 shows average efficiency scores by year for both the asymmetric and symmetric noise models. In years where the OLS residuals are of the ‘wrong skewness’, the conventional SF model predicts no inefficiency (i.e., the average efficiency score is 1). We observe this in about half of the cases. In each of those years, our model estimates inefficiency (the average efficiency score is around 0.975). In about 10% of the years, the average efficiencies from both models are the same. This happens in years when the skewness of the OLS residuals is ‘correct’ and the estimated skewness coefficient in our model is indistinguishable from 0 and is statistically insignificant (red circles in Fig. 9). Considering both what we have seen here and our simulations, there is evidence that our approach can identify inefficiency in each year of our sample.

Fig. 10

The average of the efficiency score estimated by N-Exp and SN-Exp models by year

5 Conclusions

In this paper, we propose to model asymmetric noise in production analysis. We discussed how to estimate a production or cost function with asymmetric noise and extended this model for a skew-normal noise distribution for stochastic frontier analysis. Our methods result in closed form solutions for the log-likelihood function and inefficiency. We are able to incorporate determinants of these components (heteroskedasticity, inefficiency and skewness) in an estimation procedure that jointly estimates all parameters of interest. The set of the proposed models will be instrumental to researchers who wish, for example, to model risk associated with the outcome variable by allowing for asymmetry in the error term with or without inefficiency.

We showcased these methods in simulations as well as in three separate empirical applications, including one that showed that our approach is able to estimate efficiency scores when OLS residuals are of the “wrong skewness”. Given that we have produced user-friendly R and Stata packages, we believe that these techniques can easily be applied across a wide range of fields within production analysis.