1 Introduction

Partial differential equations (PDE) show their effectivness to overcome various issues appearing in the fields of mathematical and physical sciences. Due to the roots in different fields of sciences, the ideology of PDEs, both linear and nonlinear, is one of the highest and more active fields of modern mathematics (Melike and Mehmet 2018; Hosseini et al. 2017; Raza 2021; Bhatti and Lu 2019). Nonlinear PDEs (NLPDE) have a giant influence on nonlinear mathematical forms in engineering, physics, biology, fluid mechanics, condensed matter physics, nonlinear optics (Khater et al. 2000; Ali et al. 2020; Sağlam Özkan et al. 2021; Seadawy and Cheemaa 2019; Younas et al. 2020; Rizvi et al. 2020; Helal and Seadawy 2009), etc. Higher-order NLSEs are the main segments for NLPDEs. There is plenty of well-known NLSEs, like derivative NLSE (Younas et al. 2020), cubic-quartic NLSE (Gao et al. 2019), Kundu Mukherjee Naskar model (He 2020), Gross Pitaevskii equation (Feng et al. 2021), Fokas-Lenells equation (Ahmed et al. 2019), and many other. A large number of integration techniques have been introduced to get particular solutions for NLSEs; like improved F-expansion method (Gao and Wang 2020), \(exp((\frac{-\Psi '}{\Psi }) \eta )\)-expansion scheme (Seadawy 2019), extended direct algebraic technique (Ahmed et al. 2019), new extended-auxiliary equation architectonic (seadawy et al. 2018), generalized Kudryashov mechanism (Gaber et al. 2019), extended auxiliary equation approach (Akram et al. 2021), \(\tan (\Phi (\rho )/2)\)-expansion technique (Raza et al. 2020), \(\Phi ^6\)-model expansion approach (Seadawy et al. 2021), etc.

Analytic solutions of some well-known NLSEs have been investigated in (Li et al. 2015; Seadawy 2015; Arshad et al. 2017; Ahmed et al. 2019; Chen et al. 2020). In optical fibers, the propagation of solitons may be appropriately specified by variable coefficient NLSEs (VCNLSE) (Malomed 2006). To raise the transmission rate ultrashort pulses (picosecond or less) are usually used as data bearers, for which higher-order dispersion can’t be neglected. Therefore, it’s important to explore the analytical fams of soliton solutions of NLPDEs that include higher-order specifications, particularly to find the proper solutions of higher-order VCNLSEs, from a logical and scientific point of view. Here we contemplate FVCNLSE as given by (Yang et al. 2018),

$$\begin{aligned}&i p_x + A(x) \bigg (\frac{1}{2} p_{tt}+ p |p|^2 \bigg ) -i B(x) \bigg (p_{ttt} +6 |p|^2 p_t \bigg ) +C(x) \bigg (p_{tttt} +6 p^* p_t^2 +4 p |p_t|^2 +8 |p|^2 p_{tt} +2 p^2 p_{tt}^* +6 p |p|^4 \bigg ) \nonumber \\ & \quad-i D(x) \bigg (p_{ttttt} +10 |p|^2 +p_{ttt} +30 |p|^4 p_t +10 p p_t p_{tt}^* +10 p p_t^* p_{tt} +20 p^* p_t p_{tt} +10 p_t^2 p_t^* \bigg ) = 0, \end{aligned}$$
(1)

which can be used as an integrable pattern to characterize the proliferation of ultrashort pulses in inharmonious optical fibers. Here \(p = p(x,t)\) is a complex function, x is the formalized transmission distance, t is the delayed time, and asterisk stands for the complex conjugate. Physically, the parameters A(x), B(x), C(x) and D(x) represents the group velocity, third-order, fourth-order, and fifth-order dispersion respectively. This model with constant quantities has been verified to be entirely integrable by using the Lax pair and Darboux transmutations (Chowdury et al. 2014). However, x-dependent coefficients A(x), B(x), C(x), and D(x) have not been studied there. An exhaustive study of integrability setting for the x-dependent parameters of VCNLSE needs to be a subject of independent work. Now we’ll study the above model for lump and their interactions with kink, periodic and rogue waves (Yang et al. 2018; Rizvi et al. 2020; Zhou et al. 2019; Kofane et al. 2017; Liu 2018; Seadawy et al. 2021; Ma and Li 2020; Ma et al. 2020). Lump solitons are analytically localized in all directions. The implementations of lump waves are greatly comprehensive, like distant ghost waves that emerge and dissolve unpredictably and uncertainly, notably, COVID-19. Rogue waves with heights exceed about 18 meters are powerful nonlinear waves that have the ability to produced huge damages even for massive ships. They are sizably much bigger as compared to the normal sea waves. There is no conformity for how and when they appear, the maximum height of the rogue wave recorded 25 meters (Olagnon 2017; Korpinar et al. 2020; Ali et al. 2020).

Now to investigate the above model, we’ll use the complex substitution \(p = r + i s\), which transforms Eq. (1) into the following real and Img parts,

$$\begin{gathered} - {s_x} + \frac{1}{2}A(x)(2r({r^2} + {s^2}) + {r_{tt}}) + B(x)(6({r^2} + {s^2}){s_t} + {s_{ttt}}) \hfill \\ \quad + C(x)(6{r^5} + 12{r^3}{s^2} + 6r{s^4} + 10rr_t^2 + 2(5{r^2} + 3{s^2}){r_{tt}} \hfill \\ \quad + {r_{tttt}} + 12s{r_t}{s_t} - 2rs_t^2 + 4rs{s_{tt}}) + D(x)(10s_t^3 + 20r{r_t}{s_{tt}} + 10{s_t} \hfill \\ \quad (3{r^4} + 6{r^2}{s^2} + 3{s^4} + r_t^2 + 2r{r_{tt}} + 4s{s_{tt}}) + 10({r^2} + {s^2}){s_{ttt}} + {s_{ttttt}}) = 0, \hfill \\ \quad {r_x} + \frac{1}{2}A(x)(2s({r^2} + {s^2}) + {s_{tt}}) - B(x)(6({r^2} + {s^2}){r_t} + {r_{ttt}}) \hfill \\ \quad + C(x)(6{s^5} + 12{r^2}{s^3} + 6{r^4}s + 10ss_t^2 + 2(5{s^2} + 3{r^2}){s_{tt}} + \hfill \\ \quad {s_{tttt}} + 12r{r_t}{s_t} - 2sr_t^2 + 4rs{r_{tt}}) - D(x)(10r_t^3 + 20s{r_{tt}}{s_t} + 10{r_t}(3{r^4} \hfill \\ \quad + 6{r^2}{s^2} + 3{s^4} + s_t^2 + 2s{s_{tt}} + 4r{r_{tt}}) + 10({r^2} + {s^2}){r_{ttt}} + {r_{ttttt}}) = 0. \hfill \\ \end{gathered}$$
(2)

Now we use this system in the next sections to find out new analytical solutions for our concern model. We present distinct possible choices of solitons and interaction solutions, by adjusting the real parameters of the concerning model, based on the gained results. Particularly, we will establish a probability to have pulse thickness of two merging solitons growing after a collision, without a variation in their sizes. The paper is arranges in proceeding pattern: in sec. 2, we study lump solutions, in sec. 3, we present lump interaction with two kink waves, in sec. 4, we obtain lump solution with periodic waves, in sec. 5, we study rogue wave solutions, in sec. 6, we presents results periodic cross lump waves solutions, in sec. 7, we discuss our obtained results and at the end, in sec. 8, we give concluding remarks.

2 Lump solutions

To attain lump solutions we use the following log forms,

$$\begin{aligned} r = 2 {\left( {\ln u} \right) _{t}},~~~~~~~~ s = 2 {\left( {\ln v} \right) _{t}}. \end{aligned}$$
(3)

Eq. (3) transforms Eq. (2) into the following bilinear forms,

$$\begin{aligned}&480 C(x) v^6 u_t^5 - 40 u v^4 u_t^3 (13 C(x) v^2 u_{tt} +34 D(x) u_t (v_t^2 -v v_{tt})) \nonumber \\&\quad +10 u^2 v^3 u_t (-32 D(x) u_t^2 v_t^3 + 16 v u_t v_t (4 D(x) \nonumber \\&\quad v_t u_{tt} +3 u_t (C(x) v_t +D(x) v_{tt})) +v^3 (A(x) u_t^2 +14 C(x) u_{tt}^2 \nonumber \\&\quad +12 C(x) u_t u_{ttt}) - 16 D(x) v^2 u_t (4 u_{tt} v_{tt} +u_t v_{ttt})) \nonumber \\&\quad - \cdots - 32 C(x) v v_t^2 (3 v_t u_{tt} +2 u_t v_{tt}) +2 u^5 (-1200 D(x) v_t^6\nonumber \\&\quad +2240 D(x) v v_t^4 v_{tt} -10 v^2 v_t^2 (3 B(x) v_t^2 + 99 D(x) v_{tt}^2 + 44 D(x) v_t v_{ttt}) +v^3 (70 D(x) v_{tt}^3 + 280 D(x) v_t v_{tt} v_{ttt} +v_t^2 (36 B(x) v_{tt} \nonumber \\&\quad +70 D(x) v_{tttt} )) -v^4 (3 B(x) v_{tt}^2 + 10 D(x) v_{ttt}^2 +15 D(x) v_{tt} v_{tttt} +v_t (4 B(x) v_{ttt} \nonumber \\&\quad +6 D(x) v_{ttttt} -v_x )) +v^5 (B(x) v_{tttt} +D(x) v_{tttttt} -v_{xt} )) = 0, \nonumber \\&\quad 2400 D(x) v^5 u_t^6 -4480 D(x) u v^5 u_t^4 u_{tt} +20 u^2 v^3 u_t^2 (12 C(x) v u_t^2 v_t \nonumber \\&\quad +120 D(x) u_t^2 v_t^2 +v^2 (3 B(x) u_t^2 +99 D(x) u_{tt}^2 \nonumber \\& \quad+ 44 D(x) u_t u_{ttt})) -4 u^3 v^2 (-80 D(x) u_t^3 v_t^3 +8 C(x) v^2 u_t^2 (2 v_t u_{tt}\nonumber \\&\quad +3 u_t v_{tt}) +8 v u_t^2 v_t (90 D(x) v_t u_{tt} +u_t (-3 C(x) v_t \nonumber \\&\quad +10 D(x) v_{tt} )) +v^3 (35 D(x) u_{tt}^3 +140 D(x) u_t u_{tt} u_{ttt} +u_t^2 (18 B(x) u_{tt}\nonumber \\&\quad +35 D(x) u_{tttt} ))) + \cdots + 8 v^2 (5 D(x) u_{tt} v_{tt}^2 \nonumber \\&\quad +10 D(x) v_t (v_{tt} u_{ttt} +u_{tt} v_{ttt}) +v_t^2 (3 B(x) u_{tt} \nonumber \\&\quad +5 D(x) u_{tttt})) +v^4 (B(x) u_{tttt} +D(x) u_{tttttt} -u_{xt}))) = 0. \end{aligned}$$
(4)

Now u and v in the bilinear form can be assumed as, (Helal and Seadawy 2009),

$$\begin{aligned} u = \chi _1^{2} + \chi _2^{2} + g_0, ~~~~~ v = \chi _1^{2} + \chi _2^{2} + h_0, \end{aligned}$$
(5)

where \(\chi _{1}=b_{1} x+ b_{2} t,\) and \(\chi _{2}=b_{3} x+ b_{4} t\). However, \(b_i\)’s, \(g_0\) and \(h_0\) are real -valued constants. Now, inserting u and v into Eq. (4) and collecting all powers of x and t, which implies us the following nonzero parameters:

Set I:

$$\begin{aligned}&b_1 = i b_3, b_2 = \frac{\frac{29435}{2} i C(x)^2 b_3 }{A(x) (495 D(x) A(x) - 3857 B(x) C(x))},\nonumber \\&\quad b_3 = b_3, g_0 = \frac{75378472575 b_3^2 C(x)^5}{A(x)^3 (495 D(x) A(x) - 3857 B(x) C(x))^2}, \nonumber \\ & \text{ and } \nonumber \\&\quad b_1 = \frac{\sqrt{-8+\sqrt{273} b_3}}{\sqrt{209}},\nonumber \\&\quad b_2 = \frac{4205 \sqrt{\frac{1}{209}(-8+\sqrt{273})} (16+\sqrt{273}) b_3 C(x)^2}{2 A(x) (495 A(x) D(x) - 3857 B(x) C(x))}, b_3 =b_3, \nonumber \\&\quad h_0 = -\frac{1538336175 (4504 + 273 \sqrt{273}) b_3^2 C(x)^5}{209 A(x)^3 (3857 B(x) C(x) -495 D(x) A(x))^2}. \end{aligned}$$
(6)

Using these parameters into Eq. (5) and then by using Eq. (3), we get:

$$\begin{aligned} r= \, & {} 4 b_2 \left( \frac{\left( b_2 t +i b_3 x \right) }{\left( g_0 +b_3^2 x^2 +(b_2 t +i b_3 x)^2 \right) } \right) , \nonumber \\ s= \, &{} 4 b_2 \left( \frac{\left( b_2 t +i b_3 x \right) }{\left( b_3^2 x^2 +(b_2 t +i b_3 x)^2 \right) } \right) , \nonumber \\ & \text{ and } \nonumber \\ r= \, &{} 4 b_2 \left( \frac{b_2 t + b_1 x}{b_3^2 x^2 + (b_2 t + b_1 x)^2} \right) ,\nonumber \\ s= \, &{} 4 b_2 \left( \frac{b_2 t + b_1 x}{h_0 + b_3^2 x^2 + (b_2 t + b_1 x)^2} \right) . \end{aligned}$$
(7)

The values of the parameters are mentioned in Eq. (6). Now, r and s gives the required solution for Eq. (1),

$$\begin{aligned}&p_{1}(x , t) = \frac{(4 + 4 i) \left( 29435 C(x)^2 t - 7714 A(x) B(x) C(x) x + 990 A(x)^2 D(x) x \right) \left( (-5121690 - 5121690 i) C(x)^3 + \Delta \right) }{t \left( 29435 C(x)^2 t - 15428 A(x) B(x) C(x) x + 1980 A(x)^2 D(x) x \right) \left( -10243380 C(x)^3 + \Delta \right) }, \nonumber \\&\quad p_{2}(x , t) = \frac{8410 \sqrt{\frac{1}{209}(-8+\sqrt{273})} (16+\sqrt{273}) b_3 C(x)^2 \Omega }{A(x) (495 A(x) D(x) - 3857 B(x) C(x)) (b_3^2 x^2 + \Omega ^2)} + \frac{8410 i \sqrt{\frac{1}{209}(-8+\sqrt{273})} (16+\sqrt{273}) b_3 C(x)^2 \Omega }{A(x) (495 A(x) D(x) - 3857 B(x) C(x)) (-\Delta _1 + b_3^2 x^2 + \Omega ^2) }, \end{aligned}$$
(8)

Here \(\Delta = 29435 A(x) C(x)^2 t^2 - 15428 A(x)^2 B(x) C(x) t x + 1980 A(x)^3 D(x) t x,\)    \(\Delta _1 = \frac{1538336175 (4504 + 273 \sqrt{273}) b_3^2 C(x)^5}{209 A(x)^3 (3857 B(x) C(x) -495 D(x) A(x))^2},\)   and   \(\Omega = \frac{4205 \sqrt{\frac{1}{209}(-8+\sqrt{273})} (16+\sqrt{273}) b_3 C(x)^2 t}{2 A(x) (495 A(x) D(x) - 3857 B(x) C(x))} + \frac{\sqrt{-8 +\sqrt{273} b_3} x}{\sqrt{209}}\).

Fig. 1
figure 1

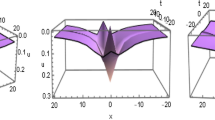
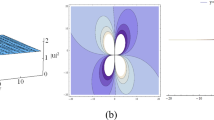
Graphs of \(p_{1}(x,t)\) in Eq. (8) at \(A(x)=-0.7, B(x)=0.5, C(x)=1, D(x)=-1\) respectively. Solution shows the x-type bright solitons

Full size image
Fig. 2
figure 2

Graphs of \(p_{2}(x,t)\) in Eq. (8) at \(A(x)=-0.6, B(x)=0.9, C(x)=1, D(x)=-1, b_3=3\) respectively. Solution shows a bright soliton

Full size image

Set II:

$$\begin{aligned}&b_2 = i b_4, b_3 = -\frac{49}{18} \frac{B(x) b_4 A(x)}{C(x)}, b_4 = b_4, h_0 = -\frac{7776}{161} \frac{b_4^2 C(x)}{A(x)}, \nonumber \\ & \text{ and }\nonumber \\&\quad b_2 = i b_4, b_3 = -\frac{637}{720} \frac{B(x) b_4 A(x)}{C(x)}, b_4 = b_4, h_0 = -\frac{7776}{91} \frac{b_4^2 C(x)}{A(x)}. \end{aligned}$$
(9)

Using these parameters into Eq. (5) and then by using Eq. (3), we get:

$$\begin{aligned} r = \frac{2 \left( -2 b_4^2 t +2 b_4(b_4 t +b_3 x )\right) }{-b_4^2 t^2 + \left( b_4 t + b_3 x \right) ^2}, ~~~~~~ s = \frac{2 \left( -2 b_4^2 t +2 b_4(b_4 t +b_3 x )\right) }{h_0 -b_4^2 t^2 + \left( b_4 t + b_3 x \right) ^2}. \end{aligned}$$
(10)

The values of the parameters are mentioned in Eq. (9). Now, r and s gives the required solution for Eq. (1),

$$\begin{aligned}&p_{3}(x , t) = \frac{(72 + 72 i) C(x) \left( (1259712 - 1259712 i) C(x)^3 + 284004 A(x)^2 B(x) C(x) t x - 386561 A(x)^3 B(x)^2 x^2 \right) }{(36 C(x) t - 49 A(x) B(x) x) \left( 2519424 C(x)^3 + 284004 A(x)^2 B(x) C(x) t x - 386561 A(x)^3 B(x)^2 x^2 \right) }, \nonumber \\&\quad p_{4}(x , t) = \frac{(2880 + 2880 i) C(x) \left( (2015539200 - 2015539200 i) C(x)^3 + 83472480 A(x)^2 B(x) C(x) t x - 36924979 A(x)^3 B(x)^2 x^2 \right) }{(1440 C(x) t - 637 A(x) B(x) x) \left( 4031078400 C(x)^3 + 83472480 A(x)^2 B(x) C(x) t x - 36924979 A(x)^3 B(x)^2 x^2 \right) }. \end{aligned}$$
(11)
Fig. 3
figure 3

Graphs of \(p_{3}(x,t)\) in Eq. (11) at \(A(x)=-1, B(x)=2, C(x)=-0.5\) respectively. Solution shows the multiple parallel bright solitons

Full size image
Fig. 4
figure 4

Graphs of \(p_{4}(x,t)\) in Eq. (11) at \(A(x)=0.4, B(x)=-0.5, C(x)=1\) respectively. Solution shows multiple bright solitons which are rapidly increasing their size

Full size image

3 Lump interaction with kink-waves

To attain kink interaction solutions we use the following forms,

$$\begin{aligned} u = \chi _1^{2} + \chi _2^{2} + e^{\varrho _1} + g_0, ~~~~~ v = \chi _1^{2} + \chi _2^{2} + e^{\varrho _2} + h_0, \end{aligned}$$
(12)

where \(\chi _{1}=b_{1} x+ b_{2} t,\) \(\chi _{2}=b_{3} x+ b_{4} t,\) \(\varrho _1=a_1 x +a_2 t\) and \(\varrho _2=a_3 x +a_4 t\) However, \(b_i\)s, \(a_i\)s, \(g_0\) and \(h_0\) are real -valued constants. Now, inserting u and v into Eq. (4) and collecting all powers of x, t, \(e^{a_1 x +a_2 t}\) and \(e^{a_3 x +a_4 t}\), which implies us the following nonzero parameters:

Set I:

$$\begin{aligned}&b_2 = i b_4, b_3 = -\frac{116025}{821762} \frac{A(x)^2 \sqrt{-\frac{35 A(x)}{1282 C(x)}} h_0}{C(x) b_4},\\&\quad b_4 = b_4, a_1 = a_1, a_2 = \sqrt{-\frac{35 A(x)}{1282 C(x)}}, a_3 = a_3, h_0 = h_0, \end{aligned}$$

and

$$\begin{aligned} b_2= \, &{} b_4 \sqrt{\frac{67 A(x) - 12 a_4 \left( 12 B(x) + 5 a_4 (-71 C(x) + 100 a_4 D(x)) \right) }{9 A(x) + 4 a_4 \left( 18 B(x) + 5 a_4 (39 C(x) + 20 a_4 D(x)) \right) }},\nonumber \\ a_1= \, &{} a_1, a_3 = a_3, a_4 = a_4, b_4 = b_4, \nonumber \\ b_3= \, &{} -\frac{4}{5} a_4 b_4 \left( -19 A(x) + 2 a_4 (9 B(x) + 70 a_4 (-9 C(x) + 10 a_4 D(x))) \right) . \end{aligned}$$
(13)

Using these parameters into Eq. (12) and then by using Eq. (3), we get:

$$\begin{aligned} r= \, &{} \frac{2 \left( a_2 e^{a_2 t +a_1 x} -2 b_4^2 t +2 b_4(b_4 t +b_3 x) \right) }{e^{a_2 t +a_1 x} - b_4^2 t^2 + (b_4 t +b_3 x)^2 }, s = {} \frac{2 \left( -2 b_4^2 t +2 b_4(b_4 t +b_3 x) \right) }{e^{a_3 x} +h_0 - b_4^2 t^2 + (b_4 t +b_3 x)^2},\nonumber \\ \text{ and } \nonumber \\ r= \, &{} \frac{2 \left( \Lambda +2 b_4(b_4 t -\frac{4}{5} a_4 b_4 \left( -19 A(x) + 2 a_4 (9 B(x) + 70 a_4 (-9 C(x) + 10 a_4 D(x))) \right) x) \right) }{\nonumber }\\&\quad {e^{a_1 x} +\frac{\Lambda }{2} t + (b_4 t -\frac{4}{5} a_4 b_4 \left( -19 A(x) + 2 a_4 (9 B(x) + 70 a_4 (-9 C(x) + 10 a_4 D(x))) \right) x)^2 }, \nonumber \\ s= \, &{} \frac{2 \left( a_4 e^{a_4 t +a_3 x} + \Lambda +2 b_4(b_4 t -\frac{4}{5} a_4 b_4 \left( -19 A(x) + 2 a_4 (9 B(x) + 70 a_4 (-9 C(x) + 10 a_4 D(x))) \right) x) \right) }{\nonumber }\\&\quad {e^{a_4 t +a_3 x} +\frac{\Lambda }{2} t + (b_4 t -\frac{4}{5} a_4 b_4 \left( -19 A(x) + 2 a_4 (9 B(x) + 70 a_4 (-9 C(x) + 10 a_4 D(x))) \right) x)^2 }. \end{aligned}$$
(14)

Now, r and s gives the required solution for Eq. (1),

$$\begin{aligned} p_{5}(x , t)& = 2 \left [ \frac{\sqrt{-\frac{35 A(x)}{1282 C(x)}} e^{\sqrt{-\frac{35 A(x)}{1282 C(x)}} t +a_1 x} -2 b_4^2 t +2 b_4(b_4 t -\frac{116025 A(x)^2 \sqrt{-\frac{35 A(x)}{1282 C(x)}} h_0 x}{821762 C(x) b_4}) }{e^{\sqrt{-\frac{35 A(x)}{1282 C(x)}} t +a_1 x} -b_4^2 t^2 +(b_4 t -\frac{116025 A(x)^2 \sqrt{-\frac{35 A(x)}{1282 C(x)}} h_0 x}{821762 C(x) b_4})} \right. \nonumber \\&\quad \left.+\frac{i \left( -2 b_4^2 t + 2 b_4 (b_4 t -\frac{116025 A(x)^2 \sqrt{-\frac{35 A(x)}{1282 C(x)}} h_0 x}{821762 C(x) b_4}) \right) }{e^{a_3 x} +h_0 - b_4^2 t^2 +(b_4 t -\frac{116025 A(x)^2 \sqrt{-\frac{35 A(x)}{1282 C(x)}} h_0 x}{821762 C(x) b_4})^2} \right ], \nonumber \\ \quad p_{6}(x , t) &= 2 \left [ \frac{\Lambda +2 b_4(b_4 t -\frac{4}{5} a_4 b_4 \left( -19 A(x) + 2 a_4 (9 B(x) + 70 a_4 (-9 C(x) + 10 a_4 D(x))) \right) x) }{e^{a_1 x} +\frac{\Lambda }{2} t + (b_4 t -\frac{4}{5} a_4 b_4 \left( -19 A(x) + 2 a_4 (9 B(x) + 70 a_4 (-9 C(x) + 10 a_4 D(x))) \right) x)^2 } \right. \nonumber \\& \quad \left.+ \frac{i \left( a_4 e^{a_4 t +a_3 x} + \Lambda +2 b_4(b_4 t -\frac{4}{5} a_4 b_4 \left( -19 A(x) + 2 a_4 (9 B(x) + 70 a_4 (-9 C(x) + 10 a_4 D(x))) \right) x) \right) }{e^{a_4 t +a_3 x} +\frac{\Lambda }{2} t + (b_4 t -\frac{4}{5} a_4 b_4 \left( -19 A(x) + 2 a_4 (9 B(x) + 70 a_4 (-9 C(x) + 10 a_4 D(x))) \right) x)^2 } \right ], \end{aligned}$$
(15)

where \(\Lambda = \frac{2 b_4^2 (67 A(x) - 12 a_4 (12 B(x) + 5 a_4 (-71 C(x) + 100 a_4 D(x)))) t}{9 A(x) + 4 a_4 (18 B(x) + 5 a_4 (39 C(x) + 20 a_4 D(x)))}\).

Fig. 5
figure 5

Graphs of \(p_{5}(x,t)\) in Eq. (15) at \(A(x)=2, C(x)=0.2, a_1=3, a_3=-5, b_4=5, h_0=-2\) respectively. Solution shows one large and one small size bright solitons

Full size image
Fig. 6
figure 6

Graphs of \(p_{6}(x,t)\) in Eq. (15) at \(A(x)=1, B(x)=3, C(x)=-3, D(x)=-2, a_1=4, a_3=5, a_4=-2, b_4=1\) respectively. Solution shows dark and bright solitons

Full size image

Set II:

$$\begin{aligned}&b_1 = \frac{i (10 b_3 b_4 - 45 A(x) a_2^3 g_0 + 246 a_2^5 C(x) g_0)}{10 b_4}, b_2 = i b_4, b_3 = b_3, b_4 = b_4, a_1 = a_1, a_2 = a_2, a_3 = a_3, g_0 = g_0, \nonumber \\ & \text{ and } \nonumber \\&b_1 = b_1, b_3 = b_3, b_4 = b_4, a_1 = a_1, a_2 = \sqrt{\frac{2}{3595}}\sqrt{-\frac{5 B(x) + 8 a_4 (C(x) + 25 a_4 D(x))}{D(x)}}, a_3 = a_3, a_4 = a_4. \end{aligned}$$
(16)

Using these parameters into Eq. (12) and then by using Eq. (3), we get:

$$\begin{aligned}&r = \frac{2 \left( a_2 e^{a_2 t +a_1 x} +2 b_4(b_4 t +b_3 x) +2 i b_4 (i b_4 t + b_1 x) \right) }{e^{a_2 t +a_1 x} +g_0 +(b_4 t +b_3 x)^2 + (i b_4 t + b_1 x)^2}, ~~~ s = \frac{2 \left( 2 b_4(b_4 t +b_3 x) +2 i b_4 (i b_4 t + b_1 x) \right) }{e^{a_3 x} + (b_4 t +b_3 x)^2 + (i b_4 t + b_1 x)^2}, \nonumber \\ & \text{ and } \nonumber \\&r = \frac{2 \left( a_2 e^{a_2 t +a_1 x} +2 b_4(b_4 t +b_3 x) \right) }{e^{a_2 t +a_1 x} +b_1^2 x^2 + (b_4 t + b_3 x)^2}, ~~~ s = \frac{2 \left( a_4 e^{a_4 t +a_3 x} +2 b_4 (b_4 t + b_3 x) \right) }{e^{a_4 t +a_3 x} +b_1^2 x^2 + (b_4 t + b_3 x)^2}. \end{aligned}$$
(17)

The values of the parameters are mentioned in Eq. (16). Now, r and s gives the required solution for Eq. (1),

$$\begin{aligned}&p_{7}(x , t) = 2 \left [ \frac{i \left( 2 b_4(b_4 t +b_3 x) +2 i b_4 (i b_4 t + \frac{i (10 b_3 b_4 - 45 A(x) a_2^3 g_0 + 246 a_2^5 C(x) g_0) x}{10 b_4}) \right) }{e^{a_3 x} + (b_4 t +b_3 x)^2 + (i b_4 t + \frac{i (10 b_3 b_4 - 45 A(x) a_2^3 g_0 + 246 a_2^5 C(x) g_0) x}{10 b_4})^2} \right. \nonumber \\&\quad \left.+\frac{a_2 e^{a_2 t +a_1 x} +2 b_4(b_4 t +b_3 x) +2 i b_4 (i b_4 t + \frac{i (10 b_3 b_4 - 45 A(x) a_2^3 g_0 + 246 a_2^5 C(x) g_0) x}{10 b_4}) }{e^{a_2 t +a_1 x} +g_0 +(b_4 t +b_3 x)^2 + (i b_4 t + \frac{i (10 b_3 b_4 - 45 A(x) a_2^3 g_0 + 246 a_2^5 C(x) g_0) x}{10 b_4})^2} \right ], \nonumber \\ \nonumber \\&\quad p_{8}(x , t) = 2 \left [\frac{\sqrt{\frac{2}{3595}}\sqrt{-\frac{5 B(x) + 8 a_4 (C(x) + 25 a_4 D(x))}{D(x)}} e^{\sqrt{\frac{2}{3595}}\sqrt{-\frac{5 B(x) + 8 a_4 (C(x) + 25 a_4 D(x))}{D(x)}} t +a_1 x} +2 b_4(b_4 t +b_3 x) }{e^{\sqrt{\frac{2}{3595}}\sqrt{-\frac{5 B(x) + 8 a_4 (C(x) + 25 a_4 D(x))}{D(x)}} t +a_1 x} +b_1^2 x^2 + (b_4 t + b_3 x)^2}\right. \nonumber \\&\quad \left. + \frac{i \left( a_4 e^{a_4 t +a_3 x} +2 b_4 (b_4 t + b_3 x) \right) }{e^{a_4 t +a_3 x} +b_1^2 x^2 + (b_4 t + b_3 x)^2} \right ]. \end{aligned}$$
(18)
Fig. 7
figure 7

Graphs of \(p_{7}(x,t)\) in Eq. (18) at \(A(x)=1, B(x)=0.5, a_1=-2, a_2=5, a_3=-1, b_3=1, b_4=-4, g_0=1\) respectively. Figure represents bright wave solutions

Full size image
Fig. 8
figure 8

Graphs of \(p_{8}(x,t)\) in Eq. (18) at \(B(x)=0.6, C(x)=-1, D(x)=-0.5, a_1=2, a_3=4, a_4=-2, b_1=-6, b_3=2, b_4=10\) respectively. Solution shows equal sizes dark and bright solitons

Full size image

4 Lump interaction with periodic-wave

To attain kink interaction solutions we use the following forms,

$$\begin{aligned} u = \chi _1^{2} + \chi _2^{2} + b_0 \cos (\varrho _1) + g_0, ~~~~~ v = \chi _1^{2} + \chi _2^{2} + b_0 \cos (\varrho _2) + h_0, \end{aligned}$$
(19)

where \(\chi _{1}=b_{1} x+ b_{2} t,\) \(\chi _{2}=b_{3} x+ b_{4} t,\) \(\varrho _1=a_1 x +a_2 t\) and \(\varrho _2=a_3 x +a_4 t\). However, \(b_i\)’s, \(a_i\)’s, \(g_0\) and \(h_0\) are real -valued constants. Now, inserting u and v into Eq. (4) and collecting all powers of x, t, \(\cos (a_1 x +a_2 t)\), \(\sin (a_1 x +a_2 t)\), \(\cos (a_3 x +a_4 t)\) and \(\sin (a_3 x +a_4 t)\), which implies us the following nonzero parameters:

Set I:

$$\begin{aligned}&b_0 = b_0, b_1 = b_1, b_2 = i b_4, b_3 = b_3, b_4 = b_4, a_1 = a_1, a_2 = \frac{1}{2} \sqrt{\frac{3}{35}} \sqrt{-\frac{A(x)}{C(x)}}, \nonumber \\&\quad a_3 = a_3, a_4 = \frac{1}{2} \sqrt{\frac{A(x)}{7 C(x)} - \frac{6 B(x)}{5 D(x)}}, \nonumber \\ & \text{ and } \\&\quad b_0 = b_0, b_1 = b_1, b_2 = i b_4, b_3 = b_3, b_4 = b_4, g_0 = g_0, h_0 = h_0, a_3 = a_3, ~~\nonumber \\&\quad a_1 = \frac{633}{242} \sqrt{\frac{3}{11}} B(x) \left( \frac{B(x)}{D(x)}\right) ^{3/2}, a_2 = \frac{1}{2} \sqrt{\frac{3}{11}} \sqrt{\frac{B(x)}{D(x)}}. \nonumber \end{aligned}$$
(20)

Using these parameters into Eq. (19) and then by using Eq. (3), we get:

$$\begin{aligned}&r = \frac{2 \left( 2 i b_4 (i b_4 t +b_1 x) +2 b_4 (b_4 t + b_3 x) -a_2 b_0 \sin (a_2 t +a_1 x) \right) }{(i b_4 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + b_0 \cos (a_2 t +a_1 x)}, ~~~ s = \frac{2 \left( 2 i b_4 (i b_4 t +b_1 x) +2 b_4 (b_4 t + b_3 x) -a_4 b_0 \sin (a_4 t +a_3 x) \right) }{(i b_4 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + b_0 \cos (a_4 t +a_3 x)}, \nonumber \\ & \text{ and } \nonumber \\&r = \frac{2 \left( 2 i b_4 (i b_4 t +b_1 x) +2 b_4 (b_4 t + b_3 x) -a_2 b_0 \sin (a_2 t +a_1 x) \right) }{g_0 + (i b_4 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + b_0 \cos (a_2 t +a_1 x)}, ~~~~~ s = \frac{2 \left( 2 i b_4 (i b_4 t +b_1 x) +2 b_4 (b_4 t + b_3 x) \right) }{h_0 + (i b_4 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + b_0 \cos (a_3 x)}. \end{aligned}$$
(21)

The values of the parameters are mentioned in Eq. (20). Now, r and s gives the required solution for Eq. (1),

$$\begin{aligned}&p_{9}(x , t) = \frac{1}{35} \left [\frac{140 (i b_1 + b_3) b_4 x -\sqrt{105} b_0 \sqrt{-\frac{A(x)}{C(x)}} \sin (\frac{1}{2} \sqrt{\frac{3}{35}} \sqrt{-\frac{A(x)}{C(x)}} t +a_1 x)}{\left( x (2 i b_1 b_4 t +b_1^2 x + b_3(2 b_4 t + b_3 x)) + b_0 \cos (\frac{1}{2} \sqrt{\frac{3}{35}} \sqrt{-\frac{A(x)}{C(x)}} t +a_1 x) \right) } \right. \nonumber \\& \quad \left.+ \frac{i \left( 140 (i b_1 + b_3) b_4 x -\sqrt{35} b_0 \sqrt{\frac{5 A(x)}{C(x)}-\frac{42 B(x)}{D(x)}} \sin (\frac{1}{2} \sqrt{\frac{A(x)}{7 C(x)} - \frac{6 B(x)}{5 D(x)}} t +a_3 x) \right) }{\left( x (2 i b_1 b_4 t +b_1^2 x + b_3(2 b_4 t + b_3 x)) + b_0 \cos (\frac{1}{2} \sqrt{\frac{A(x)}{7 C(x)} - \frac{6 B(x)}{5 D(x)}} t +a_1 x) \right) } \right ], \nonumber \\&\quad p_{10}(x , t) = 4 \left [\frac{11 (i b_1 + b_3) b_4 x - \sqrt{33} b_0 \sqrt{\frac{B(x)}{D(x)}} \sin (\frac{\sqrt{\frac{3}{11}} \sqrt{\frac{B(x)}{D(x)}} (121 D(x) t + 633 B(x)^2 x)}{242 D(x)})}{11 \left( g_0 + x (2 i b_1 b_4 t +2 b_3 b_4 t + b_1^2 x + b_3^2 x) + b_0 \cos (\frac{\sqrt{\frac{3}{11}} \sqrt{\frac{B(x)}{D(x)}} (121 D(x) t + 633 B(x)^2 x)}{242 D(x)}) \right) } \right. \nonumber \\& \quad \left. + \frac{i (i b_1 + b_3) b_4 x }{h_0 + x (2 i b_1 b_4 t +2 b_3 b_4 t + b_1^2 x + b_3^2 x) + b_0 \cos (a_3 x)} \right ]. \end{aligned}$$
(22)
Fig. 9
figure 9

Graphs of \(p_{9}(x,t)\) in Eq. (22) at \(A(x)=-0.3, B(x)=-0.6, C(x)=3, D(x)=2, a_1=5, a_3=-3, b_1=-5, b_3=3, b_4=-1.5, b_0=4\) respectively. Solution shows periodic wave interaction with bright and dark solitons

Full size image
Fig. 10
figure 10

Graphs of \(p_{10}(x,t)\) in Eq. (22) at \(B(x)=0.9, D(x)=-1, a_3=3.5, b_1=-6, b_3=-1, b_4=1, b_0=8, g_0=5, h_0=-3\) respectively. Solution shows periodic wave interaction with two bright solitons

Full size image

Set II:

$$\begin{aligned}&b_0 = b_0, b_1 = b_1, b_2 = b_2, b_3 = b_3, b_4 = b_4, a_1 = a_1, a_2 = -\frac{1}{2} \sqrt{\frac{-239 +\sqrt{1139035}}{10607}} \sqrt{\frac{A(x)}{C(x)}},\nonumber \\&\quad A_3 = a_3, g_0 = \frac{9631156 (b_2^2 + b_4^2) C(x)}{(-11324 + 3 \sqrt{1139035}) A(x)}, h_0 = \frac{9631156 (b_2^2 + b_4^2) C(x)}{3 \left( 11324 A(x) - 3 \sqrt{1139035} A(x) \right) }, \nonumber \\ & \text{ and } \nonumber \\&\quad b_0 = b_0, b_1 = b_1, b_2 = i b_4, b_3 = b_3, b_4 = b_4, h_0 = h_0, a_2 = \frac{1}{4} \sqrt{\frac{21}{110}} \sqrt{-\frac{B(x)}{D(x)}}, a_3 = a_3, \nonumber \\&\quad a_1 = \frac{\sqrt{\frac{7}{330}} \left( -\frac{B(x)}{D(x)}\right) ^{3/2} \left( 33327 B(x)^2 C(x)^2 + 7392 A(x) B(x) C(x) D(x) - 77440 A(x)^2 D(x)^2 \right) }{154880 B(x) C(x)^2}, a_4 = \frac{1}{4} \sqrt{\frac{8 A(x)}{3 C(x)} -\frac{7 B(x)}{55 D(x)}}. \end{aligned}$$
(23)

Using these parameters into Eq. (19) and then by using Eq. (3), we get:

$$\begin{aligned}&r = \frac{2 \left( 2 b_2 (b_2 t + b_1 x) +2 b_4 (b_4 t + b_3 x) +a_2 b_0 \sin (-a_2 t - a_1 x) \right) }{g_0 +( b_2 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + b_0 \cos (-a_2 t -a_1 x)}, ~~~ s = \frac{2 \left( 2 b_2 (b_2 t +b_1 x) +2 b_4 (b_4 t + b_3 x)\right) }{h_0 + (b_2 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + b_0 \cos (a_3 x)}, \nonumber \\ & \text{ and } \nonumber \\&\quad r = \frac{2 \left( 2 i b_4 (i b_4 t +b_1 x) +2 b_4 (b_4 t + b_3 x) -a_2 b_0 \sin (a_2 t +a_1 x) \right) }{(i b_4 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + b_0 \cos (a_2 t +a_1 x)}, ~~~ s = \frac{2 \left( 2 i b_4 (i b_4 t +b_1 x) +2 b_4 (b_4 t + b_3 x) -a_4 b_0 \sin (a_4 t +a_3 x) \right) }{h_0 + (i b_4 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + b_0 \cos (a_4 t + a_3 x)}. \end{aligned}$$
(24)

The values of the parameters are mentioned in Eq. (23). Now, r and s gives the required periodic waves solution for Eq. (1),

$$\begin{aligned} p_{11}(x , t)= \, &{} 2 \left [\frac{2 b_2 (b_2 t + b_1 x) +2 b_4 (b_4 t + b_3 x) -\frac{1}{2} \sqrt{\frac{-239 +\sqrt{1139035}}{10607}} b_0 \sqrt{\frac{A(x)}{C(x)}} \sin (\frac{1}{2} \sqrt{\frac{-239 +\sqrt{1139035}}{10607}} \sqrt{\frac{A(x)}{C(x)}} t - a_1 x) }{\frac{9631156 (b_2^2 + b_4^2) C(x)}{(-11324 + 3 \sqrt{1139035}) A(x)} +( b_2 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + b_0 \cos (\frac{1}{2} \sqrt{\frac{-239 +\sqrt{1139035}}{10607}} \sqrt{\frac{A(x)}{C(x)}} t - a_1 x)} \right.\nonumber \\& \quad \left. + ~~~~~~ \frac{2 i \left( b_2^2 t + b_1 b_2 x + b_4 (b_4 t + b_3 x)\right) }{\frac{9631156 (b_2^2 + b_4^2) C(x)}{3 \left( 11324 A(x) - 3 \sqrt{1139035} A(x) \right) } + (b_2 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + b_0 \cos (a_3 x)} \right ], \nonumber \\ \nonumber \\ p_{12}(x , t)= \, &{} 2 \left [\frac{i \left( 2 i b_4 (i b_4 t +b_1 x) +2 b_4 (b_4 t + b_3 x) -\frac{1}{4} b_0 \sqrt{\frac{8 A(x)}{3 C(x)} -\frac{7 B(x)}{55 D(x)}} \sin (\frac{1}{4} \sqrt{\frac{8 A(x)}{3 C(x)} -\frac{7 B(x)}{55 D(x)}} t +a_3 x) \right) }{h_0 + (i b_4 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + b_0 \cos (\frac{1}{4} \sqrt{\frac{8 A(x)}{3 C(x)} -\frac{7 B(x)}{55 D(x)}} t + a_3 x)} +~~~~~~~~~~~ \right.\nonumber \\&\quad \left. ~~~~~~ \frac{2 i b_4 (i b_4 t +b_1 x) +2 b_4 (b_4 t + b_3 x) -\frac{1}{4} \sqrt{\frac{21}{110}} b_0 \sqrt{-\frac{B(x)}{D(x)}} \sin (\Omega ) }{(i b_4 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + b_0 \cos (\Omega )} \right ], \end{aligned}$$
(25)

where \(\Omega = \frac{1}{4} \sqrt{\frac{21}{110}} \sqrt{-\frac{B(x)}{D(x)}} t + \frac{\sqrt{\frac{7}{330}} \left( -\frac{B(x)}{D(x)}\right) ^{3/2} \left( 33327 B(x)^2 C(x)^2 + 7392 A(x) B(x) C(x) D(x) - 77440 A(x)^2 D(x)^2 \right) x}{154880 B(x) C(x)^2}.\)

Fig. 11
figure 11

Graphs of \(p_{11}(x,t)\) in Eq. (25) at \(A(x)=-2, C(x)=4, a_1=-10, a_3=6, b_1=10, b_2=-8, b_3=5, b_4=15, b_0=5\) respectively. Solution shows periodic wave with bright and dark surfaces

Full size image
Fig. 12
figure 12

Graphs of \(p_{12}(x,t)\) in Eq. (25) at \(A(x)=3, B(x)=0.9, C(x)=-3, D(x)=-1, a_3=3.5, b_1=-6, b_3=-1, b_4=0.1, b_0=8, h_0=-3\) respectively. Figure shows M-shape periodic wave with two bright and one dark solitons

Full size image

5 Rogue-wave solutions

For this, we can use u and v as following,

$$\begin{aligned} u = \chi _1^{2} + \chi _2^{2} + \cosh (\varrho _1) + g_0, ~~~~~ v = \chi _1^{2} + \chi _2^{2} + \cosh (\varrho _2) + h_0, \end{aligned}$$
(26)

where \(\chi _{1}=b_{1} x+ b_{2} t,\) \(\chi _{2}=b_{3} x+ b_{4} t,\) \(\varrho _1=a_1 x +a_2 t\) and \(\varrho _2=a_3 x +a_4 t\). However, \(b_i\)’s, \(a_i\)’s, \(g_0\) and \(h_0\) are real -valued constants. Now, inserting u and v into Eq. (4) and collecting all powers of x, t, \(\cosh (a_1 x +a_2 t)\), \(\sinh (a_1 x +a_2 t)\), \(\cosh (a_3 x +a_4 t)\), \(\sinh (a_3 x +a_4 t)\), \(\cosh (a_3 x +a_4 t) \sinh (a_3 x +a_4 t)\) and \(\cosh (a_1 x +a_2 t) \sinh (a_3 x +a_4 t)\), which implies us the following nonzero parameters:

Set I:

$$\begin{aligned}&b_1 = b_1, b_2 = i b_4, b_3 = b_3, b_4 = b_4, a_1 = a_1, a_3 = -\frac{360828 \sqrt{\frac{2}{485}} B(x) \left( \frac{B(x)}{D(x)}\right) ^{3/2}}{235225}, \nonumber \\&a_4 = 3 \sqrt{\frac{2}{485}} \sqrt{\frac{B(x)}{D(x)}}, g_0 = -\frac{5}{2} h_0, h_0 = h_0, \nonumber \\ & \text{ and }\nonumber \\&b_1 = b_1, b_2 = i b_4, b_3 = b_3, b_4 = b_4, g_0 = g_0, h_0 = h_0, a_3 = a_3, ~~\nonumber \\&a_1 = \frac{3348 \left( -\frac{B(x)}{D(x)}\right) ^{5/2} D(x)}{25 \sqrt{5}}, a_2 = 3 \sqrt{-\frac{B(x)}{5 D(x)}}. \end{aligned}$$
(27)

Using these parameters into Eq. (26) and then by using Eq. (3), we get:

$$\begin{aligned}&r = \frac{2 \left( 2 i b_4 (i b_4 t +b_1 x) +2 b_4 (b_4 t + b_3 x) \right) }{g_0 + (i b_4 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + \cosh (a_1 x)}, \quad s = \frac{2 \left( 2 i b_4 (i b_4 t +b_1 x) +2 b_4 (b_4 t + b_3 x) + a_4 \sinh (a_4 t + a_3 x) \right) }{h_0 + (i b_4 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + \cosh (a_4 t + a_3 x)}, \nonumber \\ & \text{ and }\nonumber \\&\quad r = \frac{2 \left( 2 i b_4 (i b_4 t +b_1 x) +2 b_4 (b_4 t + b_3 x) +a_2 \sinh (a_2 t +a_1 x) \right) }{g_0 + (i b_4 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + \cosh (a_2 t +a_1 x)}, \quad s = \frac{2 \left( 2 i b_4 (i b_4 t +b_1 x) +2 b_4 (b_4 t + b_3 x) \right) }{h_0 + (i b_4 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + \cosh (a_3 x)}. \end{aligned}$$
(28)

The values of the parameters are mentioned in Eq. (27). Now, r and s gives the required solution for Eq. (1),

$$\begin{aligned}&p_{13}(x , t) = 2 \left [ \frac{4 (i b_1 + b_3) b_4 x }{-5 h_0 +2 x (2 i b_1 b_4 t +2 b_3 b_4 t + b_1^2 x + b_3^2 x) + 2 \cosh (a_1 x)} \right.\nonumber \\& \quad \left.+ \frac{i \left( 970 (i b_1 + b_3) b_4 x +3 \sqrt{970} \sqrt{\frac{B(x)}{D(x)}} \sinh (\frac{3 \sqrt{\frac{2}{485}} \sqrt{\frac{B(x)}{D(x)}} (235225 D(x) t - 120276 B(x)^2 x)}{235225 D(x)}) \right) }{485 \left( h_0 +x (2 i b_1 b_4 t +2 b_3 b_4 t +b_1^2 x + b_3^2 x) + \cosh (\frac{3 \sqrt{\frac{2}{485}} \sqrt{\frac{B(x)}{D(x)}} (235225 D(x) t - 120276 B(x)^2 x)}{235225 D(x)}) \right) } \right ], \nonumber \\&\quad p_{14}(x , t) = \frac{1}{5} \left [ \frac{20 i (i b_1 + b_3) b_4 x}{h_0 + x (2 i b_1 b_4 t +2 b_3 b_4 t + b_1^2 x + b_3^2 x) + \cosh (a_3 x)} \right. ~\nonumber \\&\quad \left. +\frac{20 (i b_1 + b_3) b_4 x +6 \sqrt{5} \sqrt{-\frac{B(x)}{D(x)}} \sinh (\frac{3 \sqrt{-\frac{B(x)}{D(x)}}(25 D(x) t + 1116 B(x)^2 x)}{25 \sqrt{5} D(x)})}{g_0 + x (2 i b_1 b_4 t +2 b_3 b_4 t + b_1^2 x + b_3^2 x) + \cosh (\frac{3 \sqrt{-\frac{B(x)}{D(x)}}(25 D(x) t + 1116 B(x)^2 x)}{25 \sqrt{5} D(x)})} \right ]. \end{aligned}$$
(29)
Fig. 13
figure 13

Evolution of rogue-waves with two large size bright solitons for \(p_{13}(x,t)\) in Eq. (29) at \(B(x)=1, D(x)=-1, a_1=3, b_1=-5, b_3=-4, b_4=2, h_0=-5\) respectively

Full size image
Fig. 14
figure 14

Evolution of rogue-waves with two bright and dark solitons for \(p_{14}(x,t)\) in Eq. (29) at \(B(x)=2, D(x)=-4, a_3=5, b_1=-3, b_3=-5, b_4=3, g_0=1, h_0=-2\) respectively

Full size image

Set II:

$$\begin{aligned}&b_1 = b_1, b_2 = i b_4, b_3 = b_3, b_4 = b_4, a_1 = a_1, g_0 = g_0, h_0 = h_0, \nonumber \\&a_3 = \frac{A(x) \sqrt{-\frac{A(x)}{C(x)}} (B(x) C(x) +7 A(x) D(x))}{4 C(x)^2}, a_4 = \sqrt{-\frac{A(x)}{4 C(x)}}, \nonumber \\ & \text{ and } \nonumber \\&b_1 = b_1, b_2 = b_2, b_3 = b_3, b_4 = b_4, a_1 = a_1, a_3 = a_3, a_4 = a_4, \nonumber \\&g_0 = -\frac{96}{5} \frac{C(x) (b_2^2 + b_4^2)}{A(x) - 40 C(x) a_4^2}, h_0 = \frac{16 C(x) (b_2^2 + b_4^2)}{A(x) - 40 C(x) a_4^2}. \end{aligned}$$
(30)

Using these parameters into Eq. (26) and then by using Eq. (3), we get:

$$\begin{aligned}&r = \frac{2 \left( 2 i b_4 (i b_4 t +b_1 x) +2 b_4 (b_4 t + b_3 x) \right) }{g_0 + (i b_4 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + \cosh (a_1 x)}, ~~~ s = \frac{2 \left( 2 i b_4 (i b_4 t +b_1 x) +2 b_4 (b_4 t + b_3 x) + \frac{1}{2} \sqrt{-\frac{A(x)}{C(x)}} \sinh (a_4 t + a_3 x) \right) }{h_0 + (i b_4 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + \cosh (a_4 t + a_3 x)}, \nonumber \\ & \text{ and } \nonumber \\&r = \frac{2 \left( 2 b_2 (b_2 t +b_1 x) +2 b_4 (b_4 t + b_3 x) \right) }{g_0 + (b_2 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + \cosh (a_1 x)}, ~~~~~ s = \frac{2 \left( 2 b_2 (b_2 t +b_1 x) +2 b_4 (b_4 t + b_3 x) +a_4 \sinh (a_4 t + a_3 x) \right) }{h_0 + (b_2 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + \cosh (a_4 t + a_3 x)}. \end{aligned}$$
(31)

The values of the parameters are mentioned in Eq. (30). Now, r and s gives the required solution for Eq. (1),

$$\begin{aligned}&p_{15}(x , t) = \left [ \frac{4 (i b_1 + b_3) b_4 x }{g_0 + x (2 i b_1 b_4 t +2 b_3 b_4 t + b_1^2 x + b_3^2 x) + \cosh (a_1 x)} \right.\nonumber \\& \quad\left.+ \frac{i \left( 4 (i b_1 + b_3) b_4 x + \sqrt{-\frac{A(x)}{C(x)}} \sinh (\frac{\sqrt{-\frac{A(x)}{C(x)}} (2 C(x)^2 t + A(x) B(x) C(x) x + 7 A(x)^2 D(x) x)}{4 C(x)^2}) \right) }{h_0 +x (2 i b_1 b_4 t +2 b_3 b_4 t +b_1^2 x + b_3^2 x) + \cosh (\frac{\sqrt{-\frac{A(x)}{C(x)}} (2 C(x)^2 t + A(x) B(x) C(x) x + 7 A(x)^2 D(x) x)}{4 C(x)^2}) } \right ], \nonumber \\&\quad p_{16}(x , t) = 2 \left [\frac{2 \left( b_2^2 t + b_1 b_2 x + b_4 (b_4 t + b_3 x) \right) }{-\frac{96 C(x) (b_2^2 + b_4^2)}{5(A(x) - 40 C(x) a_4^2)} + (b_2 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + \cosh (a_1 x)} \right. \nonumber \\& \quad\left. + \frac{i \left( 2 b_2 (b_2 t +b_1 x) +2 b_4 (b_4 t + b_3 x) +a_4 \sinh (a_4 t + a_3 x) \right) }{\frac{16 C(x) (b_2^2 + b_4^2)}{A(x) - 40 C(x) a_4^2} + (b_2 t +b_1 x)^2 + (b_4 t + b_3 x)^2 + \cosh (a_4 t + a_3 x)} \right ]. \end{aligned}$$
(32)
Fig. 15
figure 15

Evolution of rogue-waves with four large size bright solitons for \(p_{15}(x,t)\) in Eq. (32) at \(A(x)=2, B(x)=1, C(x)=-2, D(x)=-1, a_1=5, b_1=-3, b_3=-5, b_4=3, g_0=2, h_0=-2\) respectively. Solution shows two large size bright solitons.

Full size image
Fig. 16
figure 16

Evolution of rogue-waves with bright and dark solitons for \(p_{16}(x,t)\) in Eq. (32) at \(A(x)=2, C(x)=-2, a_1=5, a_3=6, a_4=-2, b_1=-3, b_2=4, b_3=-5, b_4=1\) respectively

Full size image

6 Periodic-cross lump waves solution

For interaction of lump with periodic and rogue waves, we can use u and v as following,

$$\begin{aligned} u = \chi _1^{2} + \chi _2^{2} + z_1 \cos (\varrho _1) + z_2 \cosh (\varrho _2) + g_0, ~~~~~ v = \chi _1^{2} + \chi _2^{2} + z_3 \cos (\varrho _1) + z_4 \cosh (\varrho _2) + h_0, \end{aligned}$$
(33)

where \(\chi _{1}=b_{1} x+ b_{2} t,\) \(\chi _{2}=b_{3} x+ b_{4} t,\) \(\varrho _1=a_1 x +a_2 t\) and \(\varrho _2=a_3 x +a_4 t\). However, \(b_i\)’s, \(a_i\)’s, \(g_0\), \(h_0\) and \(z_i\)’s are real -valued constants. Now, inserting u and v into Eq. (4) and collecting all powers of x, t, \(\cos (a_1 x +a_2 t)\), \(\sin (a_1 x +a_2 t)\), \(\cosh (a_3 x +a_4 t)\), \(\sinh (a_3 x +a_4 t)\), \(\cos (a_1 x +a_2 t) \cosh (a_3 x +a_4 t)\) and \(\sin (a_1 x +a_2 t) \sinh (a_3 x +a_4 t)\), which implies us the following nonzero parameters:

Set I:

$$\begin{aligned}&b_1 = b_1, b_4 = b_4, a_1 = a_1, a_2 = 3 \sqrt{-\frac{110 A(x)}{5233 C(x)}}, a_3 = a_3, a_4 = 3 \sqrt{-\frac{13 A(x)}{5233 C(x)}}, \nonumber \\&g_0 = \frac{512834}{5445} \frac{b_4^2 C(x)}{A(x)}, z_2 = -\frac{11}{2} z_4, z_3 = z_3, z_4 = z_4, \nonumber \\ & \text{ and } \nonumber \\&b_1 = b_1, b_4 = b_4, a_1 = a_1, a_2 = 3 \sqrt{-\frac{2 A(x)}{53 C(x)}}, a_3 = a_3, a_4 = 3 \sqrt{-\frac{13 A(x)}{2915 C(x)}}, \nonumber \\&h_0 = \frac{5194}{99} \frac{b_4^2 C(x)}{A(x)}, z_1 = z_1, z_2 = -\frac{2}{11} z_4, z_4 = z_4. \end{aligned}$$
(34)

Using these parameters into Eq. (33) and then by using Eq. (3), we get:

$$\begin{aligned}&r = \frac{2 \left( 2 b_4^2 t + a_4 z_2 \sinh (a_4 t + a_3 x) \right) }{g_0 + b_4^2 t^2 +b_1^2 x^2 + z_2 \cosh (a_4 t +a_3 x)}, ~~~ s = \frac{2 \left( 2 b_4^2 t -a_2 z_3 \sin (a_2 t + a_1 x) + a_4 z_4 \sinh (a_4 t + a_3 x) \right) }{b_4^2 t^2 +b_1^2 x^2 + z_3 \cos (a_2 t + a_1 x) + z_4 \cosh (a_4 t + a_3 x)}, \nonumber \\ & \text{ and } \nonumber \\&r = \frac{2 \left( 2 b_4^2 t -a_2 z_1 \sin (a_2 t + a_1 x) + a_4 z_2 \sinh (a_4 t + a_3 x) \right) }{b_4^2 t^2 +b_1^2 x^2 + z_1 \cos (a_2 t + a_1 x) + z_2 \cosh (a_4 t +a_3 x)}, ~~~ s = \frac{2 \left( 2 b_4^2 t + a_4 z_4 \sinh (a_4 t + a_3 x) \right) }{h_0 + b_4^2 t^2 +b_1^2 x^2 + z_4 \cosh (a_4 t + a_3 x)}. \end{aligned}$$
(35)

The values of the parameters are mentioned in Eq. (34). Now, r and s gives the required solution for Eq. (1),

$$\begin{aligned}&p_{17}(x , t) = 2 \left [\frac{2 b_4^2 t - \frac{33}{2} \sqrt{-\frac{13 A(x)}{5233 C(x)}} z_4 \sinh (3 \sqrt{-\frac{13 A(x)}{5233 C(x)}} t + a_3 x)}{\frac{512834}{5445} \frac{b_4^2 C(x)}{A(x)} + b_4^2 t^2 +b_1^2 x^2 -\frac{11}{2} z_4 \cosh (3 \sqrt{-\frac{13 A(x)}{5233 C(x)}} t + a_3 x)} \right. \nonumber \\& \quad \left.+ \frac{i \left( 2 b_4^2 t -3 \sqrt{-\frac{110 A(x)}{5233 C(x)}} z_3 \sin (3 \sqrt{-\frac{110 A(x)}{5233 C(x)}} t + a_1 x) + 3 \sqrt{-\frac{13 A(x)}{5233 C(x)}} z_4 \sinh (3 \sqrt{-\frac{13 A(x)}{5233 C(x)}} t + a_3 x) \right) }{b_4^2 t^2 +b_1^2 x^2 + z_3 \cos (3 \sqrt{-\frac{110 A(x)}{5233 C(x)}} t + a_1 x) + z_4 \cosh (3 \sqrt{-\frac{13 A(x)}{5233 C(x)}} t + a_3 x)} \right ], \nonumber \\ \nonumber \\&p_{18}(x , t) = 2 \left [\frac{2 b_4^2 t -3 \sqrt{-\frac{2 A(x)}{53 C(x)}} z_1 \sin (3 \sqrt{-\frac{2 A(x)}{53 C(x)}} t + a_1 x) - \frac{6}{11} \sqrt{-\frac{13 A(x)}{2915 C(x)}} z_4 \sinh (3 \sqrt{-\frac{13 A(x)}{2915 C(x)}} t + a_3 x) }{b_4^2 t^2 +b_1^2 x^2 + z_1 \cos (3 \sqrt{-\frac{2 A(x)}{53 C(x)}} t + a_1 x) -\frac{2}{11} z_4 \cosh (3 \sqrt{-\frac{13 A(x)}{2915 C(x)}} t +a_3 x)} \right.\nonumber \\& \quad \left.+ \frac{i \left( 2 b_4^2 t + 3 \sqrt{-\frac{13 A(x)}{2915 C(x)}} z_4 \sinh (3 \sqrt{-\frac{13 A(x)}{2915 C(x)}} t + a_3 x) \right) }{\frac{5194}{99} \frac{b_4^2 C(x)}{A(x)} + b_4^2 t^2 +b_1^2 x^2 + z_4 \cosh (3 \sqrt{-\frac{13 A(x)}{2915 C(x)}} t + a_3 x)} \right ]. \end{aligned}$$
(36)

Set II:

$$\begin{aligned}&b_1 = b_1, b_4 = \frac{33}{7} \sqrt{\frac{5}{10466}} \sqrt{\frac{A(x) g_0}{C(x)}}, a_1 = a_1, a_2 = 3 \sqrt{\frac{13 A(x)}{5233 C(x)}}, a_3 = a_3, a_4 = 3 \sqrt{\frac{110 A(x)}{5233 C(x)}}, \nonumber \\&g_0 = g_0, z_1 = -\frac{11}{2} z_3, z_3 = z_3, z_4 = z_4, \nonumber \\ & \text{ and }\nonumber \\&b_1 = b_1, b_4 = \frac{3}{7} \sqrt{\frac{11}{106}} \sqrt{\frac{A(x) h_0}{C(x)}}, a_1 = a_1, a_2 = 3 \sqrt{\frac{13 A(x)}{2915 C(x)}}, a_3 = a_3, a_4 = 3 \sqrt{\frac{2 A(x)}{53 C(x)}}, \nonumber \\&h_0 = h_0, z_1 = z_1, z_2 = z_2, z_3 = -\frac{11}{2} z_1. \end{aligned}$$
(37)

Using these parameters into Eq. (33) and then by using Eq. (3), we get:

$$\begin{aligned}&r = \frac{2 \left( \frac{5445 A(x) g_0 t}{256417 C(x)} - a_2 z_1 \sin (a_2 t + a_1 x) \right) }{g_0 + \frac{5445 A(x) g_0 t^2}{512834 C(x)} +b_1^2 x^2 + z_1 \cos (a_2 t +a_1 x)}, ~~~ s = \frac{2 \left( \frac{5445 A(x) g_0 t}{256417 C(x)} -a_2 z_3 \sin (a_2 t + a_1 x) + a_4 z_4 \sinh (a_4 t + a_3 x) \right) }{\frac{5445 A(x) g_0 t^2}{512834 C(x)} +b_1^2 x^2 + z_3 \cos (a_2 t + a_1 x) + z_4 \cosh (a_4 t + a_3 x)}, \nonumber \\ & \text{ and }\nonumber \\&r = \frac{2 \left( \frac{99 A(x) h_0 t}{2597 C(x)} - a_2 z_1 \sin (a_2 t + a_1 x) +a_4 z_2 \sinh (a_4 t +a_3 x) \right) }{\frac{99 A(x) h_0 t^2}{5194 C(x)} +b_1^2 x^2 + z_1 \cos (a_2 t +a_1 x) +z_2 \cosh (a_4 t +a_3 x)}, ~~~ s = \frac{2 \left( \frac{99 A(x) h_0 t}{2597 C(x)} -a_2 z_3 \sin (a_2 t + a_1 x) \right) }{h_0 +\frac{99 A(x) h_0 t^2}{5194 C(x)} +b_1^2 x^2 + z_3 \cos (a_2 t + a_1 x)}. \end{aligned}$$
(38)

The values of the parameters are mentioned in Eq. (37). Now, r and s give us the required solution,

$$\begin{aligned}&p_{19}(x , t) = 6 \left [\frac{11 \left( 330 A(x) g_0 t +49 \sqrt{68029} \sqrt{\frac{A(x)}{C(x)}} C(x) z_3 \sin (3 \sqrt{\frac{13 A(x)}{5233 C(x)}} t + a_1 x) \right) }{5445 A(x) g_0 t^2 +512834 C(x) (g_0 + b_1^2 x^2) -2820587 C(x) z_3 \cos (3 \sqrt{\frac{13 A(x)}{5233 C(x)}} t + a_1 x)} \right.\nonumber \\&\quad \left. +\frac{2 i \left( 1815 A(x) g_0 t -49 \sqrt{68029} \sqrt{\frac{A(x)}{C(x)}} C(x) z_3 \sin (3 \sqrt{\frac{13 A(x)}{5233 C(x)}} t + a_1 x) + 49 \sqrt{575630} \sqrt{\frac{A(x)}{C(x)}} C(x) z_4 \sinh (\Delta ) \right) }{5445 A(x) g_0 t^2 +512834 b_1^2 C(x) x^2 +512834 C(x) z_3 \cos (3 \sqrt{\frac{13 A(x)}{5233 C(x)}} t + a_1 x) + 512834 C(x) z_4 \cosh (\Delta )} \right ], \nonumber \\ \nonumber \\&\quad p_{20}(x , t) = 2 \left [\frac{3 i \left( 330 A(x) h_0 t +49 \sqrt{37895} \sqrt{\frac{A(x)}{C(x)}} C(x) z_1 \sin (3 \sqrt{\frac{13 A(x)}{2915 C(x)}} t + a_1 x) \right) }{5 \left( 99 A(x) h_0 t^2 +5194 C(x) (h_0 + b_1^2 x^2) -28567 C(x) z_1 \cos (3 \sqrt{\frac{13 A(x)}{2915 C(x)}} t + a_1 x) \right) } \right. \nonumber \\&\quad \left.+ \frac{\frac{99 A(x) h_0 t}{2597 C(x)} -3 \sqrt{\frac{13 A(x)}{2915 C(x)}} z_1 \sin (3 \sqrt{\frac{13 A(x)}{2915 C(x)}} t + a_1 x) + 3 \sqrt{\frac{2 A(x)}{53 C(x)}} z_2 \sinh (\Omega )}{\frac{99 A(x) h_0 t^2}{5194 C(x)} + b_1^2 x^2 +z_1 \cos (3 \sqrt{\frac{13 A(x)}{2915 C(x)}} t + a_1 x) + z_2 \cosh (\Omega )} \right ], \end{aligned}$$
(39)

where \(\Delta = 3 \sqrt{\frac{110}{5233}} \sqrt{\frac{A(x)}{C(x)}} t + a_3 x\),  and  \(\Omega = 3 \sqrt{\frac{2}{53}} \sqrt{\frac{A(x)}{C(x)}} t + a_3 x.\)

Fig. 17
figure 17

Evolution of periodic rogue and lump solitons for \(p_{17}(x,t)\) in Eq. (36) at \(A(x)=3, C(x)=-1, a_1=4, a_3=9, b_1=-3, b_4=8, z_3=-1, z_4=2\) respectively

Full size image
Fig. 18
figure 18

Evolution of periodic rogue and lump solitons for \(p_{20}(x,t)\) in Eq. (39) at \(A(x)=4, C(x)=-2, a_1=4, a_3=9, b_1=-5, z_1=3, z_2=2, h_0=-1\) respectively

Full size image

7 Result and discussions

Here, we’ll discuss some already published work on FVCNLSE and our newly gained results. The FVCNLSE has been investigated by various researchers, like: Lan investigated soliton and breather solutions based on Darboux transformations for FVCNLSE (Lan 2020). Zhao et al. obtained dark one, two and three -soliton solutions for FVCNLSE (Zhao et al. 2016). Huang et al. studied soliton stability, dark solitons and interactions with dark two solitons for FVCNLSE (Huang et al. 2019). Liu et al. studied multi-soliton, and interactions of one, two and three solitons for FVCNLSE (Liu et al. 2020). Huang investigated integrability and dark solutions for FVCNLSE (Huang 2019).

In this work, we investigated lump solutions, lump with kink, periodic waves, rogue-waves, and periodic cross lump waves for FVCNLSE with the aid of some new ansatz forms. All new results have been shown in graphical ways by assigning real values to the parameters. Figures 1, 2, 3, 4 represents lump solutions for \(p_1\), \(p_2\), \(p_3\) and \(p_4\) respectively. Figures 5, 6, 7, 8 represents lump with kink solutions for \(p_5\), \(p_6\), \(p_7\) and \(p_8\) respectively. In Figures 9,10, 11, 12 we successfully obtained periodic wave solutions with lump solitons for \(p_9\), \(p_{10}\), \(p_{11}\) and \(p_{12}\). Figures (13, 14, 15, 16) shows the rogue waves solutions for \(p_{13}\), \(p_{14}\), \(p_{15}\) and \(p_{16}\) respectively. We can see in \(p_{13}\) when \(h_0 \rightarrow \infty\) then \(p_{13} \rightarrow 0\), and similarly in \(p_{14}\) & \(p_{15}\) when \(g_0 + h_0 \rightarrow \infty\) then \(p_{14} ~ \& ~ p_{15} \rightarrow 0\). Figure (17, 18) represents the evaluation of lump, periodic and rogue waves for \(p_{17}\) and \(p_{20}\) respectively. From solutions \(p_{17}\) to \(p_{20}\) we can see that A(x) and C(x) both are not be equal to zero, when they are zero then our solutions will be undefined.

8 Concluding remarks

In this article, we studied FVCNLSE and obtained various lump and interaction solutions with the aid of some new ansatz transformations. For this model we successfully achieved twenty new proper solutions and also show them in 3D, 2D and contour shapes. These new forms are effective and powerful in solving more nonlinear models.