Multiple lump and rogue wave for time fractional resonant nonlinear Schrödinger equation under parabolic law with weak nonlocal nonlinearity

Abstract

This article retrieve lump, lump with one kink and rogue wave soliton for the time fractional resonant nonlinear Schrödinger equation with parabolic law having weak nonlocal nonlinearity. According to theory of dynamical systems, Schrödinger equation may be converted into plane systems. We use Hirota bilinear method to obtained these solutions. At the end, we present graphical representation of our results in various dimensions.

1 Introduction

Nonlinear partial differential equations (NLPDE) play a basic role to solve various issues appear in different fields of mathematical and physical sciences such as physics, chemistry, biology and engineering (Ahmed et al. 2019; Akhmediev et al. 2009; Akram et al. 2021). In NLPDEs, higher order nonlinear Schrödinger equations (NLSEs) are main sectors for nonlinear optics which interpret the proliferation specifically short pulse in optical fibers and have large appliances in telecommunication system and ultrafast signal routing etc. The NLSE have a huge impact on nonlinear mathematical model in condensed matter physics, fluid mechanics and nonlinear optics (Ali et al. 2020; Biswas et al. 2018; Chabchoub et al. 2011; Chen et al. 2020; Dianchen et al. 2018). There are so many renowned NLSEs such as Kundu Mukherjee Naskar model (Dong et al. 2019), derivative NLSE (Dysthe et al. 2008), Fokas–Lenells equation (Ekici et al. 2017) and so many other. Nowadays fractional NLSE has so many applications in different fields of sciences particularly in the field of optics, where the fractional order may be fractional diffraction effect, space fractional order or t-fractional order (Eslami et al. 2013; Farah et al. 2020; Foroutan et al. 2018; Gaber et al. 2019; Ghaffar et al. 2020). Since last two decades, so many integration schemes have been used to get soliton solutions for various NLSEs like; the semi-inverse method (Dong et al. 2019), Kudryashove scheme (Ghanbari et al. 2020), extended mapping method (He 2020), HBM (Ismael et al. 2020), generalized exponential rational function scheme (Kumar et al. 2014), extended auxiliary equation method (Longhi 2015), $(G'/G)$ expansion method (Ma and Zhou 2018), $exp((-\psi '/ \psi )\eta )$-expansion method (Ozkan et al. 2020) and Seadawy techniques (Rizvi et al. 2020a, b; Sarwar and Rashidi 2016; Seadawy and Cheemaa 2019a, b). Here we consider TFRNLSE under parabolic law with weak nonlocal nonlinearity to obtain multiple lump and rogue wave solutions. The governing model for TFRNLSE is given by Seadawy and Cheemaa (2019a)

$$\begin{aligned} i {\frac{{\partial ^\beta u}}{\partial t^\beta }} +au_{xx}+b\left\{ c_1|u|^2+c_2|u|^4+c_3(|u|^2)_{xx}\right\} u+c\left\{ {\frac{{|u|_{xx}}}{|u|}} \right\} u=0,~~~~~0<\beta <1, \end{aligned}$$

(1)

where $\frac{{\partial ^\beta u}}{\partial t^\beta },$ is conformable derivative operator in t-direction and $\beta \in (0,1)$. Eq. (1) describes the proliferation of optical pulse in nonlinear optical fibers, where $u = u(x,t)$ is a complex function which show a normalized complex amplitude of the pulse envelope in nonlinear optical fibers, x is the normalized proliferation distance, t represents the related time, while a,  b and c are nonzero real constants.

Conformal Derivative: $Let~ h:(0,\infty )\rightarrow R,$ then conformable fractional derivative (CFD) of h order $\beta$ is defined as Seadawy and Cheemaa (2019a),

$$\begin{aligned} S_{\beta }(h)(t)=\lim _{\theta \rightarrow 0} \frac{h(t + \theta t^{1-\beta }) - h(t)}{\theta } \end{aligned}$$

(2)

$\forall ~t > 0,$ $\beta \in (0,1).$

If the CFD of h order $\beta$ exists, then h is $\beta$-differentiable. Let $\beta \in (0,1)$ and h, g be $\beta$-differentiable at $t > 0,$ then some properties of CFD are as follows:

• (i)   $S_\beta (x h+y g)=xS_\beta (h)+yS_\beta (g),~~x,y \in R;$

• (ii)  $S_\beta (hg)=hS_\beta (g)+gS_\beta (h);$

• (iii)  $S_\beta (\frac{h}{g})=\frac{gS_\beta (g)-hS_\beta (g)}{g^2};$

• (iv)  $S_\beta (t^\nu )=\nu t^{\nu -\beta },~~\nu \in R;$

• (v)  $S_\beta (\phi )=0, ~~ \forall$ constant function $h(t)=\phi ;$

• (vi)  $S_{\beta }(h)(t)=t^{1-\beta }\frac{dh}{dt};$

• (vii)  Suppose $h,g:[0,\infty )\rightarrow R,$ then $S_\beta (h \circ g)(t)=t^{1-\beta } g'(t)h'(g(t))$.

Consider the fractional transformation (Seadawy et al. 2019), given by:

$$\begin{aligned} \tau =\frac{t^\beta }{\beta } \end{aligned}$$

(3)

Now after using Eq. (3) into Eq. (1), we get the following NLSE:

$$\begin{aligned} i {\frac{{\partial u}}{\partial \tau }} +au_{xx}+b\left\{ c_1|u|^2+c_2|u|^4+c_3(|u|^2)_{xx}\right\} u+c\left\{ {\frac{{|u|_{xx}}}{|u|}} \right\} u=0,~~~~~0<\alpha <1, \end{aligned}$$

(4)

Now we will study the above model for multiple lump and interaction solutions (Seadawy et al. 2019a, b, 2020; Singh et al. 2016; Solli et al. 2008). Lump solitons are rationally localised in all space directions. The applications of lump waves are very wide, such as various ghost waves which appear and disappear unexpectedly and unpredictably, particularly, covid-19. Lump solutions, studied in various fields like biology, finance, engineering, non-linear optics, chemistry, atmosphere and physics etc. HBM is a very helpful technique to compute algorithms for formulation of multiple solitons (Suret et al. 2016; Trki et al. 2012; Wazwaz 2008; Younas et al. 2020). The main purpose is to find multiple lump solution for Eq. (4), based on bilinear method.

In order to solve Eq. (4), we substitute $u=p+iq$, where $|u|=\sqrt{p^2+q^2}$. Thus the Eq. (4) may be converted into real and imaginary parts given as:

$$\begin{aligned} {\left\{ \begin{array}{ll} -A^2 q_\tau +A^2 a p_{xx}+A^2 b p\{Ac_1+A^2 c_2+2Bc_3\}+cp\{-C^2+AB\}=0,\\ A^2 p_\tau +A^2 a q_{xx}+A^2 b q\{Ac_1+A^2 c_2+2Bc_3\}+cq\{-C^2+AB\}=0. \end{array}\right. } \end{aligned}$$

(5)

where $A=p^2+q^2,$ $B=pp_{xx}+qq_{xx}+p_x^2 +q_x^2,$ $C=pp_x +qq_x,$ while $p(x,\tau ),$ and $q(x,\tau )$ are complex wave dependent variables appeared in the physical systems, including plasma physics, nonlinear optics and others.

The contents of this paper are organised as: In Sect. 2, we evaluate the lump solutions for TFRNLSE. In Sect. 3, we find out lump one stripe interactional solutions. In Sect. 4, the brief discussion of rogue wave solutions for Eq. (4) will be given. In Sect. 5, results and discussions about our newly obtained and previous results will be presented and in Sect. 6, we give concluding remarks.

2 Lump solution

To find lump solutions of Eq. (5), we use transformation (Younas et al. 2021),

$$\begin{aligned} p ={\frac{{6}}{\rho }}{\left( {\ln g} \right) _{x}}~,~~~ q ={\frac{{6}}{\omega }}{\left( {\ln h} \right) _{x}}~. \end{aligned}$$

(6)

Which transforms Eq. (5) in bilinear form,

$$\begin{aligned} {\left\{ \begin{array}{ll} 36b{c_{1}}{\rho ^2}{\omega ^8}{g^2}{h^8}g_x^7 +2a{\rho ^4}{\omega ^8}{g^2}{h^8}g_x^7 + 2c{\rho ^4}{\omega ^8}{g^2}{h^8}g_x^7 + 1296bc_2{\omega ^8}{h^8}g_x^9+ \ldots + \\ c{\rho ^8}{\omega ^4}{g^8}{h^4}g_x h_x^3{h_{xxx}}+144bc_3{\rho ^6}{\omega ^4}{g^6}{h^4}g_x^3 h_x^3{h_{xxx}}+72bc_3{\rho ^8}{\omega ^2}{g^8}{h^2}g_x h_x^5{h_{xxx}} = 0,\\ {\rho ^3}{\omega ^9}{g^2}{h^9}g_\tau g_x^5 -36bc_1{\rho ^2}{\omega ^8}{g^2}{h^8}g_x^6 h_x - 2c{\rho ^4}{\omega ^8}{g^2}{h^8}g_x^6 h_x -1296bc_2{\omega ^8}{h^8}g_x^8 h_x- \ldots \\ -c{\rho ^8}{\omega ^4}{g^8}{h^4}h_x^4{h_{xxx}}-144bc_3{\rho ^6}{\omega ^4}{g^6}{h^4}g_x^2 h_x^4{h_{xxx}}-72bc_3{\rho ^8}{\omega ^2}{g^8}{h^2} h_x^6 {h_{xxx}} = 0. \end{array}\right. } \end{aligned}$$

(7)

Now the function g and h in Eq. (8) can be assumed as Zhang and Pang (2019), we set g and h in the bilinear form (7) as,

$$\begin{aligned} g=\xi _{1}^{2}+\xi _{2}^{2}+a_{2}, ~~~~h=\xi _{1}^{2}+\xi _{2}^{2}+a_{3}. \end{aligned}$$

(8)

where $\xi _1=a_{0}x+\tau ,$ $\xi _2=a_{1}x+\tau$. However, $a_{j}~( 0 \le j \le 3)$ are all real parameters to be measured. Now, putting g and h into Eq. (8) and associating the coefficients of the x and $\tau$, then we use Eq. (6) and find p and q which relate to u(x, t),  having fractional transformation Eq. (3), implies us the subsequent result on parameters:

Set I When $a_0 = 0,$ we get the following solutions:

$$\begin{aligned} {\left\{ \begin{array}{ll} {a_1} = {a_1} ,{a_2} = {a_2},{a_3} = {a_3},\rho =\frac{6\sqrt{-\frac{-2a_3^2 bc1+2bc_1 a_2^2}{a+c}}}{a_2},\omega =\frac{6\sqrt{-\frac{2a_3^2 bc1-2bc_1 a_2^2}{a+c}}}{a_3}, \\ {a_1} = {a_1} ,{a_2} =0,{a_3} = {a_3},\omega =\omega ,\rho =\frac{1}{10}\sqrt{-350+10\sqrt{385}}\omega ~. \end{array}\right. } \end{aligned}$$

(9)

parameters in Eq. (9), leads the lump solutions to Eq. (5):

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{11}(x,t)=\frac{2 a_1 a_2 \left( a_1 x +\frac{t^\beta }{\beta }\right) }{ \sqrt{-\frac{2a_2^2 bc1-2a_3^2 bc_1}{a+c}}\left( a_2+\left( a_1 x+\frac{t^\beta }{\beta } \right) ^2+\frac{t^{2\beta }}{\beta ^2}\right) }+\frac{2i a_1 a_3 \left( a_1 x +\frac{t^\beta }{\beta }\right) }{ \sqrt{-\frac{-2a_2^2 bc1+2a_3^2 bc_1}{a+c}}\left( a_3+\left( a_1 x+\frac{t^\alpha }{\alpha } \right) ^2+\frac{t^{2\alpha }}{\alpha ^2} \right) }, \\ u_{12}(x,t)=-\frac{120ia_1\left( a_1 x+\frac{t^\beta }{\beta }\right) }{\sqrt{350-10 \sqrt{385}}\left( \left( a_1 x+\frac{t^\beta }{\beta }\right) ^2+\frac{t^{2\beta }}{\beta ^2}\right) \omega } + \frac{12ia_1\left( a_1 x+\frac{t^\beta }{\beta }\right) }{\left( a_3+\left( a_1x+\frac{t^\beta }{\beta } \right) ^2+\frac{t^{2\beta }}{\beta ^2} \right) \omega } . \end{array}\right. } \end{aligned}$$

(10)

Set II

$$\begin{aligned} {\left\{ \begin{array}{ll} {a_1} = {a_1},{a_2} = -\frac{25}{72} a_3,{a_3} = {a_3},\omega =\omega ,\rho =\sqrt{-1}\omega ,\\ {a_1} = {a_1},{a_2} =0,{a_3} = {a_3},\omega =36\sqrt{130}\sqrt{-\frac{bc_1}{122528a+58373c} },\rho =18\sqrt{-\frac{10 bc_1}{17504a+8339c}}. \end{array}\right. } \end{aligned}$$

(11)

parameters in Eq. (11), implies the lump solutions to Eq. (5):

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{21}(x,t) =-\frac{12ia_1\left( a_1 x+\frac{t^\beta }{\beta }\right) }{ \left( -\frac{25a_3}{72}+\left( a_1 x+\frac{t^\beta }{\beta } \right) ^2 +\frac{t^{2\beta }}{\beta ^2}\right) \omega }+\frac{12ia_1\left( a_1 x+\frac{t^\beta }{\beta }\right) }{ \left( a_3+\left( a_1 x+\frac{t^\beta }{\beta }\right) ^2 +\frac{t^{2\beta }}{\beta ^2}\right) \omega }, \\ u_{22}(x,t)=\frac{\sqrt{\frac{2}{5}}a_1\left( a_1 x+\frac{t^\beta }{\beta } \right) }{3\sqrt{-\frac{bc_1}{17504a+8339c}}\left( \left( a_1 x+\frac{t^\beta }{\beta } \right) ^2+\frac{t^{2\beta }}{\beta ^2}\right) } + \frac{ia_1\left( a_1 x+\frac{t^\beta }{\beta } \right) }{3\sqrt{130}\sqrt{-\frac{bc_1}{122528a+58373c}}\left( a_3+\left( a_1 x+\frac{t^\beta }{\beta } \right) ^2+\frac{t^{2\beta }}{\beta ^2}\right) }. \end{array}\right. } \end{aligned}$$

(12)

Fig. 1

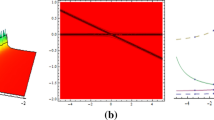
The graphs of the solution $u_{11}(x,t)$ in Eq. (10) are shown via suitable parameters $a_1=-3, a_2=-1,a_3=b=5,a=-1,c_1=1,c=2$. Three-dimensional graphs at (i) $\beta =0.95$, (ii) $\beta =0.48$, and (iii) $a_1=-1, a_2=1,a_3=6,b=7,a=-2,c_1=3,c=4,\beta =0.55$ respectively

Fig. 2

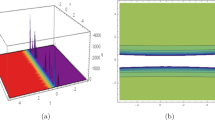
The graphs of the solution $u_{12}(x,t)$ in Eq. (10) are shown via suitable parameters $a_1=0.1, a_3=-0.4,\omega =3$. Three-dimensional graphs at (i) $\beta =0.18$, (ii) $\beta =0.718$, and (iii) $a_1=-5, a_3=1,\omega =3,\beta =0.008$ respectively

Fig. 3

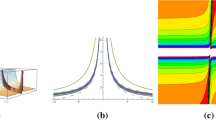
The profiles of the solution $u_{21}(x,t)$ in Eq. (12) are shown by different choices of parameters $a_1=-3, a_3=1, \omega =5$. Three-dimensional graphs at (i) $\beta =0.008$, (ii) $\beta =0.558$, and (iii) $a_1=-1, a_3=3, \omega =10,\beta =0.88$ respectively

Fig. 4

The profiles of the solution $u_{22}(x,t)$ in Eq. (12) are shown by different choices of parameters $a_1=-5, a_3=1, a=2,b=-3,c=1.5,c_1=2$. Three-dimensional graphs at (i) $\beta =0.006$, (ii) $a_3=-6,$ $\beta =0.45$, and (iii) $a_1=1, a_3=-3, a=1,b=-2,c=2,c_1=1,\beta =0.76$ respectively

Fig. 5

The corresponding contour profiles for Fig. 1 successively

Fig. 6

The corresponding contour profiles for Fig. 2 successively

Fig. 7

The associating contour graphs for Fig. 3 respectively

Fig. 8

The corresponding contour profiles for Fig. 4 successively

3 Lump-one stripe soliton interaction solution

For the purpose of mixed lump and soliton solutions, the g and h in bilinear equation can be assumed as,

$$\begin{aligned} g=\xi _{1}^{2}+\xi _{2}^{2}+a_{2}+c_0 exp(\eta _1), ~~~~h=\xi _{1}^{2}+\xi _{2}^{2}+a_{3}+c_0 exp(\eta _2). \end{aligned}$$

(13)

where $\xi _1=a_{0}x+\tau ,$ $\xi _2=a_{1}x+\tau ,$ $\eta _1=m_1 x+\tau ,$ $\eta _2=m_2 x+\tau ,$ However, $a_{i}( 0 \le i \le 3)$,$c_0$ and $m_{1},$ $m_{2}$ are all real parameters to be found. Now, inserting g and h in Eq. (6) which relate to u(x, t),  having fractional transformation Eq. (3), implies us the subsequent result on parameters:

Set I When $a_1 =m_2=0,$ we get the following solutions:

$$\begin{aligned} {\left\{ \begin{array}{ll} {a_0} ={a_0},{a_2} ={a_2},{a_3}=0,{c_0}={c_0},{m_1}={m_1},\omega =\omega ,\rho = \sqrt{-\frac{a+c}{a}}\omega , \\ {a_0} ={a_0},{a_2} =0,{a_3}={a_3},{c_0}={c_0},\omega =\omega ,{m_1}=2\sqrt{-\frac{\frac{1}{15}\sqrt{-1}\sqrt{5}}{c} },\rho =\frac{3}{5}\sqrt{-1}\sqrt{5}\omega . \end{array}\right. } \end{aligned}$$

(14)

parameters in Eq. (14), leads the required solutions to Eq. (5):

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{11}(x,t) = \frac{6\left( c_0 e^{m_1x+\frac{t^\beta }{\beta }}m_1+2a_0\left( a_0x+\frac{t^\beta }{\beta }\right) \right) }{\sqrt{-\frac{a+c}{a}}\left( a_2+c_0 e^{m_1x+\frac{t^\beta }{\beta }}+\left( a_0x+\frac{t^\beta }{\beta }\right) ^2+\frac{t^{2\beta }}{\beta ^2} \right) \omega }+\frac{12ia_0\left( a_0x+\frac{t^\beta }{\beta }\right) }{\left( c_0e^\frac{t^\beta }{\beta }+\left( a_0x+\frac{t^\beta }{\beta }\right) ^2+ \frac{t^{2\beta }}{\beta ^2} \right) \omega },\\ u_{12}(x,t)=\frac{12ia_0 \left( a_0x+\frac{t^\beta }{\beta }\right) }{\left( a_3+c_0e^{\frac{t^\beta }{\beta }}+\left( a_0x+\frac{t^\beta }{\beta }\right) ^2+\frac{t^{2\beta }}{\beta ^2} \right) \omega }- \frac{2i\sqrt{5}\left( \frac{2\sqrt{-\frac{i}{c}}c_0\Delta }{\sqrt{3}5^{1/4}}+2a_0\left( a_0x+\frac{t^\beta }{\beta }\right) \right) }{\left( c_0\Delta +\left( a_0x+\frac{t^\beta }{\beta }\right) ^2+\frac{t^{2\beta }}{\beta ^2}\right) \omega }. \end{array}\right. } \end{aligned}$$

(15)

where $\Delta =e^{\frac{2\sqrt{-\frac{i}{c}}x}{\sqrt{3}5^{1/4}}+\frac{t^\beta }{\beta }},$

Set IIWhen $a_1 =m_1=0,$ we get the following solutions:

$$\begin{aligned} {\left\{ \begin{array}{ll} {a_0} ={a_0},{c_0}={c_0},{m_2}={m_2},\omega =\omega ,\rho = \frac{1}{3}\sqrt{-5}\omega ,{a_2}={a_3}=-\frac{4224}{5}\frac{a_0^2bc_3}{\omega ^2(8a+13c)},\\ {a_0}={a_0},{a_2}=0,{c_0}={c_0},{m_2}={m_2},\omega =2\sqrt{-\frac{58bc_1+18bc_3m_2^2}{24a+29c}},\rho =6\sqrt{-\frac{-58bc_1-18bc_3m_2^2}{120a+145c}},{a_3}=-\frac{480a_0^2(c+a)}{(8a-27c)m_2^2}. \end{array}\right. } \end{aligned}$$

(16)

parameters in Eq. (16), implies the required solutions to Eq. (5):

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{21}(x,t) =\frac{6i\left( c_0 e^{m_2x+\frac{t^\beta }{\beta }}m_2+2a_0\left( a_0x+\frac{t^\beta }{\beta }\right) \right) }{\left( c_0 e^{m_2x+\frac{t^\beta }{\beta }}+\left( a_0x+\frac{t^\beta }{\beta }\right) ^2+\frac{t^{2\beta }}{\beta ^2}-\frac{4224a_0^2bc_3}{5(8a+13c)\omega ^2} \right) \omega }-\frac{36ia_0\left( a_0x+\frac{t^\beta }{\beta }\right) }{\sqrt{5}\left( c_0e^\frac{t^\beta }{\beta }+\left( a_0x+\frac{t^\beta }{\beta }\right) ^2+ \frac{t^{2\beta }}{\beta ^2}-\frac{4224a_0^2bc_3}{5(8a+13c)\omega ^2}\right) \omega }, \\ u_{22}(x,t)=\frac{3i\left( c_0e^{m_2x+\frac{t^\beta }{\beta }}m_2+2a_0\left( a_0x+\frac{t^\beta }{\beta }\right) \right) }{\sqrt{-\frac{58bc_1+18bc_3m_2^2}{24a+29c}} \left( c_0e^{m_2x+\frac{t^\beta }{\beta }}- \frac{480a_0^2(c+a)}{(8a-27c)m_2^2}+\left( a_0x+\frac{t^\beta }{\beta }\right) ^2+\frac{t^{2\beta }}{\beta ^2}\right) } + \frac{2a_0\left( a_0x+\frac{t^\beta }{\beta }\right) }{\sqrt{-\frac{-58bc_1-18bc_3m_2^2}{120a+145c}} \left( c_0e^{\frac{t^\beta }{\beta }}\left( a_0x+\frac{t^\beta }{\beta }\right) ^2+\frac{t^{2\beta }}{\beta ^2}\right) }. \end{array}\right. } \end{aligned}$$

(17)

Fig. 9

The profiles of the solution $u_{11}(x,t)$ in Eq. (15) via various choices of parameters $a_0=1,a_2=-0.3,c_0=0.8,a=-0.6,c=-0.5,m_1=-0.3,\omega =8$. Contour profiles at (i) $\beta =0.15$, (ii) $\beta =0.489$, and (iii) $a_0=-5,a_2=2,c_0=3,a=1,c=-2,m_1=4,\omega =7,\beta =0.99$ respectively

Fig. 10

The profiles of the solution $u_{12}(x,t)$ in Eq. (15) via various choices of parameters $a_0=-0.8,a_3=-0.1,c_0=0.5,c=-2,\omega =5$. Contour profiles at (i) $\beta =0.15$, (ii) $\beta =0.66$, and (iii) $a_0=-1,a_3=3,c_0=1,c=-2,\omega =12,\beta =0.85$ respectively

Fig. 11

The shapes of the solution $u_{21}(x,t)$ in Eq. (17) are shown by various choices of parameters $a_0=-4,c_0=4,a=-2,b=1,c=2,c_3=-3,m_2=3,\omega =5$. 3D graphs at (i) $\beta =0.098$, (ii) $\beta =0.89$, and (iii) $a_0=-1,c_0=1,a=-1,b=-1,c=1,c_3=3,m_2=2,\omega =9,\beta =0.898$ successively

Fig. 12

The shapes of the solution $u_{22}(x,t)$ in Eq. (17) are shown by various choices of parameters $a_0=-5,c_0=3,m_2=1,a=1,b=-1,c=2,c_1=3,c_3=4$. 3D graphs at (i) $\beta =0.115$, (ii) $\beta =0.665$, and (iii) $a_0=-1,c_0=5,m_2=3,a=-2,b=4,c=-3,c_1=1,c_3=2,\beta =0.85$ successively

Fig. 13

The relating contour graphs for Fig. 9 respectively

Fig. 14

The relating contour graphs for Fig. 10 respectively

Fig. 15

The associating contour profiles for Fig. 11 respectively

Fig. 16

The relating contour graphs for Fig. 12 respectively

4 Rogue wave solutions

For rogue wave solution, g and h in bilinear form can be assumed as Zhang and Pang (2019),

$$\begin{aligned} g=\xi _{1}^{2}+\xi _{2}^{2}+a_{2}+b_0 cosh(\eta _1), ~~~~h=\xi _{1}^{2}+\xi _{2}^{2}+a_{3}+b_0 cosh(\eta _2). \end{aligned}$$

(18)

where $\xi _1=a_{0}x+\tau ,$ $\xi _2=a_{1}x+\tau ,$ $\eta _1=n_1 x+\tau ,$ $\eta _2=n_2 x+\tau ,$

However, $a_{i}( 0 \le i \le 3)$,$b_0,$ $n_{1}$ and $n_{2}$ are all real parameters to be measured. Now, inserting g and h in Eq. (6), which relate to u(x, t),  having fractional transformation Eq. (3), implies us the subsequent result on parameters:

Set I When $a_1 = 0,$ we get the following solutions:

$$\begin{aligned} {\left\{ \begin{array}{ll} {a_0} = {a_0},{a_2} =0,{b_0} = {b_0},{n_1}={n_1},{n_2}={n_2},\omega =\omega ,\rho =\frac{1}{14}\sqrt{-15}\sqrt{14}\omega ,{a_3} =\frac{1}{210}\frac{a_0(182a_0\rho ^2+630n_2\rho ^2+195a_0\omega ^2+375n_2\omega ^2)}{n_2^2 \rho ^2},\\ {a_0} = {a_0},{a_3} =0,{b_0} = {b_0},{n_2}={n_2},\omega =\omega ,\rho =\frac{1}{5}\sqrt{-42}\omega ,{a_2} =\frac{1096}{3}\frac{a_0^2 c}{n_2^2(1323c+3925a)},{n_1}=\sqrt{-\frac{1}{6850}\frac{17199c+51025a}{c}}n_2. \end{array}\right. } \end{aligned}$$

(19)

parameters in Eq. (19), leads the required Rogue wave solutions to Eq. (5):

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{11}(x,t)=-\frac{2i\sqrt{\frac{42}{5}}\left( 2a_0\left( a_0x+\frac{t^\beta }{\beta }\right) +b_0n_1sinh\left[ n_1x+\frac{t^\beta }{\beta }\right] \right) }{\omega \left( \left( a_0x+\frac{t^\beta }{\beta }\right) ^2+\frac{t^{2\beta }}{\beta ^2}+b_0n_1cosh\left[ n_1x+\frac{t^\beta }{\beta }\right] \right) } + \frac{6i\left( 2a_0\left( a_0x+\frac{t^\beta }{\beta }\right) +b_0n_2sinh\left[ n_2x+\frac{t^\beta }{\beta }\right] \right) }{\omega \left( \frac{4a_0}{3n_2}+\left( a_0x+\frac{t^\beta }{\beta }\right) ^2+\frac{t^{2\beta }}{\beta ^2}+b_0n_2cosh\left[ n_1x+\frac{t^\beta }{\beta }\right] \right) }, \\ u_{12}(x,t)=\frac{6i\left( 2a_0\left( a_0x+\frac{t^\beta }{\beta }\right) +b_0n_2sinh\left[ n_2x+\frac{t^\beta }{\beta }\right] \right) }{\omega \left( \left( a_0x+\frac{t^\beta }{\beta }\right) ^2+\frac{t^{2\beta }}{\beta ^2}+b_0cosh\left[ n_2x+\frac{t^\beta }{\beta }\right] \right) } - \frac{5i\sqrt{\frac{6}{7}}\left( 2a_0\left( a_0x+\frac{t^\beta }{\beta }\right) +\frac{b_0\sqrt{-\frac{51025a+17199c}{c}}n_2sinh[\Delta ] }{5\sqrt{274}}\right) }{\omega \left( \frac{1096a_0^2c}{3(3925a+1323c)n_2^2}+\left( a_0x+\frac{t^\beta }{\beta }\right) ^2+\frac{t^{2\beta }}{\beta ^2}+b_0cosh[\Delta ] \right) } . \end{array}\right. } \end{aligned}$$

(20)

where $\Delta =\left( \frac{\sqrt{-\frac{51025a+17199c}{c}}n_2x}{5\sqrt{274}}+\frac{t^\beta }{\beta }\right) .$

Fig. 17

The profiles of the solution $u_{11}(x,t)$ in Eq. (20) via various choices of parameters $a_0=-5,b_0=4,n_1=1,n_2=3,\omega =5$. 3D graphs at (i) $\beta =0.15$, (ii) $\beta =0.665$, and (iii) $a_0=-3,b_0=5,n_1=-1,n_2=1,\omega =10,\beta =0.965$ respectively

Fig. 18

The profiles of the solution $u_{12}(x,t)$ in Eq. (20) via various choices of parameters $a_0=5,b_0=3,a=-3,c=5,n_2=4,\omega =9$. 3D graphs at (i) $\beta =0.25$, (ii) $\beta =0.65$, and (iii) $a_0=-0.3,b_0=0.1,a=-0.6,c=3,n_2=-1,\omega =5,\beta =0.94$ successively

Fig. 19

The relating contour graphs for Fig. 17 respectively

Fig. 20

The relating contour graphs for Fig. 18 respectively

5 Result and discussions

In this segment, we will give a detailed comparison of our freshly obtained outcomes with the earlier one. Many scientists used distinct schemes to obtain quantum solutions for NLSEs. Chen et al. obtained bell shaped, periodic waves, kink shaped, anti kink, Jacobi elliptic solutions and other solitary wave solutions using bifurcation theory for TFRNLSE with parabolic law nonlinearity (Seadawy and Cheemaa 2019a). Triki et al. obtained used so many nonlinearities to get drk and bright solitons with the aid of ansatz method for time dependent RNLSE (Zhang et al. 2015). Ekici et al. studied Kerr-law and parabolic-law nonlinearity for RNLSE by using $(G'/G)$-expansion norm (Zhao and Ma 2017). Eslami et al. obtained new exact 1-soliton solutions by using simplest equation technique for RNLSE (Zheng et al. 2019), Biswas et al. achieved dark and singular optical soliton for RNLSE with dual-power law nonlinearity (Zhong et al. 2016), etc. In this work, we construct lump, lump with one kink and rogue wave solutions for TFRNLSE with the help of HBM. Figures 1 and 2 represent the first geometric lump solution for Eq. (1) graphically. Figure 1(i) at $\beta =0.95$ u expressed 3D shape making one bright and two dark lump solutions and one bright lump also appearing which is small in size. Figure 1(ii) we observe two lump solution of equal size and shape at $\beta =0.48$, one is bright and one is dark. In Fig. 3(iii) we change all parametric values and see three lump solution one is bright which is disappearing and two dark solutions. Figure 2(i) for $\beta =0.18$ we observe three bright lump solutions one is at their maximum value and remanning two are small in size. Figure 2(ii) at $\beta =0.718$ only one bright lump solution is appeared. Figure 2(iii) we achieved two bright lump solutions of equal sizes at different parametric values. Figures 5 and 6 represented the contour profiles of Figs. 1 and 2 respectively. Figures 3 and 4 represented the second geometric lump solution for Eq. (1) graphically. In Fig. 3 we study the behaviour of two bright lump solutions in (i) two bright lump solution where u has maximum. In (ii) one lump solution is at their max. and the other is disappearing and in (iii) we see again two bright solution where u has max. at different parametric values. In Fig. 4 we seen the behaviour of bright lump solution (i) u has max (ii) waves disappearing (iii) continuous flow with hight and low amplitude at different sets of values. Figures 7 and 8 represented the contour profiles of Figs. 3 and 4 respectively. Figures 9 and 10 represent the first geometric Lump-one stripe solution for Eq. (1) graphically. Figure 9(i) at $\beta =0.15$ we observe two dark lump solution having equal amplitude but different in shape and one bright lump solution of large amplitude. By increasing $\beta$ we see two bright lump solutions of equal size and shapes and one dark lump solution of large amplitude appears (ii). In (iii) we see the crest surface of two bright lump solutions for different sets of values. Figure 10(i) we observe a continuous flow of large and small amplitude of bright and dark lump solutions. In (ii) at $\beta =0.66$, we see the parallel flow of bright lump solutions. we see three bright lump solution for different parametric values in (iii). Figures 13 and 14 represent the contour profile of Figs. 9 and 10 respectively. Figures 11 and 12 represented the second geometric Lump-one stripe solution for Eq. (1) graphically. In Figs. 11 and 12 (i) (ii) and (iii) we observe the breakdown of bright lump solution from large to small-amplitude waves for different sets of values, where some times a large-amplitude wave appear rapidly and very next instant it disappears. Figures 15 and 16 represent the contour profile of Figs. 11 and 12 respectively. Figures 17 and 18 represented the first geometric rogue wave solution for Eq. (1) graphically. Figure 17(i) we see the multiple dark and bright lump solutions having different sizes. Figure 17(ii), By increasing $\beta$ dark lump solution disappears only bright solutions remaining having different in sizes. In (iii) we have seen the upper face of two bright solutions for a different set of values. Figure 18(i) at $\beta =0.25,$ we achieve one bright and one dark lump solution having a different shape. In (ii) we see one dark and two bright solutions for $\beta =0.65$ which are different in size and shape. In (iii) multiple lump solutions appear rapidly having the same shape but different in amplitude. Figures 19 and 20 represent the contour profile of Figs. 11 and 12 successively.

6 Concluding remarks

In this manuscript, we obtained the lump, multiple lumps and rogue wave solutions for TFRNLSE by Hirota bilinear approach. We got various forms of lump solition solutions, like one bright and dark, one bright with two dark and multiple bright lump solitons. For observing the physical performance of our model we set up 3D and contour plots for different sets of values. We also explained the structure of our results graphically for more understanding. The obtained results show that expected method is stable.