An SEQAIHR model to study COVID-19 transmission and optimal control strategies in Hong Kong, 2022

Abstract

During the COVID-19 pandemic, one of the major concerns was a medical emergency in human society. Therefore it was necessary to control or restrict the disease spreading among populations in any fruitful way at that time. To frame out a proper policy for controlling COVID-19 spreading with limited medical facilities, here we propose an SEQAIHR model having saturated treatment. We check biological feasibility of model solutions and compute the basic reproduction number ($R_0$). Moreover, the model exhibits transcritical, backward bifurcation and forward bifurcation with hysteresis with respect to different parameters under some restrictions. Further to validate the model, we fit it with real COVID-19 infected data of Hong Kong from 19th December, 2021 to 3rd April, 2022 and estimate model parameters. Applying sensitivity analysis, we find out the most sensitive parameters that have an effect on $R_0$. We estimate $R_0$ using actual initial growth data of COVID-19 and calculate effective reproduction number for same period. Finally, an optimal control problem has been proposed considering effective vaccination and saturated treatment for hospitalized class to decrease density of the infected class and to minimize implemented cost.

1 Introduction

COVID-19 is a dangerous disease, first found in December 2019 and after that it spreads throughout the world rapidly. On January 7, 2020, novel coronavirus was identified as the cause behind these disease [1]. WHO reported identification of this virus, warned world about its emergence and named as SARS-CoV-2  [2, 3]. Symptoms of this disease are dry cough, fever, and tiredness. Some patients may have pains and aches, nasal congestion, diarrhea or sore throat. Some people may be infected by very mild symptoms. About 80 % people recover from COVID-19 without hospital treatment [4]. Self-isolation is an important policy to avoid COVID-19 transmission in community.

In the preliminary stages, number of patients doubled within a little more than a week. By mid-February, 2020 the virus outbreak affected the USA, European countries like France, Italy, Germany, Spain, UK, middle eastern countries like Iran. On March, 2020 WHO declared COVID-19 as a pandemic outbreak [5]. According to reports, almost one-third of population was under lockdown to slow down the devastating effects of the pandemic [6]. COVID-19 pandemic shows immense negative affect on socioeconomic, education and other global aspects. Medical emergency becomes more gruesome day by day. Therefore, it is necessary to formulate a model to describe development and disease transmission. The model will also support policymakers to take decision for controlling disease based on the effective assumptions [7, 8].

Mathematical modeling of such pandemics is very operational to estimate the outcome. For many years, researchers are using mathematical models to deal with infectious disease outbreaks and as a result, there are different kinds of epidemic models. The most well-known epidemic model is the SIR model also known as Kermack–McKendrick [9] model. The infectious diseases like measles, mumps, rubella etc., create permanent immunity in the system which gives us the recovered (R) portion of the population. The diseases like tuberculosis have incubation period where patients are asymptomatic but infected and this portion of the population are considered in the model as the exposed (E) individuals [10]. There are many other different models that have been formulated over the years. To investigate the COVID-19 disease dynamics, authors have been formulated large number of models and gave guidelines to control it  [11,12,13,14,15,16,17,18,19].

Biswas et al. [11] proposed an SEAIQHR model to study COVID-19 outbreak in India. They discussed coronavirus dynamics and some interventions policies to control the spread of the disease. In [12], authors considered an SEIR model to show the severity of COVID-19 in Italy. They showed affect of panic/tension/anxiety on population for the first wave. Ghosh et al. [13]introduced an SEQIR model with saturated treatment and studied COVID-19 scenario in Italy. In [14], authors discussed effect of vaccination and crowding effect on coronavirus disease. To study transmission dynamics and control strategies for COVID-19 in India, Mondal and Khajanchi [15] proposed an SAIQJR model. Authors divided susceptible populations into two classes, namely conscious and unconscious susceptibles in [16]. They also considered asymptomatic, symptomatic, hospitalized and recovered population to frame out a COVID-19 model. Ali et al. [17] studied a fractional COVID-19 model with vaccination. In [18], authors discussed the spread of COVID-19 among health workers in Iran and showed the effect of vaccination on mitigation of COVID-19 among health workers. In [19], authors proposed a robust sliding mode controller to mitigate COVID-19 spreading through social distancing, medical treatment and vaccination.

Here we extend the work of [11], where authors proposed an SEAIQHR model to examine the scenario of spreading disease in India. In [11], authors supposed that susceptible populations affected by interaction with symptomatic infected, asymptomatic infected, quarantined and hospitalized populations, but they did not consider any type of treatment for hospitalized population. Moreover, asymptomatic people can move to symptomatic class after showing symptoms, this is also overlooked. Authors considered COVID-19-induced death in symptomatic, quarantine and hospitalized class, but in reality symptomatic infected and quarantined people move to hospitalized class after heavier infection, therefore it is not necessary to consider COVID-19-induced death rate in above-mentioned two classes.

In this paper, we propose an SEQAIHR model to examine COVID-19 transmission dynamics saturated treatment for hospitalized class and validate model with infected data of Hong Kong from 19th December, 2021 to 3rd April, 2022. Here we suppose that susceptible people are infected by interaction with asymptomatic infected, symptomatic infected and hospitalized classes only as the number of infected by quarantine class is negligible, for this reason here we do not consider infection produced by quarantined class. We consider effective vaccination for susceptible population in optimal control problem, which is very realistic in current situation. Also, we suppose some parts of asymptomatic population move to infected class after showing symptoms and we consider COVID-19-induced death rate only for hospitalized class, since only severely infected people are moved to hospitalized class.

The main findings of this paper are given in below:

• 1. The model undergoes through transcritical, backward bifurcation and forward bifurcation with hysteresis at $R_0 = 1$.

• 2. Validate model with COVID-19 infected data of Hong Kong from 19th December, 2021 to 3rd April, 2022, estimate model parameters and identify sensitive parameters.

• 3. $R_0$ is estimated using actual COVID-19 infected data and R(t) is found for same period.

• 4. Finally we consider an optimal control problem with vaccination to find out optimal value of the considered controls to reduce or prevent the influence of the disease among population and minimize implemented cost.

Organization of the paper is as follows: We formulate an SEQAIHR model in Sect. 2. In Sect. 3, biological properties of proposed model have been discussed. $R_0$ and different types equilibria are addressed in Sect. 4. In Sect. 5, we show stability of disease free and endemic equilibria. We examine transcritical, backward and forward bifurcation with hysteresis of the considered model in Sect. 6. In Sect. 7, we validate model with COVID-19 infected data of Hong Kong from 19th December, 2021 to 3rd April, 2022 and estimate model parameters. In Sect. 8, sensitivity analysis of proposed model has been studied to find out most effective model parameters which have effect on $R_0$. In Sect. 9, we estimate $R_0$ from initial growth data of COVID-19 and find R(t). An optimal control problem has been constructed to identify optimal value of controls to minimize influence of the disease in Sect. 10. Finally, we thoroughly discuss about this study in Sect. 11.

2 Model formulation

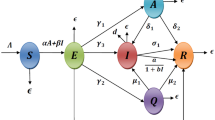
In this paper, our intention is to propose a model for discussing the devastate phenomenon of the world due to gruesome spreading of coronavirus. The outbreak of novel coronavirus takes gigantic form which is intensely denunciation to mankind. Initially there was no proper medical treatment for coronavirus but many actions were being taken by government such as lockdown, social distancing, individual hygienic cautions etc. Concerning all the matters, we adopt a deterministic model to predict the mechanism of coronavirus disease transmission as well as implementation of intervention strategies to combat the severe outbreak of this pandemic. Based on health situations, we split total population (N) into seven different compartments, namely susceptible populations (S) , exposed populations (E) , quarantined populations (Q), asymptomatic infected populations (A) , symptomatic infected populations (I) , hospitalized populations (H) and recovered populations (R) i.e. $N(t) = S(t) + E(t) + Q(t) + A(t) + I(t) + H(t) + R(t)$ at any t. To formulate the deterministic model, the following assumptions are taken into consideration:

• 1. Constant recruitment rate (C) in susceptible population.

• 2. Normal death rate $(\mu )$ in every class.

• 3. Susceptible population becomes exposed after interaction with asymptomatic, symptomatic and hospitalized population at a proportion $\beta _{1}$, $\beta _{2}$, $\beta _{3}$, respectively.

• 4. Exposed populations move to quarantined, asymptomatic and symptomatic infected compartment at a proportion $\alpha _{1}$, $\alpha _{3}$ and $\alpha _{2}$, respectively.

• 5. Quarantined populations are taken under observation, when symptoms are developed, they are immediately transferred to hospitalized compartment at proportion $\gamma _{1}$ otherwise they leave quarantined compartment at rate $\gamma _{2}$ and enter to recovered compartment.

• 6. Symptomatic infected compartment moves to hospitalized compartment at proportion of $\delta _1$. On the other hand, if symptoms are reduced with days for self-immunity of human system, they are moved to recovered compartment at proportion $\delta _{2}$.

• 7. The asymptomatic population moves to recovered compartment at proportion $\nu _{1}$ and they transform to symptomatic infected compartment at proportion $\nu _{2}$.

• 8. Since a huge number of humans are infected in very short period of time and due to limited medical resources, required treatment may be delayed. To include the effect of treatment delay, here we consider a saturated treatment function $\dfrac{aH}{1 + bH}$ where a and b are cure rate and delayed parameter of treatment, respectively. The hospitalized class cure from the disease at rate $\sigma$ for self-immunity and die for disease at proportion d.

Fig. 1

Flow diagram of COVID-19 model as proposed in (1)

Incorporating all the assumptions given above, the disease transmission dynamics of coronavirus is presented in Fig. 1 and the corresponding differential equations are given in Eq. (1).

$$\begin{aligned} {\left\{ \begin{array}{ll} \dfrac{\textrm{d}S}{\textrm{d}t} = C - \dfrac{ S (\beta _{1} A + \beta _{2} I + \beta _{3} H)}{N} - \mu S \ \equiv f_1 \ \ (\text {say}) \\ \dfrac{\textrm{d}E}{\textrm{d}t} = \dfrac{ S (\beta _{1} A + \beta _{2} I + \beta _{3} H)}{N} - ( \alpha _{1}+ \alpha _{2}+ \alpha _{3} + \mu )E \\ \qquad \qquad \equiv f_2 \ \ (\text {say}) \\ \dfrac{\textrm{d}Q}{\textrm{d}t} = \alpha _{1} E - (\gamma _{1} + \gamma _{2} + \mu )Q \ \equiv f_3 \ \ (\text {say}) \\ \dfrac{\textrm{d}A}{\textrm{d}t} = \alpha _{3} E - (\nu _{1} + \nu _{2} + \mu )A \ \equiv f_4 \ \ (\text {say}) \\ \dfrac{\textrm{d}I}{\textrm{d}t} = (\alpha _{2} E + \nu _{2} A) - (\delta _{1} + \delta _{2} + \mu )I \ \equiv f_5 \ \ (\text {say}) \\ \dfrac{\textrm{d}H}{\textrm{d}t} = (\gamma _{1} Q + \delta _{1} I) - \dfrac{aH}{1 + bH }- (\sigma + d + \mu ) H \\ \qquad \qquad \equiv f_6 \ \ (\text {say}) \\ \dfrac{\textrm{d}R}{\textrm{d}t} = (\gamma _{2} Q + \delta _{2} I + \nu _{1} A + \sigma H) + \dfrac{aH}{1 + bH } - \mu R \\ \qquad \qquad \equiv f_7 \ \ (\text {say}) \end{array}\right. } \end{aligned}$$

(1)

with initial conditions $S(0) > 0$, $E(0) \ge 0$, $Q(0) \ge 0$, $A(0) \ge 0$, $I(0) \ge 0$, $H(0) \ge 0$, $R(0) \ge 0$ at any instant $t\ge 0$ and model parameters in model system (1) are given in the following Table 1.

Table 1 Description of model parameters

3 Basic properties of mathematical model

Here we show all solutions of the proposed model (1) satisfying initial conditions are non-negative and bounded for any time $t\ge 0.$ Adopted mathematical model is biologically valid if all solutions are non-negative and bounded at any instant for non-negative initial conditions. The non-negativity and boundedness are established in Theorems 1 and 2, respectively.

Theorem 1

All solutions $\left\{ S(t), E(t), Q(t), A(t), I(t),\right. \left. H(t), R(t)\right\}$ of model system (1) are non-negative satisfying initial conditions $S(0) > 0$, $E(0) \ge 0$, $Q(0) \ge 0$, $A(0) \ge 0$, $I(0) \ge 0$, $H(0) \ge 0$, $R(0) \ge 0$ at any instant $t\ge 0$.

Proof

Integrating first equation of the model (1) and satisfying initial conditions, we have

$$\begin{aligned}&S(t) = S(0) \ \exp \left( - \int ^{t}_{0}\left\{ \dfrac{ (\beta _{1} A + \beta _{2} I + \beta _{3} H)}{N} + \mu \right\} \textrm{d}u \right) \\&\quad + \int ^{t}_{0} C \ \exp \left( \int ^{v}_{0} \left\{ \dfrac{(\beta _{1} A + \beta _{2} I + \beta _{3} H)}{N} + \mu \right\} \textrm{d}u \right) dv \\&\quad \times \ \exp \left( - \int ^{t}_{0}\left\{ \dfrac{ (\beta _{1} A + \beta _{2} I + \beta _{3} H)}{N} + \mu \right\} \textrm{d}u \right) > 0. \end{aligned}$$

Hence S(t) is positive $\forall$ t > 0. Similarly, considering other equations of model system (1) using the same procedure one can easily show $E(t) \ge 0$, $Q(t) \ge 0$, $A(t) \ge 0$, $I(t) \ge 0$, $H(t) \ge 0$, $R(t) \ge 0$ at any time $t\ge 0$. Therefore all solutions $\left\{ S(t), E(t), Q(t), A(t), I(t), H(t), R(t)\right\}$ of system (1) are non-negative satisfying initial conditions at any time $t\ge 0$. $\square$

Theorem 2

The closed feasible region $\varOmega$ given by

$$\begin{aligned}{} & {} \varOmega = \left\{ (S, E, Q, A, I, H, R) \in \mathbb {R}^{7}_{+} : \right. \\{} & {} \quad \left. 0 < S + E + Q + A + I + H + R \le \dfrac{C}{\mu } \right\} \end{aligned}$$

is a positively attracting region of model system (1) with non-negative initial condition in $\mathbb {R}^{7}_{+}$.

Proof

Summing all equations of system (1) and noting $N = S + E + Q + A + I + H + R$, we get

$\dfrac{\textrm{d}N}{\textrm{d}t} = C - \mu N - \textrm{d}H < \mu \left( \dfrac{C}{\mu } - N \right)$

Integrating the last inequality and letting $t \longrightarrow \infty$, we get $N\longrightarrow \dfrac{C}{\mu }$ and hence $N(t) \le \dfrac{C}{\mu } \forall t \ge 0$.

Therefore set $\varOmega$ is a positively invariant region presented by model (1). Hence our proposed model is biologically as well as mathematically well defined in feasible invariant set $\varOmega$  [20]. $\square$

4 Basic reproduction number $(R_{0})$ and different types of equilibria

First we compute $R_0$ of the considered COVID-19 model (1), then we describe different number of equilibria based on value of $R_0$.

4.1 Basic reproduction number $(R_{0})$

$R_{0}$ is a threshold quantity in disease transmission dynamics. It helps to health planners to identify whether disease will die out or eradicate in a population. It is defined as the average number of secondary infections per unit time from a single susceptible in its entire infection period. If disease-free equilibrium point exists, then we can compute $R_0$ using next generation matrix approach  [21, 22].

Here disease-free equilibrium point $E_0 \left( \dfrac{C}{\mu }, 0, 0, 0,\right. \left. 0, 0, 0\right) .$ According to [21, 22], the new infection matrix F and disease elimination matrix V are given by

$$\begin{aligned}{} & {} F = \left( \begin{array}{ccccc} 0 &{} 0 &{} \beta _{1} &{} \beta _{2} &{} \beta _{3} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array} \right) \ and \nonumber \\ {}{} & {} V = \left( \begin{array}{ccccc} D_{0} &{} 0 &{} 0 &{} 0 &{} 0 \\ - \alpha _{1} &{} D_{1} &{} 0 &{} 0 &{} 0 \\ - \alpha _{3} &{} 0 &{} D_{2} &{} 0 &{} 0 \\ - \alpha _{2} &{} 0 &{} - \nu _{2} &{} D_{3} &{} 0 \\ 0 &{} - \gamma _{1} &{} - \delta _{1} &{} 0 &{} D_{4} \end{array} \right) , \end{aligned}$$

where $D_{0} = \alpha _{1} + \alpha _{2} + \alpha _{3} + \mu$, $D_{1} = \gamma _{1} + \gamma _{2} + \mu$, $D_{2} = \nu _{1} + \nu _{2} + \mu$, $D_{3} = \delta _{1} + \delta _{2} + \mu$, $D_{4} = a + \sigma + d + \mu ,$ The value of $R_{0}$ is spectral radius of $F V^{- 1}$ which is $R_{0} = \dfrac{\beta _{1} \alpha _{3}}{D_{0}D_{2}}$ + $\dfrac{\beta _{2}(\alpha _{2} D_{2} + \alpha _{3} \nu _{2})}{D_{0}D_{2}D_{3}}$ + $\dfrac{\beta _{3}(D_{1}D_{2}\alpha _{2}\delta _{1}+ D_{1}\alpha _{3}\delta _{1} \nu _{2} + D_{2} D_{3} \alpha _{1} \gamma _{1})}{D_{0}D_{1}D_{2} D_{3} D_{4}}$.

The interesting result is obtained from the expression of $R_0$, it contains three separate expressions arise from proportion of infection for asymptomatic compartment (A), proportion of infection for symptomatic compartment (I) and last term is proportion of infection for hospitalized compartment (H).

4.2 Different types of equilibria

Along with $E_0$ the system contains the endemic equilibrium $E^{*}(S^{*}, E^{*}, Q^{*}, A^{*}, I^{*}, H^{*}, R^{*})$ where $S^{*} = \dfrac{C- D_0 E^{*}}{\mu }$, $Q^{*} = \dfrac{\alpha _1}{D_1}E^{*}$, $A^{*} = \dfrac{\alpha _3}{D_3}E^{*}$, $I^{*} = \dfrac{\alpha _2 D_3 + \gamma _2 \alpha _3}{D_2 D_3}E^{*}$, $E^{*} = \dfrac{1}{\rho _1}\left\{ D_4 H^{*} - \dfrac{ab H^{{*}^2}}{1 + b H}\right\}$, $\rho _1 = \left\{ \dfrac{\gamma _1 \alpha _1}{D_1} + \dfrac{\delta _1(\alpha _2 D_3 + \gamma _2 \alpha _3) }{D_2 D_3}\right\}$ and $H^{*}$ satisfies the equation

$$\begin{aligned} e_0 H^{{*}^3} + e_1 H^{{*}^2} + e_2 H^{*} + e_3 = 0 \end{aligned}$$

(2)

where all coefficients $e_i, i = 0, 1, 2, 3$ are given in “Appendix-I”.

But from the above expression, it is very difficult to find the exact number of endemic equilibria. For this purpose, here we find number of endemic equilibria numerically considering the empirical values of model parameters $\beta _1 = 0.42, \beta _2 = 0.6, \beta _3 = 0.2, \mu = 0.06, \alpha _1 = 0.08, \alpha _2 = 0.1, \alpha _3 = 0.2, \gamma _1 = 0.15, \gamma _2 = 0.25, \delta _1 = 0.15, \delta _2 = 0.25, \nu _1 = 0.2, \nu _2 = 0.15, a = 1.8, b = 20, \sigma = 0.1, d = 0.02$. In Fig. 2 we represent the I- component of different endemic equilibrium point(s) with respect to $R_0$. From Fig. 2a, c it is clear that there may exist zero or two endemic with one coincident endemic equilibrium point for $R_0 < 1.$ Also from Fig. 2a–c there may exist one or three or two with one coincident endemic equilibria for $R_0 > 1.$ The number of equilibrium point(s) under different conditions is summarized in Lemma 1. The results are biologically interpreted in Sect. 6.3.

Lemma 1

(i) For model (1) always exists $E_0$.

(ii) Model (1) has no or two or one coincident endemic equilibria for $R_0 < 1.$

(iii) Model (1) has one or three or two with one coincident endemic equilibria for $R_0 > 1.$

Fig. 2

Number and nature of endemic equilibria with respect to $R_0$ for a $C = 4$, b $C =$9, c $C = 15$ and other parameters are given above

5 Stability analysis of different equilibria

Here we show stability of $E_0$ and $E^{*}$ depending on basic reproduction number $(R_{0})$. Now Jacobian matrix of model (1) at $E^{*}(S^*, E^*, Q^*, A^*, I^*, H^*, R^*)$ is denoted by $J_{E^{*}}$ and its expression is given by,

$$\begin{aligned} J_{E^{*}} = \left( \begin{array}{ccccccc} - a_1 &{} 0 &{} 0 &{} - a_2 &{} - a_3 &{} - a_4 &{} 0 \\ a_1 &{} - D_{0} &{} 0 &{} a_2 &{} a_3 &{} a_4 &{} 0 \\ 0 &{} \alpha _{1} &{} - D_{1} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \alpha _{3} &{} 0 &{} - D_{2} &{} 0 &{} 0 &{} 0 \\ 0 &{} \alpha _{2} &{} 0 &{} \nu _{2} &{} -D_{3} &{} 0 &{} 0 \\ 0 &{} 0 &{} \gamma _{1} &{} \delta _{1} &{} 0 &{} - a_{5} &{} 0 \\ 0 &{} 0 &{} \gamma _{2} &{} \delta _{2} &{}\nu _{1} &{} a_6 &{} - \mu \end{array} \right) \end{aligned}$$

(3)

where $a_1 = \dfrac{( \beta _1 A^* + \beta _2 I^* + \beta _3 H^*)}{N} + \mu ,$ $a_2 = \dfrac{S^* \beta _1}{N},$ $a_3 = \dfrac{S^* \beta _2}{N}$, $a_4 = \dfrac{S^* \beta _3}{N}$, $a_5 = \dfrac{a}{(1 + b H^*)^2} + (\delta + d + \mu )$, $a_6 = \sigma + \dfrac{a}{(1 + bH^*)^2}.$

The eigenvalues of Jacobian matrix $J_{E_{0}}$ at $E_0$ are $- \mu$, $- \mu$ and remaining five are roots of equation:

$$\begin{aligned} x^5 + c_{1} x^4 + c_{2} x^3 + c_{3} x^2 + c_{4} x + c_{5} = 0 \end{aligned}$$

(4)

where the coefficients $c_i, i = 1, 2, 3, 4, 5$ and some part of theorem given in “Appendix-II”.

If $R_{0} < 1$ then all coefficients of Eq. (4) are positive that means there is no change in sign for $R_{0} < 1$. By Descartes rule of sign we can conclude that Eq. (4) has no positive root if $R_{0} < 1$ i.e. all eigenvalues of $J_{E_{0}}$ are negative for $R_{0} < 1$. So, $E_{0}$ is locally asymptotically stable for $R_{0} < 1$ otherwise $E_{0}$ is unstable.

The above result is summarized in the following corollary.

Corollary 1

For $R_{0} < 1$, $E_{0}$ is locally asymptotically stable and unstable otherwise.

Now we consider a Lyapunov function [23] as, L(S, E, Q, A, I, H, R)= $E+ Q + A + I + H$ which is positive invariant for all members of the set $\varOmega$.

$$\begin{aligned} Then\quad \dfrac{\textrm{d}L}{\textrm{d}t} = \dfrac{\textrm{d}E}{\textrm{d}t} + \dfrac{\textrm{d}Q}{\textrm{d}t} + \dfrac{\textrm{d}A}{\textrm{d}t} + \dfrac{\textrm{d}I}{\textrm{d}t} + \dfrac{\textrm{d}H}{\textrm{d}t} \end{aligned}$$

i.e. $\dfrac{\textrm{d}L}{\textrm{d}t} = \left( \nu _{1} + \mu \right) \left( R_{e} - 1 \right) A + \left( \delta _{2} + \mu \right) \left( R_{f} - 1 \right) I + (a + \sigma + d + \mu )\left( R_{g} - 1 \right) H - \mu E - \mu Q$ where $R_{e} = \dfrac{\beta _{1}}{\delta _{2} + \mu } <R_{0}$, $R_{f} = \dfrac{\beta _{2}}{\nu _{1} + \mu } <R_{0}$, $R_{g} = \dfrac{\beta _{3}}{a + \sigma + d + \mu } <R_{0}$.

Therefore $\dfrac{\textrm{d}L}{\textrm{d}t}< 0$ if $R_{0} < 1$ and hence by Lyapunov’s stability theorem it follows that $E_{0}$ is globally stable [24]. This result is summarized in the following corollary.

Corollary 2

For $R_{0} < 1$, $E_{0}$ is globally asymptotically stable.

It is clear from above two theorems that for $R_{0} < 1$ then the model (1) is stable that means disease will eradicate from the system.

Next we shall discuss stability of endemic equilibrium $E^*$.

One of the characteristic root of $J_{E^{*}}$ is $- \mu$ and other roots satisfy the following equation:

$$\begin{aligned} x^6 + b_{1} x^5 + b_{2} x^4 + b_{3} x^3 + b_{4} x^2 + b_{5} x + b_6 = 0\nonumber \\ \end{aligned}$$

(5)

where $b_{i}, i = 1, 2 , 3, 4, 5, 6$ are given in “Appendix-III”.

Since one eigenvalue of $J_{E^{*}}$ is negative, therefore system (1) is asymptotically stable at $E^*$ if other roots of the Eq. (5) are negative real or have negative real part. The stability can be theoretically verified using Routh–Hurwitz criteria [25] but we are omitting this due to the large expressions. This result is summarized in the following corollary.

Corollary 3

For $R_{0} > 1$, $E^*$ is locally asymptotically stable and unstable otherwise.

6 Bifurcation analysis

In this section, we discuss transcritical bifurcation, backward bifurcation about $R_{0} = 1$ and forward bifurcation with hysteresis. The condition $R_{0} = 1$ equivalent to $a = a^{[TB]}$ where

$a^{[TB]} = \dfrac{\beta _{3}(D_{1}D_{2}\alpha _{2}\delta _{1}{+} D_{1}\alpha _{3}\delta _{1} \nu _{2} {+} D_{2} D_{3} \alpha _{1} \gamma _{1})}{D_{0}D_{1}D_{2} D_{3} D_{4}}\left( 1 - \dfrac{\beta _{1} \alpha _{3}}{D_{0}D_{2}} {-} \dfrac{\beta _{2}(\alpha _{2} D_{2} {+} \alpha _{3} \nu _{2})}{D_{0}D_{2}D_{3}} \right) ^{- 1}$ − $(d + \sigma + \mu )$ or $\beta _2 = \beta _2^{[BB]}$ where $\beta _{2}^{[BB]} = \dfrac{D_{0} D_{2} D_{3}}{(\alpha _{2} D_{2} {+} \alpha _{3} \nu _{2})}\left[ 1 {-}\right. \left. \dfrac{\beta _{1} \alpha _{3}}{D_{0}D_{3}}{ -} \dfrac{\beta _{3}(D_{1}D_{3}\alpha _{2}\delta _{1}{+} D_{1}\alpha _{3}\delta _{1} \nu _{2} {+} D_{2} D_{3} \alpha _{1} \gamma _{1})}{D_{0}D_{1}D_{2} D_{3} D_{4}} \right]$.

In Theorem 3 we shall investigate transcritical bifurcation and Theorem 4 we shall examine backward bifurcation.

6.1 Transcritical bifurcation

Theorem 3

Model (1) goes through transcritical bifurcation about $E_{0}$ as cure rate parameter (a) passes critical value $a = a^{[TB]}$ with $\dfrac{2 \mu (v_{2} {+} v_{3} {+} v_{4} {+} v_{5} {+} v_{6} {+} v_{7})(\beta _{1} v_{4} {+} \beta _{2} v_{5} {+} \beta _{3} v_{6})}{C} \ne 2 a b v_{6}^{2} w_{6}$.

Proof

In order to check occurrence of transcritical bifurcation at $E_{0}$ of model (1), we need to verify transversality conditions of Sotomayor’s theorem [26]. First we consider a function f(S, E, Q, A, I, H, R) with seven components given as below:

$$\begin{aligned} f(S, E, Q, A, I, H, R) = \left( \begin{array}{ccccccc} f_{1}&f_{2}&f_{3}&f_{4}&f_{5}&f_{6}&f_{7} \end{array} \right) ^\textrm{T}\nonumber \\ \end{aligned}$$

(6)

where $f_1, f_2, f_3, f_4, f_5, f_6, f_7$ are defined in Eq. (1).

The determinant value of $J_{E_{0}}$ is $D_{0} D_{1} D_{2} D_{3} D_{4} (1 - R_{0})$, which vanishes at $a = a^{[TB]}$. Thus, at $a = a^{[TB]}$(equivalently $R_0 = 1$), $J_{E_{0}}$ has a zero eigenvalue.

Let $V = (v_{1} \ v_{2} \ v_{3} \ v_{4} \ v_{5} \ v_{6} \ v_{7})^\textrm{T}$ and $W = (w_{1} \ w_{2} \ w_{3} \ w_{4} \ w_{5} \ w_{6} \ w_{7})^\textrm{T}$ be two eigenvectors of $J_{E_{0}}(a^{[TB]})$ and $J_{E_{0}}^\textrm{T}(a^{[TB]})$, respectively, for the zero eigenvalue then $v_{1} = -$ $\dfrac{\mu }{D_{0}}$, $v_{2} = 1$, $v_{3} = \dfrac{\alpha _{1}}{D_{1}}$, $v_{4} = \dfrac{\alpha _{3}}{D_{2}}$, $v_{5} = \dfrac{\alpha _{2}D_{1}D_{2} + \alpha _{3} \nu _{2} D_{1}}{D_{1}D_{2}D_{3}}$, $v_{6} = \dfrac{\alpha _{1} \gamma _{1} D_{2} D_{3} + \alpha _{2} \delta _{1} D_{1} D_{2} + \alpha _{3} \delta _{1} \nu _{2} D_{1}}{D_{1} D_{2}D_{3} D_{4}}$, $v_{7} = \dfrac{\alpha _{1} \gamma _{2} D_{3} + \alpha _{3} \nu _{1} D_{1}}{\mu D_{1} D_{3}}$ $+ \tfrac{\begin{array}{l}[\delta _{2} D_{4} (\alpha _{2} D_{1} D_{3} {+} \alpha _{3} \nu _{2} D_{1}) {+} (\sigma {+} a)(\alpha _{1} \gamma _{1} D_{2} D_{3} \\ + \alpha _{2} \delta _{1} D_{1} D_{2} {+} \alpha _{3} \delta _{1} \nu _{2} D_{1})]\end{array}}{\mu D_{1} D_{2} D_{3} D_{4}}$. and $w_{1} = 0$, $w_{2} = 1$, $w_{3} = \frac{\beta _{3} \gamma _{1}}{D_{1} D_{4}}$, $w_{4} = \frac{\beta _{1} D_{3} D_{4} + \beta _{2} \nu _{2} D_{4} + \beta _{3} \delta _{1} \nu _{2}}{D_{2} D_{3} D_{4}}$, $w_{5} = \frac{\beta _{2} D_{4} + \beta _{3} \delta _{1}}{D_{3} D_{4}}$, $w_{6} {=} \frac{\beta _{3}}{D_{4}}$, $w_{7} {=} 0$. Then we get, $W^T f_{a}(E_{0};a^{[TB]})$ = 0. $W^T \left( Df_{a}(E_{0};a^{[TB]}) V\right) = - \dfrac{\beta _{3} (\alpha _{1} \gamma _{1} D_{2} D_{3} + \alpha _{2} \delta _{1} D_{1} D_{2} + \alpha _{3} \delta _{1} \nu _{2} D_{1})}{D_{1} D_{2}D_{3} D_{4}^{2}}$ $\ne$ 0. and $W^T \left( D^2f(E_{0};\mu _{1}^0) (V,V)\right)$ = $- \dfrac{2 \mu (v_{2} {+} v_{3} {+} v_{4} {+} v_{5} {+} v_{6} {+} v_{7})(\beta _{1} v_{4} {+} \beta _{2} v_{5} {+} \beta _{3} v_{6})}{C} {+} 2 a b v_{6}^{2} w_{6}$ $\ne$ 0.

Thus all conditions of Sotomayor’s theorem for transcritical bifurcation are satisfied, therefore model (1) goes through transcritical bifurcation at $E_{0}$ as cure rate parameter a passes critical value $a = a^{[TB]}$. $\square$

In Fig. 3, we have presented the one parameter bifurcation diagram with respect to $R_0$ (considering a as inbuilt parameter). It is clear from the figure, stability of disease free equilibrium exchanges at $R_0 = 1$ through creation of one stable endemic equilibrium, therefore occurrence of transcritical bifurcation is verified at $R_0 = 1$ numerically. Biologically this result is highly important because if $a > a^{[TB]}$ i.e. $R_0 < 1$ then no disease will persist and otherwise disease will persist in the system. Thus we get an lower value of the cure rate due to treatment below which disease will persistent in the system.

Fig. 3

Transcritical bifurcation diagram with respect to $R_0$ for the empirical values of the parameters $C = 10, \beta _1 = 0.52, \beta _2 = 0.6, \beta _3 = 0.35, \mu = 0.82, \alpha _1 = 0.08, \alpha _2 = 0.1, \alpha _3 = 0.2, \gamma _1 = 0.15, \gamma _2 = 0.25, \delta _1 = 0.15, \delta _2 = 0.25, \nu _1 = 0.2, \nu _2 = 0.15, b = 20, \sigma = 0.1, d = 0.06$. Blue, green line corresponding to stable equilibrium points and red line corresponding to unstable equilibria. (Color figure online)

6.2 Backward bifurcation

Theorem 4

Model (1) has backward bifurcation at $R_{0} = 1$ with respect to disease transmission rate $\beta _{2}$ for symptomatic infected individuals if $2 a b w_{6} v_{6}^{2}$ > $\frac{2 \mu (v_{2} + v_{3} + v_{4} + v_{5} + v_{6} + v_{7})( \beta _{1} v_{4} + \beta _{2}^{[BB]} v_{5} + \beta _{3} v_{6})}{C}$.

Proof

To determine the necessary condition for backward bifurcation theorem, Castillo–Chavez and Song theorem [27] will be used at $R_{0} = 1$ which is equivalent to $\beta _2 = \beta _2^{[BB]}$.

Since $det(J_{E_{0}}) = D_{0} D_{1} D_{2} D_{3} D_{4} (1 - R_{0}) = 0$ for critical value $\beta _2 = \beta _{2} ^{[BB]}$, therefore $J_{E_{0}}$ has a zero eigenvalue corresponding to $\beta _{2} = \beta _{2}^{[BB]}$. Let $W = (w_{1} \ w_{2} \ w_{3} \ w_{4} \ w_{5} \ w_{6} \ w_{7})^\textrm{T}$ and $V = (v_{1} \ v_{2} \ v_{3} \ v_{4} \ v_{5} \ v_{6} \ v_{7})$ be left and right eigenvectors, respectively, of $J_{E_{0}}$ corresponding to eigenvalue zero where the values of $w_i, v_i$ are given in Theorem 3.

The discriminant quantity used in Castillo–Chavez and Song backward bifurcation theorem are

$$\begin{aligned} {\left\{ \begin{array}{ll} \psi = \sum _{k, i, j = 1} ^{7} w_{k}v_{i}v_{j} \dfrac{\partial ^2 f_{k}}{\partial x_{i} \partial x_{j}}(0,0) = 2 a b w_{6} v_{6}^{2} - \dfrac{2 \mu (v_{2} + v_{3} + v_{4} + v_{5} + v_{6} + v_{7})( \beta _{1} v_{4} + \beta _{2}^{[BB]} v_{5} + \beta _{3} v_{6})}{C} \\ \phi = \sum _{k, i = 1} ^{7} w_{k}v_{i} \dfrac{\partial ^2 f_{k}}{\partial x_{i} \partial \beta _{3}}(0,0) = v_{4} > 0. \end{array}\right. } \end{aligned}$$

(7)

where $x_{1} = S$, $x_{2} = E$, $x_{3} = Q$, $x_{4} = A$, $x_{5} = I$, $x_{6} = H$, $x_{7} = R$.

Here, $\phi$ is always positive and by Castillo–Chavez and Song’s theorem, system (1) experiences backward bifurcation at $R_{0} = 1$ if $\psi > 0$ which is equivalent to the condition as stated in theorem. $\square$

Fig. 4

Backward bifurcation diagram at $R_0 = 1$ (blue, green line corresponding to stable equilibrium points and red, magenta line corresponding to unstable equilibrium points) for $C = 10, \beta _1 = 0.42, \beta _3 = 0.2, \mu = 0.06, \alpha _1 = 0.08, \alpha _2 = 0.1, \alpha _3 = 0.2, \gamma _1 = 0.15, \gamma _2 = 0.25, \delta _1 = 0.15, \delta _2 = 0.25, \nu _1 = 0.2, \nu _2 = 0.15, a = 0.3, b = 20, \sigma = 0.1, d = 0.02$. (Color figure online)

In Fig. 4, we have presented the backward bifurcation diagram considering $R_0$ as bifurcation parameter ($\beta _2$ is the inbuilt parameter). There exists a critical value of $R_0$ (say $R_0^{*} = 0.9459$) such that for $R_0^{*}< R_0 < 1$ the system (1) contains two endemic equilibrium points with lower endemic state is unstable and higher endemic state is stable. Thus disease persists in the system $R_0 <1$ also. Hence the system experiences backward bifurcation with respect to $\beta _2$. Biologically bi-stability occurs for $R_0 <1$. Another importance of backward bifurcation is the eradication of disease depends not only on $R_0$ but also on initial population density. Thus for $R_0 < 1$ there is a critical value of $\beta _2$ say $\beta _2^{[BB]}$ below which disease will eradicate from the system.

6.3 Forward bifurcation with hysteresis

Forward bifurcation occurs when two local stable branches exist at $R_0 = 1$ [25]. In Fig. 2a one stable endemic equilibrium bifurcates forwardly from $R_0 = 1$, therefore Fig. 2a exhibits forward bifurcation at $R_0 = 1$ [25]. Now we discuss one uncommon type bifurcation, namely forward bifurcation with hysteresis [28, 29]. This type of bifurcation occurs when three endemic equilibrium exist with two outer stable endemic and one inner unstable endemic in very small region of $R_0 > 1$ [28, 29]. Figure 2a shows the above said qualitative phenomenon therefore Fig. 2b indicates system exhibits forward bifurcation with hysteresis. This type bifurcation has one more critical case. In Fig. 2c we see that, in very small region of $R_0 > 1$ three endemic equilibria exist with two stable endemic and one unstable endemic. At the same time, in very small region of $R_0 < 1$, similar qualitative nature of backward bifurcation occurs therefore smaller infected endemic is unstable and higher infected endemic is stable. These two cases combined represent forward bifurcation with hysteresis [28, 29].

Fig. 5

a Fitting model to cumulative cases in Hong Kong. b Residuals of the fit. c Bar diagram from 19th December, 2021 to 3rd April, 2022

Table 2 Parameter values and their sensitivity indexes

7 Model validation and parameter estimation

Here we check validity of proposed COVID-19 model fitting it with COVID-19 infected data of Hong Kong from 19th December, 2021 to 3rd April, 2022 [30]. In this context, we use least square minimization technique for cumulative infected data of COVID-19 [25]. The main principle for least square technique is to minimize sum of the square error. Model fitness will be reasonably good if sum of the squares of the vertical distances between real reported data and the model predicted data are as small as possible i.e. we have to minimize $f(\xi , n)$ where

$$\begin{aligned}f(\xi , n) = \sum _{i = 1}^{n} \left( Y_i - I(t_i) \right) ^2, \end{aligned}$$

$\xi$ denotes set of the model parameters, $Y_i$ denotes cumulative real infected data for ith observation, $I(t_i)$ denotes cumulative infected data of model prediction for ith observation and n denotes the total days which are used for model fitting. The cumulative model predicted data satisfies equation

$$\begin{aligned}\dfrac{\textrm{d}I(t_j)}{\textrm{d}t} = \alpha _{2} E + \nu _{2} A.\end{aligned}$$

The minimization of $f(\xi , n)$ is quite difficult for analytic procedure. We have taken help of MATLAB fmincon minimization package for fitting the model and estimating the model parameters. We consider birth rate, normal death rate as 222.432, 0.0000322 which are collected from  [31] and COVID-19-induced death rate as 0.00697 which is taken from [30]. Also we take value of $\alpha _2$ as 0.1 as duration of incubation period lies between 2 to 14 days. The remaining parameters are estimated which are enlisted in second column of Table 2. The total error for estimating model parameters is $1.510 \times 10^{11}$. The number of cumulative infected real data and the model predicted data is given in Fig. 5a. Residuals and bar diagram of the data fitting are given in Fig. 5b, c. From the Fig. 5, we observe that the vertical distances between real infected cumulative data and model predicted cumulative infected data are very small; therefore we can decide that fitness of model is good. Also residuals are randomly distributed in Fig. 5b which indicates data is fitted well [25].

Fig. 6

Effect on symptomatic infected class (I) with respect to parameter a $\beta _1$, b $\beta _2$, c $\beta _3$, d $\alpha _3$, e $\nu _1$, f $\alpha _1$, g a, h $\sigma$

8 Sensitivity analysis

Since from December 2021, the number of daily COVID-19 infected people is increasing day by day for Hong Kong. Therefore our motive will be, how we can minimize the COVID-19 transmission among community. To reduce the rate of disease spreading, we have to take proper intervention policies which is equivalent to identify most sensitive parameters which have most influence on the proposed model i.e. on $R_0$. Since, $R_0$ is defined as average number of secondary infection produced by an infected people during its entire lifespan as an infected host, therefore parameters whose impact on disease transmission dynamics, they should affect $R_0$. Hence, to decrease the invade of disease transmission, we have to find out these types of sensitive model parameters. By controlling these parameters, we can able to reduce COVID-19 transmission among population, since in this case value of $R_0$ will be also reduced. To find out sensitivity of parameters, we have to estimate variation of $R_0$ with respect to variation of different model parameters. Here, we use normalized sensitivity index method  [12, 32, 33] to calculate the value of sensitivity index of model parameters. In this method, the sensitivity index of $R_0$ with respect to model parameter $\rho$ is given by $\varGamma ^{\rho }_{R_0} = \dfrac{\partial R_0}{\partial \rho } \times \dfrac{\rho }{R_0}$. The parameter with higher sensitivity index implies that model parameter has more impact on $R_0$. The positive (negative) sign of sensitivity index implies $R_0$ will increase with increasing (decreasing) value of that model parameter. In our study, the sensitivity indexes of parameters are given in fourth column of Table 2. The most positive sensitive model parameters of the proposed model are $\beta _1$, $\beta _2$, $\beta _3$, $\alpha _3$ and most negative sensitive model parameters are $\nu _1$, $\alpha _1$, a, $\sigma$. It is clear from Table 2 that, if we increase (decrease) value of $\beta _1,$ $\beta _2$, $\beta _3$, $\alpha _3$ by 10 %, the value of $R_0$ will be increased (decreased) by 3.57 %, 1.97 %, 4.44 %, 1.54 %, respectively. Similarly, if we decrease (increase) values of $\nu _1$, $\alpha _1$, a, $\sigma$ by 10 %, then value of $R_0$ will be increased (decreased) by 3.65 %, 2.49 %, 2.28 %, 1.84 %, respectively. This kind of study will be helpful for health planners to control or prevent COVID-19 transmission in the population.

8.1 Effect of different sensitive parameters on symptomatic infected compartment (I)

In this section, we show the effect of positive indexes parameters $\beta _1$, $\beta _2$, $\beta _3$, $\alpha _3$ and negative indexes parameters $\nu _1$, $\alpha _1$, a, $\sigma$ on symptomatic infected class (I). It is clear from Fig. 6a–d that density of symptomatic infected class (I) increases (decreases) with increasing (decreasing) values of parameters $\beta _1$, $\beta _2$, $\beta _3$, $\alpha _3$. In each case we increase the values of parameters $\beta _1$, $\beta _2$, $\beta _3$, $\alpha _3$ by 10 %, the corresponding effect on symptomatic infected class (I) is shown in Fig. 6a–d. Since $\beta _1$, $\beta _2$, $\beta _3$, $\alpha _3$ are positive indexes parameters hence number of symptomatic infected class (I) increases with increasing value of $\beta _1$, $\beta _2$, $\beta _3$, $\alpha _3$. Similarly from Fig. 6e–h we see that density of symptomatic infected class (I) decreases (increases) with increasing (decreasing) values of the parameters $\nu _1$, $\alpha _1$, a, $\sigma$. In each case we increase the values of the parameters $\nu _1$, $\alpha _1$, a, $\sigma$ by 10%, the corresponding effect on symptomatic infected class (I) is shown in Fig. 6e–h. As $\nu _1$, $\alpha _1$, a, $\sigma$ are negative indexes parameters hence number of symptomatic infected class (I) decreases with increasing value of $\nu _1$, $\alpha _1$, a, $\sigma$.

9 Estimation of $R_0$ and R(t) for COVID-19 outbreak in Hong Kong

Here we estimate $R_0$ using initial growth rate of actual infected data in Hong Kong and also estimate time-dependent effective reproduction number from daily new infected COVID-19 cases in Hong Kong.

9.1 Estimation of $R_0$ from actual infected data of Hong Kong

Many methods exist mathematically and also statistically to estimate $R_0$ from actual infected data [34]. Here, we estimate $R_0$ from initial infected COVID-19 data of Hong Kong, as theory developed in [35]. First, we assume that cumulative cases $C(t) \propto \exp (\zeta t)$ where $\zeta$ is force of the infection. Also number of exposed, quarantined, asymptomatic, infected and hospitalized human varies with $\exp (\zeta t)$. Therefore, we get

$$\begin{aligned} {\left\{ \begin{array}{ll} E \sim E_0 \, \exp (\zeta t) \\ Q \sim I_0 \, \exp (\zeta t) \\ A \sim A_0 \, \exp (\zeta t) \\ I\sim I_0 \, \exp (\zeta t) \\ H \sim H_0 \, \exp (\zeta t) \end{array}\right. } \end{aligned}$$

(8)

where $E_0, Q_0, A_0, I_0, H_0$ are constants. Again, we suppose that at early stage of COVID-19 outbreak, the density of infected people is negligible compared to total susceptible population, therefore we can consider $S(t) = N(t) = \dfrac{C}{\mu }$. Putting values of E, Q, A, I, H from relation (8) in model (1), we get,

$$\begin{aligned} {\left\{ \begin{array}{ll} (\zeta + D_0) E_0 = \beta _1 A_0 + \beta _2 I_0 + \beta _3 H_0, \\ (\zeta + D_1) Q_0 = \alpha _1 E_0, \\ (\zeta + D_2) A_0 = \alpha _3 E_0, \\ (\zeta + D_3) I_0 = \alpha _2 E_0 + \nu _2 A_0, \\ (\zeta + D_4) H_0 = \gamma _1 Q_0 + \delta _1 I_0. \end{array}\right. } \end{aligned}$$

(9)

Determining $\beta _1$, $\beta _2$ & $\beta _3$, from relations of (9) and then putting in $R_0$, we get,

$$\begin{aligned} R_0= & {} \dfrac{\zeta + D_0}{M D_0}\left[ \dfrac{\alpha _2 D_2 + \alpha _3 \nu _2}{D_2 D_3} + \dfrac{k_1 \alpha _3}{D_2} \right. \nonumber \\{} & {} \left. + \dfrac{k_2 \left( D_1 D_2 \alpha _2 \delta _1 + D_1 \alpha _3 \delta _1 \nu _2 + D_2 D_3 \alpha _1 \gamma _1 \right) }{D_1 D_2 D_3 D_4} \right] \nonumber \\ \end{aligned}$$

(10)

where

$$\begin{aligned}{} & {} M = \dfrac{\alpha _2}{\zeta + D_3} + \dfrac{\nu _2 \alpha _3}{(\zeta + D_2)(\zeta + D_3)}+\dfrac{k_1 \alpha _3}{\zeta + D_2}\\{} & {} \quad + \dfrac{k_2 \gamma _1 \alpha _1}{(\zeta + D_1)(\zeta + D_4)}+ \dfrac{k_2 \delta _1 \alpha _2}{(\zeta + D_3)(\zeta + D_4)}\\{} & {} \quad + \dfrac{k_2 \delta _1 \nu _2 \alpha _3}{(\zeta + D_2)(\zeta + D_3)(\zeta + D_4)}, k_1 = \dfrac{\beta _1}{\beta _2}, k_2 = \dfrac{\beta _3}{\beta _2}. \end{aligned}$$

For estimating $R_0$ from (10), we have to estimate $\zeta$ and here we use estimated values of model parameters which are given in second column of Table 2. Based on  [36], number of per day new cases varies as $\zeta (t)$. Next we plot daily new COVID-19 infected case versus cumulative infected COVID-19 cases C(t) in Hong Kong from 19th December, 2021 to 3rd April, 2022 (see Fig. 7a). Here we fit a linear regression line by adopting least square methodology to the exponential cumulative growth data. $\zeta$ is represented by the slope of fitted line (see Fig. 7b). Therefore, the estimated value of $\zeta$ is $0.195 \pm 0.007 \, day^{-1}$ and using relation (10) along with $\zeta$, we get the estimated value of $R_0$ is 4.360 with lower and upper value as 4.203 and 4.519, respectively.

Fig. 7

a Time series of new cases of COVID-19 in Hong Kong from 19th December, 2021 to 3rd April, 2022, b daily number of infected cases against cumulative number of infected cases from 19th December, 2021 to 3rd April, 2022

9.2 Effective reproduction number (R(t))

In disease spreading dynamics, $R_0$ plays a crucial role. Depending on value of $R_0$, we can conclude whether disease persists or eradicates from population. If value of $R_0 < 1$, then disease eradicates from population, at the same time if $R_0 > 1$ then disease persists in population. From the definition of $R_0$, it can be assumed that $R_0$ is always constant. But in reality, the value of $R_0$ is not always constant that means its value varies with time. Especially for COVID-19 disease, when disease starts to spread in population at first, its rate of disease transmission increases gradually, then at a time it will take its peak position, after that disease transmission rate starts to decrease. Therefore, value of reproduction number varies always. In this context, we study time varying reproduction number, known as effective reproduction number R(t) [37]. From the value of R(t), researchers can identify the trend of the disease and also predict about an epidemic outbreak. Therefore, health planners can take proper control policies to control or prevent transmission of disease based on value of R(t). To estimate the value of R(t), we use real infected COVID-19 data of Hong Kong from 19th December, 2021 to 3rd April, 2022. There are several methods available to estimate R(t), but here we use the methodology as developed in  [38, 39]. For estimation of R(t), we use equation,

$$\begin{aligned} R(t) = \dfrac{b(t)}{\int _0^\infty b(t-\lambda ) h(\tau ) \textrm{d} \tau } \end{aligned}$$

(11)

where b(t) represents number of new infected COVID-19 case in tth day and $h(\tau )$ represents generation interval distribution for COVID-19 transmission in Hong Kong. Let exposed, quarantined, asymptomatic, infected and hospitalized people leave their corresponding class at a rate $D_{0} = \alpha _{1} + \alpha _{2} + \alpha _{3} + \mu$, $D_{1} = \gamma _{1} + \gamma _{2} + \mu$, $D_{2} = \nu _{1} + \nu _{2} + \mu$, $D_{3} = \delta _{1} + \delta _{2} + \mu$, $D_{4} = a + \sigma + d + \mu$, respectively. So, generation interval distribution is combination of the exponential functions $D_0 e^{- D_0 t}$, $D_1 e^{- D_1 t}$, $D_2 e^{- D_2 t}$, $D_3 e^{- D_3 t}$ and $D_4 e^{- D_4 t}$, then the formula is given as

$$\begin{aligned} h(t)= \sum _{i = 1}^4 \dfrac{D_0 D_1 D_2 D_3 D_4 e^{- D_i t}}{\varPi _{j=1, j\ne i}^2(D_j - D_i)} \end{aligned}$$

(12)

with mean $T = \dfrac{1}{D_0} + \dfrac{1}{D_1} + \dfrac{1}{D_2} + \dfrac{1}{D_3} + \dfrac{1}{D_4}$ and $\tau > 0$. The above said formula is valid only when $\zeta > \min \left\{ - D_0, - D_1, - D_2, - D_3, -D_4 \right\}$.

Using estimated model parameter values, we calculate effective reproduction number and the figure of it is given in Fig. 8. We see that values of R(t) always greater than unity except 27th to 29th day but after 90th day, value of R(t) lies below unity. Therefore we can conclude that after 90 days disease starts to decrease.

Fig. 8

Effective reproduction number R(t) for COVID-19 cases in Hong Kong from 19th December, 2021 to 3rd April, 2022

10 Optimal control problem

Coronavirus spread worldwide from December, 2019. It took dangerous form for human civilization in very short time. Initially government of every country faced problem to reduce infection. To control the invade of infection, many countries adopted full or partial lockdown based on their countries financial loss. By adopting lockdown, government could able to reduce interaction between susceptible population with asymptomatic or symptomatic infected population. But to avoid financial loss, many countries unlocked lockdown after few months and gave restriction for maintaining home isolation of the symptomatic infected persons. We discuss different available ways in formulation of optimal control problem. The main purpose to use optimal control in COVID-19 problem, is to reduce number of asymptomatic, infected, symptomatic infected and hospitalized people and at the same time, we have to remember to minimize vaccination or treatment cost [40, 41]. Now, if we apply constant rate of vaccination or treatment, then implementation cost may be very high. Therefore we have to use time-dependent control to reduce infected population as well as implemented cost in a finite time. Now, we formulate an optimal control problem for considered SEQAIHR model.

We consider COVID-19 infected data of Hong Kong from 19th December, 2021 to 3rd April, 2022, at that period vaccination was started and without loss of any generality we can assume that vaccination has been done to maximum number of populations. Let $a_1$ be the rate of vaccination and $v_1$ be efficiency of vaccination where $0 \le v_1 \le 1$. We define $u_1 = a_1 v_1$ $(0 \le u_1 \le 1)$ is the rate of effective vaccination at this rate successful immunized vaccinated peoples move to recovered class  [42,43,44,45,46]. Therefore here we assume that the vaccinated peoples who will not be affected by coronavirus again, hence these vaccinated people will move to recovered class. Further, we use saturated type treatment for hospitalized class, therefore we can here consider a treatment control parameter $u_2$ for treatment function, hence it takes the form $\dfrac{a u_2 H}{1 + b u_2 H}$ where $0 \le u_2 \le 1$. Generally, values of $u_1$ and $u_2$ lie between 0 to 1, since a part of population is vaccinated or took treatment. Here, we consider both controls $u_1$ and $u_2$ as function of time t. Thus, we reformulate considered model (1) for optimal control problem as given below:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dfrac{\textrm{d}S}{\textrm{d}t} = C - \dfrac{ S (\beta _{1} A + \beta _{2} I + \beta _{3} H)}{N}\\ \qquad \qquad - u_1 S - \mu S \\ \dfrac{\textrm{d}E}{\textrm{d}t} = \dfrac{ S (\beta _{1} A + \beta _{2} I + \beta _{3} H)}{N}\\ \qquad \qquad - ( \alpha _{1}+ \alpha _{2}+ \alpha _{3} + \mu )E \\ \dfrac{\textrm{d}Q}{\textrm{d}t} = \alpha _{1} E - (\gamma _{1} + \gamma _{2} + \mu )Q \\ \dfrac{\textrm{d}A}{\textrm{d}t} = \alpha _{3} E - (\nu _{1} + \nu _{2} + \mu )A \\ \dfrac{\textrm{d}I}{\textrm{d}t} = (\alpha _{2} E + \nu _{2} A) - (\delta _{1} + \delta _{2} + \mu )I \\ \dfrac{\textrm{d}H}{\textrm{d}t} = (\gamma _{1} Q + \delta _{1} I) - \dfrac{a u_2 H}{1 + b u_2 H }\\ \qquad \qquad - (\sigma + d + \mu ) H \\ \dfrac{\textrm{d}R}{\textrm{d}t} = (\gamma _{2} Q + \delta _{2} I + \nu _{1} A + \sigma H)\\ \qquad \qquad + \dfrac{a u_2 H}{1 + b u_2 H } + u_1 S - \mu R \end{array}\right. } \end{aligned}$$

(13)

The objective functional $M(u_1, u_2)$, which has to minimize is given below,

$$\begin{aligned}{} & {} M(u_1, u_2)\nonumber \\ {}{} & {} = \int ^T_0 \left( A_1 S+ A_2 H + \dfrac{1}{2} B_1 u_1^2 + \dfrac{1}{2} B_2 u_2^2\right) \textrm{d}t \end{aligned}$$

(14)

constants $A_1$, $A_2$ denote loss due to presence of susceptible class (S), hospitalized class (H) and Constants $B_1$, $B_2$ denote loss due to implementation of two controls $u_1$, $u_2$. The cost function in (14) contains two types of terms, those are: (i) the cost of infection/loss in population (i.e. first two terms) and (ii) cost of vaccination (i.e. last two terms). It is chosen in quadratic form to make it convex such that the minimum value exists. Another important observation of quadratic form in biological point of view is the severity of “giving too much vaccine to an individual” [47]. The optimal problem is implemented for time interval [0, T], therefore after time T, both controls will be stopped. Thus, we have to identify an optimal pair $(u_1^{*}, u_2^{*})$ such that

$$\begin{aligned} M(u_1^{*}, u_2^{*}) = \min \left\{ M(u_1, u_2) : (u_1, u_2) \in U \right\} \end{aligned}$$

(15)

where U is given by

$$\begin{aligned}U = \left\{ (u_1(t), u_2(t)) : 0 \le u_i \le 1, i = 1, 2, t \in [0, T] \right\} \end{aligned}$$

$u_1(t)$ and $u_2(t)$ as Lebesgue measurable functions.

It is clear that integrand of cost functional $M(u_1, u_2)$ is convex function for $u_1$ and $u_2$. Again, by Theorem 2, all solutions of system (1) are bounded, in similar manner we can show that solutions of system (13) are bounded, which implies that system (13) satisfies Lipschitz condition for state variables. This concludes the existence of $(u_1^{*}, u_2^{*})$ such that $M(u_1^{*}, u_2^{*})$ is minimized. The above result is summarized in the following remark:

Remark

There exists optimal control pair $(u_1^{*}, u_2^{*})$ for which $M(u_1^{*}, u_2^{*}) = \min \left\{ M(u_1, u_2) : (u_1, u_2) \in U \right\}$.

Theorem 5

For $(u_1^{*}, u_2^{*})$ and $(S^{*}, E^{*}, Q^{*}, A^{*}, I^{*}, H^{*}, R^{*})$ of system (13) and (14) which minimizes $M(u_1, u_2)$ on U, there exists $\lambda _1$, $\lambda _2$, $\lambda _3$, $\lambda _4$, $\lambda _5$, $\lambda _6$, $\lambda _7$ satisfying

$$\begin{aligned} {\left\{ \begin{array}{ll} \dfrac{\textrm{d} \lambda _1(t)}{\textrm{d}t} = - A_1 + (\lambda _1 - \lambda _2)\dfrac{(\beta _1 A + \beta _2 I + \beta _3 H)(E+ Q+ A+ I+ H +R)}{(S+ E+ Q+ A+ I+ H +R)^2} + (\lambda _1 - \lambda _7)u_1 + \lambda _1 \mu \\ \dfrac{\textrm{d} \lambda _2(t)}{\textrm{d}t} = (\lambda _1 - \lambda _2)\dfrac{S(\beta _1 A + \beta _2 I + \beta _3 H)}{(S+ E+ Q+ A+ I+ H +R)^2} + (\lambda _2 - \lambda _3) \alpha _1 + (\lambda _2 - \lambda _5) \alpha _2 + (\lambda _2 - \lambda _4) \alpha _3 + \lambda _2 \mu \\ \dfrac{\textrm{d} \lambda _3(t)}{\textrm{d}t} = (\lambda _1 - \lambda _2)\dfrac{S(\beta _1 A + \beta _2 I + \beta _3 H)}{(S+ E+ Q+ A+ I+ H +R)^2} + (\lambda _3 - \lambda _6) \gamma _1 + (\lambda _3 - \lambda _7) \gamma _1 + \lambda _3 \mu \\ \dfrac{\textrm{d} \lambda _4(t)}{\textrm{d}t} = (\lambda _1 - \lambda _2)S\dfrac{\beta _1(S+ E+ Q+ I+ H +R)- (\beta _2 I + \beta _3 H)}{(S+ E+ Q+ A+ I+ H +R)^2} + (\lambda _4 - \lambda _7) \nu _1 + (\lambda _4 - \lambda _5) \nu _2 + \lambda _4 \mu \\ \dfrac{\textrm{d} \lambda _5(t)}{\textrm{d}t} = (\lambda _1 - \lambda _2)S\dfrac{\beta _2(S+ E+ Q+ A+ H +R)- (\beta _1 A + \beta _3 H)}{(S+ E+ Q+ A+ I+ H +R)^2} + (\lambda _5 - \lambda _6) \delta _1 + (\lambda _5 - \lambda _7) \delta _2 + \lambda _5 \mu \\ \dfrac{\textrm{d} \lambda _6(t)}{\textrm{d}t} = -A_2 + (\lambda _1 - \lambda _2)S\dfrac{\beta _3(S+ E+ Q+ A+ I + R)- (\beta _1 A + \beta _2 I)}{(S+ E+ Q+ A+ I+ H +R)^2} + (\lambda _6 - \lambda _7) \dfrac{a u_2}{(1 + b u_2 H)^2} \\ \ \ \ \ \ \ \ \ \ \ \ + (\lambda _6 - \lambda _7) \sigma + \lambda _6 (d+ \mu ) \\ \dfrac{\textrm{d} \lambda _7(t)}{\textrm{d}t} = (\lambda _1 - \lambda _2)\dfrac{S(\beta _1 A + \beta _2 I +\beta _3 H)}{(S+ E+ Q+ A+ I+ H +R)^2} +\lambda _7 \mu \end{array}\right. } \end{aligned}$$

(16)

with transversality condition

$$\begin{aligned} \lambda _i(T) = 0, i= 1, 2, 3 , 4, 5, 6, 7 \end{aligned}$$

and $(u_1^{*}, u_2^{*})$ is given by

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{1}^{*}(t) = \min \left( \max \left( 0, \dfrac{(\lambda _{1} - \lambda _{7})S^*}{B_{1}} \right) , 1 \right) \\ u_{2}^{*}(t) = \min \left( \max \left( 0, \overline{u}_{2} \right) , 1 \right) \end{array}\right. } \end{aligned}$$

(17)

where $\overline{u}_{2}$ is non-negative root of $u_2 B_2(1 + b u_2 H^{*})^2 = (\lambda _6 - \lambda _7) (a-b) H^{*}$.

Proof

To prove this theorem, we have to use Pontryagin’s maximum principle  [13, 41, 48]. We construct Lagrangian $L(S, E, Q, A, I, H, R, u_1, u_2)$ of (13) as

$$\begin{aligned}{} & {} L(S, E, Q, A, I, H, R, u_1, u_2) = A_1 S+ A_2 H \nonumber \\{} & {} \quad + \dfrac{1}{2} B_1 u_1^2 + \dfrac{1}{2} B_2 u_2^2 \end{aligned}$$

(18)

and Hamiltonian H as

$$\begin{aligned}{} & {} \quad H_1(S, E, Q, A, I, H, R, u_1, u_2, \lambda _1, \nonumber \\{} & {} \quad \quad \lambda _2, \lambda _3, \lambda _4, \lambda _5, \lambda _6, \lambda _7, t) \nonumber \\{} & {} \quad = A_1 S+ A_2 H + \dfrac{1}{2} B_1 u_1^2 + \dfrac{1}{2} B_2 u_2^2 + \lambda _1 \dfrac{\textrm{d}S}{\textrm{d}t} \nonumber \\{} & {} \quad + \lambda _2 \dfrac{\textrm{d}E}{\textrm{d}t} + \lambda _3 \dfrac{\textrm{d}Q}{\textrm{d}t} + \lambda _4 \dfrac{\textrm{d}A}{\textrm{d}t} + \lambda _5 \dfrac{\textrm{d}I}{\textrm{d}t} \nonumber \\{} & {} \quad + \lambda _6 \dfrac{\textrm{d}H}{\textrm{d}t} + \lambda _7 \dfrac{\textrm{d}R}{\textrm{d}t} \end{aligned}$$

(19)

satisfying adjoint equations

$$\begin{aligned} \dfrac{\textrm{d} \lambda _1(t)}{\textrm{d}t}{} & {} = - \dfrac{\partial H_1}{\partial S}, \dfrac{\textrm{d} \lambda _2(t)}{\textrm{d}t} = - \dfrac{\partial H_1}{\partial E}, \dfrac{\textrm{d} \lambda _3(t)}{\textrm{d}t}\nonumber \\ {}{} & {} = - \dfrac{\partial H_1}{\partial Q}, \dfrac{\textrm{d} \lambda _4(t)}{\textrm{d}t} = - \dfrac{\partial H_1}{\partial A}, \dfrac{\textrm{d} \lambda _5(t)}{\textrm{d}t}\nonumber \\{} & {} \quad = - \dfrac{\partial H_1}{\partial I}, \dfrac{\textrm{d} \lambda _6(t)}{\textrm{d}t} = - \dfrac{\partial H_1}{\partial H}, \end{aligned}$$

(20)

$$\begin{aligned}{} & {} \quad \dfrac{\textrm{d} \lambda _7(t)}{\textrm{d}t} = - \dfrac{\partial H_1}{\partial R} \end{aligned}$$

(21)

with

$$\begin{aligned} \lambda _i(T) = 0, i= 1, 2, 3 , 4, 5, 6, 7 \end{aligned}$$

.

Solving (20), we see $\lambda _1, \lambda _2, \lambda _3, \lambda _4, \lambda _5, \lambda _6, \lambda _7$ satisfy the equations which are given in Eq. (16) with $\lambda _i(T) = 0, i= 1, 2, 3 , 4, 5, 6, 7$.

Fig. 9

Time series of controls and different populations in presence of control (blue line) and without control (red line): a exposed population, b quarantined population c asymptomatic population, d infected population, e hospitalized population, f recovered population, g total infected hosts, h $u_1$ control, i $u_2$ control

Now, we use optimality conditions $\dfrac{\partial H_1}{\partial u_1}$ & $\dfrac{\partial H_1}{\partial u_2}$ at $(u_1^{*}, u_2^{*})$, thus we get

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{1}^{*}(t) = \min \left( \max \left( 0, \dfrac{(\lambda _{1} - \lambda _{7})S^*}{B_{1}} \right) , 1 \right) \\ u_{2}^{*}(t) = \min \left( \max \left( 0, \overline{u}_{2} \right) , 1 \right) \end{array}\right. } \end{aligned}$$

where $\overline{u}_{2}$ is non-negative root of $u_2 B_2(1 + b u_2 H^{*})^2 = (\lambda _6 - \lambda _7) (a-b) H^{*}$.

It is obvious that $\dfrac{\partial ^2 H_1}{\partial u_1^2} > 0$, $\dfrac{\partial ^2 H_1}{\partial u_2^2} > 0$ and $\dfrac{\partial ^2 H_1}{\partial u_1^2} \dfrac{\partial ^2 H_1}{\partial u_1^2} > \left( \dfrac{\partial ^2 H_1}{\partial u_1 u_2} \right) ^2$ at $(u_1^{*}, u_2^{*})$.

Thus, considered optimal control problem is minimized at optimal value $(u_1^{*}(t), u_2^{*}(t))$. $\square$

Now we verify theoretical findings of optimal control (13), we solve numerically using forward-backward sweep method. Here, we consider time interval [0, 108] days i.e. after 108 days both controls will be stopped. To simulate the problem, we consider parameter values from Table 2 with $A_1 = 0.01$, $A_2 = 0.01$, $B_1 = 1000$, $B_2 = 0.0001$ with initial conditions 7604299, 15, 4, 7, 6, 5, 0. From Fig. 9a–f, we compare density of exposed, quarantined, asymptomatic, infected, hospitalized, recovered population when system is in control or in without control. From Fig. 9a–e, we see density of exposed, quarantined, asymptomatic, infected, hospitalized population is reduced when system is in control. In Fig. 9g, we show density of total infected population i.e. asymptomatic, infected and hospitalized population is also reduced when system with control. In Fig. 9h–i, we show optimal path of control variables $u_1$ and $u_2$.

11 Conclusion

In this paper we consider an SEQAIHR model with three infected classes namely asymptomatic (A), symptomatic infected (I) and hospitalized class (H) to visualize the pandemic situation of Hong Kong, 2022. Here we consider saturated treatment rate in hospitalized class to include effect of the limited medical facility. First we examine biological significance of model solutions. Then we compute $R_0$ which has effective role to control disease outbreak. It is verified that the model may have maximum three endemic equilibria for $R_0 >1$ and also may have maximum two endemic equilibria for $R_0 <1$. The stability of disease free and endemic equilibrium point is expressed in terms of $R_0$. Further, we show the model exhibits transcritical, backward and forward bifurcation with hysteresis.

To validate the proposed model, we fit model with COVID-19 infected data of Hong Kong from 19th December, 2021 to 3rd April, 2022 and also estimate the model parameters. Then, we use sensitivity analysis to identify the most sensitive parameters which have more impact on $R_0$. From estimation of $R_0$, we see that value of $R_0$ lies between 4.20 and 4.51, therefore COVID-19 takes a fatal form in population. Also, from R(t), we see that its values lie between from 1.44 to 12.87 and also we observe that after 90 days the value of effective reproduction number less than unity therefore we can conclude that after 90 days disease will die out from population.

Finally, we perform an optimal control problem considering effective vaccination control and saturated treatment control. Numerically we give a comparative study of each class with population under control and without control. We think that our study will give some lay out for health planners to take some decision about pandemic outbreak. For future work, one can extend the proposed SEQAIHR model by considering separate vaccinated class V to study the effect of vaccination for populations.

Appendices

Appendices

Appendix-I: Expressions of $e_{i}, i = 0, 1, 2 , 3$

$$\begin{aligned}{} & {} e_0 = - D_0 D_1 D_2^2 D_3^2 a^2 \alpha _1 b^2 \mu - D_0 D_1 D_2^2 D_3^2 D_4^2 \alpha _1 b^2 \mu \\{} & {} \quad -D_0 D_1^2 D_2 D_3^2 a^2 \alpha _2 b^2 \mu -D_0 D_1^2 D_2 D_3^2 D_4^2 \alpha _2 b^2 \mu \\{} & {} \quad -D_0 D_1^2 D_2 D_3^2 a^2 \alpha _2 b^2 \beta _2 -D_0 D_1^2 D_2 D_3^2 D_4^2 \alpha _2 b^2\\{} & {} \quad \beta _2 -D_0 D_1^2 D_2^2 D_3 a^2 \alpha _3 b^2 \beta _1 -D_0 D_1^2 D_2^2 D_3 a^2 \alpha _3 b^2 \mu \\{} & {} \quad -D_0 D_1^2 D_2^2 D_3 D_4^2 \alpha _3 b^2 \beta _1 -D_0 D_1^2 D_2^2 D_3 D_4^2 \alpha _3 b^2 \mu \\{} & {} \quad + D_0 D_1 D_2 D_3 D_5 a b^2 \mu + 2 D_0 D_1^2 D_2^2 D_3^2 D_4 a b^2 \mu \\{} & {} \quad -D_0 D_1 D_2 D_3 D_4 D_5 b^2 \mu + D_0 D_1 D_2 D_3 D_5 a b^2 \beta _3\\{} & {} \quad -D_0 D_1 D_2 D_3 D_4 D_5 b^2 \beta _3 + D_0 D_1 D_2 D_3 D_5 a b^2\\{} & {} \quad \sigma -D_0 D_1^2 D_2 D_3^2 a^2 \alpha _2 b^2 \delta _2 -D_0 D_1^2 D_2^2 D_3 D_4^2 \alpha _3 b^2 \nu _1 \\{} & {} \quad -D_0 D_1^2 D_2^2 D_3 a^2 \alpha _3 b^2 \nu _1- D_0 D_1 D_2 D_3 D_4 D_5 b^2 \sigma - D_0 D_1 D_2^2 D_3^2 D_4^2 \\{} & {} \quad \alpha _1 b^2 \gamma _2 - D_0 D_1 D_2^2 D_3^2 a^2 \alpha _1 b^2 \gamma _2 -D_0 D_1^2 D_2 D_3^2 D_4^2 \\{} & {} \quad \alpha _2 b^2 \delta _2 + D_0^2 D_1^2 D_2^2 D_3^2 a^2 b^2+ D_0^2 D_1^2 D_2^2 D_3^2 D_4^2 b^2 \\{} & {} \quad + 2 D_0 D_1^2 D_2 D_3 D_4 a \alpha _3 b^2 \mu \nu _2+ 2 D_0 D_1^2 D_2 D_3 D_4 a \alpha _3 b^2 \beta _3 \nu _2 \\{} & {} \quad + 2 D_0 D_1^2 D_2 D_3 D_4 a \alpha _3 b^2 \delta _2 \nu _2 + 2 D_0 D_1^2 D_2^2 D_3 D_4 a \alpha _3 b^2 \nu _1 \\{} & {} \quad -D_0 D_1^2 D_2 D_3 D_4^2 \alpha _3 b^2 \delta _2 \nu _2 -D_0 D_1^2 D_2 D_3 a^2 \alpha _3 b^2 \delta _2 \nu _2\\{} & {} \quad + 2 D_0 D_1 D_2^2 D_3^2 D_4 a \alpha _1 b^2 \gamma _2 + 2 D_0 D_1^2 D_2 D_3^2 D_4 a \alpha _2 b^2 \delta _2 \\{} & {} \quad -D_0 D_1^2 D_2 D_3 a^2 \alpha _3 b^2 \beta _2 \nu _2 - D_0 D_1^2 D_2 D_3 a^2 \alpha _3 b^2 \mu \nu _2\\{} & {} \quad + 2 D_0 D_1^2 D_2 D_3^2 D_4 a \alpha _2 b^2 \beta _2 + 2 D_0 D_1^2 D_2 D_3^2 D_4 a \alpha _2 b^2 \mu \\{} & {} \quad -D_0 D_1^2 D_2^2 D_3^2 a^2 b^2 \mu -D_0 D_1^2 D_2 D_3 D_4^2 \alpha _3 b^2 \beta _2 \nu _2 \\{} & {} \quad -D_0 D_1^2 D_2 D_3 D_4^2 \alpha _3 b^2 \mu \nu _2+ 2 D_0 D_1 D_2^2 D_3^2 D_4 a \alpha _1 b^2 \mu \\{} & {} \quad + 2 D_0 D_1^2 D_2^2 D_3 D_4 a \alpha _3 b^2 \beta _1 +2 D_0 D_1^2 D_2^2 D_3 D_4 a \alpha _3 b^2 \mu \\{} & {} \quad - 2 D_0^2 D_1^2 D_2^2 D_3^2 D_4 a b^2 - D_0 D_1^2 D_2^2 D_3^2 D_4^2 b^2 \mu ,\\{} & {} \quad e_1 = D_0 D_1 D_2 D_3 D_5 a b \mu + 2 D_0 D_1^2 D_2^2 D_3^2 D_4 a b \mu \\{} & {} \quad - 2 D_0 D_1 D_2^2 D_3^2 D_4^2 \alpha _1 b \gamma _2 -C D_1 D_5 a \alpha _3 b^2 \beta _2 \nu _2\\{} & {} \quad - 2 D_0 D_1 D_2 D_3 D_4 D_5 b \beta _3 - 2 D_0 D_1 D_2 D_3 D_4 D_5 b \mu \\{} & {} \quad + D_0 D_1 D_2 D_3 D_5 a b \beta _3 + C D_0 D_1 D_2 D_3 D_5 a b^2 + C D_1 D_2 D_4 D_5 \alpha _3 b^2 \beta _1\\{} & {} \quad -C D_1 D_2 D_5 a \alpha _3 b^2 \beta _1 + C D_1 D_3 D_4 D_5 \alpha _2 b^2 \beta _2 \\{} & {} \quad -C D_1 D_3 D_5 a \alpha _2 b^2 \beta _2 + C D_1 D_4 D_5 \alpha _3 b^2 \beta _2 \nu _2 \\{} & {} \quad - 2 D_0 D_1^2 D_2^2 D_3^2 D_4^2 b \mu + D_0 D_1 D_2 D_3 D_5 a^2 b - 2 D_0^2 D_1^2 D_2^2 D_3^2 D_4 a b\\{} & {} \quad + 2 D_0 D_1 D_2^2 D_3^2 D_4 a \alpha _1 b \mu - 2 D_0 D_1^2 D_2 D_3 D_4^2\\{} & {} \quad \alpha _3 b \mu \nu _2 - 2 D_0 D_1 D_2^2 D_3^2 D_4^2 \alpha _1 b \mu - C D_0 D_1 D_2 D_3 D_4 D_5 b^2 \\{} & {} \quad - 2 D_0 D_1^2 D_2 D_3^2 D_4^2 \alpha _2 b \\{} & {} \quad \mu - 2 D_0 D_1^2 D_2^2 D_3 D_4^2 \alpha _3 b \mu - 2 D_0 D_1^2 D_2 D_3^2 D_4^2 \alpha _2 b \beta _2\\{} & {} \quad - D_0 D_1 D_2 D_3 D_4 D_5 a b - 2 D_0 D_1^2 D_2^2 D_3 D_4^2 \alpha _3 b \beta _1\\{} & {} \quad - 2 D_0 D_1 D_2 D_3 D_4 D_5 b \sigma + D_0 D_1 D_2 D_3 D_5 a b \sigma \\{} & {} \quad - 2 D_0 D_1^2 D_2 D_3^2 D_4^2 \alpha 2 b \delta _2 - 2 D_0 D_1^2 D_2^2 D_3 D_4^2 \alpha _3 b \nu _1 \\{} & {} \quad + 2 D_0 D_1^2 D_2 D_3 D_4 a \alpha _3 b \delta _2 \nu _2 + 2 D_0 D_1^2 D_2 D_3 D_4 a \alpha _3 b \beta _2 \nu _1 \\{} & {} \quad + 2 D_0 D_1^2 D_2 D_3 D_4 a \alpha _3 b \mu \nu 2 - 2 D_0 D_1^2 D_2 D_3 D_4^2 \alpha _3 b \beta _2 \nu _2\\{} & {} \quad + 2 D_0 D_1^2 D_2 D_3^2 D_4 a \alpha _2 b \mu \\{} & {} \quad + 2 D_0 D_1^2 D_2^2 D_3 D_4 a \alpha _3 b \mu +2 D_0 D_1^2 D_2 D_3^2 D_4 a \alpha _2 b \beta _2 \\{} & {} \quad + 2 D_0 D_1^2 D_2^2 D_3 D_4 a \alpha _3 b \beta _4 +2 D_0 D_1^2 D_2^2 D_3 D_4 a \alpha _3 b \nu _1 \\{} & {} \quad + 2 D_0^2 D_1^2 D_2^2 D_3^2 D_4^2 b - 2 D_0 D_1^2 D_2 D_3 D_4^2 \alpha _3 b \delta _2 \nu _2\\{} & {} \quad + 2 D_0 D_1^2 D_2 D_3^2 D_4 a \alpha _2 b \delta _2 + 2 D_0 D_1 D_2^2 D_3^2 D_4 a \alpha _1 b \gamma _2+ C D_5^2 b^2 \beta _3,\\{} & {} \quad e_2 = - D_0 D_1 D_2^2 D_3^2 D_4^2 \alpha _1 \gamma _2- D_0 D_1^2 D_2 D_3^2 D_4^2 \alpha _2 \delta _2\\{} & {} \quad - D_0 D_1^2 D_2^2 D_3 D_4^2 \alpha _3 \nu _1 - D_0 D_1 D_2^2 D_3^2 D_4^2 \alpha _1 \mu \\{} & {} \quad -D_0 D_1 D_2 D_3 D_4 D_5 \beta _3 - D_0 D_1 D_2 D_3 D_4 D_5 \sigma \\{} & {} \quad - D_0 D_1^2 D_2^2 D_3 D_4^2 \alpha _3 \beta _1 - D_0 D_1^2 D_2^2 D_3 D_4^2 \alpha _3 \mu \\{} & {} \quad -D_0 D_1^2 D_2 D_3^2 D_4^2 \alpha _2 \beta _3 -D_0 D_1^2 D_2 D_3^2 D_4^2 \alpha _2 \mu - D_0 D_1 D_2 D_3 D_4 D_5 \mu \\{} & {} \quad - D_0 D_1 D_2 D_3 D_4 D_5 a -C D_1 D_5 a \alpha _3 b \beta _2 \nu _2 -D_0 D_1^2 D_2 D_3 D_4^2 \alpha _3 \delta _2 \nu _2 \\{} & {} \quad -C D_1 D_2 D_5 a \alpha _3 b \beta _1 + 2 C D_1 D_3 D_4 D_5 \alpha _2 b \beta _2\\{} & {} \quad -C D_1 D_3 D_5 a \alpha _2 b \beta _2 + 2 C D_1 D_4 D_5 \alpha _3 b \beta _2 \nu _2 \\{} & {} \quad -D_0 D_1^2 D_2 D_3 D_4^2 \alpha _3 \beta _2 \nu _2 -D_0 D_1^2 D_2 D_3 D_4^2 \alpha _3 \mu \nu _2\\{} & {} \quad - 2 C D_0 D_1 D_2 D_3 D_4 D_5 b+ C D_0 D_1 D_2 D_3 D_5 a b \\{} & {} \quad + 2 C D_1 D_2 D_4 D_5 \alpha _3 b \beta _1 + D_0^2 D_1^2 D_2^2 D_3^2 D_4^2\\{} & {} \quad + 2 C D_5^2 b \beta _3- D_0 D_1^2 D_2^2 D_3^2 D_4^2 \mu , \\{} & {} \quad e_3 = -C D_0 D_1 D_2 D_3 D_4 D_5 + C D_1 D_2 D_4 D_5 \alpha _3 \beta _1\\{} & {} \quad + C D_1 D_3 D_4 D_5 \alpha _2 \beta _2 + C D_1 D_4 D_5 \alpha _3 \beta _2 \nu _2 + C D_5^2 \beta _3. \end{aligned}$$

Appendix-II: Expressions of $c_{i}, i = 1, 2 , 3, 4, 5$ and some part of Corollary 1

$$\begin{aligned}{} & {} c_{1} = D_{0} + D_{1} + D_{2} + D_{3} + D_{4},\\{} & {} c_{2} = D_{4} (D_{0} + D_{1} + D_{2} + D_{3}) + (D_{0} D_{1} + D_{1} D_{2} \\{} & {} \quad + D_{1} D_{3} + D_{2} D_{3}) + D_{0} D_{2}\\{} & {} \quad \left( 1 - R_{a} \right) + D_{0} D_{3} \left( 1 - R_{b} \right) ,\\{} & {} c_{3} = \left[ D_{1} D_{3} ( D_{2} + D_{4}) + D_{2} D_{4} (D_{1} + D_{3})\right] \\{} & {} \quad + D_{0} \left\{ D_{1} (D_{2} + D_{3} + D_{4})+ D_{3}(D_{2} + D_{4}) + D_{2} D_{4}\right\} \left( 1 - R_{c} \right) ,\\{} & {} c_{4} = D_{1} D_{2} D_{3} D_{4} \\{} & {} \quad + \left\{ D_{0} (D_{1} D_{2} D_{3} + D_{1} D_{2} D_{4} + D_{1} D_{3} D_{4} + D_{2} D_{3} D_{4})\right\} \\{} & {} \quad \left( 1 - R_{d} \right) ,\\{} & {} c_{5} = D_{0} D_{1} D_{2} D_{3} D_{4} \left( 1 - R_{0} \right) ,\\{} & {} \quad \text {and }\\{} & {} R_{a} = \dfrac{\beta _{1} \alpha _{3}}{D_{0} D_{2}}< R_{0}, \quad R_{b} = \dfrac{\beta _{2} \alpha _{2}}{D_{0} D_{3}}< R_{0},\\{} & {} R_{c} = \dfrac{\beta _{1} \alpha _{3} (D_{1} + D_{2} + D_{4})}{D_{0} D_{3} (D_{1} + D_{2} + D_{4}) + D_{0} \left( D_{1} D_{2} + D_{2} D_{4} + D_{4} D_{1}\right) } \\{} & {} \quad + \ \dfrac{\beta _{2} \left\{ \alpha _{3} \nu _{2} + \alpha _{2} (D_{1} + D_{3} + D_{4}) \right\} }{D_{0} D_{2} (D_{1} + D_{3} + D_{4})+ D_{0} \left( D_{1} D_{3} + D_{3} D_{4} + D_{4} D_{1}\right) } \\{} & {} \quad + \dfrac{\beta _{3} \left( \alpha _{1} \gamma _{1} + \alpha _{2} \delta _{1}\right) }{D_{0} D_{1} D_{4} + D_{0} D_{2} D_{4} + D_{0} (D_{1} D_{2} + D_{2} D_{3} + D_{3} D_{4} + D_{3} D_{1})}\\ {}{} & {} \qquad \qquad<R_{0},\\{} & {} \quad R_{d} = \beta _{2}\left\{ \dfrac{\alpha _{3} \nu _{2} (D_{1} + D_{4})}{D_{0} D_{2} D_{3} (D_{1} + D_{4}) + D_{0} D_{1} D_{4} (D_{2} + D_{3})}\right. \\{} & {} \quad \left. + \dfrac{\alpha _{2} \left\{ D_{2}(D_{1} + D_{4}) + D_{1} D_{4} \right\} }{ D_{0} D_{2} \left\{ D_{3} (D_{1} + D_{4}) + D_{1} D_{4} \right\} + D_{0} D_{1} D_{3} D_{4} } \right\} \\{} & {} \quad + \beta _{3}\left\{ \dfrac{\alpha _{2} \delta _{1} (D_{1} + D_{2})}{D_{0} D_{3} D_{4} (D_{1} + D_{2}) + D_{0} D_{1} D_{2} (D_{3} + D_{4})}\right. \\{} & {} \quad \left. + \dfrac{\alpha _{1} \gamma _{1} (D_{2} + D_{3})}{ D_{0} D_{1} D_{4} (D_{2} + D_{3}) + D_{0} D_{2} D_{3}( D_{1} + D_{4} } \right\} \\{} & {} \quad + \dfrac{\beta _{3} \alpha _{3} \delta _{1} \nu _{2}}{D_{0} D_{2} D_{3} D_{4} + D_{0}D_{1}(D_{2} D_{3} + D_{3} D_{4} + D_{4} D_{2}) } \\{} & {} \quad + \dfrac{\beta _{1} \alpha _{3} D_{4} (D_{1} + D_{2})}{D_{0} D_{2} D_{4} (D_{1} + D_{3}) + D_{0} D_{1} D_{3}(D_{2} + D_{4})} < R_{0}. \end{aligned}$$

Appendix-III: Expressions of $b_{i}, i = 1, 2 , 3, 4, 5, 6$

$$\begin{aligned}{} & {} b_1 = a_5+D_3+D_2+D_1+D_0+a_1,\\{} & {} b_2 = D_0 D_1+ D_0 D_2+ D_0\\{} & {} \quad D_3+ D_0 a_1+ D_0 a_5+ D_1 D_2+ D_1 D_3 \\{} & {} \quad +D_1 a_1+ D_1 a_5+ D_2 D_3+ D_2 a_1+D_2 a_5+ D_3 a_1+D_3 a_5 \\{} & {} \quad +a_1 a_5-a_2 \alpha _2-a_3 \alpha _3,\\{} & {} b_3 = D_0 D_1 D_2+ D_0 D_1 D_3+ D_0 D_1 a_1\\{} & {} \quad + D_0 D_1 a_5+ D_0 D_2 D_3+ D_0 D_2 a_1+ D_0 D_2 a_5\\{} & {} \quad + D_0 D_3 a_1+ D_0 D_3 a_5+ D_0 a_1 a_5+ D_1 D_2 D_3\\{} & {} \quad + D_1 D_2 a_1+ D_1 D_2 a_5+ D_1 D_3 a_1 + D_1 D_3 a_5\\{} & {} \quad + D_1 a_1 a_5- D_1 a_2 \alpha _2-D_1 a_3 \alpha _3\\{} & {} \quad + D_2 D_3 a_1+ D_2 D_3 a_5\\{} & {} \quad + D_2 a_1 a_5- D_2 a_3 \alpha _3+ D_3 a_1a_5\\{} & {} \quad - D_3 a_2 \alpha _2- a_2 a_5 \alpha _2- a_2 \alpha _3 \nu _2\\{} & {} \quad -a_3 a_5 \alpha _3- a_4 \alpha _1\gamma _1- a_4 \alpha _2 \delta _1,\\{} & {} b_4 = D_2 D_1 D_0 a_1-a_4 \alpha _3 \delta _1 \nu _2+ D_0 D_1 D_2 D_3\\{} & {} \quad + D_0 D_1 D_3 a_1+ D_0 D_2 D_3 a_1+ D_1 D_2 D_3 a_1- D_1 D_2 a_3 \alpha _3\\{} & {} \quad - D_1 D_3 a_2 \alpha _2- D_1 a_2 \alpha _3 \nu _2-D_1 a_4 \alpha _2 \delta _1\\{} & {} \quad - D_2 a_4 \alpha _1 \gamma _1- D_3 a_4 \alpha _1 \gamma _1-D_3 a_4 \alpha _2 \delta _1\\{} & {} \quad + D_0 D_1 D_2 a_5+ D_0 D_1 D_3 a_5\\{} & {} \quad + D_0 D_1 a_1 a_5+ D_0 D_2 D_3 a_5+ D_0 D_2 a_1 a_5\\{} & {} \quad + D_0 D_3 a_1 a_5+ D_1 D_2 D_3 a_5\\{} & {} \quad + D_1 D_2 a_1 a_5+ D_1 D_3 a_1 a_5 -D_1 a_2 a_5 \alpha _2\\{} & {} \quad - D_1 a_3 a_5 \alpha _3+ D_2 D_3 a_1 a_5\\{} & {} \quad - D_2 a_3 a_5 \alpha _3- D_3 a_2 a_5 \alpha _2- a_2 a_5 \alpha _3 \nu _2,\\{} & {} b_5 = D_3 D_2 D_1 D_0 a_1- D_1 D_3 a_4 \alpha _2 \delta _1\\{} & {} \quad -D_2 D_3 a_4 \alpha _1 \gamma _1-D_1 a_4 \alpha _3 \delta _1 \nu _2\\{} & {} \quad + D_0 D_1 D_2 D_3 a_5+ D_0 D_1 D_2 a_1 a_5+ D_0 D_1 D_3 a_1 a_5\\{} & {} \quad + D_0 D_2 D_3 a_1 a_5+ D_1 D_2 D_3 a_1 a_5- D_1 D_2 a_3 a_5 \alpha _3\\{} & {} \quad - D_1 D_3 a_2 a_5 \alpha _2- D_1 a_2 a_5 \alpha _3 \nu _2,\\{} & {} b_6 = a_5 D_3 D_2 D_1 D_0 a_1. \end{aligned}$$