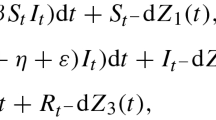Asymptotic behavior of a stochastic SIR model with general incidence rate and nonlinear Lévy jumps

Abstract

In this paper, we consider a stochastic SIR epidemic model with general disease incidence rate and perturbation caused by nonlinear white noise and L$\acute{e}$vy jumps. First of all, we study the existence and uniqueness of the global positive solution of the model. Then, we establish a threshold $\lambda$ by investigating the one-dimensional model to determine the extinction and persistence of the disease. To verify the model has an ergodic stationary distribution, we adopt a new method which can obtain the sufficient and almost necessary conditions for the extinction and persistence of the disease. Finally, some numerical simulations are carried out to illustrate our theoretical results.

1 Introduction

The study of epidemic dynamics is to establish a mathematical model which can reflect the biological mechanisms according to the occurrence, development and environmental changes of diseases, and then to show the evolution of diseases through the study of dynamics of the model. Theories of Kermack and McKendrick laid the foundation for subsequent study of infectious disease dynamics and the generation of the most classic SIR epidemic model [1]. Since then, a large number of papers have focused on the dynamics of SIR infectious disease model [2,3,4,5,6]. And this model is usually used to denote some diseases with permanent immunity such as herpes, rabies, syphilis, whooping cough, smallpox, and measles, etc. We refer the readers to [7,8,9] for more details. In this paper, we assume that the mortality due to disease is not very high and the average daily increase in people over a period of time is constant. Then, the classic epidemic model can be given by:

$$\begin{aligned} \left\{ \begin{array}{l} d S(t)=\left( \alpha -\beta S(t)I(t)-\mu S(t)\right) d t,\\ d I(t)=\left( \beta S(t)I(t)-(\mu +\rho +\gamma )I(t)\right) d t,\\ d R(t)=\left( \gamma I(t)-\mu R(t)\right) d t, \end{array} \right. \end{aligned}$$

(1)

where S(t), I(t), R(t) represent the density of susceptible individuals, infected individuals and individuals recovered from the disease at time t, respectively. The parameter $\alpha$ denotes the recruitment rate of the population, $\beta$ is the transmission coefficient between S(t) and I(t), $\mu$ is the natural mortality rate, $\rho$ is the mortality due to disease, and $\gamma$ is the recovery rate. All of the parameters $\alpha$, $\beta$, $\mu$, $\rho$, $\gamma$ are assumed to be positive.

It is well known that the bilinear incidence rate $\beta S(t)I(t)$ describes the number of people infected by all the patients in a unit of time t (i.e., the number of new cases). However, studies have shown there exist many biological factors that may contribute to nonlinearity of transmission rate (refer [10] and the references therein ). The nonnegligible interactions between organisms caused by the nonlinear incidence of disease have attracted many scholars to consider more complex incidence functions. For example, a study on the transmission of cholera epidemic in Bari, Italy, 1973 attracted Capasso and Serio’s attention to SIR epidemic model with saturated incidence [11], they put forward the nonlinear incidence rate $\frac{\beta SI}{1+aI}$, which can avoid the unboundedness of the contact rate on the cholera epidemic. This incidence rate measures the behavioral change of the disease and saturation effect as the number of infected individuals increases. That is, $\frac{\beta SI}{1+aI}$ will converge to a saturation point when I is large. In addition, Chong et al. [12] considered a model of avian influenza with half-saturated incidence $\frac{\beta SI}{H+I}$, where $\beta >0$ denotes the transmission rate and H denotes the half-saturation constant which means the density of infected individuals in the population that yields 50$\%$ possibility of contracting avian influenza. Huo and coworkers [13] proposed a rumor transmission model with Holling-type II incidence rate given by $\frac{\lambda SI}{m+S}$. Kashkynbayev and Rihan [14] studied the dynamics of a fractional-order epidemic model with general nonlinear incidence rate functionals and time-delay, they proposed that the model applied to the incidence rate $\frac{\beta S^{n}I}{1+\eta S^{n}}$, $n \ge 2$. Furthermore, they adopted the Holling-type III functional response $\frac{\beta S^{2} I}{1+\eta S^{2}}$ for numerical simulation to implement the theoretical results. In [15], authors assumed that the infection rate of HIV-1 was given by the Beddington–DeAngelis incidence function $\frac{\beta SI}{1+aS+bI}$, obviously, with the different values of a and b, this nonlinear incidence rate can be transformed into Holling-type II or saturation incidence function. Similarly, when Alqahtani performed the stability and numerical analysis of a SIR epidemic system (COVID-19), they also adopted the Beddington–DeAngelis incidence function $f(S,I)=\frac{\beta _{1}SI}{a_{1}+a_{2}S+a_{3}I}$ [16]. Besides, Ruan et al. proposed an epidemic model with nonlinear incidence rate $\frac{kI^{l}S}{1+\alpha I^{h}}$ in [17], where $kI^{l}$ measures the infection force of the disease and $\frac{1}{1+\alpha I^{h}}$ measures the inhibition effect from the behavioral change of the susceptible individuals when their number increases or from the crowding effect of the infective individuals. In [18], Rohith and Devika modeled the COVID-19 transmission dynamics using a susceptible-exposed-infectious-removed model with a nonlinear incidence rate $\frac{\beta _{0}SI}{1+\alpha I^{2}}$. Khan et al. [19] presented the dynamics of a fractional SIR model with a general incidence rate f(I)S which contained several most famous generalized forms. In addition, there are a lot of other studies on the subject (see [20,21,22,23,24,25,26,27]). In this paper, we take a more general incidence rate F with two variables S(t) and I(t) which will contain a number of common incidence rate mentioned in studies before. To be specific, model (1) turns into the following form:

$$\begin{aligned} \left\{ \begin{array}{l} d S(t)=\left( \alpha -F(S(t),I(t))I(t)-\mu S(t)\right) d t,\\ d I(t)=\left( F(S(t),I(t))I(t)-(\mu +\rho +\gamma )I(t)\right) d t,\\ d R(t)=\left( \gamma I(t)-\mu R(t)\right) d t. \end{array} \right. \end{aligned}$$

(2)

Throughout this paper, we assume the general incidence rate F(S, I) has the following properties.

Assumption 1

Suppose that F(S(t), I(t)) is locally Lipschitz continuous for both variables with $F(0,I)=0$ , $\forall I \ge 0$. Furthermore, F is continuous at $I=0$ uniformly, that is

$$\begin{aligned} \lim _{I \rightarrow 0}\sup _{S \ge 0}\{\left| F(S,I) - F(S,0)\right| \} = 0. \end{aligned}$$

Suppose further that F(S, I) is a function non-decreasing in S, non-increasing in I and satisfies the following condition:

$$\begin{aligned} \frac{\partial F(S,I)}{\partial S} \le c, \end{aligned}$$

where c is a positive constant.

Remark 1

Note that the incidence rate F(S, I) contains all the disease incidence functions listed in this paper. In summary, it includes the bilinear incidence rate ($F(S,I)=\beta S$) [28], saturated incidence rate ($F(S,I)=\frac{\beta S}{1+mI}$) [11, 29, 30], half-saturated incidence rate ($F(S,I)=\frac{\beta S}{m+I}$) [12, 31], Holling-type II incidence rate ($F(S,I)=\frac{\beta S}{m+S}$) [13], Holling-type III incidence rate ($F(S,I)=\frac{\beta S^{2}}{(m_{1}+S)(m_{2}+S)}$) [14], the Beddington–DeAngelis incidence rate ($F(S,I)=\frac{\beta S}{1+m_{1}S+m_{2}I}$) [15, 32, 33] and some other nonlinear incidence rates that are not listed here.

However, from the perspective of ecology and biology, the transmission process of infectious diseases, the contact between people, the movement of people and so on are inevitably affected by various environmental disturbances [34], such as temperature, water supply or climate change, whereas the above deterministic model does not consider the effects of any random factors. May [35] has revealed that some main parameters in epidemic model, such as the birth rates, death rates and spread rates of disease, are affected by environmental noise to a certain extent. In addition, as we know, Brownian motion is the main choice for simulating random motion and noise in continuous-time system modeling. This choice is soundly based on the good statistical characteristics of Brownian motion. For example, Brownian motion has finite moments of all orders, continuous sample-path trajectories, and there are powerful analytical tools that can solve the Brownian motion problem. Thus, we aim at stochastic epidemic model which contains white noise on the basis of the deterministic model (see [36, 37]).

In order to better simulate the impact of environmental noise during disease transmission, follow the methods of Liu and Jiang [38], nonlinear perturbation is considered in this paper, because the random perturbation may be dependent on square of the state variables S, I and R. Specifically, we assume the perturbations of S, I, R have the following form, respectively.

$$\begin{aligned} \begin{aligned}&S: -\mu \rightarrow -\mu + (\sigma _{11}+\sigma _{12} S){\dot{B}}_{1}(t),\\&I: -\mu \rightarrow -\mu + (\sigma _{21}+\sigma _{22} I){\dot{B}}_{2}(t),\\&R: -\mu \rightarrow -\mu + (\sigma _{31}+\sigma _{32} R){\dot{B}}_{3}(t), \end{aligned} \end{aligned}$$

where $B_{1}(t), B_{2}(t)$ and $B_{3}(t)$ are mutually independent standard Brownian motions. $\sigma _{ij}^{2}>0$, $i=1,2,3$, $j=1,2$ are the intensities of white noise. Thus, after taking into account the nonlinear perturbation of white noise, model (2) turns into the form of

$$\begin{aligned} \left\{ \begin{array}{l} d S(t)=\left( \alpha -F(S(t),I(t))I(t)-\mu S(t)\right) d t \\ \;\quad \qquad \quad +\left( \sigma _{11}S(t)+\sigma _{12}S^{2}(t)\right) d B_{1}(t), \\ d I(t)=\left( F(S(t),I(t))I(t)-(\mu +\rho +\gamma )I(t)\right) d t\\ \;\quad \qquad \quad +\left( \sigma _{21}I(t)+\sigma _{22}I^{2}(t)\right) d B_{2}(t),\\ d R(t)=\left( \gamma I(t)-\mu R(t)\right) d t \\ \;\quad \qquad \quad +\left( \sigma _{31}R(t)+\sigma _{32}R^{2}(t)\right) d B_{3}(t). \end{array} \right. \end{aligned}$$

(3)

Brownian motion has many excellent properties, but in some cases advantages can also be disadvantages. In the population ecosystem, it is inevitable to suffer some abrupt massive disturbances. These disturbances could be major catastrophes, like tsunamis, hurricanes, tornadoes, earthquakes and floods, etc.; and they also could be serious, large-scale diseases, such as avian influenza, COVID-19, SARS, dengue fever and Hemorrhagic fever caused by the Ebola virus, etc. Once these disasters occur, they usually lead to drastic fluctuations in the population of the region, and even a jump in the number of people. In other words, these disturbances will lead to discontinuous sample-path trajectories in the corresponding mathematical model. Therefore, Brownian motion cannot be simply used to describe these kinds of environmental disturbances. In order to explain the above phenomenon more accurately, a stochastic differential equation with jump should be considered to continue the study of epidemic dynamics system.

According to Liu et al. [39], the jump times are always random, and the waiting time of jumps is similar to L$\acute{e}$vy jumps. In addition, according to the theory of Eliazar and Klafter [40], L$\acute{e}$vy motions—performed by stochastic processes with stationary and independent increments—constitute one of the most important and fundamental family of random motions. Consequently, some scholars incorporated jump process into the system and there have been a number of specific studies of epidemiological models with L$\acute{e}$vy jumps up to now. Bao et al. took the lead in considering the competitive LotKa-Volterra population dynamics with jumps in [41] and gave some results to reveal the effect of jump process on the system. In [42], authors used the stochastic differential equation with jumps to study the asymptotic behavior of stochastic SIR model. Some other studies can be found in [43, 44] and the references therein. To the best of the authors’ knowledge, there is little literature on stochastic SIR epidemic model with general disease incidence and second-order perturbation of white noise and L$\acute{e}$vy jumps. Inspired by the above, we develop model (3) with L$\acute{e}$vy jumps:

$$\begin{aligned} \left\{ \begin{array}{l} d S(t)=\left( \alpha -F\left( S(t^{-}),I(t^{-})\right) I(t^{-})-\mu S(t^{-})\right) d t\\ \qquad \qquad \quad +\left( \sigma _{11}S(t^{-})+\sigma _{12}S^{2}(t^{-})\right) d B_1(t)\\ \qquad \qquad \quad +\int _{\mathbb {Y}}\left( f_{11}(u)S(t^{-})+f_{12}(u)S^{2}(t^{-})\right) {\widetilde{N}}\left( d t,d u\right) ,\\ d I(t)=\left( F\left( S(t^{-}),I(t^{-})\right) I(t^{-})-\left( \mu +\rho +\gamma \right) I(t^{-})\right) d t\\ \qquad \qquad \quad +\left( \sigma _{21}I(t^{-})+\sigma _{22}I^{2}(t^{-}) \right) d B_2(t)\\ \qquad \qquad \quad +\int _{\mathbb {Y}}\left( f_{21}(u)I(t^{-})+f_{22}(u)I^{2}(t^{-}) \right) {\widetilde{N}}\left( d t,d u\right) ,\\ d R(t)=\left( \gamma I(t^{-})-\mu R(t^{-})\right) d t +\left( \sigma _{31}R(t^{-})\right. \\ \left. \qquad \qquad \quad +\sigma _{32}R^{2}(t^{-})\right) d B_{3}(t)\\ \qquad \qquad \quad +\int _{\mathbb {Y}}\left( f_{31}(u)R(t^{-})+f_{32}(u)R^{2}(t^{-}) \right) {\widetilde{N}}\left( d t,d u\right) , \end{array} \right. \end{aligned}$$

(4)

where $S(t^{-})$, $I(t^{-})$, $R(t^{-})$ are the left limit of S(t), I(t) and R(t), respectively. $N(\cdot ,\cdot )$ is a Poisson counting measure with characteristic measure $\lambda$ on a measurable subset $\mathbb {Y}$ of $[0,\infty )$ with $\lambda (\mathbb {Y}) < \infty$, and the compensated Poisson random measure is defined by ${\widetilde{N}}(d t, d u) = N(d t, d u) - \lambda (d u)d t$. Throughout this paper, we assume that $B_{i}(t)$, $i = 1, 2, 3$ and $N(\cdot ,\cdot )$ are independent and all the coefficients of the system are positive. Since the dynamics of recovered population has no impact on the disease transmission dynamics of model (4), hence, we can omit the third equation in system (4) for convenience.

Assumption 2

$$\begin{aligned} \int _{\mathbb {Y}}f_{ij}^{2}(u)\lambda (d u) < \infty . \end{aligned}$$

According to this assumption, we can derive that $\int _{\mathbb {Y}}\left( \ln (1+f_{ij}(u))\right) ^{2}\lambda (d u)$

$< \infty$, which implies that the intensities of L$\acute{e}$vy jumps are not very big.

As far as we know, few papers have studied the effects of a SIR epidemic model with general incidence rate and perturbed by both nonlinear white noise and L$\acute{e}$vy jumps. Therefore, this paper presents a great challenge to the theoretical analysis of the model. The main innovation and contribution in this paper is that we provide a sufficient and almost necessary condition under which the disease disappears and persists. In a deterministic model, the persistence and extinction of the disease are usually reflected by the stability of the equilibrium point, while in a stochastic model, we usually discuss the existence of the stationary distribution. The common way to prove the existence of ergodic stationary distribution is the theory of Has’minskii [45], and the key to the theory is to establish befitting Lyapunov functions. However, only sufficient conditions for the existence and uniqueness of ergodic stationary distribution can be obtained by these conventional methods [46,47,48]. To perfect the results, in this paper, we adopt a novel method which is a combination of classical Lyapunov functions and methods introduced in [49]. Finally, we obtain the desired sufficient and almost necessary condition for persistence of the disease and get a threshold $\lambda$. To be more specific, in case of $\lambda <0$, the number of the infected population will tend to zero exponentially which means the disease will become extinct. In case $\lambda >0$, system (4) exists an ergodic stationary distribution on $\mathbb {R}_{+}^{2}$ which means the disease will persist in the population.

The structure of this paper is arranged as follows. In Sect. 2, we first give some preliminary knowledge that may be used in this paper, including the exponential martingale inequality with L$\acute{e}$vy jumps and the local martingale’s strong law of large numbers. Section 3 proves the existence and uniqueness of the global positive solution in system (4). In order to obtain a threshold to determine the extinction and persistence of the disease, we discuss the existence of ergodic stationary distribution of the equation on the boundary where the infected individuals are absent in Sect. 4, and then we define a $\lambda$ which is a key in this paper. The extinction and the ergodic stationary distribution of the disease in model (4) are given in Sects. 5 and 6, respectively. Finally, several numerical simulation examples are conducted to illustrate our main research results.

2 Preliminaries

Unless otherwise stated, throughout this paper, let ($\varOmega$, ${\mathcal {F}}$, $\{{\mathcal {F}}_t\}_{t\ge 0}$, P) be a complete probability space with a filtration $\{{\mathcal {F}}_t\}_{t\ge 0}$ satisfying the usual conditions. We denote $\mathbb {R}_+=[0,\infty )$, $\mathbb {R}_+^n=\{x_{i}\in \mathbb {R}^n:x_i>0,i=1,2,\cdots ,n\}$.

Now we shall give some primary basic knowledge in stochastic population systems with L$\acute{e}$vy jumps, more details on L$\acute{e}$vy process can be found in [50].

Definition 1

X is a L$\acute{e}$vy process if:

• (1) X(0) = 0 a.s.;

• (2) X has independent and stationary increments;

• (3) X is stochastically continuous, i.e., for all $a > 0$ and $s>0$,

  $$\begin{aligned} \lim _{t \rightarrow s}P(\left| X(t)-X(s) \right| > a) = 0. \end{aligned}$$

In general, let x(t) be a d-dimensional L$\acute{e}$vy process on $t \ge 0$ presented as the following stochastic differential equation with L$\acute{e}$vy jumps

$$\begin{aligned} d x(t)= & {} f(t^{-})d t + g(t^{-})d B(t) \nonumber \\&+ \int _{\mathbb {Y}}\gamma (t^{-},u){\widetilde{N}}(d t,d u), \end{aligned}$$

(5)

where $f \in {\mathcal {L}}^{1}(\mathbb {R}_{+},\mathbb {R}^{d})$, $g \in {\mathcal {L}}^{2}(\mathbb {R}_{+},\mathbb {R}^{d \times m})$ and $\gamma \in {\mathcal {L}}^{1}(\mathbb {R}_{+} \times \mathbb {Y},\mathbb {R}^{d})$.

B(t)=$\{\left( B_{t}^{1}, B_{t}^{2}, \cdots , B_{t}^{m}\right) ^{T}\}_{t \ge 0}$ is an m-dimensional Brownian motion defined on the complete probability space $(\varOmega , {\mathcal {F}} , P)$. Integrating both sides of (5) from 0 to t, we can get

$$\begin{aligned} x(t)= & {} x(0) + \int _{0}^{t}f(s^{-})d s + \int _{0}^{t}g(s^{-})d B(s)\\&+ \int _{0}^{t}\int _{\mathbb {Y}}\gamma (s^{-},u){\widetilde{N}}(d s,d u). \end{aligned}$$

Let $C^{2,1}(\mathbb {R}^{d} \times \mathbb {R}_{+} ; \mathbb {R})$ denote the family of all real-valued functions V(x, t) defined on $\mathbb {R}^{d} \times \mathbb {R}_{+}$ such that they are continuously twice differentiable in x and once in t. For any function $U \in C^{2,1}(\mathbb {R}^{d} \times \mathbb {R}_{+}; \mathbb {R})$, define the differential operator ${\mathcal {L}}U(x(t),t)$ as follows:

$$\begin{aligned} \begin{aligned} {\mathcal {L}}U(x(t),t)&=U_{t}(x(t),t)+U_{x}(x(t),t)f(t)\\&\quad + \frac{1}{2}trace(g^{T}(t)U_{xx}(x(t),t)g(t))\\&\quad + \int _{\mathbb {Y}}\left( U(x(t)+\gamma (t,u),t)\right. \\&\quad \left. -U(x(t),t) {-} U_{x}(x(t),t)\gamma (t,u)\right) \lambda (d u), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} U_{t}= & {} \frac{\partial U}{\partial t} ,\; U_{x}=\left( \frac{\partial U}{\partial x_{1}}, \cdots , \frac{\partial U}{\partial x_{d}}\right) ,\; U_{xx}\\= & {} \left( \begin{array}{ccc} \frac{\partial ^{2} U}{\partial x_{1}\partial x_{1}} &{} \cdots &{} \frac{\partial ^{2} U}{\partial x_{1}\partial x_{d}}\\ \vdots &{} \vdots &{} \vdots \\ \frac{\partial ^{2} U}{\partial x_{d}\partial x_{1}} &{} \cdots &{} \frac{\partial ^{2} U}{\partial x_{d}\partial x_{d}} \end{array} \right) . \end{aligned}$$

According to the It${\hat{o}}$’s formula,

$$\begin{aligned}\begin{aligned} d U(x(t),t)&={\mathcal {L}}U(x(t),t)d t + U_{x}g(t)d B(t) \\&+ \int _{\mathbb {Y}}\left( U(x(t)+\gamma (t,u),t)\right. \\&\left. -U(x(t),t)\right) {\widetilde{N}}(d t, d u). \end{aligned} \end{aligned}$$

Next, we shall introduce the exponential martingale inequality with jumps as follows [41].

Definition 2

Assume that $g \in {\mathcal {L}}^{2}(\mathbb {R}_{+},\mathbb {R}^{d \times m}), \gamma \in {\mathcal {L}}^{1}(\mathbb {R}_{+} \times \mathbb {Y},\mathbb {R}^{d})$. For any constants $T , \alpha , \beta > 0$,

$$\begin{aligned} \begin{aligned} \mathbb {P}&\bigg \{ \sup _{0 \le t \le T}\left[ \int _{0}^{t}g(s)d B(s) - \frac{\alpha }{2}\int _{0}^{t}\left| g(s)\right| ^{2}d s\right. \\&\quad \left. + \int _{0}^{t}\int _{\mathbb {Y}}\gamma (s,u){\widetilde{N}}(d s, d u)\right. \\&\quad \left. - \frac{1}{\alpha }\int _{0}^{t}\int _{\mathbb {Y}}\left( e^{\alpha \gamma (s,u)}-1-\alpha \gamma (s,u)\right) \lambda (d u)d s\right] > \beta \bigg \}\\&\quad \le e^{-\alpha \beta }. \end{aligned} \end{aligned}$$

To make the theory more complete, the following lemma cited by [50] is concerning the local martingale’s strong law of large numbers.

Lemma 1

Assume that M(t) is a local martingale vanishing at $t=0$, define

$$\begin{aligned} \rho _{M}(t):=\int _{0}^{t}\frac{d\left\langle M\right\rangle (s) }{(1+s)^{2}},\;\;\; t \ge 0, \end{aligned}$$

where $\left\langle M\right\rangle (t) :=\left\langle M, M \right\rangle (t)$ is Meyer’s angle bracket process.

If $\lim _{t \rightarrow \infty }\rho _{M}(t) < \infty \;\;a.s.$ holds, then

$$\begin{aligned} \lim _{t \rightarrow \infty }\frac{M(t)}{t}=0 \;\;a.s.. \end{aligned}$$

From the relevant introduction in [51], we cite the proposition as follows.

Remark 2

Assume that

$$\begin{aligned} \varGamma _{loc}^{2}:=\left\{ \gamma (t,u)\; \text {predictable} \bigg \vert \int _{0}^{t}\int _{\mathbb {Y}}\left| \gamma (t,u) \right| ^{2}\lambda (d u)d t < \infty \right\} . \end{aligned}$$

For any $\gamma \in \varGamma _{loc}^{2}$,

$$\begin{aligned} M(t):=\int _{0}^{t}\int _{\mathbb {Y}}\gamma (s,u){\widetilde{N}}(d s, d u), \end{aligned}$$

then one can see that

$$\begin{aligned}&\left\langle M \right\rangle (t)=\int _{0}^{t}\int _{\mathbb {Y}}\left| \gamma (s,u)\right| ^{2}\lambda (d u)d s, \;\;\;\; \\&\quad \left[ M \right] (t)=\int _{0}^{t}\int _{\mathbb {Y}}\left| \gamma (s,u)\right| ^{2}{\widetilde{N}}(d s, d u), \end{aligned}$$

where $\left[ M \right] (t)=\left[ M,M\right] (t)$ denotes the quadratic variation process of M(t).

3 Existence and uniqueness of the global positive solution

In order to study the dynamics of an epidemic system, the first thing we concerned is whether the solution of model (4) is global and positive. Here, we give the following conclusion which is a fundamental condition for the long time behavior of model (4).

Theorem 1

For any initial value $(S(0),I(0))\in \mathbb {R}_+^2$, stochastic system (4) has a unique positive solution $(S(t),I(t))\in \mathbb {R}_+^2$ on $t\ge 0$, and the solution will remain in $\mathbb {R}_+^2$ with probability one.

Proof

Our proof is motivated by the methods of [34]. Since the drift and diffusion (i.e., the coefficients of model (4)) are locally Lipschitz continuous, hence there is a unique local solution $\left( S(t),I(t) \right)$ on $t \in [ 0,\rho _{e} )$ for any given initial value $\left( S(0),I(0) \right) \in \mathbb {R}_{+}^{2}$, where $\rho _{e}$ is an explosion time. To testify this solution is global, we only need to show that $\rho _{e} = \infty$ a.s.. Let $k_{0} > 0$ be sufficiently large such that both S(0) and I(0) can lie within the interval $[ \frac{1}{k_{0}} , k_{0} ]$. For each integer $k \ge k_{0}$, define the following stopping time

$$\begin{aligned} \tau _{k}=\inf \bigg \{t \in ( 0,\rho _{e} ) : S(t) \notin \left( \frac{1}{k}, k \right) \text {or} \; I(t) \notin \left( \frac{1}{k},k \right) \bigg \}. \end{aligned}$$

Apparently, $\tau _{k}$ is increasing as $k \rightarrow \infty$. Set $\tau _{\infty }=\lim _{k \rightarrow \infty }\tau _{k}$, hence $\tau _{\infty } \le \rho _{e}$ a.s.. Once we prove that $\tau _{\infty }=\infty$ a.s., then we can get $\rho _{e}=\infty$ and $\left( S(t), I(t) \right) \in \mathbb {R}_{+}^{2}$ a.s..

If $\tau _{\infty } < \infty$ a.s., then there exists a pair of constants $T > 0$ and $0< \varepsilon <1$ such that $P( \tau _{\infty } \le T ) > \varepsilon$. Hence, there is an integer $k_{1} \ge k_{0}$ such that $P( \tau _{k} \le T ) \ge \varepsilon$ for all $k \ge k_{1}$.

Define a $C^{2}$-function V: $\mathbb {R}_+^2 \rightarrow \mathbb {R}_+$ as follows:

$$\begin{aligned} V(S,I) {=} (1+S)^p -1 -p\log S +I^p -1 -p\log I, \end{aligned}$$

where $0<p<1$. The nonnegativity of V(S, I) is due to $k-1-\log k \ge 0$ for $k \ge 0$. It is easy to see V(S, I) is continuously twice differentiable with respect to S and I.

Applying It${\hat{o}}$’s formula to function V(S, I), we have

$$\begin{aligned} \begin{aligned}&d V(S,I)={\mathcal {L}}V(S,I)d t+\left( p(1+S)^{p-1}-\frac{p}{S}\right) \\&\quad \left( \sigma _{11}S+\sigma _{12}S^{2}\right) d B_{1}(t)\\&\quad +\left( pI^{p-1}-\frac{p}{I}\right) \left( \sigma _{21}I+\sigma _{22}I^{2} \right) d B_{2}(t)\\&\quad +\int _{\mathbb {Y}}\left( (1+S+f_{11}(u)S+f_{12}(u)S^{2})^{p}\right. \\&\quad \left. -(1+S)^{p} \right) {\widetilde{N}}(d t,d u)\\&\quad -p\int _{\mathbb {Y}} \left( \log (S+f_{11}(u)S+f_{12}(u)S^{2})-\log S \right) \\&\quad {\widetilde{N}}(d t,d u)\\&\quad +\int _{\mathbb {Y}}\left( (I+f_{21}(u)I+f_{22}(u)I^{2})^{p}-I^{p}\right) {\widetilde{N}}(d t,d u)\\&\quad -p\int _{\mathbb {Y}}\left( \log \left( I+f_{21}(u)I+f_{22}(u)I^{2}\right) -\log I\right) \\&\quad {\widetilde{N}}(d t,d u), \end{aligned} \end{aligned}$$

(6)

where

$$\begin{aligned}&{\mathcal {L}}V(S,I) = p(1+S)^{p-1}\left( \alpha - F(S,I)I - \mu S \right) \\&\quad + \frac{p(p-1)}{2}(1+S)^{p-2}(\sigma _{11}S+\sigma _{12}S^{2})^{2}\\&\quad +\int _Y\left( \left( 1+S+f_{11}(u)S+f_{12}(u)S^{2}\right) ^p -(1+S)^p\right. \\&\quad \left. -p(1+S)^{p-1}(f_{11}(u)S+f_{12}(u)S^{2}) \right) \lambda (d u)\\&\quad -\frac{p\alpha }{S}+\frac{pF(S,I)I}{S}+p\mu +\frac{p\sigma _{11}^2}{2} +\frac{p\sigma _{12}^2}{2}S^{2} \\&\quad + p\sigma _{11}\sigma _{12}S\\&\quad -p\int _Y\left( \log \left( S+f_{11}(u)S+f_{12}(u)S^{2}\right) -\log S\right. \\&\quad \left. -\frac{1}{S}\left( f_{11}(u)S+f_{12}(u)S^{2} \right) \right) \lambda (d u)+pF(S,I)I^{p}\\&\quad - p\left( \mu +\rho +\gamma \right) I^{p} + \frac{p(p-1)}{2}I^{p-2}\\&\quad \left( \sigma _{21}I+\sigma _{22}I^{2}\right) ^{2} \\&\quad +\int _Y\left( \left( I+f_{21}(u)I+f_{22}(u)I^{2}\right) ^p-I^{p}\right. \\&\quad \left. \quad -pI^{p-1}\left( f_{21}(u)I+f_{22}(u)I^2\right) \right) \lambda (d u)\\&\quad -pF(S,I)+p(\mu +\rho +\gamma )+\frac{p\sigma _{21}^2}{2} +\frac{p\sigma _{22}^2}{2}I^{2}\\&\quad +p\sigma _{21}\sigma _{22}I\\&\quad -p\int _Y\left( \log \left( I+f_{21}(u)I+f_{22}(u)I^{2}\right) -\log I\right. \\&\quad \left. -\frac{1}{I}\left( f_{21}(u)I+f_{22}(u)I^2\right) \right) \lambda (d u).\\ \end{aligned}$$

For any $0< p <1$, by the inequation $x^{r} \le 1+r(x-1)$ for $x \ge 0,\;\; 0 \le r \le 1$, we have

$$\begin{aligned} \begin{aligned}&\int _{\mathbb {Y}}\left( \left( 1+S+f_{11}(u)S+f_{12}(u)S^{2}\right) ^{p} -(1+S)^{p}\right. \\&\left. \qquad -p(1+S)^{p-1}\left( f_{11}(u)S+f_{12}(u)S^{2}\right) \right) \lambda (d u)< 0,\\&\int _{\mathbb {Y}}\left( I+f_{21}(u)I+f_{22}(u)I^{2}\right) ^{p}-I^{p} \\&-pI^{p-1}\left( f_{21}(u)I+f_{22}(u)I^{2}\right) \lambda (d u) < 0. \end{aligned} \end{aligned}$$

On the basis of Assumption 1 and the above results, then

$$\begin{aligned}&{\mathcal {L}}V(S,I) \le p\alpha -pF(S,I)I(1+S)^{p-1}-p\mu S(1+S)^{p-1}\\&\quad +\frac{p(p-1)}{2}(1+S)^{p}\left( \frac{\sigma _{11}S +\sigma _{12}S^2}{1+S}\right) ^2\\&\quad -\frac{p\alpha }{S}+pcI+p\mu +\frac{p\sigma _{11}^2}{2}\\&\quad +\frac{p\sigma _{12}^2}{2}S^2+p\sigma _{11}\sigma _{12}S+p \int _{\mathbb {Y}}\\&\quad \left( f_{11}(u)+f_{12}(u)S\right) \lambda (d u)\\&\quad +pF(S,I)I^p-p(\mu +\rho +\gamma )I^p\\&\quad +\frac{p(p-1)}{2}I^{p+2} \left( \frac{\sigma _{21}+\sigma _{22}I}{I}\right) ^2\\&\quad -pF(S,I)+p(\mu +\rho +\gamma )+\frac{p\sigma _{21}^2}{2} +\frac{p\sigma _{22}^2}{2}I^2\\&\quad +p\sigma _{21}\sigma _{22}I+p\int _{\mathbb {Y}}\left( f_{21}(u) +f_{22}(u)I\right) \lambda (d u)\\&\le p\alpha +p\mu +\frac{p\sigma _{11}^2}{2}+p(\mu +\rho +\gamma ) +\frac{p\sigma _{21}^2}{2}\\&\quad +p\int _{\mathbb {Y}}\left( f_{11}(u)+f_{21}(u)\right) \lambda (d u) -\frac{p(1-p)}{2}(1+S)^{p}\\&\quad \left( \frac{\sigma _{11}S+\sigma _{12}S^2}{1+S} \right) ^2\\&\quad -\frac{p(1-p)}{2}I^{p+2}\left( \sigma _{22}+\frac{\sigma _{21}}{I} \right) ^2+pF(S,I)I^p+\frac{p\sigma _{12}^2}{2}S^2\\&\quad +\frac{p\sigma _{22}^2}{2}I^2+pcI+p\sigma _{11}\sigma _{12}S +p\sigma _{21}\sigma _{22}I\\&\quad +p\int _{\mathbb {Y}}f_{12}(u)\lambda (d u)S + p\int _{\mathbb {Y}}f_{22} (u)\lambda (d u)I\\&\le p\left( \alpha +2\mu +\rho +\gamma +\frac{\sigma _{11}^2+\sigma _{21}^2}{2}\right. \\&\left. +\int _{\mathbb {Y}}\left( f_{11}(u)+f_{21}(u)\right) \lambda (d u)\right) \\&\quad -\frac{p(1-p)}{2}min\{\sigma _{11},\sigma _{12}\}^2(1+S)^{p}S^{2}\\&\quad -\frac{p(1-p)}{2}\sigma _{22}^{2}I^{p+2}+pcSI^{p}\\&\quad +\frac{p}{2}\left( \sigma _{12}^{2}S^{2}+\sigma _{22}^{2}I^{2}\right) \\&+\left( pc+p\sigma _{21}\sigma _{22}+p\int _{\mathbb {Y}}f_{22}(u) \lambda (d u)\right) I\\&\quad +\left( p\sigma _{11}\sigma _{12}+p\int _{\mathbb {Y}}f_{12}(u) \lambda (d u)\right) S\\&\le k_{2}+p\left( \alpha +2\mu +\rho +\gamma +\frac{\sigma _{11}^2 +\sigma _{21}^2}{2}+p\int _{\mathbb {Y}}\right. \\&\quad \left. \left( f_{11}(u)+f_{21}(u)\right) \lambda (d u)\right) \\&=:k_{3}, \end{aligned}$$

where

$$\begin{aligned}\begin{aligned}&k_{2}=\sup _{S\ge 0,I\ge 0} \bigg \{-\frac{p(1-p)}{2}min\{\sigma _{11}, \sigma _{12}\}^2(1+S)^{p}S^{2}\\&\quad -\frac{p(1-p)}{2}\sigma _{22}I^{p+2}\\&\quad +pcSI^{p}+\frac{p}{2}\left( \sigma _{12}^{2}S^{2}+\sigma _{22}^{2}I^{2} \right) \\&\quad +\left( pc+p\sigma _{21}\sigma _{22}+p\int _{\mathbb {Y}}f_{22}(u)\lambda (d u) \right) I\\&\quad +\left( p\sigma _{11}\sigma _{12}+p\int _{\mathbb {Y}}f_{12}(u)\lambda (d u)\right) S\bigg \}. \end{aligned} \end{aligned}$$

Integrating both sides of (6) from 0 to $\tau _{k}\wedge T$ and then taking expectations

$$\begin{aligned} \begin{aligned}&EV\left( S(\tau _{k}\wedge T),I(\tau _{k}\wedge T)\right) \\&\quad \le V\left( S(0), I(0)\right) +k_{3}E\left( \tau _{k}\wedge T\right) \\&\quad \le V\left( S(0),I(0)\right) +k_{3}T. \end{aligned} \end{aligned}$$

Let $\varOmega _{k}=\{ \tau _{k}\le T \}$ for $k \ge k_{1}$, then we have $p( \varOmega _{k} ) \ge \varepsilon$. Note that for every $\omega \in \varOmega _{k}$, $S( \tau _{k},\omega )$ or $I( \tau _{k},\omega )$ equals either k or $\frac{1}{k}$. Consequently,

$$\begin{aligned} \begin{aligned}&V\left( S(0),I(0) \right) +k_{3}T \ge E[ I_{\varOmega _{k}}V( S(\tau _{k}, \omega ),I(\tau _{k},\omega ) ) ]\\&\quad \ge \varepsilon \bigg [\left( (1+k)^{p}-1-p\log k\right) \\&\quad \wedge \left( (1+\frac{1}{k})^{p}-1-p\log \frac{1}{k}\right) \\&\quad \wedge \left( k^{p}-1-p\log k\right) \wedge \left( \frac{1}{k^{p}}-1-p\log \frac{1}{k}\right) \bigg ], \end{aligned} \end{aligned}$$

where $I_{\varOmega _{k}}$ is the indicator function of $\varOmega _{k}$. Taking $k \rightarrow \infty$, we obtain that $\infty > V\left( S(0),I(0)\right) +k_{3}T = \infty$ which is a contradiction, therefor we have $\tau _{\infty } = \infty$ a.s. (i.e., S(t) and I(t) will not explode in a finite time with probability one). The conclusion is confirmed. $\square$

4 Exponential ergodicity for the system without disease

In this section, a threshold $\lambda$ will be defined by exploring the exponential ergodicity of a one-dimensional disease-free system. To proceed, we first consider the following equation if there is no infective at time $t = 0$:

$$\begin{aligned} \begin{aligned}&d{\hat{S}}(t)=\left( \alpha -\mu {\hat{S}}(t)\right) d t+\left( \sigma _{11} {\hat{S}}(t)+\sigma _{12}{\hat{S}}^{2}(t)\right) d B_1(t)\\&\quad +\int _{\mathbb {Y}}\left( f_{11}(u){\hat{S}}(t)+f_{12}(u){\hat{S}}^{2}(t) \right) {\widetilde{N}}\left( d t,d u\right) . \end{aligned} \end{aligned}$$

(7)

In terms of the comparison theorem, it is easy to check out that $S(t) \le {\hat{S}}(t)$, $\forall t \ge 0$ a.s. provided $S(0) = {\hat{S}}(0) > 0$. In order to obtain the exponential ergodicity of model (7), we first give the following lemma which has been discussed in [38].

Lemma 2

The following equation

$$\begin{aligned}&d{\bar{S}}(t)=\left( \alpha -\mu {\bar{S}}(t)\right) d t\nonumber \\&\quad +\left( \sigma _{11}{\bar{S}}(t)+\sigma _{12}{\bar{S}}^{2}(t)\right) d B_1(t),\;{\bar{S}}(0)>0 \end{aligned}$$

(8)

admits an ergodic stationary distribution with the density:

$$\begin{aligned} \begin{aligned}&\pi ^{*} (x) = Qx^{-2-\frac{2(2\alpha \sigma _{12}+\mu \sigma _{11})}{\sigma _{11}^{3}}}\\&\quad \left( \sigma _{11} +\sigma _{12}x \right) ^{-2+\frac{2(2\alpha \sigma _{12}+\mu \sigma _{11})}{\sigma _{11}^{3}}}\\&\quad e^{-\frac{2}{\sigma _{11}\left( \sigma _{11}+\sigma _{12}x\right) } \left( \frac{\alpha }{x}+\frac{2\alpha \sigma _{12}+\mu \sigma _{11}}{\sigma _{11}} \right) }, \end{aligned} \end{aligned}$$

(9)

where Q is a constant such that $\int _{0}^{\infty }\pi ^{*}(x)d x=1, x\in (0,\infty )$ and it follows $\lim _{t \rightarrow \infty }\frac{1}{t}\int _{0}^{t}{\bar{S}}(\tau )d \tau =\int _{0}^{\infty }x\pi ^{*}(d x) \;\;a.s..$

Theorem 2

Markov process ${\hat{S}}(t)$ is exponentially ergodic and it has a unique stationary distribution denoted by ${\bar{\pi }}$ on $\mathbb {R_+}$.

Proof

In order to prove the existence of the ergodic stationarity of ${\hat{S}}(t)$, according to [49], it is equivalent to proving the following two conditions: (a) The auxiliary process ${\bar{S}}(t)$ determined by (8) has a positive transition probability density with respect to Lebesgue measure. (b) There exists a nonnegative $C^{2}$-function $V({\hat{S}}(t))$ such that ${\mathcal {L}}V({\hat{S}}(t)) \le -H_{2}V({\hat{S}}(t))+H_{1}$, in which $H_{1}, H_{2}$ are positive constants. In view of Lemma 2, condition (a) has been given; therefore, we just need to verify condition (b) in the following.

Consider the Lyapunov function

$$\begin{aligned} V({\hat{S}}(t))=\frac{\left( 1+{\hat{S}}(t)\right) ^{p}}{p} - \ln {\hat{S}}(t), \end{aligned}$$

where $0< p < 1$.

Applying It${\hat{o}}$’s formula , one sees that

$$\begin{aligned}&{\mathcal {L}}\left( \frac{\left( 1+{\hat{S}}(t)\right) ^{p}}{p} - \ln {\hat{S}}(t)\right) \\&\quad =\left( 1+{\hat{S}}\right) ^{p-1}\left( \alpha -\mu {\hat{S}}\right) +\frac{p-1}{2}\left( 1+{\hat{S}}\right) ^{p-2}\\&\quad \left( \sigma _{11}{\hat{S}}+\sigma _{12}{\hat{S}}^{2}\right) ^{2}\\&\quad +\int _{\mathbb {Y}}\left( \frac{\left( 1+{\hat{S}}+f_{11}(u){\hat{S}} +f_{12}(u){\hat{S}}^{2}\right) ^{p}}{p}-\frac{\left( 1+{\hat{S}} \right) ^{p}}{p}\right. \\&\quad \left. \quad -\left( 1+{\hat{S}}\right) ^{p-1}\left( f_{11}(u) {\hat{S}}+f_{12}(u){\hat{S}}^{2}\right) \right) \lambda (d u)\\&\quad -\frac{\alpha }{{\hat{S}}}+\mu +\frac{\left( \sigma _{11}{\hat{S}} +\sigma _{12}{\hat{S}}^{2}\right) ^{2}}{2{\hat{S}}^{2}}\\&\quad -\int _{\mathbb {Y}}\left( \ln \left( {\hat{S}}+f_{11}(u){\hat{S}} +f_{12}(u){\hat{S}}^{2}\right) -\ln {\hat{S}}\right. \\&\left. -\left( f_{11}(u)+f_{12}(u) {\hat{S}}\right) \right) \lambda (d u)\\&\le -\mu \left( 1+{\hat{S}}\right) ^{p}-\frac{\alpha }{{\hat{S}}} +\mu (1+{\hat{S}})^{p-1}+\alpha (1+{\hat{S}})^{p-1}\\&\quad +\frac{p-1}{2}\left( 1+{\hat{S}}\right) ^{p}\left( \frac{\sigma _{11} {\hat{S}}+\sigma _{12}{\hat{S}}^{2}}{1+{\hat{S}}}\right) ^{2}+\mu \\&\quad +\frac{\left( \sigma _{11}+\sigma _{12}{\hat{S}}\right) ^{2}}{2}\\&\quad +\frac{\left( 1+{\hat{S}}\right) ^{p}}{p}\int _{\mathbb {Y}}\\&\quad \left( \left( 1+\frac{{\hat{S}}}{1+{\hat{S}}}f_{11}(u) +\frac{{\hat{S}}^{2}}{1+{\hat{S}}}f_{12}(u)\right) ^{p}-1\right. \\&\quad \left. -p\left( \frac{{\hat{S}}}{1+{\hat{S}}}f_{11}(u)+\frac{{\hat{S}}^{2}}{1+{\hat{S}}}f_{12}(u)\right) \right) \lambda (d u)\\&\quad +\int _{\mathbb {Y}} \left( f_{11}(u)+f_{12}(u){\hat{S}} -\ln (1+f_{11}(u)\right. \\&\quad \left. +f_{12}(u){\hat{S}})\right) \lambda (d u). \end{aligned}$$

By reason of the inequations $\frac{1}{x}-1+\ln x \ge 0$ for $x \ge 0$ and $x^{r}\le 1+r(x-1)$ for $x \ge 0$, $0 \le r \le 1$, we derive that

$$\begin{aligned}\begin{aligned} {\mathcal {L}}V({\hat{S}}(t))&\le -\mu p \frac{\left( 1+{\hat{S}} \right) ^{p}}{p}+\alpha \ln {\hat{S}} +\mu (1+{\hat{S}})^{p-1}\\&\quad +\alpha (1+{\hat{S}})^{p-1}\\&\quad -\frac{1-p}{2}\min \{\sigma _{11}, \sigma _{12}\}^{2}\left( 1+{\hat{S}} \right) ^{p}{\hat{S}}^{2}\!+\!\mu \\&\quad +\frac{\left( \sigma _{11}+\sigma _{12} {\hat{S}}\right) ^{2}}{2}\\&\quad +\int _{\mathbb {Y}}\left( f_{11}(u)+f_{12}(u){\hat{S}}\right. \\&\quad \left. -\ln (1+f_{11}(u) +f_{12}(u){\hat{S}})\right) \lambda (d u) \\&\le -\mu p \frac{\left( 1\!+\!{\hat{S}}\right) ^{p}}{p}\!-\!\alpha (-\ln {\hat{S}})+\max \{h,1\}\\&\le -\min \{\mu p , \alpha \}\left( \frac{\left( 1+{\hat{S}}(t) \right) ^{p}}{p} - \ln {\hat{S}}(t)\right) \\&\quad + \max \{h,1\}\\&=-H_{2}V({\hat{S}}(t))+H_{1}, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} H_{1}&=\max \{h,1\},\;\;\; H_{2}=\min \{\mu p , \alpha \},\\ h=&\sup _{{\hat{S}}\in [0 , \infty )}\bigg \{\mu (1+{\hat{S}})^{p-1} +\alpha (1+{\hat{S}})^{p-1}\\&\quad -\frac{1-p}{2}\min \{\sigma _{11}, \sigma _{12}\}^{2} \left( 1+{\hat{S}}\right) ^{p}{\hat{S}}^{2} \\&\quad +\mu +\frac{\left( \sigma _{11} +\sigma _{12}{\hat{S}}\right) ^{2}}{2}\\&\quad +\int _{\mathbb {Y}}\left( f_{11}(u)+f_{12}(u){\hat{S}}-\ln (1+f_{11}(u)\right. \\&\quad \left. +f_{12}(u){\hat{S}})\right) \lambda (d u)\bigg \}. \end{aligned}$$

This completes the proof of the theorem. $\square$

Remark 3

For any ${\bar{\pi }}$-integrable f(x): $\mathbb {R}_{+}^{2} \rightarrow \mathbb {R}$, according to the ergodicity of ${\hat{S}}(t)$,

$$\begin{aligned} \lim _{t \rightarrow \infty }\frac{1}{t}\int _{0}^{t}f\left( {\hat{S}}(\tau )\right) d \tau =\int _{0}^{\infty }f\left( x\right) {\bar{\pi }}(d x). \end{aligned}$$

Furthermore, integrating both sides of (7) from 0 to t and then taking expectation, then it yields

$$\begin{aligned}&\lim _{t \rightarrow \infty }\frac{\mathbb {E}{\hat{S}}(t)}{t}=\alpha -\mu \lim _{t \rightarrow \infty }\frac{1}{t}\int _{0}^{t}\mathbb {E}{\hat{S}}(\tau )d \tau \\&\quad = \alpha -\mu \mathbb {E}\int _{0}^{\infty }x{\bar{\pi }}(d x), \end{aligned}$$

combining the above result and $\lim _{t \rightarrow \infty }\frac{\mathbb {E}{\hat{S}}(t)}{t}=0$, we can obtain

$$\begin{aligned} \lim _{t \rightarrow \infty }\frac{1}{t}\int _{0}^{t}{\hat{S}}(\tau )d \tau =\int _{0}^{\infty }x{\bar{\pi }}(d x) = \frac{\alpha }{\mu }. \end{aligned}$$

Remark 4

Now, we define a critical value which will play an important role in determining the extinction and persistence of the disease.

$$\begin{aligned} \begin{aligned} \lambda =&\int _{0}^{\infty }F\left( x, 0\right) {\bar{\pi }}(d x) \\&- \left( \mu + \rho + \gamma + \frac{\sigma _{21}^{2}}{2} + \int _{\mathbb {Y}}\left( f_{21}\left( u\right) \right. \right. \\&\left. \left. -\ln \left( 1+f_{21}\left( u\right) \right) \right) \lambda \left( d u\right) \right) . \end{aligned} \end{aligned}$$

(10)

According to Assumption (1), one can see that $F(S,I) \le cS$, hence,

$$\begin{aligned}&\int _{0}^{\infty }F\left( x,0\right) {\bar{\pi }}(d x) \le c\int _{0}^{\infty }x{\bar{\pi }}(d x)\\&\quad =\lim _{t \rightarrow \infty }\frac{c}{t}\int _{0}^{t}{\hat{S}}(\tau )d \tau =\frac{c\alpha }{\mu } < \infty . \end{aligned}$$

Therefore, $\lambda$ is well defined.

5 Extinction of the disease

In this section, we will present sufficient conditions for the demise of the disease, which will provide theoretical guidance for the prevention and control of the spread of disease. The following theorem is vital in this paper.

Theorem 3

Let $\left( S(t),I(t)\right)$ be the solution of system (4) with any given positive initial value $\left( S(0) , I(0)\right) \in \mathbb {R}_{+}^{2}$, then it has the property

$$\begin{aligned} \lim _{t \rightarrow \infty }\frac{\ln I(t)}{t} \le \lambda \;\;a.s.. \end{aligned}$$

If $\lambda < 0$ holds, I(t) will go to zero exponentially with probability one.

Proof

Applying It${\hat{o}}$’s formula to $\ln I(t)$, we have

$$\begin{aligned}&d \ln I(t) \nonumber \\&\quad =\left( F(S,I)-\left( \mu + \rho + \gamma \right) -\frac{\left( \sigma _{21}I+\sigma _{22}I^{2}\right) ^{2}}{2I^{2}} \right. \nonumber \\&\quad \left. + \int _{\mathbb {Y}}\left( \ln \left( I+f_{21}(u)I +f_{22}(u)I^{2}\right) \right. \right. \nonumber \\&\quad \left. \left. -\ln I-\left( f_{21}(u)+f_{22}(u)I\right) \right) \lambda \left( d u\right) \right) d t \nonumber \\&\quad + \left( \sigma _{21}+\sigma _{22}I\right) d B_{2}(t) \nonumber \\&\quad + \int _{\mathbb {Y}} \left( \ln \left( I+f_{21}(u)I+f_{22}(u)I^{2}\right) -\ln I\right) {\widetilde{N}}(d t , d u) \nonumber \\&\quad \le \left( F({\hat{S}},0)-\left( \mu + \rho + \gamma + \frac{\sigma _{21}^{2}}{2} + \int _{\mathbb {Y}}\right. \right. \nonumber \\&\quad \left. \left. \left( f_{21}(u) -\ln \left( 1+f_{21}(u)\right) \right) \lambda (d u) \right) \right. \nonumber \\&\quad \left. -\sigma _{21}\sigma _{22}I - \frac{\sigma _{22}^{2}}{2}I^{2}\right. \nonumber \\&\quad \left. + \int _{\mathbb {Y}}\left( \ln \left( 1+\frac{f_{22}(u)I}{1+f_{21}(u)}\right) - f_{22}(u)I\right) \lambda (d u)\right) d t \nonumber \\&\quad + \sigma _{21}d B_{2}(t)+\sigma _{22}Id B_{2}(t)\nonumber \\&\quad + \int _{\mathbb {Y}}\ln \left( 1+f_{21}(u)\right) {\widetilde{N}}(d t , d u) \nonumber \\&\quad + \int _{\mathbb {Y}}\ln \left( 1+\frac{f_{22}(u)I}{1+f_{21}(u)}\right) {\widetilde{N}}(d t , d u). \end{aligned}$$

(11)

Integrating both sides of (11), we obtain

$$\begin{aligned} \ln I(t)&\le \ln I(0)-\frac{\sigma _{22}^{2}}{2}\int _{0}^{t}I^{2}(\tau )d \tau - \int _{0}^{t}\sigma _{21}\sigma _{22}I(\tau )d \tau \nonumber \\&\quad + \int _{0}^{t}\left( F({\hat{S}}(\tau ),0)-\left( \mu + \rho + \gamma + \frac{\sigma _{21}^{2}}{2} \right) \right) d \tau \nonumber \\&\quad + \int _{0}^{t}\int _{\mathbb {Y}}\left( f_{21}(u)-\ln \left( 1+f_{21}(u)\right) \right) \lambda (d u)d \tau \nonumber \\&\quad -\int _{0}^{t}\int _{\mathbb {Y}}\left( \ln \left( 1 +\frac{f_{22}(u)I(\tau )}{1+f_{21}(u)}\right) -f_{22}(u)I(\tau )\right) \nonumber \\&\quad \lambda (d u)d \tau \nonumber \\&\quad + \int _{0}^{t}\sigma _{21}d B_{2}(\tau )+\int _{0}^{t} \sigma _{22}I(\tau )d B_{2}(\tau ) \nonumber \\&\quad + \int _{0}^{t}\int _{\mathbb {Y}}\ln \left( 1+f_{21}(u)\right) {\widetilde{N}}(d \tau , d u) \nonumber \\&\quad +\int _{0}^{t}\int _{\mathbb {Y}}\ln \left( 1+\frac{f_{22}(u)I(\tau )}{1+f_{21}(u)}\right) {\widetilde{N}}(d \tau , d u) \nonumber \\&=\ln I(0)- \int _{0}^{t}\sigma _{21}\sigma _{22}I(\tau )d \tau - \frac{\sigma _{22}^{2}}{2}\int _{0}^{t}I^{2}(\tau )d \tau \nonumber \\&\quad + \int _{0}^{t}\left( F({\hat{S}}(\tau ),0)-\left( \mu + \rho + \gamma + \frac{\sigma _{21}^{2}}{2}\right) \right) d \tau \nonumber \\&\quad -\int _{0}^{t}\int _{\mathbb {Y}}\left( f_{21}(u)-\ln \left( 1+f_{21}(u)\right) \right) \lambda (d u)d \tau \nonumber \\&\quad + \int _{0}^{t}\int _{\mathbb {Y}}\left( \ln \left( 1+\frac{f_{22}(u)I(\tau )}{1+f_{21}(u)}\right) -f_{22}(u)I(\tau ) \right) \nonumber \\&\quad \lambda (d u)d \tau \nonumber \\&\quad + \int _{0}^{t}\sigma _{22}I(\tau )d B_{2}(\tau ) + w_{1}(t)+ w_{2}(t) \nonumber \\&\quad + \int _{0}^{t}\int _{\mathbb {Y}}\ln \left( 1+\frac{f_{22}(u)I(\tau )}{1+f_{21}(u)}\right) {\widetilde{N}}(d \tau , d u), \end{aligned}$$

(12)

where

$$\begin{aligned} \begin{aligned}&w_{1}(t)=\int _{0}^{t}\sigma _{21}d B_{2}(\tau ),\;\;w_{2}(t)=\int _{0}^{t}\int _{\mathbb {Y}}\ln \\&\quad \left( 1+f_{21}(u)\right) {\widetilde{N}}(d \tau , d u). \end{aligned} \end{aligned}$$

It is obvious that $\left\langle w_{1},w_{1}\right\rangle (t) =\sigma _{21}^{2}t$. In view of Remark 2, one can obtain that $\left\langle w_{2},w_{2}\right\rangle (t)=t\int _{\mathbb {Y}}\left( \ln \left( 1+f_{21}(u)\right) \right) ^{2}\lambda (d u)$. Consequently, according to the strong law of large numbers presented in Lemma 1 we have

$$\begin{aligned} \lim _{t \rightarrow \infty }\frac{w_{1}(t)}{t}=0, \;\lim _{t \rightarrow \infty }\frac{w_{2}(t)}{t}=0\;\;a.s.. \end{aligned}$$

Furthermore, on the basis of exponential martingale inequality introduced in Definition 2, we choose $\alpha =1$, $\beta =2\ln n$, then it follows

$$\begin{aligned} \begin{aligned}&P\bigg \{\sup _{0 \le t \le n}\left( \int _{0}^{t} \sigma _{22}I(\tau )d B_{2}(\tau ) - \frac{1}{2}\int _{0}^{t} \sigma _{22}^{2}I^{2}(\tau )d \tau \right. \\&\qquad \qquad \;\;\left. + \int _{0}^{t}\int _{\mathbb {Y}}\ln \left( 1+\frac{f_{22}(u)I(\tau )}{1+f_{21}(u)}\right) {\widetilde{N}}(d \tau , d u)\right. \\&\qquad \qquad \;\;\left. - \int _{0}^{t}\int _{\mathbb {Y}} \left( 1+\frac{f_{22}(u)I(\tau )}{1+f_{21}(u)}-1\right. \right. \\&\qquad \qquad \;\;\left. \left. -\ln \left( 1+\frac{f_{22}(u)I(\tau )}{1+f_{21}(u)}\right) \right) \lambda (d u)d \tau \right) \ge 2\ln n\bigg \} \le \frac{1}{n^{2}}, \end{aligned} \end{aligned}$$

since $\sum \frac{1}{n^{2}} < \infty$, the Borel–Cantelli lemma implies that there exist a set $\varOmega _{0} \in {\mathcal {F}}$ with $P(\varOmega _{0})=1$ and an integer-valued random variable $n_{0}$ such that for every $\omega \in \varOmega _{0}$,

$$\begin{aligned} \begin{aligned}&\sup _{0 \le t \le n}\left( \int _{0}^{t}\sigma _{22}I(\tau )d B_{2}(\tau ) - \frac{1}{2}\int _{0}^{t}\sigma _{22}^{2}I^{2}(\tau )d \tau \right. \\&\quad \left. + \int _{0}^{t}\int _{\mathbb {Y}}\ln \left( 1+\frac{f_{22}(u)I(\tau )}{1+f_{21}(u)}\right) {\widetilde{N}}(d \tau , d u)\right. \\&\quad \left. - \int _{0}^{t}\int _{\mathbb {Y}} \left( 1+\frac{f_{22}(u)I(\tau )}{1+f_{21}(u)}-1\right. \right. \\&\quad \left. \left. -\ln \left( 1+\frac{f_{22}(u)I(\tau )}{1+f_{21}(u)}\right) \right) \lambda (d u)d \tau \right) \le 2\ln n, \quad \text {if} \; n \ge n_{0}. \end{aligned} \end{aligned}$$

That is, for all $0 \le t \le n$ and $n \ge n_{0}$ a.s., it follows

$$\begin{aligned} \begin{aligned}&\int _{0}^{t}\sigma _{22}I(\tau )d B_{2}(\tau ) \\&+ \int _{0}^{t} \int _{\mathbb {Y}}\ln \left( 1+\frac{f_{22}(u)I(\tau )}{1+f_{21}(u)}\right) {\widetilde{N}}(d \tau , d u)\le 2\ln n \\&+ \frac{\sigma _{22}^{2}}{2}\int _{0}^{t}I^{2}(\tau )d \tau + \int _{0}^{t}\int _{\mathbb {Y}}\left( \frac{f_{22}(u)I(\tau )}{1+f_{21}(u)}\right. \\&\left. -\ln \left( 1+\frac{f_{22}(u)I(\tau )}{1+f_{21}(u)}\right) \right) \lambda (d u)d \tau . \end{aligned} \end{aligned}$$

Then, substituting the above results into (12) deduces that

$$\begin{aligned}\begin{aligned}&\frac{\ln I(t)-\ln I(0)}{t}\\&\quad \le \frac{1}{t}\int _{0}^{t} \left( F({\hat{S}}(\tau ),0)-\left( \mu + \rho + \gamma + \frac{\sigma _{21}^{2}}{2}\right) \right) d \tau \\&\quad -\frac{1}{t}\int _{0}^{t}\int _{\mathbb {Y}}\left( f_{21}(u) -\ln \left( 1+f_{21}(u)\right) \right) \lambda (d u)d \tau \\&\quad +\frac{2\ln n}{t} -\frac{1}{t} \int _{0}^{t}\int _{\mathbb {Y}}\\&\quad \left( f_{22}(u)I(\tau ) - \frac{f_{22}(u)I(\tau )}{1+f_{21}(u)}\right) \lambda (d u)d \tau \\&\quad -\frac{1}{t}\int _{0}^{t}\sigma _{21}\sigma _{22}I(\tau )d \tau +\frac{w_{1}(t)}{t}+\frac{w_{2}(t)}{t}\\&\le \frac{1}{t}\int _{0}^{t}\left( F({\hat{S}}(\tau ),0) -\left( \mu + \rho + \gamma + \frac{\sigma _{21}^{2}}{2}\right) \right) d \tau \\&\quad -\frac{1}{t}\int _{0}^{t}\int _{\mathbb {Y}}\left( f_{21}(u) -\ln \left( 1+f_{21}(u)\right) \right) \lambda (d u)d \tau \\&\quad +\frac{2\ln n}{t}+\frac{w_{1}(t)}{t}+\frac{w_{2}(t)}{t}, \end{aligned} \end{aligned}$$

for all $0 \le t \le n$ and $n \ge n_{0}$ a.s..

Therefore, for almost all $\omega \in \varOmega _{0}$, if $n \ge n_{0}$, $0 < n-1 \le t \le n$, by taking the limit of both sides we obtain

$$\begin{aligned} \begin{aligned}&\limsup _{t \rightarrow \infty }\frac{\ln I(t)}{t}\le \lim _{t \rightarrow \infty }\frac{1}{t} \\&\int _{0}^{t}\left( F({\hat{S}} (\tau ),0)d \tau -\left( \mu + \rho + \gamma + \frac{\sigma _{21}^{2}}{2} \right) \right) d \tau \\&\quad -\lim _{t \rightarrow \infty }\frac{1}{t}\int _{0}^{t}\int _{\mathbb {Y}} \left( f_{21}(u)-\ln \left( 1+f_{21}(u)\right) \right) \lambda (d u)d \tau \\&\quad + \lim _{n \rightarrow \infty }2\frac{\ln n}{n-1} \\&\le \int _{0}^{\infty }F\left( x, 0\right) {\bar{\pi }} (d x) -\left( \mu + \rho + \gamma + \frac{\sigma _{21}^{2}}{2}\right. \\&\quad \left. + \int _{\mathbb {Y}}\left( f_{21}(u)-\ln \left( 1+f_{21}(u)\right) \right) \lambda (d u) \right) = \lambda \,\,a.s.. \end{aligned} \end{aligned}$$

If $\lambda < 0$, then $\limsup _{t \rightarrow \infty }\frac{\ln I(t)}{t} < 0$, i.e., $\lim _{t \rightarrow \infty }I(t)=0$ a.s., which means the disease will die out in a long term. $\square$

6 Ergodic stationary distribution

In biology, the persistence of disease is closely related to the balance and stability of the entire ecosystem. In theoretical research, different from the deterministic model, the stochastic model has no endemic equilibrium point, so there is no way to get the desired result by analyzing the stability of the equilibrium point. In this part, we will investigate the existence of the ergodic stationary distribution of model (4) in a new way on the basis of the method mentioned in [53,54,55].

Theorem 4

Assume that $\lambda > 0$, for any initial value $\left( S(0) , I(0)\right) \in \mathbb {R}_{+}^{2}$, system (4) has a unique stationary distribution $\pi$ and it has ergodic property.

Furthermore, the following assertions are valid.

• (a) For any $\pi$-integrable f(x,y) : $\mathbb {R}_{+}^{2} \rightarrow \mathbb {R}$, it follows that

  $$\begin{aligned}&\lim _{t \rightarrow \infty }\frac{1}{t}\int _{0}^{t}f(S(\tau ),I(\tau ))d \tau \\&\quad =\int _{\mathbb {R}_{+}^{2}} f(x,y)\pi (d x, d y) \, a.s.. \end{aligned}$$

• (b) $\lim _{t \rightarrow \infty }||P(t,(S(0),I(0)),\cdot )-\pi ||=0$, $\forall (S(0),I(0)) \in \mathbb {R}_{+}^{2}$, where

  $P(t,(S(0),I(0)),\cdot )$ is the transition probability of (S(t),I(t)).

Proof

At first, we define a $C^{2}$-function

$$\begin{aligned} \begin{aligned} {\widehat{V}}(S(t),I(t))=&M\left( -\ln I(t)+\frac{c}{\mu } \left( {\hat{S}}(t)-S(t)\right) \right) \\&- \ln S(t)+\frac{\left( 1+S(t)\right) ^{p}}{p}+\frac{I^{p}(t)}{p}, \end{aligned} \end{aligned}$$

where p $\in (0,1)$, M is a positive constant which satisfies $-M\lambda + L \le -2$ and constant L will be determined later. In view of $\hat{S(t)}-S(t)>0, \forall t \ge 0$ and the partial derivative equations, it is easy to know that the following function has a minimum point, i.e.,

$$\begin{aligned}&{\widehat{V}}(S(t),I(t))\ge -M\ln I(t)-\ln S(t)+\frac{\left( 1+S(t)\right) ^{p}}{p}\\&\quad +\frac{I^{p}(t)}{p}\ge l_{1}. \end{aligned}$$

Then, we consider the following nonnegative function

$$\begin{aligned} V(S(t),I(t))={\widehat{V}}(S(t),I(t))-l_{1}. \end{aligned}$$

Denote

$$\begin{aligned} \begin{aligned}&V_{1}=-\ln I(t),\; V_{2}={\hat{S}}(t)-S(t), \;V_{3}=-\ln I(t)\\&\quad +\frac{c}{\mu }\left( {\hat{S}}(t)-S(t)\right) ,\\&V_{4}=-\ln S(t),\; V_{5}=\frac{\left( 1+S(t)\right) ^{p}}{p},\; V_{6}=\frac{I^{p}(t)}{p}. \end{aligned} \end{aligned}$$

An application of It${\hat{o}}$’s formula , one can see that

$$\begin{aligned}&{\mathcal {L}}(V_{1}) = - F(S,I) + \left( \mu + \rho + \gamma \right) +\frac{\left( \sigma _{21} +\sigma _{22}I\right) ^{2}}{2}\nonumber \\&\quad +\int _{\mathbb {Y}}\left( f_{21}(u)+f_{22}(u)I \right. \nonumber \\&\quad \left. - \ln \left( 1+f_{21}(u) +f_{22}(u)I\right) \right) \lambda \left( d u\right) \nonumber \\&= - F(S,I) + \mu + \rho + \gamma + \frac{\sigma _{21}^{2}}{2}\nonumber \\&\quad + \int _{\mathbb {Y}}\left( f_{21}(u)-\ln \left( 1+f_{21}(u)\right) \right) \lambda (d u)\nonumber \\&\quad +\sigma _{21}\sigma _{22}I+\frac{\sigma _{22}^{2}}{2}I^{2}\nonumber \\&\quad +\int _{\mathbb {Y}}\left( f_{22}(u)I-\ln \left( 1+\frac{f_{22}(u)I}{1+f_{21}(u)}\right) \right) \lambda (d u)\nonumber \\&\le - F({\hat{S}},0) + \mu + \rho + \gamma + \frac{\sigma _{21}^{2}}{2}\nonumber \\&\quad + \int _{\mathbb {Y}}\left( f_{21}(u)-\ln \left( 1+f_{21}(u)\right) \right) \lambda (d u)\nonumber \\&\quad +F({\hat{S}},0)-F(S,0)+F(S,0)-F(S,I)\nonumber \\&\quad +\left( \sigma _{21}\sigma _{22}+\int _{\mathbb {Y}}f_{22}(u) \lambda (d u)\right) I+\frac{\sigma _{22}^{2}}{2}I^{2}\nonumber \\&\le - F({\hat{S}},0) + \mu + \rho + \gamma + \frac{\sigma _{21}^{2}}{2} +c({\hat{S}}-S)\nonumber \\&\quad + \int _{\mathbb {Y}}\left( f_{21}(u)-\ln \left( 1+f_{21}(u)\right) \right) \lambda (d u)\nonumber \\&\quad +F(S,0)-F(S,I)\nonumber \\&\quad +\left( \sigma _{21}\sigma _{22}+\int _Yf_{22}(u)\lambda (d u)\right) I +\frac{\sigma _{22}^{2}}{2}I^{2}.\nonumber \\ \end{aligned}$$

(13)

$$\begin{aligned}&{\mathcal {L}}(V_{2})=-\mu ({\hat{S}}-S)+F(S,I)I\nonumber \\&\quad \le -\mu ({\hat{S}}-S)+cSI, \end{aligned}$$

(14)

where Assumption 1 has been used.

Combining Eqs. (13) and (14), we obtain

$$\begin{aligned} \begin{aligned} {\mathcal {L}}(V_{3})&\le -\int _{0}^{\infty }F(x, 0){\bar{\pi }} (d x) + \mu + \rho + \gamma + \frac{\sigma _{21}^{2}}{2} \\&\quad + \int _{\mathbb {Y}}\left( f_{21}(u)-\ln \left( 1+f_{21}(u)\right) \right) \lambda (d u)\\&\quad +\int _{0}^{\infty }F(x, 0){\bar{\pi }}(d x ) \\&\quad -F({\hat{S}}, 0) +F(S,0)-F(S,I)\\&\quad +\left( \sigma _{21}\sigma _{22}+\int _{\mathbb {Y}}f_{22}(u)\lambda (d u)\right) I\\&\quad +\frac{\sigma _{22}^{2}}{2}I^{2}+\frac{c^{2}}{\mu }SI. \end{aligned} \end{aligned}$$

Moreover,

$$\begin{aligned}&{\mathcal {L}}(V_{4}) = -\frac{\alpha }{S}+\mu + \frac{F(S,I)I}{S} +\frac{1}{2}\left( \sigma _{11}+\sigma _{12}S\right) ^{2}\\&\quad +\int _{\mathbb {Y}}\left( f_{11}(u)+f_{12}(u)S\right. \\&\quad \left. -\ln \left( 1+f_{11}(u) +f_{12}(u)S\right) \right) \lambda (d u)\\&\quad \le -\frac{\alpha }{S}+\mu +\frac{\sigma _{11}^{2}}{2}+cI+\sigma _{11} \sigma _{12}S\\&\quad +\frac{\sigma _{12}^{2}}{2}S^{2}+\int _{\mathbb {Y}}\left( f_{11}(u) +f_{12}(u)S\right) \lambda (d u)\\&\quad = -\frac{\alpha }{S}+\mu +\frac{\sigma _{11}^{2}}{2} +\int _{\mathbb {Y}}f_{11}(u)\lambda (d u)+cI\\&\quad +\left( \sigma _{11}\sigma _{12}+\int _{\mathbb {Y}}f_{12}(u)\lambda (d u)\right) S+ \frac{\sigma _{12}^{2}}{2}S^{2}. \\&{\mathcal {L}}(V_{5}) \le \left( 1+S\right) ^{p-1}\left( \alpha -F(S,I)I-\mu S\right) \\&\quad -\frac{1-p}{2}\left( 1+S\right) ^{p-2}\left( \sigma _{11}S +\sigma _{12}S^{2}\right) ^{2}\\&\quad +\frac{\left( 1+S\right) ^{p}}{p}\int _{\mathbb {Y}} \left( \left( 1+\frac{S}{1+S}f_{11}(u)+\frac{S^{2}}{1+S}f_{12}(u)\right) ^{p} -1\right. \\&\quad \left. -p\left( \frac{S}{1+S}f_{11}(u)+\frac{S^{2}}{1+S}f_{12}(u)\right) \right) \lambda (d u)\\&\quad \le \alpha -\frac{1-p}{2}\min \{\sigma _{11},\sigma _{12}\}^{2}(1+S)^{p}S^{2}. \\&{\mathcal {L}}(V_{6})=\left( F(S,I)I-(\mu +\rho +\gamma )I\right) I^{p-1}\\&\quad -\frac{1-p}{2}I^{p-2}\left( \sigma _{21}I+\sigma _{22}I^{2}\right) ^{2}\\&\quad +\frac{I^{p}}{p}\int _{\mathbb {Y}}\left( \left( \left( 1+f_{21} +f_{22}I\right) ^{p}\right. \right. \\&\quad \left. \left. -1-p\left( f_{21}+f_{22}I\right) \right) \right) \lambda (d u)\\&\quad \le cSI^{p}-\frac{1-p}{2}\sigma _{22}^{2}I^{p+2}. \end{aligned}$$

Now, combining the inequalities what we have got above, it follows

$$\begin{aligned}&{\mathcal {L}}V(S,I) \le -M\lambda + M\left( F(S,0)-F(S,I)\right) \\&\quad +M\left( \sigma _{21}\sigma _{22}+\int _{\mathbb {Y}}f_{22}(u) \lambda (d u)\right) I\\&\quad + \frac{\sigma _{22}^{2}}{2}MI^{2} + \frac{c^{2}}{\mu }MSI - \frac{\alpha }{S}+\mu +\frac{\sigma _{11}^{2}}{2}\\&\quad +\int _{\mathbb {Y}}f_{11}(u)\lambda (du)\\&\quad +cI+\left( \sigma _{11}\sigma _{12}+\int _{\mathbb {Y}}f_{12}(u) \lambda (d u)\right) S+ \frac{\sigma _{12}^{2}}{2}S^{2} + \alpha \\&\quad -\frac{1-p}{2}\min \{\sigma _{11},\sigma _{12}\}^{2}(1+S)^{p}S^{2}\\&\quad + cSI^{p} -\frac{1-p}{2}\sigma _{22}^{2}I^{p+2} \\&\quad + M\left( \int _{0}^{\infty }F(x,0){\bar{\pi }} (d x) - F({\hat{S}},0) \right) \\&\le -M\lambda + L - \frac{\alpha }{S} -\frac{1-p}{4}\min \{\sigma _{11}, \sigma _{12}\}^{2}(1+S)^{p}S^{2}\\&\quad -\frac{1-p}{4}\sigma _{22}^{2}I^{p+2}+\frac{\sigma _{22}^{2}}{2}MI^{2} + \frac{c^{2}}{\mu }MSI\\&\quad + M\left( F(S,0)-F(S,I)\right) \\&\quad + M\left( \sigma _{21}\sigma _{22}+\int _{\mathbb {Y}}f_{22}(u) \lambda (d u)\right) I\\&\quad + M\left( \int _{0}^{\infty }F(x,0){\bar{\pi }} (d x) - F({\hat{S}},0) \right) \\&=G(S,I) + M\left( \int _{0}^{\infty }F(x,0){\bar{\pi }} (d x) - F({\hat{S}},0)\right) , \end{aligned}$$

where

$$\begin{aligned} L= & {} \sup _{t\rightarrow \infty }\bigg \{\mu +\frac{\sigma _{11}^{2}}{2} +\int _{\mathbb {Y}}f_{11}(u)\lambda (d u)+cI\\&+\left( \sigma _{11}\sigma _{12}+\int _{\mathbb {Y}}f_{12}(u) \lambda (d u)\right) S\\&+\frac{\sigma _{12}^{2}}{2}S^{2} + \alpha \\&-\frac{1-p}{4}\min \{\sigma _{11},\sigma _{12}\}^{2}(1+S)^{p}S^{2}\\&+ cSI^{p} -\frac{1-p}{4}\sigma _{22}^{2}I^{p+2}\bigg \},\\ G(S,I)= & {} -M\lambda + L - \frac{\alpha }{S}\\&-\frac{1-p}{4}\min \{\sigma _{11},\sigma _{12}\}^{2}(1+S)^{p}S^{2}\\&-\frac{1-p}{4}\sigma _{22}^{2}I^{p+2}+\frac{\sigma _{22}^{2}}{2}MI^{2} + \frac{c^{2}}{\mu }MSI\\&+ M\left( F(S,0)-F(S,I)\right) \\&+ M\left( \sigma _{21}\sigma _{22}+\int _{\mathbb {Y}}f_{22}(u)\lambda (d u)\right) I. \end{aligned}$$

From the expression of G(S, I), we can deduce that

Case 1. If $S \rightarrow 0^{+}$, then it is obvious that $G(S,I) \rightarrow -\infty$;

Case 2. If $S \rightarrow +\infty$, obviously we have $G(S,I) \rightarrow -\infty$;

Case 3. If $I \rightarrow +\infty$, then $G(S,I) \rightarrow -\infty$;

Case 4. If $I \rightarrow 0^{+}$, it is easy to see that

$$\begin{aligned} \begin{aligned} G(S,I)&\le -M\lambda + L +\frac{\sigma _{22}^{2}}{2}MI^{2} + \frac{c^{2}}{\mu }MSI \\&+ M\left( F(S,0)-F(S,I)\right) \\&+ M\left( \sigma _{21}\sigma _{22}+\int _{\mathbb {Y}}f_{22}(u)\lambda (d u)\right) I, \end{aligned} \end{aligned}$$

according to Assumption 1, F(S, I) is continuous at $I=0$ uniformly, hence it is obvious that $F(S,0)-F(S,I)$ tends to 0 as I tends to $0^{+}$. Consequently, we obtain that

$$\begin{aligned} G(S,I) \le -M\lambda +L \le -2. \end{aligned}$$

Now we proceed to define the bounded closed set

$U_{\varepsilon }=\left\{ (S,I) \in \mathbb {R}_{+}^{2} , \varepsilon \le S \le \frac{1}{\varepsilon } , \varepsilon \le I \le \frac{1}{\varepsilon }\right\}$, taking $\varepsilon >0$ sufficiently small. From what we have discussed it follows that

$$\begin{aligned} G(S,I) \le -1 , \;\;\forall (S,I) \in \mathbb {R}_{+}^{2} \setminus U_{\varepsilon }. \end{aligned}$$

On the other hand, for any $(S,I) \in \mathbb {R}_{+}^{2}$, there exists a positive constant H such that $G(S,I) \le H$. Consequently, we have

$$\begin{aligned} \begin{aligned}&-\mathbb {E}\left( V(S(0),I(0))\right) \le \mathbb {E}\left( V(S(t),I(t)) \right) \\&\quad -\mathbb {E}\left( V(S(0),I(0))\right) \\&\quad =\int _{0}^{t}\mathbb {E}\left( {\mathcal {L}}V(S(\tau ),I(\tau ))\right) d \tau \\&\quad \le \int _{0}^{t}\mathbb {E}\left( G\left( S(\tau ),I(\tau )\right) \right) d \tau \\&\quad +M\mathbb {E}\left( \int _{0}^{t}\int _{0}^{\infty }F(x,0){\bar{\pi }}(d x)d \tau \right. \\&\quad \left. -\int _{0}^{t}F({\hat{S}}(\tau ),0)d \tau \right) . \end{aligned} \end{aligned}$$

According to the ergodicity of ${\hat{S}}(t)$, we get

$$\begin{aligned}\begin{aligned} 0&\le \liminf _{t \rightarrow \infty }\frac{1}{t}\int _{0}^{t}\mathbb {E} \left( G(S(\tau ),I(\tau )) \right) d \tau \\&=\liminf _{t \rightarrow \infty }\frac{1}{t}\int _{0}^{t}\left( \mathbb {E} (G(S(\tau ),I(\tau )))I_{\{(S(\tau ),I(\tau ))\in U_{\varepsilon }^{c}\}} \right. \\&\quad \left. +\mathbb {E}(G(x(s),y(s)))I_{\{(S(\tau ),I(\tau )) \in U_{\varepsilon }\}}\right) d \tau \\&\le \liminf _{t \rightarrow \infty }\frac{1}{t}\int _{0}^{t}\left( -P((S(\tau ), I(\tau ))\in U_{\varepsilon }^{c})\right. \\&\left. +HP((S(\tau ),I(\tau ))\in U_{\varepsilon }) \right) d \tau \\&\le -1+(1+H)\liminf _{t \rightarrow \infty }\frac{1}{t}P((S(\tau ),I(\tau ))\in U_{\varepsilon })d \tau , \end{aligned} \end{aligned}$$

which follows that

$$\begin{aligned}&\liminf _{t \rightarrow \infty }\frac{1}{t}\int _{0}^{t}P(\tau ,(S(0),I(0)),U_{\varepsilon })d \tau \nonumber \\&\quad \ge \frac{1}{1+H},\;\forall (S(0),I(0))\in \mathbb {R}_{+}^{2}, \end{aligned}$$

(15)

where $P(t,(S(0),I(0)),\cdot )$ is the transition probability of (S(t), I(t)). Inequality (15) and the invariance of $\mathbb {R}_{+}^{2}$ imply that there exist an invariant probability measure of system (x(t), y(t)) on $\mathbb {R}_{+}^{2}$. Furthermore, the independence between standard Brownian motions $B_{i}(t)$,  $i=1,2,3$ indicates that the diffusion matrix is non-degenerate. In addition, it is easy to see the existence of an invariant probability measure is equivalent to a positive recurrence. Therefore, system (4) has a unique stationary distribution $\pi$ and it has the ergodic property. On the other hand, assertions (a) and (b) can refer to [13, 56]. The proof is complete. $\square$

Lemma 3

Assume that $\left( S(t), I(t)\right)$ is the positive solution of system (4) with initial value $\left( S(0), I(0) \right) \in \mathbb {R}_{+}^{2}$, then for any $0\le \theta \le 1$, there exists a positive constant $K(\theta )$ such that

$$\begin{aligned} \lim _{t \rightarrow \infty }\sup \mathbb {E}S^{\theta }\le K(\theta ),\;\lim _{t \rightarrow \infty }\sup \mathbb {E}I^{\theta }\le K(\theta ). \end{aligned}$$

Proof

Consider the Lyapunov function

$$\begin{aligned} V(S(t),I(t))=(1+S+I)^{\theta }. \end{aligned}$$

By simple calculation on the basis of It${\hat{o}}$’s formula, we obtain

$$\begin{aligned}\begin{aligned}&d V(S(t),I(t))\\&=\left[ \theta (1+S+I)^{\theta -1}\left( \alpha -\mu S -\left( \mu +\rho +\gamma \right) I \right) \right. \\&\quad \left. +\frac{\theta (\theta -1)}{2}(1+S+I)^{\theta -2} \left( \left( \sigma _{11}S+\sigma _{12}S^{2}\right) ^{2}\right. \right. \\&\quad \left. \left. +\left( \sigma _{21}I+\sigma _{22}I^{2} \right) ^{2} \right) \right. \\&\quad \left. +\int _{\mathbb {Y}}\left( \left( 1+S+I+f_{11}S +f_{12}S^{2}+f_{21}I+f_{22}I^{2}\right) ^{\theta } \right. \right. \\&\quad \left. \left. -\left( 1+S+I \right) ^{\theta } \right. \right. \\&\quad \left. \left. -\theta \left( 1+S+I\right) ^{\theta -1}\left( f_{11}S +f_{12}S^{2}+f_{21}I+f_{22}I^{2}\right) \right) \right. \\&\quad \left. \lambda (d u)\right] d t \\&\quad + \theta \left( 1+S+I\right) ^{\theta -1}\left[ \left( \sigma _{11}S +\sigma _{12}S^{2}\right) d B_{1}(t)\right. \\&\quad \left. +\left( \sigma _{21}I+\sigma _{22}I^{2} \right) d B_{2}(t)\right] \\&\quad + \int _{\mathbb {Y}}\left( \left( 1+S+I+f_{11}S+f_{12}S^{2}+f_{21}I+f_{22}I^{2}\right) ^{\theta }\right. \\&\quad \left. -\left( 1+S+I \right) ^{\theta }\right) {\widetilde{N}}(d t, d u). \end{aligned} \end{aligned}$$

Applying It${\hat{o}}$’s formula to $e^{\eta t}V(S(t),I(t))$, we have

$$\begin{aligned}&d (e^{\eta t}V(S(t),I(t))) \nonumber \\&=\eta e^{\eta t}V(S(t),I(t))+e^{\eta t}d V(S(t),I(t)) \nonumber \\&=e^{\eta t} \eta (1+S+I)^{\theta }+e^{\eta t} \left( \theta (\alpha +\mu )(1+S+I)^{\theta -1}\right. \nonumber \\&\quad \left. -\theta \mu (1+S+I)^{\theta }-\theta (\rho +\gamma ) I(1+S+I)^{\theta -1}\right) d t \nonumber \\&\quad +\frac{\theta (\theta -1)}{2}e^{\eta t}(1+S+I)^{\theta -2} \left( \left( \sigma _{11}S+\sigma _{12}S^{2}\right) ^{2}\right. \nonumber \\&\quad \left. +\left( \sigma _{21}I+\sigma _{22}I^{2} \right) ^{2} \right) d t \nonumber \\&\quad +e^{\eta t}\int _{\mathbb {Y}} \left( \left( 1+S+I+f_{11}S +f_{12}S^{2}+f_{21}I+f_{22}I^{2}\right) ^{\theta }\right. \nonumber \\&\quad \left. -\left( 1+S+I\right) ^{\theta }\right. \nonumber \\&\quad \left. -\theta \left( 1+S+I\right) ^{\theta -1} \left( f_{11}S+f_{12}S^{2}+f_{21}I+f_{22}I^{2}\right) \right. \nonumber \\&\quad \left. \lambda (d u) \right) d t\nonumber \\&\quad +e^{\eta t} \theta (1+S+I)^{\theta -1}\left[ \left( \sigma _{11}S +\sigma _{12}S^{2}\right) d B_{1}(t)\right. \nonumber \\&\quad \left. +\left( \sigma _{21}I+\sigma _{22}I^{2} \right) d B_{2}(t)\right] \nonumber \\&\quad + e^{\eta t}\int _{\mathbb {Y}}\left( \left( 1+S+I+f_{11}S+f_{12}S^{2} +f_{21}I+f_{22}I^{2}\right) ^{\theta }\right. \nonumber \\&\quad \left. -\left( 1+S+I \right) ^{\theta }\right) {\widetilde{N}}(d t, d u), \end{aligned}$$

(16)

where $\eta$ is a positive constant which satisfies $\eta >\mu \theta$.

Denote

$$\begin{aligned} G&=\theta (\alpha +\mu )(1+S+I)^{\theta -1}-(\eta -\mu \theta )(1+S+I)^{\theta }\\&\quad -\theta (\rho +\gamma ) I(1+S+I)^{\theta -1}\\&\quad +\frac{\theta (\theta -1)}{2}(1+S+I)^{\theta -2}\left( \left( \sigma _{11}S +\sigma _{12}S^{2}\right) ^{2} \right. \\&\left. \quad +\left( \sigma _{21}I+\sigma _{22}I^{2} \right) ^{2} \right) \\&\quad +\int _{\mathbb {Y}}\left( \left( 1+S+I+f_{11}S+f_{12}S^{2}+f_{21}I +f_{22}I^{2}\right) ^{\theta } \right. \\&\quad \left. -\left( 1+S+I\right) ^{\theta }\right. \\&\quad \left. -\theta \left( 1+S+I\right) ^{\theta -1}\right. \\&\quad \left. \left( f_{11}S+f_{12}S^{2}+f_{21}I+f_{22}I^{2}\right) \right) \lambda (d u). \end{aligned}$$

According to the inequation

$$\begin{aligned}\begin{aligned}&x^{r}\le 1+r(x-1),\;x\ge 0,\;0\le r\le 1,\\&\left| \sum _{i=1}^{k}a_{i}\right| ^{p} \le k^{p-1}\sum _{i=1}^{k}\left| a_{i}\right| ^{p},\;p\ge 1, \end{aligned} \end{aligned}$$

it follows

$$\begin{aligned} \begin{aligned} G\le&\theta (\alpha +\mu )(1+S+I)^{\theta -1}-(\eta -\mu \theta ) (1+S+I)^{\theta }\\&-\frac{\theta (1-\theta )}{54}\min \{\sigma _{12}^{2},\sigma _{22}^{2}, 1\}(1+S+I)^{\theta +2} \\&\le K(\theta ),\;\theta \in [0,1]. \end{aligned} \end{aligned}$$

Integrating both sides of (16) from 0 to t and then taking expectations

$$\begin{aligned} \mathbb {E}\left( e^{\eta t}V(S(t),I(t))\right) \le V(S(0),I(0))+\frac{K(\theta )(e^{\eta t}-1)}{\eta } \end{aligned}$$

This completes the proof. $\square$

Table 1 Parameters of the epidemic system (4)

Remark 5

If $\theta =1$, by virtue of Lemma 3 and Theorem 4, one can see that

$$\begin{aligned} \begin{aligned}&\lim _{t \rightarrow \infty }\frac{1}{t}\int _{0}^{t}S(\tau )d \tau =\int _{\mathbb {R}_{+}^{2}}x\pi (d x, d y),\\&\lim _{t \rightarrow \infty }\frac{1}{t}\int _{0}^{t}I(\tau )d \tau =\int _{\mathbb {R}_{+}^{2}}y\pi (d x, d y) \;\;a.s.. \end{aligned} \end{aligned}$$

Although information about the stationary distribution $\pi$ is not known yet, the above result implies that S(t) and I(t) are persistent in the mean.

7 Examples and numerical simulations

7.1 Numerical simulation only with white noise

In this section, we give some numerical simulation examples to illustrate the effect of disturbances on the SIR epidemic model. Since it is difficult to get the explicit value of $\lambda$, we first consider the following equation with saturated incidence rate but without the perturbation of L$\acute{e}$vy jumps, i.e., $f_{ij}=0$, $i=1,2,3$, $j=1,2$.

$$\begin{aligned} \left\{ \begin{array}{l} d S(t)=\left( \alpha -\mu S(t)-\frac{\beta S(t)I(t)}{1+mI(t)}\right) d t +\left( \sigma _{11}S(t)\right. \\ \qquad \quad \quad \quad \left. +\sigma _{12}S^{2}(t)\right) d B_{1}(t), \\ d I(t)=\left( \frac{\beta S(t)I(t)}{1+mI(t)}-(\mu +\rho +\gamma )I(t)\right) d t \\ \qquad \quad \quad \quad +\left( \sigma _{21}I(t)+\sigma _{22}I^{2}(t) \right) d B_{2}(t),\\ d R(t)=\left( \gamma I(t)-\mu R(t)\right) d t +\left( \sigma _{31}R(t)\right. \\ \qquad \quad \quad \quad \left. +\sigma _{32}R^{2}(t)\right) d B_{3}(t), \end{array} \right. \end{aligned}$$

(17)

Fig. 1

Simulations of the solution in stochastic system (17) with white noise $\sigma _{11}=\sigma _{12}=\sigma _{21}=\sigma _{22}=\sigma _{31}=\sigma _{32}=0.01$. The graph shows that the three sub-populations are persistent, which means that the disease will spread among people

The values of parameters in model (17) and initial values of S, I, R are shown in the following table.

Example 1

Consider model (17) with parameters in Table 1, we take the white noise intensities as $\sigma _{ij}=0.01$, $i=1,2,3$, $j=1,2$. By using MATLAB software, we compute that

$$\begin{aligned}\begin{aligned} \lambda&=\int _{0}^{\infty }F(x,0)\pi ^{*}(d x)-(\mu +\rho +\gamma +\frac{\sigma _{21}^{2}}{2})\\&=\beta \int _{0}^{\infty }x\pi ^{*}(d x)-(\mu +\rho +\gamma +\frac{\sigma _{21}^{2}}{2})\approx 0.046>0, \end{aligned} \end{aligned}$$

According to Theorem 4, this means that the disease will persist and system (17) has an unique ergodic stationary distribution. Through the trajectory images of S(t), I(t) and R(t) shown in Fig. 1, one can easily find that the number of all the three sub-populations fluctuated around a nonzero number, which means that the disease persists in a long term.

Next, we choose other parameter values such that $\lambda <0$, which can indicate the disease will be extinct in a long time. The only difference between the two examples is the intensities of white noise. Consider model (17) with $\sigma _{11}=0.01, \sigma _{12}=0.01, \sigma _{21}=0.8, \sigma _{22}=0.01,\sigma _{31}=0.01,\sigma _{32}=0.01$, then by software we obtain $\lambda \approx -0.274<0.$ According to Theorem 3, we can know that I(t) will go to zero exponentially with probability one while S(t) converges to the ergodic process ${\bar{S}}(t)$. Through the curve trajectories in Fig. 2, one can see that the number of infected and recovered populations tends to zero eventually, and this implies that the disease can be brought under control and stopped spreading among people.

Fig. 2

Simulations of the solution in stochastic system (17) with white noise $\sigma _{11}=0.01, \sigma _{12}=0.01, \sigma _{21}=0.8, \sigma _{22}=0.01,\sigma _{31}=0.01, \sigma _{32}=0.01$. The curves in the graph show that both the infected and the recovered population will eventually decrease to zero, which means that the disease will eventually disappear

Fig. 3

Simulations of the solution in stochastic system (18) with white noise $\sigma _{ij}=0.01$, $i=1,2,3$, $j=1,2$ and jump noise $f_{ij}=0.01$, $i=1,2,3$, $j=1,2$. The curves in the figure indicate a persistent presence of susceptible, infected and recovered individuals

Fig. 4

Simulations of the solution in stochastic system (18) with white noise $\sigma _{ij}=0.01$, $i=1,2,3$, $j=1,2$ and jump noise $f_{11}=f_{12}=f_{31}=f_{32}=0.01$ while ${21}=f_{22}=0.8$. As time goes on, the number of infected and recovered people tends to zero, which means that the disease will stop spreading and eventually disappear

7.2 Numerical simulation with white noise and L$\acute{e}$vy jumps

Although we cannot get the exact mathematical expression of $\lambda$ at present, some corresponding visualized results can be obtained by numerical simulation. Now, we take into account the interference of L$\acute{e}$vy jumps to study the effects of this noise. At first, we present the equation.

$$\begin{aligned} \left\{ \begin{array}{l} d S(t)=\left( \alpha -\mu S(t^{-})-\frac{\beta S(t^{-})I(t^{-})}{1+mI(t^{-})}\right) d t \\ \qquad \qquad \quad +\left( \sigma _{11}S(t^{-})+\sigma _{12}S^{2}(t^{-}) \right) d B_{1}(t)\\ \qquad \qquad \quad +\int _{\mathbb {Y}}\left( f_{11}(u)S(t^{-})+f_{12}(u)S^{2}(t^{-}) \right) \\ \qquad \qquad \times {\widetilde{N}}\left( d t,d u\right) , \\ d I(t)=\left( \frac{\beta S(t^{-})I(t^{-})}{1+mI(t^{-})}-(\mu +\rho +\gamma )I(t^{-})\right) d t\\ \qquad \qquad \quad +\left( \sigma _{21}I(t^{-})+\sigma _{22}I^{2}(t^{-}) \right) d B_{2}(t)\\ \qquad \qquad \quad +\int _{\mathbb {Y}}\left( f_{21}(u)I(t^{-})+f_{22}(u)I^{2}(t^{-}) \right) \\ \qquad \qquad \times {\widetilde{N}}\left( d t,d u\right) ,\\ d R(t)=\left( \gamma I(t^{-})-\mu R(t^{-})\right) d t +\left( \sigma _{31}R(t^{-})\right. \\ \qquad \qquad \quad \left. +\sigma _{32}R^{2}(t^{-})\right) d B_{3}(t)\\ \qquad \qquad \quad +\int _{\mathbb {Y}}\left( f_{31}(u)R(t^{-})+f_{32}(u)R^{2}(t^{-}) \right) \\ \quad \qquad \quad \times {\widetilde{N}}\left( d t,d u\right) , \end{array} \right. \end{aligned}$$

(18)

Example 2

Based on the parameter values in Table 1, we set the intensities of white noise and L$\acute{e}$vy noise as $\sigma _{ij}=f_{ij}=0.01$, $i=1,2,3$, $j=1,2$. When the noise intensities are relatively small, the effect of external disturbance on epidemic system (18) is weak, in addition, the dynamic properties of the stochastic model are similar to those of the deterministic model. From Fig. 3, it is easy to see that the numbers of S(t), I(t), R(t) are stable in the mean which also indicates that the disease will be persistent in a long term under the relatively weak noise.

On the other hand, we increase the intensity of L$\acute{e}$vy noise and set it to $f_{21}=f_{22}=0.8$. It is obvious that the only difference between the two examples is the value of $f_{21}$ and $f_{22}$. Now, the external noise plays an important role in the dynamics of disease transmission, and its influence on the stochastic system cannot be ignored. Through the curve trajectories in Fig. 4, it is obvious that the susceptible still remain stable on average, while both the infected and the recovered disappeared eventually. This also reflects that when there is a strong external disturbance, the disease can be controlled and does not spread in the population.

Based on the numerical simulations above, it is easy to find that both white noise and L$\acute{e}$vy jumps can suppress the spread of the disease. As the intensities of the white noise and L$\acute{e}$vy jumps increase, the disease disappeared eventually.

8 Conclusion

Based on the pervasiveness of randomness in nature, which includes mild noises and some massive, abrupt fluctuations, a stochastic SIR epidemic model with general disease incidence rate and L$\acute{e}$vy jumps is studied in this paper. Through rigorous theoretical analysis, we first present that the solution of model (4) is global and unique. Then, we investigate the existence of exponential ergodicity for the corresponding one-dimensional disease-free system (7) and a threshold $\lambda$ is established, which is represented by the stationary distribution ${\bar{\pi }}$ of (7) and the parameters in model (4). Through the symbol of the threshold, we can classify the extinction and persistence of the disease. To be specific, when $\lambda <0$, the number of the infected population will tend to zero exponentially which means the disease will extinct finally. Meanwhile, in case of $\lambda >0$, system (4) exists an ergodic stationary distribution on $\mathbb {R}_{+}^{2}$ which also means the disease is permanent.

However, since the explicit analytic formula of invariant measure ${\bar{\pi }}$ cannot be obtained so far, the exact expression of $\lambda$ cannot be known accordingly, whereas from the threshold we can still get a series of dynamic behaviors and characteristics of model (4). According to the mathematical expression of the threshold $\lambda$, a surprising finding is that neither $f_{11}(u)$ nor $f_{12}(u)$ has an effect on the value of $\lambda$. In addition, both the linear perturbation parameters $\sigma _{21}$ of white noise and $f_{21}(u)$ of L$\acute{e}$vy jumps have a negative effect on the value of $\lambda$, while the second-order perturbation parameters have little effect.

In our numerical simulation, one can easily find that when the intensities of noises are relatively small, the disease will persist. However, with the increase in noise intensity, the curves of the solution (S, I, R) to model (4) fluctuate more obvious. Finally, when noise intensity is relatively high, the number of infected and recovered people tends to zero, which indicates that the disease tends to disappear. In other words, it implies that both the white noise and L$\acute{e}$vy jumps can suppress the outbreak of the disease.