Rigid impacts of three-dimensional rocking structures

Abstract

Studies of rocking motion aim to explain the remarkable earthquake resistance of rocking structures. State-of-the-art assessment methods are mostly based on planar models, despite ongoing efforts to understand the significance of three-dimensionality. Impacts are essential components of rocking motion. We present experimental measurements of free-rocking blocks on a rigid surface, focusing on extreme sensitivity of impacts to geometric imperfections, unpredictability, and the emergence of three-dimensional motion via spontaneous symmetry breaking. These results inspire the development of new impact models of three-dimensional facet and edge impacts of polyhedral objects. Our model is a natural generalization of existing planar models based on the seminal work of George W. Housner. Model parameters are estimated empirically for rectangular blocks. Finally, new perspectives in earthquake assessment of rocking structures are discussed.

1 Introduction

Rocking is the typical response of many structures to dynamic loads such as earthquakes. Rocking structures include masonry columns, arches, walls [7, 15, 16, 23], innovative earthquake protection structures such as rocking shear-walls and frames [14, 38], and some tanks, machines or vehicles [4, 18, 22]. Understanding the non-smooth dynamics of rocking motion is essential to properly design and to assess the safety of these structures.

Rocking motion of quasi-rigid objects is an example of contact-induced hybrid multibody dynamics, where episodes of continuous motion are interrupted by short impacts. Rocking is inherently nonlinear, which prevents the use of the theory of linear vibrations [21]. Moreover the time history of motion is notoriously unpredictable in many cases for two reasons [8, 35]. The lack of reliable and accurate impact models is a central problem of research concerning rocking motion. Modeling friction and transitions between stick and slip is another crucial question, even though the motion of many rocking structures (such as slender blocks) appears to be free of slip, and in such cases impact models are the only source of difficulty.

Fig. 1

Three types of rocking impacts: edge impact in a planar model (a), and in a three-dimensional model (b); and facet impact in a 3D model (c)

Impacts between hard objects have a very short duration. Accordingly, impact models used in the context of rigid body dynamics often take the mathematical form of an instantaneous mapping assigning a post-impact velocity to given pre-impact velocity state. Such discrete models are phenomenological descriptions of a complex, multi-scale physical process, and thus they are often unable to provide accurate predictions. In the case of straight impacts at a point contact, the coefficient of restitution is the standard phenomenological parameter, describing the motion in the normal direction. In the case of oblique frictional impacts, additional parameters are required to describe how the tangential and rotational motion of the colliding objects change during the impact process. Among others, a Coulomb-type coefficient of friction and the tangential coefficient of restitution are often used in this context. The parameters of impact maps are most often determined empirically and they are affected by various factors including material properties of the colliding objects (stiffness, strength, ductility, etc.), and other mechanical parameters (e.g., masses, velocity of collision, frictional characteristics of surfaces) [35].

The impacts of rocking objects occur in the presence of linear contact (Fig. 1a, b) or surface contact (Fig. 1c). Both contact setups are geometrically degenerate in the sense that points within a spatially extended region establish contact simultaneously. Degeneracy implies that the impact map is significantly affected by those geometric imperfections of the contact region, which are comparable in size to the deformations of the objects during an impact. In the case of light impacts of a quasi-rigid block on a hard surface (a common situation in the context of rocking motion), this mechanism manifests itself as extreme sensitivity to geometric imperfection, which is in sharp contrast with the more predictable motion of objects on a compliant surface [12]. For example, the slightest concavity of the base of a rigid, planar rocking block results in the concentration of contact forces at the vertices (Fig. 2a), whereas a slightly convex, polyhedral base may gives rise to a rapid sequence of very light impacts sweeping along the whole edge (Fig. 2b). Obviously, the two types of impact affect the angular velocity of the block differently.

Unlike other factors affecting the outcome of an impact, geometric imperfection varies among specimens in an unpredictable way. We believe that it has crucial role in the commonly observed unpredictability and irreproducibility of motion trajectories observed in physical experiments. The presence of such an effect limits the use of the traditional approach of impact modeling: empirically calibrated impact models cannot predict time histories. This feature of geometric imperfections is our motivation to develop an impact model that takes into account the effect of imperfections. We think that such a model is an important initial step toward the ability to assess the safety of rocking structure in the presence of unpredictability and irreproducibility.

Fig. 2

Illustration of geometric imperfections and their effect on a planar rocking impact. A concave edge results in the impact model of Housner [23] (a). A slightly convex edge (b) induces no energy loss. The models proposed by Ther and Kollár [36] (c), and by Kallitzonis [24] (d) are consistent with other types of imperfection. For an arbitrary imperfection, the possible outcomes of the impact can be parameterized by a single scalar $\lambda$ representing the location of the resultant $\varvec{\rho }$ of the impulsive forces (e)

Housner’s classical impact model for a planar rocking block [23] assumes that the impulse transmitted during a rocking impact occurs at the corner of the block, which is consistent with the assumption of a slightly concave base surface (Fig. 2a). In contrast, physical experiments clearly indicate significant deviation from the predictions of Housner’s model [3, 5, 20, 28, 31, 32, 36]. More recently, several authors proposed empirical model corrections [3, 5, 20, 28, 31], or a priori chosen geometric imperfections [36], to match the mean value of experimental measurements. Very recently, a few authors have proposed to consider the possibility of arbitrary geometric imperfections, in order to reproduce not only the mean, but also the observed variability of experimental results [10]. In the present paper, we revisit the problem of the planar rocking block, and present previous results using a unified approach in Sect. 2.

While the planar models uncover important aspects of rocking motion, real rocking motion is three dimensional, either because of out-of-plane excitation or as the result of spontaneously emerging out-of-plane motion even under planar initial motion and excitation.

Relatively, few works treat rocking as a 3D problem. The rocking motion of a rigid cylinder has been known for long time to be inherently three dimensional [34]. Rocking cylindrical columns have been studied numerically by using rigid models [25, 37] as well as the discrete element method [1]. Some experimental investigations focusing on the spatial rocking behavior of ancient cylindrical columns have also been reported [19, 30]. It is notable however that cylindrical blocks behave differently than polyhedral objects as they typically roll smoothly instead of undergoing impacts due to the lack of sharp vertices.

The first numerical model of 3D free rocking motion of a polyhedral block [26] focused on continuous motion, and did not propose an impact model. A similar analysis of an arbitrary rigid body with rectangular base by [40] proposed a natural 3D extension of Housner’s impact model by assuming that the impact impulse is concentrated at a vertex of the object. In addition, the effect of slip was investigated in several papers [10, 11, 13].

Several authors including [11, 17, 40] pointed out that the overturning of a 3D block can occur under excitations which are lower than those which overturn a corresponding 2D block. Hence, 3D models are important for earthquake assessment. At the same time, none of these works attempted to systematically investigate the set of possible outcomes of three-dimensional impacts and the role of geometric imperfections. In order to fill this gap, we introduce three impact parameters in the case of facet impacts, and two parameters for edge impacts, which capture all physically relevant outcomes of an impact without slip. Thereby, we obtain for the first time a universal 3D rigid impact model. The impact parameters of some free rocking blocks are determined through fitting simulated trajectories to experimental data. We use these results as well as basic physical laws to estimate the relevant ranges of model parameters.

The rest of the paper is organized as follows. In Sect. 2, we review the most common rigid, planar models of rocking impacts in a unified framework focusing on the case of a single monolithic block, and on the role of geometric imperfection. Then, we present an experimental demonstration of transition from planar-free rocking motion into three-dimensional rocking by a spontaneous symmetry breaking. This experiment illustrates the crucial role of geometric imperfections. In Sect. 4, we develop the new, three-dimensional model of rocking impacts, which is highly analogous to planar models, but it can account for spontaneous symmetry-breaking. The experimental results are revisited in Sect. 5, and the parameters of the new impact model are fitted empirically. Section 6 concludes the work, and outlines future steps toward the successful application of spatial impact models in earthquake design.

Fig. 3

Rocking impact of a free-standing block in two dimensions

2 A review of planar impact models

Consider a rigid, planar, rectangular object with mass m, and mass moment of inertia about the center of mass (COM) $\theta$. Immediately before the impact, the block rocks around vertex $V_b$, until the base $V_bV_a$ hits the ground. Let h and b denote the height of the COM of the block, and the half-length of $V_bV_a$, according to Fig. 3.

When the base of the block hits the ground, all points along $V_bV_a$ come into contact simultaneously, and contact forces may emerge anywhere along $V_bV_a$. Housner’s model [23] assumes that

• H1: immediately before the impact, the block rotates about $V_b$

• H2: the rotational momentum of the block about the vertex $V_a$ colliding to the ground is preserved

• H3: the vertex $V_a$ stays in sticking contact with the ground after the impact

These assumptions determine uniquely the post-impact angular velocity of the block in terms of the pre-impact value as follows.

According to assumption H1, the velocity vector of the COM is $\mathbf {v}^-=\omega ^-\cdot [h,-b]^\mathrm{T}$. Similarly, assumption H3 implies that the post-impact COM velocity is $\mathbf {v}^+=\omega ^+\cdot [h,b]^\mathrm{T}$. The preservation of angular momentum about point $V_a$

$$\begin{aligned} \theta \omega ^-\!+\!mh^2\omega ^-\!-\!m b^2\omega ^- \!=\! \theta \omega ^+\!+\!mh^2\omega ^+\!+\!m b^2\omega ^+ \end{aligned}$$

(1)

yields

$$\begin{aligned} \omega ^+=r \cdot \omega ^- \end{aligned}$$

(2)

where

$$\begin{aligned} r=r_\mathrm{Hou}:=\frac{\theta +mh^2-mb^2}{\theta +mh^2+m b^2} \end{aligned}$$

(3)

The scalar r will be referred to as angular velocity reduction factor (AVRF).

If we introduce the following notions

• sticking impact: an impact where the impact point has 0 post-impact tangential velocity

• inelastic impact: an impact where the impact point has 0 post-impact normal velocity

then assumptions H2–H3 can be formulated in a more concise way as:

• H4: a single, perfectly inelastic sticking impact occurs at the vertex $V_a$

While Housner’s model does not include explicit assumptions about geometric imperfections, assumption H4 is consistent with certain geometric imperfections (Fig. 2a) but inconsistent with others.

Many experimental works confirmed that the linear relationship (2) is a good approximation but the AVRF (3) derived using Housner’s assumptions underestimates experimentally measured values [9, 36]. The inaccuracy of the model has been attributed to the fact that H2 is not more than an a priori assumption [33]. To address this limitation, several works suggested improved models using either empirical modifications of the AVRF or modifications in Housner’s initial assumptions [6, 27, 28]. For example, Kalliontzis et al. [24] proposed using a reduced effective width of the base, which was motivated by the fact that small deformations of the underlying surface give rise to a spatially extended contact region along the base during the impact. The effective width introduces a free parameter $0\le \nu \le 1$ into the model and the corresponding value of r

$$\begin{aligned} r=r_\mathrm{Kal}:=\frac{\theta +mh^2-m\nu ^2 b^2}{\theta +mh^2+m\nu ^2 b^2} \end{aligned}$$

(4)

can be anywhere in the interval $r\in (r_\mathrm{Housner},1)$.

Ther and Kollár [36] pointed out the crucial role of geometric imperfections in the case of a hard underlying surface. In order to improve model accuracy, they proposed an a priori infinitesimally small geometric imperfection (Fig. 2c), which implies that a rocking impact consists of a sequence of two elementary impacts at points M and $V_a$ of Fig. 3. The smallness of the imperfection means that its effect on the physical properties (m, $\theta$) of the block is negligible. Furthermore, the points $V_b$, M, $V_a$ are almost collinear, and the elementary impacts occur within very short time. This assumptions allowed them to estimate the effect of the two elementary impacts according to

• H5: The outcome of a sequence of elementary impacts can be calculated as if they occurred immediately after one another in the nominal impact configuration of the perfect block.

In addition, H4 was replaced by a more general assumption

• H4a: whenever a point of the imperfect surface hits the ground, a perfectly inelastic sticking impact occurs.

They showed that the corresponding AVRF

$$\begin{aligned} r=r_\mathrm{TK}:=\frac{\theta +mh^2}{\theta +mh^2+m b^2} \end{aligned}$$

(5)

closely matched the mean value of many physical experiments. Wittich and Hutchinson [39] examined a model with arbitrary geometric imperfection and demonstrated how the corresponding value of r can be determined under assumptions H1, H4a, H5. Interestingly, the previously mentioned model of Kallitzonis [24] is also equivalent of assuming a hard surface with geometric imperfection in the form of a concave section surrounded by two identical convex segments (Fig. 2d).

Chatzis et al. [10] seems to be the first one to notice that the linear momentum transferred along the base during the impact process can be replaced by an instantaneous resultant momentum $[P_x,P_y]^\mathrm{T}$ under assumptions H1, H3. All possible outcomes of the impact can be parameterized by a single scalar $\lambda$ representing the position of the resultant impact force (Fig. 2e). Accordingly, they proposed to use assumptions H1, H3 together with

• H2a: the rotational momentum of the block about a specified internal impact point of the base given by the parameter $\lambda$ is preserved

The AVRF now becomes

$$\begin{aligned} r=r_\mathrm{Cha}:=\frac{\theta +mh^2-m\lambda b^2}{\theta +mh^2+m\lambda b^2} \end{aligned}$$

(6)

Importantly, the model of [10] is universal in the following sense: it captures all possible post-impact states through a single scalar parameter $\lambda$. On the other hand, the approach of [10] does not give a hint on how to choose $\lambda$. Clearly, many different factors may affect $\lambda$ (e.g., material properties, impact velocity, etc.). Among these, the key role of geometric imperfections was first pointed out by [36, 39].

One can also set up theoretical bounds on the parameter $\lambda$. The straightforward assumptions of nonnegative energy absorption implies $0\le \lambda$, whereas unilateral nature of contact forces implies $-1\le \lambda \le 1$. Housner’s assumptions correspond to $\lambda =1$, and a slightly convex base (as in Fig. 2b) would induce an impact with $\lambda \approx 0$ under assumptions H1, H4a, and H5. We notice without proof that all values in the interval $\lambda \in (0,1)$ can be realized by choosing an appropriate geometric imperfection. Thus, the resulting AVRF $r_\mathrm{Cha}(\lambda )$ can take arbitrary values within the interval $(r_\mathrm{Hou},1)$.

It is noticeable that some experimental works report AVRF values below $r_\mathrm{Hou}$, which would correspond to $\lambda >1$ [5, 20]. Impact parameter values beyond theoretical bounds are typically caused by unmodeled effects such as slip [5] or additional energy absorption of pin joints in the experimental device [20] .

In Sect. 4, we develop a similar model of three-dimensional rocking impacts involving edge and surface contacts. Our contribution consists of a parameterization of all possible outcomes in order to ensure universality of the new model. Theoretical limits of the model parameters will also be identified.

3 Spontaneous emergence of out-of-plane motion in physical experiments

3.1 The experimental setup

The free rocking motion of eight stone blocks (Fig. 4) with identical nominal heights h and half width $b_{1}$ but different half depths $b_{2}$ has been investigated. The blocks were manufactured from the same solid granite slug. Examining the sliced surfaces, no cavities or cracks were found, so the blocks were considered to be homogeneous. The density of the granite blocks is $\rho = 2692 \pm 43\, \mathrm{kg}/\mathrm{m}^3$.

Fig. 4

Stone blocks used in the experiment and the coordinate system attached to the rocking block

The motion of the blocks was recorded with the aid of an X-IMU inertial motion unit device produced by X-IO Technologies. We use an orthogonal coordinate frame fixed to the rocking block (Fig. 4) such that the x-axis is parallel to the edge of length $b_1$ and the z-axis points vertically up. During the experiments, each block shown in Fig. 4 was tilted in the xz plane and released five times. Then, each block was turned upside down, and the experiments were repeated. The two settings will be referred to as positions A and B.

The bodies were released from a state of edge contact with initial angular velocity close to 0 and an initial inclination angle slightly below the neutral position of the block ($\varphi _n = 0.245$ rad). The initial inclinations were for all experiments in the range of 0.17 rad $<\varphi _0 < 0.24$ rad. The support medium was a solid granite block of size 50 by 40 by 20 cm resting on a massive steel support.

Before the recorded experiments, some preliminary tests were run using 120 fps action cameras (GoPro Hero 8 Black) to investigate the effect of sliding and bouncing during impact. The front- and side-view of the block were recorded, and the frames of the movie were analyzed. No visible signs of sliding and or bouncing were observed.

Figure 5 shows time history data of three experimental tests. The first two belong to granite block three, but the experiment was carried out in positions A and B, respectively. The last test belongs to block eight, which has a larger depth. Panels (a, d, g) show components of the angular velocity, where nonzero values of $\omega _x$ or $\omega _z$ are both signs of spatial motion. Panels (b, e, h) depict Euler angles $\varphi _x$, $\varphi _y$ and $\varphi _z$ representing the attitude of the block using the zyx convention. (That is, a general rotation is the composition of three consecutive rotations about the local z, y, and x axes by angles $\varphi _z$, $\varphi _y$ and $\varphi _x$.)

The X-IMU estimates time histories of the acceleration vector, angular velocity vector, attitude, and local magnetic field vector using on-board sensors including accelerometers, a triple-axis gyroscope, and magnetometers. Two operation modes are offered by the device. The attitude heading reference system (AHRS) modes combine all sensor data including the magnetometer. We observed that the big amount of steel equipment in the laboratory caused large systematic errors, and thus this mode could not be used. The inertial measurement unit (IMU) mode excludes magnetometer data. This mode provides sufficiently accurate angular velocity estimations, but large drift was observed in some of the attitude estimations (see Fig. 5e). Throughout the experiment, we used IMU mode with 256 Hz rate, and the drift of attitude data was compensated as described below (Fig. 5c, f, i). The modified Euler angles were determined as follows:

• The local maximum points of $|\omega _y|$ in the angular velocity diagram were located numerically.

• These points mark the moment of an impact in which an edge of length $b_1$ is in contact with the ground. Thus, the $\varphi _y$ Euler angle should be zero

• A piecewise linear error function was added to the Euler angles to enforce 0 value of the appropriate components at the impact times.

The same correction steps were also repeated for the $\varphi _x$ Euler angles.

3.2 Results of the experiment

Despite the xz plane being a plane of reflection symmetry, significant out-of-plane motion was observed in almost all cases (Fig. 5). In addition, large differences were observed between the A and B positions, whereas multiple trials in the same position yielded more similar results. Both phenomena are the results of manufacturing imprecisions of the object, and our observations suggest that minor imperfections of the block strongly affect rocking motion. For blocks with large depth, we recorded lateral motion emerging from time to time, but decaying very rapidly, so motion appeared to be planar most of the time (Fig. 5g).

Fig. 5

Measured angular velocities (a, d, g), Euler angles (b, e, h), and corrected Euler angles (c, f, i) of the third block rocking in positions A (a–c) and B (d–f) as well as the eighth block rocking in position A. Note large drift in e. The corresponding OPMF and AVRF values are given above the diagrams

In order to quantify these observations, two quantities were determined for every experimental trial:

• the out-of-plane motion factor (OPMF) is the ratio of the maximal absolute values of the Euler angles corresponding to out-of-plane and in-plane rotation $\varPhi = \max _t|\varphi _x(t)|/\max _t|\varphi _y(t)|$ during the entire course of the rocking motion after the first impact.

• the AVRF was estimated based on ten subsequent local maximum values of the corrected $|\varphi _y|$ inclination angle ($\varphi _{y,i}$; $i=1,2,\dots ,10$) of the block. First, the vertical uplift of the COM at the maximal inclination angles was calculated as $u_{i}=h\sin \varphi _{y,i}-b_1(1-\cos \varphi _{y,i})$. Then, an AVRF value corresponding to two adjacent maximum values was calculated as $r_{\mathrm{exp},i}=\sqrt{u_{i+1}/u_{i}}$. The final estimated AVRF $r_\mathrm{EXP}$ was the median of the nine values corresponding to one single experimental trial.

The measured AVRF and OPMF values for different values of block depth ($b_2$) are shown in Fig. 6. The out-of-plane motion factor was found to be as high as 0.1 for low values of $b_2$, which is the result of spontaneous symmetry breaking induced by geometric imperfections. High dispersion of the AVRF data is likely also caused by imperfections, which can be explained by planar models. However the AVRF data also suggests that average values depend on $b_2$, which cannot be explained by planar models. The amount of experimental data is insufficient to draw detailed conclusions about the role of $b_2$; however, the presented results clearly indicate that such an effect exists. This is our motivation to present a new three-dimensional impact model.

Fig. 6

Mean and standard deviation of measured out-of-plane motion factors (a) and angular velocity ratios (b) for each position (A or B) of the eight blocks

4 A new, three-dimensional impact model

This section is devoted to development of our new impact model. First, a general description of hybrid rocking motion is given to clarify the role and the types of impacts. Then, the basic idea of the new impact model is presented in Sect. 4.2. This is followed by a general formula applicable to all types of impact maps (Sect. 4.3). The initial formula is further developed into a fully explicit expression in terms of impact parameters, which is applicable to edge impacts (Sect. 4.4) and to two different types of facet impacts (Sects. 4.5–4.6). A unified map applicable to any facet impact is given (Sect. 4.7). Finally, we establish some theoretical bounds of impact parameters (Sects. 4.8–4.9) .

4.1 The role of impacts during rocking motion

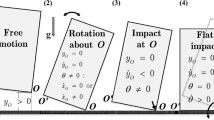
Three-dimensional rocking motion of quasi-rigid, convex, polyhedral objects is a combination of continuous and discrete components. Contact-free motion is barely observed except for perhaps very small amplitude bouncing motion. Accordingly, models of rocking motion often ignore the possibility of free flight. Slip may or may not be significant depending on contacting materials and geometry of the objects. Here, we keep focusing on slip-free motion, which is the most common behavior of slender blocks unless the underlying surface is slippery. With these restrictions, the possible contact modes of motion are surface contact (i.e., rest), edge contact (rocking around the edge) and vertex contact (rocking possibly with spin component). Transitions between these modes occur through impacts. More specifically, rocking under vertex contact typically ends when all points along an adjacent edge of the block reach the ground simultaneously giving rise to an edge impact. The typical post-impact motion of slender rocking object is rocking about the other endpoint of that edge. In a similar fashion, rocking about an edge terminates when all points of the base facet reach the ground simultaneously, giving rise to a facet impact. Then, the typical post-impact mode is rocking about a vertex or another edge of that facet.

In addition, vertex contact terminating in a facet impact is also possible but non-generic, so it is not discussed here.

Fig. 7

Transitions during two- and three-dimensional rocking motion

It is worth noting that sustained edge or facet contact (rest) can not be created by any of the single impact transitions listed above. One of the special features of rocking motion is the accumulation of infinite sequence of impacts in finite time intervals, which is often called Zeno behavior [2, 8]. In planar models, a Zeno point occurs when motion stops. For three-dimensional models, a Zeno sequence of edge impacts may terminate in a state of rest or in a state of sustained edge contact (i.e., rocking). A Zeno sequence of facet impacts may only terminate in a state of rest. Figure 7 provides a schematic overview of the possible contact modes and generic transitions between them, including Zeno behavior.

4.2 Overview of the impact model

Similarly to planar impacts, three-dimensional rocking blocks have sustained contact at an edge or at a vertex immediately before an impact. Hence, it is reasonable to use an extension of assumption H1 (see Sect. 2). In addition, it is also reasonable to ignore the possibility of free flight and slip, similarly to assumption H3 in Sect. 2.

Analogously to planar rocking, we will approximate the impact by an instantaneous mapping of velocities. Then, the outcome of the impact is uniquely determined by the spatial distribution of impulsive forces transferred to the object along the edge or facet involved in the impact, and the exact time history of force during the impact process does not matter. Moreover, we can further simplify the description by considering the resultant of the impulsive forces in the spirit of Chatzis et al. [10].

Fig. 8

Resultants of distributed impulses in two and three dimensions. a Planar impulse distributed along a line. b Wrench representation of a three-dimensional impulse distributed along a surface. c Modified wrench representation of the same impulse. d Modified wrench representation of an impulse distributed along a line section $V_bV_a$

There are however some differences between planar and spatial impacts. We have seen that an arbitrary distributed planar impulse is equivalent of a single resultant impulse $\varvec{\rho }$, which can be represented by its components $\rho _x$, $\rho _y$ and its location $x_R$ (Fig. 8a). Two parameters are determined by the kinematic constraints associated with no slip and no liftoff, and thus the possible outcomes of a planar impact can be parameterized by one scalar parameter (which was denoted by $\lambda$ in Sect. 2).

In contrast, the resultant of a spatially distributed three-dimensional impulse has six independent parameters, and representation of the distributed impulse by an equivalent single resultant impulse (which has only five parameters) is in general not possible. In the field of robotics, a distributed force is often represented by a ’wrench’: a resultant force vector $\varvec{\rho }=[\rho _x,\rho _y,\rho _z]$ along an appropriately chosen line of action (specified by two parameters) and an additional torque vector of magnitude $\tau$ parallel to $\varvec{\rho }$. This representation is unique. Impulses can be represented in a completely analogous way by a resultant impulse and an angular impulse, which can be parameterized by three components $\rho _x,\rho _y,\rho _z$, two coordinates $x_R,y_R$ of the resultant $\varvec{\rho }$ as well as by the magnitude of the torque $\tau$ (Fig. 8b).

For convenience, we will use a slightly different representation of the distributed impulsive impact forces by using a ’modified wrench’, which consists of the resultant impulse $\varvec{\rho }=(\rho _x,\rho _y,\rho _z)$ and an additional vertical angular impulse vector of magnitude $\tau$. The coordinates $x_R,y_R$ are used to specify the line of action of $\varvec{\rho }$ (Fig. 8c, d).

The modified wrench representation is unique provided that $\rho _z\ne 0$. Its parameters can be calculated in the case of facet impact as follows. Assume that the distributed impulse acts over a facet $\mathcal {F}$ lying in the $x-y$ coordinate plane and it is given by the function $\mathbf {p}(x,y)$ with components $p_x(x,y),p_y(x,y),p_z(x,y)$. Then, the parameters of the modified wrench are calculated by surface integrals:

$$\begin{aligned} \varvec{\rho }&=\int _\mathcal {F}\mathbf {p}(x,y)\mathrm{d}S \end{aligned}$$

(7)

$$\begin{aligned} x_R&= \rho _z^{-1} \int _\mathcal {F}xp_z(x,y)\mathrm{d}S \end{aligned}$$

(8)

$$\begin{aligned} y_R&= - \rho _z^{-1} \int _\mathcal {F}yp_z(x,y)\mathrm{d}S \end{aligned}$$

(9)

$$\begin{aligned} \tau&= \int _\mathcal {F} xp_y(x,y) - yp_x(x,y)\mathrm{d}S. \end{aligned}$$

(10)

For edge impacts, $\mathbf {p}$ is distributed along that edge, and analogous linear integrals are used to determine the resultant. If the distribution of the impulse is discrete, then summation can be used instead of integration.

The main advantage of the modified wrench representation is the fact that for arbitrary $p_z(x,y)\ge 0$, the possible locations of the point $R:(x_R,y_R,0)$ are exactly the points of the facet $\mathcal {F}$ according to (8)–(9). Similarly, for an edge impact, the possible locations of $R:(x_R,y_R,0)$ are exactly the points of the edge $V_bV_a$ involved in the impact. The latter will allow us later to use a single scalar parameter $\lambda$ instead of $x_R$ and $y_R$.

Fig. 9

Components of the post-impact angular velocity $\varvec{\omega }^+$ after an edge impact of a homogenous block with $b_1=b_2=5\,\hbox {cm}$, $h=20\,\hbox {cm}$ $m=1\,\hbox {kg}$ at tilt angle of $5^{\circ }$ for pre-impact angular velocity $\varvec{\omega }^-=[1,0,0]^\mathrm{T}$

4.3 General formula of the impact map

Consider a three-dimensional impact of a rocking block with mass m and moment of inertia tensor ${\varvec{\varTheta }}$. Let $\mathbf {u}_x$, $\mathbf {u}_y$, $\mathbf {u}_z$ denote unit vectors along the coordinate axes.

The pre- and post-impact velocity of the center of mass, and angular velocity are $\mathbf {v}^-$, $\mathbf {v}^+$, $\varvec{\omega }^-$, $\varvec{\omega }^+$. Let $V_b$, and $V_a$ denote points of contact before and after the impact. (These points are unique in the case of rocking about a vertex, but non-unique in the case of rocking about an edge.) Let R denote the point where the modified wrench of the impact impulse intersects the xy plane. The corresponding position vectors are $\mathbf {r}_b$, $\mathbf {r}_a$, $\mathbf {r}_R$, and $\mathbf {r}_c$ is the position vector of the COM.

The impact map $\varvec{\omega }^-\rightarrow \varvec{\omega }^+$ can be expressed as follows. The kinematic constraints of rocking motion immediately before and after the impact yield

$$\begin{aligned}&\mathbf {v}^-=\varvec{\omega }^-\times (\mathbf {r}_c-\mathbf {r}_b) \end{aligned}$$

(11)

$$\begin{aligned}&\mathbf {v}^+=\varvec{\omega }^+\times (\mathbf {r}_c-\mathbf {r}_a) \end{aligned}$$

(12)

The angular impulse momentum theorem applied to point R yields

$$\begin{aligned} (\mathbf {r}_c-\mathbf {r}_R)&\times (m\mathbf {v}^+)+{\varvec{\varTheta }}\varvec{\omega }^+ =\nonumber \\&(\mathbf {r}_c-\mathbf {r}_R)\times (m\mathbf {v}^-)+{\varvec{\varTheta }}\varvec{\omega }^- + \tau \mathbf {u}_z \nonumber \\ \end{aligned}$$

(13)

One can replace the cross products in (11)–(13) by matrix multiplication, using the matrix

$$\begin{aligned} \mathbf {R}_b= \begin{bmatrix} 0&{}\quad -\mathbf {u}_z^\mathrm{T}(\mathbf {r}_b-\mathbf {r}_c)&{} \quad \mathbf {u}_y^\mathrm{T}(\mathbf {r}_b-\mathbf {r}_c)\\ \mathbf {u}_z^\mathrm{T} (\mathbf {r}_b-\mathbf {r}_c)&{}\quad 0&{}\quad -\mathbf {u}_x^\mathrm{T} (\mathbf {r}_b-\mathbf {r}_c)\\ -\mathbf {u}_y^\mathrm{T} (\mathbf {r}_b-\mathbf {r}_c)&{}\quad \mathbf {u}_x^\mathrm{T} (\mathbf {r}_b-\mathbf {r}_c)&{}\quad 0 \end{bmatrix} \end{aligned}$$

(14)

and two other matrices $\mathbf {R}_R$, $\mathbf {R}_a$ composed in the same way:

$$\begin{aligned} \mathbf {v}^-&=\mathbf {R}_b\varvec{\omega }^- \end{aligned}$$

(15)

$$\begin{aligned} \mathbf {v}^+&=\mathbf {R}_a\varvec{\omega }^+ \end{aligned}$$

(16)

$$\begin{aligned} -\mathbf {R}_R(m\mathbf {v}^+)+{\varvec{\varTheta }} \varvec{\omega }^+&= -\mathbf {R}_R(m\mathbf {v}^-)+{\varvec{\varTheta }}\varvec{\omega }^- + \tau \mathbf {u}_z \end{aligned}$$

(17)

Then, $\varvec{\omega }^+$ can be expressed as

$$\begin{aligned} \varvec{\omega }^+ = ({\varvec{\varTheta }}-m\mathbf {R}_R\mathbf {R}_a)^{-1}\left[ ({\varvec{\varTheta }}-m\mathbf {R}_R\mathbf {R}_b)\varvec{\omega }^-+\tau \mathbf {u}_z\right] \end{aligned}$$

(18)

4.4 Explicit formula for edge impacts

In this case, $V_b$, and $V_a$ are the two endpoints of the edge involved in the impact, and R is a point along the edge. Hence, one can introduce the scalar parameter $\lambda$ such that

$$\begin{aligned} \mathbf {r}_R=\frac{\mathbf {r}_a+\mathbf {r}_b}{2}+\lambda \frac{\mathbf {r}_a-\mathbf {r}_b}{2} \end{aligned}$$

(19)

which also implies that $\mathbf {R}_R=(\mathbf {R}_a+\mathbf {R}_b)/2+\lambda (\mathbf {R}_a-\mathbf {R}_b)/2$. Thereby, we obtain from (18) a closed-form expression of the impact map in terms of known quantities and two impact parameters $\lambda$ and $\tau$:

$$\begin{aligned} \varvec{\omega }^+&= \left( {\varvec{\varTheta }}-m \frac{\mathbf {R}_a+\mathbf {R}_b+\lambda (\mathbf {R}_a-\mathbf {R}_b)}{2} \mathbf {R}_a\right) ^{-1}... \nonumber \\&\quad ... \cdot \left( \left( {\varvec{\varTheta }}-m \frac{\mathbf {R}_a+\mathbf {R}_b+\lambda (\mathbf {R}_a-\mathbf {R}_b)}{2} \mathbf {R}_b\right) \varvec{\omega }^-+\tau \mathbf {u}_z\right) \end{aligned}$$

(20)

Fig. 10

Notation of edge impacts (a) and facet impacts (b) illustrated by a rectangular block of size $2b_1$ by $2b_2$ by h. In b, we assumed that the index of the $V_b$ vertex is $b=2$

Figure 9 illustrates the dependence of the impact map on the impact parameters. The dominant effect of $\lambda$ is to set the amount reduction in the component of the angular velocity vector perpendicular to the impacting edge (which is the x component in the case illustrated by the figure), whereas $\tau$ affects dominantly the z component of angular velocity, and if the tilt angle $\alpha$ of the block is not 0, then $\tau$ also affects the third (in this case: y) component.

Later, Sect. 5 shows that one can fix $\tau =0$, and the remaining impact parameter $\lambda$ still allows a reasonable fitting of simulated trajectories to experimental measurements.

4.5 Explicit formula of facet impact followed by vertex contact

Let $V_i,i=1,2,\dots ,n$ denote the vertices of the facet involved in the impact and $\mathbf {r}_i$ the corresponding position vectors. Before a facet impact, the object rocks about an edge adjacent to that facet in general, which means two immobile vertices. Let $V_{b-1},V_b$ ($b\in \{1,2,\dots ,n\}$) be the pre-impact axis of rotation. (The index $b-1$ should be understood modulo n).

Immediately after the impact, the object rocks either about a vertex or about an edge of the base facet (see Fig. 7). Here, we discuss the first scenario.

So now, $V_a$, $a\in \{1,2,3,\dots ,n\}$ is the unique vertex contacting the ground after the impact. As before, the impact is given by the general formula (18).

In this case, $\mathbf {r}_R$ cannot be expressed in terms of a single scalar parameter $\lambda$. Instead, one can use two parameters $x_R$ and $y_R$. Alternatively, if the facet is rectangular, then it is convenient to introduce two dimensionless parameters $\lambda _\mathrm{lon}$, $\lambda _\mathrm{lat}$ according to Fig. 10b such that

$$\begin{aligned} \mathbf {r}_R\!=\!\frac{\mathbf {r}_1+\cdots +\mathbf {r}_4}{4}\!+\!\frac{\mathbf {r}_{b+1}-\mathbf {r}_{b}}{2}\lambda _\mathrm{lon}\!+\!\frac{\mathbf {r}_{b}-\mathbf {r}_{b-1}}{2}\lambda _\mathrm{lat}. \end{aligned}$$

(21)

Then, the explicit expression of the impact map in terms of the impact parameters is given by (18), and (21) using the notation (14) for fixed values of a.

Importantly, the index a of the post-impact point of contact $V_a$ cannot be chosen a priori in the case of a facet impact. The feasibility of all values of a can be tested one by one by evaluating the impact map, and by checking the requirements associated with unilateral contact:

$$\begin{aligned} \mathbf {u}_z^\mathrm{T}\mathbf {v}^+&> \mathbf {u}_z^\mathrm{T}\mathbf {v}^- \end{aligned}$$

(22)

$$\begin{aligned} \mathbf {u}_z^\mathrm{T}(\mathbf {v}^++\varvec{\omega }^+\times \mathbf {r}_i)&\ge 0 \end{aligned}$$

(23)

for $i=1,2,\dots ,n$. The first formula reflects that unilateral contact forces should increase $\mathbf {u}_z^\mathrm{T}\mathbf {v}$, and the second one means that none of the vertices penetrates into the ground after the impact.

Ideally, this process should always provide a unique feasible solution; however, this is not true in general. As illustration, we show numerical results of this process for a rectangular block of mass $m=1\,\hbox {kg}$, and sizes $b_1=5\,\hbox {cm}$; $b_2= 3\,\hbox {cm}$; $h=20\,\hbox {cm}$ in Fig. 11. We assumed $b=2$ (i.e., rocking about $V_1V_2$ before the impact) and pre-impact angular velocity $\varvec{\omega }^-=[0,-1,0]^\mathrm{T}$. Each panel corresponds to a fixed value of $\tau$. The figure shows numerically identified regions of the impact parameters where $a=3$ and those where $a=4$, i.e., the impact is followed by rocking about vertex $V_3$ and vertex $V_4$, respectively. In addition, there are regions of the impact parameters where no feasible solution exists, and others where there are two solutions.

The observed non-existence of the solution means that there are non-trivial ranges of the impact parameters, which are physically impossible. In addition, non-uniqueness means that there are ranges of the parameter values where the chosen parameterization of impact is ambiguous.

Fig. 11

Illustration of a facet impact of a block. Background colors show the index a of the vertex in contact with the ground after the impact. Dash-dotted lines depict the singularity of (18). Dashed rectangles depict the region (27); the energy bound (26) is satisfied in the region above the continuous curves

In order to get rid of nonuniqueness and nonexistence, we will postulate that

$$\begin{aligned} \mathbf {u}_z^\mathrm{T}\varvec{\omega }^+=0, \end{aligned}$$

(24)

i.e., there is no ‘spinning’ motion immediately after an impact. This assumption can be used to express $\tau$ explicitly from (18) after both sides of (18) have been multiplied by vector $\mathbf {u}_z^\mathrm{T}$ from left. In the case of a homogeneous cuboid block, we obtain the trivial result $\tau =0$. Equation (24) is merely an assumption which does not follow from physical laws; however, it is plausible, as dry friction is likely to eliminate the spinning component of motion when a whole facet is in contact with the ground. As we will see, this assumption is also in agreement with experimental results.

Finally, (24) guarantees a unique feasible solution as shown in Fig. 11a. In particular, the impact is followed by rocking about $V_3$ if $\lambda _\mathrm{lat}>0$ and rocking about $V_4$ if $\lambda _\mathrm{lat}<0$. A sketch of the proof of uniqueness is presented in “Appendix.”

Fig. 12

Contour plot of the x and y components of the post-impact angular velocity $\varvec{\omega }^+$ after a facet impact of a block with $m=1\,\hbox {kg}$, $b_1=5\,\hbox {cm}$; $b_2= 3\,\hbox {cm}$; $h=20\,\hbox {cm}$. The pre-impact angular velocity is $\varvec{\omega }^=[0,-1,0]$, which corresponds to rocking around edge $V_1V_2$. Note that the third component of $\varvec{\omega }^+$ is 0 by (24). The component $\mathbf {u}_y\varvec{\omega }^+$ is non-smooth function of the impact parameters at $\lambda _\mathrm{lat}=0$ because the post-impact mode of contact depends on the sign of $\lambda _\mathrm{lat}$

4.6 Explicit formula of facet impact followed by edge contact

Similarly to the previous type of facet impact, the explicit expression of the impact map is given by (18), and (21) using the notation (14). In contrast to the previous case, there are two immobile vertices immediately after the impact (say $V_a$ and $V_{a-1}$); furthermore, the kinematics of rotation implies that (24) must be satisfied. In the case of a slender cuboid block, it is easy to see that $V_{a-1}V_a$ must be the edge of the base facet opposite to $V_{b-1}V_b$. Furtermore, these constraints imply that $\lambda _\mathrm{lat}=\tau =0$, whereas $\lambda _\mathrm{lon}$ can be arbitrary. Hence, we only have one free parameter. This is not surprising given that facet impact followed by edge contact is essentially an example of two-dimensional hybrid rocking motion. Hence, in this case, the impact map is identical to the one-parameter map of planar rocking impacts of [10] revised by us in Sect. 2.

4.7 Unified impact map of facet impacts

Our findings in the previous two subsections imply that the two types of facet impacts can be given by one single impact map as shown in Fig. 11a. The impact map has two parameters: $\lambda _\mathrm{lat}$, and $\lambda _\mathrm{lon}$. Every parameter value delivers a unique solution, and the type of post-impact motion is determined by the sign of $\lambda _\mathrm{lat}$. For example, if pre-impact motion is rocking about $V_1V_2$, then post-impact motion of rocking about vertex $V_3$ if $\lambda _\mathrm{lat}>0$; rocking about the edge $V_3V_4$ if $\lambda _\mathrm{lat}=0$, and rocking about $V_4$ if $\lambda _\mathrm{lat}<0$.

The dependence of the impact map on the parameters is shown in Fig. 12. The map is continuous everywhere but non-smooth at $\lambda _\mathrm{lat}=0$. The dominant effect of $\lambda _\mathrm{lon}$ is to set the amount of reduction in the component of $\varvec{\omega }^+$, which is parallel to $\varvec{\omega }^-$ , whereas $\lambda _\mathrm{lat}$ controls the emergence of an angular velocity component perpendicular to $\varvec{\omega }^-$.

If a rocking block has large width to depth ratio (like blocks 7 and 8 in Fig. 4), the experimentally observed motion is usually almost perfectly planar. In contrast, our new impact model introduces large lateral angular velocity component unless $\lambda _\mathrm{lat}$ is very close to 0. This apparent contradiction can be resolved by noting the behavior of simulated blocks after such an impact. The facet impact is followed by spatial motion involving a sequence of edge impacts. Large depth value implies that the lateral component of the motion decays very rapidly (relatively to the time-scale of the longitudinal motion) and disappears through a Zeno point even if $\lambda _\mathrm{lat}$ was not very close to 0. After this short transient, our model predicts planar motion in agreement with experiments.

4.8 Theoretical limits of parameters of edge impacts

Similarly to planar impacts, the parameters $\lambda$, $\tau$ of edge impacts capture all possible outcomes, but it remains to find theoretical limits of these parameters. As we have seen, $\lambda$ determines the position of the resultant $\varvec{\rho }$, which must belong to the segment $V_bV_a$. From this observation, we obtain the limits

$$\begin{aligned} -1\le \lambda \le 1. \end{aligned}$$

(25)

Secondly, the impacts may not increase the kinetic energy of the rocking block. The kinetic energy of a rigid body rotating by angular velocity $\varvec{\omega }$ about a fixed point X can be calculated as $\frac{1}{2}\varvec{\omega }^{T}(\varvec{\varTheta }+ m \mathbf {R}_x^\mathrm{T}\mathbf {R}_x)\omega$ where $\mathbf {R}_x$ is the matrix composed from $\mathbf {r}_x$ according to (14). Then, we have

$$\begin{aligned} \varDelta E&:= \frac{1}{2}\varvec{\omega }^{+T} \left( \varvec{\varTheta }+ m \mathbf {R}_a^\mathrm{T}\mathbf {R}_a \right) \varvec{\omega }^+ - \dots \nonumber \\&\quad \dots - \frac{1}{2}\varvec{\omega }^{-T}\left( \varvec{\varTheta }+ m \mathbf {R}_b^\mathrm{T}\mathbf {R}_b \right) \varvec{\omega }^- \le 0. \end{aligned}$$

(26)

The region of the $\tau -\lambda$ parameter plane consistent with the last two contraints is always bounded, as $\lambda$ is bounded by (25), and for each value of $\lambda$, $\varDelta E$ is a quadratic function of $\tau$ with positive leading coefficient. It should also be noted that for $\tau =0$, (26) implies $\lambda \ge 0$ in analogy with previous findings about planar impacts. Figure 13 illustrates these bounds for various values of $\varvec{\omega }^-$. It should be noted that the contour lines are not affected by multiplication of $\varvec{\omega }^-$ by a constant factor, nor by adding an arbitrary y component to $\varvec{\omega }^-$.

Fig. 13

Energy balance of an edge impact of a homogenous block of size 10 cm by 10 cm by 40 cm and total mass 1 kg at tilt angle of $5^{\circ }$ for several pre-impact angular velocities. The regions of the parameter plane on the right sides of the curves result in reduction in the kinetic energy

Another theoretical bound is provided by a singularity of the inverted matrix ${\varvec{\varTheta }}-m\mathbf {R}_R\mathbf {R}_a$ in (18). We note without proof that such singularites do exist, but for slender blocks, they appear for large values of $\lambda$, which are irrelevant due to (25) .

There is at least one more theoretical bound for edge impacts, which reflects the fact that the torque $\tau$ originates from frictional forces generated by tangential motion during the impact, thus it cannot be arbitrary.

Finding the induced constraints of $\tau$ is beyond the scope of this work.

4.9 Theoretical limits of parameters of facet impacts

For facet impacts, bounds similar to those of edge impacts apply. First of all, the point R must be a point of the impacting facet. In the case of rectangular facets, this means

$$\begin{aligned} -1&\le \lambda _\mathrm{lat}\le 1\nonumber \\ -1&\le \lambda _\mathrm{lon}\le 1 \end{aligned}$$

(27)

The energy bound (26) (solid curves in Fig. 11) as well as the singularity of (18) (dash-dotted curves in Fig. 11) are also applicable to facet impacts. Again, we note without proof that the singularity appears for irrelevant ranges of $(\lambda _\mathrm{lat},\lambda _\mathrm{lon})$ provided that the block under investigation is slender. In addition, there are bounds of $\tau$ similarly to edge impacts that we do not investigate in this paper.

5 Empirical fitting of impact parameters

5.1 Methods

We now revisit the experimental tests introduced in Sect. 2. The motion always starts with the following phases of motion:

• 1. inital rocking about edge $V_1V_2$

• 2. facet impact

• 3. motion with sustained contact at $V_3$ and/or $V_4$. This phase includes one or several episodes of rocking about vertex $V_3$, vertex $V_4$ or about edge $V_3V_4$. Each such episode is followed by an edge impact at edge $V_3V_4$. The number of impacts may also be infinite in the case that a Zeno point occurs during this phase of motion.

• 4. an edge impact or a facet impact when $V_1$ and/or $V_2$ reaches the ground again

In order to reproduce the observed motion numerically, we developed a custom-made code in MATLAB environment, which simulates rocking motion on any vertex or edge as dictated by the Newton–Euler equations of rigid body motion. This was complemented with event detection algorithms to detect impact times and Zeno points, as well as numerical implementations of the impact maps. The code follows the logical structure of Fig. 7.

This code is capable of simulating rocking motion of a block if the physical properties of the block (size, mass, moment of inertia), the initial time of release $t_0$, initial tilt angle $\alpha$, the parameters of edge impacts at edge $V_3V_4$ during phase 3 ($\lambda$, $\tau$) and the parameters of the first facet impact in phase 2 ($\lambda _\mathrm{lat}$, $\lambda _\mathrm{lon}$, $\tau$) are specified.

The aim of this code is to find optimal values of the initial conditions and impact parameters, matching the experimentally measured trajectories. To that end, we introduce the error function

$$\begin{aligned} \epsilon (t_0,\alpha ,\dots ) =&(t_\mathrm{end}-t_0)^{-1}\nonumber \\&\times \int _{t_0}^{t_\mathrm{end}} | \varvec{\omega }_{m}(t)-\varvec{\omega }_{s}(t,t_0,\alpha ,\dots )|\mathrm{d}t \end{aligned}$$

(28)

where $t_\mathrm{end}$ is the time when the sequence of episodes listed above ends. $\varvec{\omega }_{m}$, and $\varvec{\omega }_{s}$ are measured and simulated angular velocity functions, and $\varvec{\omega }_{s}$ depends on the initial conditions and model parameters introduced above. In order to reduce the number of unknown parameters, we fix $\tau =0$ both for edge and for facet impacts. In addition, we assume that each of the $\lambda$, $\lambda _\mathrm{lat}$, $\lambda _\mathrm{lon}$ impact parameters take constant values along an individual rocking test. The unknown initial conditions ($t_0$, $\alpha$) and the model parameters $\lambda$, $\lambda _\mathrm{lat}$, $\lambda _\mathrm{lon}$ have been determined by semi-automated numerical minimization of the error function $\epsilon$: a rough fitting was first obtained by trial-and-error, the results of which was used as initial guess in the fminsearch numerical optimization algorithm of MATLAB software [29].

An example of trajectory fitting is shown in Fig. 14, and the optimum values are summarized in Fig. 15 for both position (A or B). The fitting of $\lambda _\mathrm{lat}$ was omitted for blocks 7 and 8, for which lateral motion decayed very rapidly. In the next two subsections, two important observations about these results are presented.

Fig. 14

Left: circles show measured angular velocities of block 4 in a free rocking test. Solid line shows simulated trajectories with optimized parameters: $t_0=2.33\,\hbox {s}$; $\alpha =0.197\,\hbox {rad}$; $\lambda =2.185$; $\lambda _\mathrm{lat}=-2.032$; $\lambda _\mathrm{lon}=0.197$. Right: magnified detail of the previous diagrams. Note that each impact induces an instantaneous jump in the angular velocity, however in some cases the jump is too small to be visible

Fig. 15

Numerically fitted impact parameters for the A and B positions of blocks 1 to 8

5.2 Variability of impact parameters

The first observation from Fig. 15 is the presence of large variability in the parameter values. This is partly caused by inaccurate measurement data. For example, impacts often cause rapid oscillations in measured angular velocity values (see Fig. 14), which is likely an artifact caused by mechanical vibration of the gyroscopes. Variation of initial tilt angles in the experimental tests may also contribute to variance of fitted parameter values because the impact maps often depend on impact velocities in a nontrivial way. Phenomena neglected by the model (bouncing, slip, elastic deformations, etc.), may also contribute to inaccuracy of fitting and noise in the fitted parameter values. All these factors call for a more extensive and controlled experimental campaign to properly calibrate the impact model in the future.

However, it is important to note that sensitivity of impacts to geometric imperfections could in itself cause large variability. Experiments using positions A and B of the same columns involve different geometric imperfections. Even subsequent tests of the same column in the same position involve different imperfections, due to moving over different areas of the underlying surface or due to the possible presence of small grains under the rocking blocks. The observed variability is thus more than just a weakness of our model, the experiments, or the analysis. Sensitivity implies that the anticipated result of model calibration is a realistic range of model parameters rather than specific values. Accordingly, impact parameters should be treated as uncertain parameters during the analysis of rocking motion. In particular, earthquake response analysis should verify the safety of a rocking structure for a whole range of impact parameter values rather than for single values of those parameters. This can be done via repeated simulations to assess the safety of one single block under a given excitation.

5.3 Violation of theoretical bounds

A closer look at the fitted $\lambda _\mathrm{lon}$ parameter values reveals that they are in the range (0, 1.5). This is consistent with the bound (26); however, the limit (25) is often violated by $\lambda _\mathrm{lon}$ values exceeding 1. In general, the violation of a theoretical bound indicates limitations of a model such as unmodeled effects (e.g., bouncing, slip, pivoting friction, or finite duration of impacts) or some simplifying assumption (e.g., using constant values of impact parameters during each individual motion sequence). In this particular case, large $\lambda$ means unexpectedly high reduction in angular velocity. We suspect that this may be caused by neglected energy loss during continuous rocking motion due to pivoting friction or micro-slip. The same explanation applies to the unexpectedly high $\lambda$ parameter values of edge impacts.

The fitted $\lambda _\mathrm{lat}$ values are in the interval $(-5,5)$, which is far beyond the limit (27). As in the previous case, we have no rigorous explanation for the violation of (27); however, we suspect that the results are caused by neglected small-scale bouncing motion as explained below.

One of the widely established assumptions in the literature of planar rocking motion is perfectly inelastic impacts (see assumption H4 in Sect. 2) despite the obvious fact that this assumption is not justified the materials used in experimental studies. Why is then inelasticity considered as acceptable? We believe that episodes of bouncing are indeed present in the experiments; however, they are of short duration and small amplitude. More specifically, rocking motion is a behavior of blocks with relatively small width-to-height (b/h) ratio (Fig. 3). The kinematics of rotational motion implies that the base of the block hits the ground with low velocity (compared to the translational velocity of other points of the block). Consequently, bouncing motion after the impact will also have low initial lift-off velocity. The emerging bouncing motion is similar to the motion of a rigid bouncing ball, where the process ends with a Zeno point followed by sustained contact. The maximum height of bouncing is proportional to the square of the liftoff velocity and the total duration of the bouncing sequence is linearly proportional to the initial liftoff velocity. That is, both quantities are small. From a practical point of view, these properties imply that bouncing is a transient behavior that has little effect on the dynamics, and it is also difficult to observe.

The observations presented above can be extended to spatial rocking motion, nevertheless even small-scale bouncing may have large effect on the emerging out-of-plane angular velocity. To illustrate this phenomenon, imagine a facet impact, in which the resultant of the impact momentum acts near vertex $V_3$ (see Fig. 11). Then, the model predicts rocking about vertex $V_4$ after the impact. If the impact is not ideally inelastic, then more vertical momentum is transferred to the block than the momentum predicted by the inelastic model. The surplus momentum causes the block to jump in the air, and to undergo bouncing at $V_4$ instead of smooth rocking. Moreover, the surplus momentum at $V_3$ during the impact is compensated by less momentum transferred to $V_4$ after the impact than the momentum generated by pure rocking motion during the same time interval. The surplus momentum emerging at $V_3$ instead of $V_4$ amplifies the out-of-plane angular velocity of the block after the facet impact. This is similar to the effect of large $|\lambda _\mathrm{lat}|$ values.

Hence, our second important observation is that the optimal fit of impact parameters to experimental results may yield parameter values contradicting previously found theoretical limits. Such violations indicate limitation of the model. We were able to identify neglected phenomena, which have similar effects to parameter values exceeding theoretical bounds. This finding suggests that the practical applicability of the model might be improved if one uses empirically determined ranges of impact parameters exceeding theoretical limits. At the same time, further exploration of this idea is left for future work.

6 Conclusions

The remarkable earthquake resistance of rocking structures inspires ongoing efforts to understand the characteristic features of rocking. The challenges of the analysis include strong nonlinearity (even at small amplitudes), hybrid dynamics (sudden impacts and continuous motion), and in the case of quasi-rigid blocks and supports, geometric sensitivity associated with edge and facet impacts. Models used for the analysis of rocking motion often use various simplifying assumptions, such as rigidity, inelastic impacts, slip-free motion, and planar motion.

Our work was inspired by the well-known observation that free rocking blocks on hard surfaces tend to transition from planar motion to spatial rocking via spontaneous symmetry breaking. This is caused by microscopic geometric imperfections of the block, which have macroscopic effect on the motion due to the extreme geometric sensitivity of edge and facet impacts of quasi-rigid objects. This phenomenon cannot be explained by currently available models, and calls for a new modeling approach, which is three dimensional and non-deterministic. As a first step toward such a model, we proposed a new universal, three-dimensional impact model, which can be used in the context of rigid body dynamics. Universality means that all reasonable outcomes of the impact are described by a small set of impact parameters. Our new model is a natural extension of the planar impact model [10], which uses one single impact parameter.

The parameters of the new impact model have been fitted to some free-rocking experiments. The results show that the parameters are quite unpredictable, which is not surprising as they are influenced by the effect of unknown geometric imperfections. We made initial steps toward identifying possible values of the impact parameters; however, more experimental data will be required to accurately identify their relevant ranges and probability distributions.

The long-term goal of our research effort is to improve current methods of assessing the earthquake resistance of rocking structures. We foresee that the inherently three-dimensional nature of rocking motion affects the ability of a structure to resist earthquakes without overturning. Moreover, the unpredictability of impact parameters suggests that parametric studies may be necessary to assess the safety of a single structure.

A Uniqueness of the facet impact map

It was demonstrated by numerical simulation (Fig. 11) that for some values of the impact parameters, the facet impact map may have no feasible solution or multiple feasible solutions. However, Fig. 11a strongly suggests that there is always one unique solution under (24) (or equivalently $\tau =0$). Here, we sketch the proof of uniqueness in this case.

For fixed values of the impact parameters $\lambda _\mathrm{lat},\lambda _\mathrm{lon},\tau$, the three components $\rho _x,\rho _y,\rho _z$ of an impact impulse could be determined by using (12). This vector equation can be decomposed to three scalar equation including the constraints of no slip at point $V_a$:

$$\begin{aligned}&\mathbf {u}_x^\mathrm{T}(\mathbf {v}^++\varvec{\omega }^+\times \mathbf {r}_a)=0 \end{aligned}$$

(29)

$$\begin{aligned}&\mathbf {u}_y^\mathrm{T}(\mathbf {v}^++\varvec{\omega }^+\times \mathbf {r}_a)=0 \end{aligned}$$

(30)

as well as inelasticity

$$\begin{aligned} \mathbf {u}_z^\mathrm{T}(\mathbf {v}^++\varvec{\omega }^+\times \mathbf {r}_a)=0. \end{aligned}$$

(31)

It is straightforward to show by direct calculation that $\mathbf {v}^++\varvec{\omega }^+\times \mathbf {r}_a$ is a linear function of $\varvec{\rho }$ for fixed values of a. As a consequence, the no slip conditions and the inequality (22) determine the direction of the vector $\varvec{\rho }$ (i.e., $\varvec{\rho }/|\varvec{\rho }|$) uniquely. At the same time, inelasticity (31) can be used to determine the length $|\varvec{\rho }|$. Moreover, for slender blocks and realistic values of impact parameters, $\mathbf {u}_z^\mathrm{T}(\mathbf {v}^++\varvec{\omega }^+\times \mathbf {r}_a)$ is a strictly increasing function of $|\varvec{\rho }|$.

If (24) holds, then the no-slip conditions (29)–(30) associated with different values of a become equivalent. Hence, for all values of a, the direction $\varvec{\rho }/|\varvec{\rho }|$ of the impact impulse will be the same. The length $|\varvec{\rho }|$ is however determined by (31) and it will be different for each value of a. Among these values, the largest one will provide a unique feasible solution as it implies that (31) is true, whereas for all values $i\ne a$, the inequality (23) will be satisfied instead.

In contrast, if (24) does not hold, then the no-slip conditions (29)–(30) are not equivalent, hence the direction of $\varvec{\rho }$ may be different for each value of a. Thus, the arguments outlined above are not applicable.