Modeling Ellipsoidal Block Impacts by an Advanced Rheological Model

Abstract

In this paper, an advanced rheological model for impacts of ellipsoidal blocks on deformable ground surfaces, introducing the effects of block eccentricity and orientation at impact, is presented. This allows us to assess impact penetration and force, restitution coefficients, and block trajectories. A parametric analysis was carried out by considering different block aspect ratios, impact angles and initial block orientations at impact. The results are presented in terms of restitution coefficients, penetration and force time histories, maximum penetration depth, maximum force and rotational/total kinetic ratios. Impacts along the major block axis, versus those along minor axis, are characterized by larger penetrations (ranging from 3.3 to 50%), shorter impact durations (ca 50%) and very slightly larger vertical forces (ranging from 0.3 to 60%) according to the model parameter used. In contrast, the impact angle is shown to strongly affect maximum penetration and force values, and markedly increase rotation at impact. Analogously, normal restitution coefficient is severely dependent on impact angle, with a variation of more than two orders of magnitude. A mathematical expression for computing the energetic restitution coefficient from the normal and tangential apparent restitution coefficients and the ratio between the rotation and total kinetic energy is proposed. This overcomes the drawback of classical restitution coefficients greater than one when a change in block rotation occurs allowing us to bracket the coefficient of restitutions values to support and improve classical rock fall simulations also highlighting their intrinsic limitations. Finally, the effects of block geometry and initial angular velocity on rockfall simulations were analyzed by implementing the approach in the HyStone simulation code. The simulated frequencies of the maximum height during each ballistic trajectory follow an exponential distribution, whereas those for normal and tangential apparent restitution coefficients follow normal distributions.

Highlights

• A new rheological model for impacts of ellipsoidal blocks is formulated.

• The model provides impact variables for different impact angles, initial orientations and block shape.

• Model results are used to compute restitution coefficients.

• Rockfall numerical simulations with HyStone implementing the extended impact model are performed.

• Statistical distributions of the normal and tangential apparent restitution coefficients are examined.

1 Introduction

Rock falling starts from the release of one or more blocks from a source area (detachment phase) and a consequent downslope movement under the action of gravity (propagation phase) (Varnes and Cruden 1996) until their arrest (deposition phase). As observed in Umili et al. (2023), the geological conditions of the rock mass govern the block geometry and volume statistics.

The motion of the blocks in the transition zone is characterized by a succession of ballistic and bouncing motions causing a sequence of interactions between block and ground surface.

In order to mitigate the rockfall risk, many defence systems have been conceived in the past and their design requires the definition of both kinematic and dynamic quantities such as rockfall mass volume, horizontal and vertical travelling distances, falling height, block trajectory as well as energetic level and penetration at the impact on ground surface and defence structures (Chau et al. 2002; Zhang et al. 2017; Lambert et al. 2021).

The above quantities are usually assessed by means of computer-based simulations and for this purpose many codes based on the lumped mass (material point) approach, the rigid body approach (Leine et al. 2014), and finally, the discrete element modelling method with either single or multi-particle blocks (Shen et al. 2020) have been implemented. Apart from Leine et al. (2014), the remaining models generally introduce a double description for the block geometry when the motion is computed: during free flying, the block geometry is summarized in the inertial moments, while during the impacts the block is assumed to be a rigid sphere or an ellipsoid (Bozzolo and Pamini 1986; Azzoni et al. 1995) in a point-like contact with the ground surface.

Free flying, sliding and rotation are well understood and adequately modelled, whereas the impact on both surface soil/rock material (Chau et al. 2002; Bourrier et al. 2011) and protection structures (Lambert and Bourrier 2013; Zhang et al. 2017) is still a major research subject.

The most commonly employed strategy to simulate the impact process consists in considering the block as a material point and assessing the bouncing velocity components by means of restitution coefficients (i.e. the ratio between pre- and post-impact velocity components, Giani et al. 2004; Spadari et al. 2012; Pfeiffer and Bowen 1989; Gischig et al. 2015; Azzoni et al. 1995; Chau et al. 2002; Asteriou et al. 2012; Leine et al. 2014). Restitution coefficients are a whole measure implicitly including all the characteristics of an impact process, as block and substrate deformation, sliding at the contact point, changes between the linear and rotational momentum. Consequently, all this information is lost in this approaches. Hence, the study of the impact process is reduced to the evaluation of the appropriate values of restitution coefficients. It has been suggested that these coefficients depend only on the impacting materials (block and substrate) leading to miscalculations, because the block response is governed, as shown by the experimental evidence (e.g. Chau et al. 2002) by many factors. Habib (1977) introduced a scaling factor controlled by a parameter, ${k}_{\mathrm{v}}$, to discriminate between almost elastic impacts for low energetic contents and inelastic for high impact velocities (Asteriou et al. 2012). Based on this strategy, Pfeiffer and Bowen (1989) proposed empirical relationships to correct the restitution coefficients by means of factors dependent on block velocity and mass.

Since restitution coefficients represent a measure of the energy dissipated during impact, with a lower value corresponding to a lower output mechanical energy (i.e. a larger dissipation) they should be less than or equal to one (no loss of mechanical energy).

As was already observed by Spadari et al. (2012), when the rotational degree of freedom is taken into account, the apparent restitution coefficients, evaluated with the reference of the block centre of mass, can be larger than one. This result apparently contradicting with the second thermodynamic principle, may be explained by taking block rotation into account (Leine et al. 2014). To solve this problem, some authors introduced the distinction between the contact and the apparent restitution coefficients according to the position where the velocity components are referred to the computation of the restitution coefficients. Vijayakumar et al. (2012) proposed a mathematical relationship between the apparent and contact restitution coefficient in which the role of block geometry is evident.

Empirical relationships to evaluate the restitution coefficients model only the velocity effect while the block size, shape and initial impact configuration are not taken into consideration because of their empirical nature not accounting for the physics of the impact. Bozzolo and Pamini (1986) introduced the shape effect by considering ellipsoidal blocks at the impact with rotation at the point-like contact between block and slope surface. Yan et al. (2020) proposed a 3D approach in which the block has a complex polyhedron geometry randomly generated and satisfying two sphericity and concavity requirements. The contact force is computed by means of a bilinear function with parameters not depending on the block geometry, orientation and velocity at impact. Torsello et al. (2021) simulated blocks with a polyhedral geometry by using the RAMMS rock builder tool and the ROCKFALL code to simulate the generated blocks, whereas Bourrier and Acary (2022) studied propagation by considering the block geometry during free-fall and rolling phases.

The Distinct Element Method (DEM) and the Non-Smooth Contact Dynamics (NSCD) can easily account for these factors (Bourrier et al. 2008, 2010; Shen et al. 2020). These simulations can provide information about the impact physics but they are still computationally consuming and for this reason, they cannot be used for multiple (determinist and stochastic) rockfall simulations requiring thousands of block simulations. This approach was also used by Chang et al. (2011) to investigate the effect of block shape on its rotation, trajectory and the main variables used in the design of protection structures, while Garcia et al. (2022) used a DEM with sphero-polyhedral block shapes to reproduce the in situ experimental tests.

Another approach makes use of rheological models to describe the impact process by using a combination of simple constitutive models to obtain the restitution velocity components and the restitution coefficients from numerical integration, once initial conditions and model parameters are set (Dattola et al. 2021). Such an approach based on a macro-element equivalent foundation was proposed by di Prisco and Vecchiotti (2006, 2010) to model the interaction between the block and the deformable ground surface. The macro-element constitutive relationship is based on a visco-plastic model and an elasto-damping element introduced to represent the near field and deep substrate mechanical behavior, respectively. The block was assumed to be spherical, with inhibited rotation so that two degrees of freedom, normal and tangential displacements, were considered. Since the rheological approach allows to reproduce all the above-mentioned dependencies by improving the corresponding constitutive equations, this strategy was followed by Dattola et al. (2021) to consider also the rotational component for prismatic blocks with a polygonal base.

In this paper, this last advanced model has been modified with the following aims: (i) introducing an advanced macro-element model in which the block has an ellipsoidal shape with an additional rotational degree of freedom; (ii) investigating the influence of ellipsoidal shape, and especially force-eccentricity, on the block rotational behaviour, (iii) analysing restitution coefficients dependency and proposing a generalization of the restitution coefficient approach by taking the rotational energy and the transition between rotational and translational moments into account; (iv) studying the effect of block geometry on rock fall run-out.

The paper is organized as follows: in the second section, the ellipsoidal shape model, the generalization of the restitution coefficient and the Vijayakumar et al. (2012) expression relating the effective and apparent restitution coefficients are presented. The third section presents numerical results in terms of block penetration (displacement), impact force, rotation and coefficients of restitution. Finally, the discussions and the conclusions sections are presented.

2 Model

The here proposed model extends the one proposed in Dattola et al. (2021) for prismatic blocks, in which eccentricity does not play a role because of symmetry and, consequently, variation of rotational velocity is less relevant for the final block trajectory.

2.1 Model Formulation

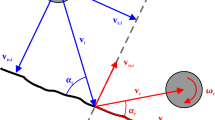
Mathematical expressions and unknowns vectors are formulated in the local reference system, in which normal and tangential directions (perpendicular and parallel to the slope, respectively) are considered (Fig. 1).

Fig. 1

Reference system of normal and tangential axes $n-t$ adopted to analyze the block impact on a slope with inclination, $\omega$. The impact angle ${\theta }^{in}$ and restitution angle ${\theta }^{out}$ are shown together with the impact and bouncing translational and angular velocities. Impact (I) and the bouncing (B) points are also shown

During the impact, block and soil interact with each other exchanging contact forces and contact momentum applied at the centre of gravity of the contact surface which evolves during the impact. This interaction between soil and block is modelled by means of an equivalent foundation, whose size is a function of block penetration and rotation, as well as the block shape. Therefore, the problem of evaluating the block motion during the impact and the force acting on the soil is split up in two sub-systems: (i) the rigid block motion and (ii) an equivalent foundation with its constitutive relationships.

The block motion is described by means of three degrees of freedom, the normal and tangential displacements of its centre of gravity and the block rotation around it assumed to be positive in clockwise direction. The block obeys the linear momentum balance equation written considering both the contact forces and the block self-weight. The linear momentum equation is the same as in Dattola et al. (2021) in which both the mass and inertia moment referred to the axis orthogonal to the motion plane $n-t$ and passing through the center of gravity are updated considering the new block shape.

The constitutive macro-element relationships are based on the same rheological model proposed in Dattola et al. (2021) (see Fig. 2 for the normal impact case) in which the constitutive equations of each element are updated to take into account of the ellipsoidal shape without changing the model parameters apart the block dimensions. The updated equations are given briefly in the Appendices B and C.

Fig. 2

Rheological models for the case of normal impact

The impact between the block and the soil is considered concluded, when at least one of the conditions between loss of adherence and toppling of the equivalent foundation is satisfied. In the former case, the block detaches from the ground surface and it flies, whereas toppling of the equivalent foundation takes place when the block touches the ground and the resultant of the contact forces lies on one side vertex of the equivalent foundation (i.e. the downward vertex of the equivalent foundation), which is also the point of instantaneous rotation, and the block starts rolling.

The linear moment equilibrium equation applied to the block, together with the compatibility and constitutive equations, forms a system of differential equations that admits a unique solution during block impact. The solution of this system provides the evolution of all contact variables, such as block displacement, velocity, acceleration, contact forces and energies.

2.2 Block Geometry

Many authors (e.g., Bozzolo and Pamini 1986; Cancelli and Crosta 1994; Chau et al. 2002) demonstrated that the block geometry affects the impact process and the restitution coefficients, by controlling both bouncing velocity and block angular velocity. In the proposed rheological constitutive equations, the geometry is taken into account synthetically by means of three functions of the block displacement component: the tangential and out-of-plane dimensions of the equivalent foundation ${B}_{t}={B}_{t}({u}_{n}^{bl},{\theta }^{bl})$ and ${B}_{w}= {B}_{w}\left({u}_{n}^{bl},{\theta }^{bl}\right)$, the normal and tangential arms of the contact force components, ${r}_{n}={r}_{n}({u}_{n}^{bl},{\theta }^{bl})$ and ${r}_{t}={r}_{t}({u}_{n}^{bl},{\theta }^{bl})$, respectively (see Fig. 17 in the D.4 Appendix D) where ${u}_{n}^{bl}$ and ${\theta }^{bl}$ are the normal displacement of the block centre of gravity and the block rotation, respectively.

In appendix $\mathrm{C}$, the above functions are derived for ellipsoidal blocks (Fig. 3), starting from those for spherical (di Prisco and Vecchiotti 2006), prismatic and cylindrical blocks (Dattola et al. 2021). For the sake of simplicity, the cross-section orthogonal to the major axis of ellipsoid is assumed to be circular with a radius of ${R}^{bl}$ (Fig. 3). The block shape is described by the aspect ratio ${A}_{r}={H}^{bl}/{R}^{bl}$ (i.e. ${A}_{r}=1$ represents a spherical block).

Fig. 3

Evolution of the impact of an ellipsoidal block at four different steps: a at the impact onset for an impact velocity ${v}^{in}$ and impact angle ${\theta }^{in}$ for an initial block orientation ${\theta }_{0}^{bl}$; b block penetration phase with a downward oriented normal velocity component and inner block rotation ${\theta }^{bl}$; c block rebound phase with an upward normal velocity component and inner block rotation ${\theta }^{bl}$, and finally d the exit phase (i.e. loss of contact) with restitution velocity ${v}^{out}$, restitution angle ${\theta }^{out}$ and restitution block orientation ${\theta }_{\mathrm{f}}^{bl}$

In principle, the model can take into consideration the out-of-plane dimension, related to the block mass value and to the out-of-plane pseudo-foundation dimension, affecting the block motion and the restitution coefficients. Nevertheless, for the sake of simplicity, this factor is not discussed in the following, since as was already clarified in Fig. 3, the authors considered exclusively rotational ellipsoids (i.e. with a circular section).

The block initial orientation (${\theta }_{0}^{bl}$) is the angle between the major semi-axis and the normal direction.

2.3 Energetic Restitution Coefficient

In this section, a mathematical relationships connecting the apparent normal and tangential restitution with the energetic restitution coefficient is derived. The obtained expression highlights also the role played by the impacting angle, the rotational kinetic energy ratio before and after the impact.

Let us consider an impact with the following assumptions: (i) the block impacts on a planar substrate with a fixed inclination; (ii) no dissipation is due to the air drag (i.e. air resistance is considered to be negligible if compared with the dissipated energy during the impact) and (iii) differently from Bozzolo and Pamini (1986), in which the instantaneous rotation centre coincides with the contact point, we does not impose the position of instantaneous rotation centre, (iv) the block is rigid so that no block shape and/or size changes are admitted and, finally, (v) neither fragmentation, nor spalling and chipping are considered, implying the block mass and inertia moment do not change during impact. During impact the block total kinetic energy reduces due to dissipation. If it is assumed that the z-coordinate value of the block centre of gravity does not change just before and after the impact (i.e. the block potential energy does not change), then the variation in the block mechanical energy is due only to the change in kinetic energy. Since block rotation is enabled the kinetic energy is the sum of the translational kinetic energy ${E}_{\mathrm{kt}}\left(t\right)$ and the rotational kinetic energy ${E}_{\mathrm{kr}}\left(t\right)$. Furthermore, during impact the block centre of mass moves in a vertical plane, then it is possible to split up the velocity vector in the normal (${v}_{n}$) and tangential (${v}_{{t}})$ components and, in turn, by using the apparent normal (${e}_{n}=-{v}_{n}^{f}/{v}_{n}^{0})$ and tangential (${e}_{{t}}$) apparent restitution coefficients, the velocity components can be written in terms of ${v}_{n0}$ and ${v}_{t0}$, the normal and tangential components (before the impact), respectively. The translational kinetic energy can be written as:

$${E}_{\mathrm{kt}}\left(t\right)={E}_{\mathrm{kt}0}\left({e}_{n}^{2}{\mathrm{cos}}^{2}{\theta }^{in}+{e}_{t}^{2}{\mathrm{sin}}^{2}{\theta }^{in}\right),$$

(1)

where ${E}_{\mathrm{kt}0}$ is the initial value of the translational kinetic energy, and ${\theta }^{in}$ is the impact angle, (i.e. the angle between the initial velocity vector and the ground normal) (Fig. 3b). The rotational kinetic energy ratios at the beginning and the end of impact are:

$${R}_{r0}=\frac{{ E}_{\mathrm{kr}0}}{{E}_{\mathrm{k}0}},$$

(2)

and

$${R}_{r}=\frac{{ E}_{\mathrm{kr}}\left(t\right)}{{E}_{\mathrm{k}}\left(t\right)},$$

(3)

in which ${E}_{\mathrm{kr}0}$ and ${E}_{k0}$ are the initial rotational kinetic energy and the initial kinetic energy, respectively. The kinetic energy is written as:

$${E}_{k}\left(t\right)=\frac{1-{R}_{r0}}{1-{R}_{r}}\left({e}_{n}^{2}{\mathrm{cos}}^{2}{\theta }^{in}+{e}_{t}^{2}{\mathrm{sin}}^{2}{\theta }^{in}\right){E}_{k0},$$

(4)

and, therefore, the following formulation for the energetic restitution coefficient (Heidenreich 2004) is obtained:

$$\overline{e }=\sqrt{\frac{{E}_{k}}{{E}_{k0}}}= \sqrt{\frac{1-{R}_{t0}}{1-{R}_{t}}\left({e}_{n}^{2}{\mathrm{cos}}^{2}{\theta }^{in}+{e}_{t}^{2}{\mathrm{sin}}^{2}{\theta }^{in}\right)}\le 1.$$

(5)

2.4 Apparent Normal Versus Effective Normal Restitution Coefficients

When both block shape and size are taken into account, the above definition of restitution coefficients is not sufficient. In fact, if the restitution coefficients are referred to the velocity components at the centre of mass, they embed both the ground material dissipation and the block rotation effects. For this reason, Vijayakumar et al. (2012), in their analysis based on the rigid body approach, distinguished the effective normal from the apparent normal restitution coefficient. The first one was defined by using the normal velocity components at contact point, whereas the second one at the gravity centre of the block. In the case of an elliptical block, under the assumption of instantaneous impact, rigid block and rigid impacted material, these authors found that the apparent restitution coefficient ${e}_{n}$ is given by the following expression:

$${e}_{n}=\frac{{I}_{\mathrm{bl}}}{{I}_{\mathrm{bl}}+{m}_{\mathrm{bl}}{r}_{t}^{2}}{e}_{n}^{*}-\frac{{m}_{\mathrm{bl}}{r}_{t}^{2}}{{I}_{\mathrm{bl}}+{m}_{\mathrm{bl}}{r}_{t}^{2}}+\left(1+{e}_{n}^{*}\right)\frac{{r}_{{t}}^{2}{I}_{\mathrm{bl}}}{{I}_{\mathrm{bl}}+{m}_{\mathrm{bl}}{r}_{t}^{2}}\frac{{\dot{\theta }}_{0}}{{v}_{\mathrm{bl}0,n}},$$

(6)

being ${e}_{n}^{*}$ the contact restitution coefficient. In this formula the geometrical effects are included in the inertia moment ${I}_{\mathrm{bl}}$, the initial block configuration in the horizontal arm ${r}_{t}$ and the block angular velocity in the ${\dot{\theta }}_{0}/{v}_{\mathrm{bl}0,n}$ ratio.

Vijayakumar et al. (2012) proved, by using the above expression, that:

• (i) for spherical blocks (as a special ellipsoid of revolution), ${e}_{n}^{*}$ and ${e}_{n}$ are coincident;

• (ii) increasing the shape ratio for low values of contact restitution coefficients, the apparent restitution coefficients can be negative (Fig. 8);

• (iii) when the initial rotational velocity is increased the apparent restitution coefficient increases and, for high values of normal restitution coefficients, the apparent restitution coefficients can be larger than one.

3 Parametric Analyses

In this work, a series of parametric simulations was carried out to investigate the impact process for ellipsoidal blocks and to evaluate the change in rotation and rotational velocity. The model parameters employed in all simulations (Table 1), which are the same of the set 02 by Dattola et al. (2021) concern a very dense sand stratum.

Table 1 Model parameter values adopted in the parametric analyses following Dattola et al. (2021)

The parametric analysis included five groups of numerical simulations in which some parameters are changed within a prefixed range. The list of the varied parameters along with the groups and the range of values is reported in Table 2.

Table 2 List of variables changed in the parametric analyses for different impact modes

For the sake of comparison, block mass ${m}^{bl}$ and its initial velocity modulus ${v}^{in}$ were kept constant and equal to $100$ kg and $14.0$ m/s, respectively, so that the initial kinetic energy at impact was equal for all the simulations. To this purpose, the block sizes were conveniently adjusted in terms of aspect ratio by means of the following relationships:

$${R}^{bl}= \sqrt[3]{\frac{3{m}^{bl}}{4\pi {\rho }^{bl}{A}_{r}}}; {H}^{bl}={A}_{r}\sqrt[3]{\frac{3{m}^{bl}}{4\pi {\rho }^{bl}{A}_{r}}},$$

(7)

being ${\rho }^{bl}$ the density of the block material.

It is worth noting that the variable parameters were only geometrical and kinematical, that is block shape ratio, orientation, and impact angle.

Initially, vertical impacts on a horizontal ground surface, considering only the orientations along the major or minor axes, were considered. This allowed to exclude rotational components generated at the impact by force moments (i.e. eccentricity). Then, inclined impacts were taken into consideration with blocks characterized by a rotational motion. Results were expressed initially in terms of vertical displacements and forces to put in evidence the impact dynamics, and, subsequently normal and tangential restitution coefficients were used and discussed since these coefficients are commonly implemented, owing to a series of simplifying assumptions, in many rockfall simulation codes.

3.1 Block Dynamics

As previously mentioned, block geometry and orientation at impact play an important role, in affecting both block penetration and generated force, the main variables in the design of rockfall protection structures. In the parametric analysis, spherical blocks were also considered for comparison since this shape is commonly employed in rockfall analyses.

In Fig. 4a, b, the evolution with time of vertical displacement and vertical force are reported, considering blocks with different aspect ratios impacting along the major axis. The vertical displacement trends are characterized by an increment up to a peak. Then, blocks with a low value of the aspect ratio stop while blocks with higher aspect ratio experience a vertical displacement reduction till block detachment from the soil. Both peak vertical displacement and time increase with ${A}_{r}$.

Fig. 4

a Vertical displacement versus time and b vertical force as a function of time for blocks with different aspect ratio, ${A}_{r}$ (${A}_{r}=1$ for a sphere), impacting vertically and aligned to major axis

The maximum force reduces with increasing ${A}_{r}$, while the peak time increases with ${A}_{r}$.

A comparison between blocks impacting vertically with major and minor axes with different ${A}_{r}$ values was performed and the results were plotted in terms of maximum vertical displacement in Fig. 5a and maximum vertical force in Fig. 5b.

Fig. 5

a Maximum vertical displacement and b maximum vertical impact force for different values of the aspect ratio, ${A}_{r}$, considering blocks impacting parallel with the major and minor axis (filled and empty squares) with no rotational component

For all the aspect ratios, the blocks impacting along the major axis exhibit larger values of the maximum vertical displacement, that increases with ${A}_{r}$, and the same trend is observed for impacts along the minor axis. The maximum vertical displacement of the spherical block is the minimum of the two trends. The maximum vertical forces are affected by the block ${A}_{r}$ for both the orientations (Fig. 5b) and in particular, they decrease with ${A}_{r}$ for blocks impacting with both the minor axis and the major axis.

For inclined impacts, the problem is not symmetric anymore and block rotation takes place coupling the block displacements, since normal and tangential forces generate momentum. Under this condition, the impact process depends on block shape, orientation at impact (${\theta }_{0}$) and impact angle (${\theta }^{in}$). The impact angle (${\theta }^{in}=20^\circ$) and the initial block orientation (${\theta }_{0}=0^\circ$-impacting along the major axis) were fixed and results are reported in Fig. 6, where block rotation and rotational energy ratio (${R}_{r}$), defined as the ratio between rotational (${E}_{\mathrm{kr}}$) and total kinetic energy (${E}_{k}$), were used. The trends of vertical displacement and force, as a function of ${A}_{r}$, coincide with those relative to vertical impacts (Fig. 6a, b).

Fig. 6

Results for an ellipsoidal block for impacts with ${\theta }^{in}=20^\circ$ and ${\theta }_{0}=0^\circ$. The blocks differ for A_r: a time evolution of vertical displacement; b vertical force vs time; c increment of inner block rotation, ${\theta }^{bl}-{\theta }_{0}^{bl}$, as a function of time; d rotational kinetic energy ratio with time

During impact, the rotation increases monotonically (Fig. 6c). The rotational energy ratio increases monotonically until a maximum. Subsequently, blocks with lower shape ratios experience a slight reduction.

In Fig. 7, the results obtained by considering different impact angles, ${\theta }^{in}$, and ${A}_{r}$ are illustrated. The maximum vertical displacement reduces with increasing the impact angle and increases with ${A}_{r}$. On the contrary, the maximum vertical force reduces with increasing ${A}_{r}$ and for increasing impact angles. For increasing ${A}_{r}$ values, the increment of block rotation reduces apart from the spherical block, whose value is intermediate. Furthermore, the trend of block rotation with ${A}_{r}$ is characterized by a peak for all ${A}_{r}$ values. The evolution of the maximum rotational energy ratio with impact angle is characterized by a peak and its value increases with ${A}_{r}$, although this increment is less evident for higher values of ${A}_{r}$.

Fig. 7

Influence of impact angle for different A_r and ${\theta }^{in}$ values for blocks impacting along the major axis. a Maximum vertical displacement, b maximum normal force; c inner block rotation (${\theta }^{bl}$), d maximum value of the rotational energy ratio

3.2 Apparent Restitution Coefficients

The proposed model describes in detail the impact process, but in practical problems, global variables such as apparent normal and tangential restitution coefficients, maximum penetration depth and block rotation are usually employed or required for defensive work design. In particular, restitution coefficients make the simulations for extended stochastic modelling more efficient.

It is well known (Asteriou et al. 2012; Asteriou and Tsiambaos 2018; Asteriou 2019) impacts and relative coefficients of restitution are influenced, among the others, by block geometry, size and orientation, impact angle and velocity. In this section, the effects of block geometry and orientation, as well as ${\theta }^{in}$ on the global variables were investigated.

In Fig. 8, the effects of block orientation and ${A}_{r}$ on global variables are shown. Normal restitution coefficient for blocks impacting with the major axis (Fig. 8a) increases with ${A}_{r}$, whereas an opposite trend is observed for blocks impacting along the minor axis. Furthermore, the normal restitution coefficients for blocks impacting with the major axis are larger than the normal restitution coefficient for blocks impacting along the minor axis while the spherical block takes an intermediate value.

Fig. 8

Vertical impacts considering different ${\theta }_{0}$ values: a normal restitution coefficient for vertical impacts and blocks oriented along either major and minor axes; b normal restitution coefficient for blocks with different ${A}_{r}$ values impacting vertically and with different ${\theta }_{0}$ values; c maximum penetration depth as a function of the initial block rotation and d variation of the block rotation as a function of the initial block rotation and ${A}_{r}$ considering vertical impacts; e maximum values of the normal force, vs initial block orientation; f maximum contact moment as a function of initial block orientation

When ${\theta }_{0}^{bl}$ (Fig. 8b) is considered, a symmetric trend is observed with respect to the 90° and a “swallow wings” trend is observed and the difference between maximum and minimum values of normal restitution coefficient, obtained by changing the block orientation, increases with ${A}_{r}$. Analogous consideration holds true for the maximum penetration depth (Fig. 8c).

When the line between contact point and the center of gravity is not aligned to either major or minor axes, even a vertical impact produces, as shown in Fig. 8d, a variation in block rotation. The variation in the rotation is antisymmetric because if the initial block orientation causes the center of mass to move to the right with respect to the normal then the block rotates clockwise. In the opposite condition, the block undergoes an anti-clockwise rotation. The variation of the block orientation, for the same ${\theta }_{0}^{bl}$, increases with ${A}_{r}$ until 2.5 then it reduces. This is due to two antagonistic factors: the increase in ${A}_{r}$ causes not only an increase in ${r}_{t}$ (tangential arm) but also an increase in block penetration. The former effect facilitates the block rotation, the latter one prevents it.

In Fig. 8e, the evolution of the maximum normal force with the initial block orientation and for different ${A}_{r}$ values is reported. The trend is symmetric with respect to 90° (i.e. impact along the minor axis) and for this limit value the influence of the A_r is reversed (i.e. larger A_r corresponds to lower maximum normal force). The maximum absolute value of the contact moment versus the initial block orientation, for different aspect ratios, is shown in Fig. 8f. The trend is symmetric with respect to the 90° initial block orientation for lower values of ${A}_{r}$ a clear trend is visible but for higher values of ${A}_{r}$ no specific trend is observed.

When inclined impacts of blocks aligned along the major or the minor axis are considered, the results, in terms of normal and tangential restitution coefficients, shown in Fig. 9 are obtained. When ${A}_{r}$ increases normal restitution coefficients decrease whereas an opposite trend is observed for the tangential one (Fig. 9a, b). For ${A}_{r}>1,$ the trend of normal restitution coefficient is not monotonic and for $0<{\theta }^{in}\le 50^\circ$ becomes negative. ${e}_{n}$ is these cases negative since ${e}_{n}$ is calculated as a function of the center of mass velocity, whereas the detachment between block and soil is a function of the contact velocity. For sufficiently large of ${\theta }^{in}$ values the normal restitution coefficient rapidly increases since the plastic slider activates at the very beginning of the impact. In contrast, when the blocks impact with the minor axis, both coefficients decreases with increasing ${A}_{r}$ (Fig. 9c, d).

Fig. 9

Model results for inclined impacts for different ${A}_{r}$: a, b normal and tangential restitution coefficients versus impact angle considering blocks oriented along the major axis; c, d normal and tangential restitution coefficients vs impact angle considering blocks oriented along the minor axis

Numerical simulations were also performed by assuming ${c}_{\mathrm{v}}=0.5$, ${\gamma }_{\mathrm{v}}=1.70$ and ${\gamma }_{\mathrm{v}}=0.85$. The results are shown in the supplementary materials. The observed trends are qualitatively similar to those discussed in this section. These parametric numerical simulations were performed to investigate the effects of viscous parameters on kinematic and dynamic variables.

3.3 Multi-Impacts and Block-Run-Out

As already stated, rockfall simulations describe blocks trajectories during impacts, free fly, rolling and sliding motions, ending up when the block kinetic energy is very small. The assessment of the block trajectory allows to compute important variables for the design of protection structures, such as the maximum trajectory height, the run-out distance and the maximum block velocity.

These variables are also important rockfall hazard mapping, and they are controlled by slope inclination, block geometry and orientation, angular velocity, normal and tangential restitution coefficients. To study the influence of block geometry and initial angular velocity on the trajectory, the HyStone numerical simulation code (Agliardi and Crosta 2003) was extended by implementing the proposed impact model. In order to focus the attention on block geometry and its angular velocity, a bi-planar topography was used (Fig. 10), with a $230$ m slope height (${H}_{{s}}$), inclined at $\omega = 30^\circ$ with respect to the horizontal plane (horizontal projected distance ${L}_{s1}=400$ m) and a final $600$ m long horizontal plateau (${L}_{s2}$). The initial block translational velocity was $20$ m/s inclined of $10^\circ$ with respect to the horizontal axis, while, in agreement with Caviezel et al. (2021) and Buzzi et al. (2012), the initial angular velocity ranged from $0^\circ$/s to ${20{,}000}^\circ$/s. To study the block geometry effects, ${A}_{r}$ was varied between $1.0$ (sphere) and $4.0$ (markedly elongated ellipsoid), by keeping constant the block mass m = $100$ kg, whereas both initial block translational and rotational kinetic energies were the same for all the numerical simulations.

Fig. 10

Biplanar slope profile and describing parameters used in the HyStone numerical simulations with ellipsoidal blocks of different aspect ratio A_r

The impact parameters were maintained as those of the previous simulation (reported in Table 1).

The first investigated parameter was ${A}_{r}$, by assuming blocks to be initially oriented along the major axis and initial angular velocity to be nil. The results, together with the slope profile, are reported in Fig. 11. Since initial conditions (i.e., velocity, angular velocity and orientation) coincide and motion equations during the first free-flight are independent of block shape, all blocks (Fig. 11a) trajectories superimpose for $x<250$ m. Except for the spherical block, after the first impact, blocks start rolling. The spherical block starts rolling after three small bouncing (Fig. 11b, c). All the blocks reach the horizontal plane where they stop at different distances (Fig. 11c).

Fig. 11

Simulation results obtained by the HyStone code considering ellipsoidal blocks with ${A}_{r}$ values ranging between $1.0$ (spherical block) and $4.0$ (strongly elongated ellipsoidal block) with parameters ${c}_{\mathrm{v}}=1.0$ and ${\gamma }_{\mathrm{v}}=8.70$: a block trajectory; b block vertical elevation with respect to the ground; c block translational velocity; d block rotational velocity. Thick black line represents the bilinear slope profile (Fig. 10)

As is well known, the maximum vertical elevation of falling blocks is essential to design position and dimensions of protection structures (e.g. fences, nets and embankments). For this reason, in Fig. 11b, block elevation histories are illustrated. Again, only spherical block elevation history differ from the others.

The translational velocity moduli, referred to the centre of mass, histories are reported in Fig. 11c: four phases are evident:

• (i) the free-fall phase, from the source area to the impact, during which the trend is parabolic, typical of ballistic-type motion,

• (ii) a practically instantaneous energy reduction, due to the energy dissipation associated with the impact,

• (iii) a subsequent linear increase, occurring during rolling, accelerated for the steep inclination,

• (iv) a parabolic reduction due to the achievement of the horizontal plane, where the energy dissipation for rolling is not balanced by a change in altitude, until the arrest of the block.

Apart from the spherical block, the results relative to the different blocks markedly differ when the horizontal plane is reached (along the inclined plane the translational velocity differs but the scale employed in the plot does not allow to capture such a difference).

The evolution of the rotational velocity component is illustrated in Fig. 11d. The rotational velocity components are constant when blocks fly, whereas at impact, they vary abruptly, since contact forces generate moments. Finally, during the rolling phase, the rotational velocity components increase linearly when the blocks move along the inclined slope and decrease with parabolic trends until the blocks stop, when they move along the horizontal plane.

Subsequently, the role of initial angular velocity has been investigated for all the previous ${A}_{r}$ values (in this case all blocks are oriented along the major axis). The initial angular velocity was varied in the range 0°/s–20,000°/s, a range sufficiently wide in the light of the real case data available in the literature (e.g. Buzzi et al. 2012; Caviezel et al. 2021).

The values of the maximum vertical elevation above the slope profile for each portion of ballistic trajectory and for all the block trajectories are expressed in terms of number of blocks in Fig. 12.

Fig. 12

Number of blocks distribution of the above ground vertical elevation for each ballistic jump considering different ${A}_{r}$, for ${\gamma }_{\mathrm{v}}=0.85$ and 1.70, and different initial rotational velocity ${v}_{r}$ (0.0°/s, 2500°/s, 5000°/s, 7500°/s, 10,000°/s, 12,500°/s, 15,000°/s, 17,500°/s, 20,000°/s). The best fitting exponential equation is reported

As is evident, the trend of these histograms and data scatter markedly depend on block shape, even if, in general, the number of blocks reduces progressively with vertical elevation.

In the supplementary material, the results obtained by performing the same simulations but by using ${c}_{\mathrm{v}}=0.5$ and ${\gamma }_{\mathrm{v}}=1.70$ and ${\gamma }_{\mathrm{v}}=0.85$ are reported.

4 Discussion

4.1 Impact Force and Penetration

Block shape role in affecting impacts and bouncing (Bozzolo and Pamini 1986; Azzoni et al. 1995; Vijayakumar et al. 2012; Leine et al. 2014; Glover 2015) is largely recognized in the scientific literature. As stated by Yan et al. (2018), the effects of both block shape and orientation are usually neglected, due to the difficulties to study irregular shapes, lithology and rock mass subdivision (Fityus et al. 2013). Block shape affects impact force and penetration depth, normal and tangential restitution coefficients and, thus, block velocity after the impact. These, in turns, are fundamental to simulate block trajectory and, consequently, to locate and design correctly protection structures and to prepare hazard maps, when using models based on restitution coefficients. As well, the contact force and its maximum value at impact are fundamental in the design of protection structures in case of direct impact on the structure or on a cushion layer interposed between block and structure. The effects of the geometry on the contact force was investigated by Yan et al. (2018), by means of the finite element method (LS-DYNA code), in which the contact option is enabled to study the interaction between a concrete slab and the ellipsoidal block. Block shape was described through the sphericity index ${S}_{{p}}$, defined as:

$${S}_{{p}}={A}_{r}^{-\frac{2}{3}},$$

(8)

making possible a comparison with our results. Yan et al. (2018) computed, the evolution of the impact force for three block orientations and different impacting velocities, but for the same block mass. They found that a reduction in ${S}_{{p}}$ (i.e. passing from spherical to ellipsoidal blocks) or, equivalently, an increase in ${A}_{r}$, induces a reduction in the maximum impact force. We confirmed this result for all impact inclinations and ${A}_{r}$ values, although the impacted material is different (Figs. 6, 7b). Shen et al. (2019, 2020) performed DEM simulations with ellipsoidal and irregularly shaped blocks constituted by a clump of particles, impacting on horizontal layers made up of the same particles used for the block. They confirmed the decrease in the maximum impact force for increasing ${A}_{r}$ values and for different falling heights (i.e. velocity), in agreement with our results (Fig. 5b).

As far as block penetration is concerned, Shen et al. (2019) demonstrated its increase with ${A}_{r}$. This was confirmed by our simulations (Fig. 6a) for vertical impacts with vertex (Dattola et al. 2021), for inclined (Fig. 7a) and for vertical impacts (Fig. 8c) and different orientations of ellipsoidal blocks. Hence, our results allow a more general description of impact and could definitely support the design of countermeasures.

4.2 Coefficients of Restitution

As mentioned above, modelling based on coefficients of restitution is still adopted in many analyses and modelling codes. Experimental and in situ results showed that normal restitution coefficients can be larger than one, especially when the angle between block velocity vector and ground surface normal (i.e. the complementary of the impact angle) is very low. This effect was attributed to block rotation, increasing the normal restitution velocity component in comparison with the corresponding one at impact. Since the amount of rotation is controlled by the arms of the normal contact force components, elongated blocks markedly show this effect. Generally, the proposed solutions started from the hypothesis of a point-like contact around which the block rotates (Bozzolo and Pamini 1986; Azzoni and De Freitas 1995; Azzoni et al. 1995; Glover 2015). Usually, restitution coefficients can be computed by employing different approaches being the rigid body impact mechanics the most popular. According to it, both body and contact plane are rigid, and the deformations, developing in regions near the contact point, are taken into account by a dummy element, virtually interposed between block and contact plane (Ashayer 2007). The equations have been expressed in impulse terms with additional assumptions needed to solve the problem (see Bozzolo and Pamini 1986; Descoeudres and Zimmermann 1987; Azzoni et al. 1995). Unlike our approach, no constitutive equations describing the impacted material were proposed. This implies irreversible deformations were not considered and, therefore, block sinking into the contact plane (material) is not calculated. In addition, the absence of constitutive equations prevents the calculation of the contact forces. Hence, in our approach, the penetration of the block into the ground surface introduces a major improvement in the model capabilities strongly influencing the results.

To highlight the relationship among block rotation, contact geometry and apparent restitution coefficients, the contact restitution coefficients are compared with apparent restitution coefficient values calculated by using our impact model (Eq. 6) and the Vijayakumar et al. (2012) model (Fig. 13). The comparison is accomplished for different initial block orientations and initial rotational velocities, in the case of an ellipsoidal block with ${A}_{r}=2.0$. In case of no initial rotation, all the graphs (Fig. 13a) are symmetric with respect to the initial block rotation at $90^\circ$. This symmetry is lost when blocks have an initial rotational velocity and the degree of asymmetry increases with its intensity (Fig. 13b–d). The apparent restitution coefficients, both for the proposed and the Vijayakumar et al. (2012) model, become negative (i.e. the normal velocity after the impact referred to the block centre of mass is directed downward, nevertheless the normal velocity at the contact point is directly upward) for a large range of initial block orientations and initial angular velocity. On the contrary, both contact and energetic restitution coefficients are always positive. In fact, the contact coefficient is computed considering the normal velocity at contact point which is always positive since the blocks bounce. This is not true for the apparent restitution coefficient even if the blocks bounce. In fact, the block rotational velocity at the exit is so high that causes a reversal of the normal velocity at the centre of mass where the apparent coefficients are computed. Therefore the contact velocity after the impact is directed upward while the normal velocity at the centre of mass, due to the rotation, is directed downward. In case of no initial rotational velocity, all the coefficients are the same for blocks impacting with the major or minor axes, because in these cases, the blocks do not generate rotational velocities. In case of spherical blocks, apparent and contact restitution coefficients coincide since the block rotation does not affect the normal velocity at the centre of mass.

Fig. 13

Apparent normal, contact point (i.e. contact restitution coefficient) and global restitution (Eq. 18) coefficients computed by using the here proposed model, the Vijayakumar et al. (2012) model (Eq. 20) for different values of the initial block rotational velocity: a no rotational velocity; b 500°/s; c 1500°/s and d 2000°/s

Rigid body contact mechanics was used by Ashayer (2007) in case of ellipsoidal blocks to obtain normal restitution velocities, normal restitution coefficient and restitution angular velocity. Under the same initial conditions, the results agree both in terms of normal restitution coefficient/normal velocity and rotation with those reported in Fig. 8.

Ashayer (2007) performed also DEM numerical simulations of ellipsoidal blocks constituted by a clump of circular particles by means of a modified particle–particle and particle–wall contact law. By increasing the number of clump particles the results converge to those obtained by performing rigid body simulations and, thereby, to our results. This furtherly supports the capabilities of the here proposed model.

Bozzolo and Pamini (1986) proposed a rigid body model for ellipsoidal blocks calculating translational and rotational velocity components after impact by imposing rigid rotation at the contact point and conservation of angular momentum. They validated the model by discussing the experimental results of three real rock falls. Although geometry and parameters are different from those employed by the authors, their number of blocks distribution of the maximum ballistic height decreases similarly to our results (Fig. 12) and the same holds for simulations by Azzoni et al. (1995).

Finally, with the reference the numerical results obtained by employed HyStone code and describe in Figs. 11 and 12, the authors assessed ${e}_{n}$ and ${e}_{t}$ for all impacts. The number of blocks distributions of all these values are plotted Fig. 14. The higher value of number of blocks have normal restitution coefficient in the range from 0.75 to 1.0 (mean values of $\mu =0.67$) and a tangential coefficient from 0.7 to 1.1 ($\mu =0.92)$. As already observed by Bourrier et al. (2012) for in situ tests, owing to block rotation and block elongated geometry, both coefficients the number of blocks follows a normal distribution and both coefficients can reach values well above 1.

Fig. 14

Number of blocks distributions of a the apparent normal restitution coefficient and b the apparent tangential restitution coefficient obtained by the HyStone simulations for a bi-planar slope (see Fig. 11) considering all the block shapes and all the initial angular velocity values

5 Conclusions

In situ observations and laboratory experimental results have demonstrated that the block shapes and their orientations at impact central restitution coefficients and consequently the block trajectory simulations. This information is not usually taken into account in rockfall simulation codes in which simplified block geometries are usually employed and the observed variabilities of the real cases are simulated by a stochastic approach. This work partially overcomes the previous drawbacks because the effects of block geometry and initial block orientation are simulated by means of an advanced and flexible impact model that extended our previous model to blocks with ellipsoidal shape with different aspect ratios and consequently embedding block eccentricity.

The model successfully reproduced the trends of main design variables and restitution coefficients observed in the laboratory and DEM numerical models, stressing the role of the block shape ratio, initial orientation and impact angle.

Inclined impacts reveals analogous trends and consequently the previous considerations can be shared.

For block impacting vertically with the longest axis or inclined the maximum penetration increases and the maximum vertical forces decrease with the increase of the block aspect ratio. An opposite trend was observed for blocks with horizontal long axis. Hence, the design of protection structures by using spherical design blocks is not conservative.

The importance of initial block orientation in vertical impacts on restitution coefficients and block rotation was shown. The main result is the strong variation of the restitution coefficients for slight variation of the initial block orientation. Furthermore, this work confirm that the block shape and rotation can result in negative values of the apparent restitution coefficients as observed in situ tests. We demonstrated that block rotation is not sufficient to generate negative values of restitution coefficients, but they are the result of the combinations of block rotation and elongated geometries: in these combinations upwardly vertical velocity at the contact point and downwardly vertically velocity at the centre of mass was observed. A comparison between the contact restitution coefficients, two apparent restitution coefficients and energetic restitution coefficient demonstrated that the negative values of the apparent restitution coefficients increase with initial block rotation, affectingly consequently the rockfall simulations.

The impact model was implemented into the HyStone rockfall simulation code and a parametric analysis on a bi-planar slope at varying the block shape ratio, block angular velocity and initial block orientation were carried out. The results in terms of maximum height and the apparent restitution coefficients were in accordance with the in situ observation and numerical simulation results. The HyStone numerical simulations allowed us to conclude that the variability observed both in situ and experimentally can be predicted in a deterministic way considering directly the block rotation and the block shape and referring the variability only to the initial condition. This implies that the effects due to the block geometry that are usually modelled in rockfall simulations by modifying the model parameters can be directly obtained by considering the variability in the initial block conditions.

Appendices

Appendix A List of Symbols

1.1 Scalar

${\alpha }_{\mathrm{vt}}$: tangential coefficient of the hardening rule

${\alpha }_{\mathrm{vR}}$: rotational coefficient of the hardening rule

$\gamma$: soil unit weight

${\gamma }_{\mathrm{v}}$: viscou-plastic coefficient

${\Delta }_{1}$: visco-plastic coefficient

${\Delta }_{2}$: viscous plastic coefficient

${\dot{\lambda }}^{ps}$: plastic slider multiplier

$\nu$: Poisson’s coefficient

${\varphi }^{{{\prime}}}$: soil friction angle

${\varphi }_{\mathrm{b}}^{{{\prime}}}$: block soil friction angle

${\eta }_{\mathrm{N}}$: normal visco-damping coefficient

${\eta }_{\mathrm{T}}$: tangential visco-damping coefficient

${\eta }_{\mathrm{R}}$: rotational visco-damping coefficient

${\theta }^{in}$: impact angle

${\theta }^{out}$: bouncing angle

${\theta }_{0}^{bl}$: initial block orientation

${\dot{\theta }}_{0}$: angular velocity at impact

${\dot{\theta }}_{\mathrm{f}}$: angular velocity at bouncing

$\psi$: coefficient for the computation of the rotational generalized force

${\rho }^{bl}$: block density

${\rho }_{\mathrm{c}}$: visco-plastic hardening variable

${\dot{\rho }}_{\mathrm{c}}$: visco-plastic hardening variable rate

$\omega$: slope angle

${A}_{r}$: aspect ratio

${b}_{\rho }$: visco-plastic hardening rule

${B}_{t}$: equivalent foundation size along the tangential direction

${B}_{w}$: equivalent foundation size along the out-of-plane direction

${c}_{\mathrm{v}}$: visco-plastic coefficient

${D}_{r0}$: initial soil density

${E}_{\mathrm{kt}}$: block kinetic energy

${E}_{\mathrm{kt}0}$: block kinetic energy at impact

${e}_{n}$: apparent normal restitution coefficient

${e}_{n}^{*}$: contact normal restitution coefficient

${e}_{t}$: apparent tangential restitution coefficient

$\overline{e }$: energetic restitution coefficient

${f}^{ps}$: plastic function of the plastic slider

${J}_{{s}}$: shape correction factor

${k}_{\mathrm{E}}$: coefficient of the elastic law

${H}^{bl}$: block major axis

${m}^{bl}$: block mass${n}_{\mathrm{E}}$: exponent of the elastic law

${R}^{bl}$: block minus axis or radius

${r}_{n}$: normal arm

${R}_{r0}:$rotational kinetic ratio

${R}_{r0}$: rotational kinetic ratio at impact

${R}_{{s}}$: shape ratio

${r}_{t}$: tangential arm

${S}_{\mathrm{ef}}$: shape coefficient of the elastic law

${S}_{{p}}$: sphericity index

${v}_{0}^{bl}$: impact velocity modulus

${v}_{\mathrm{f}}^{bl}$: bouncing velocity modulus

${u}_{D}^{bl}$: normal block sinking

1.2 Vector

${{\varvec{b}}}_{\mathrm{L}}$: elasto-damping function

${{\varvec{b}}}_{\mathrm{ps}}$: plastic slider flow rule function

${{\varvec{b}}}_{\mathrm{vp}}$: visco-plastic flow rule function

${\varvec{L}}$: contact force

${\varvec{Q}}$: generalized force

${{\varvec{u}}}^{bl}$: block displacement

${{\varvec{u}}}^{ed}$: elasto-damping displacement

${\dot{{\varvec{u}}}}^{ed}$: elasto-damping velocity

${{\varvec{u}}}_{D}^{bl}$: generalize block displacement

${{\varvec{u}}}^{ps}$: plastic slider displacement

${{\varvec{u}}}^{vp}$: visco-plastic displacement

${\dot{{\varvec{u}}}}^{vp}$: visco-plastic velocity

${{\varvec{v}}}_{0}^{bl}$: impact velocity

${{\varvec{v}}}_{\mathrm{f}}^{bl}$: bouncing velocity

1.3 Matrix

${{\varvec{C}}}_{\mathrm{bl}}$: Compatibility matrix

Appendix B Model Equations and Compatibility Equation for an Ellipsoidal Block

The rheological model system equation (see Dattola et al. 2021) can be synthetically by the following system of six differential equations

$${{\varvec{u}}}^{{\varvec{b}}{\varvec{l}}}={{\varvec{C}}}_{\mathrm{bl}}^{-1}({{\varvec{u}}}^{{\varvec{v}}{\varvec{p}}}+{{\varvec{u}}}^{{\varvec{p}}{\varvec{s}}}+{{\varvec{u}}}^{{\varvec{e}}{\varvec{d}}})\quad {\text{ Compatibility condition}}$$

$${\varvec{L}}={{\varvec{b}}}_{\mathrm{L}}\left({B}_{t},{B}_{w},{{\varvec{u}}}^{ed},{\dot{{\varvec{u}}}}^{ed}\right) \quad {\text{ Elasto-damping element}}$$

$${\dot{{\varvec{u}}}}^{vp}={{\varvec{b}}}_{\mathrm{vp}}\left({\varvec{Q}}\left({\varvec{L}},{B}_{t}\right),{\rho }_{c}\right) \quad {\text{Visco-plastic flow rule}}$$

$${\dot{\rho }}_{\mathrm{c}}={b}_{\rho }\left({\varvec{Q}}\left({\varvec{L}},{B}_{t}\right),{\rho }_{c}\right) \quad {\text{Visco-plastic hardening rule}}$$

$${\dot{{\varvec{u}}}}^{ps}={{\varvec{b}}}_{ps}\left({\dot{\lambda }}^{ps},{\varvec{L}}\right) \quad {\text{ Plastic slider flow rule}}$$

$${f}^{ps}\left({\varvec{L}}\right){\dot{\lambda }}^{ps}=0 \quad {\text{ Consistency condition}}.$$

(9)

The other equations represent the constitutive equations of each element of the rheological model as summarized in the following. ${{\varvec{b}}}_{\mathrm{L}}$ is a function depending on the visco-elastic displacement (${{\varvec{u}}}^{ed})$ and velocity $\left({\dot{{\varvec{u}}}}^{ed}\right)$, ${{\varvec{u}}}^{vp}$ stands for visco-plastic displacement, ${\varvec{Q}}$ is the generalized force vector for the macro-element, ${B}_{t}$ and ${B}_{w}$ are the equivalent foundation sizes along the tangential and out-of-plane directions, respectively (i.e. the size of the instantaneous block footprint during the impact), ${\rho }_{\mathrm{c}}$ is an hardening variable and ${{\varvec{b}}}_{\mathrm{vp}}$ is a function representing the visco-plastic flow rule; ${b}_{\rho }$ is a function representing the hardening rule describing the evolution of the hardening variable, ${{\varvec{u}}}^{ps}$ is the plastic slider displacement, ${\lambda }^{ps}$ is the plastic multiplier for the plastic slider, ${{\varvec{b}}}_{\mathrm{ps}}$ represents the plastic slider flow rule. Finally, ${f}^{ps}$ is the plastic function for the plastic slider. The mathematical expressions of the above functions and vectors are the same as in Dattola et al. (2021) apart from the expressions regarding the block geometry which are reported in the appendixes.

Differently from the spherical blocks, in the ellipsoidal blocks, the sinking of the block normal into the ground does not coincide with the normal displacement of its centre of gravity. Indeed, in Fig. 15 it is shown that the normal displacement of centre of gravity ${u}_{n}^{bl}$ in case of spherical block coincides with normal block sinking ${u}_{D}^{bl}$, whereas the ${u}_{D}^{bl}$ in case of an ellipsoidal block is a function of ${u}_{n}^{bl}$ and the block rotation ${\theta }^{bl}$.

Therefore the compatibility equation proposed in Dattola et al. (2021) must be updated to take into account the difference between ${u}_{n}^{bl}$ and ${u}_{D}^{bl}$.

Fig. 15

Comparison between the block normal sinking, ${u}_{D}^{bl}$, into the ground and the normal displacement for center of mass ${u}_{n}^{bl}$ for the: a spherical block; b ellipsoidal block

The normal displacement of the elasto-damping component becomes

$$\left[\begin{array}{c}{u}_{n}^{ed}\\ {u}_{t}^{ed}\\ {\theta }^{ed}\end{array}\right]=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& -{r}_{n}\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{u}_{D}^{bl}\\ {u}_{t}^{bl}\\ {\theta }^{bl}\end{array}\right]-\left[\begin{array}{c}{u}_{n}^{vp}\\ {u}_{t}^{vp}\\ {\theta }^{vp}\end{array}\right]-\left[\begin{array}{c}{u}_{n}^{ps}\\ {u}_{t}^{ps}\\ {\theta }^{ps}\end{array}\right],$$

(10)

or in compact form

$${{\varvec{u}}}^{ed}={{\varvec{C}}}^{bl}{{\varvec{u}}}_{D}^{bl}-{{\varvec{u}}}^{vp}-{{\varvec{u}}}^{ps},$$

(11)

being ${{\varvec{u}}}^{vp}$, ${{\varvec{u}}}^{ps}$ and ${{\varvec{u}}}^{ed}$ the visco-plastic, plastic slider and elasto-damping displacement vectors, respectively defined as in Dattola et al. (2021), ${{\varvec{C}}}^{bl}$ the compatibility matrix, and finally vector ${{\varvec{u}}}_{D}^{bl}$ is:

$${{\varvec{u}}}_{D}^{bl}=\left[\begin{array}{c}{u}_{D}^{bl}\\ {u}_{t}^{bl}\\ {\theta }^{bl}\end{array}\right].$$

(12)

The computation of ${u}_{\mathrm{D}}^{bl}$ is given in the Appendix C after introducing ellipsoidal shape equations.

Appendix C Correction Factor for the Elastic Stiffness Coefficient

The effect of the block shape on the normal elastic stiffness coefficient (${k}_{n}$) is enclosed in the correction factor which, in turn, depends on the shape ratio ${R}_{{s}}$ Dattola et al. (2021). In this appendix only the updating of the shape ratio and the correction factors for the blocks with ellipsoidal shape are reported with respect to Dattola et al. (2021). The shape ratio is updated as:

$${R}_{{s}}=\frac{\mathrm{max}\left({B}_{t}, {B}_{w}\right)}{\mathrm{min}\left({B}_{t},{B}_{w}\right)}\ge 1,$$

(13)

where ${B}_{t}$ and ${B}_{w}$ are the sizes of the equivalent foundation footprint along the tangential and out-of-plane axes. To obtain an expression for the correction factor the values reported in Gazetas (1983) were interpolated resulting in the equation:

$${J}_{{s}}\left({R}_{{s}}\right)=0.957\cdot \mathrm{exp}\left(0.0394 {R}_{{s}}\right).$$

(14)

Appendix D Ellipsoidal Shape Equations

Differently from the spherical and prismatic blocks (see Dattola et al. 2021), the ellipsoidal blocks imply a more sophisticated computation of the equivalent foundation footprint defined as the intersection of the impacting block with the impact plane considering both the extremes points. This complexity is due to the out-plane size of the equivalent foundation that in general evolves differently from the in plane size. Therefore the problem cannot be solved in two dimensions and a 3D local reference system was introduced. This system has a normal ($n$) and tangential axis ($t$) as in Dattola et al. (2021) and a third axis ($w$) perpendicular to the others.

This appendix presents mathematical expressions for the size of the equivalent foundation along the tangential (${B}_{t}$) and out-plane (${B}_{w})$ axes, the normal, ${r}_{n}$, and tangential ${r}_{{t}}$ arms of the contact forces components with respect to the block centre of mass and the block sinking into the soil (${u}_{D}$).

Initially both the parametric and the Cartesian equations of the ellipsoid surface were written. Subsequently the intersection of the ellipsoidal shape with the impacting plane was taken into consideration. Finally the computation of the block sinking in the normal direction (${u}_{D}^{bl}$) was carried out.

4.1 Parametric and Cartesian Equations of the Ellipsoidal Block

The parametric equation of the ellipsoidal block is given by the following equations system:

$$\left\{\begin{array}{l}n={u}_{n}^{bl}-{r}_{y0}+\left({H}^{bl} \mathrm{sin}{\varphi }_{p}\mathrm{cos}{\theta }_{p}\right) {\mathrm{cos}}{\theta }^{bl}+\left({R}^{bl} \mathrm{sin}{\varphi }_{p}\mathrm{sin}{\theta }_{p}\right)\mathrm{sin}{\theta }^{bl}\\ t=-\left({H}^{bl} \mathrm{sin}{\varphi }_{p}\mathrm{cos}{\theta }_{p}\right)\mathrm{sin}{\theta }^{bl}+\left({R}^{bl} \mathrm{sin}{\varphi }_{p}\mathrm{sin}{\theta }_{p}\right)\mathrm{cos}{\theta }^{bl}\\ w={R}^{bl} \mathrm{cos}{\varphi }_{p}\end{array},\right.$$

(15)

in ${\varphi }_{p}\in \left[0;\pi \right]$ and ${\theta }_{p}\in \left[0;2\pi \right]$ where ${r}_{y0}$ is the normal coordinate of the block centre of mass at the impact onset computed by imposing is tangency condition to the impact plane. Its value is given by the following expression:

$${r}_{y0}=\sqrt{{\left({H}^{bl}\right)}^{2}{\mathrm{cos}}^{2}{\theta }_{0}+{\left({R}^{bl}\right)}^{2}{\mathrm{sin}}^{2}{\theta }_{0}.}$$

(16)

The Cartesian equation of the ellipsoid is given by:

$$\frac{{\left[\left(n-{u}_{n}^{bl}+{r}_{y0}\right)\mathrm{cos}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)-\left(t-{u}_{t}^{bl}\right)\mathrm{sin}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)\right]}^{2}}{{\left({H}^{bl}\right)}^{2}}+\frac{{\left[\left(n-{u}_{n}^{bl}+{r}_{y0}\right)\mathrm{sin}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)+\left(t-{u}_{t}^{bl}\right)\mathrm{cos}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)\right]}^{2}}{{\left({R}^{bl}\right)}^{2}}+\frac{{w}^{2}}{{\left({H}^{bl}\right)}^{2}}=1.$$

(17)

4.2 Intersection Between the Ellipsoidal Surface and the Impact Plane

Once the block penetrates into the substrate material, the impact plane (i.e. ground surface) intersects the block. Here we present the mathematical expression for: (i) the equivalent foundation size and, (ii) the normal and tangential arms.

The intersection of the ellipsoid with the impact plane is solved by imposing the following algebraic system

$$\left\{\begin{array}{l}\frac{{\left[\left(n-{u}_{n}^{bl}+{r}_{y0}\right)\mathrm{cos}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)-\left(t-{u}_{t}^{bl}\right)\mathrm{sin}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)\right]}^{2}}{{\left({H}^{bl}\right)}^{2}}+\frac{{\left[\left(n-{u}_{n}^{bl}+{r}_{y0}\right)\mathrm{sin}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)+\left(t-{u}_{t}^{bl}\right)\mathrm{cos}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)\right]}^{2}}{{\left({R}^{bl}\right)}^{2}}+\frac{{w}^{2}}{{\left({H}^{bl}\right)}^{2}}=1\\ n=0\end{array}\right..$$

(18)

After some algebraic manipulation, the following equation is obtained:

$$\frac{{\left(t+\frac{{b}_{1}}{{r}_{y}}-{u}_{t}^{bl}\right)}^{2}}{\frac{{b}_{2}+{b}_{1}^{2}}{{r}_{y}^{2}}}+\frac{{w}^{2}}{\frac{{b}_{2}+{b}_{1}^{2}}{{\left({H}^{bl}\right)}^{2}}}=1,$$

(19)

which is an ellipse centred in $\left(0;{u}_{t}^{bl}-\frac{{b}_{1}}{ry};0\right)$ and semi-axes:

$${a}_{t}=\sqrt{\frac{{b}_{2}+{b}_{1}^{2}}{{r}_{y}^{2}},}$$

(20)

$${a}_{w}=\sqrt{\frac{{b}_{2}+{b}_{1}^{2}}{{\left({H}^{bl}\right)}^{2}}},$$

(21)

where

$$\left\{\begin{array}{l}{r}_{y}=\sqrt{{\left({H}^{bl}\right)}^{2}{\mathrm{cos}}^{2}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)+{\left({R}^{bl}\right)}^{2}{\mathrm{sin}}^{2}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)}\\ {b}_{1}=\frac{\left({r}_{y0}-{u}_{n}^{bl}\right)\left[{\left({R}^{bl}\right)}^{2}+{\left({H}^{bl}\right)}^{2}\right]\mathrm{sin}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)\mathrm{cos}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)}{{r}_{y}}\\ {b}_{2}={\left({R}^{bl}\right)}^{2}{\left({H}^{bl}\right)}^{2}-{\left({r}_{y0}-{u}_{n}^{bl}\right)}^{2}\left[{\left({H}^{bl}\right)}^{2}+{\left({R}^{bl}\right)}^{2}-{r}_{y}^{2}\right]\end{array}\right..$$

(22)

The vertex points of this ellipse are

$$\left\{\begin{array}{l}{A}_{t1}=\left(0, {u}_{t}^{bl}-\frac{{b}_{1}}{ry}-{a}_{t};0\right)\\ {A}_{t2}=\left(0, {u}_{t}^{bl}-\frac{{b}_{1}}{ry}+{a}_{t};0\right)\\ {A}_{w1}=\left(0, {u}_{t}^{bl}-\frac{{b}_{1}}{ry};-{a}_{w}\right)\\ {A}_{w2}=\left(0, {u}_{t}^{bl}-\frac{{b}_{1}}{ry};+{a}_{w}\right)\end{array}\right..$$

(23)

4.3 Extremes Points

According to the ellipsoidal position, the equivalent foundation size computed considering also the extremes points (Fig. 16) (${C}_{t}$ and ${A}_{t}$) computed by imposing the vertical tangency to the meridian section of the ellipsoidal block.

The extremes point coordinates are given by the following expressions:

$$\left\{\begin{array}{l}{C}_{t1}=\left({n}_{1},{t}_{1};0.0\right)\\ {C}_{t2}=\left({n}_{2},{t}_{2};0.0\right)\end{array} \quad \mathrm{if} {t}_{1}\le {t}_{2}\right.,$$

(24)

or

$$\left\{\begin{array}{l}{C}_{t1}=\left({n}_{2},{t}_{2};0.0\right)\\ {C}_{t2}=\left({n}_{1},{t}_{1};0.0\right)\end{array} \quad \mathrm{if} {t}_{1}>{t}_{2}\right.,$$

(25)

and

$$\left\{\begin{array}{l}{C}_{w1}=\left(-H+{u}_{t}^{bl},0.0;-{R}^{bl}\right)\\ {C}_{w2}=\left(-H+{u}_{t}^{bl},0.0;+{R}^{bl}\right)\end{array}\right.,$$

(26)

where

$$\left\{\begin{array}{l}{n}_{1}={u}_{n}^{bl}-{r}_{y0}+{H}^{bl}\mathrm{cos}{\theta }_{p1}\mathrm{cos}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)+{R}^{bl}\mathrm{sin}{\theta }_{p1}\mathrm{sin}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)\\ {t}_{1}={u}_{t}^{bl}-{H}^{bl}\mathrm{cos}{\theta }_{p1}\mathrm{sin}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)+{R}^{bl}\mathrm{sin}{\theta }_{p1}\mathrm{cos}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right) \end{array}\right.,$$

(27)

and

$$\left\{\begin{array}{l}{n}_{2}={u}_{n}^{bl}-{r}_{y0}+{H}^{bl}\mathrm{cos}{\theta }_{p2}\mathrm{cos}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)+{R}^{bl}\mathrm{sin}{\theta }_{p2}\mathrm{sin}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)\\ {t}_{2}={u}_{t}^{bl}-{H}^{bl}\mathrm{cos}{\theta }_{p2}\mathrm{sin}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)+{R}^{bl}\mathrm{sin}{\theta }_{p2}\mathrm{cos}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right) \end{array}\right.,$$

(28)

and the angles ${\theta }_{p1}$ and ${\theta }_{p2}$ are

$$\left\{\begin{array}{l}{\theta }_{p1}= -\mathrm{arctan}\left(\frac{{R}^{bl}}{{H}^{bl}\mathrm{tan}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)}\right)\\ {\theta }_{p2}=\pi -\mathrm{arctan}\left(\frac{{R}^{bl}}{{H}^{bl}\mathrm{tan}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)}\right) \end{array}\right..$$

(29)

Fig. 16

Extremes points (${C}_{t}$), intersection point (${A}_{t}$) and equivalent foundation size (${B}_{t}$) along the tangential direction ($t$) for the case with: a the extreme points above the impact plane; b only one extreme point below the impact plane and c both extreme points below the impact plane

4.4 Normal and Tangential Arms During Block Sinking

From Fig. 16 it is possible to define the following points:

$$D{t}_{1}=\left\{\begin{array}{l}{A}_{t1} \quad \mathrm{if} {n}_{Ct1}<0\\ {C}_{t1} \quad \mathrm{if} {n}_{Ct1}\ge 0 \end{array}\right.,$$

(30)

$$D{t}_{2}=\left\{\begin{array}{l}{A}_{t2} \quad \mathrm{if} {n}_{Ct2}<0\\ {C}_{t2} \quad \mathrm{if} {n}_{Ct2}\ge 0 \end{array}\right.,$$

(31)

$$D{w}_{1}=\left\{\begin{array}{l}{A}_{w1} \quad \mathrm{if} {n}_{Cw1}<0\\ {C}_{w1} \quad \mathrm{if} {n}_{Cw1}\ge 0 \end{array}\right.,$$

(32)

$$D{w}_{2}=\left\{\begin{array}{l}{A}_{w2} \quad \mathrm{if} {n}_{Cw2}<0\\ {C}_{w1} \quad \mathrm{if} {n}_{Cw2}\ge 0 \end{array}\right..$$

(33)

Consequently the equivalent foundation sizes are:

$${B}_{t}={t}_{Dt2}-{t}_{Dt1},$$

(34)

and for the out of plane:

$${B}_{w}={w}_{Dw2}-{w}_{Dw1},$$

(35)

The normal and tangential arms are given by, respectively:

$${r}_{n}={r}_{y0}-{u}_{n}^{bl},$$

(36)

$${r}_{t}=\frac{{t}_{Dt1}+{t}_{Dt2}}{2}-{u}_{t}^{bl}.$$

(37)

By imposing the tangency block condition at impact, the block sinking is computed as:

$${u}_{D}^{bl}=\mathrm{max}\left\{{n}_{1};{n}_{2}\right\},$$

(38)

where

$$\left\{\begin{array}{l}{n}_{1}={u}_{n}^{bl}-{r}_{y0}+{H}^{bl}{\mathrm{cos}}{\theta }_{p1}\mathrm{cos}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)+{R}^{bl}\mathrm{sin}{\theta }_{p1}\mathrm{sin}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)\\ {n}_{2}={u}_{n}^{bl}-{r}_{y0}+{H}^{bl}{\mathrm{cos}}{\theta }_{p2}\mathrm{cos}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)+{R}^{bl}\mathrm{sin}{\theta }_{p2}\mathrm{sin}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)\end{array}\right.,$$

(39)

where ${\theta }_{p1}$ and ${\theta }_{p2}$ are the solutions of the following trigonometric equation:

$$-{H}^{bl}\mathrm{tan}{\theta }_{{p}}\mathrm{cos}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)+{R}^{bl}\mathrm{cos}{\theta }_{p}\mathrm{sin}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right),$$

(40)

which is are

$$\left\{\begin{array}{l}{\theta }_{p1}=\mathrm{arctan}\left[\frac{{R}^{bl}}{{H}^{bl}}\mathrm{tan}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)\right]\\ {\theta }_{p2}=\pi +\mathrm{arctan}\left[\frac{{R}^{bl}}{{H}^{bl}}\mathrm{tan}\left({\theta }_{0}^{bl}+{\theta }^{bl}\right)\right]\end{array},\right.$$

(41)

in case ${\mathrm{cos}}{\theta }_{p}\ne 0$ or otherwise (Fig. 17)

$$\left\{\begin{array}{l}{\theta }_{p1}=\frac{\pi }{2}\\ {\theta }_{p2}=\frac{3}{2}\pi \end{array}\right..$$

(42)

Fig. 17

Shape and sizes (${B}_{t} \; {\mathrm{and}} \; {B}_{w}$) of the equivalent foundation footprint (red line) reported with the tangential arm (${r}_{t}$) for a block impacting on a horizontal layer