1 Introduction

Since December 2019, a number of unexplained pneumonia cases have been discovered by some hospitals in Wuhan, Hubei Province, China, and have been confirmed as acute respiratory infections caused by coronavirus disease in 2019 [1]. On February 11, 2020, the World Health Organization (WHO) named a coronavirus disease 2019 as ‘COVID-19.’ So far, there have been 2,335,180 patients with COVID-19 worldwide, and 161,491 have died (latest data as of writing time April 20th 17:05, 2020 [2]). The case data of the world top six most affected countries on April 2, 2020, and April 20, 2020, are shown in Table 1. The COVID-19 has spread globally, seriously endangering people’s lives and health, and leading to a huge impact on the economy, education and daily life of various countries. At present, only some provinces in China have resumed physical teaching for students in junior and high school graduation years, while students from colleges, universities, and elementary schools across the country are taking online courses. In the last few days, the Ministry of Education of China informed that the national unified examination for admissions to general universities and colleges is delayed by one month [3]. The International Olympic Committee officially announced in a statement that the Tokyo 2020 Olympics will be celebrated from July 23 to August 8, 2021 [4].

Table 1 Case data of the world top six most affected countries
Full size table

During the spread of epidemic, national medical staff, scientific research teams, and epidemiological research experts are all struggling to contribute to the fight against the epidemic and have achieved very important results in China. Many important treatment methods and theoretical results will provide valuable experience for the world. The team led by Academician Zhong Nanshan pointed out in the medical paper [5] that the median incubation period of the new coronavirus is 3 days, with a minimum of 0 days and a maximum of 24 days. On February 11, 2020, Yang et al. took 8866 patients as a research sample and reached an important conclusion that the estimated basic reproductive number \({\mathfrak {R}}_{0}=3.77\) [6]. Another estimate of \({\mathfrak {R}}_{0}=2.7\) was also based on surveillance data, but the methodology was different from [7]. The basic reproductive number is a mathematical concept of epidemic dynamics, which represents the number of people infected by a patient during their average illness period. The team of Professor Xiao of Xi’an Jiaotong University put forward a concept of mean control reproductive number [8]. This concept is novel and provides a new theoretical analysis method for the later stage of epidemic dynamics. Since the article was published early in the epidemic and the amount of data is not comprehensive, the \({\mathfrak {R}}_{0}\) calculation was not recognized by the academic community. However, the epidemic model proposed by epidemiologists can characterize the transmission mechanism of epidemic and predict the final scale of the disease, and then provide valuable guidance for the overall epidemic prevention work of our society. More relevant research results can also be found in the latest literature [9, 10].

Now we are in an era of the Internet with information explosion. Information is speeding quickly and in various forms. Currently, popular and active social software worldwide includes WhatsApp, Facebook Messenger, Network platform, Instagram, QQ, Twitter, Line, etc. There are hundreds of millions or even billions of registered users of these social software. For example, the registered number of WhatsApp has exceeded 1.5 billion [11]). As a platform for free speech, the Internet has also become a means of disseminating many online rumors and even affected the stability of society. In particular, during the epidemic, the spread of some unconfirmed news caused social panic and disrupted normal life order. For example, on January 31, some media reported that the Chinese patent medicine Shuanghuanglian oral solution can inhibit the new coronavirus [2]. After the news was released, some Shuanghuanglian-related products in some domestic pharmacies were out of stock, causing market confusion. On March 9, the news of ‘Universities and middle schools in Beijing will open on April 6 and elementary schools and kindergartens will open on April 20’ was circulated among multiple network platform groups and friends. However, on the evening of March 11, the Beijing Municipal Education Commission made it clear that this is a false message [12]. In addition, some people spread rumors on the Internet that the price of daily necessities will increase sharply, causing some citizens to snap up living supplies, thus causing market chaos. Such events are endless. The spread of rumors disturbed people’s sight and caused extremely bad influence.

Combined with the information dissemination properties of the network platform, the number of friends of a user is an important factor affecting the spread of rumors. The number of user friends determines the user’s ability to spread information (rumors). This is based on a reasonable hypothesis that the number of friends of a user is mainly determined by the length of registration. Therefore, longer registration time forms larger friend cycle and further creates greater rumor impact. If the user’s registration time is abstracted as ‘age,’ the spreading mechanism of the rumor on the network platform can be characterized by the SIR model with the ‘age’ structure. Considering the above analysis, for the rumor propagation features of the network platform, we establish a SIR model with ‘age’ structure of spread rumors. The ignorants are divided into those with higher education level and lower education level, and short-term online education is carried out. The main contributions of this paper are summarized as follows

  1. (1)

    Considering that different users have different registration times which leads to different abilities to spread rumors, we denote ‘age’ as the user’s registration time as an important variable factor. Unlike previous models, the distance between the geographic location of a user and the rumor source is taken as an important factor [13].

  2. (2)

    Considering that the education level of the individual has an important influence on the spread of rumors, the users are divided into two categories according to their educational level. Compared with treating all users as ignorant [14], it can describe the spreading rules of rumors more reasonably.

  3. (3)

    The improvement in education level requires a long period. Our model first introduces short-term online education and quantitatively analyzes its inhibitory effect on the spread of rumors. This will be an important means to effectively control the spread of rumors.

In this paper, we will propose a novel epidemic-like model to quantitatively describe the law of rumor spread and then consider education as a control measure of the spread of rumors. The remainder of this paper is organized as follows. In Sect. 2, the latest achievements of rumor propagation research are reviewed. The establishment of rumor propagation model is described in Sect. 3. In Sect. 4, we analyze dynamic behavior of the model. In Sect. 5, due to the spread of rumors, the importance of education is summarized and some suggestions are given. The numerical simulations are introduced in Sect. 6. Some brief conclusions are presented in Sect. 7.

2 Related work

Rumors refer to remarks that have no corresponding factual basis but are fabricated and promoted through certain means [15, 16]. In the past few years, we have seen many examples of rumors that have a huge negative impact, and these rumors are often accompanied by major accidents. As an example, in April 2013, many rumors about the H7N9 epidemic were spread throughout China, which triggered the great panic among the masses and even posed a threat to social stability [17]. With the rapid development of information technology, rumor propagation is mainly carried by social media rather than traditional word of mouth. Network platform is the most popular social media platform in China with the largest number of users. In the second quarter of 2019, the monthly active users of WeChat platform had reached 1.13 billion [18]. Although the emergence of network platform allows people to communicate easily, it also makes the rumors spread uncontrollably in the circle of friends. Therefore, it is extremely meaningful to study the mechanism of rumor propagation on the network platform and propose an approach to effectively suppress the spread of rumors.

The spread of rumors in social networks has attracted widespread attention from scholars at home and abroad [19, 20]. In particular, a series of rumor spreading models based on the SIR dynamics model of infectious disease transmission have achieved fruitful results in theoretical research. In 1960, the DK model, the earliest rumor spreading model, was developed by Daley and Kendal [21]. In this model, the population is divided into three categories, namely Ignorant, Spreader, and Stifler, corresponding to susceptible, infected, and removed people in the infectious disease model. Afterward, Maki et al. [22] proposed an additional hypothesis to improve the DK model and formed the MT model. Because the DK and MT models are only applicable to small-scale social networks and do not take into account the topological properties of the networks, these classical propagation models are not sufficient to adapt to complex social interaction systems.

In small-world networks, Zanette [23] first combined the complex network with the rumor propagation model to analyze the dynamic behavior of rumor spreading. Furthermore, the author considered the topological properties of underlying network and put forward a useful stochastic approach on a scale-free network [24]. On the basis of complex networks, a series of studies on different mechanisms in the spreading of rumors have received sustained attention. Nekovee et al. [25] introduced the forgetting mechanism into the SIR rumor spreading model, arguing that rumor spreaders might forget the rumors and turn them into immune. In this model, the forgetting rate is considered as a constant, but Zhao et al. [26] proposed that the forgetting rate is a function that changes with time. The trust mechanism established between the ignorant nodes and the spreader nodes was proposed by [27].

Combining the research results of the above literature, the stifling rate, the forgetting rate and the trust rate are three crucial factors that affect the spread of rumors. However, there is very little literature regarding the impact of the educational level of ignorant on the spread of rumors. In practice, the education level of ignorant is the most significant factor affecting their ability to judge rumor. Particularly, based on the SIR model, Afassinou [28] introduced a SEIR model applying a forgetting mechanism and a factor of the educational level of the population. His research demonstrated that increasing the educational level of the population promotes the termination of rumor communication. Nevertheless, unfortunately, the education level of the ignorant with lower education cannot be improved in a short period of time, but to prevent the spread of rumors, it is necessary to take measures for the ignorant of lower education, such as short-term online education.

On the other hand, the rumor spreading models mentioned above are based on the classical SIR model of ordinary differential equations (ODE), which considers that the number of the ignorants, the spreaders and the stiflers are only a function of time t. In the new media era, the study of rumor spreading models needs to combine the characteristics of social software to disseminate information. Zhu et al. [29] pointed out that with the rapid development of mobile communication devices, the traditional ODE-based rumor propagation model may not be suitable for describing rumor spread in online social networks. According to partial differential equation (PDE), Wang et al. [30] further proposed a linear diffusive model to understand the diffusion process of information in both temporal and spatial dimensions. Zhu et al. [31] investigated a PDE mathematical model that considers a delayed feedback controller, which effectively controls the diffusion of adverse information in online social networks. Zhu et al. [32] proposed a delayed reaction–diffusion rumor propagation model based on partial differential equations, and they obtained the local stability of equilibrium point and the condition of Hopf bifurcation. The exact solutions and nonlinear dynamics are of importance for the study of partial differential equations [33,34,35,36,37]. Some results have been derived recently for kinds of nonlinear partial differential equations [38,39,40,41,42]. On the basis of the model established by partial differential equations, scholars believe that rumor spread is not only related to time but also to space [43, 44]. Thus, it is more reasonable to study the rumor spread mechanism from both temporal and spatial dimensions than the ODE-based model.

For spatiotemporal dynamics of rumor propagation, we hold different views from the literature [29,30,31,32, 43, 44]. We believe that in the instant messaging network platform, the distance from the information source is irrelevant. Instead, the ability of platform users to spread information is more important, such as the number of friends a user has. In the next section of the model establishment process, we will elaborate on our views.

3 Mathematical modeling

This paper uses the network platform as a research carrier to study rumor spreading mechanism. We assume that N(t) is the number of network platform users at time t. For two users A and B, the number of friends they have has a distinct influence on the spread of rumor spreading, as illustrated in Fig. 1. The arrow indicates the direction in which the information can be transmitted. Any user can be either a communicator of the message or a receiver of the message. Users who are connected in a straight line are usually not online for a long time and do not participate in any interaction on the platform which is referred to as inactive users. Obviously, the impact of A users posting a message is greater than that of B users.

We abstract the ability of a user to distribute messages as influence weights, which are usually related to the number of friends they have (especially active users). If the variable y represents the influence weight of the user, the total number of users can be regarded as a bivariate distribution function for time t and weight y. Usually, users with long registration time have more friends, and the spreading influence is greater. Let a be the duration of the network platform user’s registration, we define a as the age of the user. In this paper, we always have the following assumption

Assumption 1

The influence weight of network platform users is positively related to the duration of the network platform user’s registration. That is, \(y=ka\), \(k>0\), \(a\in [0, M]\), where M is a network platform user expiration date (maximum age).

Fig. 1
figure 1

The influence weight of users

Full size image

Based on Assumption 1, the total number of N can be expressed as the bivariate distribution function N(a, t) with age structure a at time t. Assume that the number of users is a constant, there is no new user registration, and there are no inactive users (or logout). Within the time interval \([t,t+\mathrm {d}t]\), it is obvious that the equation \(\mathrm {d}t=\mathrm {d}a\) is satisfied; that is, the increment of time is equal to the increment of age. At time \(t+\mathrm {d}t\), the number \(N(a,t+\mathrm {d}t)\,\mathrm { d}a\) of users with age in interval \([a,a+\mathrm {d}a]\) should be equal to the number \(N(a-\mathrm {d}t,t)\,\mathrm {d}a\) of at the time t with age in interval \([a-\mathrm {d}t,a+\mathrm {d}a-\mathrm {d}t]\). Then, we have

$$\begin{aligned} N(a,t+\mathrm {d}t)\,\mathrm {d}a=N(a-\mathrm {d}t,t)\,\mathrm {d}a. \end{aligned}$$

Therefore, applying the Taylor formula of the binary function to the above, the following equation can be derived

$$\begin{aligned} \frac{\partial N(a,t)}{\partial t}+\frac{\partial N(a,t)}{\partial a}=0,\,\quad \quad N(0,a)=N_{0}(a). \end{aligned}$$

In fact, a social platform has new users registered all the time, and some users leave or become inactive users. A similar set of first-order nonlinear partial differential equations has been used to model population dynamics of sickle cell anemia, a genetically inherited disease [45]. In the next subsection, we discuss the impact of these two scenarios on the total number of users.

3.1 New user registration

Assuming the registration rate of the network platform is \(\alpha (a)\), the total number of users registered in the time interval \([t,t+\mathrm {d}t]\) is

$$\begin{aligned} \left( \int _{0}^{M}\alpha (a)N(a,t)\,\mathrm {d}a\right) \mathrm {d}t. \end{aligned}$$

On the other hand, the total number of users registered in the time interval \([t,t+\mathrm {d}t]\) should be equal to the total number of users with age in interval \([0,\mathrm {d}t]\); then, we have

$$\begin{aligned} N(0,t)\mathrm {d}t=\left( \int _{0}^{M}\alpha (a)N(a,t)\,\mathrm {d}a\right) \mathrm {d}t. \end{aligned}$$
(1)
Fig. 2
figure 2

Rumor spreading process

Full size image

The above formula gives the calculation method of the number of new users registered to the network platform, which is equivalent to the input item. With the continuous input of new users, some users never participate in the dissemination of information and become inactive users. Such a user needs to be regarded as an invalid user and cannot be counted.

3.2 The presence of inactive users

Assume that \(\mu (a-\mathrm {d}a)\) is the probability that a user with age in the interval \([a-\mathrm {d}t,a]\) becomes an inactive user per unit time. In the time interval \([t,t+\mathrm {d}t]\), the number of users whose age increases from \([a-\mathrm {d}t,a]\) to \([a,a+\mathrm {d}a]\) is \(\mu (a-\mathrm {d}a)\mathrm {d}t N(a,t)\,\mathrm {d}a\). Therefore, we get

$$\begin{aligned}&N(a-\mathrm {d}t,t)\,\mathrm {d}a-N(a,t+\mathrm {d}t)\,\mathrm {d}a\\&\quad =\mu (a-\mathrm {d}a)\mathrm {d}t N(a,t)\,\mathrm {d}a \end{aligned}$$

where we assume that the inactive network platform users have no effect on the entire information circle and are not counted in the total number of users. Using the Taylor formula to expand the two ends of the above equation and discard the high-order terms, we obtain

$$\begin{aligned}&\left[ N(a,t)-\frac{\partial N}{\partial a}\mathrm {d}t\right] -\left[ N(a,t)+\frac{\partial N}{\partial t}\mathrm {d}t\right] \\&\quad =[\mu (a)-\mu '(a)\mathrm {d}a]\mathrm {d}t\left[ N(a,t)-\frac{\partial N}{\partial a}\mathrm {d}t\right] . \end{aligned}$$

Noticing \(\mathrm {d}t=\mathrm {d}a\) and omitting the term of \((\mathrm {d}t)^{2}\), we get the following partial differential equation

$$\begin{aligned} \frac{\partial N(a,t)}{\partial a}+\frac{\partial N(a,t)}{\partial t}=-\mu (a)N(a,t). \end{aligned}$$
(2)

The initial conditions corresponding to above equation are

$$\begin{aligned} N(a,0)=N_{0}(a), \end{aligned}$$
(3)

where \(N_{0}(a)\) represents the distribution density of the initial user. Synthesizing (1), (2), and (3), a partial differential equation (PDE) model of network platform users development is obtained as follows

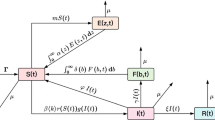
$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial N(a,t)}{\partial a}+\frac{\partial N(a,t)}{\partial t}=-\mu (a)N(a,t),\\ N(a,0)=N_{0}(a),\quad a\ge 0,\\ N(0,t)=\int _{0}^{M}\alpha (a)N(a,t)\,\mathrm {d}a, \quad a \ge 0.\\ \end{array}\right. \end{aligned}$$
(4)

We subdivide the network platform users into three different classes. And let S(a, t), I(a, t) and R(a, t) be the age densities of, respectively, the ignorant users, spreading users and immune users at time t. Furthermore, we divide the susceptible users into higher-educators class \(S_{h}(a,t)\) and lower-educators class \(S_{l}(a,t)\). Obviously, the relationship between the number of different classes of users and the total number of users is formulated as follows

$$\begin{aligned} S_{h}(a,t)+S_{l}(a,t)+I(a,t)+R(a,t)=N(a,t). \end{aligned}$$
(5)

3.3 Rumor spreading process

The main process of rumor spreading on network platform is shown in Fig. 2. The force of spreading for the spreaders rumor denoted by \(\lambda _{h}(a)\) and \(\lambda _{l}(a)\) is defined by [46,47,48]

$$\begin{aligned} \lambda _{h}(a,t)= & {} k_{h}(a)\int _{0}^{+\infty }\sigma (a)I(a,t)\,\mathrm {d}a,\\ \lambda _{l}(a,t)= & {} k_{l}(a)\int _{0}^{+\infty }\sigma (a)I(a,t)\,\mathrm {d}a, \end{aligned}$$

where \(\sigma (a)\) is age-specific spread rate, \(k_{h}(a)\) and \(k_{l}(a)\) are age-specific contact rates that spreaders contact higher-educator users and lower-educator users, respectively. The others major parameters are given in Table 2.

Table 2 Major parameters
Full size table

All parameters are evaluated in the interval [0, 1], satisfying \(0\le \lambda _{l}(a)+\beta _{l}(a)\le 1\), \(0\le \lambda _{h}(a)+\beta _{h}(a)+\gamma _{l}(a)\le 1\), \(\lambda _{l}(a)\ge \lambda _{h}(a)\) and \(\beta _{l}(a)\le \beta _{h}(a)\). When an ignorant user contacts a spreader, who will become a spreader by listening to rumors or become an immune user by being able to recognize the truth. Of course, education is the key factor that determines whether an ignorant user can recognize rumors. Based on this inspiration, we introduce a short-term network education control mechanism \(\gamma _{l}(a)\) for the ignorant users with low educational level. There are two factors that either the rumor becomes outdated or the spreader loses interest in the rumor, which causes the rumor spreader to become an immune. Under the above assumptions, the spread of the rumor can be described by the following partial differential equations

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial S_{h}(a,t)}{\partial t}+\frac{\partial S_{h}(a,t)}{\partial a}= -[\lambda _{h}(a,t)+\beta _{h}(a)]S_{h}\\ \quad \quad -\mu (a)S_{h},\\ \frac{\partial S_{l}(a,t)}{\partial t}+\frac{\partial S_{l}(a,t)}{\partial a}=-[\lambda _{l}(a,t)+\beta _{l}(a) \\ \quad \quad +\gamma _{l}(a)]S_{l}-\mu (a)S_{h},\\ \frac{\partial I(a,t)}{\partial t}+\frac{\partial I(a,t)}{\partial a}=\lambda _{h}(a,t)S_{h}+\lambda _{l}(a,t)S_{l} \\ \quad \quad -\mu (a) I-\delta (a) I,\\ \frac{\partial R(a,t)}{\partial t}+\frac{\partial R(a,t)}{\partial a}=\beta _{h}(a)S_{h}+[\beta _{l}(a)+\gamma _{l}(a)]S_{l} \\ \quad \quad -\mu (a) R+\delta (a) I,\\ S_{h}(a,0)=S_{h0}(a),\,\,S_{l}(a,0)=S_{l0}(a),\\ \quad \quad I(a,0)=I_{0}(a),\,\,R(a,0)=R_{0}(a),\\ S_{h}(0,t)=\int _{0}^{M}\alpha (a)N(a,t)\,\mathrm {d}a, \\ \quad \quad S_{l}(0,t)=\int _{0}^{M}\alpha (a)N(a,t)\,\mathrm {d}a,\\ I(0,t)=0,\,\,R(0,t)=0. \end{array}\right. \nonumber \\ \end{aligned}$$
(6)

We assume that the total number of users of the network platform is an equilibrium, and the number of newly registered users per unit time is equal to the number of inactive users. This means that

$$\begin{aligned} \int _{0}^{+\infty }\alpha (a)e^{-\int _{0}^{a}\mu (\tau )\,\mathrm {d}\tau }\,\mathrm {d}a=1, \quad \text {and}\quad N(a,t)=N(a). \end{aligned}$$

We introduce four new variables as follows

$$\begin{aligned} s_{h}(a,t)= & {} \frac{S_{h}(a,t)}{N(a)},\quad s_{l}(a,t)=\frac{S_{l}(a,t)}{N(a)},\\ i(a,t)= & {} \frac{I(a,t)}{N(a)},\quad r(a,t )=\frac{R(a,t)}{N(a)}. \end{aligned}$$

It is easy to obtain that \(s_{h}(a,t)+s_{l}(a,t)+i(a,t)+r(a,t)=1\) and

$$\begin{aligned} \lambda _{h}(a,t)= & {} k_{h}(a)\int _{0}^{+\infty }\sigma (a)N(a)i(a,t)\,\mathrm {d}a,\\ \lambda _{l}(a,t)= & {} k_{l}(a)\int _{0}^{+\infty }\sigma (a)N(a)i(a,t)\,\mathrm {d}a. \end{aligned}$$

Then, model (6) can be rewritten as follows

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial s_{h}(a,t)}{\partial t}+\frac{\partial s_{h}(a,t)}{\partial a}= -[\lambda _{h}(a,t)+\beta _{h}(a)]s_{h},\\ \frac{\partial s_{l}(a,t)}{\partial t}+\frac{\partial s_{l}(a,t)}{\partial a}=-[\lambda _{l}(a,t)+\beta _{l}(a)+\gamma _{l}(a)]s_{l},\\ \frac{\partial i(a,t)}{\partial t}+\frac{\partial i(a,t)}{\partial a}=\lambda _{h}(a,t)s_{h}+\lambda _{l}(a,t)s_{l}-\delta (a) i,\\ \frac{\partial r(a,t)}{\partial t}+\frac{\partial r(a,t)}{\partial a}=\beta _{h}(a)s_{h}+[\beta _{l}(a)+\gamma _{l}(a)]s_{l} \\ \quad \quad +\delta (a) i,\\ s_{h}(a,0)=s_{h0}(a),\,\,s_{l}(a,0)=s_{l0}(a),\\ \quad \quad i(a,0)=i_{0}(a),\,\,r(a,0)=r_{0}(a),\\ s_{h}(0,t)+s_{l}(0,t)=1,\,\,i(0,t)=r(0,t)=0.\\ \end{array}\right. \nonumber \\ \end{aligned}$$
(7)

To facilitate the study, we normalized model (6) and converted it into model (7). The two models are equivalent. In the next section, we will do a comprehensive analysis of the dynamic behavior of model (7).

4 Existence and stability of solution

To study the dynamics of the model, the global existence of the solution should be ensured firstly. This is also a necessary condition to verify the rationality of our proposed model. In the next subsection, we will prove the existence and uniqueness of solution.

4.1 Existence and uniqueness of solution

Consider the initial boundary value problem of model (6) as an abstract Cauchy problem on the Banach space \(X:={\mathcal {L}}^{1}(0,\,M;\,C^{2})\) that is the set of equivalence classes of Lebesgue integrable functions from \([0,\,m]\) to \(C^{2}\) equipped with the \({\mathcal {L}}^{1}\)-norm. Let A be a linear operator defined by \(A: D(A)\rightarrow X\) with norm

$$\begin{aligned} Ax=\left( \begin{array}{l} -\left[ \frac{\partial }{\partial a}+\beta _{h}(a)+\mu (a)\right] x_{1}\\ -\left[ \frac{\partial }{\partial a}+\beta _{l}(a)+\gamma _{l}(a)+\mu (a)\right] x_{2}\\ -\left[ \frac{\partial }{\partial a}+\delta (a)+\mu (a)\right] x_{3}\\ -\left[ \frac{\partial }{\partial a}+\mu (a)\right] x_{4} \end{array},\right) \end{aligned}$$

and a nonlinear operator defined by \(F: X\rightarrow X\) with norm

$$\begin{aligned} F(x)=\left( \begin{array}{l} -\left[ k_{h}(a)\int _{0}^{+\infty }\sigma (a)N(a)x_{3}\,\mathrm {d}a\right] x_{1}\\ -\left[ k_{l}(a)\int _{0}^{+\infty }\sigma (a)N(a)x_{3}\,\mathrm {d}a\right] x_{2}\\ \left[ k_{h}(a)\int _{0}^{+\infty }\sigma (a)N(a)x_{3}\,\mathrm {d}a\right] x_{1}\\ \qquad +\left[ k_{l}(a)\int _{0}^{+\infty } \sigma (a)N(a)x_{3}\,\mathrm {d}a\right] x_{2}\\ \beta _{h}(a)x_{1}+\beta _{l}(a)x_{2}+\gamma _{l}(a)x_{2}+\delta (a)x_{3} \end{array}\right) . \end{aligned}$$

Then, model (6) can be rewritten to an abstract Cauchy problem as follows

$$\begin{aligned} \frac{\mathrm {d}u(t)}{\mathrm {d}t}=Au(t)+F(u(t)), \end{aligned}$$
(8)

where \(u(t)=(s_{h}(a,t),s_{l}(a,t),i((a,t),r(a,t))\).

Theorem 1

The initial boundary value problem of model (6) has a unique nonnegative classical solution on X with respect to \((s_{h}(a,0),s_{l}(a,0),i(a,0),r(a,0))\in D(A)^{T}\).

Proof

It is easily obtained that the operator A is the infinitesimal generator of \(C_{0}\)-semigroup \(T(t),\,\, t\ge 0\), and F is continuously Frechet differentiable on X. Then, for each \(u_{0}\in X\), there exist a maximal interval of existence [0, m) and a unique continuous differential mild solution \(t\rightarrow u(t,u_{0})\) (see [47]) from [0, m) such that

$$\begin{aligned} u(t,u_{0})=T(t)u_{0}+\int _{0}^{t}T(t-s)F(u(s,u_{0}))\,\mathrm {d}s, \end{aligned}$$

where either \(m=+\infty \) or \(m<+\infty \) and \(\lim _{t\rightarrow m}\Vert u(t,u_{0})\Vert =\infty \). Since \(\Vert N(a,t)\Vert =N(a)<+\infty \), we can obtain \(m=+\infty \). The proof is completed. \(\square \)

Rewriting model (6) as an abstract Cauchy equation in vector form, we obtained that model (6) admits a unique nonnegative classical solution by using the \(C_{0}\)-semigroup theory. Since model (6) and model (7) are equivalent, model (7) also has a unique nonnegative classical solution.

4.2 Existence of steady-state solution

The equilibrium point of the autonomous model, which indicates a state where the system model reaches dynamic equilibrium, has an important physical significance. This equilibrium is usually the level of balance we expect the system to eventually reach. Similarly, there are steady-state solutions that are independent of time variables for nonautonomous models. In particular, general models also have marginal equilibrium state from the perspective of mathematics. However, such a marginal equilibrium has no practical significance. For model (7), our goal is to reduce the amount of i(a, t). Of course, \(i(a,t)=0\) is also unrealistic. For a network platform with nearly one billion users, we can only control and reduce the spread of rumors, which is difficult to completely ban. Therefore, we only study the existence of the positive steady-state solution of model (7).

Theorem 2

If the basic reproductive number of rumor \({\mathfrak {R}}_{0}>1\), then there exists a steady-state solution \(X^{*}=(s_{h}^{*}(a),s_{l}^{*}(a),i^{*}(a),r^{*}(a))\) of model (7), where \({\mathfrak {R}}_{0}=H(0)\), and

$$\begin{aligned} H(V^{*})=: & {} \int _{0}^{+\infty }\sigma (a)N(a)\int _{0}^{a}[k_{h}(\xi )s_{h}^{*}(\xi )\\&\quad +k_{l}(\xi )s_{l}^{*}(\xi )] \,e^{-\int _{\xi }^{a}\delta (\tau )\,\mathrm {d}\tau }\,\mathrm {d}\xi \,\mathrm {d}a,\\ s_{h}^{*}(a)= & {} s_{h}^{*}(0)e^{-\int _{0}^{a}[V^{*}k_{h}(\tau )+\beta _{h}(\tau )]\,\mathrm {d}\tau },\\ s_{l}^{*}(a)= & {} s_{l}^{*}(0)e^{-\int _{0}^{a}[V^{*}k_{l}(\tau )+\beta _{l}(\tau )+\gamma (\tau )]\,\mathrm {d}\tau }. \end{aligned}$$

Proof

\(X^{*}=(s_{h}^{*}(a),s_{l}^{*}(a),i^{*}(a),r^{*}(a))\) as a time-independent solution of model (7) that satisfies

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\mathrm {d}s_{h}^{*}(a)}{\mathrm {d}a}= -[\lambda _{h}^{*}(a)+\beta _{h}(a)]s_{h}^{*}(a),\\ \frac{\mathrm {d}s_{l}^{*}(a)}{\mathrm {d}a}=-[\lambda _{l}^{*}(a)+\beta _{l}(a)+\gamma _{l}(a)]s_{l}^{*}(a),\\ \frac{\mathrm {d}i^{*}(a)}{\mathrm {d}a}=\lambda _{h}^{*}(a) s_{h}^{*}(a)+\lambda _{l}^{*}(a)s_{l}^{*}(a)-\delta (a) i^{*}(a),\\ \frac{\mathrm {d}r^{*}(a)}{\mathrm {d}a}=\beta _{h}(a)s_{h}^{*}(a)+[\beta _{l}(a)+\gamma _{l}(a)]s_{l}^{*}(a)+\delta (a) i^{*}(a),\\ s_{h}^{*}(0)+s_{l}^{*}(0)=1,\,\,i^{*}(0)=r^{*}(0)=0,\\ \end{array}\right. \end{aligned}$$
(9)

where

$$\begin{aligned} \lambda _{h}^{*}(a)= & {} k_{h}(a)\int _{0}^{+\infty }\sigma (a)N(a)i^{*}(a)\,\mathrm {d}a,\\ \lambda _{l}^{*}(a)= & {} k_{l}(a)\int _{0}^{+\infty }\sigma (a)N(a)i^{*}(a)\,. \end{aligned}$$

Let \(\int _{0}^{+\infty }\sigma (a)N(a)i^{*}(a)\,\mathrm {d}a=: V^{*}\), then we have \(\lambda _{h}^{*}(a)=: k_{h}(a)V^{*}\) and \(\lambda _{l}^{*}(a)=: k_{l}(a)V^{*}\). By solving equation (9) directly, we get

$$\begin{aligned} i^{*}(a)= & {} \int _{0}^{a}V^{*}[k_{h}(\xi )s_{h}^{*}(\xi )+k_{l}(\xi )s_{l}^{*}(\xi )]\nonumber \\&\times \, e^{-\int _{\xi }^{a}\delta (\tau ) \,\mathrm {d}\tau }\,\mathrm {d}\xi , \end{aligned}$$
(10)

and

$$\begin{aligned} r^{*}(a)= & {} \int _{0}^{a}\{\beta _{h}(\xi )s_{h}^{*}(\xi )+[\beta _{l}(\xi )+\gamma _{l}(\xi )]\nonumber \\&\times \, s_{l}^{*}(\xi )+\delta (\xi ) i^{*}(\xi )\}\,\mathrm {d}\xi . \end{aligned}$$
(11)

Substituting (10) into (11) and changing the order of integration, we have

$$\begin{aligned} r^{*}(a)= & {} \int _{0}^{a}\{\beta _{h}(\xi )s_{h}^{*}(\xi )+[\beta _{l}(\xi )+\gamma _{l}(\xi )]s_{l}^{*}(\xi )\} \,\mathrm {d}\xi \nonumber \\&+V^{*}\int _{0}^{a}[k_{h}(\xi )s_{h}^{*}(\xi )+k_{l}(\xi )s_{l}^{*}(\xi )]\nonumber \\&\times \, \int _{\xi }^{a}\delta (\eta )e^{-\int _{\xi }^{\eta }\delta (\tau )\,\mathrm {d}\tau }\,\mathrm {d}\eta \,\mathrm {d}\xi . \end{aligned}$$
(12)

From the first and second equations of (9), we get

$$\begin{aligned} s_{h}^{*}(a)= & {} s_{h}^{*}(0)e^{-\int _{0}^{a}[V^{*}k_{h}(\tau )+\beta _{h}(\tau )]\,\mathrm {d}\tau },\nonumber \\ s_{l}^{*}(a)= & {} s_{l}^{*}(0)e^{-\int _{0}^{a}[V^{*}k_{l}(\tau )+\beta _{l}(\tau )+\gamma (\tau )]\,\mathrm {d}\tau }. \end{aligned}$$
(13)

For any \(V^{*}>0\), substituting \(V^{*}\) into (13), there is a unique \(s^{*}_{h}(a)\) and \(s^{*}_{l}(a)\) corresponding to it. Substituting \(s^{*}_{h}(a)\) and \(s^{*}_{l}(a)\) into (12) can solve \(r^{*}(a)\). For the same reason, substituting \(s^{*}_{h}(a)\) and \(s^{*}_{l}(a)\) into (10) can solve \(i^{*}(a)\). That is to say, each \(V^{*}\) corresponds to the unique equilibrium state \((s^{*}_{h}(a), s^{*}_{l}(a),i^{*}(a),r^{*}(a))\). Next, we discuss the existence of \(V^{*}\). Substituting \(i^{*}(a)\) into \(\int _{0}^{+\infty }\sigma (a)N(a)i^{*}(a)\,\mathrm {d} a=: V^{*}\), and both sides divide by \(V^{*}\), we have

$$\begin{aligned} 1= & {} \int _{0}^{+\infty }\sigma (a)N(a)\int _{0}^{a}[k_{h}(\xi )s_{h}^{*}(\xi )+k_{l}(\xi )s_{l}^{*}(\xi )]\nonumber \\&\times e^{-\int _{\xi }^{a}\delta (\tau ) \,\mathrm {d}\tau }\,\mathrm {d}\xi \,\mathrm {d}a=:H(V^{*}). \end{aligned}$$
(14)

We define \({\mathfrak {R}}_{0}=H(0)\). It is easy to see that the existence of a steady-state solution in model (7) which is equivalent to equation (14) has a positive solution. We can claim that \(i^{*}(a)<1\) because \(s^{*}_{h}(a)+ s^{*}_{l}(a)+i^{*}(a)+r^{*}(a)=1\). Therefore, we get

$$\begin{aligned} H(V^{*})= & {} \frac{1}{V^{*}}\int _{0}^{+\infty }\sigma (a)N(a)r^{*}(a)\,\mathrm {d}a\\< & {} \frac{\sigma _{\max }}{V^{*}}\int _{0}^{+\infty }N(a)\,\mathrm {d}a=\frac{\sigma _{\max }N}{V^{*}}, \end{aligned}$$

where \(\sigma _{\max }=\max \{\sup _{[0,+\infty )}\sigma (a)\}\). Obviously, we get that \(H(\sigma _{\max }N)<1\) when the \(V^{*}=\sigma _{\max }N\). As can be seen from expressions (14) and (13), we obtain that \(H(V^{*})\) is monotonically decreasing with respect to \(V^{*}\). In view of the theorem conditions \({\mathfrak {R}}_{0}=H(0)>1\), then from the properties of continuous functions, we have Eq. (14) that has a unique positive solution \({\bar{V}}^{*}\) in \((0,\sigma _{\max }N)\). The proof is completed. \(\square \)

4.3 Stability of steady-state solution

In this section, we focus on the stability of the steady-state solution of model (7). \({\hat{s}}_{h}(a,t)\), \({\hat{s}}_{l}(a,t)\), \({\hat{i}}(a,t)\), \({\hat{r}}(a,t)\) and \({\hat{V}}\) are linear perturbations of the steady-state solutions \(s_{h}^{*}(a)\), \(s_{l}^{*}(a)\), \(i^{*}(a)\), \(r^{*}(a)\) and \(V^{*}\), respectively. It is easy to see that the stability of the steady-state solution is equivalent to the linear disturbance tending to zero. We assume that the perturbations of model (7) have the following exponential solution

$$\begin{aligned} {\hat{s}}_{h}(a,t)= & {} {\bar{s}}_{h}(a)e^{\lambda t},\,\,{\hat{s}}_{l}(a,t)={\bar{s}}_{l}(a)e^{\lambda t},\nonumber \\ {\hat{i}}(a,t)= & {} {\bar{i}}(a)e^{\lambda t},\,\,{\hat{r}}(a,t)={\bar{r}}(a)e^{\lambda t},\, {\hat{V}}={\bar{V}}e^{\lambda t}.\nonumber \\ \end{aligned}$$
(15)

Theorem 3

If the condition \(f(\xi )\ge 0\) is satisfied, then the steady-state solution of model (7) is locally asymptotically stable, where

$$\begin{aligned} f(\xi )= & {} V^{*}k_{h}(\xi )s_{h}(\xi )+k_{h}(\xi )s ^{*}_{h}(\xi )\\&+V^{*}k_{l}(\xi )s_{l}(\xi )+k_{l}(\xi )s^{*}_{l}(\xi )\\= & {} k_{h}(\xi )s ^{*}_{h}(\xi )-V^{*}k_{h}(\xi )\int _{0}^{\xi }e^{-\lambda (a-\eta )}k_{h}(\eta )s_{h}^{*}(\eta )\\&\times e^{-\int _{\eta }^{\xi }[k_{h}(\tau )V^{*}+\beta _{h}(\tau )] \,\mathrm {d}\tau }\,\mathrm {d}\eta \\&+k_{l}(\xi )s^{*}_{l}(\xi )-V^{*}k_{l}(\xi )\int _{0}^{\xi }e^{-\lambda (a-\eta )}k_{l}(\eta )s_{l}^{*}(\eta )\\&\times e^{-\int _{\eta }^{\xi }[k_{l}(\tau )V^{*}+\beta _{l}(\tau )+\gamma _{l}(\tau )]\,\mathrm {d}\tau }\,\mathrm {d}\eta .\\ \end{aligned}$$

Proof

From (15), we can get the following approximate model

$$\begin{aligned} \left\{ \begin{array}{l} \lambda {\bar{s}}_{h}(a)+\frac{\mathrm {d} {\bar{s}}_{h}(a)}{\mathrm {d} a}= -k_{h}(a)V^{*}{\bar{s}}_{h}-k_{h}(a){\bar{V}}s^{*}_{h} \\ \quad -\beta _{h}(a){\bar{s}}_{h},\\ \lambda {\bar{s}}_{l}(a)+\frac{\mathrm {d} {\bar{s}}_{l}(a)}{\mathrm {d} a}= -k_{l}(a)V^{*}{\bar{s}}_{l}-k_{l}(a){\bar{V}}s^{*}_{l} \\ \quad -\beta _{l}(a){\bar{s}}_{l}-\gamma _{l}(a){\bar{s}}_{l},\\ \lambda {\bar{i}}(a)+\frac{\mathrm {d} {\bar{i}}(a)}{\mathrm {d} a}= k_{h}(a)V^{*}{\bar{s}}_{h}+k_{h}(a){\bar{V}}s^{*}_{h}\\ \quad +k_{l}(a)V^{*}{\bar{s}}_{l}+k_{l}(a){\bar{V}}s^{*}_{l}-\delta (a) {\bar{i}},\\ \lambda {\bar{r}}(a)+\frac{\mathrm {d} {\bar{r}}(a)}{\mathrm {d} a}= \beta _{h}(a){\bar{s}}_{h}+[\beta _{l}(a)+\gamma _{l}(a)]{\bar{s}}_{l} \\ \quad +\delta (a) {\bar{i}},\\ {\bar{s}}_{h}(0)+{\bar{s}}_{l}(0)={\bar{i}}(0)={\bar{r}}(0)=0,\\ \end{array}\right. \end{aligned}$$

Note that the intensities of the perturbation can take on either positive or negative. For the convenience of analysis, we make a variable substitution as

$$\begin{aligned} s_{h}(a)= & {} \frac{{\bar{s}}_{h}(a)}{{\bar{V}}},\,\,s_{l}(a)=\frac{{\bar{s}}_{l}(a)}{{\bar{V}}},\\ i(a)= & {} \frac{{\bar{i}}(a)}{{\bar{V}}},\,\,r(a)=\frac{{\bar{r}}(a)}{{\bar{V}}}. \end{aligned}$$

Then, we can obtain the following system as

$$\begin{aligned} \left\{ \begin{array}{l} \lambda s_{h}(a)+\frac{\mathrm {d} s_{h}(a)}{\mathrm {d} a}= -k_{h}(a)V^{*}s_{h}-k_{h}(a)s^{*}_{h}\\ \quad -\beta _{h}(a)s_{h},\\ \lambda s_{l}(a)+\frac{\mathrm {d} s_{l}(a)}{\mathrm {d} a}= -k_{l}(a)V^{*}s_{l}-k_{l}(a)s^{*}_{l}-\beta _{l}(a)s_{l}\\ \quad -\gamma _{l}(a)s_{l},\\ \lambda i(a)+\frac{\mathrm {d}i(a)}{\mathrm {d} a}= k_{h}(a)V^{*}s_{h}+k_{h}(a)s^{*}_{h}+k_{l}(a)V^{*}s_{l}\\ \quad +k_{l}(a)s^{*}_{l}-\delta (a) i,\\ \lambda r(a)+\frac{\mathrm {d} r(a)}{\mathrm {d} a}= \beta _{h}(a)s_{h}+[\beta _{l}(a)+\gamma _{l}(a)]s_{l}\\ \quad +\delta (a) i,\\ s_{h}(0)+s_{l}(0)=i(0)=r(0)=0,\\ \end{array}\right. \nonumber \\ \end{aligned}$$
(16)

with

$$\begin{aligned} \int _{0}^{+\infty }\sigma (a)N(a)i(a)\,\mathrm {d}a=1. \end{aligned}$$
(17)

By solving the third equation and fourth equation of model (16), directly we obtain

$$\begin{aligned} i(a)= & {} \int _{0}^{a}e^{-\lambda (a-\xi )}[V^{*}k_{h}(\xi )s_{h}(\xi )+k_{h}(\xi )s ^{*}_{h}(\xi )\nonumber \\&+ V^{*}k_{l}(\xi )s_{l}(\xi )+k_{l}(\xi )s^{*}_{l}(\xi )]\nonumber \\&\times e^{-\int _{\xi }^{a}\delta (\tau )\,\mathrm {d}\tau }\,\mathrm {d}\xi , \end{aligned}$$
(18)
$$\begin{aligned} r(a)= & {} \int _{0}^{a}e^{-\lambda (a-\xi )}\{\beta _{h}(\xi )s_{h}(\xi )+[\beta _{l}(\xi )+\gamma _{l}(\xi )]s_{l}(\xi )\nonumber \\&+\,\delta (\xi ) i(\xi )\}\,\mathrm {d}\xi , \end{aligned}$$
(19)
$$\begin{aligned} s_{h}(a)= & {} -\int _{0}^{a}e^{-\lambda (a-\xi )}k_{h}(\xi )s_{h}^{*}(\xi )e^{-\int _{\xi }^{a}[k_{h}(\tau )V^{*}+\beta _{h}(\tau )] \,\mathrm {d}\tau }\,\mathrm {d}\xi ,\nonumber \\ \end{aligned}$$
(20)

and

$$\begin{aligned} s_{l}(a)= & {} -\int _{0}^{a}e^{-\lambda (a-\xi )}k_{l}(\xi )s_{l}^{*}(\xi )\nonumber \\&\times e^{-\int _{\xi }^{a}[k_{l}(\tau )V^{*}+\beta _{l}(\tau )+\gamma _{l}(\tau )]\,\mathrm {d}\tau }\,\mathrm {d}\xi . \end{aligned}$$
(21)

Obviously, \(s_{h}(a)\) and \(s_{l}(a)\) are negative. Precisely, we assume that

$$\begin{aligned}&V^{*}k_{h}(\xi )s_{h}(\xi )+k_{h}(\xi )s ^{*}_{h}(\xi )+V^{*}k_{l}(\xi )s_{l}(\xi )+k_{l}(\xi )s^{*}_{l}(\xi )\\&\quad =k_{h}(\xi )s ^{*}_{h}(\xi )-V^{*}k_{h}(\xi )\int _{0}^{\xi }e^{-\lambda (a-\eta )}k_{h}(\eta )s_{h}^{*}(\eta )\\&\qquad \times e^{-\int _{\eta }^{\xi }[k_{h}(\tau )V^{*}+\beta _{h}(\tau )]\,\mathrm {d}\tau }\,\mathrm {d}\eta \\&\qquad +\,k_{l}(\xi )s^{*}_{l}(\xi )-V^{*}k_{l}(\xi )\int _{0}^{\xi }e^{-\lambda (a-\eta )}k_{l}(\eta )s_{l}^{*}(\eta )\\&\qquad \times e^{-\int _{\eta }^{\xi }[k_{l}(\tau )V^{*}+\beta _{l}(\tau )+\gamma _{l}(\tau )]\,\mathrm {d}\tau }\,\mathrm {d}\eta =:f(\xi ) \end{aligned}$$

Substituting i(a) into (17), we obtain

$$\begin{aligned} 1= & {} \int _{0}^{+\infty }\sigma (a)N(a)i(a)\,\mathrm {d}a\\= & {} \int _{0}^{+\infty }\sigma (a)N(a)\int _{0}^{a}e^{-\lambda (a-\xi )}f(\xi )e^{-\int _{\xi }^{a}\delta (\tau ) \,\mathrm {d}\tau }\,\mathrm {d}\xi \,\mathrm {d}a\\=: & {} Q(\lambda ). \end{aligned}$$

In view of the condition of Theorem 3, we get that \(Q(\lambda )\ge 0\) and \(Q(\lambda )\) is decreasing function of \(\lambda \) and \(Q(\lambda )\rightarrow 0\) as \(\lambda \rightarrow +\infty \).

$$\begin{aligned}&Q(0) =\int _{0}^{+\infty }\sigma (a)N(a)\int _{0}^{a}\left( k_{h}(\xi )s ^{*}_{h}(\xi )-V^{*}k_{h}(\xi )\right. \\&\qquad \left. \times \int _{0}^{\xi }k_{h}(\eta )s_{h}^{*}(\eta ) e^{-\int _{\eta }^{\xi }[k_{h}(\tau )V^{*}+\beta _{h}(\tau )]\,\mathrm {d}\tau }\,\mathrm {d}\eta \right) \\&\qquad +\left( k_{l}(\xi )s^{*}_{l}(\xi )-V^{*}k_{l}(\xi )\int _{0}^{\xi }k_{l}(\eta )s_{l}^{*}(\eta )\right. \\&\qquad \left. \times e^{-\int _{\eta }^{\xi }[k_{l}(\tau )V^{*}+\beta _{l}(\tau )+\gamma _{l}(\tau )]\,\mathrm {d}\tau }\,\mathrm {d}\eta e^{-\int _{\xi }^{a}\delta (\tau )\,\mathrm {d}\tau }\,\mathrm {d}\xi \right) \,\mathrm {d}a\\&\quad =\int _{0}^{+\infty }\sigma (a)N(a)\int _{0}^{a}k_{h}(\xi )s ^{*}_{h}(\xi )+k_{l}(\xi )s^{*}_{l}(\xi )\\&\qquad \times e^{-\int _{\xi }^{a}\delta (\tau )\,\mathrm {d}\tau }\,\mathrm {d}\xi \,\mathrm {d}a\\&\qquad -\int _{0}^{+\infty }V^{*}k_{h}(\xi )\int _{0}^{\xi }k_{h}(\eta )s_{h}^{*}(\eta )\\&\qquad \times e^{-\int _{\eta }^{\xi }[k_{h}(\tau )V^{*}+\beta _{h}(\tau )] \,\mathrm {d}\tau }\,\mathrm {d}\eta e^{-\int _{\xi }^{a}\delta (\tau )}\,\mathrm {d}\xi \,\mathrm {d}a\\&\qquad -\int _{0}^{+\infty }V^{*}k_{l}(\xi )\int _{0}^{\xi }k_{l}(\eta )s_{l}^{*}(\eta )\\&\qquad \times e^{-\int _{\eta }^{\xi }[k_{l}(\tau )V^{*}+\beta _{l}(\tau )+\gamma _{l}(\tau )]\,\mathrm {d}\tau }\,\mathrm {d}\eta e^{-\int _{\xi }^{a}\delta (\tau )\,\mathrm {d}\tau }\,\mathrm {d}\xi \,\mathrm {d}a. \end{aligned}$$

It is easy to see that the first integral above is equal to one, and the second integral and the third integral are negative terms. Therefore, we obtain that \(Q(0)<1\). Then, in view of monotonicity of \(Q(\lambda )\), we get that equation \(Q(\lambda )=1\) has a unique real solution which is negative and all complex solutions have real parts smaller than the unique real solution. Therefore, the steady-state solution of model (7) is locally asymptotically stable by the Lyapunov stability theory. The proof is completed. \(\square \)

5 Analysis of educational factors

In this section, we mainly focus on the impact of educational factors on the spread of rumors. The educational factors mainly refer to the education level of the ignorant and the short-term education of the network. First, the ignorant users are divided into higher educators and lower educators to study the rumor spreading mechanism, without considering the short-term network education factor, namely \(\gamma _{l}=0\). In fact, this is based on the theory that the higher the level of education is, the stronger the ability of users to identify rumors is. Therefore, short-term online education is provided for ignorant people at the bottom of education to improve their ability to recognize rumors. Finally, we give reasonable suggestions and feasible measures for our analysis results.

5.1 The influence of education level

According to the rumor spreading mechanism established by model (7), we define the final size of rumor spreading to include the following two factors

  1. (1)

    Setting the scale of the rumor effect \(M=\int _{0}^{+\infty }i^{*}(a)\,\mathrm {d}a\), where M represents the total number of rumor harms in the whole process of rumor spreading to the equilibrium state.

  2. (2)

    Network final health status is \(r^{*}(a)\), where \(r^{*}(a)\) represents the proportion of users who have the ability to identify rumors when they reach equilibrium. It can represent the ability of the network to ultimately resist rumors.

Obviously, the smaller the M is, the less harmful it is to be affected by rumors before the equilibrium state. The greater the \(r^{*}(a)\) is, the stronger the ability of the network to resist rumors is. We define \(K=\frac{s_ {h}(0,t)}{s_ {h}(0,t)+s_{l}(0,t)}\) to represent users with higher education proportion of total users in initial moment, which also represents the overall level of education of the entire user community. In this case, we also assume that short-term network education factor \(\gamma _{l}=0\). In particular, we assume that all users in the initial state have not received higher education, namely. Then, the model can be changed to the following form

$$\begin{aligned} \left\{ \begin{array}{l} \frac{\partial s_{l}(a,t)}{\partial t}+\frac{\partial s_{l}(a,t)}{\partial a}=-[\lambda _{l}(a,t)+\beta _{l}(a)]s_{l},\\ \frac{\partial i(a,t)}{\partial t}+\frac{\partial i(a,t)}{\partial a}=\lambda _{l}(a,t)s_{l}-\delta (a) i,\\ \frac{\partial r(a,t)}{\partial t}+\frac{\partial r(a,t)}{\partial a}=\beta _{l}(a)s_{l}+\delta (a) i,\\ \,\,s_{l}(a,0)=s_{l0}(a),\,\,i(a,0)=i_{0}(a),\,\,r(a,0)=r_{0}(a),\\ s_{l}(0,t)=1,\,\,i(0,t)=r(0,t)=0.\\ \end{array}\right. \nonumber \\ \end{aligned}$$
(22)

Similar to the analysis of Theorem 3, we can get a positive steady-state solution for model (22) \({\tilde{X}}^{*}({\tilde{s}}_{_{l}}^{*}(a),{\tilde{i}}^{*}(a),{\tilde{r}}^{*}(a))\). In view of \(\lambda _{l}(a)\ge \lambda _{h}(a)\) and \(\beta _{l}(a)\le \beta _{h}(a)\), we can obtain the conclusion \(M=\int _{0}^{+\infty }i^{*}(a)\,\mathrm {d}a< {\tilde{M}}=\int _{0}^{+\infty }{\tilde{i}}^{*}(a)\,\mathrm {d}a\) and \(r^{*}(a)>{\tilde{r}}^{*}(a)\). Furthermore, using explicit expressions (10), (12) and (13), we can achieve that M decreases as K increases, and \(r^{*}(a)\) increases as K increases.

Case 1 Positive effects of college students during the spread of COVID-19

The outbreak began during the winter vacation of 2019, and Chinese universities have not yet announced the start of classes. This causes all the college students and graduate students to stay at home. These senior intellectuals are distributed in every family in the community, which has significantly improved the education level of social groups. (In fact, when students are concentrated on campus, they do not participate in social activities, which is equivalent to an invalid user.) That is, the \(K=\frac{s_ {h}(0,t)}{s_ {h}(0,t)+s_{l}(0,t)}\) of model (22) becomes larger. From the above theoretical analysis, it can be concluded that the total number of rumor harms \(Q=\int _{0}^{+\infty }i^{*}(a)\,\mathrm {d}a\) will decrease and the proportion of users with the ability to identify rumors \(r^{*}(a)\) will increase. This is true. During this outbreak of COVID-19, senior intellectuals have a strong ability to identify rumors, and they can spread scientific epidemic prevention knowledge and related information in the community in time. These measures have inhibited the spread of rumors and passed positive energy for social stability.

In short, the theoretical results show that the level of education directly affects the final size of rumor spreading. The more users with higher education in the network are, the smaller the influence of rumors is, and the stronger the ability of the network to resist rumors is.

Fig. 3
figure 3

Dynamic characteristics of i(a, t) and r(a, t)

Full size image

5.2 Control by short-term online education

Through the above analysis, we know that improving the user’s education level is an effective means to control the final size spread of rumors. However, the overall education level of a network group is basically maintained in a short period of time. Therefore, it is highly necessary to carry out network short-term education for users with low education level. Based on the conclusions of the previous subsection, we can conclude that M decreases as \(\gamma _{l}(a)\) increases, and \(r^{*}(a)\) increases as \(\gamma _{l}(a)\) increases.

In this paper, we mainly considered two important factors affecting the rumor spreading education level K and short-term online education \(\gamma _{l}(a)\). Education level K is uncontrollable in the short term. However, the short-term network education \(\gamma _{l}(a)\) is an effective way to control the rumor spreading. To this end, we give the following suggestions

  1. (1)

    For the rumors that appear in social networks and further ferment, the media should promptly correct, disclose the false information of rumors and report the negative impact and social harm that rumors spread. The media needs to take advantage of its platform’s speed and credibility to expand the scope of the report, so as to awaken more rumors and stop the spread of rumors.

  2. (2)

    The government and other administrative departments should popularize popular science knowledge and improve the basic quality of citizens. At the same time, each social network user should strengthen network information security education and strive to improve their ability to identify true and false information.

  3. (3)

    Credible experts clarify the facts of rumors in time and can effectively reduce the spread of rumors, thereby reducing the density of rumors spread in social networks. For example, credible experts can publish authoritative opinions in time through the news media, which can effectively reduce the confusion of the people.

Case 2 Positive effects of credible experts and official media during the spread of COVID-19

Human beings need a cognitive process when facing sudden disasters. So far, we have not figured out the source of the new coronavirus pneumonia. There are many speculations about the etiology of pneumonia in the early days. Academician Zhong Nanshan, an authoritative expert, clarified at the press conference that the outbreak of COVID-19 occurred in Wuhan, but there is no evidence that the source is also in Wuhan. This is a scientific question. It is irresponsible to make conclusions casually before you figure it out. This eliminates the doubts of the masses. Some rumors disappeared as a result. The three control suggestions mentioned above can be attributed to short-term online education \(\gamma _{l}(a)\). In view of model (7), we note that \(\gamma _{l}(a)s_{l}(a, t)\) is reduced from \(s_{l}(a,t)\) to r(a, t); that is, through short-term online education, some people with lower education level can recognize rumors and become rumors immune. This is consistent with our theoretical analysis conclusion (12): \(r^{*}(a)\) increases as \(\gamma _{l}(a)\) increases. For COVID-19 such a fierce emergency, it is of great significance for the official media, government departments and authoritative experts in the field of doctors to publish reliable information in a timely manner, which can effectively control the spread of some rumors and reduce the anxiety of the masses.

Fig. 4
figure 4

Comparison diagram about the influence of education level for i(a, t)

Full size image
Fig. 5
figure 5

Comparison diagram about the influence of education level for r(a, t)

Full size image
Fig. 6
figure 6

Comparison diagram about short-term online education control

Full size image

6 Numerical simulation

In this section, we simulate and analyze the dynamic characteristics of the proposed rumor propagation model through simulations with MATLAB as well as the influence of education level and short-term online education factors on the spread of rumors.

Example 1

The dynamic characteristics of model (7)

To show the dynamic characteristics model (7), the basic parameters of the model we selected are as follows

$$\begin{aligned} \lambda _{h}(a,t)= & {} \sin (0.05a+t),\\ \beta _{h}(a)= & {} \frac{\exp (-a)}{1+\exp (-a)}+0.1,\\ \delta (a)= & {} \frac{\exp (-a)}{1+\exp (-a)},\\ \lambda _{l}(a,t)= & {} \sin (0.05a+t)+0.1, \beta _{l}(a)\\= & {} \frac{\exp (-a)}{1+\exp (-a)},\\ \gamma _{l}(a)= & {} \frac{0.01\exp (-a)+0.1}{0.01\exp (-a)+1}, \end{aligned}$$

where the initial value condition of model (7) is

$$\begin{aligned} s_{h}(0,t)= & {} 0.01\sin (t)+0.1,\\ s_{l}(0,t)= & {} 0.01\sin (t)+0.9,\\ i(0,t)= & {} 0,\quad r(0,t)=0 \end{aligned}$$

and the boundary value condition of model (7) is

$$\begin{aligned} s_{h}(a,0)= & {} 0.01\sin (a)+0.1,\\ s_{l}(a,0)= & {} 0.01\sin (a)+0.9,\\ i(a,0)= & {} 0,\quad r(a,0)=0. \end{aligned}$$

Theorem 1 proves the existence of nonnegative classical solution of model (6) and model (7). The dynamic characteristics of i(a, t) and r(a, t) of model (7) are shown in Fig. 3. Note that the maximum value of i(a, t) is close to 0.2, which means that at some point 20% of the participants are involved in the spread of rumors. In particular, in a critical period such as the outbreak of COVID-19, the harm caused by rumors to society is huge.

Example 2

The influence of education level

In this example, we assume that the short-term online education strength \(\gamma _{l}(a)=0\) by using the control variable method. The curve family of i(a) (or r(t)) at different times t is depicted as (a) of Fig. 4 (or Fig. 5). For each curve (a) of Fig. 4 (or Fig. 5), it means the change of i(a) (or r(t)) at a time t with age a. We can see that the variable a has an important influence on i (or r) at different times. For a fixed a, the variation law of i(t) (or r(t)) with time t is shown in (b) of Fig. 4 (or Fig. 5). To visualize the numerical results, the fixed age \(a=6\), then i(a, t) (or r(a, t)) is simplified to a unary function about time t. To verify the results of the theoretical analysis of the influence of education level on communication in Sects. 4 and 5, we took four different K(t) as follows

$$\begin{aligned} K=K_{1}(t)= & {} \frac{0.01\sin (t)+0.1}{0.01\sin (t)+0.1+0.01\sin (t)+0.9},\\ K=K_{2}(t)= & {} \frac{0.01\sin (t)+0.2}{0.01\sin (t)+0.2+0.01\sin (t)+0.8},\\ K=K_{3}(t)= & {} \frac{0.01\sin (t)+0.3}{0.01\sin (t)+0.3+0.01\sin (t)+0.7},\\ K=K_{4}(t)= & {} \frac{0.01\sin (t)+0.4}{0.01\sin (t)+0.4+0.01\sin (t)+0.6}. \end{aligned}$$

It is easy to calculate that \(K_{1}(t)\approx 10\%\), \(K_{2}(t)\approx 20\%\), \(K_{1}(t)\approx 30\%\), \(K_{4}(t)\approx 40\%\) and \(K_{1}(t)<K_{2}(t)<K_{3}(t)<K_{4}(t)\). In the (c) of Fig. 4 (or (c) of Fig. 5), we use red, pink, blue and black lines to represent i(t) (or r(t)) change trend with time which with the initial value conditions are \(K_{1}(t)\), \(K_{2}(t)\), \(K_{3}(t)\) and \(K_{4}(t)\), respectively. Obviously, as the education level K(t) to increase, i(t) gradually decreases and r(t) gradually increases, which is consistent with theoretical analysis results of Sect. 5.1. In other words, as the number of higher education users continues increase, the spread of rumors M will decrease. According to the data released by the Ministry of Education of China, as of 2018, the number of people who have obtained college diplomas or above accounted for 13% of the total population of the country [3]. Therefore, our selection of \( K_ {1} (t) \) is reasonable. With the continuous improvement of China’s education level, this data will definitely increase.

Example 3

Control by short-term online education

The innovation of this paper is that we added the control factor of online short-term education \( \ gamma_ {l} (a) \) to the model. Similar to the previous two Examples, the fixed age \(a=6\) and \(K=K_{1}(t)\). We choose four different \(\gamma _{l}(a)\) as follows

$$\begin{aligned} \gamma _{l1}(a)= & {} \frac{0.01\exp (-a)+0.1}{0.01\exp (-a)+1},\\ \gamma _{l2}(a)= & {} \frac{0.01\exp (-a)+0.2}{0.01\exp (-a)+1},\\ \gamma _{l3}(a)= & {} \frac{0.01\exp (-a)+0.3}{0.01\exp (-a)+1},\\ \gamma _{l4}(a)= & {} \frac{0.01\exp (-a)+0.4}{0.01\exp (-a)+1}. \end{aligned}$$

In Fig. 6, we use red, pink, blue, and black lines to represent i(t) (or t(t)) change trend with time in different short-term online education control factors \(K_{1}(t) \), \(K_{2}(t)\), \(K_{3}(t)\) and \(K_{4}(t)\), respectively. Obviously, as the short-term online education control factors K(t) increase, i(t) gradually decreases and r(t) gradually increases, which are shown in a and b of Fig. 6. This is consistent with theoretical analysis results of Sect. 5.2. In fact, as we suggested in Sect. 5.2, the short-term online education is the fastest and most effective way to control rumors. For example, during the outbreak of COVID-19, the government released official news in a timely manner, and the official news media updated the data in a timely manner, which played an important role in stabilizing public sentiment and resisting the spread of rumors.

7 Conclusion

In this paper, we have established a rumor propagation model based on the structure of nonautonomous partial differential equations. Combined with the law of users’ dissemination of information, three important factors are considered: the user’s education level, registration time, and short-term online education. The existence and uniqueness of the positive solution of model (7) are obtained by using \(C_{0}\)-semigroup theory. If the basic reproductive number of rumor \({\mathfrak {R}}_{0}>1\), then model (7) admits a steady-state solution. Furthermore, the stability of local asymptotically of steady-state solution is obtained. For an online platform with a large number of users, it is only an ideal state to completely eliminate the spread of rumors. Therefore, we did not consider the marginal equilibrium of model (7), which is meaningless. By analyzing the main influencing factors of i(a, t) in the steady-state solution, it is an effective means to reduce its number scale. The interesting conclusion of this article is that improving education level and conducting short-term online education are important strategies for effectively controlling the spread of rumors. The numerical simulation verified the correctness and feasibility of the theoretical results.

Since the outbreak of COVID-19, it has brought huge disasters to all countries in the world, including the direct impact of people’s lives and health, economic development, transportation, education, employment and other aspects. In addition, the spread of the epidemic has also brought many indirect impacts on people, such as people’s panic during the epidemic. Psychological research shows that when people face sudden crises, they will have different degrees of anxiety, nervousness and other excessive reactions. These overreactions can damage the immune system and cause physical and mental illness. This article mainly focuses on the laws and control of the spread of related rumors during the epidemic. Quantitative analysis and evaluation guide us to effectively control the spread of rumors and alleviate the negative psychological impact of COVID-19.