Method of shaft crack detection based on squared gain of vibration amplitude

Abstract

Rotating machines are exposed to different faults such as shaft cracks, bearing failures, rotor misalignment, stator to rotor rub, etc. Therefore, turbo-generators, aircraft engines, compressors, pumps, and many other rotating machines should be constantly diagnosed to warn about the probable appearance of a possible rotor failure. Unfortunately, despite the ongoing work on various rotor fault detection methods, there are still very few techniques that can be considered as reliable and applicable in practical problems. The difficulty lies in the fact that usually the fault introduces very subtle local changes in the overall structure of the rotor. The symptoms of these changes must be isolated and extracted from a wide spectrum of vibration data obtained from sensors measuring the vibrations of the machine. The measured data are usually disturbed with some noise or other disturbances, and that is why the detection of a possible rotor fault is even more difficult. The paper presents a new rotor fault detection method. The method is based on a new diagnostic model of rotor signals and external disturbances. The model utilizes auto-correlation functions of measured rotor’s vibrations. By proper processing of the measured vibration data, the influence of environmental disturbances is completely compensated and reliable indications of the possible rotor fault are obtained. The method has been tested numerically using the finite element model of the rotor and then verified experimentally at the shaft crack detection test rig. The results are presented in a readable graphical form and confirm high sensitivity and reliability of the method.

1 Introduction

Different faults such as shaft cracks, bearing failures, rotor misalignment, stator to rotor rub, etc., can affect the normal operation of rotating machinery. If not detected early, such failures can lead to dangerous damages or even catastrophic accidents. Therefore, it is important to constantly monitor the technical condition of a given rotating machine and quickly react to possible changes resulting from developing failures.

Traditional rotor fault detection methods are based on vibration signal analysis. Vibrations of the rotor are measured at the bearings by proximity probes (eddy current, reluctance, fiberoptic or laser sensors) and then amplified and analyzed at dynamic signal analyzers or specialized data acquisition devices equipped with dedicated software. Usually, fast Fourier transform (FFT) [1,2,3,4,5,6,7,8] is applied. This way, additional components at Fourier spectra increase [3,4,5, 9,10,11,12] in the overall amplitude of vibrations or phase variations [1, 7, 8, 11] can be observed and used as indications for rotor failure detection and warning. For these purposes steady-state (obtained at the constant rotating speed of the machine) [2, 3, 5, 6, 11] or transient (e.g., obtained during run-up or run-down of the machine) [7, 13,14,15,16,17,18] vibration data may be applied.

Soffker et al. [19] undertook comparison of the two approaches used for crack detection in rotating machinery: signal-based and model-based. As a modern model-based technique, the PI-observer-based method was used. Also a novel signal-based approach, based on support vector machine (SVM) and wavelets as an example for a modern machine learning technique, was introduced. When compared to complicated model-based [20,21,22,23,24,25], modal testing [26, 27] or non-traditional [13, 14, 28,29,30,31,32] techniques, the methods based on vibration signal analysis are quick, low cost and simple. They utilize popular, commonly used measurement equipment and well-established computational procedures and software. They may be applied continuously online during normal (steady-state) machine operation. Therefore, they have already found and are expected to extend their practical applications in different real-life rotor damage detection problems.

First research reports on signal-based methods appeared at early eighties. Bently and Muszynska [11] observed changes in absolute shaft position, vibration amplitude and steadily increasing 1${\times }$ component in the FFT spectra. The appearance of 1${\times }$ component has been also confirmed by Werner [8]. Saavedra and Cuitino [6] conducted a theoretical and experimental analysis of horizontally rotating shafts demonstrating that the 2${\times }$ component at the FFT spectrum appears at half the first critical speed value if the transverse shaft crack develops. The 2${\times }$ component has been also studied by Allen and Bohanick [9], Bently and Muszynska [1], Lazzeri et al. [12], Kulesza and Sawicki [2]. Additional components in the vibration spectra due to the crack have been reported by Bachschmid et al. [10], Ishida et al. [33], and Sinou and Lees [27]. Patel and Darpe [5] reported a stronger 1${\times }$ component in axial and torsional frequency responses in case of parallel misalignment and very strong 3${\times }$ component in case of angular misalignment. Szolc et al. [34] used Monte Carlo numerical simulations of coupled nonlinear lateral–torsional–axial vibrations of the rotor with transverse crack to generate dynamic responses for various possible crack locations and depths. To detect and localize the crack, Szolc et al. applied and compared four identification methods: the nearest-point method (NP), the Nedler–Mead method (NM), the orthogonal projection method (OP) and the local sample method (LS).

Another signal-based method for shaft crack detection has been proposed by Gasch and Liao [35]. This method analyzes changes in orbit shapes of the cracked rotating shaft. Vibration signal of the shaft is decomposed into forward and backward orbits of 1${\times }$, 2${\times }$ and 3${\times }$ frequencies, and a continuous monitoring of the backward harmonics can indicate the crack. Changes in orbit shapes indicating different rotor faults have been also considered by Patel and Darpe [5], Goldman et al. [36], Sinou and Lees [27], Wang et al. [37], Al-Shudeifat et al. [38], Han and Chu [39].

Investigating different variants of the method of orbit shape changes in a two-disk accelerating/decelerating shaft, Al-Shudeifat [40] recently observed an interesting phenomenon of additional backward whirl frequencies. These frequencies appeared not below any critical forward whirl frequency (as usually accepted), but just above the forward whirl frequencies, and only in the presence of shaft crack. These observations have been verified experimentally and explained theoretically by sign changes in gyroscopic matrices of the disks.

Nevertheless, the fast Fourier transform remains a common approach, when signal-based damage detection methods are applied. More sophisticated signal processing techniques, like auto-/cross-correlation or power spectral density functions, i.e., the techniques based on statistical data analysis, are less popular.

Ha et al. [41] utilized auto-correlation functions with properly selected windowing and time synchronous averaging for condition monitoring of planetary gears in window turbines. They were able to identify a fault signature in the planet’s tooth even in a case when the amount of the available stationary vibration data was limited. Ni et al. [42] considered auto-/cross-correlation functions of multiple excitations applied to a mechanical structure. The functions were divided into two parts: the time-variant one associated with unit response functions depending on structural parameters, and the time-invariant one depending on the energy of the excitation force. By using these auto-/cross-correlation functions and the model updating technique, Ni et al. [42] were able to identify small cracks in a steel structure. A simple technique based on auto-correlation functions of the vibration data obtained from the cracked bar was proposed by Ramsagar and Pardue [43]. The effectiveness of this method was demonstrated experimentally for a set of aluminum bars with different depths of a crack. Similar technique was used by Zubaydi et al. [44] to detect small cracks in stiffened plates being the models of ship hulls. Comparing auto-correlation functions of healthy and cracked plates, they confirmed the effectiveness of this simple method, especially in the presence of external disturbances and measurement noise. Zhang and Schmidt [45] introduced a correlation function matrix, consisting of cross-correlation functions between combinations of the vibration responses measured at different points of the 12-bar mechanical structure. Defining a special damage index for this matrix-based damage indicator, they confirmed numerically the ability of the method not only to detect but also to locate the local stiffness changes in the structure.

The application of correlation function-based signal processing techniques for rotor fault detection problems is not reported frequently. A possible use of auto-correlation functions to average vibration signals obtained from the rotating shaft was suggested by Gosiewski and Sawicki in [46]. In [47] the authors used the decorrelation technique, based on power spectral density functions, to separate vibration signals from the superposed signal. Seibold and Weinert [25] utilized auto-correlation functions to compare the outputs of extended Kalman filters in a filter bank and thus to locate the crack along the length of a shaft. Sekhar [31] defined the coherence measure based on auto-correlation functions to estimate the probability of shaft cracks in a rotor.

The present paper introduces a new signal-based approach for rotor fault detection [48,49,50,51]. The method is based on auto-correlation and power spectral density functions of the vibration signals measured at the bearings of the rotating shaft. Environmental signals (e.g., external disturbances, sensor noise etc.) affecting the operation of the machine are also included in the diagnostic model. By proper signal transformations including the calculation of squared amplitude gains of measured signals, the method is able to eliminate the influence of adverse disturbances on a diagnostic model of the machine. This way, the effectiveness of damage indications can be considerably improved. The ability to reject the influence of external disturbance signals on the diagnostic model is a unique feature of the proposed method which differs it from other traditional, signal-based diagnostic methods.

The method was developed by Lindstedt [48, 49] and applied successfully to various diagnostic problems of turbine blades [48,49,50,51,52,53] and jet engines [54]. The present paper unifies the mathematical foundations of the method and explains its possible application for rotor fault detection problems. Provided numerical and experimental results confirm its high effectiveness and reliability when applied to shaft crack detection.

2 Mathematical foundations

2.1 Squared amplitude gain of signals

In diagnostics of machines, the technical condition $\mathbf{A}(\vartheta )$ of a given mechanical structure can be evaluated based on vector $\mathbf{y}(t)$ of operational signals$y_k (t)$ measured by sensors, $k=1,2,\ldots ,n_\mathrm{m}$. The information about the ambient environment affecting the operation of this structure (external disturbances, sensor noise, etc.) can be presented as vector $\mathbf{x}(t)$ of environmental signals$x_l (t)$, $l=1,2,\ldots ,n_\mathrm{u}$. Here, $n_\mathrm{m}$ and $n_\mathrm{u}$ are the numbers of operational and environmental signals.

Fig. 1

Operational and environmental signals in two time intervals

Environmental signals $\mathbf{x}(t)$ disturb the normal operation of the machine and affect also operational signals $\mathbf{y}(t)$. Therefore, the technical condition $\mathbf{A}(\vartheta )$ of the machine can be defined by the mutual relationship between signals $\mathbf{y}(t)$ and $\mathbf{x}(t)$ at the current moment $\vartheta _1$ of the diagnostic time interval and at the moment $\vartheta _0$ of the beginning of this time interval [49]

$$\begin{aligned} \mathbf{A}(\vartheta )=\mathbf{f}(\mathbf{y}(t)_{\vartheta _0 },\mathbf{x}(t)_{\vartheta _0 },\mathbf{y}(t)_{\vartheta _1 },\mathbf{x}(t)_{\vartheta _1 }) \end{aligned}$$

(1)

where $\mathbf{A}(\vartheta )$ is the matrix of parameters that define the technical condition of the machine, t is time in terms of Newton’s definition (for diagnostic examinations) and $\vartheta$ is time in terms of Bergson’s definition (for diagnostic inference).

This relation between signals $\mathbf{y}(t)$ and $\mathbf{x}(t)$ can be presented in the form of the following state equation

$$\begin{aligned} {{\dot{\mathbf{y}}}}(t)_\vartheta =\mathbf{A}(\vartheta )\mathbf{y}(t)_\vartheta +\mathbf{B}(\vartheta )\mathbf{x}(t)_\vartheta \end{aligned}$$

(2)

where $\mathbf{B}(\vartheta )$ is the matrix of coefficients that define how intensely the environment affects the given machine.

For a given pair of signals $y_k (t)$ and $x_l (t)$, the relations given by Eq. (2) can be transformed to the following form

$$\begin{aligned} y_k (s)=G_{kl} (s)x_l (s) \end{aligned}$$

(3)

where $y_k (s)$ and $x_l (s)$ are Laplace’s transforms of time signals $y_k (t)$ and $x_l (t)$ (having initial conditions equal to zero) and $G_{kl} (s)$ is a transfer function defining the relation between $y_k (s)$ and $x_l (s)$.

From the basic properties of power spectral density analysis, the squared amplitude gain $W^{2}(\omega )$ of the operational signal $y_k (t)$ related to the environmental signal $x_l (t)$ can be obtained as [55]

$$\begin{aligned} W^{2}(\omega )=\left| {G_{kl} (j\omega )} \right| ^{2}=\frac{S_{yy} (\omega )}{S_{xx} (\omega )} \end{aligned}$$

(4)

where $G_{kl} (j\omega )$ is the frequency response version of transfer function $G_{kl} (s)$, $j\omega$ is the imaginary part of complex variable s and $S_{yy} (\omega )$, $S_{xx} (\omega )$ are power spectral density functions of signals $y_k (t)$ and ${x}_{l}(t)$.

Using Wiener–Khinchin theorem, power spectral density functions $S_{yy} (\omega )$ and $S_{xx} (\omega )$ can be calculated as Fourier transforms of the corresponding auto-correlation functions $R_{yy} (\tau )$ and $R_{xx} (\tau )$ [55]

$$\begin{aligned} S_{yy} (\omega )={\mathbb {F}}\left[ {R_{yy} (\tau )} \right] , \quad S_{xx} (\omega )={\mathbb {F}}\left[ {R_{xx} (\tau )} \right] \end{aligned}$$

(5)

where

$$\begin{aligned} R_{yy} (\tau )= & {} \mathop {\int }_{-\infty }^\infty {y_k (t)y_k (t-\tau )d\tau }, \nonumber \\ R_{xx} (\tau )= & {} \mathop {\int }_{-\infty }^\infty {x_l (t)x_l (t-\tau )d\tau } \end{aligned}$$

(6)

and ${\mathbb {F}}\left[ {f(\tau )} \right]$ denotes Fourier transform of a time function $f(\tau )$ and $\tau$ is time shift variable.

Equations (2)–(4) may be seen as different diagnostic models of a given machine as they express relations between operational $y_k (t)$ and environmental $x_l (t)$ signals on the one hand and technical parameters of the machine $\mathbf{A}(\vartheta )$ on the other.

The relation defined with Eq. (4) is particularly important as it can be used to eliminate environmental signals $x_l (t)$ from the diagnostic model of the machine. This is explained in detail in the next section.

2.2 Elimination of environmental signals from the diagnostic model

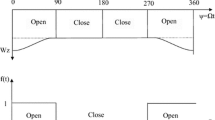
Consider two time intervals $\Delta t_1$ and $\Delta t_2$ ($\Delta t_1 =\Delta t_2)$ at which operational $y_k (t)$ and environmental $x_k (t)$ signals are analyzed (Fig. 1). According to Eq. (4) the squares of amplitude gains $W_1^2 (\omega )$, $W_2^2 (\omega )$ of signal $y_k (t)$ related to signal $x_l (t)$ in time intervals $\Delta t_1$, $\Delta t_2$ can be calculated as

$$\begin{aligned} W_1^2 (\omega )=\frac{S_{yy1} (\omega )}{S_{xx1} (\omega )}, \quad W_2^2 (\omega )=\frac{S_{yy2} (\omega )}{S_{xx2} (\omega )} \end{aligned}$$

(7)

where $S_{yy1} (\omega )$, $S_{xx1} (\omega )$ and $S_{yy2} (\omega )$, $S_{xx2} (\omega )$ are power spectral density functions of $y_k (t)$ and $x_l (t)$ signals in subsequent time intervals $\Delta t_1$ and $\Delta t_2$. Note that $S_{xx1} (\omega )$ and $S_{xx2} (\omega )$ functions cannot be calculated since environmental signal $x_l (t)$ is not measured directly. However, if a very short time distance $\Delta t_0$ between time intervals $\Delta t_1$ and $\Delta t_2$ is assumed, then power spectral density functions $S_{xx1} (\omega )$ and $S_{xx2} (\omega )$ can be considered as equal, i.e.,

$$\begin{aligned} S_{xx1} (\omega )=S_{xx2} (\omega ) \end{aligned}$$

(8)

This assumption can be explained by the observation that if the time distance $\Delta t_0$ between time intervals $\Delta t_1$ and $\Delta t_2$ is short, then environmental signal $x_l (t)$ in those time intervals may be considered as unchanged.

Including Eq. (7), a new diagnostic model $W_{21}^2 (\omega )$ describing the technical condition of the tested machine can be introduced in the following form

$$\begin{aligned} W_{21}^2 (\omega )=\frac{W_2^2 (\omega )}{W_1^2 (\omega )} \end{aligned}$$

(9)

Applying Eqs. (8) and (9) yields

$$\begin{aligned} W_{21}^2 (\omega )=\frac{S_{yy2} (\omega )}{S_{yy1} (\omega )} \end{aligned}$$

(10)

Note that by taking the quotient of $W_2^2 (\omega )$ and $W_1^2 (\omega )$ the power spectral density functions $S_{xx1} (\omega )$, $S_{xx2} (\omega )$ of environmental signals $x_l (t)$ have been removed from the new diagnostic model $W_{21}^2 (\omega )$. This way, the influence of environmental signals $x_l (t)$ on the new model $W_{21}^2 (\omega )$ has been eliminated. Of course, the new model still describes the technical condition of the tested machine, as it relates operational $y_k (t)$, environmental $x_k (t)$ signals and parameters $\mathbf{A}(\vartheta )$ of the machine (retrace the sequel of Eqs. (3), (4), (7) and (10). However, this model is evaluated using only measured operational signals $y_k (t)$, with no need to include direct measurements of environmental signals $x_l (t)$. What is more important, environmental signals do not disturb diagnostic indications of the new model, although they still disturb operational signals $y_k (t)$.

2.3 Condition monitoring based on the new diagnostic model

In order to use the proposed diagnostic model for condition monitoring, the operational signals $y_k (t)$ of a given machine are measured and sampled with time period $h>0$. Then, prescriptive numbers N of signal samples in two adjacent time intervals $\Delta t_1$ and $\Delta t_2$ are collected into two separable sets $y_{k1} (n)$ and $y_{k2} (n)$, $n=0,1,2,\ldots ,N$. The number N of signal samples in each set must be chosen carefully to ensure proper statistical assessment of measured operational signals $y_{k1} (n)$ and $y_{k2} (n)$. Next, to reduce frequency leakage, signals $y_{k1} (n)$ and $y_{k2} (n)$ are scaled by Hanning window $H_\mathrm{w} (n)$

$$\begin{aligned} H_\mathrm{w} (n)=\frac{1}{2}\left( {1-\cos \left( {2\pi \frac{n}{N}} \right) } \right) , \quad n=0,1,2,\ldots ,N\nonumber \\ \end{aligned}$$

(11)

to form new signals $y_{\mathrm {H}k1} (n)$ and $y_{\mathrm {H}k2} (n)$

$$\begin{aligned} y_{\mathrm {H}k1} (n)=H_\mathrm{w} (n)y_{k1} (n), \quad y_{\mathrm {H}k2} (n)=H_\mathrm{w} (n)y_{k2} (n)\nonumber \\ \end{aligned}$$

(12)

Then, discrete auto-correlation functions $R_{yy1} (m)$, $R_{yy2} (m)$ of the scaled signals $y_{\mathrm {H}k1} (n)$ and $y_{\mathrm {H}k2} (n)$ are calculated, as follows

$$\begin{aligned} R_{yy1} (m)= & {} \sum _{n=0}^{N-1} {y_{\mathrm {H}k1} } (n)y_{\mathrm {H}k1} (n-m),\nonumber \\ R_{yy2} (m)= & {} \sum _{n=0}^{N-1} {y_{\mathrm {H}k2} } (n)y_{\mathrm {H}k2} (n-m) \end{aligned}$$

(13)

where $m=-\,(N-1),\ldots ,-1,0,1,\ldots ,+(N-1)$.

Discrete auto-correlation functions $R_{yy1} (m)$, $R_{yy2} (m)$ are then approximated with smooth approximating functions, to obtain analytical representations $R_{yy1} (\tau )$, $R_{yy2} (\tau )$. As approximating functions the polynomials may be used [50, 51], resulting in the following forms of the auto-correlation functions:

$$\begin{aligned} R_{yy1} (\tau )= & {} a_r \tau ^{r}+{a}_{r-1} \tau ^{(r-1)}+\cdots +a_1 \tau +a_0, \nonumber \\ R_{yy2} (\tau )= & {} b_r \tau ^{r}+b_{r-1} \tau ^{(r-1)}+\cdots +b_1 \tau +b_0\nonumber \\ \end{aligned}$$

(14)

where $a_j$, $b_j$ are coefficients of the polynomials, $j=0,1,2,\ldots ,r$.

The order r of the polynomials should be selected carefully—too low order will result in inaccurate approximations, too high order—in an excessive number of polynomial coefficients and longer calculation times.

Based on analytical representations, the auto-correlation functions $R_{yy1} (\tau )$, $R_{yy2} (\tau )$ Laplace transforms ${\mathbb {F}}\left[ {R_{yy1} (\tau )} \right]$, ${\mathbb {F}}\left[ {R_{yy2} (\tau )} \right]$, and power spectral density functions $S_{yy1} (\omega )$, $S_{yy2} (\omega )$ are calculated according to Eq. (5). Next, the power spectral density functions $S_{yy1} (\omega )$, $S_{yy2} (\omega )$ are introduced into Eq. (15). For polynomial approximation, the diagnostic model $W_{12}^2 (\omega )$ is obtained in the following form

$$\begin{aligned} W_{21}^2 (\omega )= & {} \frac{S_{yy2} (\omega )}{S_{yy1} (\omega )}\nonumber \\= & {} \frac{B_r s^{r}+B_{r-1} s^{r-1}+\cdots +B_1 s+B_0 }{A_r s^{r}+A_{r-1} s^{r-1}+\cdots +A_1 s+A_0 }\nonumber \\ \end{aligned}$$

(15)

where

$$\begin{aligned} B_j= & {} b_{r-j} (r-j)!, \quad A_j =a_{r-j} (r-j)!, \nonumber \\ j= & {} 0,1,2,\ldots ,r \end{aligned}$$

(16)

The technical condition of the machine is then evaluated by calculating relative changes $\Delta A_j$, $\Delta B_j$ in model parameters, defined as follows

$$\begin{aligned} \Delta A_j =\frac{A_j -\bar{{A}}_j }{\bar{{A}}_j }, \quad \Delta B_j =\frac{B_j -\bar{{B}}_j }{\bar{{B}}_j } \end{aligned}$$

(17)

where $A_j$, $B_j$ are values of the $W_{21}^2 (\omega )$ model parameters evaluated at the moment $\vartheta _1$ and $\bar{{A}}_j$, $\bar{{B}}_j$ are mean values of these parameters evaluated during subsequent measurements within the period between $\vartheta _0$ (beginning of the monitoring process) and $\vartheta _1$ (the current moment at the monitoring process).

2.4 Damage maps

To simplify the evaluation of technical condition of a given machine, relative changes $\Delta A_j$, $\Delta B_j$ of $W_{21}^2 (\omega )$ diagnostic model are classified into three damage threshold ranges and presented in a convenient graphical way, termed as a damage map [52, 53]. The damage map of the machine is created as described below.

The three damage threshold ranges are defined with mean $\overline{\Delta A} _j$, $\overline{\Delta B} _j$ and standard deviation $\sigma _{A_j }$, $\sigma _{B_j }$ values of relative changes $\Delta A_j$, $\Delta B_j$, where

$$\begin{aligned} \overline{\Delta A} _j =\frac{1}{K}\sum _k^K \Delta A_j (k), \quad \overline{\Delta B} _j =\frac{1}{K}\sum _k^K \Delta B_j (k)\nonumber \\ \end{aligned}$$

(18)

and

$$\begin{aligned}&\sigma _{A_j } =\sqrt{\frac{1}{K}\sum _k^K {\left( {\Delta A_j (k)-\overline{\Delta A} _j } \right) ^{2}} }, \nonumber \\&\quad \sigma _{B_j } =\sqrt{\frac{1}{K}\sum _k^K {\left( {\Delta B_j (k)-\overline{\Delta B} _j } \right) ^{2}} } \end{aligned}$$

(19)

Here, $\Delta A_j (k)$ and $\Delta B_j (k)$ are relative changes in model parameters evaluated at time moment $\vartheta _k$, $\vartheta _0 \le \vartheta _k \le \vartheta _1$, and K is the number of those evaluations.

Fig. 2

Test rig: a photograph, b schematic of the rotor, c schematic of tested shafts: 2-ball bearings; 3-eddy current position sensors; 7-tested shaft

The three damage threshold ranges are assumed as

$$\begin{aligned} \overline{\Delta A} _j \pm \sigma _{A_j }, \quad \overline{\Delta A} _j \pm 2\sigma _{A_j }, \quad \overline{\Delta A} _j \pm 3\sigma _{A_j } \end{aligned}$$

(20)

for $\Delta A_j$, and

$$\begin{aligned} \overline{\Delta B} _j \pm \sigma _{B_j }, \quad \overline{\Delta B} _j \pm 2\sigma _{B_j }, \quad \overline{\Delta B} _j \pm 3\sigma _{B_j } \end{aligned}$$

(21)

for $\Delta B_j$.

The damage map is then created in a form of a color table of K rows and 2r columns, where each row contains color indications of whether at a given time moment $\vartheta _k$ the value of a given relative change $\Delta A_j$ and $\Delta B_j$ falls within one of the three damage ranges. The colors in subsequent cells in a given row are assigned as follows:

• 1. If at a given time moment $\vartheta _k$, relative changes $\Delta A_j$ or $\Delta B_j$ are within the first damage threshold range, i.e., if

  $$\begin{aligned}&\left( {\overline{\Delta A} _j -\sigma _{A_j } } \right) \le \Delta A_j \le \left( {\overline{\Delta A} _j +\sigma _{A_j } } \right) \quad \hbox {or}\nonumber \\&\left( {\overline{\Delta B} _j -\sigma _{B_j } } \right) \le \Delta B_j \le \left( {\overline{\Delta B} _j +\sigma _{B_j } } \right) \end{aligned}$$

  (22)

  then the indication of the respective relative change $\Delta A_j$ or $\Delta B_j$ in a given kth row, jth column becomes green.

• 2. If at a given time moment $\vartheta _k$, relative changes $\Delta A_j$ or $\Delta B_j$ are within the second damage threshold range, then the indication of the respective relative change $\Delta A_j$ or $\Delta B_j$ in a given kth row, jth column becomes dark blue.

• 3. If at a given time moment $\vartheta _k$, relative changes $\Delta A_j$ or $\Delta B_j$ are within the third damage threshold range, then the indication of the respective relative change $\Delta A_j$ or $\Delta B_j$ in a given kth row, jth column becomes red.

• 4. If at a given time moment $\vartheta _k$, relative changes $\Delta A_j$ or $\Delta B_j$ are above the third damage threshold range, then the indication of the respective relative change $\Delta A_j$ or $\Delta B_j$ in a given kth row, jth column becomes black.

It is clear that damage maps defined in this way should be predominantly green for a healthy machine. For the machine with any damage in structure, the predominant colors should be red and black.

3 Experimental test rig

The proposed damage detection method has been verified experimentally at a shaft crack detection test rig utilized at Bialystok University of Technology (Fig. 2a). The main component of the rig is a rotor supported by two ball bearings 2 and driven by an adjustable-speed electric motor 9 (Fig. 2b). The rotor consists of three parts connected by cones 5, flanges 6 and screws to ensure axial symmetry of the rotor on the one hand, and quick and simple reconfiguration of tested shafts 7 on the other. The outermost parts of the rotor are two short shafts with balancing disks 4 attached to them. The shafts are the unchanging components of the rotor, and they are supported by the bearings. The middle part of the rotor is the tested shaft 7, which can be changed. Shafts of different diameters and lengths with or without transverse cracks can be attached to the unchanging parts of the rotor (Fig. 2c). This way, different configurations of the rotor can be tested. Radial positions of the shaft near the left bearing are measured by two eddy current sensors 3, rotated by $45^{\circ }$ from horizontal and vertical axes (Fig. 2a).

Fig. 3

Finite element model of the rotor: a discretization of the shaft, b shaft cross section at the crack, c models of tested shafts

During the experiments, three configurations of the rotor have been tested (2c): Cnf1 with uncracked shaft and Cnf2, Cnf3 with cracked shafts. In Cnf2 the crack is located at the 1/4 shaft length to the left, and in Cnf3—at the 1/4 shaft length to the right. The length of the tested shaft is 250 mm, and its diameter is 16 mm. A thin notch simulating the crack is cut perpendicularly to the shaft axis using the electrodischarging machining. The relative depth of the crack is $\mu =25$%, where $\mu =a/d$, and a is absolute crack depth, d is diameter of shaft cross section.

4 Model of the rotor

Simulation tests of a finite element model of the cracked rotor have been performed to numerically evaluate the effectiveness of the proposed method. The model of the rotor (Fig. 3) has been formulated using the methodology presented in [2, 56,57,58].

The shaft is discretized into $n=53$ elements of equal lengths having 6 degrees of freedom at each node (Fig. 3a). These are beam finite elements with circular cross sections. The two disks are modeled as rigid bodies of given masses and moments of inertia. The rotor is supported by two ball bearings located between 10th and 11th, and 44th and 45th nodes. Vertical and horizontal displacements of the shaft are measured by two proximity sensors located at the 15th and 43rd nodes.

Breathing cracks can be introduced into the 24th or 32nd finite elements (Cnf2 or Cnf3 configuration, see Figs. 2c, 3c), by using the stress energy release rate approach proposed in [2, 56,57,58]. The model of the crack is schematically presented in Fig. 3b.

Fig. 4

Simulation frequency response of the uncracked rotor, $\mu =0$% (Cnf1): a no noise, b$\sigma =10^{-7}$ m noise

Fig. 5

Simulation frequency response of the cracked rotor $\mu =25$% (Cnf2): a no noise, b$\sigma =10^{-7}$ m noise

Fig. 6

Simulation frequency response of the cracked rotor $\mu =25$% (Cnf3): a no noise, b$\sigma =10^{-7}$ m noise

After assembling shaft elements and including bearing and disk dynamics, the rotor-bearing system in local coordinates can be presented with the following equation of motion:

$$\begin{aligned} \mathbf{M}\ddot{\mathbf{q}}+(\mathbf{D}_\mathrm{d} +\varOmega \mathbf{D}_\mathrm{g}){ {\dot{\mathbf{q}}}}+\mathbf{K}[\mathbf{q}(t)]\mathbf{q}=\mathbf{G}+\mathbf{P}_\mathrm{u} \end{aligned}$$

(23)

where $\mathbf{M}$, $\mathbf{D}_\mathrm{d}$, $\mathbf{D}_\mathrm{g}$,$\mathbf{K}[\mathbf{q}(t)]$ are mass, damping, gyroscopic and stiffness matrices; $\mathbf{G}$ and $\mathbf{P}_\mathrm{u}$ are vectors of gravity and unbalance; $\mathbf{q}$ is a vector of rotor displacements; and $\varOmega$ is the rotational speed. Here $\mathbf{M}$, $\mathbf{D}_\mathrm{d}$, $\mathbf{D}_\mathrm{g}$,$\mathbf{K}[\mathbf{q}(t)]$ are $6n\times 6n$ dimensional matrices, and $\mathbf{G}$, $\mathbf{P}_\mathrm{u}$, $\mathbf{q}$ are $6n\times 1$ dimensional vectors. Due to the breathing mechanism of the crack, the stiffness matrix $\mathbf{K}[\mathbf{q}(t)]$ is not constant but depends on rotor displacements $\mathbf{q}(t)$ which are in turn time dependent. To evaluate the forces on the crack edge, the new response vector $\mathbf{q}$ is used to find the response in the rotor-fixed coordinates ${q}^{\mathrm {r}}$. The nodal forces P are then presented by:

$$\begin{aligned} \left[ {P} \right] =\left[ {K} \right] ^{r}\left\{ {q} \right\} ^{r} \end{aligned}$$

(24)

Details about the breathing mechanism of the crack are well explained in [2, 56]. The components of the matrices are given in “Appendix 1” section.

Fig. 7

Simulated shaft positions at $\varOmega =800$ rpm, a no noise, b$\sigma =10^{-7}$ m noise

5 Simulation results

Using the FE model of the rotor presented in Fig. 3, vibration responses of the rotor have been calculated at the constant rotational speed of $\varOmega =800$ rpm.

The parameters of the rotor have been assumed as follows: Young’s modulus $E=208$ GPa, density $\rho =7850$ kg/m3, Poisson’s ratio $\nu =0.3$, radial stiffness and damping coefficients of the bearings $k_{\mathrm{b}} =3.4\times 10^{6}$ N/m, $d_{\mathrm{b}} =10$ Ns/m, and rotor eccentricity $\varepsilon =7\times 10^{-5}$ m. The simulations have been conducted for the rotor without the shaft crack (Cnf1) and with the crack of depth values $\mu =25$% (Cnf2 and Cnf3). To simulate measurement disturbances, additional white noise of standard deviation $\sigma =10^{-7}$ m has been added to the calculated vibration responses.

5.1 Simulation frequency response

To initially validate the correctness of the model, simulation frequency responses of the rotor have been calculated and are presented in Figs. 4a, b, 5a, b and 6a, b. Note that the results shown in Figs. 4b, 5b and 6b have been disturbed with an additional white noise of $\sigma =10^{-7}$ m.

As can be seen in Fig. 4a, b simulation vibration response of the uncracked rotor contains only one strong frequency component located at 1${\times }$ synchronous frequency of the rotor, i.e., at $f=13.3$ Hz ($\varOmega =800$ rpm). This is a typical response of a linear model of the rotor with no crack.

In the simulated response of the cracked rotor, additional 2${\times }$ and 4${\times }$ frequency peaks appear, as can be seen in Figs. 5a, b and 6a, b. These 2${\times }$ and 4${\times }$ components result from the nonlinear breathing mechanism of the crack.

5.2 Simulation damage maps

Simulated shaft positions in y axis with and without noise are presented in Fig. 7a, b. These positions have been calculated for the rotor rotating with a constant speed of $\varOmega =800$ rpm. It can be seen (the zoomed portions of Fig. 7) that the vibration amplitudes of the uncracked as well as the cracked rotor are almost the same, and the 25% deep crack cannot be detected by searching for possible changes in vibration amplitude or in the orbits. Therefore, the proposed method based on auto-correlation functions is applied and tested by simulations.

According to the method, the vibration response of the rotor is analyzed in two separate time intervals $\Delta t_1$ and $\Delta t_2$ (Fig. 8). These time intervals are applied in the following manner: $\Delta t_1$ is located to the left from a recognized peak value, and $\Delta t_2$—to the right. The number n of signal samples in each time interval is constant and is selected arbitrarily to cover the most of the increasing/decreasing parts of the vibration response during one revolution of the rotor. For the rotating speed of 800 rpm, the number of samples is $n=299$, while the sampling frequency $f=8000$ Hz.

Fig. 8

Time intervals for auto-correlation calculations–simulated vertical positions of the shaft rotating at $\varOmega =800$ rpm with no noise

Fig. 9

Simulation auto-correlation functions of a selected vibration peak: a at time interval $\Delta t_1$, no noise, b at time interval $\Delta t_2$, no noise, c at time interval $\Delta t_1$, $\sigma =10^{-7}$ m noise, b at time interval $\Delta t_2$, $\sigma =10^{-7}$ m noise

Shaft vibrations $y_{k1} (n)$ and $y_{k2} (n)$ in each time interval $\Delta t_1$, $\Delta t_2$ are scaled by Hanning window (Eq. 11), and then auto-correlation functions $R_{yy1} (m)$, $R_{yy2} (m)$ of the obtained signals $y_{\mathrm {H}k1} (n)$, $y_{\mathrm {H}k2} (n)$ are calculated (Eq. 13). Example functions $R_{yy1} (m)$, $R_{yy2} (m)$ obtained for both time intervals of a selected vibration peak are shown in Fig. 9. It is obvious that the direct comparison of the auto-correlation functions is difficult. Therefore, their analytical representations $R_{yy1} (\tau )$, $R_{yy2} (\tau )$ are calculated (Eq. 14) and relative changes $\Delta A_j$, $\Delta B_j$ in model parameters (Eq. 17) are used to assess the appearance of a probable shaft crack. After several initial calculations, the order r of the approximating polynomials (Eq. 14) has been chosen as $r=6$ resulting in the coefficient of determination $R^{2}>0.997$. Next, threshold ranges (Eq. 20) for individual parameter changes $\Delta A_j$, $\Delta B_j$ are calculated and damage maps are created. Auto-correlation analysis is conducted in a series of $K=30$ subsequent peaks. The results obtained for each peak in a series are averaged over the number of peaks. The number of $K=30$ peaks is selected to ensure a statistically representative data sample.

Fig. 10

Simulation damage map of the uncracked rotor (Cnf1); $\varOmega =800$ rpm

Fig. 11

Simulation damage maps (no noise) at $\varOmega =800$ rpm: a uncracked rotor (Cnf1), b, c cracked rotor (Cnf2 and Cnf3)

Damage maps obtained for the three considered configurations of the rotor are presented in Figs. 10, 11 and 12. Figure 10 explains the structure of the damage map for the uncracked shaft (Cnf1). The map consists of 30 rows indicating the location of relative changes $\Delta A_j$, $\Delta B_j$ within respective threshold ranges $\overline{\Delta A} _j \pm \sigma _{A_j }$, $\overline{\Delta A} _j \pm 2\sigma _{A_j }$, $\overline{\Delta A} _j \pm 3\sigma _{A_j }$ and $\overline{\Delta B} _j \pm \sigma _{B_j }$, $\overline{\Delta B} _j \pm 2\sigma _{B_j }$, $\overline{\Delta B} _j \pm 3\sigma _{B_j }$ at 30 vibration peaks. Damage maps for other rotor configurations are created in a similar manner (Figs. 11, 12). Figures 11 (with no noise) and 12 (with $\sigma =10^{-7}$ m noise) contain two sets of 30 peak series registered for each rotor configuration (Cnf1–Cnf3). Rotation numbers at which vibration peaks are analyzed have been chosen freely (in a randomized way).

The indications of a possible shaft crack in the rotor shown in Fig. 11 (with no noise) are clearly visible. The damage maps of the healthy rotor (Cnf1) are predominantly green, while the maps of the cracked rotor (Cnf2, Cnf3) are predominantly black. For a noisy case, similar indications are observed (Fig. 12)—damage maps of the cracked rotor are completely different than the maps of the cracked rotor. These changes in damage maps reflect the technical condition of the rotor and confirm the effectiveness of the proposed method in the simulated case.

Fig. 12

Simulation damage maps ($\sigma =10^{-7}$ m noise) at $\varOmega =800$ rpm: a uncracked rotor (Cnf1), b, c cracked rotor (Cnf2 and Cnf3)

6 Experimental results

6.1 Experimental frequency response

Frequency responses of the rotor obtained experimentally are presented in Fig. 13a–c. As can be seen experimental vibration response of the uncracked rotor contains not only the 1${\times }$ synchronous frequency of the rotor located at $f=13.3$ Hz ($\varOmega =800$ rpm) but also its multiples at 2${\times }$, 3${\times }$, 4${\times }$. These additional 2${\times }$, 3${\times }$, 4${\times }$ components are the main differences in frequency responses of the uncracked rotor obtained experimentally and by simulations (compare Figs. 4 and 13). In real rotor systems, these additional components appear as a result of inevitable nonlinearities that are always present even in healthy rotors [17, 26].

As can be seen in Fig. 13, frequency responses of the uncracked as well as the cracked rotor are almost the same. Therefore, it becomes clear that the changes in the frequency response of the rotor (appearance of additional frequency components or increase in their amplitudes) cannot be used as reliable shaft crack indications.

Fig. 13

Experimental frequency responses of the rotor, a uncracked rotor (Cnf1), b, c cracked rotor (Cnf2 and Cnf3)

6.2 Experimental damage maps

Example time histories of vertical shaft positions obtained for the rotor rotating with a constant speed of 800 rpm are shown in Fig. 14. The evident difference between the responses in Fig. 14 is in the amplitudes of vibration. However, there is no clear trend in these changes—the amplitude for the cracked shaft may be larger (Cnf3) or smaller (Cnf2) than for the uncracked (Cnf1) shaft. This observation is true for other experimentally registered cases, not shown in Fig. 14, and confirms, what has already been noticed in Sect. 5.2 (and in literature), that the amplitude changes cannot be considered as reliable shaft crack indications. Note also that the obtained vibration responses are disturbed with some measurement noise. Therefore, the proposed method may be applied, expecting that due to its ability to eliminate the influence of external disturbances, and independence on absolute amplitude values, the obtained crack indications will be more robust.

Fig. 14

Experimental shaft positions at $\varOmega =800$ rpm

According to the method, also in the experimental case the vibration response of the rotor is analyzed in two separate time intervals $\Delta t_1$ and $\Delta t_2$ (Fig. 15). To detect the peaks, a simple procedure is applied in which the measured vibration response is approximated with a sine function.

Fig. 15

Time intervals for auto-correlation calculations–experimental vertical positions of the shaft rotating at $\varOmega =800$ rpm

Example auto-correlation functions $R_{yy1} (m)$, $R_{yy2} (m)$ are shown in Fig. 16. The differences between these functions obtained for the uncracked and cracked rotor are larger than in the simulated case (compare Figs. 9 and 16), yet again their analytical representations $R_{yy1} (\tau )$, $R_{yy2} (\tau )$ are calculated (Eq. 14) and relative changes $\Delta A_j$, $\Delta B_j$ in model parameters (Eq. 17) are used to create damage maps and assess the possible appearance of a shaft crack.

Fig. 16

Experimental auto-correlation functions of a selected vibration peak: a at time interval $\Delta t_1$, b at time interval $\Delta t_2$

Experimental damage maps obtained for the three considered configurations of the rotor are presented in Fig. 17. The indications of a possible shaft crack in the rotor shown in Fig. 17 are clearly visible. The damage maps of the healthy rotor (Cnf1) are predominantly green. The maps of the cracked rotor (Cnf2, Cnf3) are predominantly black. Again the predominant colors in each map reflect the technical condition of the rotor and confirm the effectiveness of the proposed method also in the experimental case.

Fig. 17

Experimental damage maps at $\varOmega =800$ rpm: a uncracked rotor (Cnf1), b, c cracked rotor (Cnf2 and Cnf3)

When comparing the simulation and experimental results, it appears that the proposed method is even more sensitive to shaft cracks when applied experimentally than when introduced in a simulation procedure. As can be seen in experimentally obtained Fig. 17b, c damage maps are almost black. Similar damage maps with mostly black areas are obtained in an undisturbed simulation case in Fig. 11. For noisy simulation results in Fig. 12, the damage maps are only red/blue for the case of the cracked shaft.

This suggests that the white noise added to the simulation data does not accurately regenerate the real disturbances that are present in the tested rotating machine. Furthermore, the practical sensitivity of the method may be even higher than predicted by simulation calculations. This is because the mathematical model does not include all physical phenomena that exist in a real rotor.

Therefore, it is expected that the practical applicability of the method will by high enough to detect not only large ($\mu >25$%) but also small cracks. However, to check and confirm this expectations, experimental tests for rotors of different shaft crack depths and locations are required and are underway.

7 Conclusions

The rotor fault detection method presented in the paper is based on auto-correlation and power spectral density functions of the rotor vibration response measured at the bearings. The response is analyzed in two separate time intervals. When the intervals are in a close vicinity to each other, the influence of external disturbances is eliminated. Therefore, each change in the parameters of the diagnostic model shall be interpreted as the change in the technical condition of the machine.

Shaft crack indications are clearly readable and presented in a form of distinctive color maps, where the predominant green implies the healthy shaft, and the predominant black—the cracked shaft. The exact locations of the colors at the damage maps may be different, as the diagnostic thresholds are defined with mean and standard deviation, i.e., with statistic parameters. Therefore, not the exact locations but predominance of a given color are important. The rotations at which vibration peaks are analyzed can be chosen freely, yet still the obtained damage maps clearly reflect the technical condition of the rotor.

Provided experimental and simulation results confirm that the method is able to reliably indicate the fault even in the presence of variable amplitude values and relatively high measurement disturbances. The method is simple and uses only the measured vibration data. No initial preparation of the rotor for tests is required. The machine can be monitored continuously online. This gives chance for future practical implementation of the method.

However, at the current state of its development, the method cannot indicate the depth or location of the shaft crack. It can only warn about a possible malfunction of the rotor, i.e., it can inform a diagnostic staff, that the overhaul of the machine is required (when the damage map is predominantly blue and red), or that the replacement of the rotor can be considered (when the damage map is predominantly red and black).

The efficiency of the method has been confirmed only for shaft crack detection problems. Based on the positive results obtained, it is expected that the method can also accurately predict the appearance of other malfunctions, e.g., rubbing or misalignment. However, experimental verification is needed, which is underway.

Appendix 1: Matrices of the rotor model

The forms of the matrices introduced in the motion Eq. (23) are explained below.

Symmetrical inertia matrix of the shaft finite element:

$$\begin{aligned} \mathbf{M}=\rho l\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {m_{1,1} }&{} {m_{1,2} }&{} {m_{1,3} }&{} {m_{1,4} }&{} \cdots &{} {m_{1,11} }&{} {m_{1,12} } \\ &{} {m_{2,2} }&{} {m_{2,3} }&{} {m_{2,4} }&{} \cdots &{} {m_{2,11} }&{} {m_{2,12} } \\ &{} &{} {m_{3,3} }&{} {m_{3,4} }&{} \cdots &{} {m_{3,11} }&{} {m_{3,12} } \\ &{} &{} &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ &{} &{} &{} &{} &{} {m_{11,11} }&{} {m_{11,12} } \\ \hbox {sym.}&{} &{} &{} &{} &{} &{} {m_{12,12} } \\ \end{array} }} \right] ,\nonumber \\ \end{aligned}$$

(A.1)

where the nonzero elements lying on the main diagonal and above it are as follows:

$$\begin{aligned}&m_{1,1} =\frac{A}{3},\quad m_{1,2} =\frac{A}{6},\\&m_{2,2} =\frac{13A}{35}+\frac{6I_3 }{5l^{2}},\quad m_{2,6} =\frac{11Al}{210}+\frac{I_3 }{10l},\\&m_{2,8} =\frac{9A}{70}+\frac{I_3 }{5l^{2}},\quad m_{2,12} =\frac{-13Al}{420}+\frac{I_3 }{10l}, \\&m_{3,3} =\frac{13A}{35}+\frac{6I_2 }{5l^{2}},\quad m_{3,5} =\frac{-11Al}{210}-\frac{I_2 }{10l},\\&m_{3,9} =\frac{9A}{70}-\frac{6I_2 }{5l^{2}},\quad m_{3,11} =\frac{13Al}{420}-\frac{I_2 }{10l}, \\&m_{4,4} =\frac{I_1 }{3},\quad m_{4,10} =\frac{I_1 }{6}, \\&m_{5,5} =\frac{Al^{2}}{105}+\frac{2I_2 }{15},\quad m_{5,9} =-\,m_{3,11},\\&m_{5,11} =\frac{-Al^{2}}{140}-\frac{I_2 }{30},\\&m_{6,6} =\frac{Al^{2}}{105}+\frac{2I_3 }{15},\quad m_{6,8} =-\,m_{2,12},\\&m_{6,12} =\frac{-Al^{2}}{140}-\frac{I_3 }{30},\\&m_{7,7} =m_{1,1},\\&m_{8,8} =m_{2,2},\quad m_{8,12} =-\,m_{2,6},\\&m_{9,9} =m_{3,3},\quad m_{9,11} =-\,m_{3,5},\\&m_{10,10} =m_{4,4},\\&m_{11,11} =m_{5,5},\\&m_{12,12} =m_{6,6}. \end{aligned}$$

Symmetrical stiffness matrix of the shaft finite element:

$$\begin{aligned} \mathbf{K}=\frac{E}{l}\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {k_{1,1} }&{} {k_{1,2} }&{} {k_{1,3} }&{} {k_{1,4} }&{} \cdots &{} {k_{1,11} }&{} {k_{1,12} } \\ &{} {k_{2,2} }&{} {k_{2,3} }&{} {k_{2,4} }&{} \cdots &{} {k_{2,11} }&{} {k_{2,12} } \\ &{} &{} {k_{3,3} }&{} {k_{3,4} }&{} \cdots &{} {k_{3,11} }&{} {k_{3,12} } \\ &{} &{} &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ &{} &{} &{} &{} &{} {k_{11,11} }&{} {k_{11,12} } \\ \hbox {sym.}&{} &{} &{} &{} &{} &{} {k_{12,12} } \\ \end{array} }} \right] ,\nonumber \\ \end{aligned}$$

(A.2)

where the nonzero elements lying on the main diagonal and above it are as follows:

$$\begin{aligned}&k_{1,1} =A, \quad k_{1,7} =-\,k_{1,1},\\&k_{2,2} =\frac{12I_3 }{l^{2}},\quad k_{2,6} =\frac{6I_3 }{l},\\&k_{2,8} =-\,k_{2,2},\quad k_{2,12} =k_{2,6},\\&k_{3,3} =\frac{12I_2 }{l^{2}},\quad k_{3,3} =\frac{-6I_2 }{l},\\&k_{3,9} =-\,k_{3,3},\quad k_{3,11} =k_{3,5},\\&k_{4,4} =\frac{I_1 }{2\left( {1+\nu } \right) },\quad k_{4,10} =-\,k_{4,4},\\&k_{5,5} =4I_2,\quad k_{5,9} =-\,k_{3,5},\quad k_{5,11} =2I_2,\\&k_{6,6} =4I_3,\quad k_{6,8} =-\,k_{2,6},\quad k_{6,12} =2I_3,\\&k_{7,7} =k_{1,1},\\&k_{8,8} =k_{2,2},\quad k_{8,12} =-\,k_{2,6},\\&k_{9,9} =k_{3,3},\quad k_{9,11} =k_{3,5},\\&k_{10,10} =k_{4,4}, \\&k_{11,11} =k_{5,5},\\&k_{12,12} =k_{6,6}. \end{aligned}$$

Anti-symmetrical gyroscopic matrix of the shaft finite element:

$$\begin{aligned} \mathbf{D}_G =2\rho \left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {d_{1,1} }&{} {d_{1,2} }&{} {d_{1,3} }&{} {d_{1,4} }&{} \cdots &{} {d_{1,11} }&{} {d_{1,12} } \\ &{} {d_{2,2} }&{} {d_{2,3} }&{} {d_{2,4} }&{} \cdots &{} {d_{2,11} }&{} {d_{2,12} } \\ &{} &{} {d_{3,3} }&{} {d_{3,4} }&{} \cdots &{} {d_{3,11} }&{} {d_{3,12} } \\ &{} &{} &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ &{} &{} &{} &{} &{} {d_{11,11} }&{} {d_{11,12} } \\ \hbox {antisym.}&{} &{} &{} &{} &{} &{} {d_{12,12} } \\ \end{array} }} \right] ,\nonumber \\ \end{aligned}$$

(A.3)

where the nonzero elements lying above diagonal are as follows:

$$\begin{aligned} d_{2,3}= & {} -\frac{13Al}{35},\quad d_{2,5} =-\frac{11Al^{2}}{210},\quad d_{2,9} =-\frac{9Al}{70},\\ d_{2,11}= & {} -\frac{13Al^{2}}{420},\quad d_{3,6} =d_{2,5},\quad d_{3,8} =-\,d_{2,9},\\ d_{3,12}= & {} d_{2,11},\quad d_{5,6} =-\frac{Al^{3}}{105},\quad d_{5,8} =d_{2,11}, \\ d_{5,12}= & {} -\frac{Al^{3}}{140},\quad d_{6,9} =d_{2,11},\quad d_{6,11} =-\,d_{5,12}, \\ d_{8,9}= & {} d_{2,3},\quad d_{8,11} =-\,d_{2,5},\\ d_{9,12}= & {} -\,d_{2,5},\quad d_{11,12} =d_{5,6}. \end{aligned}$$

In the above formulas A is the cross-sectional area of the shaft element, l is the length of the shaft element, $I_1$, $I_2$ and $I_3$ are the moments of inertia of the cross section of the shaft element with respect to the $x_1$, $x_2$, $x_3$ axis, $\rho$ is the density, E the Young’s modulus and $\nu$ the Poisson’s ratio of the rotor material.