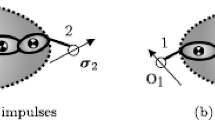Index-3 divide-and-conquer algorithm for efficient multibody system dynamics simulations: theory and parallel implementation

Abstract

There has been a growing attention to efficient simulations of multibody systems, which is apparently seen in many areas of computer-aided engineering and design both in academia and in industry. The need for efficient or real-time simulations requires high-fidelity techniques and formulations that should significantly minimize computational time. Parallel computing is one of the approaches to achieve this objective. This paper presents a novel index-3 divide-and-conquer algorithm for efficient multibody dynamics simulations that elegantly handles multibody systems in generalized topologies through the application of the augmented Lagrangian method. The proposed algorithm exploits a redundant set of absolute coordinates. The trapezoidal integration rule is embedded into the formulation and a set of nonlinear equations need to be solved every time instant. Consequently, the Newton–Raphson iterative scheme is applied to find the system coordinates and joint constraint loads in an efficient and highly parallelizable manner. Two divide-and-conquer-based mass-orthogonal projections are performed then to circumvent the effect of constraint violation errors at the velocity and acceleration level. Sample open- and closed-loop multibody system test cases are investigated in the paper to confirm the validity of the approach. Challenging simulations of multibody systems featuring long kinematic chains are also performed in the work to demonstrate the robustness of the algorithm. The details of OpenMP-based parallel implementation on an eight-core shared memory computer are presented in the text and the parallel performance results are extensively discussed. Significant speedups are obtained for the simulations of small- to large-scale multibody open-loop systems. The mentioned features make the proposed algorithm a good general purpose approach for high-fidelity, efficient or real-time multibody dynamics simulations.

1 Introduction

1.1 Background

Computational efficiency has traditionally been a major concern of researchers developing algorithms for multibody dynamics simulations. Considerable improvements in computer architectures have taken place during the last years, enabling the efficient simulation of larger and more complex mechanical systems. Also the expectations about the performance that a multibody software tool can deliver have grown at the same pace. Nowadays, there are a large number of industry and academic applications that require efficient and accurate code execution. Some of these demand real-time performance, such as Hardware- and Human-in-the-Loop (HiL) settings, e.g., simulators and test benches for physical components in the automotive industry. HiL applications require specialized multibody formulations to decrease the turnaround time associated with the evaluation of multibody system dynamics. Real-time multibody simulators are typically connected to virtual reality environments and motion platforms to provide realistic feedback to users. Therefore, the efficiency of multibody dynamics algorithms is determinant for the ability of these applications to meet their performance requirements.

1.2 Related work

The availability of distributed computing environments and parallel architectures, equipped with inexpensive multi-core processors and graphical processor units, has encouraged researchers to develop parallel multibody dynamics algorithms [35]. Featherstone’s Divide-and-Conquer Algorithm (DCA) [16] is among the most popular ones. Its binary-tree structure allows distributing the computations among several processing cores in a scalable and relatively simple way. In open chains with n bodies, it can achieve $O\left( \log \left( n \right) \right)$ performance if enough processors are available [25]. The DCA constitutes the building block of dozens of methods and parallel codes for multibody dynamics [26]. Some of these introduced changes in the way originally proposed to deal with closed kinematic loops [34] and other constraints [37]. Others extended the algorithm to enable the consideration of flexible bodies [25, 32], discontinuities in system definition [33], and contacts [5]. Computational improvements to the initial algorithm have been published as well such as techniques to keep constraint drift under control [24, 31] and optimized variants of the algorithm for computer architectures with reduced computational resources [10]. The practical applications of the DCA are multiple and range from the simulation of simple linkages and multibody chains to molecular dynamics [29, 38].

The DCA scheme does not specify the way in which the system of equations of motion must be formulated and several approaches can be followed to do this. A spatial formulation of the Newton–Euler equations was used in the initial definition of the algorithm and subsequently adopted by many of the formalisms that were derived from it, e.g., [10, 34]. However, other expressions of the dynamics equations can be used as well. The Articulated Body Algorithm (ABA) [15] was combined with the DCA in [6] to deliver significant speedups in computation times. Hamilton’s canonical equations were used in [7, 8] and showed good properties regarding the satisfaction of kinematic constraints. Augmented Lagrangian methods with configuration- and velocity-level mass-orthogonal projections have also been employed [28]; the resulting algorithm has been proven to behave robustly during the simulation of mechanical systems with redundant constraints and singular configurations. It should be noted however that there are alternative, non-DCA, ways to formulate the equations of motion for parallel computing environments. The first logarithmic order algorithm (called Constraint Force Algorithm) for computation of the dynamics of multibody chain systems was proposed in [18, 19]. In [17], the authors investigated and expanded the CFA algorithm to deal with arbitrary joint types. It was found that the CFA could be written in terms of articulated body inertias [15]. It was also found that recursive calculation of articulated body inertias for short branches off the main chain can be calculated efficiently. Recent developments in this context can be found in [27], where a modified version of the CFA algorithm is presented for the simulation of flexible multibody systems in arbitrary topologies.

Augmented Lagrangian methods are common in multibody literature. Many of them were derived from the penalty formulation in [3], in which the constraint reactions were made proportional to the violation of kinematic constraints at the configuration, velocity, and acceleration levels. An augmented Lagrangian algorithm was also proposed in [3] that complemented the penalty formulation with a set of modified Lagrange multipliers, evaluated iteratively, to satisfy more accurately the kinematic constraints and obtain stable and precise simulations for wider ranges of penalty factors. Mass-orthogonal projections were introduced in [4] to ensure the satisfaction of the constraints down to machine-precision levels. An index-3 algorithm, in which the dynamics equations were combined with the Newmark integration formulas to produce an iterative method in Newton–Raphson form was described in [4] as well. Such method was later improved to deliver real-time performance in [11, 12], and to handle nonholonomic constraints in [13]. This index-3 augmented Lagrangian algorithm with projections of velocities and accelerations (ALi3p) has shown very good efficiency and robustness in the simulation of multibody systems in real-time industrial applications, e.g., [14]. The ALi3p and the DCA were first combined for the simulation of open-loop chains in [30]. This work greatly extends the early work by delivering a generalized formulation for multi-rigid body system dynamics.

1.3 Contribution

In this paper, we propose a novel and generalized index-3 divide and conquer formulation for multi-rigid body dynamics that elegantly handles redundant constraints and potential singular configurations that may appear in such simulations. Unlike the methods reported in e.g., [26, 28] that follow an index-1 approach, here we deliberately make use of an index-3 augmented Lagrangian formulation. Instead of formulating the system dynamics at the acceleration level, here, the system coordinates are the primary variables of the problem. Accordingly, the projected quantities are the system generalized velocities and accelerations, instead of the generalized coordinates and velocities. The proposed algorithm exploits a redundant set of absolute coordinates and leads to three broad and highly parallelizable computational sub-procedures: Newton–Raphson phase for the solution of nonlinear discretized equations of motion and two stages of mass-orthogonal projections for improving the quality of the solutions. Various numerical test cases are presented in the text to indicate the properties of the formulation. Small-scale open- and closed-loop systems are investigated and analyzed, and the results are verified against an external solver. Long-chain dynamics is investigated in order to report the accuracy and stability of the formulation for large-scale systems. The stability of the algorithm is demonstrated for a chain composed of 128 links at step size $\Delta t=0.01\text { s}$. Sequential and parallel performance results are presented in the text to illustrate the ability of the proposed algorithm to reduce the turnaround time of the simulations. This work also includes the analysis of scalability of the proposed parallel algorithm and reports significant speedups captured on a parallel shared memory computer with eight cores. The successful combination of index-3 formulation and recursive divide-and-conquer algorithm may be essential in performing efficient or real-time simulations of complex multibody systems.

2 Equations of motion for constrained spatial systems

Before embarking on the divide-and-conquer formulation, the general form of the equations of motion for constrained spatial multibody system (MBS) is recalled. The system dynamics is formulated in terms of a set of absolute coordinates involving Euler parameters. Consider n bodies that form a multibody system (MBS). The composite set of generalized coordinates for the system is denoted as $\mathbf{q }=\left[ \mathbf{q }_1^T\quad \mathbf{q }_2^T\quad \ldots \quad \mathbf{q }_{n}^T\right] ^T$, where vector $\mathbf{q }$ contains the absolute coordinates of all bodies in the system. For a particular body i the vector of absolute coordinates can be written as a $7\times 1$ quantity $\mathbf{q }_i=\left[ \mathbf{r }_i^T,\mathbf{p }_i^T\right] ^T,\quad i=1,\ldots ,n$, where $\mathbf{r }_i=\left[ x_i\quad y_i\quad z_i\right] ^T$ refers to the global Cartesian coordinates of the body-fixed centroidal coordinate frame $(x_iy_iz_i)$ and $\mathbf{p }_i=\left[ e_{0i}\quad e_{1i}\quad e_{2i}\quad e_{3i}\right] ^T=\left[ e_{0i}\quad \mathbf{e }_i^T\right] ^T$ corresponds to a set of four Euler parameters that describe the orientation of body i with respect to the global reference frame $(x_0y_0z_0)$. Rigid bodies in an MBS system are interconnected by l joints. It is assumed that there are m holonomic (and scleronomic) constraint equations imposed on the system:

$$\begin{aligned} \varvec{{\Phi }}(\mathbf{q })= \begin{bmatrix} \varvec{{\Phi }}_1^T,\varvec{{\Phi }}_2^T,\ldots ,\varvec{{\Phi }}_{l}^T \end{bmatrix}^T =\mathbf{0 }_{m\times 1}. \end{aligned}$$

(1)

In the following derivations, there is a necessity to evaluate first and second time derivatives of constraint conditions expressed in Eq. (1). The velocity and acceleration constraint equations can be expressed as:

$$\begin{aligned}&\dot{\varvec{{\Phi }}}\equiv \varvec{{\Phi }}_{\mathbf{q }}\dot{\mathbf{q }}=\mathbf{0 }_{m\times 1}, \end{aligned}$$

(2)

$$\begin{aligned}&\ddot{\varvec{{\Phi }}}\equiv \varvec{{\Phi }}_{\mathbf{q }}\ddot{\mathbf{q }}+{\dot{\varvec{{\Phi }}}_{\mathbf{q }}\dot{\mathbf{q }}} =\varvec{{\Phi }}_{\mathbf{q }}\ddot{\mathbf{q }}-\pmb {\upgamma }=\mathbf{0 }_{m\times 1}, \end{aligned}$$

(3)

where $\varvec{{\Phi }}_{\mathbf{q }}$ is the constraint Jacobian matrix of size m and n. In addition, the Euler parameter normalization constraints must hold. For $i=1,\ldots ,n$ one may define position, velocity, and acceleration level constraint equations:

$$\begin{aligned} \Psi _i&\equiv \mathbf{p }_i^T\mathbf{p }_i-1=0, \end{aligned}$$

(4)

$$\begin{aligned} \dot{\Psi }_i&\equiv \mathbf{p }_i^T\dot{\mathbf{p }}_i=\left[ \mathbf{0 }_{1\times 3},\mathbf{p }_i^T\right] \begin{bmatrix}\dot{\mathbf{r }}_i \\ \dot{\mathbf{p }}_i\end{bmatrix}={\Psi }_{i\mathbf{q }_i}\dot{\mathbf{q }}_i=0, \end{aligned}$$

(5)

$$\begin{aligned} \ddot{\Psi }_i&\equiv \mathbf{p }_i^T\ddot{\mathbf{p }}_i+\dot{\mathbf{p }}_i^T\dot{\mathbf{p }}_i= \Psi _{i\mathbf{q }_i}\ddot{\mathbf{q }}_i-{\upnu }_i=0, \end{aligned}$$

(6)

where ${\Psi }_{i\mathbf{q }_i}$ is the normalization constraint Jacobian matrix of size $1\times 7$ and $\upnu _i$ is that part of the acceleration level constraint equation that is dependent on Euler parameters $\mathbf{p }_i$ and its time derivatives $\dot{\mathbf{p }}_i$. Let us define the following (singular) matrix for particular body i

$$\begin{aligned} \mathbf{M }_i=\begin{bmatrix} m_i\mathbf{I }_{3\times 3}&\mathbf{0 } \\ \mathbf{0 }&4\mathbf{G }_i^T\mathbf{J }'_i\mathbf{G }_i \\ \end{bmatrix},\quad i=1,\ldots ,n, \end{aligned}$$

(7)

where $m_i$ is the mass of body i, $\mathbf{J }'_i$ is the inertia matrix expressed with respect to centroidal coordinate frame $(x_iy_iz_i)$, and $\mathbf{G }_i=\left[ -\mathbf{e }_i,-\widetilde{\mathbf{e }}_i+e_{0i}\mathbf{I }_{3\times 3}\right]$ is a useful $3\times 4$ matrix that involves Euler parameters that fulfills the relation $\varvec{{\upomega }}^{'}_{i}=2\mathbf{G }_i\dot{\mathbf{p }}_i$ ($\varvec{{\upomega }}^{'}_{i}$ – angular velocity of body i expressed in the body-fixed coordinate frame) and $\widetilde{\mathbf{e }}_i$ is a skew-symmetric matrix. Then, the vector of generalized forces acting on body i can be expressed as:

$$\begin{aligned} \mathbf{Q }_i= \begin{bmatrix} \mathbf{f }_i \\ 2\mathbf{G }_i^T\mathbf{n }'_i-8\dot{\mathbf{G }}_i^T\mathbf{J }'_i\mathbf{G }_i\dot{\mathbf{p }}_i \end{bmatrix},\quad i=1,\ldots ,n. \end{aligned}$$

(8)

The active forces $\mathbf{f }_i$ acting on body i are expressed in the global reference frame ($x_0y_0z_0$), whereas active torques $\mathbf{n }'_i$ are expressed in the body-fixed centroidal coordinate frame. Finally, the Euler parameter form of constrained equations of motion for spatial multibody system can be expressed as: [23]

(9)

where $\varvec{{\upgamma }}$ and $\varvec{{\upnu }}$ are the stacked vectors defined in the following way: $\varvec{{\upgamma }}=\left[ \varvec{{\upgamma }}_1^T,\ldots ,\varvec{{\upgamma }}_l^T\right] ^T$ and $\varvec{{\upnu }}=\left[ \varvec{{\upnu }}_1^T,\ldots ,\varvec{{\upnu }}_n^T\right] ^T$. Additionally, the following terms are formed:

$$\begin{aligned} \mathbf{M }&=diag(\mathbf{M }_1,\ldots ,\mathbf{M }_n),\quad \mathbf{Q }=\begin{bmatrix}\mathbf{Q }_1^T,\ldots ,\mathbf{Q }_n^T\end{bmatrix}^T. \end{aligned}$$

(10)

Moreover, the vector of Lagrange multipliers $\varvec{{\uplambda }}$ that corresponds to constraint reactions at joints and the vector of Lagrange multipliers $\varvec{{\upmu }}$ associated with Euler normalization constraints are given as:

$$\begin{aligned} \pmb {\uplambda }= \begin{bmatrix} \pmb {\uplambda }_{\pmb {1}}^{\pmb {T}},\pmb {\uplambda }_{\pmb {2}}^{\pmb {T}},\pmb {\ldots }, \pmb {\uplambda }_{\pmb {l}}^{\pmb {T}} \end{bmatrix}_{m\times 1}^T,\quad \varvec{{\upmu }}= \begin{bmatrix} {\upmu }_1,{\upmu }_2,\ldots ,{\upmu }_{n} \end{bmatrix}_{n\times 1}^T.\nonumber \\ \end{aligned}$$

(11)

Please note that Eq. (9) demonstrates an index-1 form of constrained equations of motion for multi-rigid body systems. The actual index-3 equations of the algorithm put forward in this paper, which make use of the expressions and symbols recalled here, are detailed in Sect. 3.

3 Algorithm formulation

3.1 Two articulated rigid bodies

This subsection will serve as an introduction to the derivation of the divide-and-conquer-based formulation proposed in this paper. Specifically, consider two representative bodies A and B demonstrated in Fig. 1a. The bodies are connected to each other by joint 2 and form only a part of the whole multibody system. Body A and body B are also connected to the rest of multibody system by joint 1 and joint 3, respectively.

Fig. 1

Two articulated bodies and generalization in the form of compound bodies. a Two articulated bodies, b compound bodies

Equations of motion for constrained bodies A and B can be written similarly as in Eq. (9). For convenience that will become clear later in this section, the equations of motion for body A and B are exressed in the form of two functions $\mathbf{g }_A$ and $\mathbf{g }_B$:

$$\begin{aligned} \mathbf{g }_A\equiv \mathbf{M }_A\ddot{\mathbf{q }}_A+\mathbf{F }_A^{1} +\mathbf{F }_A^{2} +{{\Psi }_{A\mathbf{q }_A}^{T}}{\upmu }_A-\mathbf{Q }_A&= \mathbf{0 }, \end{aligned}$$

(12)

$$\begin{aligned} \mathbf{g }_B\equiv \mathbf{M }_B\ddot{\mathbf{q }}_B+\mathbf{F }_B^{2} +\mathbf{F }_B^{3} +{{\Psi }_{B\mathbf{q }_B}^{T}}{\upmu }_B-\mathbf{Q }_B&=\mathbf{0 }, \end{aligned}$$

(13)

where $\mathbf{F }_A^{1}$, $\mathbf{F }_A^{2}$ are constraint loads at joints 1 and 2, which are acting on body A, whereas the vectors $\mathbf{F }_B^{2}$, $\mathbf{F }_B^{3}$ correspond to constraint forces at joint 2 and 3 that are acting on body B. Moreover, the following conditions are hold

$$\begin{aligned} \mathbf{F }_A^{1}&={\varvec{{\Phi }}_{\mathbf{q }_A}^{1T}}\varvec{{\uplambda }}_1, \mathbf{F }_A^{2}={\varvec{{\Phi }}_{\mathbf{q }_A}^{2T}}\varvec{{\uplambda }}_2,\nonumber \\ \mathbf{F }_B^{2}&={\varvec{{\Phi }}_{\mathbf{q }_B}^{2T}}\varvec{{\uplambda }}_2, \mathbf{F }_B^{3}={\varvec{{\Phi }}_{\mathbf{q }_B}^{3T}}\varvec{{\uplambda }}_3. \end{aligned}$$

(14)

Let us also note that the equivalent mass matrices $\mathbf{M }_A$, $\mathbf{M }_B$ of size $7\times 7$ in Eqs. (12) and (13) are singular. This issue is particularly inconvenient for the developement of the divide-and-conquer algorithm. In this form, one cannot calculate absolute accelerations from the equations of motion. Later in this section, this problem will be alleviated by two-stage use of the augmented Lagrangian method. In this work, a single-step trapezoidal rule is employed to integrate the equations of motion for constrained multibody system. Although there are many single-step integrators used in multibody applications, the employed trapezoidal scheme proved to be a reasonable choice to keep a balance between computational requirements, accuracy, and stability of numerical calculations. The raised issues may be especially important in real-time applications [11, 12, 14]. The difference equations at the velocity and acceleration level can be written as

$$\begin{aligned} \dot{\mathbf{q }}&\!=\!\frac{2}{\Delta t}{\mathbf{q }}+\hat{\dot{\mathbf{q }}},\quad \text {where} \quad \hat{\dot{\mathbf{q }}}=-\Big (\frac{2}{\Delta t}\overline{\mathbf{q }}+\dot{\overline{\mathbf{q }}}\Big ), \end{aligned}$$

(15)

$$\begin{aligned} \ddot{\mathbf{q }}&\!=\!\frac{4}{\Delta t^2}{\mathbf{q }}+\hat{\ddot{\mathbf{q }}}, \quad \text {where} \quad \hat{\ddot{\mathbf{q }}}=-\Big (\frac{4}{\Delta t^2}\overline{\mathbf{q }}+\frac{4}{\Delta t}\dot{\overline{\mathbf{q }}}+\ddot{\overline{\mathbf{q }}}\Big ). \end{aligned}$$

(16)

Please note that subscripts indicating time instants have been intentionally omitted due to simplicity reasons. It is assumed that $\mathbf{q }_{k+1}\equiv \mathbf{q }$ (next time-instant) and $\mathbf{q }_{k}\equiv \overline{\mathbf{q }}$ (current time-instant), where k is the index associated with arbitrary kth time-instant. Now, let us introduce Eqs. (15), (16) into Eqs. (12) and (13) at the $k+1$ (next) time-instant. After scaling the resulting equations by $\frac{\Delta t^2}{4}$, we get

$$\begin{aligned}&\mathbf{M }_A\mathbf{q }_{A}+\frac{\Delta t^2}{4}\left( \mathbf{F }_{A}^{1}+\mathbf{F }_{A}^{2}+ {{\Psi }_{A\mathbf{q }_A}^{T}}{\upmu }_A-\mathbf{Q }_{A}+\mathbf{M }_A\hat{\ddot{\mathbf{q }}}_{A}\right) =\mathbf{0 }, \end{aligned}$$

(17)

$$\begin{aligned}&\mathbf{M }_B\mathbf{q }_{B}+\frac{\Delta t^2}{4}\left( \mathbf{F }_{B}^{2}+\mathbf{F }_{B}^{3}+ {{\Psi }_{B\mathbf{q }_B}^{T}}{\upmu }_B-\mathbf{Q }_{B}+\mathbf{M }_B\hat{\ddot{\mathbf{q }}}_{B}\right) =\mathbf{0 }. \end{aligned}$$

(18)

The algebraic relations (17) and (18) constitute a discretized form of equations of motion (12) and (13) expressed at the next time-instant. The relations form a system of nonlinear equations with positions $\mathbf{q }_A$, $\mathbf{q }_B$ and Lagrange multipliers as unknowns. The discretized equations may be solved through use of the Newton–Raphson procedure and by taking predicted positions, velocities, accelerations, and Lagrange multipliers as initial guesses for the next time-instant. The linearized form of Eqs. (17) and (18) can be written as:

$$\begin{aligned}&\underline{\check{\mathbf{M }}}_A\Delta \mathbf{q }_{A}+\frac{\Delta t^2}{4}\left( \Delta \mathbf{F }_{A}^{1}+\Delta \mathbf{F }_{A}^{2}+ \underline{{\Psi }}_{A\mathbf{q }_A}^{T}\Delta {\upmu }_A\right) \nonumber \\&\quad = -\frac{\Delta t^2}{4}\underline{\mathbf{g }}_A, \end{aligned}$$

(19)

$$\begin{aligned}&\underline{\check{\mathbf{M }}}_B\Delta \mathbf{q }_{B}+\frac{\Delta t^2}{4}\left( \Delta \mathbf{F }_{B}^{2}+\Delta \mathbf{F }_{B}^{3}+ \underline{{\Psi }}_{B\mathbf{q }_B}^{T}\Delta {\upmu }_B\right) \nonumber \\&\quad = -\frac{\Delta t^2}{4}\underline{\mathbf{g }}_B, \end{aligned}$$

(20)

where $\underline{\check{\mathbf{M }}}_A=\mathbf{M }_A-\frac{\Delta t}{2}\frac{\partial \mathbf{Q }_A}{\partial \mathbf{q }_A}-\frac{\Delta t^2}{4}\frac{\partial \mathbf{Q }_A}{\partial \dot{\mathbf{q }}_A}$, $\underline{\check{\mathbf{M }}}_B=\mathbf{M }_B-\frac{\Delta t}{2}\frac{\partial \mathbf{Q }_B}{\partial \mathbf{q }_B}-\frac{\Delta t^2}{4}\frac{\partial \mathbf{Q }_B}{\partial \dot{\mathbf{q }}_B}$ are non-invertible $7\times 7$ matrices and the terms $\frac{\partial \mathbf{Q }}{\partial \mathbf{q }}$, $\frac{\partial \mathbf{Q }}{\partial \dot{\mathbf{q }}}$ represent contribution of elastic and damping forces, respectively, provided that they exist. The quantities $\Delta \mathbf{q }_A=\mathbf{q }_A-\underline{\mathbf{q }}_A$, $\Delta \mathbf{q }_B=\mathbf{q }_B-\underline{\mathbf{q }}_B$ denote increments in positions. In turn, the vectors $\pmb {\Delta }\pmb {\uplambda }_1=\pmb {\uplambda }_1-\underline{\pmb {\uplambda }}_1$, $\Delta \pmb {\uplambda }_2=\pmb {\uplambda }_2-\underline{\pmb {\uplambda }}_2$, $\Delta \pmb {\uplambda }_3=\pmb {\uplambda }_3-\underline{\pmb {\uplambda }}_3$ are used to define the increments in constraint loads at joints $\Delta \mathbf{F }_A^1=\underline{\varvec{{\Phi }}}_{\mathbf{q }_A}^{1T}\Delta \pmb {\uplambda }_1$, $\Delta \mathbf{F }_A^2=\underline{\varvec{{\Phi }}}_{\mathbf{q }_A}^{2T}\Delta \pmb {\uplambda }_2$, and $\Delta \mathbf{F }_B^2=\underline{\varvec{{\Phi }}}_{\mathbf{q }_B}^{2T}\Delta \pmb {\uplambda }_2$, $\Delta \mathbf{F }_B^3=\underline{\varvec{{\Phi }}}_{\mathbf{q }_B}^{3T}\Delta \pmb {\uplambda }_3$. Moreover, the quantities $\Delta {\upmu }_A=\upmu _A-\underline{\upmu _A}$, $\Delta {\upmu }_B=\upmu _B-\underline{\upmu _B}$ represent the increments in Lagrange multipliers associated with normalization constraints. Let us note that the Newton–Raphson scheme is an iterative procedure, that is why we have used the underlined symbols to indicate the quantities from previous iteration within the same time-instant.

Now, let us turn our attention to the increments $\Delta {\upmu }_A$ and $\Delta {\upmu }_B$. The augmented Lagrangian method allows one to formulate the following relations

$$\begin{aligned} \begin{aligned}&\Delta \upmu _A=\upalpha {\Psi }_A(\mathbf{q }_A)\approx \upalpha (\underline{\Psi }_A+\underline{{\Psi }}_{A\mathbf{q }_A}\Delta \mathbf{q }_A), \\&\Delta \upmu _B=\upalpha {\Psi }_B(\mathbf{q }_B)\approx \upalpha (\underline{\Psi }_B+\underline{{\Psi }}_{B\mathbf{q }_B}\Delta \mathbf{q }_B), \end{aligned} \end{aligned}$$

(21)

where $\upalpha$ is a large penalty factor (usually of the order of $10^6$ – $10^9$) that affects convergence rate. The equations expressed in (21) may be directly introduced into Eqs. (19) and (20), respectively, to obtain an almost final algebraic form of discretized and linearized equations of motion:

$$\begin{aligned}&\underline{\check{\check{\mathbf{M }}}}_A\Delta \mathbf{q }_A+ \frac{\Delta t^2}{4}\left( \Delta \mathbf{F }_{A}^{1}+\Delta \mathbf{F }_{A}^{2}\right) \nonumber \\&\quad =-\frac{\Delta t^2}{4}(\underline{\mathbf{g }}_A-\underline{{\Psi }}_{A\mathbf{q }_A}^T\upalpha \underline{\Psi }_A), \end{aligned}$$

(22)

$$\begin{aligned}&\underline{\check{\check{\mathbf{M }}}}_B\Delta \mathbf{q }_B+ \frac{\Delta t^2}{4}\left( \Delta \mathbf{F }_{B}^{2}+\Delta \mathbf{F }_{B}^{3}\right) \nonumber \\&\quad =-\frac{\Delta t^2}{4}(\underline{\mathbf{g }}_B-\underline{{\Psi }}_{B\mathbf{q }_B}^T\upalpha \underline{\Psi }_B), \end{aligned}$$

(23)

where $\underline{\check{\check{\mathbf{M }}}}_A=\underline{\check{\mathbf{M }}}_A+\frac{\Delta t^2}{4}\underline{{\Psi }}_{A\mathbf{q }_A}^T\upalpha \underline{{\Psi }}_{A\mathbf{q }_A}$ and $\underline{\check{\check{\mathbf{M }}}}_B=\underline{\check{\mathbf{M }}}_B+\frac{\Delta t^2}{4}\underline{{\Psi }}_{B\mathbf{q }_B}^T\upalpha \underline{{\Psi }}_{B\mathbf{q }_B}$. Please note that this time the matrices $\underline{\check{\check{\mathbf{M }}}}_A$, $\underline{\check{\check{\mathbf{M }}}}_B$ are symmetric and positive definite, thus invertible. Therefore, one can write the following form of discretized equations of motion for body A and B:

$$\begin{aligned}&\Delta \mathbf{q }_A=\varvec{{\updelta }}_{i1}^{A}\Delta \mathbf{F }_A^1+\varvec{{\updelta }}_{i2}^{A} \Delta \mathbf{F }_A^2+\varvec{{\updelta }}_{i3}^{A},\quad i=1,2, \end{aligned}$$

(24)

$$\begin{aligned}&\Delta \mathbf{q }_B=\varvec{{\updelta }}_{i1}^{B}\Delta \mathbf{F }_B^2+\varvec{{\updelta }}_{i2}^{B}\Delta \mathbf{F }_B^3+\varvec{{\updelta }}_{i3}^{B},\quad i=1,2, \end{aligned}$$

(25)

where the following vector-matrix coefficients are defined:

$$\begin{aligned} \varvec{{\updelta }}_{i1}^A&=\varvec{{\updelta }}_{i2}^A=-\frac{\Delta t^2}{4}\underline{\check{\check{\mathbf{M }}}}_A^{-1}, \varvec{{\updelta }}_{i1}^B=\varvec{{\updelta }}_{i2}^B=-\frac{\Delta t^2}{4}\underline{\check{\check{\mathbf{M }}}}_B^{-1}, \end{aligned}$$

(26)

$$\begin{aligned} \varvec{{\updelta }}_{i3}^A&=-\frac{\Delta t^2}{4}\underline{\check{\check{\mathbf{M }}}}_A^{-1}(\underline{\mathbf{g }}_A-\underline{{\Psi }}_{A\mathbf{q }_A}^T\upalpha \underline{\Psi }_A),\nonumber \\ \varvec{{\updelta }}_{i3}^B&=-\frac{\Delta t^2}{4}\underline{\check{\check{\mathbf{M }}}}_B^{-1}(\underline{\mathbf{g }}_B-\underline{{\Psi }}_{B\mathbf{q }_B}^T\upalpha \underline{\Psi }_B) \end{aligned}$$

(27)

for $i=1,2$. The subscript i in Eqs. (24) and (25) means that the equations are valid for handle 1 or handle 2. Handle is a point on the physical or compound body where it has a force interaction with other bodies in the system or with the inertially invariant spatial environment through the presence of constraint loads arising from holonomic constraints. When a single, physical body, say A, is considered, handle 1 and 2 are located at the same point, i.e., at the center of mass of that body. In this case the subscript i could be suppressed, because Eq. (24) for $i=1$ and $i=2$ conveys the same information. Nevertheless, the subscripts are redundantly kept in this form to make the algorithm more consistent with its version for compound bodies. Additionally, please note that in general $\varvec{{\updelta }}_{i1}^A\ne \varvec{{\updelta }}_{i2}^A$ and $\varvec{{\updelta }}_{i1}^B\ne \varvec{{\updelta }}_{i2}^B$ for compound bodies considered later in this work. The equality relations expressed in Eqs. (26) and (27) are valid only for physical bodies when the assembly process is about to start.

3.2 Generalized formulation

Now, let us use equations (24) and (25) as a basis for further development. Specifically, let us consider a system of compound bodies A and B as depicted in Fig. 1b. Note that there are three Lagrange multipliers indicated in the figure. The vectors $\varvec{{\uplambda }}_1$ and $\varvec{{\uplambda }}_2$ correspond to the forces of interaction between body C and the rest of the multibody system, whereas constraint loads $\varvec{{\uplambda }}$ represent the forces of interaction between body A and B. Two physical bodies marked by the numbers 1 and 2 have been distinguished for each compound body A and B. The discretized and linearized form of equations of motion for the representative compound bodies A and B can be written in the form:

$$\begin{aligned} \Delta \mathbf{q }_A^{1}=\varvec{{\updelta }}_{11}^{A}\Delta \mathbf{F }_{A}^{1}+ \varvec{{\updelta }}_{12}^{A}\Delta \mathbf{F }_{A}^{2}+\varvec{{\updelta }}_{13}^{A}, \end{aligned}$$

(28)

$$\begin{aligned} \Delta \mathbf{q }_A^{2}=\varvec{{\updelta }}_{21}^{A}\Delta \mathbf{F }_{A}^{1}+ \varvec{{\updelta }}_{22}^{A}\Delta \mathbf{F }_{A}^{2}+\varvec{{\updelta }}_{23}^{A}, \end{aligned}$$

(29)

$$\begin{aligned} \Delta \mathbf{q }_B^{1}=\varvec{{\updelta }}_{11}^{B}\Delta \mathbf{F }_{B}^{1}+ \varvec{{\updelta }}_{12}^{B}\Delta \mathbf{F }_{B}^{2}+\varvec{{\updelta }}_{13}^{B}, \end{aligned}$$

(30)

$$\begin{aligned} \Delta \mathbf{q }_B^{2}=\varvec{{\updelta }}_{21}^{B}\Delta \mathbf{F }_{B}^{1}+ \varvec{{\updelta }}_{22}^{B}\Delta \mathbf{F }_{B}^{2}+\varvec{{\updelta }}_{23}^{B}. \end{aligned}$$

(31)

The objective of the first phase of the divide-and-conquer algorithm, called assembly phase, is to obtain the discretized form of equations of motion for the compound body C in the form:

$$\begin{aligned} \Delta \mathbf{q }_C^{1}=\varvec{{\updelta }}_{11}^{C}\Delta \mathbf{F }_{C}^{1}+ \varvec{{\updelta }}_{12}^{C}\Delta \mathbf{F }_{C}^{2}+\varvec{{\updelta }}_{13}^{C}, \end{aligned}$$

(32)

$$\begin{aligned} \Delta \mathbf{q }_C^{2}=\varvec{{\updelta }}_{21}^{C}\Delta \mathbf{F }_{C}^{1}+ \varvec{{\updelta }}_{22}^{C}\Delta \mathbf{F }_{C}^{2}+\varvec{{\updelta }}_{23}^{C}. \end{aligned}$$

(33)

The Lagrange multipliers $\varvec{{\uplambda }}$ associated with constraint equations $\varvec{{\Phi }}=\mathbf{0 }$ between body A and B can be found by using the augmented Lagrangian method:

$$\begin{aligned} \Delta \varvec{{\uplambda }}= & {} \varvec{{\uplambda }}-\underline{\varvec{{\uplambda }}}=\upalpha \varvec{{\Phi }}\approx \upalpha (\underline{\varvec{{\Phi }}}+\underline{\varvec{{\Phi }}}_{\mathbf{q }_A^{2}}\Delta \mathbf{q }_A^{2}+ \underline{\varvec{{\Phi }}}_{\mathbf{q }_B^{1}}\Delta \mathbf{q }_B^{1}).\nonumber \\ \end{aligned}$$

(34)

Then, substituting Eqs. (29) and (30) into Eq. (34) with the addition of Eq. (14) the following relation for increments in Lagrange multipliers is obtained

$$\begin{aligned} \Delta \varvec{{\uplambda }}=\mathbf{C }\varvec{{\Phi }}_{\mathbf{q }_A^2}\varvec{{\updelta }}_{21}^A\Delta \mathbf{F }_A^1+ \mathbf{C }\varvec{{\Phi }}_{\mathbf{q }_1^B}\varvec{{\updelta }}_{12}^B\Delta \mathbf{F }_B^2+\mathbf{C }\pmb {\upbeta }, \end{aligned}$$

(35)

where $\mathbf{C }=\left( \frac{1}{\upalpha }\mathbf{I }-\underline{\varvec{{\Phi }}}_{\mathbf{q }_A^2}\varvec{{\updelta }}_{22}^A\underline{\varvec{{\Phi }}}_{\mathbf{q }_A^2}^T -\underline{\varvec{{\Phi }}}_{\mathbf{q }_B^1}\varvec{{\updelta }}_{11}^B\underline{\varvec{{\Phi }}}_{\mathbf{q }_B^1}^T\right) ^{-1}$ and $\varvec{{\upbeta }}=\underline{\varvec{{\Phi }}}_{\mathbf{q }_A^2}\varvec{{\updelta }}_{23}^A+\underline{\varvec{{\Phi }}}_{\mathbf{q }_B^1}\varvec{{\updelta }}_{13}^B+\underline{\varvec{{\Phi }}}$. Please note that the inversion of matrix $\mathbf{C }$ exists, even in the case when constraint Jacobian matrices become rank deficient. Equation (35) is substituted back to Eqs. (28) and (31) to obtain the relations (32) and (33). The unknown matrix coefficients are recursively obtained as

$$\begin{aligned}&\varvec{{\updelta }}_{11}^C=\varvec{{\updelta }}_{11}^A+ \varvec{{\updelta }}_{12}^A\underline{\varvec{{\Phi }}}_{\mathbf{q }_{A}^2}^T\mathbf{C }\underline{\varvec{{\Phi }}}_{\mathbf{q }_{A}^2}\varvec{{\updelta }}_{21}^A, \end{aligned}$$

(36)

$$\begin{aligned}&\varvec{{\updelta }}_{12}^C=(\varvec{{\updelta }}_{21}^C)^T=\varvec{{\updelta }}_{12}^A\underline{\varvec{{\Phi }}}_{\mathbf{q }_{A}^2}\mathbf{C }\underline{\varvec{{\Phi }}}_{\mathbf{q }_{B}^1}\varvec{{\updelta }}_{12}^B, \end{aligned}$$

(37)

$$\begin{aligned}&\varvec{{\updelta }}_{22}^C=\varvec{{\updelta }}_{22}^B+ \varvec{{\updelta }}_{21}^B\underline{\varvec{{\Phi }}}_{\mathbf{q }_{B}^1}^T\mathbf{C }\underline{\varvec{{\Phi }}}_{\mathbf{q }_{B}^1}\varvec{{\updelta }}_{12}^B, \end{aligned}$$

(38)

$$\begin{aligned}&\varvec{{\updelta }}_{13}^C=\varvec{{\updelta }}_{13}^A+\varvec{{\updelta }}_{12}^A\underline{\varvec{{\Phi }}}_{\mathbf{q }_{A}^2}^T\mathbf{C }\varvec{{\upbeta }},\quad \varvec{{\updelta }}_{23}^C=\varvec{{\updelta }}_{23}^B+\varvec{{\updelta }}_{21}^B\underline{\varvec{{\Phi }}}_{\mathbf{q }_{B}^1}^T\mathbf{C }\varvec{{\upbeta }}. \end{aligned}$$

(39)

The divide-and-conquer algorithm developed here is composed of two computational stages: assembly and disassembly phase. Each phase is associated with the binary tree, which is connected to the topology of the mechanism (see [6, 16, 28, 33]). The first phase starts with the evaluation of matrix coefficients for individual bodies as in Eqs. (26) and (27). Then, the multibody system is assembled. The coefficients in Eqs. (36)–(39) form recursive formulae for coupling two physical or compound bodies A and B into one subassembly C by eliminating the constraint force between them. The process may be repeated and applied for all bodies that are included in the specified subset of bodies up to the moment when the whole MBS is constructed. Finally, a single assembly is obtained. This entity constitutes a representation of the entire multibody system modeled as a single assembly. The first phase finishes at this stage. Taking into account the boundary conditions, e.g., a connection of a chain to a fixed base body and a free floating terminal body, the second phase is started. At this stage, all constraint force increments $\Delta \varvec{{\uplambda }}$ and bodies’ positions $\Delta \mathbf{q }$ can be calculated by traversing the binary tree from root node up to leaves.

The Newton–Raphson method used here requires the evaluation of a tangent matrix and its inversion. Rather than computing the inverse of the tangent matrix, one solve the system of linear equations in which the increments $\Delta \mathbf{q }$ and $\Delta \varvec{{\uplambda }}$ are unknowns. One should note that the algorithm proposed in this paper does not really formulate an explicit tangent matrix and its inversion. In fact, the quantities are implicitly stored in a recursively generated sequence of coefficients $\varvec{{\updelta }}_{11}^C$, $\varvec{{\updelta }}_{12}^C$, $\varvec{{\updelta }}_{21}^C$, $\varvec{{\updelta }}_{22}^C$ expressed in Eqs. (36)–(39). If a regular Newton–Raphson method is used, the coefficients are updated in subsequent iterations. In this paper, we use a modified Newton–Raphson method, in which the tangent matrix (and its inverse) is held constant for a fixed number of iterations. This implies that the coefficients $\varvec{{\updelta }}_{11}^C$, $\varvec{{\updelta }}_{12}^C$, $\varvec{{\updelta }}_{21}^C$, $\varvec{{\updelta }}_{22}^C$ are constant and need not to be recomputed at every iteration. Such treatment significantly reduces the overall computational cost of the method, but it may slow down the convergence rate of the algorithm, especially, when an initial guess is improperly chosen. To be sufficiently close to the solution, we partially circumvent this effect by delivering the following initial approximations: $\mathbf{q }=\overline{\mathbf{q }}+\dot{\overline{\mathbf{q }}}\Delta t+\frac{1}{2}\ddot{\overline{\mathbf{q }}}\Delta t^2$, $\varvec{{\uplambda }}=\overline{\varvec{{\uplambda }}}$ that are computed by reusing the results that are already available. There may be unfortunate cases in which Newton–Raphson method can give highly inaccurate results or may be divergent. This situation is associated with ill-conditioning of the tangent matrix, which, in turn, indicates a pathological situation going on in a multibody system such as lock-up configuration or bifurcation point.

The iterations of the Newton–Raphson scheme presented here are continued up to the moment of convergence of the algorithm. Various stop criteria may be used. In this work, it is assumed that the convergence criterion is defined as $||\Delta \mathbf{q }||<\upepsilon$, where ||.|| is the Euclidean norm and $\upepsilon$ is a user specified tolerance. Usually 2–3 iterations are required to calculate a reasonable and stable solution for not very stringent requirements imposed on accuracy. It is worth noticing that at each iteration one has to update positions $\mathbf{q }=\underline{\mathbf{q }}+\Delta \mathbf{q }$ and Lagrange multipliers $\varvec{{\uplambda }}=\underline{\varvec{{\uplambda }}}+\Delta \varvec{{\uplambda }}$, $\varvec{{\upmu }}=\underline{\varvec{{\upmu }}}+\Delta \varvec{{\upmu }}$. Moreover velocities and accelerations are kept updated according to the difference equations (15), (16). Ultimately, the divide-and-conquer algorithm demonstrated here yields a set of positions $\mathbf{q }$ at the next time-instant that satisfy both dynamic equilibrium conditions as well as position level constraint equations.

Checking only the convergence of the positions is a common practice in multibody dynamics algorithms. Because the constraints are assumed to be holonomic (nonholonomic constraints would require a different treatment), a convergence in the positions would ensure the convergence of the Lagrange multipliers, especially if the system is not subjected to redundant constraints. Formally, the norm of the whole vector of increments $\left[ \begin{array}{cc}\Delta \mathbf{q }^T&\Delta \varvec{{\uplambda }}^T\end{array}\right] ^T$ could be used to provide a more reliable termination criterion instead of using the norm of $\Delta \mathbf{q }$ itself. The rate of convergence appears to be different for $\Delta \mathbf{q }$ and $\Delta \varvec{{\lambda }}$. The experience of the authors showed that when the Newton–Raphson scheme is convergent, the scaled norm of constraint forces $||\Delta \varvec{{\uplambda }}||\cdot \frac{\Delta t^2}{4}$ is approximately of the same order as the norm $||\Delta \mathbf{q }||$. Two consequences arise. Firstly, the convergence rate of the Lagrange multipliers is at least $\frac{\Delta t^2}{4}$ worse than the rate observed at the position level. Secondly, the smaller $\Delta t$ is, the greater the relative difference between $||\Delta \varvec{{\lambda }}||$ and $||\Delta \mathbf{q }||$ is.

3.3 Mass-orthogonal projections at the velocity level

In Sects. 3.1 and 3.2, constraint equations were imposed only at the position level. Velocities and accelerations were obtained as secondary variables through use of the difference equations (15), (16). So far no information is provided about first and second derivatives of constraint equations. It is expected that the constraint equations (2), (3) may be violated during the simulation. To circumvent this effect, mass-orthogonal projections at the velocity and acceleration level are employed [4, 11]. Usually this procedure is numerically expensive due to the iterative scheme involved in the calculations. For real-time applications, one needs a deterministic response. The mass-orthogonal projections are performed only once per integration step, just after the convergence of the Newton–Raphson procedure.

Fortunately, the calculations associated with projections can be organized in the same divide-and-conquer manner that is presented in Sects. 3.1 and 3.2. Moreover, there is a place for many computational savings. At this phase, there is no need to update the matrices $\varvec{{\updelta }}_{11}$, $\varvec{{\updelta }}_{12}$, $\varvec{{\updelta }}_{21}$, and $\varvec{{\updelta }}_{22}$ as defined in Eqs. (36)–(38). The qualitative and quantitative difference between mass-orthogonal projections scheme and the divide-and-conquer-based Newton–Raphson procedure lies in the definitions of bias terms (cf. $\varvec{{\updelta }}_{13}$, and $\varvec{{\updelta }}_{23}$) and the involved Lagrange multipliers.

Let us assume that the values $\dot{\mathbf{q }}^*$ represent perturbed quantities for which constraint equations $\varvec{{\dot{\Phi }}}$ are not completely satisfied after the convergence of the Newton–Raphson scheme. Mass-orthogonal projections [11, 12] for a two body example depicted in Fig. 1a can be written as:

$$\begin{aligned}&{\check{\mathbf{M }}}_A\dot{\mathbf{q }}_{A}+\frac{\Delta t^2}{4}\left( {\varvec{{\Phi }}}_{\mathbf{q }_A}^{1T}\varvec{{\upsigma }}_1+{\varvec{{\Phi }}}_{\mathbf{q }_A}^{2T}\varvec{{\upsigma }}_2+ {{\Psi }}_{A\mathbf{q }_A}^{T}{\upsigma }_{A}^N\right) \nonumber \\&\quad = {\check{\mathbf{M }}}_A\dot{\mathbf{q }}_{A}^*, \end{aligned}$$

(40)

$$\begin{aligned}&{\check{\mathbf{M }}}_B\dot{\mathbf{q }}_{B}+\frac{\Delta t^2}{4}\left( {\varvec{{\Phi }}}_{\mathbf{q }_B}^{2T}\varvec{{\upsigma }}_2+{\varvec{{\Phi }}}_{\mathbf{q }_B}^{3T}\varvec{{\upsigma }}_3+ {{\Psi }}_{B\mathbf{q }_B}^{T}{\upsigma }_{B}^N\right) \nonumber \\&\quad = {\check{\mathbf{M }}}_B\dot{\mathbf{q }}_{B}^*, \end{aligned}$$

(41)

where $\varvec{{\upsigma }}$ and $\upsigma ^{N}$ denote Lagrange multipliers that enforce velocity-level joint and normalization constraint equations, respectively. Please notice that there is a structural similarity between the relations (40), (41) and the expressions (19) (20) derived in the Newton–Raphson scheme. Now, let us approximate the values of the multipliers $\upsigma ^{N}_A$, $\upsigma ^{N}_B$ through use of the penalty method:

$$\begin{aligned} \upsigma _A^N\approx & {} \upalpha \dot{\Psi }_A=\upalpha \Psi _{A\mathbf{q }_A}\dot{\mathbf{q }}_A,\nonumber \\ \upsigma _B^N\approx & {} \upalpha \dot{\Psi }_B=\upalpha \Psi _{B\mathbf{q }_B}\dot{\mathbf{q }}_B. \end{aligned}$$

(42)

Upon substitution of Eq. (42) into Eqs. (40) and (41), we get

$$\begin{aligned}&\dot{\mathbf{q }}_A=\varvec{{\updelta }}_{i1}^{A}\mathbf{T }_A^1+\varvec{{\updelta }}_{i2}^{A}\mathbf{T }_A^2+\pmb {\uptheta }_{i3}^{A},\quad i=1,2, \end{aligned}$$

(43)

$$\begin{aligned}&\dot{\mathbf{q }}_B=\varvec{{\updelta }}_{i1}^{B}\mathbf{T }_B^2+\varvec{{\updelta }}_{i2}^{B}\mathbf{T }_B^3+\pmb {\uptheta }_{i3}^{B},\quad i=1,2, \end{aligned}$$

(44)

where the quantities $\varvec{{\updelta }}_{i1}^{A}$, $\varvec{{\updelta }}_{i2}^{A}$, $\varvec{{\updelta }}_{i1}^{B}$, and $\varvec{{\updelta }}_{i2}^{B}$ for $i=1,2$ are exactly the same as in Eq. (26) and pseudo-constraint forces at the velocity level are read as $\mathbf{T }_A^1={\varvec{{\Phi }}}_{\mathbf{q }_A}^{1T}\varvec{{\upsigma }}_1$, $\mathbf{T }_A^2={\varvec{{\Phi }}}_{\mathbf{q }_A}^{2T}\varvec{{\upsigma }}_2$, and $\mathbf{T }_B^2={\varvec{{\Phi }}}_{\mathbf{q }_B}^{2T}\varvec{{\upsigma }}_2$, $\mathbf{T }_B^3={\varvec{{\Phi }}}_{\mathbf{q }_B}^{3T}\varvec{{\upsigma }}_3$. The bias terms $\varvec{{\uptheta }}_{i3}^{A}$, $\varvec{{\uptheta }}_{i3}^{B}$ are calculated as:

$$\begin{aligned} \varvec{{\uptheta }}_{i3}^A={\check{\check{\mathbf{M }}}}_A^{-1}{{\check{\mathbf{M }}}}_A\dot{\mathbf{q }}_A^*, \quad \varvec{{\uptheta }}_{i3}^B={\check{\check{\mathbf{M }}}}_B^{-1}{{\check{\mathbf{M }}}}_B\dot{\mathbf{q }}_B^* ,\quad i=1,2, \end{aligned}$$

(45)

where ${\check{\check{\mathbf{M }}}}_A={\check{\mathbf{M }}}_A+\frac{\Delta t^2}{4}{{\Psi }}_{A\mathbf{q }_A}^T\upalpha {{\Psi }}_{A\mathbf{q }_A}$ and ${\check{\check{\mathbf{M }}}}_B={\check{\mathbf{M }}}_B+\frac{\Delta t^2}{4}{{\Psi }}_{B\mathbf{q }_B}^T\upalpha {{\Psi }}_{B\mathbf{q }_B}$.

Now, one can use the expressions (43), (44) derived for physical bodies in order to find analogous expressions for compound bodies. Such treatment will employ the divide-and-conquer methodology exposed in this paper. The mass-orthogonal projections for compound bodies A and B illustrated in Fig. 1b can be written as:

$$\begin{aligned} \dot{\mathbf{q }}_A^{1}=\varvec{{\updelta }}_{11}^{A}\mathbf{T }_{A}^{1}+ \varvec{{\updelta }}_{12}^{A}\mathbf{T }_{A}^{2}+\varvec{{\uptheta }}_{13}^{A}, \end{aligned}$$

(46)

$$\begin{aligned} \dot{\mathbf{q }}_A^{2}=\varvec{{\updelta }}_{21}^{A}\mathbf{T }_{A}^{1}+ \varvec{{\updelta }}_{22}^{A}\mathbf{T }_{A}^{2}+\varvec{{\uptheta }}_{23}^{A}, \end{aligned}$$

(47)

$$\begin{aligned} \dot{\mathbf{q }}_B^{1}=\varvec{{\updelta }}_{11}^{B}\mathbf{T }_{B}^{1}+ \varvec{{\updelta }}_{12}^{B}\mathbf{T }_{B}^{2}+\varvec{{\uptheta }}_{13}^{B}, \end{aligned}$$

(48)

$$\begin{aligned} \dot{\mathbf{q }}_B^{2}=\varvec{{\updelta }}_{21}^{B}\mathbf{T }_{B}^{1}+ \varvec{{\updelta }}_{22}^{B}\mathbf{T }_{B}^{2}+\varvec{{\uptheta }}_{23}^{B}. \end{aligned}$$

(49)

The purpose of the assembly phase is to obtain the expressions for compound body C in the form:

$$\begin{aligned} \dot{\mathbf{q }}_C^{1}=\varvec{{\updelta }}_{11}^{C}\mathbf{T }_{C}^{1}+ \varvec{{\updelta }}_{12}^{C}\mathbf{T }_{C}^{2}+\varvec{{\uptheta }}_{13}^{C}, \end{aligned}$$

(50)

$$\begin{aligned} \dot{\mathbf{q }}_C^{2}=\varvec{{\updelta }}_{21}^{C}\mathbf{T }_{C}^{1}+ \varvec{{\updelta }}_{22}^{C}\mathbf{T }_{C}^{2}+\varvec{{\uptheta }}_{23}^{C}. \end{aligned}$$

(51)

Again, Lagrange multipliers $\varvec{{\upsigma }}$ that enforce velocity level constraint equations $\dot{\varvec{{\Phi }}}=\mathbf{0 }$ between compound body A and B are found by using the penalty method:

$$\begin{aligned} \varvec{{\upsigma }}\approx \upalpha \dot{\varvec{{\Phi }}}=\upalpha ({\varvec{{\Phi }}}_{\mathbf{q }_A^{2}}\dot{\mathbf{q }}_A^{2}+ {\varvec{{\Phi }}}_{\mathbf{q }_B^{1}}\dot{\mathbf{q }}_B^{1}). \end{aligned}$$

(52)

After insertion of the approximation (52) into Eqs. (47) and (48), we get

$$\begin{aligned} \varvec{{\upsigma }}=\mathbf{C }\varvec{{\Phi }}_{\mathbf{q }_A^2}\varvec{{\updelta }}_{21}^A\mathbf{T }_A^1+ \mathbf{C }\varvec{{\Phi }}_{\mathbf{q }_1^B}\varvec{{\updelta }}_{12}^B\mathbf{T }_B^2+\mathbf{C }\varvec{{\upbeta }}_{vel}, \end{aligned}$$

(53)

where $\varvec{{\upbeta }}_{vel}={\varvec{{\Phi }}}_{\mathbf{q }_A^2}\varvec{{\uptheta }}_{23}^A+{\varvec{{\Phi }}}_{\mathbf{q }_B^1}\varvec{{\uptheta }}_{13}^B$. The last step of the assembly phase is to insert Eq. (53) into the expressions (46), (49) such that the following recursive formulae are generated for the bias terms $\varvec{{\uptheta }}$:

$$\begin{aligned}&\varvec{{\uptheta }}_{13}^C=\varvec{{\uptheta }}_{13}^A+\varvec{{\updelta }}_{12}^A{\varvec{{\Phi }}}_{\mathbf{q }_{A}^2}^T\mathbf{C }\varvec{{\upbeta }}_{vel},\nonumber \\&\varvec{{\uptheta }}_{23}^C=\varvec{{\uptheta }}_{23}^B+\varvec{{\updelta }}_{21}^B{\varvec{{\Phi }}}_{\mathbf{q }_{B}^1}^T\mathbf{C }\varvec{{\upbeta }}_{vel}. \end{aligned}$$

(54)

Obviously, the process presented here maintains the same assembly–disassembly structure as in the case of the Newton–Raphson scheme. Most of the matrix quantities need not be updated. Only the bias terms (54) have to be recursively calculated in order to get a clean set of velocities $\dot{\mathbf{q }}$ that fulfill velocity-level constraint equations.

3.4 Mass-orthogonal projections at the acceleration level

The same divide-and-conquer procedure may be formulated for mass-orthogonal projections at the acceleration level. Let us denote $\ddot{\mathbf{q }}^*$ as a vector of perturbed values of absolute accelerations. For a two body example presented in Fig. 1a, one can write the following expressions [11, 12]:

$$\begin{aligned}&{\check{\mathbf{M }}}_A\ddot{\mathbf{q }}_{A}+\frac{\Delta t^2}{4}\left( {\varvec{{\Phi }}}_{\mathbf{q }_A}^{1T}\varvec{{\upkappa }}_1+{\varvec{{\Phi }}}_{\mathbf{q }_A}^{2T}\varvec{{\upkappa }}_2+ {{\Psi }}_{A\mathbf{q }_A}^{T}{\upkappa }_{A}^N\right) \nonumber \\&\quad = {\check{\mathbf{M }}}_A\ddot{\mathbf{q }}_{A}^*, \end{aligned}$$

(55)

$$\begin{aligned}&{\check{\mathbf{M }}}_B\ddot{\mathbf{q }}_{B}+\frac{\Delta t^2}{4}\left( {\varvec{{\Phi }}}_{\mathbf{q }_B}^{2T}\varvec{{\upkappa }}_2+{\varvec{{\Phi }}}_{\mathbf{q }_B}^{3T}\varvec{{\upkappa }}_3+ {{\Psi }}_{B\mathbf{q }_B}^{T}{\upkappa }_{B}^N\right) \nonumber \\&\quad = {\check{\mathbf{M }}}_B\ddot{\mathbf{q }}_{B}^*, \end{aligned}$$

(56)

where $\varvec{{\upkappa }}$ and $\upkappa ^{N}$ denote Lagrange multipliers that enforce joint and normalization constraint equations at the acceleration level, respectively. The multipliers ${\upkappa }^{N}_A$, $\upkappa ^{N}_B$ are approximated by the use of the penalty method:

$$\begin{aligned} \upkappa _A^N\approx \upalpha \ddot{\Psi }_A= & {} \upalpha (\Psi _{A\mathbf{q }_A}\ddot{\mathbf{q }}_A-\upnu _A),\nonumber \\ \upkappa _B^N\approx \upalpha \ddot{\Psi }_B= & {} \upalpha (\Psi _{B\mathbf{q }_B}\ddot{\mathbf{q }}_B-\upnu _B). \end{aligned}$$

(57)

Let us insert Eq. (57) into Eq. (55) and (56), to obtain

$$\begin{aligned}&\ddot{\mathbf{q }}_A=\varvec{{\updelta }}_{i1}^{A}\mathbf{K }_A^1+\varvec{{\updelta }}_{i2}^{A}\mathbf{K }_A^2+\varvec{{\upxi }}_{i3}^{A},\quad i=1,2, \end{aligned}$$

(58)

$$\begin{aligned}&\ddot{\mathbf{q }}_B=\varvec{{\updelta }}_{i1}^{B}\mathbf{K }_B^2+\varvec{{\updelta }}_{i2}^{B}\mathbf{K }_B^3+\varvec{{\upxi }}_{i3}^{B},\quad i=1,2, \end{aligned}$$

(59)

where the pseudo-constraint forces at the acceleration level are defined as $\mathbf{K }_A^1={\varvec{{\Phi }}}_{\mathbf{q }_A}^{1T}\varvec{{\upkappa }}_1$, $\mathbf{K }_A^2={\varvec{{\Phi }}}_{\mathbf{q }_A}^{2T}\varvec{{\upkappa }}_2$, and $\mathbf{K }_B^2={\varvec{{\Phi }}}_{\mathbf{q }_B}^{2T}\varvec{{\upkappa }}_2$, $\mathbf{K }_B^3={\varvec{{\Phi }}}_{\mathbf{q }_B}^{3T}\varvec{{\upkappa }}_3$, whereas the bias terms $\varvec{{\upxi }}_{i3}^{A}$, $\varvec{{\upxi }}_{i3}^{B}$ are evaluated as:

$$\begin{aligned} \begin{aligned}&\varvec{{\upxi }}_{i3}^A={\check{\check{\mathbf{M }}}}_A^{-1}\left( {{\check{\mathbf{M }}}}_A\ddot{\mathbf{q }}_A^*+\frac{\Delta t^2}{4}\Psi _{A\mathbf{q }_A}^T\upalpha \upnu _A\right) ,\quad i=1,2\\&\varvec{{\upxi }}_{i3}^B={\check{\check{\mathbf{M }}}}_B^{-1}\left( {{\check{\mathbf{M }}}}_B\ddot{\mathbf{q }}_B^*+\frac{\Delta t^2}{4}\Psi _{B\mathbf{q }_B}^T\upalpha \upnu _B\right) ,\quad i=1,2 \end{aligned} \end{aligned}$$

(60)

Again, one can exploit the basic expressions (58), (59) in order to perform mass-orthogonal projections for compound bodies in the system (cf. Fig. 1b). One can write the following generalized expressions for the representative bodies A and B:

$$\begin{aligned} \ddot{\mathbf{q }}_A^{1}=\varvec{{\updelta }}_{11}^{A}\mathbf{K }_{A}^{1}+ \varvec{{\updelta }}_{12}^{A}\mathbf{K }_{A}^{2}+\varvec{{\upxi }}_{13}^{A}, \end{aligned}$$

(61)

$$\begin{aligned} \ddot{\mathbf{q }}_A^{2}=\varvec{{\updelta }}_{21}^{A}\mathbf{K }_{A}^{1}+ \varvec{{\updelta }}_{22}^{A}\mathbf{K }_{A}^{2}+\varvec{{\upxi }}_{23}^{A}, \end{aligned}$$

(62)

$$\begin{aligned} \ddot{\mathbf{q }}_B^{1}=\varvec{{\updelta }}_{11}^{B}\mathbf{K }_{B}^{1}+ \varvec{{\updelta }}_{12}^{B}\mathbf{K }_{B}^{2}+\varvec{{\upxi }}_{13}^{B}, \end{aligned}$$

(63)

$$\begin{aligned} \ddot{\mathbf{q }}_B^{2}=\varvec{{\updelta }}_{21}^{B}\mathbf{K }_{B}^{1}+ \varvec{{\updelta }}_{22}^{B}\mathbf{K }_{B}^{2}+\varvec{{\upxi }}_{23}^{B}. \end{aligned}$$

(64)

The Lagrange multipliers $\varvec{{\upkappa }}$ hold for acceleration level constraints $\ddot{\varvec{{\Phi }}}=\mathbf{0 }$ that indicate a joint between compound body A and B. The multipliers can be approximated through use of the penalty method :

$$\begin{aligned} \varvec{{\upkappa }}\approx \upalpha \ddot{\varvec{{\Phi }}}=\upalpha ({\varvec{{\Phi }}}_{\mathbf{q }_A^{2}}\ddot{\mathbf{q }}_A^{2}+ {\varvec{{\Phi }}}_{\mathbf{q }_B^{1}}\ddot{\mathbf{q }}_B^{1}-\varvec{{\upgamma }}). \end{aligned}$$

(65)

Let us apply an analogous procedure to that demonstrated in Sect. 3.3 and let us insert Eqs. (62), (63) into Eq. (65). The following expression for Lagrange multipliers $\varvec{{\upkappa }}$ can be obtained:

$$\begin{aligned} \varvec{{\upkappa }}=\mathbf{C }\varvec{{\Phi }}_{\mathbf{q }_A^2}\varvec{{\updelta }}_{21}^A\mathbf{K }_A^1+ \mathbf{C }\varvec{{\Phi }}_{\mathbf{q }_1^B}\varvec{{\updelta }}_{12}^B\mathbf{K }_B^2+\mathbf{C }\varvec{{\upbeta }}_{acc}, \end{aligned}$$

(66)

where $\varvec{{\upbeta }}_{acc}={\varvec{{\Phi }}}_{\mathbf{q }_A^2}\varvec{{\upxi }}_{23}^A+{\varvec{{\Phi }}}_{\mathbf{q }_B^1}\varvec{{\upxi }}_{13}^B-\varvec{{\upgamma }}$. One can finally arrive at the expressions for compound body C by substituting Eq. (66) into the relations (61), (64), to get

$$\begin{aligned} \ddot{\mathbf{q }}_C^{1}=\varvec{{\updelta }}_{11}^{C}\mathbf{K }_{C}^{1}+ \varvec{{\updelta }}_{12}^{C}\mathbf{K }_{C}^{2}+\varvec{{\upxi }}_{13}^{C}, \end{aligned}$$

(67)

$$\begin{aligned} \ddot{\mathbf{q }}_C^{2}=\varvec{{\updelta }}_{21}^{C}\mathbf{K }_{C}^{1}+ \varvec{{\updelta }}_{22}^{C}\mathbf{K }_{C}^{2}+\varvec{{\upxi }}_{23}^{C}, \end{aligned}$$

(68)

Ultimately, the bias terms $\varvec{{\upxi }}$ are evaluated from the following recursive relations:

$$\begin{aligned}&\varvec{{\upxi }}_{13}^C=\varvec{{\upxi }}_{13}^A+\varvec{{\updelta }}_{12}^A{\varvec{{\Phi }}}_{\mathbf{q }_{A}^2}^T\mathbf{C }\varvec{{\upbeta }}_{acc},\nonumber \\&\varvec{{\upxi }}_{23}^C=\varvec{{\upxi }}_{23}^B+\varvec{{\updelta }}_{21}^B{\varvec{{\Phi }}}_{\mathbf{q }_{B}^1}^T\mathbf{C }\varvec{{\upbeta }}_{acc}. \end{aligned}$$

(69)

Again, the procedure formulated here keeps the assembly-disassembly pattern with the main computational load imposed on the evaluation of the bias terms (69) and calculation of a clean set of accelerations $\ddot{\mathbf{q }}$ that satisfy acceleration level constraint equations.

3.5 Flowchart of the algorithm

Figure 2 presents a flowchart of the algorithm. The most computationally intensive parts of the formulation are marked as orange boxes. These procedures may be parallelized by using the divide-and-conquer approach proposed in the paper. The main simulation loop is repeated until the end of simulation time. The inner loop is created to implement Newton–Raphson scheme. This loop is continued up to the convergence of the iterative procedure. Please note that in real-time applications, fixed number of iterations is assumed to guarantee deterministic execution time irrespective of the convergence achieved. Two last parallelizable steps involve a process of projecting the solutions onto the constraint hypersurface at the velocity and acceleration level, respectively. One should note that the projections may be performed independently of each other providing a coarse-grained task parallelism.

Fig. 2

Flowchart of the algorithm. The orange boxes indicate the possibility to parallelize the computations according to the binary tree associated with topology of a multibody system

An extensive pseudo-code of the algorithm is also provided in the listing below. It demonstrates the algorithmic steps required to implement the scheme with references to appropriate equations presented in the text.

• 1. Initialization. Initial time $t=t_0$. Let $\mathbf{q }$, $\dot{\mathbf{q }}$ will be given. Calculate $\ddot{\mathbf{q }}$ and $\varvec{{\uplambda }}$ (e.g., see parallelizable version of the augmented Lagrangian method [28])

• 2. Start main simulation loop. Time $t=t_0+\Delta t$.

• 3. Start Newton-Raphson iteration.

  • (a) In the first Newton iteration (within each time step), predict positions for the next time-instant from Taylor series expansion: $\mathbf{q }=\overline{\mathbf{q }}+\dot{\overline{\mathbf{q }}}\Delta t+\frac{1}{2}\ddot{\overline{\mathbf{q }}}\Delta t^2$ and assume that Lagrange multipliers are taken as $\varvec{{\uplambda }}=\overline{\varvec{{\uplambda }}}$, $\varvec{{\upmu }}=\overline{\varvec{{\upmu }}}$. For each next Newton iteration assume that $\mathbf{q }=\underline{\mathbf{q }}+\Delta \mathbf{q }$, $\varvec{{\uplambda }}=\underline{\varvec{{\uplambda }}}+\Delta \varvec{{\uplambda }}$, and $\varvec{{\upmu }}=\underline{\varvec{{\upmu }}}+\Delta \varvec{{\upmu }}$.

  • (b) Predict velocities $\dot{\mathbf{q }}^*$ and accelerations $\ddot{\mathbf{q }}^*$ from (15) and (16), respectively.

  • (c) Update kinematic dependent quantities, calculate mass matrices for physical bodies, forces acting on them, and constraint equations.

  • (d) Find the matrix coefficients for individual bodies (26), (27).

  • (e) Perform assembly process according to the relations (36)–(39) until the whole system is represented as a single entity.

  • (f) Use boundary conditions (e.g., connection to the fixed base body) in order to calculate constraint loads at the boundaries of a compound body.

  • (g) Perform disassembly phase and recursively find constraint load increments $\Delta \varvec{{\uplambda }}$ from Eq. (34).

  • (h) For each body in the system, calculate position increments $\Delta \mathbf{q }$ from Eq. (24) and (25) and evaluate increments $\Delta \varvec{{\upmu }}$ from (21).

  • (i) If stop criterion (e.g., $||\Delta \mathbf{q }||<\upepsilon$) is fulfilled, then exit Newton-Raphson iteration; otherwise, go to 3(a) and repeat.

$\rightarrow$ End Newton-Raphson iteration (repeated until convergence).

• 4. Mass-orthogonal projections at the velocity level.

  • (a) Find the vector quantities evaluated for individual bodies (45).

  • (b) Proceed with assembly phase and use relations (54) to represent a multibody system as a single compound body.

  • (c) Use boundary conditions in order to calculate pseudo-constraint loads $\mathbf{T }$ at the boundaries of compound body.

  • (d) Perform disassembly phase and calculate Lagrange multipliers $\varvec{{\upsigma }}$ from Eq. (53).

  • (e) For each body in the system calculate corrected velocities $\dot{\mathbf{q }}$ from Eq. (43) and (44) and calculate the values of $\varvec{{\upsigma }}^N$ from (42).

• 5. Mass-orthogonal projections at the acceleration level.

  • (a) Find the vector quantities computed for individual bodies (60).

  • (b) Proceed with assembly phase and use relations (69) to represent a mechanical system as a single compound body.

  • (c) Use boundary conditions in order to calculate pseudo-constraint loads $\mathbf{K }$ at the boundaries of compound body.

  • (d) Perform disassembly phase and calculate Lagrange multipliers $\varvec{{\upkappa }}$ from Eq. (66).

  • (e) For each body in the system calculate a clean set of accelerations $\ddot{\mathbf{q }}$ from Eq. (58) and (59) and calculate the multipliers $\varvec{{\upkappa }}^N$ from (57).

$\rightarrow$ End main simulation loop (repeated until end of simulation time).

4 Numerical test cases

4.1 Introduction

This section presents the results of numerical simulations for several test cases. The sample mechanisms are chosen intentionally to demonstrate the performance of the formulation in case of modeling of multibody systems possessing various topologies and configurations. All bodies are modeled as rigid moving either in three dimensional space as in the case of the first example or in the plane as in the case of other examples. The length of each body in the systems is $1\text { m}$, mass $1\text { kg}$ and inertia matrix equals to $\mathbf{J }{'}=diag(1.0)\text { kgm}^2$ with respect to the axes of appropriate centroidal coordinate frames unless otherwise stated. Long-time simulations are carried out in order to investigate the properties of the algorithm in the case of open-, closed-loop systems (four-bar mechanism). The four-bar linkage, moreover, showcases the ability of the algorithm to deal with systems that feature both redundant constraints and singular configurations. Moreover, the algorithm proposed in this paper is designed to handle systems with holonomic constraints. For these reasons, the test problems proposed can be considered to be representative of a wide range of practical applications and confirm the validity of the algorithm.

4.2 Spatial double pendulum

Let us consider an open-loop multibody system as shown in Fig. 3a. The system is composed of two bodies A and B. The bodies are interconnected by spherical joints 1 and 2. The gravity force acts in the negative direction of $y_0$ axis. Initially, body A is located along $x_0$ axis, whereas body B is situated in the $x_0z_0$ plane and it is pointing at the $z_0$ direction. Moreover, the axes of centroidal coordinate frames $(x_Ay_Az_A)$ and $(x_By_Bz_B)$ are coincident with the axes of global reference frame $(x_0y_0z_0)$. As mentioned before the state of the system is described by a set of absolute coordinates. At initial time-instant Cartesian position of body A and B in the global reference frame $(x_0y_0z_0)$ are given as $\mathbf{r }_{{A}}=\left[ 0.5\quad 0.0\quad 0.0\right] ^T$, $\mathbf{r }_{{B}}=\left[ 1.0\quad 0.0\quad 0.5\right] ^T$, respectively. Linear and angular velocities of the bodies are set to zero. The penalty coefficient for the proposed approach is chosen as $\upalpha =10^6$. The maximum number of iterations in the Newton–Raphson procedure is limited to three, whereas the stop criterion for the procedure is selected to be $||\Delta \mathbf{q }||<\upepsilon =10^{-12}$. The time step for the trapezoidal integration rule is constant and equals to $\Delta t=0.01\text { s}$, while the simulation time is set to be $10\text { s}$.

Fig. 3

Sample test cases. a Spatial double pendulum; joints 1 and 2 are spherical, b Planar four-bar mechanism; joints 1–4 are revolute

Figure 4 presents positions of body A and the components of the constraint force at joint 1. Continuous lines in the plots indicate the outcome obtained by the proposed method. Circle marks represent the results produced by commercial multibody software (MSC.ADAMS). Dynamic motion of the mechanism is well reproduced through use of the proposed method and matches the results obtained by using commercial multibody solver.

On the other hand, Fig. 5 demonstrates constraint violation errors and total energy of the system as a function of simulation time. The time plots can be regarded as a kind of performance measures for the proposed approach. The sub-figure on the left shows Euclidean norm of joint and mathematical constraint equations. The sub-figure on the right demonstrates the total mechanical energy of the pendulum as a sum of kinetic energy and potential energy of the system. Constraint violation errors are kept under control with a reasonable accuracy compared to the characteristic length of each body ($L=1\text { m}$). The position constraint violation errors are fulfilled with the highest accuracy compared to the errors committed at the velocity or at the acceleration level. This is an expected outcome since the absolute positions are primary variables in the formulation. The total energy of the system is well conserved, and it is kept approximately constant at the zero level. The behavior of the curve for longer simulation scenarios has a slight tendency to energy dissipation due to the reasons explained in [20], namely the energy loss associated with velocity and acceleration projections and the dissipative behavior of the Newmark family of integrators.

Fig. 4

Positions of body A and constraint force at joint 1 for the spatial double pendulum

Fig. 5

Constraint violation errors and total energy conservation for the spatial double pendulum

4.3 Four-bar mechanism

This test case is more complex than the first example. The four-bar mechanism is one of the simplest representatives of closed-loop systems. The initial system configuration and topology are presented in Fig. 3b. The mechanism consists of three bodies A, B, and C. The bodies are interconnected to each other and the base body 0 by revolute joints 1–4. Each revolute joint introduces five constraint equations, giving 20 conditions in total. In addition, three Euler parameter normalization constraints yield 23 constraint equations imposed on the system. If absolute coordinates are used, there are 21 generalized coordinates for the three bodies. Since the mechanism possesses one degree of freedom, there must be three redundant constraints. Such over-constrained systems represent a challenge for numerical algorithms. In this situation, one has to permanently deal with rank-deficient constraint Jacobian matrices. The existence of redundant constraints might have consequences in non-uniqueness of constraint reactions [36, 41]. The other issue corresponds to a singular configuration. It is encountered when a multibody system reaches a position, in which there is a sudden change in the number of degrees of freedom. For instance, a four-bar mechanism shown in Fig. 3b reaches a singular configuration when the characteristic angle is $\upvarphi =90^{\circ }$ and the links B and C are overlapped. At this particular state, the constraint equations become dependent and the constraint Jacobian matrix temporarily loses its rank. At this point, the mechanism can theoretically take two different paths (bifurcation point). The behavior of the augmented Lagragian method in the context of multibody systems that move in the neigborhood of singular configurations is discussed more thoroughly in [21]. When the mechanism passes through the neighborhood of the singular configuration, large errors may be introduced into the solution or the simulation may completely fail. The exemplary four-bar mechanism may lose the Jacobian matrix row rank both ways.

Let us assume that initially, the characteristic angle for the four-bar mechanism is $\upvarphi =45^{\circ }$. This angle corresponds to the Cartesian position of the system shown in Fig. 3a. It is assumed that initial linear and angular velocities are set to zero. The gravity force is taken as acting in the negative $y_0$ direction. The simulation time is $30\text { s}$ with the integrator time step $\Delta t=0.01\text { s}$. The simulaton parameters are chosen to be $\upalpha =10^6$, $||\Delta \mathbf{q }||<\upepsilon =10^{-12}$, and the number of iterations in the Newton–Raphson procedure equals four. Plots of positions, velocities, accelerations and constraint loads at joint 1 for the first 10 s of the simulation are shown in Fig. 6. Since the system is conservative, the presented time histories are periodic with a dose of symmetry in the results. No sudden changes in the constraint force components are observed. The proposed approach delivers numerical results which match the outcome achieved by commercial multibody software. Circle marks in Fig. 6 represent the results produces by ADAMS. Figure 7 presents the performance of the algorithm for the simulation that lasts $30\text { s}$. As in the case of open-loop system, the proposed algorithm gives bounded response in terms of constraint violation errors as well as in terms of the total energy conservation. Constraint errors are kept under control. Due to the fact that absolute positions are treated as primary variables, positions constraint equations are fulfilled to the highest extent compared to the velocity and acceleration level conditions. The total energy of the system indicates small oscillatory behavior with a tendency to marginal energy dissipation. The dissipation is observed partly due to the mass-orthogonal projections involved in the solution process. It can be noticed that the proposed formulation handles well the system with redundant constraints, which may repeatedly pass through the neighborhood of singular configuration. The singular configuration corresponds to the point at which the four links of the mechanism are aligned on the global y axis. At this moment, the Jacobian matrix of the system constraints instantaneously loses rank and two possible motions of the theoretically 1 d.o.f. system are simultaneously possible. Details are provided in Ref. [21]. Long-time simulations were performed, and the same successful behavior was observed for that system.

Fig. 6

Numerical results for the fourbar mechanism. Position, velocity, acceleration of body A, and constraint loads at joint 1

Fig. 7

Constraint violation errors and total energy conservation for the four-bar mechanism

4.4 Multilink pendulum

In this subsection, even more complex example is demonstrated in order to show the properties of the proposed algorithm for the simulation of large-scale mechanical systems. A multi-rigid body pendulum with $n=128$ links is presented in Fig. 8 at its initial configuration. The binary tree associated with the flow of calculations is also depicted in the figure. This example may serve as a good starting point for simulating more complex systems such as cables and ropes [39]. The bodies are connected to each other by spherical joints and move planarly due to the gravity forces directed toward negative $y_0$ axis. The system is modeled as a spatial one with $7n=896$ absolute coordinates. There are $m=3\cdot 128=384$ spherical joint constraints and $n=128$ normalization constraints imposed on the system. The simulation time is $10\text { s}$, and the system is integrated with time step $\Delta t=0.01\text { s}$. Again, the number of Newton–Raphson iterations is limited to three at the most, where the stop criterion is chosen to be $||\Delta \mathbf{q }||<\upepsilon =10^{-12}$. The penalty parameter is set to be $\upalpha =10^9$. This choice stems from the fact that for smaller penalty parameters instabilities in the simulations occurred. No convergence was achieved for the penalty parameters $\upalpha =10^6$ and $\upalpha =10^7$. Wrong results were recorded for $\upalpha =10^8$.

Fig. 8

A multilink rigid-body pendulum and the binary tree associated with the system

Fig. 9

Swinging chain consisting of $n=128$ bodies falling under gravity forces

Figure 9 shows multiple snapshots of the pendulum taken at different time-instants. Initially, the bodies fall down and their kinetic energy is rapidly increased. This behavior is continued up to the moment when the maximum value of the energy is observed, which can be noticed at time $t\approx 5.22\text { s}$. After that, there is a phase of loss of kinetic energy. The behavior of the system could be better understood if we look at Fig. 10. The leftmost sub-figures illustrate Cartesian positions of the last body in the chain as well as its linear velocities. It can be noticed that there is a swinging phase and a second phase, in which a complex, low-amplitude and high-frequency motion is observed. The rightmost top sub-figure demonstrates constraint loads at joint 1, whereas the rightmost bottom sub-figure presents time histories of potential, kinetic, and total energy of the system. Figure 11 presents total constraint violation errors and how the total energy of the system evolves as a function of time. Constraint violation errors are kept under control and are stabilized for the assumed simulation time. The total energy drops temporarily to the value of $-\,46.84\text { J}$ at time $t\approx 5.22\text { s}$ and, after that, it is recovered and stabilized at the level of $-\,25\text { J}$. The energy loss is due to numerical damping introduced by numerical integrator and mass-orthogonal projections. Apart from the mentioned issues, the sudden drop in the system’s energy takes place because impact-like forces are exerted on the system when it reaches the vertical position. Nevertheless, it has a marginal effect on the simulation results. The total energy drop constitutes only a $0.06\%$ of the maximum kinetic energy of the system. The approach proposed in the paper captures correctly dynamical behavior of the long chain, and the algorithm remains stable for the analyzed test case and the assumed parameters.

Fig. 10

Numerical results for the multilink pendulum. The figure depicts position and linear velocity of point C (see Fig. 8), constraint loads at joint 1, and kinetic (KE), potential (PE), and total energy (TE) of the system

Fig. 11

Constraint violation errors and total energy conservation for the spatial multilink pendulum

One should comment on the potential source of numerical instabilities observed here when long multi-rigid-body chains are being simulated. The convergence issues reported in this paper may be associated with numerical ill-conditioning of the problem. This matter is pointed out by many researchers in the field [1, 39]. With a basic penalty formulation, usually low penalty factors result in a stable (though possibly inaccurate) solution. In the case of index-3 methods, low penalty factors can deliver wrong results, because the Newton–Raphson iteration fails to achieve convergence in a reasonable number of iterations. This issue is mentioned in Ref. [21] as well.

The algorithm presented here may suffer from another source of problems. The potential numerical instability may be laid up in the way the linearized form (19) and (20) is obtained. In fact, the linearization of the equations of motion (17), (18) reflected in Eqs. (19) and (20) is not exact. The missing terms that are omitted here (and often neglected in the augmented Lagrangian based formulations) are associated with partial derivatives of constraint loads. The derivatives take on the following form: $\varvec{{\Phi }}_{\mathbf{q }\mathbf{q }}^T\varvec{{\uplambda }}$, $\varvec{{\Psi }}_{\mathbf{q }\mathbf{q }}^T\varvec{{\upmu }}$. The symbols $\varvec{{\Phi }}_{\mathbf{q }\mathbf{q }}$ and $\varvec{{\Psi }}_{\mathbf{q }\mathbf{q }}$ indicate third-order tensors. A second-order tensor (matrix) is obtained upon appropriate multiplication of the tensors $\varvec{{\Phi }}_{\mathbf{q }\mathbf{q }}$ and $\varvec{{\Psi }}_{\mathbf{q }\mathbf{q }}$ by the vector of Lagrange multipliers $\varvec{{\uplambda }}$ and $\varvec{{\upmu }}$, respectively. Algorithmically, the mentioned higher-order terms may be added to the matrices $\underline{\check{\mathbf{M }}}_A$, $\underline{\check{\mathbf{M }}}_B$, which are originally defined below Eq. (20). Then, the updated formulas will take the following form

$$\begin{aligned} \begin{aligned}&\underline{\check{\mathbf{M }}}_A:=\underline{\check{\mathbf{M }}}_A+\frac{\varDelta t^2}{4}\left( \underline{\varvec{{\Phi }}}_{\mathbf{q }_A\mathbf{q }_A}^{1T}\underline{\varvec{{\uplambda }}}_1+\underline{\varvec{{\Phi }}}_{\mathbf{q }_A\mathbf{q }_A}^{2T}\underline{\varvec{{\uplambda }}}_2+\underline{{\Psi }}_{A\mathbf{q }_A\mathbf{q }_A}^{T}\underline{{\upmu }}_A\right) ,\\&\underline{\check{\mathbf{M }}}_B:=\underline{\check{\mathbf{M }}}_B+\frac{\varDelta t^2}{4}\left( \underline{\varvec{{\Phi }}}_{\mathbf{q }_B\mathbf{q }_B}^{2T}\underline{\varvec{{\uplambda }}}_2+\underline{\varvec{{\Phi }}}_{\mathbf{q }_B\mathbf{q }_B}^{3T}\underline{\varvec{{\uplambda }}}_3+\underline{{\Psi }}_{B\mathbf{q }_B\mathbf{q }_B}^{T}\underline{{\upmu }}_B\right) , \end{aligned} \end{aligned}$$

and the algorithm is continued in the standard way described in the paper. It should be noted that there are some parallels between this notion and the results obtained by the other authors [2, 40]. The new terms added here are similar to the concept of geometric stiffness defined for real-time simulation of complex multibody systems. This fiddly modification may improve numerical stability of the algorithm proposed here by providing more accurate forms of the tangent matrix.

5 Parallel implementation and performance results

5.1 Parallel implementation

The objectives of this section are to present the details of parallel implementation of the proposed index-3 divide-and-conquer algorithm as well as to show the performance results gathered on a shared memory parallel computer. First of all, before the simulation is started, one has to generate a binary, possibly well-balanced, tree associated with a topology of a multibody system. Parallel efficiency is highly dependent on the shape of that tree. A well-balanced binary tree creation is a key to gain optimal parallel computational cost for the simulation of systems with more general topologies. For an arbitrary multibody system, available parallel resources can be effectively utilized by shaping the binary tree to be of low height and of sufficiently large tree-width to obtain optimal turnaround time for a given parallel resource. Moreover, the height of an upper part of such tree should be minimized and the lower part of the tree should be designed in a way to distribute the computational load as evenly as possible over the available processing units. Therefore, the real problem is to design a good assembly-disassembly tree for a given mechanism so that the tree could be efficiently mapped onto the architecture of a given parallel resource, either it is a shared memory computer (as in this paper) or it is a graphics processor unit (as analyzed in [8]). The specifics of the binary tree creation for various multibody system topologies can found in other references [6, 16, 28, 33]. At the moment, it is important to note that nodes represent physical or compound bodies in the system. The same binary tree is exploited in three main algorithmic steps of the formulation, i.e., in the Newton–Raphson iteration and in the phase of mass-orthogonal projections at the velocity and acceleration level. If we look again at the exemplary system and the associated binary tree in Fig. 8, we see that parallel calculations may be performed at each level of the tree starting from the leaf nodes. In the assembly phase, the procedure traverses the tree from leaf nodes up to the root node. The root node indicates a compound body that represents a multibody system as a single entity. In the disassembly phase, the recursions are performed in the reverse order, i.e., from the root node to the leaf nodes. It should be immediately noticed that one could perform embarrassingly parallel computations at each level of the binary tree. This kind of correspondence makes the process dynamic. The computational load evolves as the procedure walks up and down the binary tree. The parallelization can be achieved at each level of the tree by assigning one node to one thread as in the case of calculations on graphics processor units, where many threads are available at the disposal of a programmer. In the case of shared memory computer, it is necessary to assign several nodes to one thread and exploit parallel constructs that take nearly the same amount of work and distribute it over the available cores in the parallel execution of a loop. The latter strategy is taken here since OpenMP compiler directives [9] are chosen to parallelize the computations. Apart from the strategy assumed here that largely parallelize calculations at each time step, there is a place for many small and embarrassingly parallel tasks that may improve overall numerical efficiency. It should be mentioned that for each body in the system the calculation of the position and Lagrange multiplier estimates together with prediction of velocities and accelerations from trapezoidal rule could be easily parallelized.

5.2 Parallel performance

The algorithm proposed in the paper is implemented in C++ by using template-based library Eigen [22] that supports fixed-size small matrix-vector operations and provides linear algebra solvers. The parallel multibody code is executed on a Linux-based shared memory parallel computer, which is equipped with two-socket motherboard, in which two quad-core processors are installed. Each processor is a Quad-Core AMD Opteron Processor 2356 (2.3GHz) with 512kB cache L2 per core and four 2GB ECC DDR-667 memory modules are set in the motherboard. The source codes are compiled with -O3 optimization flag using g++ compiler with the support of OpenMP compiler directives. In the implementation, we have used the simplest parallelization strategy that suffices to implement the algorithm. A #pragma omp for compiler directive was exploited to divide the work of the for-loop among the available threads. Moreover, private clauses were specified in order to assign which variables are local to a thread in parallel loop. The private scope has been mainly defined for the variables that store indices associated with a binary tree. Our current software implements a simulation framework for open-loop mechanical system depicted in Fig. 8, which is described in detail in Sect. 4.4. The sequential and parallel performance of the code is investigated by varying the problem size in terms of the number of bodies, which may take on the following values $n_b=2,4,8,16,32,64,128,256,512,1024$. It is also possible to change the number of threads used for calculations from 1 to 8. The total simulation time is set $10\text { s}$ with the constant time step $\Delta t=0.01\text { s}$. In real-time applications, it is a common practice to perform a fixed number of iterations, even though convergence may have been achieved already, to ensure predictability in execution time. The number of Newton–Raphson iterations has been limited to three. Moreover, the accuracy $\upepsilon =10^{-12}$ is purposefully assumed to be extremely tight to enforce that three iterations are always taken irrespective of the fulfillment of the condition $||\Delta \mathbf{q }||<\upepsilon$. A check has been performed beforehand in order to verify value of the norm $||\Delta \mathbf{q }||$ after three Newton–Raphson iterations, which is being kept below $10^{-7}$ for $n_b=2$ bodies in the system, and below $10^{-3}$ for $n_b=1024$ bodies in the pendulum. The maximum value of the norm $||\Delta \mathbf{q }||$ for other simulation scenarios are found to be in between the mentioned values. In this sense, we guarantee a minimum accuracy.

Fig. 12

Wall-clock time versus problem size and number of processing elements. a Sequential performance, b parallel performance

In order to explore the performance of the algorithm, the aggregate wall-clock time required by the Newton–Raphson scheme, mass-orthogonal projections at the velocity and at the acceleration level, is measured by using OpenMP built-in procedure omp_get_wtime(). A sequential version of the algorithm is evaluated in terms of its total execution time, expressed as a function of the problem size. Figure 12a demonstrates the timing results for sequential implementation of the algorithm as a function of the problem size. Firstly, let us observe that the total computational cost scales linearly with the number of bodies in the chain. This is not a surprising result as the recursive algorithm presented here is built on top of the divide-and-conquer algorithm [16], which exhibits linear computational complexity for sequential calculations. Secondly, the time spent in three iterations of the Newton–Raphson scheme is evaluated and observed in the same Fig. 12a. It can be concluded that this step gives major computational contribution and constitutes about 81% of the total execution time on average. The rest of the time is spent on two mass-orthogonal projections and about 9.5% is taken by each of the corrective procedures.

On the other hand, Fig. 12b presents the time measurements for parallel implementation. The wall-clock time is demonstrated as a function of the number of cores used for calculations while varying the problem size. Let us point out that adding more processing elements gives a substantial decrease in the turnaround time, which is especially observed in the case of systems possessing more than 64 bodies. It is also worth noticing that the proposed index-3 algorithm enables one to perform real-time calculations by employing additional cores. This trend is clearly seen for the chain possessing $n_b=128$ bodies, for which the real-time barrier is broken for four cores used for calculations.

There are many measures of parallel performance. It is important to study the benefits from parallelism. A number of metrics have been used based on the desired outcome of performance analysis. Speedup is a measure that captures the relative benefit of solving a problem in parallel. It is defined as the ratio of the time taken to solve a problem on a single core to the time spent to solve the same problem on a parallel computer with identical multi-core processors. Parallel efficiency is a measure of the fraction of time for which a processing element is usefully employed. Parallel efficiency is the ratio of speedup to the number of cores. In an ideal case, speedup is equal to the number of cores and efficiency is equal to one. Practically, this result is unachievable and speedup is usually less than the number of cores and efficiency is between zero and one. Figures 13a, b and 14a, b demonstrate speedup and parallel efficiency versus the problem size and the number of processing elements. Figure 13a, b illustrate that the speedup has a tendency to saturate. Larger problems yield higher speedup and parallel efficiency as it is also observed in Fig. 14a for the same number of cores. We can also see in Fig. 14a that parallel efficiency is an increasing function of the problem size, which is a desirable property with respect to utilizing parallel processors effectively and determines the degree of scalability of the software. Figure 14b demonstrates a natural tendency of the algorithm to decrease overall efficiency of the parallel program as we increase the number of cores used for calculations. One should also emphasize that the parallel performance results are promising not only for large-scale systems with hundreds of degrees of freedom but also for multibody systems possessing small number of bodies, as it may be clearly observed in Figs. 13b and 14b. This qualitative result extends the possibilities of application of the proposed index-3 divide-and-conquer algorithm to a broader range of systems.

Fig. 13

Parallel speedup versus problem size and number of processing elements

Fig. 14

Parallel efficiency versus problem size and number of processing elements

6 Summary and conclusions

In this work, the equations of motion are formulated in terms of absolute coordinates. A unified form of the algorithm is presented at the position, velocity and acceleration level. The unification manifests itself in the computational savings, because the leading matrices at the mentioned levels are evaluated only once per integration step. Also, the employed Euler parameter form of the equations of motion is particularly useful in deriving the divide and conquer algorithm presented in this paper. The associated mass matrix is invertible and the derived divide-and-conquer formulae are simpler. The equations of motion for the spatial multi-rigid body system dynamics are discretized by using a single-step trapezoidal rule as an integration scheme. The employed framework leads to the set of nonlinear algebraic equations for the bodies’ positions and for the Lagrange multipliers associated with constraint equations. These equations are solved by the Newton–Raphson procedure with the addition of the second-order predictor. It is assumed that the constraint equations for multibody systems are imposed at the position level. In consequence, one may expect the accumulation of constraint errors for velocities and accelerations. To correct the constraint violation errors, the resulting classical index-3 formulation is supplemented by the two mass-orthogonal projections.

The robustness of the formulation manifests itself in the ability of the algorithm to analyze multibody systems with redundant constraints, and the systems that may occasionally enter into singular configurations. The problems associated with such systems are reflected in numerical difficulties, and in some situations, inability of the algorithm to continue the simulation as reported. The proposed algorithm circumvents the problems by introducing the approximations of Lagrange multipliers. The key matrices in the formulation remain nonsingular, and simultaneously, the constraint equations are fulfilled within the reasonable accuracy dependent on the tolerance imposed in the calculations. Due to the necessity of the solution of nonlinear equations of motion, the proposed formulation is inherently iterative. The largest computational load is associated with iterations performed by the Newton–Raphson algorithm, where the increments in positions and Lagrange multipliers are evaluated to predict the state of the system in the next time-instant. The computational burden can be reduced each next iteration by assuming that the tangent matrix in the Newton–Raphson procedure is constant. On the other hand, the error corrections at the velocity and acceleration level are performed only once per integration step. The mass-orthogonal projections based procedures make use of the tangent matrix evaluated in the Newton–Raphson procedure. As indicated in the text, the numerical cost associated with the projections is only a small part of the burden required in the first iteration of the Newton–Raphson scheme.

The properties of the algorithm are also demonstrated for the simulation of large-scale multi-rigid-body systems. The behavior of the multilink pendulum with $n=128$ bodies is analyzed in order to investigate accuracy and stability of the formulation for long chains. It is reported in the numerical results that the proposed approach handles well such simulation scenarios by providing negligible energy drift for conservative systems. Constraint violation errors are kept under control even for high-amplitude accelerations observed during the simulation. Stable numerical simulations are performed at time step $\Delta t=0.01\text { s}$. The rich chain dynamics behavior is properly captured by guaranteeing reasonable accuracy for long-time simulations.

Finally, the divide-and-conquer scheme is employed on top of the index-3 formulation with mass-orthogonal projections. The trapezoidal rule is embedded into the solution process without the deterioration of the binary-tree structure of the algorithm. The proposed approach enables one to parallelize the involved computations at the position, velocity, and acceleration level. The details of parallel implementation on shared memory computer with eight cores are presented. Significant efficiency gains are captured for the simulation of small and medium multibody systems. Substantial decrease in turnaround time is obtained for large multibody systems ($n_b=256,512,1024$ bodies). Highly parallelizable structure of the algorithm together with the ability of the formulation to take large integration time steps by simultaneously delivering physically meaningful results with reasonable accuracy make the proposed algorithm a good general purpose approach for highly efficient or real-time multibody dynamics simulations.