Self-generated limit cycle tracking of the underactuated inertia wheel inverted pendulum under IDA-PBC

Abstract

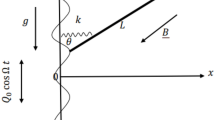
This paper deals with the tracking approach of a self-generated stable limit cycle for an underactuated mechanical system: The inertia wheel inverted pendulum (IWIP). Such system is subject to unilateral constraints limiting its swing motion. It is known that an interconnection and damping assignment passivity-based control (IDA-PBC) can be employed to control such pendulum to its upright position. In this work, we briefly show first that the IWIP can generate a stable period-1 limit cycle through a Hopf bifurcation by varying some gain parameter of the IDA-PBC. Thus, such self-generated limit cycle is used as a reference trajectory, which is chosen to be tracked by the IWIP. To achieve the tracking problem, a supplementary control input is added. Such tracking problem is reformulated as an asymptotic stabilization of the tracking error. Our fundamental approach hinges mainly on the use of the S-procedure to introduce the unilateral constraints, and the Schur complement and the matrix inversion lemma to transform bilinear matrix inequalities into linear matrix inequalities. Several simulations have been presented to corroborate the mathematical results and to show the efficiency of the proposed tracking scheme of the self-generated stable limit cycle of the controlled IWIP, even if it is subject to external disturbances, or in the presence of uncertainties in the friction parameters.

Appendices

Appendix 1: Self-generation of a limit cycle through Hopf bifurcation

In this Appendix, we show generation of a self-sustained oscillation (limit cycle) in the nonlinear dynamics of the underactuated IWIP under the IDA-PBC. Thus, we present first stability conditions of the equilibrium point $\varvec{x}_{eq}$, given by expression (9), of the nonlinear dynamics (8). Moreover, we derive conditions proving existence of the Hopf bifurcation and hence the periodic solutions in the nonlinear dynamics (8). Finally, we discuss briefly stability of the periodic solutions using the fist Lyapunov value [4]. This quantity is calculated numerically in this paper. Its mathematical description will be developed and presented in another new paper. It is worth to note that analysis of 3D or 4D nonlinear dynamics has been widely investigated, as in [91,92,93,94,95,96], just to mention a few.

1.1 Appendix 1.1: Stability of the equilibrium point

We look for determining conditions on the control gains $k_i$ $(i=1,2,3,4)$ for which the equilibrium point is stable and hence the Hopf bifurcation occurs.

For simplicity, posing $a=\frac{1}{I}$, $b=bg$ and $c=\frac{1}{I_{2}}$. Then, the characteristic equation of the Jacobian matrix (10) is defined as:

$$\begin{aligned} {\mathcal {P}}\left( \lambda \right)= & {} \lambda ^{4} + \left( k_{3}-k_{4}\right) \lambda ^{3} \nonumber \\&+ \left( a\left( \gamma -b+k_{1}\right) -ck_{2}\right) \lambda ^{2} + abk_{4}\lambda \nonumber \\&+\, abck_{2}=0 \end{aligned}$$

(74)

In order to study the stability conditions of the equilibrium point $\varvec{x}_{eq}$, we apply Routh-Hurwitz criterion, which states that all real eigenvalues and all real parts of complex conjugate eigenvalues of the characteristic polynomial ${\mathcal {P}}\left( \lambda \right)$ are negative if and only if the following conditions hold:

$$\begin{aligned} \begin{array}{ccccccc} \left( \text {i}\right) \ a_{1}>0,&\,&\left( \text {ii}\right) \ a_{3}>0,&\,&\left( \text {iii}\right) \ a_{4}>0&\text {and}&\left( \text {iv}\right) \ a_{1}a_{2}a_{3}>a_{3}^{2}+a_{1}^{2}a_{4} \end{array} \end{aligned}$$

(75)

with $a_{i}$ ($i=1,2,3,4$), are defined such that:

$$\begin{aligned} \begin{array}{ccccccc} {\mathcal {P}}\left( \lambda \right) =\lambda ^{4} + a_{1}\lambda ^{3} + a_{2}\lambda ^{2} +a_{3}\lambda + a_{4}=0 \end{array} \end{aligned}$$

(76)

Applying Routh-Hurwitz criterion (75) to the characteristic polynomial (74), and as $k_{i}>0$ for $i=1,2,3,4$, we find that necessary and sufficient conditions for the equilibrium point $\varvec{x}_{eq}$ to be asymptotically stable are:

$$\begin{aligned} {{\mathcal {C}}}_{1}= & {} k_{3}-k_{4}>0 \end{aligned}$$

(77a)

$$\begin{aligned} {{\mathcal {C}}}_{2}= & {} a\left( \gamma -b+k_{1}\right) \nonumber \\&-\,ck_{2}-ab\frac{k_{4}}{k_{3}-k_{4}}-ck_{2}\frac{k_{3}-k_{4}}{k_{4}}>0 \end{aligned}$$

(77b)

1.2 Appendix 1.2: Existence of Hopf bifurcation and periodic solutions

In this part, we will investigate existence of the Hopf bifurcation [4] at the equilibrium point regarding $k_{4}$ as the bifurcation parameter. Assume that (74) has a pure imaginary root $\lambda =\text {i} w$, $w\in {\mathbb {R}}^{+}$. Substituting it into (74) yields

$$\begin{aligned}&w^{4} - \left( a\left( \gamma -b+k_{1}\right) -ck_{2}\right) w^{2} + abck_{2} \nonumber \\&\quad +\, \text {i}w\left( -\left( k_{3}-k_{4}\right) w^{2}+abk_{4}\right) =0 \end{aligned}$$

(78)

It then follows that:

$$\begin{aligned}&w^{4} - \left( a\left( \gamma -b+k_{1}\right) -ck_{2}\right) w^{2} + abck_{2} = 0 \end{aligned}$$

(79a)

$$\begin{aligned}&\left( k_{4}-k_{3}\right) w^{2}+abk_{4} = 0 \end{aligned}$$

(79b)

From relation (79b), we obtain the following expression:

$$\begin{aligned} k_{4} = \frac{w^{2}}{ab+w^{2}}k_{3} \end{aligned}$$

(80)

We stress that w is the solution of (79a) and it depends only on the two parameters $k_{1}$ and $k_{2}$. Moreover, according to expression (80), $k_{4}$ is proportional to $k_{3}$ and it depends on w. Then, by fixing the value of the parameters $k_{1}$, $k_{2}$ and $k_{3}$, we can calculate the value of the gain $k_{4}$ at which the Hopf bifurcation occurs.

By solving relation (79a), it is easy to show that there are two solutions $w_{1}^{c}$ and $w_{2}^{c}$ defined as follows:

$$\begin{aligned}&w_{1}^{c} = \sqrt{\frac{a\left( \gamma -b+k_{1}\right) -ck_{2} - \sqrt{\left( a\left( \gamma -b+k_{1}\right) -ck_{2}\right) ^{2}-4abck_{2}}}{2}} \end{aligned}$$

(81a)

$$\begin{aligned}&w_{2}^{c} = \sqrt{\frac{a\left( \gamma -b+k_{1}\right) -ck_{2} + \sqrt{\left( a\left( \gamma -b+k_{1}\right) -ck_{2}\right) ^{2}-4abck_{2}}}{2}} \end{aligned}$$

(81b)

In (81), we have $w_{1}^{c}<w_{2}^{c}$. Actually, these two solutions, $w_{1}^{c}$ and $w_{2}^{c}$, exist if and only if the following three conditions hold:

$$\begin{aligned}&\left( a\left( \gamma -b+k_{1}\right) -ck_{2}\right) ^{2}-4abck_{2}>0 \end{aligned}$$

(82a)

$$\begin{aligned}&a\left( \gamma -b+k_{1}\right) -ck_{2}\nonumber \\&- \sqrt{\left( a\left( \gamma -b+k_{1}\right) -ck_{2}\right) ^{2}-4abck_{2}}>0 \end{aligned}$$

(82b)

$$\begin{aligned}&a\left( \gamma -b+k_{1}\right) -ck_{2} \nonumber \\&+\, \sqrt{\left( a\left( \gamma -b+k_{1}\right) -ck_{2}\right) ^{2}-4abck_{2}}>0 \end{aligned}$$

(82c)

As $k_{1}>0$ and $k_{2}>0$, then according to conditions (82b) and (82c), it follows that: $a\left( \gamma -b+k_{1}\right) -ck_{2}>0$. Therefore, relying on (82a), it easy to show that:

$$\begin{aligned} k_{1}>b-\gamma +\frac{c}{a}k_{2} + 2\sqrt{\frac{bc}{a}}\sqrt{k_{2}} \end{aligned}$$

(83)

This expression represents the condition on $k_{1}$ with respect to $k_{2}$ for the existence of the Hopf bifurcation. In addition, we emphasize that the system (8) exhibits two Hopf bifurcations at two different critical values $k_{4,1}^{c}$ and $k_{4,2}^{c}$ that are associated to $w_{1}^{c}$ and $w_{2}^{c}$, respectively. These two critical parameters $k_{4,1}^{c}$ and $k_{4,2}^{c}$ are defined like so:

$$\begin{aligned}&k_{4,1}^{c} = k_{3}\frac{a\left( \gamma -b+k_{1}\right) -ck_{2}- \sqrt{\left( a\left( \gamma -b+k_{1}\right) -ck_{2}\right) ^{2}-4abck_{2}}}{a\left( \gamma +b+k_{1}\right) -ck_{2} - \sqrt{\left( a\left( \gamma -b+k_{1}\right) -ck_{2}\right) ^{2}-4abck_{2}}} \end{aligned}$$

(84a)

$$\begin{aligned}&k_{4,2}^{c} = k_{3}\frac{a\left( \gamma -b+k_{1}\right) -ck_{2} + \sqrt{\left( a\left( \gamma -b+k_{1}\right) -ck_{2}\right) ^{2}-4abck_{2}}}{a\left( \gamma +b+k_{1}\right) -ck_{2} + \sqrt{\left( a\left( \gamma -b+k_{1}\right) -ck_{2}\right) ^{2}-4abck_{2}}} \end{aligned}$$

(84b)

For example, for $k_{1}=1.036692$, $k_{2}=0.0011$ and $k_{3}=38.4$, the two critical values of $k_{4}$ at which the Hopf bifurcation occurs are calculated to be about: $k_{4,1}^{c}=0.87159917$ and $k_{4,2}^{c}=27.19772529$. Moreover, we have: $w_{1}^{c}=1.04160466$ and $w_{2}^{c}=10.64970853$.

It is worth noting that for $k_{4}=k_{4,i}^{c}$, $(i=1,2)$, the relation ${{\mathcal {C}}}_{2}=0$ in (77b) takes place, for which the stability of the equilibrium is violated. Moreover, if the condition (83) is not satisfied, the two Hopf bifurcations disappear. In fact, there are two cases. The two Hopf bifurcations collide with each other and are replaced by only one Hopf bifurcation if the following condition is met:

$$\begin{aligned} k_{1} = b-\gamma +\frac{c}{a}k_{2} + 2\sqrt{\frac{bc}{a}}\sqrt{k_{2}} \end{aligned}$$

(85)

Hence, for such expression (90), we will obtain: $w_{1}^{c}=w_{2}^{c}=w_{\star }^{c}=\sqrt{\sqrt{abc}\sqrt{k_{2}}}$, and then:

$$\begin{aligned} k_{4,\star }^{c} = k_{3}\frac{\sqrt{ck_{2}}}{\sqrt{ab}+\sqrt{ck_{2}}} \end{aligned}$$

(86)

Moreover, if $k_{1} < b-\gamma +\frac{c}{a}k_{2} + 2\sqrt{\frac{bc}{a}}\sqrt{k_{2}}$, then no Hopf bifurcation exits.

Now, we aim at developing the analytical expression of the transversality condition for the occurrence of the Hopf bifurcation. From (74), it follows that:

$$\begin{aligned} \frac{d\lambda \left( k_{4}\right) }{dk_{4}}=\frac{\text {i}w\left( w^{2}+ab\right) }{abk_{4}-3\left( k_{3}-k_{4}\right) w^{2}+2\text {i}w\left( a\left( \gamma -b+k_{1}\right) -ck_{2}-2w^{2}\right) } \end{aligned}$$

(87)

Thus, we obtain:

$$\begin{aligned} \text {Re}\left( \frac{d\lambda \left( k_{4}\right) }{dk_{4}}\right) =\frac{2w^{2}\left( w^{2}+ab\right) \left( a\left( \gamma -b+k_{1}\right) -ck_{2}-2w^{2}\right) }{\left( abk_{4}-3\left( k_{3}-k_{4}\right) w^{2}\right) ^{2}+4w^{2}\left( a\left( \gamma -b+k_{1}\right) -ck_{2}-2w^{2}\right) ^{2}} \end{aligned}$$

(88)

It is clear that the sign of the condition (88) depends on the quantity $\vartheta = a\left( \gamma -b+k_{1}\right) -ck_{2}-2w^{2}$. Using expressions of $w_{1}^{c}$ and $w_{2}^{c}$, it follows that: $\vartheta = \sqrt{\left( a\left( \gamma -b+k_{1}\right) -ck_{2}\right) ^{2}-4abck_{2}}$ for $w=w_{1}^{c}$, and $\vartheta = -\sqrt{\left( a\left( \gamma -b+k_{1}\right) -ck_{2}\right) ^{2}-4abck_{2}}$ for $w=w_{2}^{c}$. Furthermore, based on condition (83), we obtain $\vartheta \ne 0$ for the two cases. Therefore,

$$\begin{aligned} \text {Re}\left( \frac{d\lambda \left( k_{4}\right) }{dk_{4}}\left| _{_{k_{4}=k_{4,i}^{c},w=w_{i}^{c}}}\right. \right) \ne 0 \end{aligned}$$

(89)

Accordingly, the second condition for the existence of a Hopf bifurcation [4] is also met. In addition, we have:

$$\begin{aligned}&\text {Re}\left( \frac{d\lambda \left( k_{4}\right) }{dk_{4}}\left| _{_{k_{4}=k_{4,1}^{c},w=w_{1}^{c}}}\right. \right) > 0 \end{aligned}$$

(90a)

$$\begin{aligned}&\text {Re}\left( \frac{d\lambda \left( k_{4}\right) }{dk_{4}}\left| _{_{k_{4}=k_{4,2}^{c},w=w_{2}^{c}}}\right. \right) < 0 \end{aligned}$$

(90b)

Hence, according to condition (90a) the equilibrium point is stable when $k_{4}>k_{4,1}^{c}$ and periodic solutions exist when $k_{4}<k_{4,1}^{c}$. Furthermore, according to condition (90b) the equilibrium point is stable when $k_{4}<k_{4,2}^{c}$ and periodic solutions exist when $k_{4}>k_{4,2}^{c}$. Furthermore, the period $T_{i}$ of oscillations around the bifurcation point $k_{4,i}^{c}$ is defined as follows:

$$\begin{aligned} T_{i} = \frac{2\pi }{w_{i}^{c}} \end{aligned}$$

(91)

1.3 Appendix 1.3: Stability of the periodic solutions

In order to characterize the stability of the periodic solutions generated through each Hopf bifurcation, the so-called fist Lyapunov value (coefficient) [4], say $\ell _{1}$, must be computed and analyzed for the system (8). In the bifurcation points, a positive first Lyapunov value represents a subcritical bifurcation and predicts that the system presents unstable periodic oscillations, which can fold back and coexist with the stable equilibrium point. In contrast, a negative value for $\ell _{1}$ indicates a supercritical bifurcation and stable self-oscillations emerge from the bifurcation point.

Analytical calculation of the fist Lyapunov coefficient $\ell _{1}$ can be achieved, but it is very long. It can be calculated according to the formula given in [97]. For the sake of brevity, we omit this calculation in this paper. In fact, this analysis on stability of the periodic oscillations and bifurcation through the first Lyapunov value and the center manifold theory will be developed with further details in another work. Then, in this study we will perform a numerical computation of $\ell _{1}$ using the well-known MATCONT package [97, 98]. Alonso et al. [57, 58] used the AUTO package to the numerical continuation of limit cycles and the stability index for the underactuated IWP.

Thus, using MATCONT package, the fist Lyapunov coefficient $\ell _{1}$ is computed to be: $\ell _{1,1}=3.121836\times 10^{-9}$ at $k_{4,1}^{c}=0.87159917$, whereas $\ell _{1,2}=-1.081602\times 10^{-5}$ at $k_{4,2}^{c}=27.19772529$. Therefore, as $\ell _{1,1}>0$ then the periodic solution emanating from the first Hopf bifurcation at $k_{4,1}^{c}$ is unstable, and which arises at the side where the equilibrium is stable. However, because $\ell _{1,2}<0$ hence the generated sustained oscillation at the parameter $k_{4,2}^{c}$ is stable. Moreover, this stable periodic oscillation arises at the side where the equilibrium is unstable. Relying on relation (91), the period of the stable self-sustained oscillation (stable limit cycle) around the critical parameter $k_{4,2}^{c}$ is: $T_{2}=0.5899866\,[s]$.

Appendix 2: Equivalent BMI (29b) for a IWIP with uncertain friction parameters and an external disturbance

Using the reference dynamics (16) and the uncertain disturbed nonlinear dynamics (17), we obtain the following tracking error dynamics:

$$\begin{aligned} \dot{\varvec{e}}=\varvec{ J}\varvec{e}+\varvec{ D}\left( f\left( x_{1}\right) -f\left( x_{1}^{r}\right) \right) + \varvec{ B}v + \varvec{\tilde{ J}}\varvec{x} + \varvec{\tilde{D}}\zeta \nonumber \\ \end{aligned}$$

(92)

By substituting the tracking control law (20) in (92), system (92) will be simplified as follows:

$$\begin{aligned} \dot{\bar{\varvec{e}}}=\varvec{ A}\varvec{\bar{e}}+\varvec{\bar{ D}}\left( f\left( x_{1}\right) -f\left( x_{1}^{r}\right) \right) + \varvec{\bar{ B}}w + \varvec{\tilde{ A}}\varvec{x} + \varvec{ D}_{5}\zeta \nonumber \\ \end{aligned}$$

(93)

with $\varvec{\tilde{ A}}=\left[ \begin{array}{ccc} 0 &{} 0 &{} 0\\ 0 &{} -\frac{\delta _{1}+\delta _{2}}{I} &{} \frac{\delta _{2}}{I_2}\\ 0 &{} \frac{\delta _{2}}{I} &{} -\frac{\delta _{2}}{I_2} \end{array} \right]$ and $\varvec{ D}_{5}=\left[ \begin{array}{c} 0 \\ 1\\ 0 \end{array} \right]$.

Moreover, the term $\varvec{\tilde{ A}}\varvec{x}$ in (93) can be rewritten like so: $\varvec{\tilde{ A}}\varvec{x} = \delta _{1}\varvec{ D}_{2}x_{3}+\delta _{2}\varvec{ D}_{3}x_{3}+\delta _{2}\varvec{ D}_{4}x_{4}$, with $\varvec{ D}_{2}= \frac{1}{I}\left[ \begin{array}{c} 0 \\ -1\\ 0 \end{array} \right]$, $\varvec{ D}_{3}= \frac{1}{I}\left[ \begin{array}{c} 0 \\ -1\\ 1 \end{array} \right]$, $\varvec{ D}_{4}= \frac{1}{I_{2}}\left[ \begin{array}{c} 0 \\ 1\\ -1 \end{array} \right]$.

In addition, if we consider that:

• the two uncertain friction parameters $\delta _{1}$ and $\delta _{2}$ are norm-bounded, i.e., $\delta _{1}\le \bar{\delta }_{1}$ and $\delta _{2}\le \bar{\delta }_{2}$,

• the two states $x_{3}$ and $x_{4}$ are bounded such that $\left| x_{3}\right| <\bar{x}_{3}$ and $\left| x_{4}\right| <\bar{x}_{4}$, for some constants $\bar{x}_{3}>0$ and $\bar{x}_{4}>0$,

• the disturbance $\zeta$ is bounded such that $\left| \zeta \right| <\rho$, with $\rho >0$.

then, according to Sect. 4.2 and relying on the Young relation, we obtain the following conditions:

$$\begin{aligned}&2\bar{\varvec{e}}^\mathrm{T}\varvec{ P}\varvec{\tilde{ A}}\varvec{x} \le \bar{\varvec{e}}^\mathrm{T}\varvec{ P}\left( \varvec{ M}_{2}+\varvec{ M}_{3}+\varvec{ M}_{4}\right) \varvec{ P}\bar{\varvec{e}} \nonumber \\&\quad + \left( \bar{\delta }_{1}\bar{x}_{3}\right) ^{2}\varvec{ D}_{2}^\mathrm{T}\varvec{ M}_{2}^{-1}\varvec{ D}_{2} + \left( \bar{\delta }_{2}\bar{x}_{3}\right) ^{2}\varvec{ D}_{3}^\mathrm{T}\varvec{ M}_{3}^{-1}\varvec{ D}_{3} \nonumber \\&\quad + \left( \bar{\delta }_{2}\bar{x}_{4}\right) ^{2}\varvec{ D}_{4}^\mathrm{T}\varvec{ M}_{4}^{-1}\varvec{ D}_{4} \end{aligned}$$

(94a)

$$\begin{aligned}&2\bar{\varvec{e}}^\mathrm{T}\varvec{ P}\varvec{ D}_{5}\zeta \le \bar{\varvec{e}}^\mathrm{T}\varvec{ P}\varvec{ M}_{5}\varvec{ P}\bar{\varvec{e}} + \rho ^{2}\varvec{ D}_{5}^\mathrm{T}\varvec{ M}_{5}^{-1}\varvec{ D}_{5} \end{aligned}$$

(94b)

with $\varvec{ M}_{i}=\varvec{ M}_{i}^\mathrm{T}>0$, $i=2,\ldots ,5$.

Let us pose $\varvec{ J}=\left[ \begin{array}{c} \varvec{{\mathcal {I}}} \\ \varvec{{\mathcal {I}}}\\ \varvec{{\mathcal {I}}}\\ \varvec{{\mathcal {I}}}\\ \varvec{{\mathcal {I}}} \end{array} \right]$, $\varvec{ M}=\text {diag}\left( \varvec{ M}_{1},\varvec{ M}_{2},\varvec{ M}_{3},\varvec{ M}_{4},\varvec{ M}_{5}\right)$, and $\varvec{ D}=\left[ \begin{array}{c} \gamma \varvec{\bar{ D}} \\ \bar{\delta }_{1}\bar{x}_{3}\varvec{ D}_{2} \\ \bar{\delta }_{2}\bar{x}_{3}\varvec{ D}_{3} \\ \bar{\delta }_{2}\bar{x}_{4}\varvec{ D}_{4} \\ \rho \varvec{ D}_{5} \end{array} \right]$. Thus, based on results in Sect. 4.2, the BMI (29b) will be replaced by the following one:

$$\begin{aligned} \left[ \begin{array}{cc} \varvec{ P}\varvec{ A}+\varvec{ P}\varvec{\bar{ B}}\varvec{ K} + \left( \star \right) + \varvec{ P}\varvec{ J}^\mathrm{T}\varvec{ M}\varvec{ J}\varvec{ P} +\eta _{3}\varvec{ {\mathcal {I}}}&{} -\left( \eta _{1}-\eta _{2}\right) \varvec{ C}\\ \left( \star \right) &{} \varvec{ D}^\mathrm{T}\varvec{ M}^{-1}\varvec{ D} - \epsilon \eta _{3}+4\sigma \left( \eta _{1}+\eta _{2}\right) \end{array} \right] <0 \end{aligned}$$

(95)