Adaptive sliding mode controller design for nonlinear teleoperation systems using singular perturbation method

Abstract

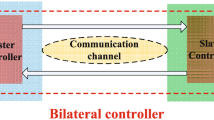
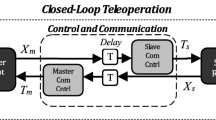
In the presence of communication latency in a bilateral teleoperation system, stability and transparency are highly regarded. The major problem with teleoperation systems is complex dynamic and subsequently designing the controller. This essay presents a novel method of controller design, based on singular perturbation framework for the bilateral teleoperation of nonlinear robots through the Internet. Using this method makes it much easier to design the controller because controller designing is done for reduced-order subsystem not full-order system. In this paper, teleoperation system dynamics was decomposed into slave (slow subsystem) and error (fast subsystem, different from master and slave), which contains position and velocity, and an adaptive sliding mode controller was designed for each of them. For constant and time-varying delay, the positions of master–slave were compared together and controlling signal was applied to the slave; therefore, they could track each other in the shortest possible time. In the simulation, the stability and performance results of teleoperation system were obtained under the proposed controller and compared with those of another approach. In this research, having higher speed and lower control signal amplitude, at the same time, elucidates the absolute superiority of the new approach.

Appendix

Proof: According to the Eq. (37) for the slow subsystem, we have:

$$\begin{aligned} \dot{\bar{{X}}}= & {} \mathop {AA}\nolimits _s \bar{{X}}+\mathop {BB}\nolimits _{Fs} \mathop F\nolimits _m (t-T)+BB_{us}\bar{{U}}(t)\nonumber \\ AA_s= & {} \left[ {{\begin{array}{cc} 0&{} 1 \\ {AA_{s21}} &{} {AA_{s22}} \\ \end{array}} } \right] ,\quad BB_{Fs} =\left[ {{\begin{array}{c} 0 \\ {BB_{Fs2}} \\ \end{array}} } \right] ,\nonumber \\ B_{us}= & {} \left[ {{\begin{array}{c} 0 \\ {BB_{us2}} \\ \end{array}} } \right] \end{aligned}$$

(54)

We can rewrite the above equation in this form:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\dot{\bar{{x}}}_1 =\bar{{x}}_2 }\\ \dot{\bar{{x}}}_2 =AA_{s21} \bar{{x}}_1 +AA_{s22} \bar{{x}}_2 +BB_{Fs2} F_m \\ \qquad -AA_{s21} \bar{{x}}_1 -AA_{s22} \bar{{x}}_2 -k_s (a_s \bar{{x}}_1 +\bar{{x}}_2 )\\ \end{array}} } \right. \end{aligned}$$

(55)

After simplification, we have:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\dot{\bar{{x}}}_1 =\bar{{x}}_2}\\ {\dot{\bar{{x}}}_2 =BB_{Fs2} F_m -a_s k_s \bar{{x}}_1 -k_s \bar{{x}}_2} \\ \end{array}} } \right. \end{aligned}$$

(56)

Equilibrium point for above system is $\left( \frac{BB_{Fs2}}{a_s k_s},0\right)$ and we must transfer it to origin; hence, we utilize a new variable to solve this problematic trouble. Therefore,

$$\begin{aligned} \left[ {{\begin{array}{c} {y_1} \\ {y_2} \\ \end{array}} } \right]= & {} \left[ {{\begin{array}{c} {\bar{{x}}_1 -\frac{BB_{Fs2}}{a_s k_s} F_m} \\ {\bar{{x}}_2} \\ \end{array}} } \right] \Rightarrow \left[ {{\begin{array}{c} {\dot{y}_1} \\ {\dot{y}_2} \\ \end{array}} } \right] \nonumber \\= & {} \left[ {{\begin{array}{c} {y_2} \\ {-a_s k_s y_1 -k_s y_2} \\ \end{array}} } \right] \end{aligned}$$

(57)

Now, we suggest following Lyapunov function for the slow subsystem with this new variable:

$$\begin{aligned} V= & {} Y^{T}PY=\left[ {{\begin{array}{cc} {y_1} &{} {y_2} \\ \end{array}} } \right] \left[ {{\begin{array}{cc} {p_1} &{} 0 \\ 0&{} {p_2} \\ \end{array}} } \right] \left[ {{\begin{array}{c} {y_1} \\ {y_2} \\ \end{array}} } \right] \nonumber \\= & {} p_1 y_1^2 +p_2 y_2^2 \Rightarrow \left\{ {{\begin{array}{l} {V(0,0)=0} \\ {V>0\quad \mathrm{for}\ Y\ne 0} \\ \mathrm{we\ show}\ \dot{V}<0 \\ \end{array}} } \right. \end{aligned}$$

(58)

Now:

$$\begin{aligned} \dot{V}= & {} \frac{\partial V}{\partial Y}\frac{\partial Y}{\partial t}=\left[ {{\begin{array}{cc} {2p_1 y_1} &{} {2p_2 y_2} \\ \end{array}} } \right] \left[ {{\begin{array}{c} {y_2} \\ {-a_s k_s y_1 -k_s y_2} \\ \end{array}} } \right] \nonumber \\= & {} 2p_1 y_1 y_2 -2a_s k_s y_1 y_2 -2k_s p_2 y_2^2 \end{aligned}$$

(59)

We choose:

$$ \begin{aligned} p_1 =a_s k_s \quad \& \quad p_2 =1\quad \& \quad a_s >0\quad \& \quad k_s >0 \end{aligned}$$

(60)

After simplification, we have:

$$\begin{aligned} \dot{V}=-2k_s y_2^2 <0 \end{aligned}$$

(61)

Therefore,

$$\begin{aligned} V=a_s k_s y_1^2 +y_2^2 \end{aligned}$$

(62)

After substitution, we have:

$$\begin{aligned} V=a_s k_s \left( \bar{{x}}_1 -\frac{BB_{Fs2}}{a_s k_s} F_m (t-T)\right) ^{2}+\bar{{x}}^{2} \end{aligned}$$

(63)

Now, we continue proof for the fast subsystem. By using Eq. (38), we have:

$$\begin{aligned} \frac{d\hat{{Z}}}{d\tau }= & {} {AA}_f \hat{{Z}}+ {BB}_{Ff} F_m (t-T)+BB_{uf} \hat{{U}}\nonumber \\ AA_f= & {} \left[ {{\begin{array}{cc} 0&{} 1 \\ {AA_{f21}} &{} {AA_{f22}} \\ \end{array}} } \right] ,\quad BB_{Ff} =\left[ {{\begin{array}{c} 0 \\ {BB_{Ff2}} \\ \end{array}} } \right] ,\nonumber \\ B_{uf}= & {} \left[ {{\begin{array}{c} 0 \\ {BB_{uf2}} \\ \end{array}} } \right] \end{aligned}$$

(64)

After rewriting the Eq. (64), we obtain:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\dot{\hat{{z}}}_1 =\hat{{z}}_2}\\ \dot{\hat{{z}}}_2 =AA_{f21} \hat{{z}}_1 +AA_{f22} \hat{{z}}_2 +BB_{Ff2} F_m \\ \quad -\,AA_{f21} \bar{{z}}_1 -AA_{f22} \hat{{z}}_2 -BB_{Ff2} F_m\\ \quad -\,k_f (a_f \hat{{z}}_1 +\hat{{z}}_2 )\\ \end{array}} } \right. \end{aligned}$$

(65)

After simplification, we reach:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\dot{\hat{{z}}}_1 =\hat{{z}}_2} \\ {\dot{\hat{{z}}}_2 =-a_f k_f \hat{{z}}_1 -k_f \hat{{z}}_2} \\ \end{array}} } \right. \end{aligned}$$

(66)

Equilibrium point for above system is in origin (0,0); therefore, we offer the following Lyapunov function for the fast subsystem:

$$\begin{aligned} W= & {} \hat{{Z}}^{T}R\hat{{Z}}=\left[ {{\begin{array}{cc} {z_1} &{} {z_2} \\ \end{array}} } \right] \left[ {{\begin{array}{cc} {r_1} &{} 0 \\ 0&{} {r_2} \\ \end{array}} } \right] \left[ {{\begin{array}{c} {z_1} \\ {z_2} \\ \end{array}} } \right] \nonumber \\= & {} r_1 \hat{{z}}_1^2 +r_2 \hat{{z}}_2^2\Rightarrow \left\{ {{\begin{array}{l} {w(0,0)=0} \\ w>0\quad \mathrm{for}\ \hat{{Z}}\ne 0\\ \mathrm{we\ show}\ \dot{W}<0\\ \end{array}} } \right. \end{aligned}$$

(67)

Now:

$$\begin{aligned} \frac{dW}{d\tau }= & {} \frac{\partial W}{\partial \hat{{Z}}} \frac{\partial \hat{{Z}}}{\partial t}=\left[ {{\begin{array}{cc} {2r_1 \hat{{z}}_1} &{} {2r_2 \hat{{z}}_2} \\ \end{array}} } \right] \left[ \! {{\begin{array}{c} {\hat{{z}}_2} \\ {-a_f k_f \hat{{z}}_1 \!-\!k_f \hat{{z}}_2} \\ \end{array}} } \!\right] \nonumber \\= & {} 2r_1 \hat{{z}}_1 \hat{{z}}_2 -2a_f k_f \hat{{z}}_1 \hat{{z}}_2 -2k_f r_2 \hat{{z}}_2^2\ \end{aligned}$$

(68)

We choose:

$$ \begin{aligned} r_1 =a_f k_f \quad \& \quad r_2 =1\quad \& \quad a_f \!>\!0\quad \& \quad k_f \!>\!0 \end{aligned}$$

(69)

After simplification, we have:

$$\begin{aligned} \dot{W}=-2k_f \hat{{z}}_2^2 <0 \end{aligned}$$

(70)

Therefore,

$$\begin{aligned} W=a_f k_f \hat{{z}}_1^2 +\hat{{z}}_2^2 \end{aligned}$$

(71)