Skip to main content
SpringerLink
Log in

Bell-polynomial approach and soliton solutions for the Zhiber–Shabat equation and (2+1)-dimensional Gardner equation with symbolic computation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

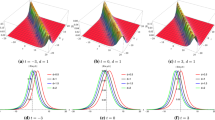
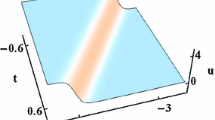
Under investigation in this paper are the Zhiber–Shabat and (2+1)-dimensional Gardner equations in quantum fields, fluids and plasmas. Via the Hirota method and symbolic computation, the Bell-polynomial approach is performed to directly bilinearize those equations. For the Zhiber–Shabat equation, based on the bilinear form with an auxiliary variable, the bell-shaped soliton, upside-down bell-shaped soliton and breather-like solutions are obtained. Figures are plotted to illustrate the elastic interactions between two upside-down bell-shaped solitons and the interaction between the breather-like. As to the (2+1)-dimensional Gardner equation, bilinear form, Bäcklund transformation, one- and two-shock wave solutions are derived. Amplitude-compression and amplification interactions are investigated analytically and graphically.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Barnett, M.P., Capitani, J.F., Von Zur Gathen, J., Gerhard, J.: Symbolic calculation in chemistry: selected examples. Int. J. Quant. Chem. 100, 80–104 (2004)

    Article  Google Scholar 

  2. Gao, Y.T., Tian, B.: On the non-planar dust-ion-acoustic waves in cosmic dusty plasmas with transverse perturbations. Europhys. Lett. 77, 15001–15006 (2007)

    Article  Google Scholar 

  3. Tyagi, M., Sujith, R.I.: The propagation of finite amplitude gasdynamic disturbances in a stratified atmosphere around a celestial body: an analytical study. Physica D 211, 139–150 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  4. Gorza, S.P., Deconinck, B., Emplit, P., Trogdon, T., Haelterman, M.: Experimental demonstration of the oscillatory snake instability of the bright soliton of the (2+1)D hyperbolic nonlinear Schrödinger equation. Phys. Rev. Lett. 106, 094101–094104 (2011)

    Article  Google Scholar 

  5. Pitaevskii, L.P., Stringari, S.: Bose–Einstein Condensation. Cambridge University Press, Cambridge (2003)

    MATH  Google Scholar 

  6. Bekir, A.: Painlevé test for some (2+1)-dimensional nonlinear equations. Chaos Solitons Fractals 32, 449–455 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  7. Matveev, V.B., Salle, M.A.: Darboux Transformations and Solitons. Springer, Berlin (1991)

    MATH  Google Scholar 

  8. Gomes, J.F., Ymai, L.H., Zimerman, A.H.: Permutability of Bäcklund transformation for N=1 supersymmetric sinh-Gordon. Phys. Lett. A 373, 1401–1404 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  9. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  10. Freeman, N.C., Nimmo, J.J.: Soliton solutions of the Korteweg–de Vries and Kadomtsev–Petviashvili equations: the Wronskian technique. Phys. Lett. A 95, 1–13 (1983)

    Article  MathSciNet  Google Scholar 

  11. Matveev, V.B.: Generalized Wronskian formula for solutions of the KdV equations: first applications. Phys. Lett. A 166, 205–208 (1992)

    Article  MathSciNet  Google Scholar 

  12. Bell, E.T.: Exponential polynomials. Ann. Math. 35, 258–277 (1934)

    Article  Google Scholar 

  13. Lambert, F., Springael, J.: On a direct procedure for the disclosure of Lax pairs and Bäcklund transformations. Chaos Solitons Fractals 12, 2821–2832 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  14. Lambert, F., Springael, J.: Soliton equations and simple combinatorics. Acta Appl. Math. 102, 147–178 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  15. Rogers, C., Shadwick, W.F.: Bäcklund Transformations and Their Applications. Academic Press, New York (1982)

    MATH  Google Scholar 

  16. Tian, B., Gao, Y.T., Zhu, H.W.: Variable-coefficient higher-order nonlinear Schrödinger model in optical fibers: variable-coefficient bilinear form, Bäcklund transformation, Brightons and symbolic computation. Phys. Lett. A 366, 223–229 (2007)

    Article  MATH  Google Scholar 

  17. Xu, T., Tian, B., Zhang, H.Q., Li, J.: Integrable decompositions for the (2+1)-dimensional Gardner equation. Z. Angew. Math. Phys. 61, 293–308 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  18. Zhang, H.Q., Tian, B., Li, J., Xu, T., Zhang, Y.X.: Symbolic-computation study of integrable properties for the (2+1)-dimensional Gardner equation with the two-singular manifold method. IMA J. Appl. Math. 74, 46–61 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  19. Zhiber, A.V., Shabat, A.B.: The Klein–Gordon equations with nontrivial groups. Sov. Phys. Dokl. 24, 607–609 (1979)

    Google Scholar 

  20. Zhiber, A.V., Shabat, A.B.: Systems of equations u x =p(u,v),v y =q(u,v) that possess symmetries. Dokl. Akad. Nauk SSSR 277, 29–33 (1984)

    MathSciNet  Google Scholar 

  21. Conte, R., Musette, M.: Link between solitary waves and projective Riccati equations. J. Phys. A 25, 5609–5623 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  22. He, B., Long, Y., Rui, W.G.: New exact bounded travelling wave solutions for the Zhiber–Shabat equation. Nonlinear Anal. 71, 1636–1648 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  23. Tang, Y.N., Xu, W., Shen, J.W., Gao, L.: Bifurcations of traveling wave solutions for Zhiber–Shabat equation. Nonlinear Anal. 67, 648–656 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  24. Borhanifar, A., Moghanlu, A.Z.: Application of the \((\frac{G'}{G})\)-expansion method for the Zhiber–Shabat equation and other related equations. Math. Comput. Model 54, 2109–2116 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  25. Unterberger, J.: On vertex algebra representations of the Schrödinger–Virasoro Lie algebra. Nucl. Phys. B 823, 320–371 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  26. Lakshmanan, M., Kalianppan, P.: Lie transformations, nonlinear evolution equations, and Painlevé forms. J. Math. Phys. 24, 795–806 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  27. Dodd, R.K., Bullough, R.K.: Bäcklund transformations for the Sine–Gordon equations. Proc. R. Soc. A, Math. Phys. Eng. Sci. 351, 499–523 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  28. Davodi, A.G., Ganji, D.D., Alipour, M.M.: Numerous exact solutions for the Dodd–Bullough–Mikhailov equation by some different methods. Selçuk J. Appl. Math. 10, 81–94 (2009)

    MathSciNet  MATH  Google Scholar 

  29. Whitham, G.B: Linear and Nonlinear Waves. Wiley-Interscience, New York (1974)

    MATH  Google Scholar 

  30. Zhang, H.Q.: New exact solutions for the sinh-Gordon equation. Chaos Solitons Fractals 28, 489–496 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  31. Krishnan, E.V., Triki, H., Labidi, M., Biswas, A.: A study of shallow water waves with Gardner’s equation. Nonlinear Dyn. 66, 497–507 (2011)

    Article  MathSciNet  Google Scholar 

  32. Konopelchenko, B.G., Dubrovsky, V.G.: Some new integrable nonlinear evolution equations in 2+1 dimensions. Phys. Lett. A 102, 15–17 (1984)

    Article  MathSciNet  Google Scholar 

  33. Konopelchenko, B.G.: Inverse spectral transform for the (2+1)-dimensional Gardner equation. Inverse Probl. 7, 739–753 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  34. Chen, Y., Yan, Z.Y.: New exact solutions of (2+1)-dimensional Gardner equation via the new Sine–Gordon equation expansion method. Chaos Solitons Fractals 26, 399–406 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  35. Anders, I.: Long-time asymptotics of non-decaying solutions of the (2+1)-dimensional Gardner equation. Asymptot. Anal. 19, 185–207 (1999)

    MathSciNet  MATH  Google Scholar 

  36. Yu, G.F., Tam, H.W.: On the (2+1)-dimensional Gardner equation: determinant solutions and pfaffianization. J. Math. Anal. Appl. 330, 989–1001 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  37. Miura, R.: Korteweg–de Vries equation and generalizations. I. A remarkable explicit nonlinear transformation. J. Math. Phys. 9, 1202–1204 (1968)

    Article  MathSciNet  MATH  Google Scholar 

  38. Lambert, F., Loris, I., Springael, J., Willox, R.: On the Hirota representation of soliton equations with one tau-function. J. Phys. Soc. Jpn. 70, 605–608 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  39. Zakharov, V.E.: What is Integrability? Springer, Berlin (1991)

    Book  Google Scholar 

  40. Wadati, M., Sanuki, H., Konno, K.: Relationships among inverse method, Bäcklund transformation and an infinite number of conservation laws. Prog. Theor. Phys. 53, 419–436 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  41. Yu, X., Gao, Y.T., Sun, Z.Y., Liu, Y.: Wronskian solutions and integrability for a generalized variable-coefficient forced Korteweg-de Vries equation in fluids. Nonlinear Dyn. 67, 1023–1030 (2012)

    Article  Google Scholar 

  42. Yu, X., Gao, Y.T., Sun, Z.Y., Liu, Y.: Solitonic propagation and interaction for a generalized variable-coefficient forced Korteweg-de Vries equation in fluids. Phys. Rev. E 83, 056601 (2011)

    Article  Google Scholar 

  43. Sun, Z.Y., Gao, Y.T., Yu, X., Liu, Y.: Amplification of nonautonomous solitons in the Bose-Einste condensates and nonlinear optics. Europhys. Lett. 93, 40004 (2011)

    Article  Google Scholar 

  44. Sun, Z.Y., Gao, Y.T., Liu, Y., Yu, X.: Soliton management for a variable-coefficient modified Korteweg-de Vries equation. Phys. Rev. E 84, 026606 (2011)

    Article  Google Scholar 

  45. Wang, L., Gao, Y.T., Gai, X.L., Sun, Z.Y.: Inelastic interactions and double Wronskian solutions for the Whitham-Broer-Kaup model in shallow water. Phys. Scr. 80, 065017 (2009)

    Article  Google Scholar 

  46. Wang, L., Gao, Y.T., Gai, X.L.: Odd-soliton-like solutions for the variable-coefficient variant boussinesq model in the long gravity waves. Z. Naturforsch. A 65, 818–828 (2010)

    Google Scholar 

  47. Sun, Z.Y., Gao, Y.T., Yu, X., Liu, W.J., Liu, Y.: Bound vector solitons and soliton complexes for the coupled nonlinear Schrödinger equations. Phys. Rev. E 80, 066608 (2009)

    Google Scholar 

Download references

Acknowledgements

This work has been supported by the Fundamental Research Funds for the Central Universities of China under Grant No. 2011BUPTYB02, and by the Specialized Research Fund for the Doctoral Program of Higher Education (No. 200800130006), Chinese Ministry of Education.

Author information

Authors and Affiliations

  1. State Key Laboratory of Information Photonics and Optical Communications, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Yu-Feng Wang, Bo Tian, Pan Wang, Min Li & Yan Jiang

  2. School of Science, Beijing University of Posts and Telecommunications, Beijing, 100876, China

    Yu-Feng Wang, Bo Tian, Pan Wang, Min Li & Yan Jiang

Authors
  1. Yu-Feng Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Bo Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Pan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Min Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Yan Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bo Tian.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Wang, YF., Tian, B., Wang, P. et al. Bell-polynomial approach and soliton solutions for the Zhiber–Shabat equation and (2+1)-dimensional Gardner equation with symbolic computation. Nonlinear Dyn 69, 2031–2040 (2012). https://doi.org/10.1007/s11071-012-0405-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-012-0405-3

Keywords

Search

Navigation