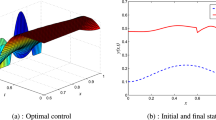
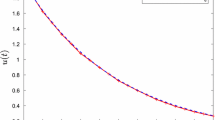
Abstract
In this paper, a solution procedure for a class of optimal control problems involving distributed parameter systems described by a generalized, fractional-order heat equation is presented. The first step in the proposed procedure is to represent the original fractional distributed parameter model as an equivalent system of fractional-order ordinary differential equations. In the second step, the necessity for solving fractional Euler–Lagrange equations is avoided completely by suitable transformation of the obtained model to a classical, although infinite-dimensional, state-space form. It is shown, however, that relatively small number of state variables are sufficient for accurate computations. The main feature of the proposed approach is that results of the classical optimal control theory can be used directly. In particular, the well-known “linear-quadratic” (LQR) and “Bang-Bang” regulators can be designed. The proposed procedure is illustrated by a numerical example.
Similar content being viewed by others
References
Riewe, F.: Noncoservative Hamiltonian and Lagrangian mechanics. Phys. Rev. E 53(2), 53–63 (1996)
Atanacković, T.M.: A generalized model for the uniaxial isothermal deformation of a viscoelastic body. Acta Mech. 159, 77–86 (2002)
Atanacković, T.M.: On a distributed derivative model of a viscoelastic body. C. R., Méc. 331, 687–692 (2003)
Sabatier, J., Agrawal, O., Tenreiro Machado, J.A. (eds.) Advances in Fractional Calculus. Springer, Berlin (2007)
Margin, R.L.: Fractional Calculus in Bioengineering. Begell House, Redding (2006)
Mainardy, F.: On the initial value problem for the fractional diffusion-wave equation. In: Rionero, S., Ruggeri, T. (eds.): Waves and Stability in Continuous Media. World Scientific, Singapore (1995)
Mainardy, F., Luchko, Y., Pagnini, G.: The fundamental solution of the space–time fractional diffusion equation. Fract. Calc. Appl. Anal. 4(2), 153–192 (2001)
Agrawal, O.P.: Solution for a fractional diffusion-wave equation defined in a bounded domain. Nonlinear Dyn. 29, 145–155 (2002)
Metzler, R., Nonnenmacher, T.F.: Fractional diffusion, waiting-time distributions, and Cattaneo-type equations. Phys. Rev. E 57(6), 6–13 (1998)
Metzler, R., Klafter, J.: Boundary value problems for fractional diffusion equations. Physica A 278, 107–125 (2000)
Atanacković, T.M., Pilipović, S., Zorica, D.: A diffusion wave equation with two fractional derivatives of different order. J. Phys. A 40, 5319–5333 (2007)
Ray, W.H., Lainiotis, D.G. (eds.): Distributed Parameter Systems—Identification, Estimation and Control. Marcel Dekker, New York (1978)
Tzafestas, S.G. (ed.): Distributed Parameter Control Systems—Theory and Application. Pergamon Press, Elmsford (1982)
Fatorini, H.O.: Infinite Dimensional Linear Control Systems—The Time-Optimal and Norm-Optimal Problems. Elsevier, Amsterdam (2005)
Liang, J., Chen, Y., Fullmer, R.: Boundary stabilization and disturbance rejection for time fractional order diffusion-wave equations. Nonlinear Dyn. 38, 339–354 (2004)
Agrawal, O.P.: A general formulation and solution scheme for fractional optimal control problems. Nonlinear Dyn. 38, 323–337 (2004)
Agrawal, O.P.: Fractional variational calculus and the transversality conditions. J. Phys. A 39, 10375–10384 (2006)
Atanacković, T.M., Konjik, S., Pilipović, S.: Variational problems with fractional derivatives: Euler–Lagrange equations. J. Phys. A 41, 095201 (2008)
Atanacković, T.M., Stanković, B.: On a class of differential equations with left and right fractional derivatives. Z. Angew. Math. Mech. 87, 537–546 (2007)
Atanacković, T.M., Stanković, B.: On a differential equation with left and right fractional derivatives. Fract. Calc. Appl. Anal. 10, 138–150 (2007)
Agrawal, O.P., Baleanu, D.: A Hamiltonian formulation and a direct numerical scheme for fractional optimal control problems. J. Vib. Control 13(9–10), 1269–1281 (2007)
Baleanu, D., Defterli, O., Agrawal, O.P.: A central difference numerical scheme for fractional optimal control problems. J. Vib. Control 15(4), 583–597 (2009)
Agrawal, O.P.: A numerical scheme for initial compliance and creep response of a system. Mech. Res. Commun. 36, 444–451 (2009)
Atanacković, T.M., Stanković, B.: On a numerical scheme for solving differential equations of fractional order. Mech. Res. Commun. 35, 429–438 (2008)
Jeličić, Z.D., Petrovački, N.: Optimality conditions and a solution scheme for fractional optimal control problems. Struct. Multidiscipl. Optim. 38, 571–581 (2009)
Petrovački, D.P.: Optimal control of a heat conduction problem. J. Appl. Math. Phys. 26, 436–480 (1975)
Petrovački, D.P.: The minimum time problem for a class of non-linear distributed parameter systems. Int. J. Control 32(1), 51–62 (1980)
Vujanović, B.D., Atanacković, T.M.: An Introduction to Modern Variational Techniques in Mechanics and Engineering. Birkhäuser, Boston (2004)
Dacorogna, B.: Direct Methods in the Calculus of Variations. Springer-Verlag, Berlin (1989)
Vujanović, B.D., Spasić, D.T.: Metodi optimizacije. Univerzitet u Novom Sadu, Fakultet tehničkih nauka (1997)
Oldham, K.B., Spanier, J.: The Fractional Calculus. Academic Press, San Diego (1974)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam (2006)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Rapaić, M.R., Jeličić, Z.D. Optimal control of a class of fractional heat diffusion systems. Nonlinear Dyn 62, 39–51 (2010). https://doi.org/10.1007/s11071-010-9697-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-010-9697-3