1 Introduction

In some applications, multibody systems may experience intermittent motions due to the collisions between different components, existence of the joint clearance, or joint locking [4, 5, 14, 18, 24, 26]. Different methods can be used to model the impact in a multibody system. These approaches have been reviewed in detail in [7, 19].

Piecewise approach has largely been used to model the impact. This technique is mainly applicable when the duration of contact is significantly short. Based on this assumption, the configuration of the system including translational and angular coordinates are considered to remain unchanged during the period of contact. However, the system experiences a discontinuous change at the velocity level. In the piecewise method, the integration of the equations of motion is halted just before the impact occurs. Then impulse–momentum equations are formed. These equations relate the change in both linear and angular momenta of the system to impulsive forces and moments. Since applied loads (forces and moments) are bounded, their impulses during the very short period of contact are ignored in the momentum balance equations. These equations along with the elastic characteristic of the impact, which is reflected in the coefficient of restitution, are then used to compute the jumps in the velocities of the system [22, 23]. These results in addition to the velocities just before the impact can now be used to find the velocities immediately after the impact. The numerical integrator uses the resulting velocities and the coordinates of the system just before the impact as a set of initial conditions to integrate the equations of motion of the system.

Another approach treats an impact as a continuous phenomenon. Allowing penetration between contacting bodies during the period of contact, this model results in a continuous change in the positions and velocities. Additionally, without interrupting the integration of equations of motion, contact forces are activated at the contact points and included in the dynamic equations of motion as long as the bodies remain in contact. In the Kelvin–Voigt viscoelastic model, the contact force is generated by a logical point-to-point linear spring–damper element [8]. However, this linear model is incapable of capturing the nonlinear nature of the impact. Furthermore, it generates a nonphysical tensile contact force if zero penetration is considered as the separation condition. To remove this shortcoming, it is assumed in [2] that the bodies separate at the moment when the contact force becomes zero, while allowing the deformation to continue after the separation of the bodies until the end of the complete restitution. This model has been further extended by using a fractional order damping element [3].

The Hertz model [10] can better capture nonlinear characteristics of the impact. In this continuous model, the force element consists of a spring with nonlinear force–penetration relationship which is obtained based on the local stress distribution. This method can only be used for impacts with elastic characteristics since it does not consider any energy dissipation. Adding a logical linear damper to the Hertz spring can further capture the energy dissipation during impact. However, the model generates a nonphysical tensile force before the complete restitution is achieved if the separation of the bodies is considered at the instant at which the penetration becomes zero [12]. To overcome this artifact, Hunt and Crossley introduced a hysteresis damping factor to modify the damping force [12]. In fact, the modification of the damping force in this model results in zero contact force and penetration at the beginning and the end of the period of contact. Although a multibody system experiences an impulsive behavior, because of the extremely short contact period, the dissipation of damping forces in the system except for the one related to the local deformation are mainly neglected. Therefore, due to the importance of local deformations at the contact point, different methods have been used to characterize the hysteresis damping factor based on the properties of the direct central impact of two spherical objects [6, 11, 15, 17, 27, 29]. Similar estimation has been presented in [16, 29] when permanent indentation after the separation is included in the model. Other estimations for the hysteresis damping factor have been developed when the force model changes during compression and restitution phases of contact [13, 20]. These estimations have been expressed in terms of the coefficient of restitution and of the geometrical and mechanical properties of the contacting bodies, which are reflected in the parameters of the Hertz contact model. Since all of these methods use approximations, in some situations the continuous model with the estimated damping factor may not necessarily recover the desired restitution based on which the estimation has been generated.

The damping coefficient has been characterized as a function of the coefficient of restitution with a model containing a linear damper connected in parallel to a spring with Hertz force-deformation property of two interacting spheres [25], where the exponent of deformation is known to be \(n = 3/2\). In this paper, we extend the characterization of the damping coefficient for a general class of Hertz spring models in which the exponent of deformation in the force–penetration relation can vary between one and two. Furthermore, it is assumed that the separation occurs when the contact force becomes zero, while either the complete restitution may have not yet been achieved or the permanent penetration may have been reached. To determine the damping coefficient, we apply an optimization process to ensure that the desired restitution is reproduced at the time of separation. In fact, this optimization is conducted on the solution of the equations governing the dynamics of the direct central impact. We further conduct a series of analytical studies and numerical experiments on the characteristics of the resulting optimal damping coefficients. It is shown that the optimal damping coefficient can analytically be expressed in terms of system properties at the time of impact such as the effective mass, penetration velocity just before the impact, coefficient of restitution, and the geometrical and mechanical properties of the contacting bodies which are reflected in the parameters of the Hertz contact model. Simulation results show that the contact force model with the proposed analytical approximation of the damping coefficient performs perfectly in recovering the desired restitution, while guarantying non-zero contact force at the time of separation.

In this paper, we first provide an overview of the continuous analysis of frictionless direct central impact in Sect. 2. This is followed by implementing the optimization-based approach to compute the damping coefficient for the zero contact force separation condition in Sect. 3. Characterization of the optimal damping coefficient through analytical investigations and numerical experiments are then conducted in Sect. 4. This is followed by numerical verification and simulation in Sects. 5 and 6, respectively. Finally, conclusions are drawn in Sect. 7.

2 Analysis of direct central impacts through continuous force models

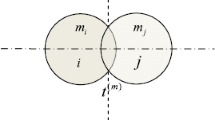
In many applications of multibody dynamics, the impact is assumed to generate a local deformation. Therefore, the most common continuous contact models are constructed based on the characteristics of the direct central impact between two objects, mainly in spherical shapes [1, 6, 11, 12, 14, 16]. Figure 1 shows the schematic of two colliding spheres of masses \(m_{i}\) and \(m_{j}\). The unit vector \(\mathbf{n}\) is the direction normal to the surface of contact. In the direct central impact it is assumed that the velocities of the colliding bodies just before the impact at \(^{-}t\), i.e. \(^{-}V_{i}\) and \(^{-}V_{j}\), lie on the axis of vector \(\mathbf{n}\). Additionally, similar to the piecewise modeling of the direct central impact, in the continuous contact model, the effect of the applied loads is considered insignificant compared to the contact force due to the very short contact duration. Therefore, as shown in Fig. 1, during the contact period only contact force \(f_{c}\) is continuously being applied to the spheres along the \(\mathbf{n}\) axis. In this scheme, the contact cycle is divided into two phases: compression and restitution. The compression phase starts at \(^{-}t\) when contact between the bodies occurs. The indentation (penetration) then increases until it reaches its maximum value, at which both bodies find the same velocity. At this moment, the restitution phase starts which is followed by a continuous decrease in the penetration until both bodies separate at \(^{+}t\) with velocities \(^{+}V_{i}\) and \(^{+}V_{j}\), respectively.

Fig. 1
figure 1

Direct central impact of two spheres

Full size image

Following the free-body diagrams of Fig. 1, we can construct the equations of motion of each body during the period of contact along the \(\mathbf{n}\) axis as

$$\begin{aligned} m_{i} \ddot{\delta }_{i} = -f_{c},\qquad m_{j} \ddot{\delta }_{j} = f_{c}, \end{aligned}$$
(1)

where \(\delta _{i}\) and \(\delta _{j}\) denote the coordinates of the mass centers of spheres \(i\) and \(j\) along the \(\mathbf{n}\) axis, respectively. Defining the penetration \(\delta \) and effective mass \(m\) as

$$\begin{aligned} \delta \triangleq & \delta _{i}-\delta _{j}, \end{aligned}$$
(2)
$$\begin{aligned} m \triangleq & \frac{m_{i}m_{j}}{m_{i}+m_{j}}, \end{aligned}$$
(3)

we develop the following Ordinary Differential Equation (ODE) governing the dynamics of the penetration:

$$\begin{aligned} m \ddot{\delta } =& - f_{c}, \\ \delta (0) =& ^{-}\delta = 0, \\ \dot{\delta }(0) =& {^{-}}{\dot{\delta }}. \end{aligned}$$
(4)

where

$$\begin{aligned} {{^{-}}{\dot{\delta }}} = {{^{-}V_{i}} - {^{-}V_{j}}}. \end{aligned}$$
(5)

The main challenge in the continuous contact model is to determine a mathematical expression for \(f_{c}\) and tune its parameters based on known information about the system during the impact in order to better capture the physics of this phenomenon. Hertz model uses stress distribution and presents the contact force as the following nonlinear spring [10]:

$$ f_{c} = k\delta ^{n}. $$
(6)

In this model, both \(k\) and \(n\) depend on the geometry and/or the material properties of the contacting bodies. For instance, for two spheres in contact or for a locally spherical surface and a plane \(n\) becomes \(3/2\), while in the contact between two locally plane surfaces \(n\) is established as one [15].

Since the Hertz model does not introduce any energy dissipation, it may not accurately present non-elastic impacts. To consider the energy dissipation during an impact, a linear damping force \(c \dot{\delta }\) is included, resulting in

$$ f_{c} = c \dot{\delta }+ k\delta ^{n}. $$
(7)

This yields the following ODE governing the dynamics of the penetration with the same initial conditions of Eq. (4):

$$\begin{aligned} m \ddot{\delta } +c \dot{\delta }+ k \delta ^{n}=0. \end{aligned}$$
(8)

The solid curve in Fig. 2 shows the behavior of this contact force versus penetration. This figure shows a non-zero compressive contact force at point \(A\) which corresponds to \(^{-}t\), the start of the compression phase. The compression continues to point \(B\) where the maximum deformation \(\delta _{m}\) is reached. The restitution phase then starts at \(B\) and continues to point \(C\) where the spheres separate. The dotted curve in this figure indicates that using this model beyond point \(C\) generates a nonphysical tensile force. Therefore, in order to avoid any contact force at the time of separation, the bodies need to be released at point \(C\) which corresponds to \(^{+}t\).

Fig. 2
figure 2

Behavior of the contact force versus penetration for different force models

Full size image

Due to computational limitations, as of several decades ago, it was not possible to predict the exact time of separation of the two bodies in forward dynamic integration of the equations of motion. Therefore, in order to overcome the artifact of tensile force of Eq. (8), Hunt and Crossley [12] proposed the damping force to be presented as \(\mu \dot{\delta }\delta ^{n}\), where \(\mu \) is called the “hysteresis damping factor”. This description for damping transforms the continuous contact force to

$$\begin{aligned} f_{c} = (\mu \dot{\delta }+ k) \delta ^{n}. \end{aligned}$$
(9)

This results in the following ODE:

$$\begin{aligned} & m \ddot{\delta } + (\mu \dot{\delta }+ k) \delta ^{n}=0, \end{aligned}$$
(10)

with the same initial conditions of Eq. (4). The dashed curve in Fig. 2 shows the behavior of this contact force versus penetration. As it is observed, colliding bodies experience zero contact force and penetration at the beginning and at the end of contact. As a result, the model does not produce a tensile force.

The hysteresis damping factor \(\mu \) in Eq. (10) is a parameter representing the dissipation of energy in an impact. Therefore, researchers have attempted to find a relationship between \(\mu \) and the corresponding coefficient of restitution since the introduction of this contact force model. The coefficient of restitution between the two colliding spheres of Fig. 1 is defined as

$$\begin{aligned} e = - \frac{{^{+}V_{i}} - {^{+}V_{j}}}{{^{-}V_{i}} - {^{-}V_{j}}} = - \frac{^{+}\dot{\delta }}{{^{-}}{\dot{\delta }}}. \end{aligned}$$
(11)

The proposed relationships between \(\mu \) and \(e\) have been derived using the following energy balance during the entire period of the direct central impact:

$$\begin{aligned} &\frac{1}{2} ~ m ({^{-}}{\dot{\delta }})^{2}(1-e^{2}) = \oint f_{c} d \delta . \end{aligned}$$
(12)

The left hand side of this equation represents the drop in the kinetic energy of the system during the impact, and the integral on the right side is the work done by the contact force during the entire cycle of impact.

Hunt and Crossley suggested the following expression approximating \(\mu \) as a function of \(e\) [12]:

$$\begin{aligned} \mu = \frac{3k(1-e)}{2({^{-}}{\dot{\delta }})}. \end{aligned}$$
(13)

Lankarani and Nikravesh [15, 17] used the general trend of Hertz contact model and expressed an estimation of the damping factor as

$$\begin{aligned} \mu = \frac{3k(1-e^{2})}{4({^{-}}{\dot{\delta }})}. \end{aligned}$$
(14)

The estimations presented in Eqs. (13) and (14) can be used if the coefficient of restitution is close to unity [6, 15, 17]. This drawback was removed with the following estimation:

$$\begin{aligned} \mu = \frac{3k(1-e)}{2 e ({^{-}}{\dot{\delta }})}, \end{aligned}$$
(15)

proposed by Hu and Gua [11]. In another attempt, using fundamental characteristics of the Kelvin–Voigt model, Ye et al. [29] and Flores et al. [6] overcame the shortcoming of Eq. (14) by estimating the damping factor as

$$\begin{aligned} \mu = \frac{8k(1-e)}{5e({^{-}}{\dot{\delta }})}. \end{aligned}$$
(16)

The estimations presented in Eqs. (15) and (16) are applicable to a wider range of coefficients of restitution [6, 11, 29]. It should be noted that these expressions have been proposed based on different approximations of the solution of Eq. (10). As such, using the estimated \(\mu \) of Eqs. (13)–(16) and solving Eq. (10) for the entire period of contact, the output coefficient of restitution

$$\begin{aligned} e_{\mathit{out}} = - \frac{{^{+}}{\dot{\delta }}}{{^{-}}{\dot{\delta }}} \end{aligned}$$
(17)

may not necessarily be the same as the desired \(e\) based on which \(\mu \) has been estimated. In other words, the estimated \(\mu \) may not accurately reproduce the desired restitution.

As reported in [9], the exact analytical solution of ODE of Eq. (10) has been presented in [21, 28]. Therefore, without any approximation, the damping factor based on which the desired restitution can be recovered is computed using the following expression [9]:

$$\begin{aligned} \mu = \frac{d ~ k}{e~({^{-}}{\dot{\delta }})}, \end{aligned}$$
(18)

where \(d\in [0,1]\) is the solution of the following equation:

$$\begin{aligned} \frac{1+\frac{d}{{e}}}{1-d} = \exp \biggl\{ d\biggl(1+\frac{1}{e}\biggr)\biggr\} . \end{aligned}$$
(19)

3 Hertz contact model with linear damping

The solid curve in Fig. 2 shows typical behavior of the Hertz contact model with linear damping, as expressed by Eq. (8). This curve clearly shows that, if the contact force is not removed from the model at point \(C\) when the two bodies separate, an undesirable tensile force will continue to be present in the equations of motion. Due to the computational deficiencies that existed several decades ago, the exact times of contact and separation such as points \(A\) and \(C\) in Fig. 2, respectively, could not be accurately detected during the integration of the equations of motion. In order to avoid such computational shortcomings, researchers adopted the contact model of Hunt and Crossley. However, as the dashed curve in Fig. 2 shows, this model artificially changes the characteristics of the original Hertz contact model with linear damping.

With advances in numerical methods and computational capabilities, most well developed numerical integrators are now capable of detecting the occurrence of an event, such as the start or the end of a contact. In order to take advantage of the existing numerical capabilities, in the study that is presented in this paper, we return to the Hertz contact model with linear damping, as expressed by Eq. (8). Then we attempt to develop an analytical formula approximating the damping coefficient \(c\) as a function of a desired value for the coefficient of restitution.

In this model, to avoid any tensile contact force during the period of impact, we assume that in the restitution phase the bodies start to separate at \(t = {}^{s}t\) provided that the contact force is zero, i.e.

$$\begin{aligned} c~{}^{s}\dot{\delta }+ k~ ({}^{s}\delta )^{n} =0, \end{aligned}$$
(20)

where

$$\begin{aligned} {}^{s}\delta = {^{+}}{{\delta }}= \delta ({}^{s}t), \qquad {}^{s}\dot{\delta }= {^{+}}{\dot{\delta }}= \dot{\delta }({}^{s}t). \end{aligned}$$
(21)

As shown in Fig. 2, in this model point \(C\) corresponds to \(t ={}^{+}t = {}^{s}t \) at which the separation occurs. In this study, \({}^{s}\delta \) could represent either a permanent penetration with no restitution after the separation or a temporary indentation which allows the continuation of the restitution after the bodies separate.

In order to find the damping coefficient \(c\) with the main objective of recovering the desired restitution \(e\), the solution of the ODE presented in Eq. (8) should yield a penetration velocity at the time of separation that satisfies the condition \(e_{\mathit{out}} = e\), where

$$\begin{aligned} e_{\mathit{out}} = - \frac{{^{+}}{\dot{\delta }}}{{^{-}}{\dot{\delta }}} = - \frac{{}^{s}\dot{\delta }}{{^{-}}{\dot{\delta }}}. \end{aligned}$$
(22)

Without using any approximation for the penetration velocity profile, in this work, we apply the following optimization process to obtain the value of \(c\):

$$ \begin{aligned} & \underset{c}{\text{minimize}} & & | e_{\mathit{out}} - e | \\ & \text{subject to} & & m\ddot{\delta } + c \dot{\delta }+ k \delta ^{n} = 0 \\ &&&\delta (0) = 0, \quad \dot{\delta }(0) = {^{-}}{\dot{\delta }} \\ &&& c~ {}^{s}\dot{\delta }+ k \,({}^{s}\delta )^{n} =0\quad (\text{at}~t={}^{s}t) \end{aligned} $$
(23)

This optimization in fact ensures that the computed damping coefficient can accurately recover the desired restitution. We note that, for given \(e\), \(m\), \({^{-}}{\dot{\delta }}\), \(k\), and \(n\), the values of \({}^{s}\delta \) and \({}^{s}\dot{\delta }\) at the time of separation \({}^{+}t = {}^{s}t\) are dependent on \(c\), which is unknown in advance.

To numerically solve the proposed optimization problem and compute the damping coefficient, any optimization technique could potentially be used. For instance, this problem has been addressed in [25] by using the method of bisection. Since most optimization methods use an iterative procedure, the optimal damping coefficient \(c_{\mathit{opt}}\) is obtained when the following condition is satisfied:

$$\begin{aligned} \frac{| e_{\mathit{out}} -e |}{e} \leq \epsilon , \end{aligned}$$
(24)

where \(\epsilon \) is a small number and \(e_{\mathit{out}}\) is defined in Eq. (22). Furthermore, in order to halt the integration process of the equations of motion at each iteration, we can use MATLAB built-in function “event” to detect the instant at which the separation condition of Eq. (20) is met. It should be noted that the result of the optimization problem automatically satisfies the energy balance of Eq. (12) since we have not used any approximation.

4 Analytical expression for optimal damping coefficient

We now conduct an analytical and a numerical investigation to characterize \(c_{\mathit{opt}}\) as a function of system parameters \(m\), \({^{-}}{\dot{\delta }}\), \(k\), \(n\), and the desired \(e\).

4.1 Analytical investigation to characterize \(c_{\mathit{opt}}\)

In this section, we analytically study some characteristics of \(c_{\mathit{opt}}\). We start with the model of Eq. (8) in the absence of damping force which reduces to the original Hertz model

$$\begin{aligned} m \ddot{\delta } = - k \delta ^{n}, \end{aligned}$$
(25)

with the following analytical solution:

$$\begin{aligned} &{\dot{\delta }^{2}} = ({^{-}}{\dot{\delta }})^{2} - \frac{2k~ \delta ^{n+1}}{m(n+1)}. \end{aligned}$$
(26)

Setting \(\dot{\delta }= 0\) yields the maximum penetration of the Hertz model as

$$\begin{aligned} \delta _{m} = \Big[\frac{(n+1)~m}{2k}{({^{-}}{\dot{\delta }})^{2}} \Big]^{\frac{1}{n+1}}. \end{aligned}$$
(27)

We note that the model of Eq. (8) contains a damping force. The dissipation due to the damping force does not allow the penetration at the separation instant to exceed the maximum indentation obtained in Eq. (27). This can mathematically be expressed as

$$\begin{aligned} {}^{s}\delta \le \delta _{m}. \end{aligned}$$
(28)

On the other hand, the damping coefficient can be obtained using the condition of Eq. (20):

$$\begin{aligned} c = -\frac{k ~ ({}^{s}\delta )^{n}}{{}^{s}\dot{\delta }}. \end{aligned}$$
(29)

Comparing Eqs. (28) and (29) yields

$$\begin{aligned} c \leq -\frac{k ~(\delta _{m})^{n}}{{}^{s}\dot{\delta }}. \end{aligned}$$
(30)

Imposing the desired restitution condition \({}^{s}\dot{\delta }= -e~({^{-}}{\dot{\delta }})\) on this inequality, we are allowed to replace \(c\) with \(c_{\mathit{opt}}\), resulting in

$$\begin{aligned} c_{\mathit{opt}} \leq \frac{k ~(\delta _{m})^{n}}{e~ ({^{-}}{\dot{\delta }})}. \end{aligned}$$
(31)

Using the maximum penetration of Eq. (27) in the absence of damping, we can express Eq. (31) as

$$\begin{aligned} c_{\mathit{opt}} \leq \frac{k}{e~({^{-}}{\dot{\delta }})} \biggl[ \frac{m(n+1)({^{-}}{\dot{\delta }})^{2}}{2k} \biggr]^{\frac{n}{n+1}}. \end{aligned}$$
(32)

This inequality can be further simplified as

$$\begin{aligned} c_{\mathit{opt}} \leq \frac{1}{e} \biggl[\biggl(\frac{n+1}{2}\biggr)^{{n}}~ k ~ ({^{-}}{ \dot{\delta }})^{{n-1}}~ m^{{n}} \biggr]^{\frac{1}{n+1}}. \end{aligned}$$
(33)

Introducing a slack variable \(\lambda \in [0,1]\), this inequality can be transformed to the following equality:

$$\begin{aligned} c_{\mathit{opt}} = \frac{\lambda }{e} \biggl[\biggl(\frac{n+1}{2}\biggr)^{{n}}~ k ~ ({^{-}}{ \dot{\delta }})^{{n-1}}~ m^{{n}} \biggr]^{\frac{1}{n+1}}. \end{aligned}$$
(34)

The natural logarithm of this equation can be expressed as

$$\begin{aligned} \mathrm{ln}\, c_{\mathit{opt}} =& \mathrm{ln}\, \lambda - \mathrm{ln}\, e + \frac{n}{n+1} \mathrm{ln}\, \frac{n+1}{2} \\ &{}+ \frac{1}{n+1} \mathrm{ln}\, k + \frac{n-1}{n+1} \mathrm{ln}\,({^{-}}{ \dot{\delta }}) +\frac{n}{n+1} \mathrm{ln}\, m. \end{aligned}$$
(35)

The inequality of Eq. (32) can alternatively be developed by rescaling penetration and time by \(\bar{\delta } = \frac{\delta }{\delta _{m}}\) and \(\bar{t} = \frac{t}{\delta _{m}/{^{-}}{\dot{\delta }}}\), respectively, and using them in the separation condition of Eq. (20) and enforcing \({}^{s}\dot{\delta } = -e \, ({^{-}}{\dot{\delta }})\) and \(\bar{\delta } \le 1\).

4.2 Computational experiments to characterize \(c_{\mathit{opt}}\)

Based on the analytical study of \(c_{\mathit{opt}}\) in the previous section, we realize that the optimal damping can be expressed using Eq. (34) or (35). The term \(\lambda \) in these equations is not just a parameter; i.e., it could potentially be a function of system properties. In the following sections, we perform four simulation experiments to investigate the dependency of \(\lambda \) on \(m\), \({^{-}}{\dot{\delta }}\), \(k\), \(n\), and the desired \(e\).

We should note that, for each of the following investigations, the value of \(\epsilon \) in Eq. (24) is selected as \(10^{-8}\). Furthermore, the curve fittings in these studies are performed using MATLAB curve-fitting toolbox.

4.2.1 Dependency of \(\lambda \) on \(m\)

In the first investigation, we numerically study the dependency of \(\lambda \) on \(m\). In order to do so, we assume that \({^{-}}{\dot{\delta }}= 1~m/s\), \(k = 1~N/m^{n}\), \(e= 0.7\). Then we sweep the effective mass and \(n\) by choosing, respectively, 200 and 50 values for these quantities linearly separated in the following ranges:

$$\begin{aligned} & 10^{-5}\leq m \leq 50~~\text{kg}, \\ & ~~~~~~1 \leq n \leq 2. \end{aligned}$$

For each resulting system, we solve the optimization problem of Eq. (23) for \(c_{\mathit{opt}}\).

Based on the optimization results, we can show the behavior of \(\ln {c_{\mathit{opt}}}\) versus \(\ln {m}\) in Fig. 3(a) for the representative values of \(n\). It is observed that this relationship can be expressed by the following linear function:

$$\begin{aligned} \ln {c_{\mathit{opt}}} = \ln {\alpha _{1}} + \beta _{1} \ln {m}, \end{aligned}$$
(36)

where \(\alpha _{1}\) and \(\beta _{1}\) are auxiliary variables. The points shown by markers • in Fig. 3(b) indicate the behavior of the slope \(\beta _{1}\) as a function of \(n\) as we solve the optimization problem. It is observed that the curve in the form of \(\frac{n}{n+1}\) can be fitted to \(\beta _{1}\) (solid line in Fig. 3(b)), resulting in

$$\begin{aligned} \ln {c_{\mathit{opt}}} = \ln {\alpha _{1}} + \frac{n}{n+1} \ln {m}, \end{aligned}$$
(37)

or equivalently,

$$\begin{aligned} c_{\mathit{opt}} = \alpha _{1}~m^{\frac{n}{n+1}}. \end{aligned}$$
(38)

We note that \(\frac{n}{n+1}\), the slope of \(\ln {m}\) which has been found through curve fitting on the solution of the optimization problem, is the same as the corresponding term in Eq. (35). Therefore, the linear relationship between \(\ln {c_{\mathit{opt}}} \) and \(\ln {m}\) in the form shown in Eq. (37) for given \({^{-}}{\dot{\delta }}\), \(k\), and \(e\) indicates that \(\lambda \) in Eq. (35) is independent of the effective mass. Furthermore, the dependency of \(c_{\mathit{opt}}\) on \(n\) confirms that \(\lambda \) should be a function of this parameter.

Fig. 3
figure 3

Characterizing effect of \(m\) on \(c_{\mathit{opt}}\)

Full size image

4.2.2 Dependency of \(\lambda \) on \({^{-}}{\dot{\delta }}\)

In this investigation, we study the dependency of \(\lambda \) on \({^{-}}{\dot{\delta }}\). We first assume that \(m = 1~\text{kg}\), \(k = 1~N/m^{n}\), \(e = 0.7\). We then sweep \({^{-}}{\dot{\delta }}\) and \(n\) by selecting, respectively, 200 and 50 values for these quantities linearly separated in the following ranges:

$$\begin{aligned} & 0.01 \leq {^{-}}{\dot{\delta }}\leq 50~\mbox{m/s}, \\ & \quad 1 \leq n \leq 2. \end{aligned}$$

For each resulting system, we solve the optimization problem of Eq. (23) for \(c_{\mathit{opt}}\). Figure 4(a) shows the behavior of \(\ln {c_{\mathit{opt}}}\) as a function of \(\ln {({^{-}}{\dot{\delta }})}\) for the selected values of \(n\). It is observed that the following linear function can describe the relationship between \(\ln {c_{\mathit{opt}}}\) and \(\ln {({^{-}}{\dot{\delta }}})\):

$$\begin{aligned} \ln {c_{\mathit{opt}}} = \ln {\alpha _{2}} + \beta _{2} \ln {({^{-}}{ \dot{\delta }})}, \end{aligned}$$
(39)

In this expression \(\alpha _{2}\) and \(\beta _{2}\) are auxiliary variables. The slope \(\beta _{2}\) is shown in Fig. 4(b) for each system with a specified \(n\) using • markers. As is shown in this figure, \(\frac{n-1}{n+1}\) is the best fit to these points, yielding

$$\begin{aligned} \ln {c_{\mathit{opt}}} = \ln {\alpha _{2}} + \frac{n-1}{n+1} \ln {({^{-}}{ \dot{\delta }})}, \end{aligned}$$
(40)

or, equivalently,

$$\begin{aligned} c_{\mathit{opt}} = \alpha _{2}~({^{-}}{\dot{\delta }})^{\frac{n-1}{n+1}}. \end{aligned}$$
(41)

It is observed that the slope of \(\ln {({^{-}}{\dot{\delta }})}\) is the same as the corresponding term in Eq. (35). As such, based on the linear relationship between \(\ln {c_{\mathit{opt}}} \) and \(\ln {({^{-}}{\dot{\delta }})}\) in the form presented in Eq. (40) for given \(m\), \(k\), and \(e\), we conclude that \(\lambda \) in Eq. (35) is independent of \({^{-}}{\dot{\delta }}\).

Fig. 4
figure 4

Characterizing effect of \({^{-}}{\dot{\delta }}\) on \(c_{\mathit{opt}}\)

Full size image

4.2.3 Dependency of \(\lambda \) on \(k\)

In previous investigations, we showed that \(\lambda \) is independent of \({^{-}}{\dot{\delta }}\) and \(m\). Therefore, in order to study the dependency of \(\lambda \) on \(k\), we assume that \(m = 1~\text{kg}\), \({^{-}}{\dot{\delta }}= 1~m/s\), and \(e = 0.7\) in Eq. (35). Then we sweep \(k\) and \(n\) by, respectively, choosing 200 and 50 values, selected in the following ranges:

$$\begin{aligned} &10^{5} \leq k \leq 10^{10}~\mbox{N}/\mbox{m}^{n}, \\ &\quad 1 \leq n \leq 2. \end{aligned}$$

For each resulting system, we solve the optimization problem in Eq. (23) for \(c_{\mathit{opt}}\). The representative results in Fig. 5(a) shows that \(\ln {c_{\mathit{opt}}}\) varies linearly as a function of \(\ln {k}\) as

$$\begin{aligned} \ln {c_{\mathit{opt}}} = \ln {\alpha _{3}} + \beta _{3} \ln {k}, \end{aligned}$$
(42)

where \(\alpha _{3}\) and \(\beta _{3}\) are auxiliary variables. The value of the slope \(\beta _{3}\) for each system with a specified \(n\) is shown in Fig. 5(b) with • markers. The best fit of \(\frac{1}{n+1}\) for \(\beta _{3}\) results in

$$\begin{aligned} \ln {c_{\mathit{opt}}} = \ln {\alpha _{3}} + \frac{1}{n+1} \ln {k}, \end{aligned}$$
(43)

or, equivalently,

$$\begin{aligned} c_{\mathit{opt}} = \alpha _{3}~k^{\frac{1}{n+1}}. \end{aligned}$$
(44)

As it is observed, the slope of \(\ln {k}\) is the same as the one in Eq. (35). Therefore, the linear relationship between \(\ln {c_{\mathit{opt}}} \) and \(\ln {k}\) in the form presented in Eq. (43) for given \(m\), \({^{-}}{\dot{\delta }}\), and \(e\) indicates that \(\lambda \) in Eq. (35) is independent of \(k\).

Fig. 5
figure 5

Characterizing effect of \(k\) on \(c_{\mathit{opt}}\)

Full size image

4.2.4 Dependency of \(\lambda \) on \(e\) and \(n\)

So far our investigations have shown that \(\lambda \) is independent of \({^{-}}{\dot{\delta }}\), \(m\), and \(k\). In order to investigate the dependency of \(\lambda \) on \(e\) and \(n\), we assume that \(m = 1~\text{kg}\), \({^{-}}{\dot{\delta }}= 1~m/s\), and \(k = 1~N/m^{n}\). We then pick 600 points for \(e\) and 100 points for \(n\) linearly separated in the following ranges:

$$\begin{aligned} 0.45 \leq& e \leq 1, \\ 1 \leq& n \leq 2. \end{aligned}$$

For each system, we solve the optimization problem of Eq. (23) for \(c_{\mathit{opt}}\). As shown in Fig. 6 for some representative values of \(n\), the optimization results indicate that the behavior of \(c_{\mathit{opt}}\) versus \(e\) obeys approximately the following pattern:

$$\begin{aligned} c_{\mathit{opt}} = \alpha ~ (e^{\beta }-1), \end{aligned}$$
(45)

where \(\alpha \) and \(\beta \) are only functions of \(n\) and computed using the following procedure. First for each individual value of \(n \in [1, 2]\), we plot \(c_{\mathit{opt}}\) vs. \(e\) (similar to the graph shown in Fig. 6), and compute the corresponding values of \(\alpha \) and \(\beta\). Figure 7 shows the resulting values of \(\alpha \) and \(\beta \) as we sweep \({n}\), which can then be curve fitted using the following expressions:

$$\begin{aligned} &\alpha = 0.3331 ~ n^{4} - 1.48~ n^{3} +3.077 ~n^{2} - 2.306~ n +1.794 , \end{aligned}$$
(46)
$$\begin{aligned} &\beta = 1.285~ n^{(0.2553)} -1.725. \end{aligned}$$
(47)

Substituting Eq. (45) for \(c_{\mathit{opt}}\), which is obtained by fitting a curve to the simulation results, into the analytical formula of Eq. (34), and knowing that \(m = 1~\text{kg}\), \({^{-}}{\dot{\delta }}= 1~m/s\), and \(k = 1~N/m^{n}\), we can express \(\lambda \) as

$$\begin{aligned} \lambda = \frac{\alpha ~(e^{\beta }-1)~e}{ (\frac{n+1}{2})^{{\frac{n}{n+1}}}}. \end{aligned}$$
(48)
Fig. 6
figure 6

Behavior of \(c_{\mathit{opt}}\) vs. \(e\); the solid curve \(c_{\mathit{opt}} = 1.59~({e}^{-0.3794}-1)\) is fitted to the optimization results for \(n = 1.2\), The dashed curve \(c_{\mathit{opt}} = 2.47~({e}^{-0.2323}-1)\) is fitted to the optimization results for \(n = 1.8\)

Full size image
Fig. 7
figure 7

Characterizing \(\alpha \) and \(\beta \) as functions of \(n\)

Full size image

4.3 Closed-form formula for \(c_{\mathit{opt}}\)

In previous sections, we concluded that \(\lambda \) is independent of \(m\), \({^{-}}{\dot{\delta }}\), and \(k\). Furthermore, we found that \(\lambda \) can be expressed in the form shown in Eq. (48). In order to present an expression for \(c_{\mathit{opt}}\) as a function of system parameters, we replace the function obtained for \(\lambda \) from Eq. (48) into Eq. (34), resulting in the following closed-form solution:

$$\begin{aligned} c_{\mathit{opt}} = \alpha ~(e^{\beta }-1)~\Big[ k ~ ({^{-}}{\dot{\delta }})^{{n-1}}~ m^{{n}}\Big]^{\frac{1}{n+1}}, \end{aligned}$$
(49)

where \(\alpha \) and \(\beta \) are computed using Eqs. (46) and (47), respectively. This expression shows that \(c_{\mathit{opt}}\) approaches 0 as \(e\) approaches 1, while the damping coefficient approaches infinity as \(e\) approaches 0. Furthermore, the exponents of \({^{-}}{\dot{\delta }}\), \(m\), and \(k\) in Eq. (49) are exact values which are in agreement with the corresponding expressions in Eq. (34), while the accuracy of the expressions for \(\alpha\) and \(\beta\) depends of the number of data points as well as the accuracy chosen to solve the optimization problem. As such, we can directly solve the optimization problem of Eq. (23) or use the expression of Eq. (49) to obtain the value of \(c_{\mathit{opt}}\).

Substituting the closed-form formula for the damping coefficient of Eq. (49) in Eq. (7), the contact force in the continuous model is expressed as

$$ f_{c} =\alpha ~(e^{\beta }-1)~\Big[ k ~ ({^{-}}{\dot{\delta }})^{{n-1}}~ m^{{n}}\Big]^{\frac{1}{n+1}}~ \dot{\delta }+ k~\delta ^{n}. $$
(50)

Finally, we can determine the magnitude of penetration at the time of separation by enforcing \({}^{s}\dot{\delta }= -e\,({^{-}}{\dot{\delta }})\) in Eq. (20) as

$$\begin{aligned} {}^{s}\delta = \biggl( \frac{{^{-}}{\dot{\delta }}~c_{\mathit{opt}} ~e }{k} \biggr)^{\frac{1}{n}}, \end{aligned}$$
(51)

where \(c_{\mathit{opt}}\) is computed using Eq. (49).

The value of \(n\) in the literature is mainly assigned to \(3/2\) which represents the contact between two spheres or a sphere and plane surface. Therefore, we explicitly express the optimal damping of Eq. (49) for \(n=3/2\) as

$$\begin{aligned} c_{\mathit{opt}} = 1.95~ (e^{-0.3}-1)~{k^{0.4}}~({^{-}}{\dot{\delta }})^{0.2}~ m^{0.6}. \end{aligned}$$
(52)

This expression has also been reported in [25].

5 Numerical verification

In this section, we perform several numerical experiments to verify the validity and accuracy of the formula of Eq. (49).

5.1 Randomly selected values for the system parameters

The closed-form formula of Eq. (49) was derived through a series of numerical investigations where arbitrary values for mass, stiffness, and initial penetration velocity were assigned to the system parameters. In order to verify that the accuracy of this formula does not depend on the assigned values, we perform the following numerical investigation.

We randomly assign values to each of the system parameters in the following ranges:

$$\begin{aligned} 10^{-5} \leq& m \leq 10^{2}~\text{kg}, \\ 10^{5} \leq& k \leq 10^{10}~~N/m^{n}, \\ 10^{-3} \leq& {^{-}}{\dot{\delta }}\leq 10^{2}~~m/s, \\ 1 \leq& n \leq 2. \end{aligned}$$

We also assign a value to the desired coefficient of restitution in the range \(10^{-4} \leq e \leq 1\). Then we determine the optimal value for \(c_{\mathit{opt}}\) using Eq. (49). We solve the following equations governing the dynamics of the continuous contact model:

$$\begin{aligned} & m~\ddot{\delta } + c_{\mathit{opt}}~ \dot{\delta }+ k~\delta ^{n} = 0, \\ &\delta (0) = {^{-}}{{\delta }}= 0, \\ &\dot{\delta }(0) = {^{-}}{\dot{\delta }}, \end{aligned}$$
(53)

and stop the simulation at \({}^{s}t\) when the separation condition of \(c_{\mathit{opt}}\,{}^{s}\dot{\delta }+ k\,({}^{s}\delta )^{n} =0\) is met. Based on the simulated value of the separation velocity, we determine \(e_{\mathit{out}}\) using Eq. (22), then the absolute error of the simulation is computed as \({|e_{\mathit{out}}-e|}\).

We repeat the above simulation 300 times for different sets of randomly selected values of system parameters \(m\), \(k\), \({^{-}}{\dot{\delta }}\), and \(n\). For each given value of \(e\), we determine the maximum absolute error. Figure 8 shows this upper bound of the absolute error versus \(e\). It is observed that the application of the formula of Eq. (49) can accurately reproduce the desired restitution.

Fig. 8
figure 8

Studying the accuracy of Eq. (49) by showing the upper bound of the absolute error vs. \(e\)

Full size image

5.2 Optimal damping for \(n = 1\)

For \(n = 1\), the system is reduced to the linear model of Kelvin–Voigt [8] presented by the following ODE:

$$\begin{aligned} &m \ddot{\delta } + c \dot{\delta }+ k \delta = 0, \\ &\delta (0) ={}^{-}\delta = 0, \\ &\dot{\delta }(0) = {^{-}}{\dot{\delta }}. \end{aligned}$$
(54)

By applying the separation condition of Eq. (20) to the exact analytical solution of this model, Butcher and Segalman [2] have proven that the exact value of the coefficient of restitution can be related to the damping ratio \(\xi \) as

$$ e_{\mathit{exact}}= \textstyle\begin{cases} \exp {\big(-\frac{\xi }{\sqrt{1-\xi ^{2}}} \tan ^{-1} ( \frac{2\xi \sqrt{1-\xi ^{2}}}{2\xi ^{2}-1})\big)} & \quad \xi < 1, \\ \big(\frac{\xi -\sqrt{\xi ^{2}-1}}{\xi +\sqrt{\xi ^{2}-1}}\big)^{( \frac{2\xi \sqrt{\xi ^{2}-1}}{2\xi ^{2}-1})} & \quad \xi >1, \end{cases} $$
(55)

where

$$\begin{aligned} \xi = \frac{c}{2 \sqrt{\mathrm{km}}}. \end{aligned}$$
(56)

It should be noted that special consideration should be made for the correct determination of the quadrant of the argument of \(\tan ^{-1}\) when \(\xi < {\sqrt{2}}/{2}\).

Using \(n =1\), we can express the damping coefficient of Eq. (49) as

$$\begin{aligned} c_{\mathit{opt}} = 1.4181~ (e^{-0.44}-1)~ \sqrt{\mathrm{km}}. \end{aligned}$$
(57)

In order to study the accuracy of Eq. (57), we assume that \(m = 1~\text{kg}\), \({^{-}}{\dot{\delta }}= 1~\mbox{m}/\mbox{s}\), and \(k = 1~\mbox{N}/\mbox{m}\). We then sweep \(e\) in the range \(10^{-4} \le e \le 1\), and use Eq. (57) to find the corresponding optimal damping coefficient. We further calculate the damping ratio for each resulting \(c_{\mathit{opt}}\) using Eq. (56) and substitute it in Eq. (55) to compute the exact value of the corresponding coefficient of restitution. Figure 9(a) shows the behavior of \(e_{\mathit{exact}}\) versus \(e\). To better compare these values, we plot the absolute error \({|e_{\mathit{exact}}-e|}\) in Fig. 9(b). It is observed that the formula presented in Eq. (57) can accurately capture the damping properties of the system.

Fig. 9
figure 9

Studying the accuracy of the formula of Eq. (57) for \(n=1\)

Full size image

6 Numerical simulation

In this section, we use the presented contact force model for the impact simulation of two pendulums and compare the results with the traditional modeling techniques. As shown in Fig. 10, each pendulum is modeled as a rod with negligible thickness and uniform mass distribution. We assume the following system parameters: \(m_{1} = 1~\text{kg}\), \(m_{2} = 0.2~\text{kg}\), \(L_{1} = 6~\mbox{m}\), \(L_{2} = 4~\mbox{m}\), and \(a = 2~\mbox{m}\). The simulation starts with the configuration shown in Fig. 10 for the rods with solid boundaries, representing the initial condition \({\theta }_{1} = \pi /12~\text{rad}\), \({\theta }_{2} = -\pi /2~\text{rad}\), and \(\dot{\theta }_{1} = \dot{\theta }_{2} = 0~\text{rad}/s\). The impact between the bodies are modeled using different techniques. First, the piecewise method with the application of the impulse–momentum formulation is used to address the dynamics of the system during impact [23]. Then, the continuous contact force model of Eq. (50), developed in this paper, is used to express the dynamics of impact during the period of contact. Finally, the Hunt–Crossley continuous contact model of Eq. (9) with the damping factor of Eq. (16) is used to simulate the dynamics of the system during the period of contact. Figure 11 shows the behavior of \(\dot{\theta }_{1}\) and \(\dot{\theta }_{2}\) for these simulations while \(e = 0.3\), \(n = 3/2\), and \(k = 10^{8}~\mbox{N}/\mbox{m}^{1.5}\) are used for the continuous contact models. It is observed that the system experiences three impacts during an 8-second simulation. The configuration of the system for the first impact is shown by bodies with dotted boundaries in Fig. 10. Furthermore, Fig. 11 shows that the presented method in this paper can capture the dynamics of the system more accurately. Figure 12 also compares the contact force versus penetration of the presented continuous model against that of the Hunt and Crossley force model of Eq. (9) with damping factor of Eq. (16) during the first period of contact.

Fig. 10
figure 10

Schematics of a two-pendulum system: the initial configuration of the system is shown by solid bodies and the configuration of the system at the first impact is shown by dotted bodies

Full size image
Fig. 11
figure 11

Comparison between the results of the simulation of the double pendulum system, solid curve: piecewise method; dashed curve: presented method with the force model of Eq. (50); dotted curve: Hunt and Crossley force model of Eq. (9) with damping factor of Eq. (16)

Full size image
Fig. 12
figure 12

Contact force vs. penetration during the first period of impact, solid curve: presented method with the force model of Eq. (50); dashed curve: Hunt and Crossley force model of Eq. (9) with damping factor of Eq. (16)

Full size image

7 Conclusion

In this paper, we have presented an analytical expression to compute the optimal damping coefficient in a class of nonlinear continuous force models. The contact force model consists of a spring–damper force element in which the spring obeys force–penetration characteristics of the Hertz model. Furthermore, it has been assumed that the exponent of the deformation in the Hertz model can be assigned values between one and two. We have applied an optimization process to compute the damping coefficient of the linear damper in the contact model such that the desired restitution is reproduced at the time of separation. Furthermore, unlike most of other reported models in literature, in which the separation condition is considered at the instant at which both penetration and contact force are zero, in this work we have considered zero contact force as the only condition for separation. After separation, either the restitution continues or permanent indentation may have been reached. As such, the presented model covers a wider range of impact problems. We have verified the validity and accuracy of the proposed formula through conducting several numerical simulations on systems with randomly-assigned parameters. Additionally, in the case of the Kelvin–Voigt model, it has been shown that the proposed formula can successfully recover the exact solution of this model. Finally, we have applied the presented formulation to demonstrate the impact of a two-pendulum system and compared the results against those of the piecewise method and the Hunt–Crossley-based continuous model.