1 Introduction

In recent years, the use of adhesively bonded joints in engineering applications has increased, especially in aerospace industries. Compared with traditional joining methods, adhesively bonded joints lower stress concentrations, reduce weight, and improve resistance to corrosion. Adhesive joining can also complicate disassembly, require careful surface preparation, and exhibit temporal and plastic responses that are not well understood (Ali and Wahab 2015). Understanding the mechanical behavior of the adhesive within a bonded joint is essential to predict joint response and strength. However, constraints from the adherends and the unbonded interfacial region between the adhesive and the adherends limit the ability of adhesives in bulk to describe thin film adhesive response (Hart-Smith 1981; Botha et al. 1983; Afendi et al. 2011).

As most adhesives are polymeric materials, they exhibit time dependence and possibly nonlinearity and plasticity under high stress and high temperature. There have been a variety of models incorporated into the finite element method (FEM) to predict the stress/strain states under monotonic and uniaxial loading. Some have used Schapery’s single integral model to describe the creep behavior and stress distribution within adhesives (Botha et al. 1983; Henriksen 1984; Roy and Reddy 1986). Popelar and Liechti modified the free volume approach of Knauss and Emri Knauss (1981), Knauss et al. (1987) by considering the effects of distortion (Popelar et al. 1997) and hydrostatic pressure (Popelar and Liechti 2003) to predict the nonlinear load-displacement response under monotonic shear tests for adhesives in Arcan specimens. The models and experiments were in good agreement. Others have extended rheological models formed with Maxwell and Kevin–Voight elements to nonlinear viscoelasticity to model the creep of adhesives (Majda and Skrodzewicz 2009; Choi and Reda Taha 2013; Houhou et al. 2014; Badulescu et al. 2015).

The foregoing nonlinear viscoelastic work concerns materials with deformation that is fully recoverable. Some polymers exhibit viscous flow, resulting in permanent deformation, which can also be described using viscoelastic principles (Silva et al. 2017; Acha et al. 2007). For other polymers, the unrecoverable deformation occurs above a yield point (which can be time- or rate-dependent Hu et al. 1996), for which several viscoplastic models have been developed. Perzyna’s viscoplastic model is often used, given its ability to accommodate a variety of yield criteria (Perzyna 1966). Pandey and Narasimhan (2001) developed a three-dimensional elasto-viscoplastic model using Perzyna’s model with a pressure-sensitive modified von Mises yield function for the stress distribution in lap joints. Su and Mackie (1993) studied the influence of creep on the thick adherend shear tests in which a two-dimensional elasto-viscoplastic model consisting of rheological elements was developed and calibrated with creep tests on bulk adhesives. Morin et al. (2015) and G’sell and Jonas (1979) developed an elasto-viscoplastic model based on the G’sell plastic model to simulate the stress response to uniaxial compressive loading with a wide range of strain rates for a structural adhesive. The results agreed with experiments.

Some materials exhibit both viscoelastic and viscoplastic behavior, which has received less attention in the literature than the responses separately. Groth (1990) studied the stress distribution in single lap joints using three different rheological viscoelastic-viscoplastic models. Rocha et al. (2019) proposed a similar rheological viscoelastic–viscoplastic-damage model that accurately described rate-dependent plasticity of an epoxy resin. Dufour et al. (2016) presented a fully coupled viscoelastic–viscoplastic damage model in which the generalized Maxwell viscoelastic model was integrated with a viscoplastic model using Raghava’s yield criterion. The model was validated on a series of tensile monotonic experiments on Arcan joints at different loading angles. Krairi and Doghri (2014) proposed a thermodynamically based viscoelastic–viscoplastic model coupling a linear Boltzmann’s integral, nonlinear hardening, and ductile damage evolution to describe the uniaxial behavior of polymers. Ilioni et al. (2018) proposed a model combining viscoelasticity with viscoplasticity considering a hydrostatic pressure-dependent yield function for the nonlinear behavior of an adhesive in an Arcan joint. The authors found that viscoplasticity had a strong influence on both shear and tensile monotonic behavior. However, there has been less work on combined viscoelastic–viscoplastic behavior involving nonlinear viscoelasticity. Frank and Brockman (2001) used molecular cooperativity with a Schapery model, incorporating the free volume approach, combined with a modified Bodner–Partom viscoplastic model (Bodner and Partom 1975, 1972) to capture the effects of pressure, strain rate and hardening on multiaxial responses for a glassy polymer. The approach found good agreement with experiment.

The foregoing has described the limited nonlinear viscoelastic–viscoplastic models describing adhesive response. This work combines a modified nonlinear viscoelastic Schapery model with Perzyna’s viscoplastic model (using the von Mises yield criterion with nonlinear kinematic hardening). The constitutive model is solved numerically by an iterative algorithm with stress corrections. The model is compared to experimental results of creep tests on scarf joints with adhesives of differing degrees of toughness.

2 Model description for adhesives

Nonlinear viscoelastic and time-dependent plastic strain has been observed during a series of stress-controlled experiments of adhesive bulk tensile coupons (Lemme and Smith 2016, 2018). At low stress levels, these adhesives exhibited only viscoelastic response with full recovery, whereas at high stress levels, both viscoelastic and viscoplastic response was observed. Accordingly, in the following, the total strain of an adhesive was decomposed into fully recoverable viscoelastic and unrecoverable viscoplastic components with the assumption that they are uncoupled:

$$ \varepsilon _{ij}^{tot} = \varepsilon _{ij}^{e} + \varepsilon _{ij}^{p}, $$
(1)

where the superscripts tot, \(e\), and \(p\) denote the total, viscoelastic, and viscoplastic components, respectively.

2.1 Viscoelastic component

Schapery’s single integral model for nonlinear viscoelasticity, which is based on the concepts of irreversible thermodynamics, was employed to describe the recoverable time-dependent responses as (Schapery 1969)

$$ \varepsilon ^{e, t} = g_{0}^{t} D_{0} \sigma ^{t} + g_{1}^{t} \int _{0}^{t} \Delta D^{\psi ^{t} - \psi ^{\tau }} \frac{d \left ( g_{2}^{\tau } \sigma ^{\tau } \right )}{d\tau } d\tau , $$
(2)

where \(\psi ^{t}\) is the effective time given by

$$ \psi ^{t} = \frac{t}{a}, $$
(3)

\(a\), \(g_{0}\), \(g_{1}\), and \(g_{2}\) are nonlinear parameters dependent on the current stress \(\sigma ^{t}\) and temperature (temperature effects were not considered here), and \(D_{0}\) is the instantaneous compliance. The transient compliance \(\Delta D^{\psi t}\) can be expressed in the form of a power-law (Tuttle and Brinson 1986; Shuangyin and Tsai 1994) or Prony series (De Prony 1795) and characterized by creep-recovery experiments (Gamby and Blugeon 1989). In this study, \(\Delta D^{\psi t}\) was expressed as a five-term Prony-series

$$ \Delta D^{\psi ^{t}} = \sum _{n =1}^{5} D_{n} \left ( 1-\exp \left ( - \lambda _{n} \psi ^{t} \right ) \right ). $$
(4)

Lai and Bakker (1996) generalized the uniaxial Schapery’s model to three dimensions for isotropic materials with the assumption that the hydrostatic and deviatoric components were fully uncoupled. The modified formulation is presented as

$$\begin{aligned} \varepsilon _{ij}^{e,t} &= e_{ij}^{e,t} + \frac{1}{3} \varepsilon _{kk}^{e,t} \delta _{ij} \\ &= \frac{1}{2} g_{0}^{t} J_{0} S_{ij}^{t} + \frac{1}{2} g_{1}^{t} \int _{0}^{t} \Delta J^{\psi ^{t} - \psi ^{\tau }} \frac{d \left ( g_{2}^{\tau } S_{ij}^{\tau } \right )}{d\tau } d\tau \\ &\quad {}+ \frac{1}{3} \left ( \frac{1}{3} g_{0}^{t} B_{0} \sigma _{kk}^{t} \delta _{ij} + \frac{1}{3} g_{1}^{t} \int _{0}^{t} \Delta B^{\psi ^{t} - \psi ^{\tau }} \frac{d \left ( g_{2}^{\tau } \sigma _{kk}^{\tau } \right )}{d\tau } d\tau \delta _{ij} \right ), \end{aligned}$$
(5)

where \(\delta _{ij}\) is the Kronecker delta, \(e_{ij}^{e,t}\), \(\varepsilon _{kk}^{e,t}\), and \(S_{ij}^{t}\) are the deviatoric strain, volumetric strain, and deviatoric stress at the current time \(t\), respectively.

The instantaneous shear compliance \(J_{0}\) and bulk compliance \(B_{0}\) are evaluated from

$$\begin{aligned} J_{0} &=2 \left ( 1+ v \right ) D_{0,} \\ B_{0} &=3 \left ( 1-2 v \right ) D_{0}, \end{aligned}$$
(6)

where \(v\) is the Poisson ratio assumed to be constant. Similarly, the transient shear and bulk compliance are determined by

$$ \Delta J^{\psi ^{t}} =2 \left ( 1+ v \right ) \Delta D^{\psi ^{t}}, $$
$$ \Delta B^{\psi ^{t}} =3 \left ( 1-2 v \right ) \Delta D^{\psi ^{t}}. $$
(7)

Substituting Eqs. (6) and (7) into Eq. (5) and employing a hereditary integral proposed by Haj-Ali and Muliana (2004), we obtain the deviatoric strain \(e_{ij}^{e,t}\) and the volumetric strain \(\varepsilon _{kk}^{e,t}\) in the recursive form as

(8)
(9)

where \(q_{ij,n}^{t- \Delta t}\) and \(q_{kk,n}^{t- \Delta t}\) are the shear and volumetric hereditary integrals at the previous time increment (\(t-\Delta t\)) for each term in the Prony series. They are updated and stored at the end of the current time increment as

$$\begin{aligned} q_{ij, n}^{t} &= e^{- \lambda _{n} \Delta \psi ^{t}} q_{ij, n}^{t -\Delta t} + \left ( g_{2}^{t} S_{ij}^{t} - g_{2}^{t -\Delta t} S_{ij}^{t -\Delta t} \right ) \frac{1- e^{- \lambda _{n} \Delta \psi ^{t}}}{\lambda _{n} \Delta \psi ^{t}}, \end{aligned}$$
(10)
$$\begin{aligned} q_{kk, n}^{t} &= e^{- \lambda _{n} \Delta \psi ^{t}} q_{kk, n}^{t -\Delta t} + \left ( g_{2}^{t} \sigma _{kk}^{t} - g_{2}^{t -\Delta t} \sigma _{kk}^{t -\Delta t} \right ) \frac{1- e^{- \lambda _{n} \Delta \psi ^{t}}}{\lambda _{n} \Delta \psi ^{t}}. \end{aligned}$$
(11)

2.2 Viscoplastic component

The evolution of the viscoplastic strain rate was given by Perzyna’s model (Perzyna 1966) with the associated flow rule

$$ \dot{\varepsilon }_{ij}^{p, t} = \dot{\lambda } m_{ij} = \eta \left \langle \phi \left ( f \right ) \right \rangle \frac{\partial f}{\partial \sigma _{ij}^{t}}, $$
(12)

where \(\eta \) is a viscosity parameter, \(\Phi \)(\(f\)) is the overstress function expressed with the yield function \(f\), and \(\left \langle \boldsymbol{\cdot } \right \rangle \) is the McCauley bracket such that

$$ \left \langle \phi \left ( f \right ) \right \rangle = \left \{ \textstyle\begin{array}{l@{\quad }l} 0, & \phi \left ( f \right ) \leq 0,\\ \left ( \frac{f}{\sigma _{y}^{0}} \right )^{N}, &\phi \left ( f \right ) >0, \end{array}\displaystyle \right . $$
(13)

where \(\sigma _{y}^{0}\) is the initial yield stress, and \(N\) is a rate sensitive constant. From Eq. (12) we can see that the viscoplastic component is activated when the yield function is larger than zero.

The von Mises yield criterion with nonlinear kinematic hardening was employed for the yield function \(f\) since it has been shown to agree with the plastic response of the adhesives considered in this work (Mohapatra 2018, 2014). The function \(f\) is written as

$$ f = \sqrt{\frac{3}{2} \left ( S_{ij}^{t} - \alpha _{ij}^{\prime \, t} \right ) \left ( S_{ij}^{t} - \alpha _{ij}^{\prime \, t} \right )} - \sigma _{y}^{0}, $$
(14)

where \(\alpha _{ij}^{\prime \, t}\) is the deviatoric backstress tensor at the current time. The evolution law of the backstress is defined from the Armstrong–Frederick model (Frederick and Armstrong 2007)

$$ \dot{\alpha }_{ij}^{t} = \frac{c}{\sigma _{y}^{0}} \left ( \sigma _{ij}^{t} - \alpha _{ij}^{t} \right ) \dot{\varepsilon }_{e}^{p, t} - \kappa \alpha _{ij}^{t} \dot{\varepsilon }_{e}^{p, t}, $$
(15)

where \(c\) is the initial kinematic hardening modulus, \(\kappa \) determines the rate at which the kinematic hardening modulus decreases with the increasing plastic deformation, and \(\dot{\varepsilon }_{e}^{p,t}\) is the rate of the effective viscoplastic strain,

$$ \dot{\varepsilon }_{e}^{p, t} = \sqrt{\frac{2}{3} \dot{\varepsilon }_{ij}^{p, t} \dot{\varepsilon }_{ij}^{p, t}}. $$
(16)

3 Numerical algorithm

3.1 Discretization

Considering a time increment \(\Delta t\), the strain history \(\varepsilon ^{t}\) at time \(t\) is obtained from the prior strain \(\varepsilon ^{t-\Delta t}\) and the change in strain over the time increment \(\Delta \varepsilon ^{t}\). Accordingly, the total strain from Eq. (1) can be presented as

$$\begin{gathered} \varepsilon _{ij}^{tot, t} = \varepsilon _{ij}^{e, t -\Delta t} + \Delta \varepsilon _{ij}^{e, t} + \varepsilon _{ij}^{p, t -\Delta t} + \Delta \varepsilon _{ij}^{p, t}, \end{gathered}$$
(17)
$$\begin{gathered} \sigma _{ij}^{t} = \sigma _{ij}^{t -\Delta t} +\Delta \sigma _{ij}^{t}. \end{gathered}$$
(18)

After some algebraic manipulation, the viscoelastic deviatoric and volumetric strain increments from Eqs. (8) and (9) can be written as

(19)
$$\begin{aligned} \Delta \varepsilon _{kk}^{e, t} &= B^{t} \sigma _{kk}^{t} - \overline{B}^{t- \Delta t} \sigma _{kk}^{t- \Delta t} - \frac{1}{3} \sum _{n=1}^{5} B_{n} \left ( g_{1}^{t} e^{- \lambda _{n} \Delta \psi ^{t}} - g_{1}^{t- \Delta t} \right ) q_{kk,n}^{t- \Delta t} \\ &\quad {}- \frac{1}{3} g_{2}^{t- \Delta t} \sum _{n=1}^{5} B_{n} \left ( g_{1}^{t- \Delta t} \frac{1- e^{- \lambda _{n} \Delta \psi ^{t- \Delta t}}}{\lambda _{n} \Delta \psi ^{t- \Delta t}} - g_{1}^{t} \frac{1- e^{- \lambda _{n} \Delta \psi ^{t}}}{\lambda _{n} \Delta \psi ^{t}} \right ) \sigma _{kk}^{t- \Delta t}. \end{aligned}$$
(20)

Assuming that the time increment \(\Delta t\) is small, we obtain the following relationship between the nonlinear viscoelastic parameters:

$$ g_{i}^{t -\Delta t} = g_{i}^{t}, i =0, 1, 2, $$
$$ \Delta \psi ^{t -\Delta \mathrm{t}} =\Delta \psi ^{t}. $$
(21)

The approximate stress increment at the beginning of each time increment may be obtained by substituting Eq. (21) into Eqs. (19) and (20):

(22)
(23)

Using the backward Euler integration method, the viscoplastic strain from Eq. (12) can be represented with the current increment as

$$ \varepsilon _{ij}^{p, t} = \varepsilon _{ij}^{p, t -\Delta t} +\Delta \varepsilon _{ij}^{p, t} = \varepsilon _{ij}^{p, t -\Delta t} + \eta \left ( \frac{f}{\sigma _{y}^{0}} \right )^{N} \frac{\partial f}{\partial \sigma _{ij}^{t}} \Delta t. $$
(24)

Similarly, the current backstress tensor is transferred into an incremental form

$$ \alpha _{ij}^{t} = \alpha _{ij}^{t -\Delta t} +\Delta \alpha _{ij}^{t} = \alpha _{ij}^{t -\Delta t} + \frac{c}{\sigma _{y}^{0}} \left ( \sigma _{ij}^{t} - \alpha _{ij}^{t} \right ) \Delta \varepsilon _{e}^{p, t} - \kappa \alpha _{ij}^{t} \Delta \varepsilon _{e}^{p, t}. $$
(25)

3.2 Viscoplastic formulation

From Eq. (16) we can see that to calculate the effective viscoplastic strain \(\Delta \varepsilon _{e}^{p,t}\), the value of \(\frac{\partial f}{\partial \sigma _{ij}^{t}}\) is needed. The derivative is presented as

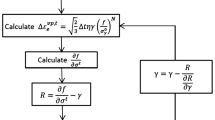
$$ \frac{\partial f}{\partial \sigma _{ij}^{t}} = \frac{\sqrt{3} ( S_{kl}^{t} - \alpha _{kl}^{\prime \,, t} )}{\sqrt{2( S_{mn}^{t} - \alpha _{mn}^{\prime \,, t} )( S_{mn}^{t} - \alpha _{mn}^{\prime \,, t} )}} \frac{\partial ( S_{kl}^{t} - \alpha _{kl}^{\prime \,, t} )}{\partial \sigma _{ij}^{t}}. $$
(26)

The yield function \(f\) depends on not only the current stress \(\sigma _{ij}^{t}\) but also on the backstress \(\alpha _{ij}^{t}\). Simultaneously, \(\alpha _{ij}^{t}\) is a function of \(\sigma _{ij}^{t}\) and \(\Delta \varepsilon _{e}^{p,t}\), whereas \(\Delta \varepsilon _{e}^{p,t}\) depends on \(f\). The interactions between each variable do not allow \(\frac{\partial f}{\partial \sigma _{ij}^{t}}\) and \(\Delta \varepsilon _{e}^{p,t}\) to be found directly. Newton’s iteration was employed to calculate the viscoplastic strain according to the flowchart shown in Fig. 1. At the beginning of the iteration, we initialize by

$$ \frac{\partial f}{\partial \sigma _{ij}^{t}} \frac{\partial f}{\partial \sigma _{ij}^{t}} = \gamma , $$
(27)

where \(\gamma \) is a constant. The increment of the effective viscoplastic strain \(\Delta \varepsilon _{e}^{p,t}\) is expressed with \(\gamma \) as

$$ \Delta \varepsilon _{e}^{p, t} = \sqrt{\frac{2}{3} \frac{\partial f}{\partial \sigma _{ij}^{t}} \frac{\partial f}{\partial \sigma _{ij}^{t}}} \Delta t\eta ( \frac{f}{\sigma _{y}^{0}} )^{N} = \sqrt{\frac{2}{3} \gamma } \Delta t\eta ( \frac{f}{\sigma _{y}^{0}} )^{N}. $$
(28)

Accordingly, the derivative of the effective strain increment with respect to the stress is given by

$$ \frac{\partial \Delta \varepsilon _{e}^{p, t}}{\partial \sigma _{ij}^{t}} = \sqrt{\frac{2}{3} \gamma } \frac{\Delta t\eta N}{f} ( \frac{f}{\sigma _{y}^{0}} )^{N} \frac{\partial f}{\partial \sigma _{ij}^{t}}. $$
(29)

The derivative of the deviatoric backstress with respect to the stress is obtained from Eq. (25) as

$$ \frac{\partial \alpha _{ij}'}{\partial \sigma _{kl}^{t}} = \frac{\left ( \frac{c}{\sigma _{y}^{0}} S_{ij}^{t} - \frac{c}{\sigma _{y}^{0}} \alpha _{ij}^{\prime \,, t} - \kappa \alpha _{ij}^{\prime \,, t} \right ) \frac{\partial \Delta \varepsilon _{e}^{p, t}}{\partial \sigma _{kl}^{t}} + \frac{c}{\sigma _{y}^{0}} \Delta \varepsilon _{e}^{p, t} \left ( \delta _{ik} \delta _{jl} - \frac{1}{3} \delta _{ij} \delta _{kl} \right )}{1+ \frac{c}{\sigma _{y}^{0}} \Delta \varepsilon _{e}^{p, t} + \kappa \Delta \varepsilon _{e}^{p, t}}, $$
(30)

whereas the derivative of the deviatoric stress with respect to the stress is expressed as

$$ \frac{\partial S_{ij}^{t}}{\partial \sigma _{kl}^{t}} = \delta _{ik} \delta _{jl} - \frac{1}{3} \delta _{ij} \delta _{kl}. $$
(31)

Substituting Eqs. (29)–(31) into Eq. (26), we obtain \(\frac{\partial f}{\partial \sigma _{ij}^{t}}\) as a function of the current stress and backstress tensors as

$$ \frac{\partial f}{\partial \sigma _{ij}^{t}} = \sqrt{\frac{3}{2}} \frac{( P \sigma _{y}^{0} - c \Delta \varepsilon _{e}^{p, t} )( S_{ij}^{t} - \alpha _{ij}^{\prime \,, t} )}{( S_{kl}^{t} - \alpha _{kl}^{\prime \,, t} )( \frac{c}{\sigma _{y}^{0}} S_{kl}^{t} - \frac{c}{\sigma _{y}^{0}} \alpha _{kl}^{\prime \,, t} - \kappa \alpha _{kl}^{\prime \,, t} ) \sqrt{\gamma } \Delta t\eta N ( \frac{f}{\sigma _{y}^{0}} )^{N -1} + P \sqrt{( S_{kl}^{t} - \alpha _{kl}^{\prime \,, t} )( S_{kl}^{t} - \alpha _{kl}^{\prime \,, t} )}}, $$
(32)

where \(P=1+ \frac{c}{\sigma _{y}^{0}} \Delta \varepsilon _{e}^{p,t} +\kappa \Delta \varepsilon _{e}^{p,t} \).

Fig. 1
figure 1

Flowchart of the viscoplastic strain calculation

Full size image

Comparing the calculated \(\frac{\partial f}{\partial \sigma _{ij}^{t}} \frac{\partial f}{\partial \sigma _{ij}^{t}}\) with the initial value of \(\gamma \), the difference is defined as

$$ R = \frac{\partial f}{\partial \sigma _{ij}^{t}} \frac{\partial f}{\partial \sigma _{ij}^{t}} - \gamma . $$
(33)

To minimize \(R\), allowing the iteration converge, \(\gamma \) is corrected at the end of every iteration according to

$$ \gamma ^{K +1} = \gamma ^{K} - \frac{R}{4 \frac{\partial R}{\partial \gamma ^{K}}} = \gamma ^{K} + \frac{\frac{\partial f}{\partial \sigma _{ij}^{t}} \frac{\partial f}{\partial \sigma _{ij}^{t}} - \gamma ^{K}}{4}. $$
(34)

The superscripts \(K\) and \(K+1\) present the \(K\)th and (\(K+1\))th iterations, respectively. It should be noted that the number 4 in Eq. (34) was used to slow down the rate of convergence, preventing \(\gamma \) from being negative without changing the iteration result. Substituting \(\gamma ^{K+1}\) into Eq. (28), the (\(K+1\))th loop begins. Once the iteration converges, namely \(R < 10^{-7}\), the viscoplastic strain increment \(\Delta \varepsilon _{ij}^{p,t}\) can be calculated from Eq. (24).

3.3 Viscoelastic–viscoplastic formulation

The viscoelastic–viscoplastic model was implemented into FE using a UMAT in ABAQUS 2016. The stress and the Jacobian matrix are required for each time increment in the UMAT. Figure 2 shows the iterative algorithm for the combined viscoelastic–viscoplastic system.

Fig. 2
figure 2

Flowchart of the viscoelastic–viscoplastic system

Full size image

At the beginning of the \(n\)th time increment \(\Delta t^{n}\), we assume the adhesive behaves viscoelastically. A trial stress increment accounting only for viscoelasticity, \(\Delta \sigma ^{tr}\), was calculated from Eqs. (22) and (23) with the nonlinear parameters and variables from the previous time history \(t-\ \Delta t^{n}\). Based on the trial stress, those parameters and the increment of the viscoelastic strain \(\Delta \varepsilon _{ij}^{e,\ t} \) were updated. To implement viscoplasticity, the backstress \(\alpha _{ij}^{t}\) and the yield function \(f\) were obtained by the trial stress. The iteration of viscoplastic strain (Fig. 1) was activated when \(f\) was larger than zero.

To decide if the calculation has converged, a strain comparison was introduced by

$$ \xi _{ij} =\Delta \varepsilon _{ij}^{tot, t} -\Delta \varepsilon _{ij}^{ext, t}, $$
(35)

where the total strain increment \(\Delta \varepsilon _{ij}^{tot, t}\) is obtained as a combination of both components,

$$ \Delta \varepsilon _{ij}^{tot, t} =\Delta \varepsilon _{ij}^{e, t} +\Delta \varepsilon _{ij}^{p, t}, $$
(36)

and \(\Delta \varepsilon _{ij}^{ext,t}\) is calculated from the stiffness matrix and external force and then passed into the UMAT. The stiffness matrix is updated for each increment from the Jacobian in the UMAT.

The root of the squared differences is defined by

$$ \xi ^{*} = \sqrt{\xi _{ij} \xi _{ij}}. $$
(37)

When \(\xi ^{*}<10^{-7}\), the iteration is assumed to be converged. If the convergence is not reached, then the stress is corrected by

$$ \sigma _{ij}^{t, K +1} = \sigma _{ij}^{t, K} - [ \frac{\partial \xi _{ij}^{K}}{\partial \sigma _{kl}^{t, K}} ]^{-1} \xi _{kl}^{K}, $$
(38)

where the superscripts \(K\) and \(K+1\) represent the \(K\)th and (\(K+1\))th iteration, respectively. In Eq. (38),

$$ \frac{\partial \xi _{ij}}{\partial \sigma _{kl}^{t}} = \frac{\partial \Delta \varepsilon _{ij}^{e, t}}{\partial \sigma _{kl}^{t}} + \frac{\partial \Delta \varepsilon _{ij}^{p, t}}{\partial \sigma _{kl}^{t}}. $$
(39)

The derivative of the viscoelastic strain increment to the stress, \(\frac{\partial \Delta \varepsilon _{ij}^{e,t}}{\partial \sigma _{kl}^{t}}\), is calculated according to the condition of the effective stress exceeding the linear viscoelastic range. The effective stress \(\overline{\sigma }^{t}\) is given as

$$ \overline{\sigma }^{t} = \sqrt{\frac{3}{2} S_{ij}^{t} S_{ij}^{t}}. $$
(40)

For nonlinear viscoelasticity, the derivative can be obtained from Eqs. (19) and (20) as

(41)

In this study the nonlinear parameters are defined as linear functions of the current effective stress \(\overline{\sigma }^{t}\):

$$ g_{i}^{t} = a_{i} \overline{\sigma }^{t} + b_{i},\quad i=0,1,2, $$
$$ a^{t} = a_{3} \overline{\sigma }^{t} + b_{3}, $$
(42)

where \(a_{i}\) and \(b_{i}\) are constants.

For linear viscoelasticity,

$$ g_{i}^{t} = a^{t} =1,\quad i=0,1,2. $$
(43)

Therefore Eq. (41) becomes

(44)

The derivative of the viscoplatic strain increment is obtained from Eq. (24) as

$$ \frac{\partial \Delta \varepsilon _{ij}^{p, t}}{\partial \sigma _{kl}^{t}} =\Delta t\eta \left ( \frac{f}{\sigma _{y}^{0}} \right )^{N} ( \frac{N}{f} \frac{\partial f}{\partial \sigma _{ij}^{t}} \frac{\partial f}{\partial \sigma _{kl}^{t}} + \frac{\partial ^{2} f}{\partial \sigma _{ij} \partial \sigma _{kl}} ). $$
(45)

In Eq. (45) the high-order derivative is given by

$$\begin{aligned} \frac{\partial ^{2} f}{\partial \sigma _{ij} \partial \sigma _{kl}} &= \frac{- \left ( G_{mn} G_{mn} \right )^{-1} G_{pq} \frac{\partial G_{pq}}{\partial \sigma _{kl}} \left ( 1- D \right ) G_{ij} - \frac{\partial D}{\partial \sigma _{kl}} G_{ij} + \left ( 1- D \right ) \frac{\partial G_{ij}}{\partial \sigma _{kl}}}{EH + \sqrt{\frac{2}{3} G_{mn} G_{mn}}} \\ &\quad {} - \frac{\left ( 1- D \right ) G_{ij} \left [ - \left ( G_{mn} G_{mn} \right )^{-1} G_{pq} \frac{\partial G_{pq}}{\partial \sigma _{kl}} EH + \frac{\partial E}{\partial \sigma _{kl}} H + \frac{\partial H}{\partial \sigma _{kl}} E \right ]}{\left ( EH + \sqrt{\frac{2}{3} G_{mn} G_{mn}} \right )^{2}}, \end{aligned}$$
(46)

where

$$ G_{ij} = S_{ij}^{t} - \alpha _{ij}^{\prime \,, t}, $$
(47)
$$ E = \frac{( S_{ij}^{t} - \alpha _{ij}^{\prime \,, t} )( \frac{c}{\sigma _{y}^{0}} S_{ij}^{t} - \frac{c}{\sigma _{y}^{0}} \alpha _{ij}^{\prime \,, t} - \kappa \alpha _{ij}^{\prime \,, t} )}{P}, $$
(48)
$$ H = \sqrt{\frac{2}{3} \frac{\partial f}{\partial \sigma _{ij}^{t}} \frac{\partial f}{\partial \sigma _{ij}^{t}}} \frac{\Delta t\eta N}{f} ( \frac{f}{\sigma _{y}^{0}} )^{N}, $$
(49)
$$ D = \frac{c \Delta \varepsilon _{e}^{p, t}}{\sigma _{y}^{0} P}, $$
(50)
$$ \frac{\partial G_{ij}}{\partial \sigma _{kl}} = \left ( \delta _{ik} \delta _{jl} - \frac{1}{3} \delta _{ij} \delta _{kl} \right ) \left ( 1- D \right ) - \frac{H}{P} \left ( \frac{c}{\sigma _{y}^{0}} S_{ij}^{t} - \frac{c}{\sigma _{y}^{0}} \alpha _{ij}^{\prime \,, t} - \kappa \alpha _{ij}^{\prime \,, t} \right ) \frac{\partial f}{\partial \sigma _{kl}^{t}}, $$
(51)
$$ \frac{\partial D}{\partial \sigma _{kl}} = \frac{cH}{\sigma _{y}^{0} P^{2}} ( P - \frac{c}{\sigma _{y}^{0}} \Delta \varepsilon _{e}^{p, t} - \kappa \Delta \varepsilon _{e}^{p, t} ) \frac{\partial f}{\partial \sigma _{kl}^{t}}, $$
(52)
$$\begin{aligned} \frac{\partial E}{\partial \sigma _{kl}} &= \left [ \frac{c}{P \sigma _{y}^{0}} \left ( S_{ij}^{t} - \alpha _{ij}^{\prime \,, t} \right ) - \frac{\kappa }{P} \alpha _{ij}^{\prime \,, t} \right ] \frac{\partial G_{ij}}{\partial \sigma _{kl}} \\ &\quad {} + \frac{G_{ij}}{P^{2}} \left [ P \left ( \frac{c}{\sigma _{y}^{0}} \frac{\partial G_{ij}}{\partial \sigma _{kl}} - \kappa \frac{\partial \alpha _{ij}^{\prime \,, t}}{\partial \sigma _{kl}} \right ) - H \left ( \frac{c}{\sigma _{y}^{0}} G_{ij} - \kappa \alpha _{ij}^{\prime \,, t} \right ) \left ( \frac{c}{\sigma _{y}^{0}} + \kappa \right ) \frac{\partial f}{\partial \sigma _{kl}^{t}} \right ], \end{aligned}$$
(53)
$$ \frac{\partial H}{\partial \sigma _{kl}} = \sqrt{\frac{2}{3} \frac{\partial f}{\partial \sigma _{mn}^{t}} \frac{\partial f}{\partial \sigma _{mn}^{t}}} \frac{\Delta t\eta N \left ( N -1 \right )}{f^{2}} ( \frac{f}{\sigma _{y}^{0}} )^{N} \frac{\partial f}{\partial \sigma _{kl}^{t}}. $$
(54)

3.4 Plane strain environment

The 3D constitutive model was used to simulate the creep-recovery behavior of a scarf joint as shown in Fig. 3. Given the high computational cost of the 3D model, the suitability of a 2D model was considered. For a shear dominated stress state, as occurs in the adhesive of the scarf joint considered here, plane stress and strain formulations provide similar solutions. Nevertheless, the relatively stiff aluminum adherends create a nearly plane strain condition in the adhesive and were used here. The stress and strain components were reduced according to

$$ \varepsilon _{13} = \varepsilon _{23} = \varepsilon _{33} = \sigma _{13} = \sigma _{23} =0, $$
(55)
$$ \sigma _{33} = \upsilon ( \sigma _{11} + \sigma _{22} ). $$
(56)
Fig. 3
figure 3

Geometry of the studied scarf joint. All dimensions are in mm

Full size image

4 Numerical simulation of the scarf joints

4.1 Mesh and boundary conditions

The scarf joint consisted of two adherends and an adhesive film with a thickness of 0.21 mm. The finite element meshes for the 2D and 3D models were created using the preprocessor in ABAQUS 2016 as shown in Fig. 4. In the 2D model (Fig. 4-a) the adherends and adhesive were mostly meshed with 4-node plane strain bilinear reduced integration with hourglass control elements (CPE4R). At the near surface-transition zone from the adherend to adhesive 3-node linear plane strain triangle elements were used for the wedge shapes. To capture the deformation within the adhesive layer, the adhesive was divided into four equal layers through the thickness. Whereas a convergence study showed minimal improvement from two layers in the adhesive, the refinement in the relatively small adhesive layer had a negligible computational cost. Similarly, the 3D model (Fig. 4-b) was meshed with 8-node linear brick, reduced integration with hourglass control elements (C3D8R), with 6-node triangular prism elements (C3D6) for the transition zone. The surface on one end of the scarf joint was constrained in all directions and rotations. The surface on the other end was allowed to deform in the longitudinal direction of the joint (\(x\)-axis). Load was applied as a pressure over the surface of the free end. Accordingly, the average shear stress in the adhesive was obtained by

$$ \tau _{12}^{adh} = \sin 10^{\circ } \cos 10^{\circ } \sigma _{xx}^{joi}, $$
(57)

where \(\tau _{12}^{adh}\) is the shear stress in the adhesive, and \(\sigma _{xx}^{joi}\) is the applied pressure.

Fig. 4
figure 4

Finite element mesh for (a) 2D model and (b) 3D model

Full size image

4.2 Parameter calibration for viscoelasticity

This work considered the response of a “standard” (Cytec FM300-2) and “toughened” (Hysol EA9696) film adhesive in a scarf joint of which the adherends were made of 2024 aluminum. The adherends were modeled elastically with a modulus of 73 GPa and Poisson’s ratio of 0.33. Both adhesives were thermoset and epoxy-based. A Poisson’s ratio of 0.38 and 0.43 (Mohapatra 2018) was used for the standard and toughened adhesive, respectively.

The model was calibrated from 10000 s creep tests of scarf joints at 20% and 50% of the ultimate shear strength (USS). Considering the linear viscoelastic response with a constant shear stress \(\sigma _{12}^{adh} =20\%\ USS\), Eq. (5) reduces to

$$ \varepsilon _{12}^{e} = \frac{1}{2} \left [ J_{0} + \sum _{n =1}^{7} J_{n} (1- e^{- \lambda _{n} t} ) \right ] \sigma _{12}^{adh}, $$
(58)

from which \(D_{o}\) was found at \(t\approx 0\), whereas the Prony series parameters were determined at \(t\gg 0\).

For nonlinear creep, Eq. (5) reduces to

$$ \varepsilon _{12}^{e} = \frac{1}{2} \left [ g_{0} J_{0} \sigma _{12}^{adh} + g_{1} g_{2} \sigma _{12}^{adh} \sum _{n =1}^{N} J_{n} \left ( 1- e^{- \lambda _{n} t} \right ) \right ], $$
(59)

whereas the associated recovery is

$$ \varepsilon _{12}^{e} = g_{2} \sigma _{12}^{adh} \left \{ \sum _{n =1}^{N} J_{n} \left [ e^{- \lambda _{n} \left ( t- t_{0} \right )} - e^{- \lambda _{n} \left ( \frac{t_{0}}{a} +t- t_{0} \right )} \right ] \right \} . $$
(60)

The nonlinear parameters \(g_{0}\), \(g_{1}\), \(g_{2}\), and \(a\) were fit to linear functions of the effective stress by Eq. (42). To provide continuity between the linear and nonlinear viscoelastic response, \(g_{1}\) for both adhesives was represented as

$$ g_{1}^{t} = a_{1} \left ( \overline{\sigma }^{t} \right )^{c_{1}} + b_{1,} $$
(61)

where \(a_{1}\), \(b_{1}\), and \(c_{1}\) are constant.

Accordingly, the instantaneous strain at 50% USS was used to obtain \(g_{0}\) from Eq. (59). The recovery strain was used to find \(g_{2}\) and \(a\) at 50% of USS from Eq. (60). Finally, the creep response was used to obtain \(g_{1}\) using Eq. (59). It should be noted that the permanent strain was subtracted from the above experimental responses at 50% USS before fitting the viscoelastic parameters, which are listed in Table 1.

Table 1 Parameters for the viscoelastic model for two adhesives
Full size table

4.3 Time-dependent plasticity

The viscoplastic parameters \(c\) and \(k\) were determined from monotonic scarf joint tests at 4448 N/min. Assuming that the adhesive was under pure shear, Eqs. (14) and (15) were combined and rewritten as

$$ \overline{\sigma } - \sigma _{y}^{0} = \sqrt{3} \sigma _{12}^{adh} - \sigma _{y}^{0} = \frac{c}{k} \left ( 1- e^{- k \varepsilon _{e}^{P}} \right ). $$
(62)

It should be noted that \(c\) and \(k\) describe the development of the yield surface, whereas \(\eta \) and \(N \) in Eq. (12) influence the time-dependent plasticity (viscoplasticity). To calibrate these two parameters, the effect of viscoplasticity in the adhesive films was considered.

A series of creep tests at 50% USS with different durations were conducted on the scarf joints. The applied load was ramped to 50% USS over 50 s for the toughened and standard adhesives and held constant until the load was removed at double the loading rate, after which the scarf joints were allowed to recover. The average adhesive strain was measured using a strain gage rosette (0∘/45∘/90∘) mounted on one side of the joint and centered over the bond line. Details of the method and its validation are presented elsewhere (Krause and Smith 2021).

The residual shear strain is shown in Fig. (5) as a function of the load duration (LD), which includes the ramp-up time. Each load duration was repeated three times, from which the average and standard deviation are reported. The residual strain increased with the load duration, showing viscoplastic behavior. The parameters \(\eta \) and \(N \) were found by fitting the residual strain as shown by the dashed lines in Fig. 5. The viscoplastic component \(\varepsilon _{12}^{p}\) in the model agreed the experiments for both adhesives. The viscoplastic parameters are listed in Table 2.

Fig. 5
figure 5

The fitting of viscoplastic components (\(\varepsilon _{12}^{p}\)) for the (a) toughened and (b) standard adhesive in scarf joints. Circles represent the measured residual strain for varying load durations (LD)

Full size image
Table 2 Parameters in viscoplastic components for von Mises yielding with kinematic hardening
Full size table

4.4 Numerical analysis

The calibration described above considered only one load duration for viscoelasticity (10,000 s) and only the permanent deformation for viscoplasticity. Using the calibrated parameters above, the predicted total shear response of the adhesive films to a load duration of 10000 s are compared with experiment for creep-recovery tests of scarf joints in Fig. 6. The experiments at 20% and 50% USS were repeated three times for the toughened and standard adhesive. As shown in Fig. 6, the nonlinear viscoelastic–viscoplastic (NEP) model showed good agreement with experiments at 20% and 50% USS for both adhesives. To show the contribution of nonlinear viscoelasticity, dotted lines in Fig. 6 describe linear-viscoelastic (LEP) response. Neglecting nonlinear viscoelasticity led to underestimating total strain for the toughened by 21% and overestimating strain for the standard adhesive by 4%. The standard adhesive experienced nonlinear stiffening, resulting in a decreasing instantaneous compliance (\(g_{0} < 1\) in Eq. (2)) in the nonlinear viscoelastic–viscoplastic model. Thus the linear viscoelastic–viscoplastic model, with a constant instantaneous compliance, overestimated the strain response.

Fig. 6
figure 6

Comparison of the creep-recovery response of (a) toughened and (b) standard adhesive in scarf joints with linear (LEP) and nonlinear (NEP) viscoelastic–viscoplastic models with 2D or 3D element formulations

Full size image

The 2D and 3D models, compared in Fig. 6, were within 1% of each other. Given the similarity of the results, and the computational efficiency of the 2D model, it was used throughout the remainder of the study. Figure 7 compares the predicted creep-recovery responses of varying load durations at 50% USS with experiment. The predicted strain response was within the experimental repeatability for creep and recovery. The predicted recovery followed the experimental response for each duration. The residual strain corresponding to the viscoplastic deformation developed nonlinearly and reached 7.2% and 3% of the total strain up to the load duration of 10000 s for the toughened and standard adhesives, respectively.

Fig. 7
figure 7

A comparison of varying creep-recovery durations of (a) toughened and (b) standard adhesive scarf joints to the nonlinear viscoelastic–viscoplastic model (NEP)

Full size image

Figure 8 compares the distributions of shear stress and strain along the center line of the adhesives at 50% USS for three cases: NEP, LEP, and nonlinear viscoelastic (NE). The NEP model shows that time reduces the shear stress concentration but magnifies the strain concentration, as observed elsewhere (Su and Mackie 1993). For both adhesives (Fig. 8(a, c)), the stress distribution predicted by the NE model changed little from 1000 to 10000 s, showing that viscoplasticity accounted for the reduced stress concentration at longer durations. In Fig. 8(b, d) the NE model produced a smaller strain concentration than the models incorporating viscoplasticity; this shows that viscoplastic response magnifies the strain concentrations in these adhesives. Note that the higher strain of the standard adhesive from NE (in comparison to the other models) is a result of nonlinear hardening for this adhesive (Fig. 8d).

Fig. 8
figure 8

A comparison of the centerline shear stress and strain of a toughened (a, b) and standard adhesive (c, d) between the nonlinear viscoelastic–viscoplastic (NEP), linear viscoelastic–viscoplastic (LEP), and nonlinear viscoelastic (NE) models

Full size image

5 Conclusion

In this study, we proposed a three-dimensional nonlinear viscoelastic–viscoplastic model combining the modified Schaper integral model and Perzyna viscoplastic model with the von Mises yield criterion and nonlinear kinematic hardening, an iterative scheme assuming only viscoelasticity initially with a correction of stress in both viscoelasticity and viscoplasticity to solve the combined system numerically. The nonlinear viscoelastic and viscoplastic parameters were calibrated from creep-recovery and monotonic tests on scarf joints with a toughened and a standard adhesive film. The existence and development of viscoplasticity was discussed by comparing the viscoplastic component of the model with residual strain from creep tests on the scarf joints. The viscoplastic strain increased nonlinearly with increasing load duration. A two-dimensional model considering plane strain was developed and compared with the 3D model in simulating the creep-recovery of the adhesives in scarf joints. A good agreement between the prediction and the experimental results was obtained. The finite element analysis showed that viscoplasticity reduced the stress concentration and magnified the strain concentration.