A viscoelastic–viscoplastic model for adhesives subjected to reversed cyclic load

Abstract

This study aims to describe a toughened adhesive’s ratcheting–recovery behavior under reversed cyclic load using a viscoelastic–viscoplastic model. As most adhesives are based on synthetic polymers, their tensile and compression response can be different. A series of load–Sunload tests were conducted on bulk adhesives and bonded joints involving tension/compression–shear loads to characterize the initial yield surface. The effect of hydrostatic stress was studied by considering the instantaneous response and yield strength under tensile and compression loads. Given the observed modulus degradation and extensive permanent strain during reversed cyclic tests, time-dependent damage factors were considered for both viscoelastic and viscoplastic responses. The model was implemented in a finite element (FE) code and used to model the shear response to reversed cyclic load with varying frequency. Good agreement between the model and experiment was obtained. The consideration of both hydrostatic stress and damage was required to describe the observed adhesive reversed cyclic response.

1 Introduction

Adhesive bonding is popular in the aerospace industry due to its high strength to weight ratio, good resistance of fatigue and corrosion, reduced stress concentration, and flexibility in bonding different materials and honeycomb structures (Wahab 2015). With the increasing use of adhesives in bonding critical aircraft parts, accurate evaluation and prediction of adhesives’ mechanical behaviors play an important role in the design and manufacturing of adhesively bonded joints.

Due to the nature of polymers, adhesives often have complex nonlinear behaviors such as viscoelasticity, plasticity, or viscoplasticity. Some adhesives behave differently in tension and compression because of the influence of hydrostatic stress on the nonlinear behaviors. Several experimental investigations involving multiaxial stress states, such as Arcan joints (Bidaud et al. 2016; Suwanpakpraek et al. 2020), lap shear joints (Srinivasan et al. 2020; Zgoul and Crocombe 2004), scarf joints (Afendi et al. 2011; Carrere et al. 2015), and tubular butt joints (Arnaud et al. 2014; Cognard et al. 2012), have shown that the yield and failure of adhesives were influenced by hydrostatic stress. Accordingly, yield criteria involving hydrostatic stress, such as Drucker–Prager (Ignjatovic et al. 1998; Morin et al. 2011), exponent Drucker–Prager (Dean et al. 2004; García et al. 2011; Srinivasan et al. 2020), and Drucker–Prager/Cap yield criteria (Ignjatovic et al. 1998; Wang and Chalkley 2000), were employed for modeling adhesives’ mechanical behaviors under multiaxial loads. In addition, some have observed that the nonlinear viscoelastic behavior of polymers is not only governed by shear but also affected by hydrostatic stress, which causes a different tensile and compression response (Buckley and Green 1976; Buckley and McCrum 1974). Popelar and Liechti (1997) proposed a modified free volume approach that included both dilatational and distortional effects on the temporal behavior for enhanced viscoelasticity in tension and reduced viscoelasticity in compression. Lai and Bakker (1996) accommodated the hydrostatic effect using viscoelastic nonlinear parameters in the Schapery model.

Adhesives are commonly used in load-bearing structures, such as wing assemblies, that are tested and deployed under fully reversed cyclic load. However, there are few published studies of adhesives under reversed cyclic load. Xia et al. (Shen et al. 2004) studied the stress–strain response of an epoxy polymer subjected to fully reversed load with different stress amplitudes. The ratcheting behavior and nonlinearity were more evident in tension than compression, which was explained by anisotropic behavior in tension and compression. They also proposed a rheological viscoelastic model with the capability of changing stiffness between loading and unloading (Xia et al. 2005). The model was able to describe the stress–strain hysteresis and ratcheting of the polymer under reversed cyclic load, but it could not predict residual strain. Krause and Smith (Krause and Smith 2021) conducted cyclic tests on adhesives in scarf joints and observed that the adhesive exhibited higher ratcheting deformation under reversed cyclic load than tension–tension cyclic load. The enhanced ratcheting during the reversed loading was attributed to kinematic hardening. Eslami et al. (2020) analyzed the load-displacement behavior and energy dissipation of a flexible adhesive by a series of monotonic and reversed cyclic tests on double-lap joints. At low and medium load rates, more damage was accumulated under cyclic load than monotonic load. Softening was also observed during cyclic loading.

In the present work, a toughened adhesive subjected to reversed cyclic load is experimentally and theoretically considered. The effects of hydrostatic stress on yielding and instantaneous elastic response were considered while modulus degradation and permanent strain were reflected by damage factors. The model was implemented into a finite element code and compared with scarf joints subjected to reversed cyclic load with varying frequencies. Good agreement with experiment was obtained. The contribution of hydrostatic stress and damage is discussed.

2 Yielding of a toughened adhesive

2.1 Experiment

The yield stress from monotonic tests is commonly found from a strain offset or the intersection of the initial and final slope of a strain–stress curve. However, adhesives often yield without a significant change in the elastic or plastic response because the temporal effect is mixed with plasticity. Therefore, in this work the yield stress was determined from strain recovery, where yielding starts at the onset of residual strain (after long recovery) from varying stress levels.

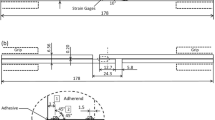
This study considered the response of a toughened (Hysol EA9696) film adhesive, which was cured at 120 °C. To investigate the effect of hydrostatic stress on yielding, monotonic tests with stress control were conducted on bulk coupons, Arcan, and scarf joints involving tension, compression, and shear conditions, as shown in Fig. 1.

Fig. 1

Test setup for (a) bulk coupon, (b) Arcan joint, and (c) scarf joint

The adhesive bulk samples were laminated from eight layers of adhesive film and cured to a thickness of 1.6 mm. Bulk coupons measuring $12 \times 12$ mm² were loaded in compression in a servo-hydraulic load frame between two lubricated parallel plates to minimize lateral constraint as shown in Fig. 1a. The coupons were loaded at 150 N/s and unloaded at 300 N/s to shorten the experiment since the unloading rate does not affect the residual strain. After the load was removed, the coupon was allowed to recover for 80,000 s or at least 200 times the loading duration where the residual strain was steady. The thickness change of each coupon was measured by a digital caliper to obtain permanent deformation.

Arcan joints bonded with the toughened adhesive film measuring 76 × 6 mm² were loaded at −45 degrees to provide a combined compression and shear stress state (Fig. 1b), while scarf joints with a scarf angle of 10 degrees over a cross section of 25 × 6 mm² were loaded under tension and compression to find shear properties (Fig. 1c). The adherends were made from 2024 T3 aluminum plates that were phosphoric acid anodized and primed before bonding. The adhesive of bonded joints was 0.2 mm thick. Load was applied to the scarf and Arcan joints along the y-axis at 148 N/s and then removed to allow recovery. The adhesive shear strain ($S_{12}$) was measured using stacked rosette strain gages (Micro-Measurements 062 WW) positioned at the center of the bond line. This method of adhesive strain measurement has been compared with the digital image correlation and extensometry, showing good reliability and accuracy in measuring the shear response of adhesives in bonded joints (Krause and Smith 2021).

2.2 Yield stress

Figure 2 shows the residual strain as a function of applied stress for different specimens, where the applied stress is the average stress over the bonding area. For the bulk coupons (Fig. 2a), the trend of residual strain indicated the yield stress in uniaxial compression at approximately 55.1 MPa. The two results of small positive residual were due to measurement error. Observing from Fig. 2b, the scarf joint’s yield shear stress in tension, 15.8 MPa, was significantly lower than in compression, which was 24.1 MPa. For the Arcan joint, the shear yield stress under compression was approaching 14.2 MPa.

Fig. 2

Residual strains as functions of applied stress in tension (Ten) and compression (Com) for the adhesive in (a) bulk and (b) bonded joints

The Arcan and scarf joint tests were under biaxial stress, which allowed yielding to include the effect of hydrostatic stress. A three-dimensional elastic FE model was employed to compare the normal and shear stress components. Table 1 shows the ratio of the normal stress ($S_{11}$) and lateral stresses ($S_{22}$ and $S_{33}$) to the shear stress ($S_{12}$), taken at the center of each joint. As expected, the shear stress was the dominant component in the scarf joint tests. The Arcan joint loaded at −45 degrees provided the ratio $S_{11}/S_{12}$ close to unity. Consequently, larger adhesive lateral stresses, due to Poisson’s effect, were present in the Arcan coupons.

Table 1 Relation between the normal and shear stress components for three different bonded joints

Using the measured average yield stress, $S_{12}$, and the ratios from Table 1, estimates of the normal stress components at yield were found and used to obtain the von Mises stress ($\sigma _{\mathrm{e}}$) and the hydrostatic stress ($\sigma _{\mathrm{h}}$) as shown in Fig. 3. Contrary to that found elsewhere (Mohapatra 2018), the yield stress was sensitive to the hydrostatic stress. Accordingly, pressure sensitive yield criteria were considered.

Fig. 3

Von Mises ($\sigma _{\mathrm{e}}$) and hydrostatic ($\sigma _{\mathrm{h}}$) components of the yield strength of each coupon type. The dashed and solid lines represent the von Mises (vM) and Drucker–Prager yield criterion (D-P), respectively

While the bulk and scarf coupons (Fig. 4b) have a nearly constant stress over their bonded regions, the Arcan joints (Fig. 4a) have a parabolic shear stress distribution and a normal stress that peaked at the bondline edge (Chen and Smith 2021b) (Cognard et al. 2008). Accordingly, the Arcan hydrostatic and von Mises stresses in Fig. 3 (based on the average yield stress) are lower than the corresponding bulk and scarf coupons. Thus, all the results in Fig. 3 are consistent with an adhesive yield strength that is dependent on the hydrostatic stress.

Fig. 4

Stress distribution along the bond line of an (a) Arcan joint at −45 degrees and (b) scarf joint with the average shear stress of 50% USS

Due to the linear relation between the von Mises stress and hydrostatic stress (Fig. 3), the Drucker–Prager yield criterion (Drucker and Prager 1952) was considered. It is modified from the von Mises criterion to include hydrostatic stress sensitivity and is widely used for polymeric materials (Quinson et al. 1997; Wang and Rose 1997) and can be written as

$$ f =\mathrm{A} I_{1} + \sqrt{\mathrm{J}_{2}} -\mathrm{B}= 3 \mathrm{A} \sigma _{\mathrm{h}} + \frac{\sigma _{e}}{\sqrt{3}} -\mathrm{B}, $$

(1)

where $I_{1}$ is the first stress invariant, $A$ and $B$ are defined as positive material constants, and $J_{2}$ is the second invariant of deviatoric stress. Fitting Eq. 1 to the yield stress of the bulk and bonded joints, a good agreement between the model (D-P) and experiment is shown in Fig. 3, where $A = 0.245$ and $B = 19$ MPa.

The toughened adhesive exhibited both viscoelastic and viscoplastic behaviors, where an overstress-based viscoplastic model (Perzyna) described the growth of permanent strain under creep and cyclic loads (Chen and Smith 2021a). Moreover, nonlinear kinematic hardening was observed for the adhesive (Mohapatra and Smith 2021). Therefore, the Drucker–Prager criterion combined with nonlinear kinematic hardening was employed for a viscoelastic–viscoplastic model in the following study.

3 Viscoelastic–viscoplastic model

3.1 Constitutive model

The total strain was decomposed into viscoelastic and viscoplastic components with the assumption that they are uncoupled,

$$ \varepsilon _{ij}^{tot} = \varepsilon _{ij}^{ve} + \varepsilon _{ij}^{vp}, $$

(2)

where the superscripts tot, $ve$, and $vp$ denote total, viscoelastic, and viscoplastic parts, respectively.

3.1.1 Viscoelastic component

The modified Schapery model (Lai and Bakker 1996) consisting of the hydrostatic and deviatoric parts was employed to describe the nonlinear viscoelastic component, which is presented as

$$\begin{aligned} \varepsilon _{ij}^{ve, t} =& e_{ij}^{ve, t} + \frac{1}{3} \varepsilon _{kk}^{ve, t} \delta _{ij} = \frac{1}{2} g_{0}^{t} J_{0} S_{ij}^{t} + \frac{1}{2} g_{1}^{t} \int _{0}^{t} \Delta J^{\psi ^{t} - \psi ^{\tau}} \frac{d \left ( g_{2}^{\tau} S_{ij}^{\tau} \right )}{d\tau} d\tau \\ & + \frac{1}{3} \left ( \frac{1}{3} g_{0}^{t} B_{0} \sigma _{kk}^{t} \delta _{ij} + \frac{1}{3} g_{1}^{t} \int _{0}^{t} \Delta B^{\psi ^{t} - \psi ^{\tau}} \frac{d \left ( g_{2}^{\tau} \sigma _{kk}^{\tau} \right )}{d\tau} d\tau \delta _{ij} \right ), \end{aligned}$$

(3)

where $\delta _{ij}$ is Kronecker delta. $e_{ij}^{ve,t}$, $\varepsilon _{kk}^{ve,t}$, and $S_{ij}^{t}$ are the deviatoric strain, volumetric strain, and deviatoric stress at the current time $t$, respectively. And $\psi ^{\mathrm{t}}$ is the effective time given by

$$ \psi ^{t} = \frac{t}{a}, $$

(4)

where $a$, $g_{0}$, $g_{1,}$ and $g_{2}$ are nonlinear viscoelastic parameters and assumed to be a function of the von Mises equivalent stress $\sigma _{\mathrm{e}}$ or

$$\begin{aligned} &g_{\mathrm{i}} = \beta _{\mathrm{i}1} \left ( \sigma _{e} \right )^{\beta _{i2}} + \beta _{\mathrm{i}3} (i=1,2), \end{aligned}$$

(5)

$$\begin{aligned} & a = \beta _{\mathrm{a}1} \left ( \sigma _{e} \right )^{\beta _{a2}} + \beta _{\mathrm{a}3}, \end{aligned}$$

(6)

where $\beta _{ij}$ ($i=1,2,a$; $j=1,2,3$) are constants.

The effect of hydrostatic stress on the viscoelastic response can be different in tension and compression. In the Schapery model, the hydrostatic effect may be reflected in the elastic response by $g_{0}$ (Haj-Ali and Muliana 2004; Lai and Bakker 1996). In this work, to encourage convergence and accommodate complex boundary conditions, $g_{0}$ was expressed as a function of $\sigma _{\mathrm{e}}$ considering both tension and compression as

$$ g_{0} = \beta _{1}^{\mathrm{j}} \left ( \sigma _{e} \right )^{\beta _{2}^{\mathrm{j}}} + \beta _{3}^{\mathrm{j}}, $$

(7)

where $\beta _{i}$ ($i=1,2,3$) are material constants, and the superscript $j$ indicates tension (+) or compression (−).

In Eq. 3, $J_{0}$ and $B_{0}$ are instantaneous elastic shear and bulk compliances, respectively. Similarly, $\Delta J$ and $\Delta B$ are transient shear and bulk compliances, respectively. The integrals in Eq. 3 present time-dependent response. The shear and bulk compliances, in turn, can be presented by uniaxial compliances

$$ J_{0} =2 \left ( 1+ \upsilon \right ) D_{0} $$

(8)

$$ B_{0} =3 \left ( 1-2 \upsilon \right ) D_{0} $$

(9)

$$ \Delta J^{\psi ^{t}} =2 \left ( 1+ \upsilon \right ) \Delta D^{\psi ^{t}} $$

(10)

$$ \Delta B^{\psi ^{t}} =3 \left ( 1-2 \upsilon \right ) \Delta D^{\psi ^{t}}, $$

(11)

where $\nu$ is the Poisson’s ratio, $D_{0}$ is the uniaxial elastic compliance, and the uniaxial transient compliance $\Delta D^{\psi t}$ was presented as a five-term Prony-series

$$ \Delta D^{\psi ^{t}} = \sum _{n =1}^{5} D_{n} \left ( 1-\exp \left ( - \lambda _{n} \psi ^{t} \right ) \right ), $$

(12)

where $D_{\mathrm{n}}$ and $\lambda _{\mathrm{n}}$ are material coefficients.

Some have expanded the Schapery model for anisotropic response by introducing compliance tensors $\Delta D_{ij}^{\psi t}$ and $D_{\mathit{oij}}$ (Poon and Ahmad 1999) or $Q_{ij}$ (Rand and Sterling 2006). This work used an isotropic model as observed experimentally (Lemme 2016) and since the scarf joint test specimens are dominated by uniaxial shear.

When polymers and adhesives are subjected to cyclic loads, damage can cause modulus degradation (Drozdov 2011; Khashaba 2020). According to the postulate of strain equivalence by Lemaitre (Lemaitre 1984), the effective modulus can be described by a damage variable $D$,

$$ E_{D} = E_{0} \left ( 1- D \right ), $$

(13)

where $E_{0}$ is the original modulus.

Therefore, the Schapery model (Eq. 3) was modified by incorporating a time-dependent damage variable to describe cyclic modulus reduction. Since the time-dependent strain is much smaller than the instantaneous elastic strain, damage was only applied to the elastic response as

$$\begin{aligned} \varepsilon _{ij}^{ve, t} =& \frac{1}{2(1- D^{ve} )} g_{0}^{t} J_{0} S_{ij}^{t} + \frac{1}{2} g_{1}^{t} \int _{0}^{t} \Delta J^{\psi ^{t} - \psi ^{\tau}} \frac{d \left ( g_{2}^{\tau} S_{ij}^{\tau} \right )}{d\tau} d\tau \\ &+ \frac{1}{3} \left ( \frac{1}{3(1- \mathrm{D}^{ve} )} g_{0}^{t} B_{0} \sigma _{kk}^{t} \delta _{ij} + \frac{1}{3} g_{1}^{t} \int _{0}^{t} \Delta B^{\psi ^{t} - \psi ^{\tau}} \frac{d \left ( g_{2}^{\tau} \sigma _{kk}^{\tau} \right )}{d\tau} d\tau \delta _{ij} \right ), \end{aligned}$$

(14)

where the damage variable $D^{ve}$ is defined by

$$ D^{\mathrm{ve}} = \sum _{i =1}^{3} a_{i} t^{i}, $$

(15)

where $a_{\mathrm{i}}$ are constants. It should be noted that the damage variable is not related to physical considerations and is phenomenological for simplicity as done elsewhere (Carraro et al. 2013; Da Costa Mattos et al. 2012; Shenoy et al. 2010).

3.1.2 Viscoplastic component

The viscoplastic strain rate was described by Perzyna’s model (Perzyna 1966) with the associated flow rule

$$ \dot{\varepsilon}_{ij}^{vp,t} = \eta \left \langle \phi \left ( f \right ) \right \rangle \frac{\partial f}{\partial \sigma _{ij}^{t}}, $$

(16)

where $\eta$ is a viscosity parameter and $\Phi (f)$ is the overstress function expressed with the yield function $f$. $\left \langle \boldsymbol{\cdot} \right \rangle$ is the McCauley bracket such that

$$ \left \langle \phi \left ( f \right ) \right \rangle = \left \{ \textstyle\begin{array}{l@{\quad }l} 0,& \phi \left ( f \right ) \leq 0\\ \left ( \frac{f}{\sigma _{y}^{0}} \right )^{N},& \phi \left ( f \right ) >0 \end{array}\displaystyle \right ., $$

(17)

where $\sigma _{y}^{0}$ is the initial yield stress and $N$ is a rate sensitive constant.

The Drucker–Prager yield criterion with nonlinear kinematic hardening was employed for the yield function (Rakic and Zivkovic 2015). The slope of each stress—strain hysteresis loop corresponds to fatigue damage (Foletti et al. 2020), which affects the viscoplastic yield stress. The yield function $f$ was written as

$$ f =\mathrm{A} I_{1} + \sqrt{\mathrm{J}_{2D}} - \left ( 1- D^{vp} \right ) \mathrm{B}=\mathrm{A} I_{1} + \sqrt{\frac{1}{2} \left ( S_{ij} - \alpha _{ij} \right ) \left ( S_{ij} - \alpha _{ij} \right )} -(1- \mathrm{D}^{vp} )\mathrm{B}, $$

(18)

where $J$_2D is the second deviatoric invariant with kinematic hardening and $\alpha$_ij is the backstress tensor describing the center of the yield surface in the deviatoric stress plane. The evolution of the backstress was defined by Armstrong–Fredrick hardening (Frederick and Armstrong 2007)

$$ \dot{\alpha}_{ij} = \frac{2}{3} c \dot{\varepsilon}_{ij}^{vp} - \kappa \alpha _{ij} \dot{\varepsilon}_{e}^{vp}, $$

(19)

where $C$ and $K$ are material parameters and $\dot{\varepsilon}_{e}^{vp}$ is the rate of the effective viscoplastic strain, or

$$ \dot{\varepsilon}_{e}^{vp} = \sqrt{\frac{2}{3} \dot{\varepsilon}_{ij}^{vp} \dot{\varepsilon}_{ij}^{vp}}. $$

(20)

The damage factor $D^{vp}$ is often presented as a function of plastic strain. Since this study only considered fixed frequencies of reversed loading, $D^{vp}$ was described as a function of time as

$$ D^{vp} = \frac{t}{t_{D}}, $$

(21)

where $t_{\mathrm{D}}$ is a reference time.

3.2 Numerical implementation

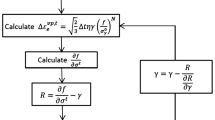
The viscoelastic–viscoplastic model was implemented into the finite element software ABAQUS 2016 via a user material subroutine (UMAT). Figure 5 shows the iterative algorithm to solve for the viscoelastic–viscoplastic system with a stress correction for each iteration. Considering a time increment from the previous (t-$\Delta$t) to the current time (t), the strain history from Eq. 2 and the current stress can be discretized as

$$ \varepsilon _{ij}^{tot, t} = \varepsilon _{ij}^{ve, t -\Delta t} + \varepsilon _{ij}^{vp, t -\Delta t} +\Delta \varepsilon _{ij}^{ve, t} +\Delta \varepsilon _{ij}^{vp, t} $$

(22)

$$ \sigma _{ij}^{t} = \sigma _{ij}^{t -\Delta t} +\Delta \sigma _{ij}^{t}. $$

(23)

At the beginning of each time increment, the material was assumed to exhibit only viscoelasticity. The viscoelastic (VE) implementation and system scheme can be found elsewhere (Chen and Smith 2021a). The viscoplastic calculation was activated once the yield function $f$ was larger than zero. Considering the interaction between $f$ and $\Delta \varepsilon _{ij}^{vp, t}$, Newton’s iteration was employed to calculate the strain iteratively, as shown in the dashed square in Fig. 5.

Fig. 5

Flowchart of the viscoelastic–viscoplastic system

A backward Euler method allowed the viscoplastic strain from Eq. 16 to be defined in the incremental form as follows:

$$ \Delta \varepsilon _{ij}^{vp,t} =\Delta \mathrm{t} \eta \left ( \frac{f}{\sigma _{y}^{0}} \right )^{N} \frac{\partial f}{\partial \sigma _{ij}^{t}} =\gamma \frac{\partial f}{\partial \sigma _{ij}^{t}}, $$

(24)

where $\gamma$ is initialized as a constant at the beginning of the iteration. Consequently, the yield function can be expressed as a function of $\gamma$ such as

$$ f = \sigma _{y}^{0} \left ( \frac{\gamma}{\Delta \mathrm{t} \eta} \right )^{\frac{1}{N}}. $$

(25)

The derivative of $f$ with respect to $\sigma _{ij}^{t}$ can be obtained by Eq. 18:

$$ \frac{\partial f}{\partial \sigma _{ij}^{t}} = \frac{\partial f}{\partial I_{1}} \frac{\partial I_{1}}{\partial \sigma _{ij}^{t}} + \frac{\partial f}{\partial J_{2 D}} \frac{\partial J_{2 D}}{\partial \sigma _{ij}^{t}} = A \delta _{ij} + \frac{S_{ij}^{t} - \alpha _{ij}^{t}}{2 \sqrt{J_{2 D}}}. $$

(26)

Consequently, the viscoplastic strain increment is obtained by combining Eq. 24 and 26:

$$ \Delta \varepsilon _{ij}^{vp, t} = \gamma A \delta _{ij} + \frac{\gamma}{2 \sqrt{J_{2 D}}} \left ( S_{ij}^{t} - \alpha _{ij}^{t} \right ). $$

(27)

The effective strain increment $\Delta \varepsilon _{e}^{vp,t}$ can be defined by Eq. 20 as

$$ \Delta \varepsilon _{e}^{vp, t} = \sqrt{\frac{2}{3} \Delta \varepsilon _{ij}^{vp, t} \Delta \varepsilon _{ij}^{vp, t}}. $$

(28)

The current backstress is $\alpha _{ij}^{t}=\alpha _{ij}^{t- \Delta t}$ at the first iteration and was corrected in the following iterations by

$$ \alpha _{ij}^{t} = \alpha _{ij}^{t -\Delta t} + \Delta \alpha _{ij}^{t}. $$

(29)

Combining Eqs. 19, 27, and 28, the backstress increment was updated by

$$ \Delta \alpha _{ij}^{t} = \frac{\frac{2}{3} c \Delta \varepsilon _{ij}^{vp, t} - \kappa \alpha _{ij}^{t -\Delta t} \Delta \varepsilon _{e}^{vp, t}}{1+ \kappa \Delta \varepsilon _{e}^{vp, t}}. $$

(30)

The yield function $f$ can be updated by substituting Eqs. 29 and 30 into Eq. 18:

$$ f =\mathrm{A} I_{1} + \sqrt{\frac{1}{2} \left ( S_{ij}^{t} - \alpha _{ij}^{t -\Delta t} + \Delta \alpha _{ij}^{t} \right ) \left ( S_{ij}^{t} - \alpha _{ij}^{t -\Delta t} + \Delta \alpha _{ij}^{t} \right )} -( 1- D^{vp} )\mathrm{B}. $$

(31)

Employing the Newton iteration method, a dynamic difference of the yield function between Eqs. 25 and 31 is required and defined as

$$\begin{aligned} \xi = &\mathrm{A} I_{1} + \sqrt{\frac{1}{2} \left ( S_{ij}^{t} - \alpha _{ij}^{t -\Delta t} + \Delta \alpha _{ij}^{t} \right ) \left ( S_{ij}^{t} - \alpha _{ij}^{t -\Delta t} + \Delta \alpha _{ij}^{t} \right )} \\ & - \left ( 1- D^{vp} \right ) \mathrm{B}- \sigma _{y}^{0} \left ( \frac{\gamma}{\Delta \mathrm{t} \eta} \right )^{\frac{1}{N}}. \end{aligned}$$

(32)

To minimize $\xi$, $\gamma$ is modified iteratively by

$$ \gamma = \gamma - \frac{\xi}{\frac{\partial \xi}{\partial \gamma}}. $$

(33)

The derivative of $\xi$ with respect to $\gamma$ is derived from Eq. 32:

$$\begin{aligned} \frac{\partial \xi}{\partial \gamma} = & \frac{\partial \sqrt{J_{2 D}}}{\partial \alpha _{ij}^{t}} \frac{\partial \alpha _{ij}^{t}}{\partial \gamma} - \frac{\sigma _{y}^{0}}{N\gamma} \left ( \frac{\gamma}{\Delta \mathrm{t} \eta} \right )^{\frac{1}{N}} = \frac{\alpha _{ij}^{t} - S_{ij}^{t}}{2 \sqrt{J_{2 D}}} \frac{\partial \alpha _{ij}^{t}}{\partial \gamma} - \frac{\sigma _{y}^{0}}{N\gamma} \left ( \frac{\gamma}{\Delta \mathrm{t} \eta} \right )^{\frac{1}{N}} \\ = &\frac{\alpha _{ij}^{t} - S_{ij}^{t}}{3 \sqrt{J_{2 D}} \left ( 1+ \kappa \Delta \varepsilon _{e}^{vp, t} \right )} \left [ C \frac{\partial f}{\partial \sigma _{ij}^{t}} - \kappa \alpha _{ij}^{t -\Delta t} \frac{\Delta \varepsilon _{mn}^{vp, t}}{\Delta \varepsilon _{e}^{vp, t}} \frac{\partial f}{\partial \sigma _{mn}^{t}}\right. \\ &\left. - \frac{\left ( 2 C \Delta \varepsilon _{ij}^{vp, t} -3 \kappa \alpha _{ij}^{t -\Delta t} \Delta \varepsilon _{e}^{vp, t} \right ) \kappa \Delta \varepsilon _{mn}^{vp, t}}{3 \left ( 1+ \kappa \Delta \varepsilon _{e}^{vp, t} \right ) \Delta \varepsilon _{e}^{vp, t}} \frac{\partial f}{\partial \sigma _{mn}^{t}} \right ] - \frac{\sigma _{y}^{0}}{N\gamma} \left ( \frac{\gamma}{\Delta \mathrm{t} \eta} \right )^{\frac{1}{N}}. \end{aligned}$$

(34)

The iteration was assumed to converge when $\xi< 10^{-6}$. The material’s Jacobian matrix was required for each time increment in the UMAT. The Jacobian matrix for the viscoelastic–viscoplastic model is

$$ \frac{\partial \Delta \varepsilon _{ij}^{t}}{\partial \sigma _{kl}^{t}} = \frac{\partial \Delta \varepsilon _{ij}^{ve, t}}{\partial \sigma _{kl}^{t}} + \frac{\partial \Delta \varepsilon _{ij}^{vp, t}}{\partial \sigma _{kl}^{t}}. $$

(35)

The derivative of the viscoplastic strain increment with respect to the current stress is derived from Eq. 19 ignoring the high order derivative, which is written as

$$ \frac{\partial \Delta \varepsilon _{ij}^{vp, t}}{\partial \sigma _{kl}^{t}} = \frac{\Delta t\eta N}{f} \left ( \frac{f}{\sigma _{y}^{0}} \right )^{N} \frac{\partial f}{\partial \sigma _{ij}^{t}} \frac{\partial f}{\partial \sigma _{kl}^{t}}. $$

(36)

A plane strain assumption has shown good agreement with the three-dimensional model (Chen and Smith 2021a). Given the reduced computational cost, the viscoelastic–viscoplastic model was simplified to the plane strain condition by

$$ \varepsilon _{13} = \varepsilon _{23} = \varepsilon _{33} = \sigma _{13} = \sigma _{23} =0 $$

(37)

$$ \sigma _{33} = \upsilon ( \sigma _{11} + \sigma _{22} ) $$

(38)

3.3 Finite element model

The model was calibrated and validated from the scarf joint experiments. The mesh and boundary conditions of the scarf joints were created with the preprocessor in ABAQUS 2016, as shown in Fig. 6 (Chen and Smith 2021b). Four-node bilinear, reduced integration with hourglass control plane strain elements (CPE4R) was used for most of the scarf joint, while three-node linear plane strain elements (CPE3) were used for the wedge shapes near the bondline edge of the scarf joint. Four layers of elements were generated through the adhesive thickness. Both ends of the scarf joint were supported and a pressure load was applied on the free end surface. The adherends were modeled as linear elastic with a modulus of 73 GPa and Poisson’s ratio of 0.33.

Fig. 6

Mesh and boundary conditions for the scarf joint

A convergence was conducted to identify an optimal mesh refinement. Figure 7 shows the normalized shear strain and von Mises stress as a function of element length along the bondline. The stress and strain were nearly unchanged when the element length was less than 0.7 mm. In the following, an element length of 0.5 mm was employed.

Fig. 7

Mesh convergence for the scarf joint

3.4 Parameter calibration

3.4.1 Viscoelastic parameters

The parameters in the viscoelastic component of the model, including the Prony series and viscoelastic nonlinear parameters, were determined from a series of creep tests of scarf joints with varying stress levels and load durations. The details can be found elsewhere (Chen and Smith 2021a, 2021b). The Prony series parameters (Eqs. 8–12) are presented in Table 2.

Table 2 The Prony series parameters

To investigate $g_{0}$ in compression, monotonic shear tests were conducted at rates of $R$ and 2$R$ on the scarf joints to various stress levels (where $R=22.2$ kN/min). Since the yield strength was not rate-dependent, their elastic response (involving $g_{o}$) was similar. At a given load, for instance, the time-dependent response at $R$ will be double that of tests at $2R$. Thus, the difference in the strain response between tests at $R$ and 2$R$ is the time-dependent portion of the response for tests done at 2$R$; and subtracting this time-dependent response from tests done at 2$R$ results in the elastic response. $g_{0}$ was obtained as a function of applied stress by fitting the experimental elastic response as shown in Fig. 8. $g_{0}$ increased more in tension than in compression, which indicates higher elastic response in tension than compression at the same stress level. Table 3 shows the viscoelastic nonlinear parameters (Eqs. 5–7).

Fig. 8

The viscoelastic parameter $g_{0}$ fitting the scarf experiment under varying shear stress levels

Table 3 Viscoelastic nonlinear parameters

To describe modulus degradation during cyclic loading, the hysteresis loops of scarf joints subjected to reversed cyclic load under stress control at 0.5 Hz were examined as shown in Fig. 9a. The loop modulus $E_{\mathrm{L}}$, defined as the slope of the straight line between the valley and peak of each loop, decreased as the cycle number increased (or in terms of compliance, the damage function is 1/(1- $D$^ve) in Eq. 14). As Fig. 9b shows, the normalized loop compliance 1/$E_{\mathrm{L}}$ ($E_{L0}$/$E_{L}$, $E_{L0}$ is the loop modulus at the first cycle) was averaged from three repeated tests (solid line) and fit to a polynomial (dashed line).

Fig. 9

Calibration of the damage factor $D$^ve on a stress-controlled reversed cyclic test at 0.5 Hz: (a) evolution of the hysteresis loops and decreasing loop modulus $E_{\mathrm{L}}$ and (b) comparison between the experimental normalized loop compliance and the fitted curve of the function of $D$^ve. Error bars correspond to one standard deviation

3.4.2 Viscoplastic parameters

The yield function $f$ was calibrated from the yield stress from bulk and scarf joints, as shown in Fig. 3. The viscoplastic parameter $\eta$ and rate-sensitive constant $N$ (which influence viscoplastic deformation) were found from the residual strains of cyclic tensile tests of scarf joints with varying frequency (Chen and Smith 2021b). Ignoring the damage effects, the nonlinear kinematic hardening parameters ($c$ and $\kappa$ in Eq. 19) were fit to a monotonic tensile test at 148 N/s as shown in Fig. 10. Since the scarf joints subjected to reversed cyclic load at 0.5 Hz broke at around 6200 cycles, $t_{\mathrm{D}}$ is defined as 12400 s. Table 4 shows the parameters for the viscoplastic model.

Fig. 10

Comparison between the fitted and experimental monotonic shear strain–stress curves of the scarf joints for the calibration of hardening parameters

Table 4 Parameters in the viscoplastic model

4 Result and discussion

4.1 Cyclic calibration at 0.5 Hz

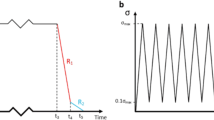
The model was compared to scarf joints subjected to reversed cyclic load at 50% USS and 0.5 Hz as shown in Fig. 11. After 1000 cycles the load was removed and the specimens were allowed to recover. The test was repeated three times, where the peak and valley strain for each cycle and the residual strain after load removal were measured. The ratcheting strain in tension was twice that observed in compression. The model (solid line) showed good agreement with the experiment at 0.5 Hz in both the loading and recovery stages.

Fig. 11

Comparison of the (a) ratcheting and (b) recovery behaviors of the toughened adhesive in scarf joints with the proposed model (Model) and model without $D$^ve (Model_Dve) or D^vp (Model_Dvp). Error bars correspond to one standard deviation

The model was compared without $D$^ve or $D$^vp (viscoelastic and viscoplastic damage, respectively). As indicated by the dotted line in Fig. 11a, the peak and valley strain increased in parallel when viscoelastic damage ($D$^ve) was removed. Their range was also smaller than experiment, showing that modulus reduction is underestimated without $D$^ve.

The dashed line in Fig. 11a removes only viscoplastic damage from the model. While the range in the peak-valley strain is comparable to experiment, they are both lower than experiment. This is a result of underestimating the permanent strain as evidenced in Fig. 11b. Thus, both the viscoelastic and viscoplastic damage factors are necessary to describe the ratcheting–recovery response of the adhesive subjected to reversed cyclic load.

4.2 Model validation at 3 Hz

The model described above was used to predict the response of scarf joints exposed to reversed cyclic load at 3 Hz. Scarf joints were loaded for 1000 and 3000 cycles and then allowed to recover. Each test was repeated three times. Figure 12 shows the comparison between the experiment and the model. Similar to the result at 0.5 Hz, nonlinearity and ratcheting were observed in tension and compression.

Fig. 12

Comparison of ratcheting–recovery behavior between the model and experiment of the scarf joints at 3 Hz with (a) 1000 and (b) 3000 cycles. Error bars correspond to one standard deviation

In prior work involving tensile cycling load, a model with a von Mises yield criterion showed good agreement with experiment (Chen and Smith 2021b). To evaluate the influence of hydrostatic stress with reversed cyclic load, the Drucker–Prager yield criterion used in this work was replaced with the von Mises yield criterion (noted vm in Fig. 12a). The model with von Mises yielding could not describe the different tensile and compressive response and did not account for the observed permanent deformation after load removal. The departure from experiment was evident after the first cycle since removing the dependence of $g_{0}$ on the hydrostatic stress led to the same tensile and compressive strain at the first cycle. Accounting for the effect of hydrostatic stress on the tensile, compressive response appears to be necessary for this adhesive when exposed to fully reversed load.

At 3000 cycles (Fig. 12b), increased ratcheting and residual strain was observed with increasing cycles. The model correctly described the ratcheting trend, while the predicted peak and residual strains were 4.3% and 1.9% lower than experiment, respectively. Overall, the model had favorable agreement with the experiment at 3 Hz.

5 Conclusion

This work studied the ratcheting–recovery behavior of a toughened adhesive subjected to reversed cyclic load. Using the residual strains from a series of load–unload experiments, a hydrostatic stress sensitive yield surface was characterized and described by a Drucker–Prager yield criterion. The effect of hydrostatic stress on viscoelasticity was included in the model and increased the adhesive’s nonlinear response. Damage was observed from modulus degradation during cyclic loading and was accompanied with permanent strain, which were described in the model using damage factors in the viscoelastic and viscoplastic components. The model showed good agreement with reversed cyclic tests of scarf joints at 0.5 and 3 Hz where the nonlinearity of ratcheting and permanent strain arose from both the effect of hydrostatic stress and damage.