Baxterisation of the fused Hecke algebra and R-matrices with gl(N)-symmetry

Abstract

We give an explicit Baxterisation formula for the fused Hecke algebra and its classical limit for the algebra of fused permutations. These algebras replace the Hecke algebra and the symmetric group in the Schur–Weyl duality theorems for the symmetrised powers of the fundamental representation of gl(N) and their quantum version. So the Baxterisation formulas presented in this paper are applicable to the R-matrices associated with these representations. In particular, all “higher spins” representations of (classical and quantum) sl(2) are covered.

A Proof of the Baxterisation formula

This appendix is devoted to the proof of Theorem 3.1. The main steps of the proof are the following:

• the fused Hecke algebra $H_{k,n}(q)$ is isomorphic to a certain projection of the usual Hecke algebra $H_{nk}(q)$;

• we write the elementary partial braidings in terms of elements in $H_{nk}(q)$;

• we show that a certain product of the usual R-matrices (9) of the Hecke algebra $H_{nk}(q)$ can be expanded as a linear combination of the elementary partial braidings;

• we identify this sum with the r.h.s. of (7) and use the factorised form in terms of usual R-matrices to show that it satisfies the braided Yang–Baxter equation (this is where the ideas of the fusion procedure appear).

1.1 Projected Hecke algebra

In the Hecke algebra $H_{nk}(q)$, we consider the elements, for $1\le i < j \le nk-1$,

$$\begin{aligned} S_{[i,j]}:=\frac{1}{[j-i+1 ]_q!} \ \prod _{i\le a\le j-1}^{\longrightarrow } \check{R}_a\big (q^{2(a-i+1)}\big )\ \check{R}_{a-1}\big (q^{2(a-i)}\big )\ \ldots \check{R}_i(q^2) \ , \end{aligned}$$

(13)

where $\check{R}_a(u)$ is given by Formula (9) and $\prod _{i\le a\le j-1}^{\longrightarrow }$ means that the product is ordered from left to right when the index a increases. This element is the image of $S_{[1,j-i+1]}$ through the embedding of $H_{j-i+1}(q)$ in $H_{nk}(q)$ given by $\sigma _a\mapsto \sigma _{a+i-1}$.

The element $S_{[1,j-i+1]}$ is the so-called q-symmetriser of the Hecke algebra $H_{j-i+1}(q)$. In fact, Formula (13) is the simplest case of the fusion formula for the Hecke algebra expressing a complete set of primitive idempotents as products of R-matrices [31]. The q-symmetrisers are well-known objects (see [6, 32]). We recall below the main properties that we will use in the following. A formula alternative to (13) is the following sum:

$$\begin{aligned} S_{[i,j]}=\frac{q^{-\frac{(j-i+1)(j-i)}{2}}}{[j-i+1]_q!}\sum _w q^{\ell (w)}\sigma _w\ , \end{aligned}$$

where the sum runs over the set of permutations of the letters $\{i,i+1,\ldots ,j\}$, the elements $\sigma _w$ are the corresponding standard basis elements of $H_{nk}(q)$, and $\ell (w)$ is the number of crossings in the standard diagram $\sigma _w$ (equivalently, the length of w). The element $S_{[i,j]}$ is a partial q-symmetriser satisfying in particular

$$\begin{aligned} S_{[i,j]}^2=S_{[i,j]}\ \ \ \ \ \text {and}\ \ \ \ \ \ \sigma _a S_{[i,j]} =S_{[i,j]}\sigma _a=q S_{[i,j]}\,,\ a=i,\ldots ,j-1. \end{aligned}$$

(14)

This implies that $S_{[i,j]}=S_{[i,j]}S_{[i',j']}$ if $i\le i'<j'\le j$. Finally, a recursion formula for these partial q-symmetrisers is:

$$\begin{aligned} S_{[i,j+1]}=\frac{1}{[j-i]_q}\sum _{a=i}^{j+1}q^{i-a} \sigma _a\sigma _{a+1}\ldots \sigma _j S_{[i,j]}\ . \end{aligned}$$

(15)

Inside the Hecke algebra $H_{nk}(q)$, we consider also the element

$$\begin{aligned} P^{(k)}:=S_{[1,k]}S_{[k+1,2k]}\ldots S_{[(n-1)k+1,nk]}\ . \end{aligned}$$

(16)

This is an idempotent (each factor is itself an idempotent and commutes with the others), and it allows us to construct $P^{(k)} H_{nk}(q)P^{(k)}$ which is an algebra with the unit $P^{(k)}$. Here, we call this algebra the projected Hecke algebra. In [25], the following proposition is established.

Proposition A.1

The fused Hecke algebra $H_{k,n}(q)$ is isomorphic to the projected Hecke algebra $P^{(k)} H_{nk}(q) P^{(k)}$.

Thanks to this proposition, we can transfer the proof of Theorem 3.1 from $H_{k,n}(q)$ to $P^{(k)} H_{nk}(q)P^{(k)}$.

1.2 Elementary partial braidings in the projected Hecke algebra

In this paragraph, we restrict ourselves to the case $n=2$. This case is sufficient when we want to study only one R-matrix. By using the isomorphism between $P^{(k)} H_{2k}(q)P^{(k)}$ and $H_{k,2}(q)$, the partial elementary braiding $\Sigma ^{(k;p)}$ reads as follows

$$\begin{aligned} \Sigma ^{(k;p)}= P^{(k)} (\sigma _k \sigma _{k+1}\ldots \sigma _{k+p-1}) (\sigma _{k-1} \sigma _{k}\ldots \sigma _{k+p-2}) \ldots (\sigma _{k-p+1} \sigma _{k-p+1}\ldots \sigma _{k}) P^{(k)} \ , \end{aligned}$$

(17)

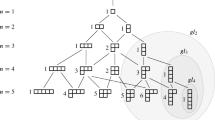
where $P^{(k)}=S_{[1,k]}S_{[k+1,2k]}$. Recall that $p\in \{0,\ldots ,k\}$ (when $p=0$, the element is simply $P^{(k)}$). The formula for $\Sigma ^{(k;p)}$ is best visualised on the following diagram:

The 4 shaded ellipses surrounding the dots $1,2, \ldots k$ and $k+1,\ldots ,2k$ in the previous diagram represent the q-symmetrisers $S_{[1,k]}$ and $S_{[k+1,2k]}$.

More generally, let $l\ge k$ and define the following elements in $H_{k+\ell }(q)$, for $0\le p\le k$,

$$\begin{aligned} \Sigma ^{(k,\ell ;p)}= P^{(k,\ell )} (\sigma _k \sigma _{k+1}\ldots \sigma _{\ell +p-1}) (\sigma _{k-1} \sigma _{k}\ldots \sigma _{\ell +p-2})\ldots (\sigma _{k-p+1} \sigma _{k-p+2}\ldots \sigma _{\ell }) P^{(\ell ,k)} \ , \end{aligned}$$

(18)

where $P^{(k,\ell )}=S_{[1,k]}S_{[k+1,k+\ell ]}$ and $P^{(\ell ,k)}=S_{[1,\ell ]}S_{[\ell +1,k+\ell ]}$. We get $\Sigma ^{(k,k;p)}=\Sigma ^{(k;p)}$. These elements are visualised on the following diagrams:

1.3 Product of R-matrices

Let us now define, in $H_{k+\ell }(q)$,

$$\begin{aligned} \check{R}^{(k,\ell )}(u) := P^{(k,\ell )} \prod _{1\le a\le k}^{\longleftarrow } \check{R}_a\left( uq^{2(1-a)}\right) \check{R}_{a+1}\left( uq^{2(2-a)}\right) \ldots \check{R}_{a+\ell -1}\left( uq^{2(\ell -a)}\right) P^{(\ell ,k)}\ , \end{aligned}$$

(19)

where $\check{R}_a\left( u\right)$ is given by (9). The arrow means that the product is ordered from right to left when the index a increases. It is a straightforward calculation, using repeatedly the braided Yang–Baxter equation satisfied by $\check{R}_i(u)$, to show that:

$$\begin{aligned} P^{(k,\ell )}\check{R}^{(k,\ell )}(u)=\check{R}^{(k,\ell )}(u)P^{(\ell ,k)}\ . \end{aligned}$$

(20)

As a consequence, only one idempotent (any one of the two) is actually needed in (19). We refer to Remark A.3 for more information on the element $\check{R}^{(k,\ell )}$.

Lemma A.2

Let $1\le k\le \ell$. The element $\check{R}^{(k,\ell )}(u)$ can be rewritten as follows

$$\begin{aligned} \check{R}^{(k,\ell )}(u)=\sum _{p=0}^{k} a^{(k,\ell )}_p(u) \ \Sigma ^{(k,\ell ;p)}\ , \end{aligned}$$

(21)

where

$$\begin{aligned} a^{(k,\ell )}_p(u) = (-q)^{k-p} \frac{ (q^{-2}\, ; \, q^{-2})_{k-p}}{(uq^{-2p}\,;\, q^{-2})_{k-p}}\left[ \begin{array}{c} k \\ p \end{array}\right] _q \left[ \begin{array}{c} \ell \\ k-p \end{array}\right] _q\ . \end{aligned}$$

(22)

Proof

We prove this lemma by induction w.r.t. k and $\ell$. For $k=\ell =1$, the definition (19) becomes

$$\begin{aligned} \check{R}^{(1,1)}(u) := \check{R}_1\left( u\right) =\sigma _1 - \frac{q-q^{-1}}{1-u} =\Sigma _1^{(1,1;1)} -\frac{q-q^{-1}}{1-u}\Sigma _1^{(1,1;0)} \end{aligned}$$

(23)

which proves Lemma for $k=\ell =1$. For $k=1$ and $\ell > 1$, the definition (19) becomes

$$\begin{aligned} \check{R}^{(1,\ell )}(u) := S_{[2,\ell +1]}\check{R}_1\left( u\right) \ldots \check{R}_\ell (uq^{2(\ell -1)}) S_{[1,\ell ]}\ . \end{aligned}$$

(24)

We use $S_{[2,\ell +1]}=S_{[2,\ell +1]} S_{[2,\ell ]}$ and the consequence of (20) to obtain:

$$\begin{aligned} \check{R}^{(1,\ell )}(u) = S_{[2,\ell +1]}\check{R}_{[1,\ell ]}^{(1,\ell -1)}(u) \check{R}_\ell (uq^{2(\ell -1)}) S_{[1,\ell ]}\ . \end{aligned}$$

(25)

The index of $\check{R}_{[1,\ell ]}^{(1,\ell -1)}(u)$ indicates that we use the embedding of $H_{\ell }(q)$ in $H_{\ell +1}(q)$ given by $\sigma _i \mapsto \sigma _i$. If we suppose that Formula (21) holds for $\ell -1$, then

$$\begin{aligned} \check{R}^{(1,\ell )}(u) = S_{[2,\ell +1]}\left( \Sigma ^{(1,\ell -1;1)} +a^{(1,\ell -1)}_0(u)\ \Sigma ^{(1,\ell -1;0)} \right) \left( \sigma _\ell - \frac{q-q^{-1}}{1-uq^{2(\ell -1)}} \right) S_{[1,\ell ]}\ .\nonumber \\ \end{aligned}$$

(26)

From the definition of $\Sigma ^{(1,\ell -1;1)}$, one obtains

$$\begin{aligned} \check{R}^{(1,\ell )}(u)&= S_{[2,\ell +1]}\left( \sigma _1\ldots \sigma _\ell -\frac{q-q^{-1}}{1-uq^{2(\ell -1)}} \sigma _1\ldots \sigma _{\ell -1}\right. \nonumber \\&\quad \left. +\,a^{(1,\ell -1)}_0(u)\sigma _\ell -\frac{q-q^{-1}}{1-uq^{2(\ell -1)}} a^{(1,\ell -1)}_0(u) \right) S_{[1,\ell ]}\nonumber \\&= \Sigma ^{(1,\ell ;1)} +S_{[2,\ell +1]} \left( -\frac{q-q^{-1}}{1-uq^{2(\ell -1)}} q^{\ell -1}\right. \nonumber \\&\quad \left. +\,a^{(1,\ell -1)}_0(u)q -\frac{q-q^{-1}}{1-uq^{2(\ell -1)}} a^{(1,\ell -1)}_0(u) \right) S_{[1,\ell ]}\ . \end{aligned}$$

(27)

To obtain the previous equality, we have used $S_{[2,\ell +1]}\sigma _\ell =q S_{[2,\ell +1]}$ and $\sigma _j S_{[1,\ell ]}=q S_{[1,\ell ]}$ (for $j=1,2, \ldots ,\ell -1$). By noticing that the expression in parenthesis in (27) is equal to $a^{(1,\ell )}_0(u)$, we prove by induction Lemma for $k=1$ and $\ell > 1$.

Let $1<k \le \ell$. By definition, one gets in $H_{k+\ell }(q)$

$$\begin{aligned} \check{R}^{(k,\ell )}(u)= & {} S_{[1,k]}S_{[k+1,k+\ell ]} \ \ \check{R}_k\big (uq^{2(1-k)}\big )\check{R}_{k+1}\big (uq^{2(2-k)}\big ) \ldots \check{R}_{k+\ell -1} \big (uq^{2(\ell -k)}\big )\nonumber \\&\times \qquad \qquad \vdots \nonumber \\&\times \check{R}_2\big (uq^{-2}\big )\check{R}_3(u) \ldots \check{R}_{\ell +1} \big (uq^{2(\ell -2)}\big )\nonumber \\&\times \check{R}_1(u)\check{R}_2(uq^2) \ldots \check{R}_\ell \big (uq^{2(\ell -1)}\big ) \ \ S_{[1,\ell ]}S_{[\ell +1,k+\ell ]} \ . \end{aligned}$$

(28)

We use that $S_{[1,k]}=S_{[1,k]}S_{[2,k]}$ and the consequence of (20) to obtain

$$\begin{aligned} \check{R}^{(k,\ell )}(u)= & {} S_{[1,k]} \ \check{R}_{[2,k+\ell ]}^{(k-1,\ell )} (uq^{-2})\ \check{R}_{[1,\ell +1]}^{(1,\ell )}(u) \ S_{[\ell +1,k+\ell ]} \end{aligned}$$

(29)

where the index of $\check{R}_{[2,k+\ell ]}^{(k-1,\ell )}(u)$ indicates that we use the embedding of $H_{k+\ell -1}(q)$ into $H_{k+\ell }(q)$ given by $\sigma _i \mapsto \sigma _{i+1}$, while the index of $\check{R}_{[1,\ell +1]}^{(1,\ell )}(u)$ indicates that we use the embedding of $H_{\ell +1}(q)$ into $H_{k+\ell }(q)$ given by $\sigma _i \mapsto \sigma _{i}$.

We use Relation (21) for $\check{R}^{(k-1,\ell )}(u)$ and the previous result for $\check{R}^{(1,\ell )}(u)$ to get

$$\begin{aligned} \check{R}^{(k,\ell )}(u) = S_{[1,k]} \ \sum _{p=0}^{k-1} a_p^{(k-1,\ell )}(uq^{-2}) \Sigma _{[2,k+\ell ]}^{(k-1,\ell ;p)} \ \Big (\sigma _1\ldots \sigma _\ell +a_0^{(1,\ell )}(u)\Big ) S_{[1,\ell ]} S_{[\ell +1,k+\ell ]}\ . \end{aligned}$$

(30)

Let $p\in \{0,\ldots ,k-1\}$. We replace $\Sigma _{[2,k+\ell ]}^{(k-1,\ell ;p)}$ using its definition. First, we have:

$$\begin{aligned}&S_{[1,k]} \Sigma _{[2,k+\ell ]}^{(k-1,\ell ;p)}\sigma _1 \ldots \sigma _\ell S_{[1,\ell ]} S_{[\ell +1,k+\ell ]} \nonumber \\&\quad =S_{[1,k]}S_{[k+1,k+\ell ]} (\sigma _k \ldots \sigma _{\ell +p}) \ldots ( \sigma _{k-p+1} \ldots \sigma _{\ell +1}) S_{[2,\ell +1]} \sigma _1 \ldots \sigma _\ell S_{[1,\ell ]} S_{[\ell +1,k+\ell ]}\nonumber \\&\quad =S_{[1,k]}S_{[k+1,k+\ell ]} (\sigma _k \ldots \sigma _{\ell +p}) \ldots ( \sigma _{k-p+1} \ldots \sigma _{\ell +1}) (\sigma _1\ldots \sigma _\ell ) S_{[1,\ell ]} S_{[\ell +1,k+\ell ]}\nonumber \\&\quad =q^{k-p-1} \Sigma ^{(k,\ell ;p+1)}\ . \end{aligned}$$

(31)

In the second equality, we use $S_{[2,\ell +1]} \sigma _1\ldots \sigma _\ell =\sigma _1\ldots \sigma _\ell S_{[1,\ell ]}$ (this is (20) when $u\rightarrow \infty$); in the last, we notice that $\sigma _1,\ldots ,\sigma _{k-p-1}$ in the last parenthesis commute with all elements on their left, and give a factor q when multiplied to $S_{[1,k]}$ (this also works for $p=0$ since there is nothing on their left then except $S_{[1,k]}S_{[k+1,k+\ell ]}$).

Second, we have, using (15) for $S_{[2,\ell +1]}$ and $S_{[2,\ell ]}S_{[1,\ell ]}=S_{[1,\ell ]}$,

$$\begin{aligned}&S_{[1,k]} \Sigma _{[2,k+\ell ]}^{(k-1,\ell ;p)}S_{[1,\ell ]} S_{[\ell +1,k+\ell ]}\nonumber \\&\quad =S_{[1,k]}S_{[k+1,k+\ell ]} (\sigma _k \ldots \sigma _{\ell +p}) \ldots ( \sigma _{k-p+1} \ldots \sigma _{\ell +1}) S_{[2,\ell +1]} S_{[1,\ell ]} S_{[\ell +1,k+\ell ]}\nonumber \\&\quad =\frac{1}{[\ell ]_q} \sum _{a=2}^{\ell +1}q^{2-a} S_{[1,k]}S_{[k+1,k+\ell ]}\nonumber \\&\qquad \underbrace{(\sigma _k \ldots \sigma _{\ell +p}) \ldots ( \sigma _{k-p+1} \ldots \sigma _{\ell +1})}_{=:x} (\sigma _a\sigma _{a+1}\ldots \sigma _\ell ) S_{[1,\ell ]} S_{[\ell +1,k+\ell ]} . \end{aligned}$$

(32)

One checks that x commutes with $\sigma _2,\ldots ,\sigma _{k-p-1}$, while $x\sigma _b=\sigma _{b+p}x$ if $b>k-p$. Thus, we have

$$\begin{aligned} S_{[1,k]}S_{[k+1,\ell +k]}\,x\sigma _b\ =\ q\,S_{[1,k]}S_{[k+1,\ell +k]} \,x\ \ \ \ \ \ \text {for any}\ n\ne k-p. \end{aligned}$$

Moreover, moving the rightmost element in each parenthesised factor of x and multiplying it to $S_{[\ell +1,k+\ell ]}$, one finds that

$$\begin{aligned} x\,S_{[\ell +1,k+\ell ]}=q^p(\sigma _k \ldots \sigma _{\ell +p-1}) \ldots ( \sigma _{k-p+1} \ldots \sigma _{\ell })\,S_{[\ell +1,k+\ell ]}\ . \end{aligned}$$

So the element whose calculation was started in (32) is equal to

$$\begin{aligned}= & {} \frac{1}{[\ell ]_q} \sum _{a=2}^{k-p}q^{k-p+2-2a} S_{[1,k]}S_{[k+1,k+\ell ]} (\sigma _k \ldots \sigma _{\ell +p}) \ldots (\sigma _{k-p+1} \ldots \nonumber \\&\sigma _{\ell +1}) (\sigma _{k-p}\sigma _{k-p+1}\ldots \sigma _\ell ) S_{[1,\ell ]} S_{[\ell +1,k+\ell ]}\nonumber \\&+\frac{1}{[\ell ]_q} \sum _{a=k-p+1}^{\ell +1}q^{\ell +p+3-2a} S_{[1,k]}S_{[k+1,k+\ell ]} (\sigma _k \ldots \sigma _{\ell +p-1}) \ldots \nonumber \\&(\sigma _{k-p+1} \ldots \sigma _{\ell }) S_{[1,\ell ]} S_{[\ell +1,k+\ell ]}\nonumber \\= & {} \frac{[k-p-1]_q}{[\ell ]_q} \Sigma ^{(k,\ell ;p+1)} +q^{2p-k+1} \frac{[\ell +p-k+1]_q}{[\ell ]_q} \Sigma ^{(k,\ell ;p)}\ . \end{aligned}$$

(33)

A straightforward verification shows that

$$\begin{aligned}&q^{-k+1}\frac{[\ell -k+1]_q}{[\ell ]_q} a_0^{(k-1,\ell )} (uq^{-2})a_0^{(1,\ell )}(u)=a_0^{(k,\ell )}(u)\,, \end{aligned}$$

(34)

$$\begin{aligned}&a_{p-1}^{(k-1,\ell )}(uq^{-2})\left( q^{k-p}+\frac{[k-p]_q}{[\ell ]_q} a_0^{(1,\ell )}(u)\right) \nonumber \\&\quad +a_{p}^{(k-1,\ell )}(uq^{-2})q^{2p-k+1} \frac{[\ell +p-k+1]_q}{[\ell ]_q}a_0^{(1,\ell )}(u)=a_p^{(k,\ell )}(u)\,, \end{aligned}$$

(35)

$$\begin{aligned}&a_{k-1}^{(k-1,\ell )}(uq^2)=a_{k}^{(k,\ell )}(u)\ . \end{aligned}$$

(36)

So we have proved that Relation (21) is also valid for k and $\ell$, which proves the lemma by induction. $\square$

1.4 Braided Yang–Baxter equation

We are now in position to prove Theorem 3.1. By using Lemma A.2, we see that in $P^{(k)}H_{kn}(q)P^{(k)}$, one gets, for $i=1,\ldots n-1$,

$$\begin{aligned} \check{R}_i^{(k)}(u) = \check{R}^{(k,k)}_i(u) \end{aligned}$$

(37)

where the index i of $\check{R}^{(k,k)}_i(u)$ indicates that we use the embedding of $H_{2k}(q)$ into $H_{nk}(q)$ given by $\sigma _a \mapsto \sigma _{a+(i-1)k}$. Therefore, we can use the factorised form given by (19) for $\check{R}_i^{(k)}(u)$. Namely, one gets

$$\begin{aligned} \check{R}_i^{(k)}(u)&:= P^{(k)} \prod _{1\le a\le k}^{\longleftarrow } \check{R}_{a+(i-1)k}\left( uq^{2(1-a)}\right) \check{R}_{a+1+(i-1)k} \left( uq^{2(2-a)}\right) \ldots \nonumber \\&\quad \check{R}_{a+\ell -1+(i-1)k} \left( uq^{2(\ell -a)}\right) P^{(k)}\ , \end{aligned}$$

(38)

Relation (20) gives in this case that $\check{R}_i^{(k)}(u)$ commutes with the projector $P^{(k)}$ so that

$$\begin{aligned} \check{R}_i^{(k)}(u)&= P^{(k)} \prod _{1\le a\le k}^{\longleftarrow } \check{R}_{a+(i-1)k}\nonumber \\&\quad \left( uq^{2(a-1)}\right) \check{R}_{a+1+(i-1)k} \left( uq^{2(a-2)}\right) \ldots \check{R}_{a-1+ik}\left( uq^{2(a-k)}\right) \ . \end{aligned}$$

(39)

It is then a standard computation to show that $\check{R}_i^{(k)}(u)$ given by (39) satisfies the braided Yang–Baxter equation (see remark below). This concludes the proof of Theorem 3.1.

Remark A.3

We recall that in fact the elements $\check{R}^{(k,l)}(u)$ given in (19) satisfy a braided Yang–Baxter equation in general (we used this when $k=l$; for $k\ne l$ one can call it a mixed Yang–Baxter equation). Namely, for $k,l,m\ge 1$ and $n=k+l+m$, we have the following equality in $H_{n}(q)$:

$$\begin{aligned} \check{R}^{(k,l)}(u)\check{R}^{(k,m)}_{[l+1,n]}(uv)\check{R}^{(l,m)}(v) =\check{R}^{(l,m)}_{[k+1,n]}(v)\check{R}^{(k,m)}(uv)\check{R}^{(k,l)}_{[m+1,n]}(u)\ , \end{aligned}$$

where an index $[a+1,n]$ indicates that we use the embedding of $H_{n-a}(q)$ in $H_{n}(q)$ given by $\sigma _i\mapsto \sigma _{i+a}$. This is a standard and straightforward computation in the context of the fusion procedure (along the lines of some calculations detailed for example in [9]). One has to use repeatedly the braided Yang–Baxter equation satisfied by $\check{R}_i(u)$. The first step is to show that:

$$\begin{aligned} S_{[1,a]}\check{R}^{(a,b)}(u)=\check{R}^{(a,b)}(u)S_{[b+1,a+b]} \ \ \ \ \text {and}\ \ \ \ S_{[a+1,a+b]}\check{R}^{(a,b)}(u) =\check{R}^{(a,b)}(u)S_{[1,b]}\ . \end{aligned}$$

Using this, in order to check the braided Yang–Baxter equation in $H_n(q)$, one can first move all projectors on one side, and then it remains only to check the braided Yang–Baxter equation satisfied by the product without the projectors in (19).

Remark A.4

Taking into account the preceding remark, one can see Lemma A.2 as the generalisation of our Baxterisation formula to the mixed situation, namely for $\check{R}^{(k,l)}(u)$ for any k, l (the condition $k\le l$ is only for convenience, the situation is symmetric in k and l). This generalised Baxterisation formula lives in the Hecke algebra $H_{k+l}(q)$. More precisely, it lives in the subspace $E^{(k,l)}:=P^{(k,l)}H_{k+l}(q)P^{(l,k)}$ which is not a subalgebra if $k\ne l$. However, one has a natural bilinear “product”:

$$\begin{aligned} E^{(k,l)}\times E^{(l,k)}\rightarrow P^{(k,l)}H_{k+l}(q)P^{(k,l)}\ . \end{aligned}$$

The subspace $P^{(k,l)}H_{k+l}(q)P^{(k,l)}$ is now a subalgebra which is also a fused Hecke algebra as defined in [25]. If $l=1$ (and k arbitrary), it admits as a quotient a similar algebra where the Hecke algebra is replaced by the Temperley–Lieb algebra. This is called in the literature the seam algebra (see for example [29]) and thus one can see a particular case of (21) as a Baxterisation formula for the seam algebra.