Introduction

The majority of landscape genetic studies to date have focused on rare, threatened, or endangered species that either naturally exist in small, fragmented populations or have done so for an evolutionarily significant period of time (Storfer et al. 2010). The few genetic studies performed on widespread plant species have found common species experience similar or greater losses in genetic diversity as rare species when populations are dramatically reduced in size and connectivity (Honnay and Jacquemyn 2006; Aguilar et al. 2008). Furthermore, genetic diversity in common, dominant plant species can have important and cascading effects on species diversity and processes throughout the ecosystem (Whitham et al. 2003; Vellend and Geber 2005). Specifically, in monotypic landscapes, genetic diversity of the foundational plant species is analogous to the role of species diversity in maintaining ecological health and ecosystem processes (Reusch and Hughes 2006; Hughes et al. 2008). Such monotypic landscapes are typical in coastal ecosystems that tend to be dominated by single-species macrophyte communities, such as eelgrass (Zostera marina L.) in seagrass beds (Reusch and Hughes 2006). Genotypic diversity (number of unique genotypes) in Z. marina has been positively correlated to shoot density, which can have a cascading positive effect on faunal abundance and other ecosystem benefits (Hughes and Stachowicz 2004, 2009; Reusch et al. 2005; Ehlers et al. 2008). Similarly, Z. marina genetic diversity (heterozygosity of individuals) was positively correlated to shoot density, nutrient retention, faunal abundance, areal productivity (Reynolds et al. 2012), and sexual and vegetative reproduction (Williams 2001; Hammerli and Reusch 2003). Positive effects of genetic diversity are especially important following disturbances, such as transplantation stress during restoration (Reynolds et al. 2012) or a warming event (Reusch et al. 2005; Ehlers et al. 2008).

Foundational plant species in salt marshes are used in ecological restoration efforts to restore coastal ecosystems that are valuable to humans and wildlife, and have been in widespread decline for decades from urban development (Kennish 2001; Gedan et al. 2009). Salt marshes provide habitat to endemic and economically important species, and supply a range of ecosystem services valued at $10,000 per hectare that include storm protection, flood attenuation, and carbon sequestration (Kennish 2001; Zedler and Kercher 2005; Kirwan and Megonigal 2013). The Gulf of Mexico coastline contains 58% of the remaining salt marsh in the United States, a total of 5480 square miles of marsh across five states (Chabreck 1988). Gulf coast salt marshes ameliorate eutrophication and have a marked effect on water quality, limiting the hypoxic effects of nutrient rich runoff from the Mississippi River (Zedler and Kercher 2005). The irregularly flooded marshes along the coasts of Mississippi, Alabama, and western Florida are dominated by the mid-marsh species black needlerush (Juncus roemerianus Scheele) (Eleuterius 1976; Stout 1984), a target species for restoration in the area (Sparks et al. 2013).

J. roemerianus is a clonal, gynodioecious macrophyte and a foundational species in salt marshes distributed from the western Gulf of Mexico in eastern Texas to the mid-Atlantic in Maryland (Eleuterius 1976; Godfrey and Wooten 1979; Stout 1984). The species plays a crucial role in the salt marsh, accreting and stabilizing sediment to create and maintain marsh habitat for other species (Pennings and Bertness 2001). Although J. roemerianus can reproduce both clonally and sexually (Eleuterius 1974, 1984), existing life history literature suggests sexual reproduction is used only in colonization of new areas, and that seedling-mediated gene flow is rare. As a result, established populations of J. roemerianus are assumed to be comprised of only a few unique genotypes (Eleuterius 1975; Stout 1984); however to our knowledge no genetic studies have been conducted to confirm these assumptions.

Gene flow among populations of J. roemerianus is achieved asexually through division and transport of vegetative ramets during storm events (USDA, NRCS 2017), and sexually through seed and pollen dispersal, of which little is known. Successful gene flow in wetland plants is dependent on both seed transport, generally via wind, water, or animals, usually birds, and establishment in habitat suitable for germination (Cronk and Fennessy 2001). While propagule dispersal mechanisms are unknown in J. roemerianus, the morphologically similar seeds of the related species, common rush (Juncus effusus L.) are dispersed by all three vectors (Neff and Baldwin 2005; Soons et al. 2008; USDA, NRCS 2017). The small size (0.6 mm) (USDA, NRCS 2017) of J. roemerianus seeds may allow for wind dispersal, (Cronk and Fennessy 2001; Neff and Baldwin 2005) or dispersal on the bodies (Cronk and Fennessy 2001), or in the excrement (Soons et al. 2008) of birds. J. roemerianus seeds can germinate when floating or submerged in water and are highly viable up to 1 year (Eleuterius 1975), potentially allowing for long distance oceanic dispersal. Across the coast, wetland habitat would facilitate seed mediated gene flow by permitting passage of wind and birds and providing suitable habitat for germination of seedlings. Areas of open ocean could facilitate long distance dispersal of seeds via tidal currents (Neff and Baldwin 2005). Conversely, developed land and forest cover would limit suitable habitat for germination, and may act as a barrier to wind or bird mediated dispersal (Delaney 2014). Pine plantations along the Gulf coast could mean both developed land and forest cover are anthropogenic barriers to gene flow. In fragmented populations such as J. roemerianus, the introduction of new genetic variants by gene flow to maintain genetic and genotypic diversity (Slatkin 1987; Hedrick 1996) is dependent on population connectivity.

Landscape genetic techniques can be used to examine the influence of landscape factors on population connectivity by associating measures of gene flow to spatial data with the potential to guide management to maintain or enhance genetic diversity in fragmented populations (Manel et al. 2003; Storfer et al. 2007; Manel and Holderegger 2013; Hall and Beissinger 2014; Keller et al. 2015). Linear regression models have emerged as an effective way to link genetic and spatial data in landscape genetics (Wagner and Fortin 2013). Gene flow among local populations (demes) or sample sites, measured indirectly using genetic distance, acts as the response variable, and landscape structure, quantified using either landscape resistance surfaces or transects, acts as the explanatory variable (van Strien et al. 2012; Hall and Beissinger 2014). Resistance surfaces are a grid representation of the landscape in which each grid cell is assigned a value symbolic of the predicted permeability of the environment within the cell (Spear et al. 2010; Zeller et al. 2012). One or more least cost paths (LCPs) among demes or sample sites are used to predict organism dispersal through the resistance surface, with either the total cost or length of the LCP used as spatial data in landscape genetic analyses (Spear et al. 2010; van Strien et al. 2012; Hall and Beissinger 2014). Transect analyses quantify landscape structure by measuring landscape composition along a straight line between demes or sites, usually by calculating the abundance of landscape features of interest (van Strien et al. 2012; Hall and Beissinger 2014). A least-cost transect analysis (LCTA) as described by van Strien et al. (2012) combines the two methods to generate LCPs along which landscape composition is quantified, so that the length of the LCP and abundance of one or more landscape features along the LCP are used as explanatory variables in a set of candidate linear models. Model selection is used to determine both potential dispersal corridors and identify landscape features that inhibit or facilitate gene flow (van Strien et al. 2012). The method could be particularly suited for understudied species lacking dispersal information, or species that are not terrestrially dispersed, such as J. roemerianus.

We examined patterns of genetic diversity and population connectivity of J. roemerianus across irregularly flooded salt marshes in the northeastern Gulf of Mexico using LCTA and model selection to address knowledge gaps and inform coastal management. We tested the hypotheses that (1) populations of J. roemerianus have low genetic diversity and are dominated by few clonal variants, (2) rare sexual reproduction leads to high population differentiation, and (3) wetland, open ocean, developed land, and forest cover will influence population connectivity. Contrary to life history literature, we predicted J. roemerianus would have greater genotypic and genetic diversity than expected of a predominantly clonal species as has been found for other clonal plant species (Ellstrand and Roose 1987; Gabrielsen and Brochmann 1998; Pluess and Stocklin 2004; Silvertown 2008; Lloyd et al. 2011); and structure into large genetic populations, indicating sexual reproduction plays a greater role in species’ life history. Wetland and open ocean were hypothesized to positively influence population connectivity and facilitate gene flow, while developed land and forest cover were predicted to impede gene flow in J. roemerianus. Results will provide information on genetic diversity and population connectivity that conservationists and managers could use to successfully and adequately preserve resiliency and evolutionary potential in this important salt marsh plant species.

Methods

Field collection

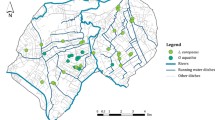
Twelve areas were selected for sample collection across the range in which Juncus roemerianus is dominant in the northeastern Gulf of Mexico. A single leaf of J. roemerianus was collected and deposited in a plastic bag, and a GPS waypoint was taken using a Garmin GPSMAP 64st at each sample point. Collection areas at the eastern (Moss Point, MS) and western (Apalachicola, FL) extent of the study area are National Estuarine Research Reserves (NERR). NERRS are established through the Coastal Zone Management Act and maintained by the National Oceanic and Atmospheric Association (NOAA) to study and protect estuarine systems. As part of an intensive case study, a total of 304 samples were collected from the Grand Bay NERR, MS in January and March 2015, and 32 samples were collected from the Apalachicola NERR, FL in May 2015 and March 2016 as part of the marker development study (Tumas et al. 2017). Thirty samples were collected from an additional ten collection areas between the two NERRs in March 2016 (Table 1; Fig. 1). Collection areas were selected based on the “Tidal Marsh” category of NOAA’s Coastal Change Analysis Program land cover atlas, using satellite imagery in Google Earth to verify J. roemerianus presence at each point. A uniform distance between collection areas was not possible due to the irregular distribution of tidal marsh along the coastline, causing distance among collection areas to vary. Distance among collection areas ranged from 22.5–353 km with an average distance of 158 km.

Table 1 Approximate geographic location and sample size of the 12 sample sites, and genotypic and genetic diversity results across the ten sample sites with Juncus roemerianus samples (Note Samples from sites CS2 and CS4 were of the related species Juncus effusus.)
Full size table
Fig. 1
figure 1

Ten Juncus roemerianus collection sites across the northeastern Gulf of Mexico from the Grand Bay NERR (GB) in eastern Mississippi to the Apalachicola NERR (AP) in northwest Florida. The orange rectangle in the geographic inset represents the study area extent. One site (CS8) was only used in genetic diversity analyses (triangle), nine sites were used in genetic diversity and landscape genetic analyses (circles), and two sites were later determined to be the morphologically similar species Juncus effusus (black circle with X). (Color figure online)

Full size image

Microsatellite amplification

Samples were genotyped using a panel of 19 polymorphic microsatellite markers, previously developed for J. roemerianus population studies (Tumas et al. 2017). DNA extractions, PCR reaction conditions, and thermal cycling parameters were as described in Tumas et al. (2017). Each sample was genotyped across a minimum of 15 loci or were re-genotyped. If more than four loci failed after re-genotyping for a sample, DNA was re-extracted and genotyped again. Eighteen percent of the samples were randomly selected and re-genotyped to test for genotyping error rate, calculated by dividing the number of mismatch genotypes by the total number of genotypes scored.

Genetic analyses

Samples were assigned to clonal genets by grouping samples with identical genotypes using ID Analysis in CERVUS (Kalinowski et al. 2007). Genotypic diversity (GD) was calculated for each site as (G − 1)/(N − 1), where G is the number of unique genotypes or clonal genets, and N is the total number of samples (Arnaud-Haond et al. 2007). A single sample was randomly selected from each clonal genet, and all other genetically identical samples were removed for all subsequent genetic analyses. Hardy–Weinberg equilibrium was tested at each locus for each study site using CERVUS, and GENEPOP (Raymond and Rousset 1995) was used to calculate linkage disequilibrium within sites. Observed heterozygosity (HO), expected heterozygosity (HE), and allelic diversity (AD) were measured for each study site using Arlequin (Excoffier and Lischer 2010). Allelic richness (AR) standardized to the smallest sample size through rarefaction was calculated using the divBasic function in the ‘diveRsity’ package in R (Keenan et al. 2013; R Core Team 2016).

Pairwise genetic distance was measured as Cavalli-Sforza chord distance (Dch) (Cavalli-Sforza and Edwards 1967) using Microsatellite Analyzer (Dieringer and Schlotterer 2003), and as Slatkin’s linearized FST calculated in Arlequin. Dch and FST were recalculated three times with three different random subsets of 30 individuals from Grand Bay NERR to account for the effect of sample size. Pearson’s correlation calculated in R was used to test for correlation between multiple estimates of genetic distance, including Dch, FST, Reynold’s FST, Nei’s genetic distance, and proportion of shared alleles that were calculated using ‘hierfstat’ in R (Goudet and Jombart 2015), Arlequin, and Microsatellite Analyzer. Isolation by distance (IBD) was examined following Rousset (1997) by fitting a regression line to FST/(1 − FST) plotted against log transformed geographic distances. Estimates of FST for the IBD analysis were calculated according to Weir and Cockerham (1984).

Population structuring was delineated using the program STRUCTURE, running 20 times for 50,000 steps after a burn-in period of 5000 steps for each of K = 1–6 (Pritchard et al. 2000). Eight sets of STRUCTURE runs were conducted with these parameters to test the effect of using admixture or no admixture models, setting populations with or without prior locations, and correlated or uncorrelated allele frequencies. Hierarchical structure within clusters was identified by performing STRUCTURE analyses on delineated genetic clusters using the above parameters. Population structure results were recalculated with a random subset of 30 individuals from the larger pool of samples collected at the Grand Bay NERR study site. The best number of genetic clusters (K) was chosen using the Evanno method in STRUCTURE HARVESTER (Earl and vonHoldt 2012). Population differentiation was also measured using a global FST derived from an AMOVA in Arlequin (Weir and Cockerham 1984).

Spatial data

Sites were defined as the centroid of all sample points within a given collection area, and were calculated by placing a minimum convex polygon around the GPS waypoint locations of the sampling points within each collection area and converting polygons to points in ArcGIS v10.4.1. Areas of the minimum convex polygons ranged from 7.85 × 10−4 to 45 km2, which was considered a small enough scale relative to the total area encompassing all sample points (15,107 km2) to be representative of the average landscape conditions of samples at each collection area. Land cover data was derived from the NOAA’s coastal change analysis program (C-CAP) land cover atlas for Mississippi, Alabama, and Florida (Coastal change analysis program (C-CAP) 2015/2016 Regional Land Cover Data—Contiguous United States, Department of Commerce, NOAA, National Ocean Service, Office for Coastal Management). Spatial layers for the three states were combined and converted to Universal Transverse Mercator (UTM) in datum D_North_American_1983 in ArcGIS. C-CAP land cover categories were grouped to create the four land cover variables (wetland, open ocean, developed land, and forest cover) hypothesized to effect J. roemerianus gene flow. Wetland was defined as categories of estuarine or palustrine emergent or scrub/shrub wetland. Open ocean was defined as water and background categories. Forest cover included deciduous, evergreen, and mixed forest; and developed land included developed low (21–49% constructed materials), medium (50–79% constructed materials), and high (80–100% constructed materials) intensity and developed open space (< 20% constructed materials) (Table S1).

Transect generation

Four sets of transects were created for LCTA, and two additional sets of transects were generated to reflect potential J. roemerianus dispersal pathways (Fig. 2). Basic, straight line transects (Euclidean) were created in ArcGIS by converting all pairs of points to lines to reflect an isolation by distance pattern with no landscape influence. Coastal transects (Digitized coastal) encompass potential routes of wind, waterfowl, or water mediated dispersal, and were created by digitizing the coastline in the C-CAP land cover layers at approximately a 1:60,000 scale. Transects for LCTA (LCTA: Wetland, LCTA: Ocean, LCTA: Developed, and LCTA: Forest) were created using the Cost Path package in ArcGIS. Cost layers were created for each landscape factor by assigning the category of interest a value of one, and all other categories a value of 100. To minimize computational demand, wetland, developed land, and forest cover layers were clipped to a 60 km buffer around the site layer, and open ocean was clipped to a 20 km buffer around the site layer. Four binary raster layers were created, one for each land cover category of interest (wetland, open ocean, developed land, and forest cover), by reclassifying the land cover dataset into 1/0 raster datasets where 1 = category of interest and 0 = everything else. The ‘raster’ and ‘rgdal’ packages in program R were used to buffer all transects by 500 m, 1, and 2 km, and extract the proportion of each land cover type across binary rasters using the mean statistic in the extract function (Hijmans 2016; Bivand et al. 2017).

Fig. 2
figure 2

Six different transect types (lines) connecting the nine sites (circles) used to measure landscape variables and distances between sites in landscape genetic analyses: a Euclidean, b digitized coastal, c LCTA: developed, d LCTA: forest, e LCTA: ocean, and f LCTA: wetland connecting pairs of study sites (red circles). (Color figure online)

Full size image

Statistical analysis

An information theoretic approach to model selection (Burnham and Anderson 2002) was applied to linear mixed effects models within a hierarchical modeling framework to examine the relationship between landscape variables and genetic distance. Due to the lack of independence in pairwise distance matrices, maximum likelihood population effects (MLPE) models were used (Clarke et al. 2002; van Strien et al. 2012). Fixed effects included the landscape variables, transect length, and the Euclidean distances between points. Pairwise genetic distances, measured as both Dch and FST, served as response variables. A random effect term was applied to each population pair to account for the dependency between pairwise distances as a result of two distances with a common node or site (van Strien et al. 2012). MLPE models were run in the R-package ‘lme4’ (Bates et al. 2015) using code developed by van Strien et al. (2012) and Helene Wagner, and adapted by Caren Goldberg.

Six candidate models relating landscape and distance variables to genetic distance were ranked using Akaike’s information criterion with second-order bias correction (AICc) (Burnham and Anderson 2002). Response variables and explanatory variables in these models were standardized around their mean to meet normality assumptions. Candidate models consisted of a full model including the four land cover variables and Euclidean distance, five land cover models, and one Euclidean distance model that acted as the null model of isolation by distance (Table 3). The five land cover models comprised a model with all four land cover variables, a model of naturally occurring land cover variables (wetland and open ocean), a model of potentially anthropogenic factors (developed land and forest cover), a model of wetland cover, and a model of developed land cover. Euclidean distance was a covariate in all models to test if land cover variables accounted for more variation in genetic distances than geographic distance alone. A separate set of four candidate models were run using the transect length of each transect type as the only explanatory variable (Table 4). The two candidate model sets were run twice using the full sample set, once for each response variable (Dch and FST). Models sets were rerun using pairwise genetic distances recalculated for three different subsets of 30 samples from the Grand Bay NERR.

Model selection across the six landscape candidate models was conducted hierarchically across buffer widths and transect types for each land cover variable under the assumption that univariate relationships would not significantly change in a multivariate framework. First, the best buffer width for each transect type was selected for each land cover variable by running single-variable models across buffer widths within transect types. Then, the best transect type for each variable was selected by running single-variable models across transect types, using the best buffer width from the prior analysis. Selection of best buffer width and transect type was made using AICc. Candidate models were then constructed using variables at the best buffer width and transect type. Signs of slope coefficients in the highest ranked candidate models were used to make inferences about the influence of landscape factors on genetic distance. Variance inflation factors between explanatory variables calculated in the R-package ‘usdm’ were used to assess multicollinearity, with a maximum factor value of 7 allowed between variables (Naimi 2015).

Results

Genetic diversity and structure

A total of 576 samples were genotyped across sites, and 310 samples represented unique genotypes that were used in all subsequent genetic diversity analyses. Samples from two of the twelve study sites (CS2 & CS4) were determined to be the closely related species Juncus effusus upon inspection in the lab, and were removed from all analyses. Genotyping error rate was 2.35%. Following a sequential Bonferroni correction, all except four loci (Jr3 & Jr86 in GB, Jr86 in CS5, and Jr33 in CS10) showed no evidence of deviation from Hardy–Weinberg equilibrium within all populations, and all except four pairs of loci (Jr13 & Jr58, Jr12 & Jr72 in GB; Jr29 & Jr33, Jr01 & Jr80 in CS10) did not exhibit linkage disequilibrium in any populations, so no loci were excluded from analysis. Genetic diversity indices and genotypic diversity were similar across the ten study sites (Table 1). Genotypic diversity averaged 0.54 across sites, and unique genotypes comprised approximately half of the samples from each site, except for sites CS3, CS7, CS8, and CS10. Sites CS3, CS7, and CS10 had more unique genotypes than other sites, while CS8 was dominated by only three clonal genets. Genetic diversity was moderate across sites, with an average allelic richness of 2.42 alleles per locus, an average expected heterozygosity of 0.57, and an average observed heterozygosity of 0.58 (Table 1). The optimal number of genetic clusters across STRUCTURE runs was K = 2, regardless of admixture, prior population location, or correlated allele frequency settings, and did not change when using a random subset of 30 samples from Grand Bay NERR. Sites clustered into a large western cluster, and a smaller eastern cluster with the division occurring between CS7 and CS8. Additional STRUCTURE analysis on the two clusters revealed a further sub-structuring in the larger western cluster into two genetic clusters, with a division between sites CS5 and CS6, and no further sub-structure in the eastern cluster (Fig. 3).

Fig. 3
figure 3

Structure plot for k = 2 across the ten sites (top) and k = 2 for the large western cluster (bottom). Probability of a sample being assigned to each cluster is on the y-axis, and samples grouped by site are on the x-axis. Clusters are delineated by color, and solid black lines represent site boundaries

Full size image

The global FST of 0.165 calculated across the ten sites using an AMOVA was significant (p < 0.001). Due to the low number of unique genotypes, CS8 was removed from pairwise genetic distance calculations, and all subsequent analyses on landscape influence. Across the remaining nine sites, all pairwise Slatkin’s linearized FST values were significant (Table S2). Genetic distance metrics calculated across the nine sites, including Dch, FST, Reynold’s FST, Nei’s genetic distance, and proportion of shared alleles, were highly correlated with a minimum Pearson’s correlation of 0.82. The plot of genetic distances against geographic distances showed a pattern of IBD and the fitted regression line had a slope of 0.2 (Fig. S1, Table 2).

Table 2 Landscape variables and information theoretic results (AICC and ΔAIC) for MLPE models using genetic distance metrics (Dch and FST) as the response variable
Full size table

Landscape variables correlated to genetic distance

Proportion developed land and Euclidean distance comprised the top model for both response variables (Dch and FST) (Table 2). However, the highest ranked transect type and buffer width for developed land (Table 3), and direction of the relationship between developed land and genetic distance differed between response variables (Table 2). When using Dch, proportion developed land was measured across digitized coastal transects buffered by 500 m and had a positive relationship with Dch in the top model. In the top model for FST, proportion developed land was measured across LCTA: Forest transects buffered by 2 km and had a negative relationship with FST. Although the direction of the relationship with proportion developed land differed between the response variables in the top model, the relationship was preserved in general based on the transect type used to measure proportion developed land. Proportion developed land had a negative relationship with Dch in a model with proportion developed land measured across LCTA: Forest transects buffered by 2 km and Euclidean distance as explanatory variables. Similarly, proportion developed land had a positive relationship with FST in a model with proportion developed land measured across digitized coastal transects buffered by 500 m and Euclidean distance as explanatory variables. Euclidean distance had a positive relationship with both measures of genetic distance across models (Table S3).

Table 3 Highest ranked transect type and buffer width for each landscape variable determined hierarchically that were used to measure each landscape variable in candidate models
Full size table

Proportion developed land was also an explanatory variable in the second and third ranked models when using both response variables. However, as in the top model, proportion developed land had a positive relationship with Dch, and a negative relationship with FST in all models in which it was an explanatory variable. Proportion forest cover measured across LCTA: Forest transects buffered by 1 km was a covariate with proportion developed land and Euclidean distance in the second ranked model and had a positive relationship for both response variables. Proportion wetland measured across LCTA: Forest transects buffered by 500 m was a covariate with proportion developed land and Euclidean distance in the third ranked model for both response variables and had a negative relationship with Dch and FST. Proportion open ocean was in the fourth and sixth models when using Dch and FST, respectively. When using Dch, proportion open ocean had a positive relationship in all models in which it was an explanatory variable, while the direction of the relationship changed between models when using FST (Table 2).

The top transect length model differed between the genetic distance measures, with digitized coastal transect length ranked highest for Dch, and LCTA: Ocean ranked highest for FST (Table 4). All transect lengths had a positive relationship to genetic distance for both metrics in the set of models examining the top ranked transect length. Top landscape and transect length candidate models, and the relationship with developed land were conserved across three different subsets of thirty samples from Grand Bay NERR (Table S4).

Table 4 Lengths of transect types and information theoretic results (AICC ΔAIC) for MLPE models using genetic distance metrics (Dch and FST) as response variables
Full size table

Discussion

Genetic diversity and structure

Measures of genetic diversity were moderate across sample sites, and unique genotypes comprised approximately half of the samples at each site on average. The only site with far fewer unique genotypes was CS8, which was most likely due to the location and area of the site. Samples from CS8 were collected around a residential dock in a highly developed region in West Bay, FL, and comprised a much smaller area than other study sites. Results aligned with our hypotheses and the greater body of clonal plant literature, but contradicted current J. roemerianus life history literature. Despite a priori expectations of investigators, most clonal plant species have been found to have intermediate levels of genotypic diversity, and to rarely produce geographically widespread clones (Ellstrand and Roose 1987; Silvertown 2008). Genetic analyses on other clonal plants have also contradicted assumptions of low genetic diversity and rare sexual reproduction (Gabrielsen and Brochmann 1998; Pluess and Stocklin 2004; Lloyd et al. 2011) including a study on the co-occurring salt marsh plant smooth cordgrass (Spartina alterniflora Loisel) (Richards et al. 2004). Only 6% of S. alterniflora samples in a study conducted on Sapelo Island, GA were clonal replicates, when populations of the species were previously assumed to be dominated by a small number of unique genotypes. Similarly, we found a greater number of unique genotypes at each study site than expected from current J. roemerianus life history literature, which assumes that the species is predominantly clonal with limited sexual reproduction (Eleuterius 1975). Only one clone, represented by samples identical at 18 markers, was shared between two sites (CS3 and CS5) that are approximately 89 km apart. All other clonal variants in the study were restricted to a single study site, indicating that, like other clonal plant species, J. roemerianus populations are composed of many unique genotypes that are not geographically widespread.

As hypothesized, J. roemerianus population structure occurred on a large scale with samples structured into two genetic clusters across the study range. We found no apparent explanation for the division between populations, as there was not an obvious landscape barrier at that location. The genetic division may instead reflect a cline of decreased genetic similarity between samples that are geographically distant. The observed genetic structure could be a result of a number of factors, including historical events, biological traits, or environmental or landscape factors not examined within the study. The large scale of genetic structure demonstrates J. roemerianus exists within two large, admixed populations, possibly indicating a high degree of intrapopulation dispersal. Long distance dispersal is believed to be rare in plants, following a leptokurtic curve with seed density declining precipitously with distance (Willson and Traveset 2000). However, genetic studies on wind-dispersed trees found higher pollen dispersal distances than expected based on the leptokurtic curve, suggesting gene flow was high enough to create effectively panmictic populations over large scales in which even isolated fragments may be connected (Ashley 2010). Oceanic (Huiskes et al. 1995) and bird mediated (Soons et al. 2008) dispersal could also allow for more frequent long distance dispersal. If more frequent long distance dispersal is causing observed structure, a higher rate of sexual reproduction would also be necessary for gene flow between habitat fragments. Conversely, the genetic structure could also reflect historic genetic patterns, possibly from a time when J. roemerianus habitat was more continuously distributed across the Gulf coast.

More localized hierarchical genetic structure in J. roemerianus was demonstrated in the sub-structuring of the large western cluster and the significant pairwise FST values among study sites. Micro differentiation between local populations is expected in plants species, resulting from local selection pressures and geographically restricted gene flow (Willson and Traveset 2000). Whereas J. roemerianus forms genetic populations that meet Hardy–Weinberg Equilibrium assumptions on a large scale, one or more evolutionary mechanisms could be creating fine scale genetic differentiation among sites. Diversifying selection is believed to generate genetic variation within clonal plants (Ellstrand and Roose 1987), and could be occurring at the scale of the study site due to variations in salinity, flooding frequency, and other environmental variables. Although our use of neutral markers limits any implications our results have for local adaptation, adaptation on such a fine scale in J. roemerianus would have important implications for conservation and restoration. Alternatively, the reduction in size of many J. roemerianus populations due to fragmentation could mean that site differentiation is driven by genetic drift at some or all of the sample sites. The rate of genetic drift is inversely proportional to population size, and can result in neutral alleles becoming randomly fixed in small populations, decreasing genetic diversity (Gillespie 2004). Even low levels of gene flow, estimated at one migrant per generation, can prevent allele fixation from genetic drift (Slatkin 1987; Young et al. 1996), highlighting the importance of population connectivity for maintaining genetic variation. Regardless of the cause of currently observed differentiation, continued fragmentation across coastal ecosystems in the Gulf of Mexico will likely have consequences for the evolutionary mechanisms driving genetic patterns in J. roemerianus, especially if population connectivity is not preserved.

Landscape factors on population connectivity

Results from the model selection were somewhat congruent with our hypotheses in that proportion developed land played an important role in population connectivity. Although, the relationship between proportion developed land and population connectivity in the top model differed when using Dch or FST as the response variable depending on the transect type used to measure developed land. Differences between the metrics may indicate our models are not robust, and that small changes in model structure results in changes in model rank and direction of relationships. However, while the majority of landscape genetics studies and other studies using LCTA (van Strien et al. 2012; Cleary et al. 2017) have examined only a single genetic distance metric, a study that examined multiple metrics also showed varying results depending on the metric selected (Goldberg and Waits 2010). Instead, difference in direction of the relationship across transects could mean landscape factors influence J. roemerianus dispersal differently depending on the surrounding landscape composition, either due to the true dispersal biology of the species or an artificial effect driven by differences in landcover variation. Other studies have demonstrated landscape genetic results can vary for a single species across different landscapes within the species’ range, either due to biological reasons (Trumbo et al. 2013), or degree of variation of land cover variables in the study landscape (Bull et al. 2011). However, greater variation in a land cover variable usually caused models containing the variable to be ranked higher, whereas in our models LCTA: Forest transects with little developed land were ranked highest. Differences in top ranked models between the genetic distance metrics may then be due to the difference in the attributes and assumptions of the genetic distance metrics themselves rather than biological or landscape factors. F statistics are measured using ratios of genetic variance within and among populations, and are based upon the island model, which assumes an infinite number of populations with the same number of individuals that give and receive the same number of migrants without regard to geographic structure (Whitlock and McCauley 1999). Conversely, Dch is a geometric distance that does not have assumptions about population size or geographic configuration, but assumes differences in allele frequencies arise from genetic drift (Cavalli-Sforza and Edwards 1967). The underlying assumptions associated with FST may make the metric less suited to multiple variable analyses than Dch, and Dch has been shown to be one of the best metrics for denoting relationships among samples (Takezaki and Nei 1996). So while FST is still the most widely used genetic distance metric in landscape genetics (Storfer et al. 2010) and can be important for comparison purposes across studies, we will make inferences about population connectivity in J. roemerianus based on results achieved when using Dch as a response variable.

Based on results from the model selection using Dch as the response variable, the most important factors influencing J. roemerianus population connectivity is proportion developed land within a 500 m buffer across digitized coastal transects and Euclidean distance. The positive relationship between Euclidean distance and genetic distance is in line with the biology of the species and other plant studies (Fievet et al. 2007; Trenel et al. 2008; Pollegioni et al. 2014). The negative impact of developed land on J. roemerianus population connectivity could be caused by inhibited seed and pollen dispersal, increased fragmentation and interpopulation distance, decreased suitable habitat for germination, or a combination of the three factors. Similar results have been found demonstrating the negative influence of human development on dispersal and species persistence in other wind-dispersed plant species, especially with increasing fragmentation in urban settings (Soons and Heil 2002; Soons et al. 2004; Williams et al. 2005). Similarly, cities can act as barriers to dispersal for urbanization-sensitive species of bird (Delaney 2014). Increasing fragmentation by human development would also increase distance among J. roemerianus populations, causing a decline in gene flow. Human development that directly reduces salt marsh area also decreases suitable habitat for germination for J. roemerianus, increasing the possibility of seeds establishing in unsuitable areas and decreasing probability of successful gene flow. Plant species have even been found to lose dispersal related traits over time with increasing habitat fragmentation (Riba et al. 2009), due to the adaptive disadvantage of dispersing into unsuitable habitat (Travis et al. 2010). Coastal areas where salt marshes occur have a high degree of human development, with a 50% loss in the last decade due solely to human modification (Kennish 2001) and 40% of the world’s human population currently residing on coasts (Gedan et al. 2009). Further habitat fragmentation by human development could have a substantial negative impact on J. roemerianus population connectivity, and possibly cause the species to lose the selective advantage of long distance dispersal.

The scale at which developed land appears to be most affecting J. roemerianus population connectivity is within a 500 m buffer zone around digitized coastal transects. Developed land was proportionally high across buffer widths along coastal transects, indicating amount or variation in the land cover variables is likely not driving the high ranking of the 500 m buffer. This result could be reflective of true J. roemerianus dispersal biology since digitized coastal transects were also the highest ranked transect type overall. Coastal winds and tides, and waterfowl dispersal could all cause dispersal to be highly concentrated around the coastline, limiting dispersal to a small area along the coast and defining a fine scale for managers to target for land management and restoration.

Implications for restoration and conservation

Our results indicate that natural populations of J. roemerianus have intermediate levels of genotypic and genetic diversity, which has important implications for salt marsh restoration technique and implementation. While there is no universal protocol for J. roemerianus restoration (Sparks et al. 2013), any projects that attempt to generate restored populations with natural levels of genetic diversity would be misled by current J. roemerianus life history literature. J. roemerianus is reported to primarily use clonal propagation to reproduce in established populations (Eleuterius 1975; Stout 1984), implying natural populations are comprised of only a few unique genotypes. Our results suggest that practitioners will need to plant a greater number of unique genotypes than this literature suggests, more on the order of 20–30 depending on the area of the restored site, to create restored populations with natural levels of genotypic diversity. Site-specific genetic diversity results can guide selection of naturally sourced transplant stock from areas of high genetic diversity. Restored populations that do not meet these criteria run the risk of founder effects such as inbreeding depression, low fitness, and low establishment rates (Hufford and Mazer 2003; Mijnsbrugge et al. 2010), and lose the positive effects of genetic diversity including resiliency (Hughes and Stachowicz 2004; Ehlers et al. 2008), ecosystem benefits (Reynolds et al. 2012), and evolutionary potential (Frankel and Soule 1981; Mills 2007). Understanding population genetic structure on the different scales explored in our study could aid in selection of genetically similar transplant stock to increase success of J. roemerianus restoration and reduce risks to native populations. Local genotypes tend to have a home-site advantage in restored populations, and transplant success has been found to be inversely related to genetic and environmental distance between the source population and restoration site (Montalvo and Ellstrand 2000; Hufford and Mazer 2003). Planting non-local genotypes in restored populations could have far reaching effects on surrounding native populations through outbreeding depression, and genetic swamping of local genotypes (Hufford and Mazer 2003; Mijnsbrugge et al. 2010). In J. roemerianus restoration, practitioners may want to select stock from within the same genetic cluster or sub-cluster to improve restoration success and prevent outbreeding depression and spread of non-local genotypes in restored areas.

Spatial results from our study can help guide management of coastal areas and J. roemerianus restoration to maintain and promote genetic diversity across the landscape. Our models suggest coastal areas within a 500 m buffer should be the most targeted by managers to preserve J. roemerianus population connectivity by limiting further urban development and implementing marsh restoration efforts. Creating new areas of marsh between existing sites could decrease isolation of extant populations, and further improve population connectivity as indicated by the positive relationship between wetland and gene flow. Using spatially explicit genetic data to inform J. roemerianus restoration and management could help shift the focus of such efforts from triage in the present to conserving persistence and evolutionary potential into the future.

Broader impacts and future directions

The methods developed for this study are applicable to other understudied species important to conservation for understanding population connectivity across the ecosystem and creating a landscape level management plan for the salt marsh. A number of current landscape genetic studies use resistance surfaces to examine and quantify the effect of landscape factors on movement and population connectivity. While resistance surfaces are useful in the field and provide more spatially explicit information than most other methods, a number of assumptions based on prior knowledge of the species must be made (Zeller et al. 2012), and the method is arguably best suited for mobile land dispersed species. As climate change and anthropogenic habitat alteration affect increasingly more non-model and understudied species, conservation efforts will need methodology that relies on less information than traditional resistance layers. Our use of multiple transect types and buffer widths greatly reduces the number of a priori assumptions needed for resistance surfaces, and requires less knowledge of species life history. Selecting from multiple transect types also allows for greater flexibility across dispersal strategies. LCTA has been successfully applied to tropical bats (Cleary et al. 2017) and common grasshoppers (Keller et al. 2013), which use flight for dispersal. This methodology is more suited to understudied plant and animal species important for conservation and restoration that generally lack necessary dispersal data for resistance surfaces, and use a wide variety of dispersal strategies. The hierarchical design we used also allows for a simplified and elegant model comparison within and among species. Examining transect types and buffer widths hierarchically reduced the number of candidate models from 177 to eight for our study, which could allow full candidate sets to be compared more easily across species for multispecies studies in the future.

While the field of landscape genetics is growing, plants studies remain relatively rare and few studies have examined salt marsh or estuarine ecosystems (Holderegger et al. 2010; Storfer et al. 2010). A 2010 survey of the landscape genetics literature found 14.5% of studies focused on plants, while only 6% occurred in salt water habitats and estuarine habitats were not listed as a category (Storfer et al. 2010). Many existing plant landscape genetic studies do not actively include landscape elements (Holderegger et al. 2010). The majority of current plant studies use mantel tests or partial mantel tests to correlate genetic measures to geographic distance measures and some measure of ecological distance measure or environmental statistic (Hirao and Kudo 2004; Fievet et al. 2007; Trenel et al. 2008; Holderegger et al. 2010; Pollegioni et al. 2014; Rico et al. 2014). Other studies have used hierarchical genetic structure, assignment tests, or overlays to draw conclusions about the influence of landscape features on gene flow and genetic patterns (Kitamoto et al. 2005; Fievet et al. 2007; Pollegioni et al. 2014). A multiple variable approach, such as that used in this study, has not been widely applied in plant studies, and would allow for greater complexity and fewer a priori assumptions than other approaches. This study also expands into an understudied system, both in the field of landscape genetics and conservation genetics. The methods developed here would be suited for continued study in salt marshes and other estuarine landscapes where many of the species lack dispersal data, and use a variety of dispersal strategies including wind, terrestrial, and oceanic. Overall, our study emphasizes the need to apply landscape genetic techniques to common species that are often understudied, but are increasingly important for conservation and restoration.

Data availability

Microsatellite markers are archived in NCBI GenBank, accession nos: KX398592, KX398593, KX398594, KX398595, KX398596, KX398597, KX398598, KX398599, KX398600, KX398601, KX398602, KX398603, KX398604, KX398605, KX398606, KX398607, KX398608, KX398609, KX398610. Sample microsatellite genotypes and coordinates are available from the corresponding author upon reasonable request.