Some remarks on equilibrium state in dynamic condition

Abstract

For dehydration of CaC₂O₄·H₂O and thermal dissociation of CaCO₃ carried out in Mettler Toledo TGA/SDTA-851^e/STAR^e thermobalance similar experimental conditions was applied: 9–10 heating rates, q = 0.2, 0.5, 1, 2, 3, 6, 12, 24, 30, and 36 K min⁻¹, for sample mass 10 mg, in nitrogen atmosphere (100 ml min⁻¹) and in Al₂O₃ crucibles (70 μl). There were analyzed changes of typical TGA quantities, i.e., T, TG and DTG in the form of the relative rate of reaction/process intended to be analyzed on-line by formula (10). For comparative purposes, the relationship between experimental and equilibrium conversion degrees was used (for $P = P^{{\ominus}}$). It was found that the solid phase decomposition proceeds in quasi-equilibrium state and enthalpy of reaction is easily “obscured” by activation energy. For small stoichiometric coefficients on gas phase side (here: ν = 1) discussed decomposition processes have typical features of phenomena analyzable by known thermokinetic methods.

Introduction

In the discussion on thermokinetic analysis of reaction/process of thermal decomposition of compounds undergoing destruction with observable weight loss:

$$ A_{\text{s}} \to B_{\text{s}} + \nu C_{\text{g}} \;{\text{or}}\; \, A_{\text{s}} \to \sum \nu C_{\text{g}} . $$

(1)

(where the stoichiometric coefficient ν is sum of coefficients for gaseous products) an important problem is description of thermodynamic conditions under which experiments are carried out. Classic ‘single kinetic triplet’ f(α) or g(α)-E-A applies to thermokinetic conditions, not necessarily equilibrium. In all conditions, due to temperature (T) and pressure (P), appropriate laws determine equilibrium degree of conversion according to:

• (1) modified van ‘t Hoff’s isobar for thermal dissociation of chemical compounds in solid state [1–5],

• (2) van Laar–Planck’s isotherm [6, 7].

Reaction course in accordance with these laws causes that its determinant are thermodynamic quantities expressed by:

$$ \alpha_{\text{eq}} - \Updelta_{\text{r}} H - T_{\text{eq}} $$

(2)

instead of ‘single kinetic triplet’.

It is proved that reaction enthalpy (Δ_r H)—as an average quantity—is independent of temperature (T) and pressure (P), when P < 3 MPa [8].

In practice, in TGA analysis, the most commonly used is experimental degree of conversion (α) at a given temperature, which must be lower than equilibrium one (α_eq) [9–11], but not always so.

A combination of both rights with regard to conditions (T, P) can be carried out using the basic relations for constant thermodynamic equilibrium of reaction:

$$ K_{\alpha } = K\left( {\frac{{P^{{\ominus}} }}{P}} \right)^{\nu } ,\quad P^{{\ominus}} = 1\;{\text{bar}} \approx 0.1\;{\text{MPa}} $$

(3)

where constant K for reaction (1) is expressed in the following manner:

$$ K = \exp \left[ {\frac{{\Updelta_{\text{r}} H}}{R}\left( {\frac{1}{{T_{\text{eq}} }} - \frac{1}{T}} \right)} \right],\;P = {\text{const}},\quad {\text{when }}T \ge T_{\text{eq}} ,\;K = 1 $$

(4)

In Eq. 4 one substitutes in accordance with Refs. [1–4]:

$$ K = \alpha_{\text{eq}}^{\nu } $$

(5)

Using the similar procedure in Eq. 3 one obtains:

$$ {\varvec{\upalpha}}_{\bf{eq}} = \alpha_{\text{eq}} \left({\frac{{P^{{\ominus}} }}{P}} \right),\quad P^{{\ominus}} > P \ge {{\upalpha}}_{\text{eq}} P^{{\ominus}} \;{\text{and}}\;0 < {{\upalpha}}_{\text{eq}} \le 1 $$

(6)

Identical results were presented in works [6, 7].

Finally, formula (6) is expressed as follows:

$$ {\varvec{\upalpha}}_{\bf{eq}} = \left( {\frac{{P^{{\ominus}} }}{P}} \right)\exp \left[ {\frac{{\Updelta_{\text{r}} H}}{\nu R}\left( {\frac{1}{{T_{\text{eq}} }} - \frac{1}{T}} \right)} \right],\quad \frac{{P^{{\ominus}} }}{P} \ge 1 $$

(7)

According to Eq. 7 intensive collection of gaseous products producing vacuum ($P^{{\ominus}} > P$) moves equilibrium line α _eq over the course deriving from isobaric conditions (4) together with (5).

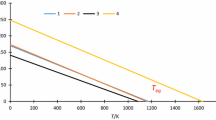
It is common to carry out studies on thermal processes just in discussed way—the example is presented in Fig. 1 quoted from [12].

Fig. 1

Seven experimental alpha (α)–temperature (T) curves for decomposition of calcium carbonate in nitrogen, obtained at different heating rates: 1, 3, 5, 7, 5, 10, 15, and 25 K min⁻¹ (data acc. [12]) on the background of equilibrium relationship (23)

Scope of the work

Basing on the analysis of thermal decomposition of two model chemical compounds (CaC₂O₄·H₂O and CaCO₃), often used as test substances, in inert atmosphere in dynamic conditions at different heating rates (q), own assessment of thermodynamic conditions of decomposition using the relative rate of reaction/process has been presented.

Basing on three-parametric equation [5], the relative rate of reaction/process was proposed for dynamic conditions [13], which results from considerations on the equilibrium course of chemical reaction of solid phase dissociation, when $P = P^{{\ominus}}$. It means that the term $r = - {{{\text{d}}\ln \alpha } \mathord{\left/ {\vphantom {{{\text{d}}\ln \alpha } {{\text{d}}\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-\nulldelimiterspace} T}} \right)}}} \right. \kern-\nulldelimiterspace} {{\text{d}}\left( {{1 \mathord{\left/ {\vphantom {1 T}} \right. \kern-\nulldelimiterspace} T}} \right)}}$ versus T should be constant, i.e., r = r _eq = const. (r in K).

Therefore there was the study carried out, in which it was assumed that relationships r versus T will be analyzed without any data selection procedure in order to analyze graphic images obtained in dynamic conditions, electronically recording the course of thermal dissociation of selected two chemical compounds in the relation: mass versus temperature.

Assumptions

Assuming in Eq. 7 $P^{{\ominus}} = P,$ after differentiation towards temperature one obtains:

$$ \frac{{{\text{d}}\ln \alpha_{\text{eq}} }}{{{\text{d}}T}} = \frac{{\Updelta_{\text{r}} H}}{{\nu RT^{2} }} $$

(8)

This result can be presented (by analogy), using equilibrium relative rate of reaction/process in the following way:

$$ r_{\text{eq}} = \frac{{\Updelta_{\text{r}} H}}{\nu R} = {\text{const}} $$

(9)

Equation 9 represents straight line parallel to temperature axis (T), limited by perpendicular at the point with coordinates [0, T _eq] (e.g., see Fig. 3 in [14]).

It was assumed that experimental data can be directly measured by TGA [13, 15]:

$$ r = - \frac{\text{DTG}}{{m_{\text{i}} - {\text{TG}}}} \cdot T^{2} $$

(10)

where m _i is initial mass (mg), DTG (mg K⁻¹) and TG (mg).

The relative rate of reaction/process is linear relationship of correlated coefficients a ₁ and a ₂ [13]:

$$ r = a_{1} - a_{2} T $$

(11)

Coefficients a ₁ and a ₂ originate from equations:

(A) [5]:

$$ \ln \alpha = a_{0} - \frac{{a_{1} }}{T} - a_{2} \ln T $$

(12)

or

(B) [16]:

$$ \ln \alpha = a_{1} \left( {\frac{1}{{T_{f} }} - \frac{1}{T}} \right) - a_{2} \ln \frac{T}{{T_{f} }} $$

(13)

Further considerations follow from comparison of temperature of maximum reaction rate T _m determined experimentally and calculated by formula (14).

According to Ref. [13] temperature of flex point (T _fp) in version [7] (formula (1–8) is identified with the T _m:

$$ T_{\text{m}} = \frac{{a_{1} }}{{1 + a_{2} + \sqrt {1 + a_{2} } }} $$

(14)

Another relationship is of thermodynamic-correlation nature and interconnects a ₁ and a ₂ by temperature T _r [16]:

$$ a_{1} = \frac{{\Updelta_{\text{r}} H}}{\nu R} + a_{2} T_{\text{r}} $$

(15)

According to Ref. [14], temperature T _r is represented by slope of straight lines (11) and (9). To some extent this is the analogue of isokinetic temperature, because (in theory) r = const. Analysis of experimental data consists in determination of linear relationships (11), while the relative rate of reaction/process is determined by formula (10). Next, formulas in forms (14) and (15) were used.

Each analysis of compounds (CaC₂O₄·H₂O and CaCO₃) was preceded by determination of activation energy according to modified Kissinger law in version [17]:

$$ \ln \frac{q}{{T_{\text{m}} }} = \ln A - \frac{E}{{RT_{\text{m}} }} $$

(16)

to confirm whether own data are within the range of data presented in literature.

The considerations were carried out in three areas: thermokinetic, thermodynamic, and relative rate. This approach follows from the fact that such considerations prevail in such order in literature.

The basic element of analysed thermoanalytical results consists in evaluation, whether the relative rate of reaction/process r calculated according to Eq. 10 versus T presents relationship (9), of which graphical image is rectangle area bounded by temperature T _eq, or linear relationship (11) with a negative slope, expressed by coefficient a ₂.

Calcium oxalate monohydrate

Thermokinetics

Thermal decomposition of CaC₂O₄·H₂O, especially at the initial stage of the process (dehydration) is still featured in both newer literature [18–23] and own works [13, 17, 24]. An example of single kinetic triplet according to Ref. [21] is expressed as:

$$ \begin{aligned} & g\left( \alpha \right) = 1 - \left( {1 - \alpha } \right)^{n} ,\quad n = { 1}. 4- 2. 4, \\ & E = { 82}. 8 3\,{\text{kJ}}\,{\text{mol}}^{ - 1} ,\;{ \ln }\;A = { 11}. 6 4 5- 1 1. 7 2 4 \;(A\;{\text{in}}\;{\text{s}}^{ - 1} ), \\ \end{aligned} $$

and according to Ref. [17]:

$$ E = 8 3. 2\;{\text{kJ}}\;{\text{mol}}^{ - 1} ,\;{ \ln }\;A = 1 4.0 5 4, \, \left( {A\;{\text{in}}\;{\text{s}}^{ - 1} } \right), $$

and from own results according to Eq. 16 was obtained:

$$ \ln \frac{q}{{T_{\text{m}} }} = 19.939 - \frac{10710.4}{{T_{\text{m}} }}, $$

(17)

i.e., E = 89.05 kJ mol⁻¹, lnA = 15.845 (A in s⁻¹).

Thermodynamics

Equation 9 is plotted on the basis of thermodynamic data for standard conditions:

• T = 298.15 K and P ≈ 0.1 MPa for dehydration according to Ref. [18]:

• ΔH = 36.4 kJ mol⁻¹, (according to Ref. [25] enthalpy of vaporization of water in 298.15 K is 44.0 kJ mol⁻¹)

• ΔG = 2.2 kJ mol⁻¹,

• ΔC _p = −10.2 J (K mol)⁻¹—originates from summing up values: ₂₉₈ C _p, Table 1 in [18] and entropy in these conditions:

• ΔS = 0.1147 kJ (K mol)⁻¹ (acc. [26]: ΔS = 0.156 kJ (K mol)⁻¹)

From these data, equilibrium temperature T _eq (also called temperature of inversion) was determined iteratively from Gibbs–Helmholtz equation and Kirchhoff’s law: when $\Updelta G \, = \, 0\quad {\text{then}}\quad T = T_{\text{eq}}$ and

$$ 36.4 - 10.2 \times 10^{ - 3} \left( {T_{\text{eq}} - 298.15} \right) - T_{\text{eq}} \left[ {0.1147 - 10.2 \times 10^{ - 3} \;\ln \left( {\frac{{T_{\text{eq}} }}{298.15}} \right)} \right] = 0 $$

(18)

next: T _eq = 317.4 K

which is to all intents and purposes consistent with the formula:

$$ T_{\text{eq}} = \frac{\Updelta H}{\Updelta S} = 36.4\frac{298.15}{{\left( {36.4 - 2.2} \right)}} = 317.3\,{\text{K}} $$

From the calculations follows the average enthalpy of reaction in the temperature range of 298–318 K: Δ_r H = 36.3 kJ mol⁻¹. Figure 2 shows relationship between degree of conversion and temperature for ten heating rates, and Fig. 3—between the relative rate of reaction/process and temperature according to Eq. 10, giving the coefficient of determination (r ²) with equilibrium line (9) limited by straight line T _eq = 318 K (45 °C) for selected heating rates (q = 0.2, 3, and 30 K min⁻¹).

Fig. 2

Ten experimental alpha (α)–temperature (T) curves for dehydration of calcium oxalate monohydrate in nitrogen, obtained at different heating rates: 0.2, 0.5, 1, 2, 3, 6, 12, 18, 24, and 30 K min⁻¹

Fig. 3

Relationship between the relative rate of reaction (r) and temperature (T) for dehydration of calcium oxalate monohydrate (3 of the 10 heating rates). Marked linear relationships (11) concerns selected experimental points

Equilibrium relationship is as follows:

$$ \ln \alpha_{\text{eq}} = 13.73 - \frac{4366.13}{T},\;T_{\text{eq}} = 318\,{\text{K}}\;\left( {45^\circ {\text{C}}} \right) $$

(19)

According to Eqs. 9 and 19 one obtains:

$$ r_{\text{eq}} = 4366.13\,{\text{K}} = {\text{const}},\;T_{\text{eq}} = 318\,{\text{K}} $$

(20)

Equation 19 was determined on the basis of thermodynamic data [18] in standard conditions, T = 298 K, and thus, referring to Eq. 5, equilibrium conversion degree (for ν = 1) in natural way concerns this reference condition. Under these considerations, Eq. 19 should be regarded as acceptable estimation, assuming that in considered temperature range thermodynamic quantities are close to standard ones.

The difference can be attributed to slightly differing values of entropy. The issue, what may be surprising here, is the fact that this is thermodynamic or maximum value at given temperature and at atmospheric pressure P = 0.1 MPa. This does not mean that at T = 298 K, the decomposition occurs and is detectable, because in the way here may be conditions of kinetic nature, e.g., very slow evaporation or atmospheric equilibrium. For this reaction, Δ_r H ≈ 36 kJ/mol is determined by the activation energy E = 80 kJ/mol (or higher) and by the heat of vaporization of water, more than 40 kJ/mol.

In turns, Fig. 4 shows experimental results that show straight lines (11). From Fig. 4 follows that each straight line (11) together with (20) intersect at a wide temperature range and not only at determined temperature T _r = 390.2 K. With the exception of q = 0.2 and 1 K min⁻¹, each straight line (for q = 0.5, 2, 3, 6, 12, 18, 24, and 30 K min⁻¹) intersects at higher temperature, i.e., 399 K.

Fig. 4

Graphical presentation of linear relation r = a ₁–a ₂ T for dehydration of calcium oxalate monohydrate

Relative rate

Table 1 presents calculated coefficients of Eq. 11 and temperature of maximum reaction rate T _m determined experimentally and calculated by Eq. 14—Fig. 5 compares the two temperatures toward q.

Table 1 The results of calculations for dehydration of CaC₂O₄·H₂O

Fig. 5

Relationship between the temperature of the maximal rate of reaction (T _m) and heating rate (q) for dehydration of calcium oxalate monohydrate

According to Fig. 2 experimental degrees of conversion α satisfy inequality α_eq > α for all heating rates q, and according to Kissinger law (as well as in version (16)) temperatures of maximum reaction rate T _m increase with increasing heating rate q. However, from Fig. 3 follows that virtually all the points showing the relative rate of reaction r in terms of temperature are outside the rectangle (20). It demonstrates relative dynamic reaction course for small heating rates (according to Table 1) for q = 0.2, 0.5, 1 K min⁻¹, moderated course (q = 1 and 3 K min⁻¹) and close to equilibrium, when a ₂ < 100 for high heating rates (q ≥ 6 K min⁻¹). Relativity of dynamics here means a reference to temperature, as well to maximum thermal rate (dα/d T) obtained at low heating rates (q), as to temperature ranges, in which conversion degree achieve the end of reaction (α → 1).

However, courses similar to the parallel (a ₂ = small) are greater in value than the expression r _eq = Δ_r H/νR = 4366.13 K and closer to the ratio E/R ≅ 10000 K.

Characteristic temperatures in these analyses are of very important control meaning, namely: T _eq and T _m, T _f as well as T _r, which are determined experimentally. For large heating rates, thermal dissociation approaches to quasi-equilibrium with a large temperature shift of the final reaction temperature T _f in relation to T _eq (T _f > T _eq). Instead, for small heating rates high values of coefficient a ₂ are observed, what means that even for the lowest heating rate, often regarded as a pseudo-isothermal (q = 0.2 K min⁻¹), occurs the largest deformation of the equilibrium distribution according to Eq. 7 by factor $\left( {T/T_{\text{f}} } \right)^{{a_{2} }}$ (Eq. 13), which gradually reaches value of 1 for a ₂ = 0 [16].

According to Fig. 5 and Table 1 the lower coefficient a ₂, the differences between fixed temperature T _m calculated by Eq. 14 become very large—only for large values of a ₂, so for very small heating rates formula (14) leads to values compatible with experiment.

Establishing the meaning of temperature T _r , for the data set in Table 1, Eq. 15 was determined:

$$ \begin{gathered} a_{1} = {11139}.5 { } + {39}0. 1 7 2a_{2} \hfill \\ \left( {r^{2} = \, 0. 9 9 9 7, \;{\text{sl}} = \, 0.0\left( 5\right)} \right) \hfill \\ \end{gathered} $$

(21)

what leads to T _r = 390.2 K.

Again, one may also note that constant term in Eq. 21 is much higher than the one resulting from enthalpy (r _eq = 4366.13 K)—the same observation is included in Ref. [16].

Calcium carbonate (calcite)

Thermokinetics

Calcium carbonate was within the frame of the project described in the report [12]—the results were analyzed and discussed further in subsequent works [27–29], and then in Ref. [16] in terms of significance of Eqs. (12–13). Results of studies on thermal dissociation of CaCO₃ discussed at the ICTAC Conference [12, 27–29], also summarized in Tables 1 and 2 in Ref. [16], were used applying Kissinger law in version (16).

It was obtained:

• for decomposition in nitrogen: E = 201.0 kJ mol⁻¹, ln A = 13.46 (A in s⁻¹) (r ² = 0.9865, sl = 0.00001), according to Ref. [12] similar values was obtained by H. O. Desseyn: ln A = 13.58 (A in s⁻¹) and E = 199 kJ mol⁻¹, but only in this one case),

• for decomposition in vacuum: E = 111.9 kJ mol⁻¹, ln A = 6.05 (A in s⁻¹) (r ² = 0.9435, sl = 0.00122)—in Ref. [12] several pairs are similar.

Next, own data analyzed according to Eq. 16 lead to equation:

$$ \begin{gathered} \ln \frac{q}{{T_{\text{m}} }} = 19.1192 - \frac{24055.9}{TE} \hfill \\ {\text{i}}.{\text{e}}.,\;E = 200.0\,{\text{kJ}}\,{\text{mol}}^{ - 1} ,\;{ \ln }\,A = { 15}.0 2 5 { }\left( {A\;{\text{in}}\;{\text{s}}^{ - 1} } \right) \hfill \\ \end{gathered} $$

(22)

Relationship between conversion degree and temperature at variable heating rates and on the background of equilibrium conversion degree is presented in Fig. 6.

Fig. 6

Nine experimental alpha (α)–temperature (T) curves for decomposition of calcium carbonate in nitrogen, obtained at different heating rates: 0.2; 0.5; 1; 3; 6; 12; 24; 30 and 36 K min⁻¹

Thermodynamics

Equilibrium relationship for calcite was taken from Ref. [16] (Δ_r H = 174.9 kJ mol⁻¹):

$$ {\rm{ln}}\,\alpha _{{{\rm{eq}}}} = 18.095 - \frac{{21039.57}}{T},\quad T_{{{\rm{eq}}}} = 1162.7\,{\rm{K}}\;(889.6^\circ {\rm{C}}) $$

(23)

that is:

$$ r_{\text{eq}} = 2 10 3 9. 5 7= {\text{const}},\quad T_{\text{eq}} = 1 1 6 2. 7\,{\text{K}} $$

(24)

Compared to the ICTAC data presented in Fig. 1, results of these studies (Fig. 6) point to an even greater shift of experimental curves of conversion degree α to the left in relation to the equilibrium curve (7) for $P^{{\ominus}}\,=\,P$ , i.e. α_eq < α.

Relative rate

In Ref. [16], it was found that a ₂ coefficients are: for decomposition in nitrogen a ₂ = 208 → 63 and for heating rate q = 1–25 K min⁻¹ (Table 1 in Ref. [16]), but they are much lower in case of decomposition in vacuum: a ₂ = 661–317, q = 1.8 to 10 K min⁻¹ (Table 2 in Ref. [16]).

Figure 7 presents—similarly as in Fig. 3—relationships of the relative rate of reaction/process according to Eq. 10, giving determination coefficient (r ²) together with the equilibrium line (23) limited by T _eq = 1162.7 K. Table 2 compiles determined coefficients of linear relationship (11) and temperature T _m (experimental) calculated by Eq. 14.

Fig. 7

Relationship between the relative rate of reaction (r) and temperature (T) for decomposition of calcium carbonate. Marked relationships (11) concerns selected experimental points, for which (r ²) reached the highest value (even for r ² = 0.2232, sl = 0.05, together with increase of q: r ² → 1)

Table 2 The results of calculations for thermal dissociation of CaCO₃

In Fig. 7 was indicated temperature T _r following from Eq. 25, because it relates to small values of a ₂ and thus exposes range closer to equilibrium. Figure 8 presents again data from Fig. 7, where straight lines (11) present experimental results.

Fig. 8

Graphical presentation of linear relation r = a ₁ − a ₂ T for decomposition of calcium carbonate

Coefficients a ₁ and a ₂ satisfy linear relationship (Fig. 9):

$$\begin{aligned} a_{1}\, =\, & 23029 + 1043.4a_{2} ,\quad 88.7 \ge a_{2} \ge 26.0 \\ & \left( {r^{2} = \,0.9911,\:{\rm{sl}} = \,0.00001} \right) \\ \end{aligned}$$

(25)

which determines T _r = 1043.4 K. Previous analyses given in Ref. [16] set different coefficients of relationship (11):

$$ \begin{aligned} & a_{1} = { 3721}. 1 { } + { 821}. 3 7a_{2} ,\quad 700 \ge a_{2} \ge 0 \\ & {\text{i}}.{\text{e}}.,\;T_{\text{r}} = { 821}. 4\,{\text{K}} \\ \end{aligned} $$

(26)

Fig. 9

Relation between coefficients: a ₁ versus a ₂ for decomposition of calcium carbonate

From Fig. 8 follows that each straight line (11) together with (24) intersect at a wide temperature range, and not only at determined temperature T _r. We note again that constant term in Eq. 25 is higher than the one resulting from enthalpy (r _eq = 21039.6 K).

Referring to Table 2, it was again established that for small values of a ₂ experimental temperature T _m is much lower than the one calculated by Eq. 14. Observed thermal dissociation of CaCO₃ can be defined as proceeding under quasi-equilibrium conditions in relation to anticipated range of characteristic temperature according to Eq. 7 for $P^{{\ominus }} = P$. Maybe this is the reason of observing more chaotic arrangement of points of Fig. 8 in comparison to Fig. 4. Approximately, when a ₂ → 0, then Eq. 13 simplifies to relationship known as temperature criterion [24, 30]: ln α = const. − E/RT, then Δ_r H → E.

Discussion

The results of investigations on thermal dissociation of two chemical substances frequently used as test compounds (standards) in thermal analysis:

• dehydration of CaC₂O₄·H₂O,

• thermal decomposition of CaCO₃ (calcite).

The investigations were carried out under identical test conditions. Previously, trial and error method was used for selection of experimental conditions—mainly heating rates, nitrogen flow, crucibles—in order to a ₂ ratio was greater than 100. According to Tables 1 and 2 in case of calcite, it was manage to get it completely, but for dehydration of oxalate—only in a large extent.

Observing the experimental conversion degrees α toward temperature profile T, one may conclude that both compounds behave differently in relation to the equilibrium curves:

• dehydration proceeds under curve resulting from relationship (19), α < α _eq ,

• thermal dissociation of carbonate proceeds above relationship (22), α > α _eq .

In detailed studies, the relative rate of reaction/process was explicitly determined from experimental data according to the formula (10), i.e., using T, TG, DTG, and m _i—deliberately it was not used the option of smoothing by Savitzky–Golay method [31], which very useful for studies of complex organic mixtures such as coal tar pitches [15].

In the range of 0 < α < 0.05–0.1 one always must take into account the occurrence of oscillations arising from expression appearing in formula (10) by the ratio −DTG/TG ∝ dα/αdT, i.e., one is close to an indeterminate form 0/0 and using filters of type [31] does not help much here.

What is puzzling, however, is how are observed such differences between temperatures of maximum reaction rate, determined experimentally and calculated by Eq. 14. Substituting empirical relationship (15) to the formula (14) yields:

$$ T_{\text{m}} = \frac{{\frac{{\Updelta_{\text{r}} H}}{\nu R} + a_{2} T_{\text{r}} }}{{1 + a_{2} + \sqrt {1 + a_{2} } }} $$

(27)

For a ₂  = 0 (and small values):

$$ T_{\text{m}} = \frac{{\Updelta_{\text{r}} H}}{2\nu R} $$

(28)

when a ₂ is large, then according to Ref. [16]

$$ T_{m} \to T_{r} $$

(29)

what, on the basis of this studies, means approaching to compliance of both temperatures T _m and T _eq.

Returning to the Eq. 28 is easy to notice that one obtains this formula, if both Eq. 8 and condition dα_eq/dT = 0 are used, thus this is the maximum occurring far beyond the scale where α_eq ⋙ 1 (compare with Ref. [32]). For these reasons, the differences [Δ_r H/2νR − (T _m)_exp] must be very large, and they decreases, when a ₂ = large.

Thus, one may note that the quasi-equilibrium conditions prevent accurate determination of enthalpy of reaction Δ_r H, because dynamic conditions directly dictate relationships dominated by activation energy E. Thermal analyses of complex organic compounds in the form of salts containing anion halogens (Cl, Br and J), as described by Błażejowski et al. [3, 4, 33–36], behave differently due to the formation of a significant volume of gas (ν ≥ 2). These compounds are characterized by thermal decomposition, combined with the total volatilization of gaseous products. From this comparison, one may even get the feeling that the presence of solid phase (ν = 1) inhibits the process of destruction and it is necessary helping it through physical occurrence (vacuum, intense collection of gaseous products, volatilization).

Conclusions

• 1. On the basis of dehydration of calcium oxalate monohydrate and thermal dissociation of calcium carbonate (calcite) in specially selected conditions, it was found that the reactions proceed in a quasi-equilibrium conditions in relation to modified van ‘t Hoff’s isobars expressed by Eq. 7 when $P^{{\ominus}} = P$. In the case of CaCO₃ were observed small values of coefficient a ₂ (maximum a ₂ = 88.65), and the experimental curves of conversion degree toward temperature profile satisfy the relation α > α_eq, what means an intense collection of gaseous product from reaction zone and, in consequence, T _eq  > T _f . In the case of dehydration of CaC₂O₄·H₂O were observed very intensive courses for small heating rates q = 0.2 to 1 K min⁻¹, what also translates to deformation equilibrium curve (7) by significant factor $(T/T_{f} )^{{a_{2} }}$ (Eq. 13), but at higher heating rates also importance of a ₂ decreases. The reference to equilibrium decomposition is consistent with expectations, because α < α_eq.

• 2. Quasi-equilibrium conditions prevent precise determination of enthalpy of reaction (Δ_r H), because dynamic conditions impose relationships dominated by activation energy (E). Despite the very significant correlation between coefficients a ₁ and a ₂ (see Refs. [37–40]), the constant term in Eq. 15 is however greater than the expression (Δ _r H/νR). For two reaction analysed in current paper it was not obtained values of a ₂ = 0 and at the same time T _f = T _eq. Temperature T _r, which is an analogue of isokinetic temperature according to Arrhenius law (here: r = r _eq = const.), may be determined by correlation—Figs. 4 and 8 indicate that the effect of convergence in one point (for one coordinate) is blurred. It should, however, be borne in mind that similar situation also concerns isokinetic temperature in isokinetic/compensation effect—for example in Ref. [41].

• 3. Formula (14)—characteristic for the model of relative rate of reaction/process (12, 13) and (11) becomes less important, when a ₂ = 0 or a ₂ = small for calculation of T _m.

• 4. In the case of dehydration of CaC₂O₄·H₂O at low heating rates q = 0.2–1 K min⁻¹ is observed high dynamics of decomposition determined by coefficient a ₂. It disappears at higher heating rates, approaching values close to but higher than r _eq = 4366.13 K (formula (20)), but significantly shifted above equilibrium temperature above T _f ⋙ T _eq. This effect is related to phase transformation of the reaction product—water that goes into the gas phase with a variable rate depending on the time and temperature. At lower temperature, but during the very long time (q = 0.2 K min⁻¹), there are more favorable conditions for the evacuation of water from solid surface. In a very short time (high heating rate q ≥ 6 K min⁻¹) high temperatures are necessary.

• 5. Formula (10) is very simple and enables on-line analysis, and in particular its linear relationship with temperature (11) becomes clearer with increasing heating rate q.

Experimental methodology

Thermal decomposition of calcium oxalate monohydrate CaC₂O₄·H₂O (Aldrich, Cat. No. 28,984-1) and calcium carbonate CaCO₃ (Mettler—Test Sample) was carried out using Mettler Toledo TGA/SDTA-851^e/STAR^e, for weight samples of 10 mg, in atmosphere of nitrogen (100 ml min⁻¹), in Al₂O₃ crucible (70 μl), for 10 heating rates: q = 0.2; 0.5; 1; 2; 3; 6; 12; 18; 24 and 30 K min⁻¹ (in the case of CaC₂O₄·H₂O) and for 9 heating rates: q = 0.2; 0.5; 1; 3; 6; 12; 24; 30 and 36 K min⁻¹ (in case of CaCO₃).

Temperatures indicated in the text by T relate to temperature of the reacting sample.

In relation to ICTAC research [12, 27–29] the scope of research was broadened on both lower (q = 0.2 K min⁻¹—it is treated as pseudo-isothermal conditions) and higher heating rates (q = 36 K min⁻¹).