Abstract
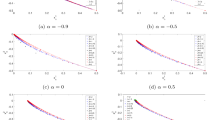
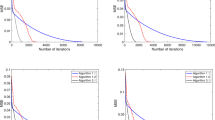
In this paper, we propose double inertial forward-backward algorithms for solving unconstrained minimization problems and projected double inertial forward-backward algorithms for solving constrained minimization problems. We then prove convergence theorems under mild conditions. Finally, we provide numerical experiments on image restoration problem and image inpainting problem. The numerical results show that the proposed algorithms have more efficient than known algorithms introduced in the literature.
Similar content being viewed by others
References
Bauschke H H, Combettes P L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces. New York: Springer, 2011
Bauschke H H, Borwein J M. Dykstra’s alternating projection algorithm for two sets. Journal of Approximation Theory, 1994, 79(3): 418–443
Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences, 2009, 2(1): 183–202
Bello Cruz J Y, Nghia T T. On the convergence of the forward-backward splitting method with linesearches. Optimization Methods and Software, 2016, 31(6): 1209–1238
Burachik R S, Iusem A N. Set-Valued Mappings and Enlargements of Monotone Operators. Boston: Springer Science Business Media, 2007
Cai J F, Cands E J, Shen Z. A singular value thresholding algorithm for matrix completion. SIAM Journal on Optimization, 2010, 20(4): 1956–1982
Combettes P L, Pesquet J C. Proximal splitting methods in signal processing//Bauschke H H, Burachik R S, Combettes P L, et al. Fixed-Point Algorithms for Inverse Problems in Science and Engineering. New York: Springer, 2011: 185–212
Combettes P L, Wajs V R. Signal recovery by proximal forward-backward splitting. Multiscale Modeling Simulation, 2005, 4(4): 1168–1200
Cui F, Tang Y, Yang Y. An inertial three-operator splitting algorithm with applications to image inpainting. arXiv:1904.11684
Davis D, Yin W. A three-operator splitting scheme and its optimization applications. Set-Valued and Variational Analysis, 2017, 25(4): 829–858
Goldstein A A. Convex programming in Hilbert space. Bulletin of the American Mathematical Society, 1964, 70(5): 709–710
Hanjing A, Suantai S. A fast image restoration algorithm based on a fixed point and optimization method. Mathematics, 2020, 8(3): 378
Kankam K, Pholasa N, Cholamjiak P. Hybrid forward-backward algorithms using linesearch rule for minimization problem. Thai Journal of Mathematics, 2019, 17(3): 607–625
Kankam K, Pholasa N, Cholamjiak P. On convergence and complexity of the modified forward-backward method involving new linesearches for convex minimization. Mathematical Methods in the Applied Sciences, 2019, 42(5): 1352–1362
Levitin E S, Polyak B T. Constrained minimization methods. USSR Computational Mathematics and Mathematical Physics, 1966, 6(5): 1–50
Moudafi A, Oliny M. Convergence of a splitting inertial proximal method for monotone operators. Journal of Computational and Applied Mathematics, 2003, 155(2): 447–454
Nesterov Y E. A method for solving the convex programming problem with convergence rate O(1/k2). Dokl Akad Nauk SSSR, 1983, 269(3): 543–547
Opial Z. Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bulletin of the American Mathematical Society, 1967, 73(4): 591–597
Osilike M O, Aniagbosor S C. Weak and strong convergence theorems for fixed points of asymptotically nonexpensive mappings. Mathematical and Computer Modelling, 2000, 32(10): 1181–1191
Polyak B T. Some methods of speeding up the convergence of iteration methods. USSR Computational Mathematics and Mathematical Physics, 1964, 4(5): 1–17
Verma M, Shukla K K. A new accelerated proximal gradient technique for regularized multitask learning framework. Pattern Recognition Letters, 2017, 95: 98–103
Wang Z, Bovik A C, Sheikh H R, Simoncelli E P. Image quality assessment: from error visibility to structural similarity. IEEE Transactions on Image Processing, 2004, 13(4): 600–612
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was supported by National Research Council of Thailand (NRCT) under grant no. N41A640094 and the Thailand Science Research and Innovation Fund and the University of Phayao under the pro ject FF66-UoE.
Electronic Supplementary Material
Rights and permissions
About this article
Cite this article
Kankam, K., Cholamjiak, P. Double Inertial Proximal Gradient Algorithms for Convex Optimization Problems and Applications. Acta Math Sci 43, 1462–1476 (2023). https://doi.org/10.1007/s10473-023-0326-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10473-023-0326-x