Derivation of the Linear Landau Equation and Linear Boltzmann Equation from the Lorentz Model with Magnetic Field

Abstract

We consider a test particle moving in a random distribution of obstacles in the plane, under the action of a uniform magnetic field, orthogonal to the plane. We show that, in a weak coupling limit, the particle distribution behaves according to the linear Landau equation with a magnetic transport term. Moreover, we show that, in a low density regime, when each obstacle generates an inverse power law potential, the particle distribution behaves according to the linear Boltzmann equation with a magnetic transport term. We provide an explicit control of the error in the kinetic limit by estimating the contributions of the configurations which prevent the Markovianity. We compare these results with those ones obtained for a system of hard disks in Bobylev et al. (Phys Rev Lett 75:2, 1995), which show instead that the memory effects are not negligible in the Boltzmann-Grad limit.

Appendices

Appendix 1: The Collision Time

We want to estimate the time spent by a the test particle in the interaction disk associated to the central potential of finite range with a uniform magnetic field perpendicular to the plane. Let be $\varepsilon ^{\alpha }\phi (r)$ with $\alpha \in [0,1/2)$ the central potential and $\varepsilon B$ the modulus of the magnetic field.

The Lagrangian of the system is

$$\begin{aligned} \mathcal {L}(r,\dot{r},\theta ,\dot{\theta })=\frac{1}{2}\dot{r}^2+\frac{1}{2}r^2\dot{\theta }^2-\varepsilon ^{\alpha }\phi ( r)+\varepsilon \frac{B}{2}r^2\dot{\theta } \end{aligned}$$

We observe that the energy of the system is conserved. Moreover the Lagrangian does not depend on the variable $\theta$, so we obtain the conservation of the conjugate momentum

$$\begin{aligned} \frac{\,d}{\,dt}\left( r^2\dot{\theta }+\varepsilon \frac{B}{2}r^2\right) =0. \end{aligned}$$

Therefore we obtain the following conserved quantities

$$\begin{aligned} \dot{r}^2+r^2\dot{\theta }^2+2\varepsilon ^{\alpha }\phi= & {} 2E,\\ r^2\dot{\theta }+\varepsilon \frac{B}{2}r^2= & {} M, \end{aligned}$$

and the equations of motion are

$$\begin{aligned} \left\{ \begin{array}{l} \dot{r}:=\frac{\,dr}{\,dt}=\sqrt{2(E-\varepsilon ^{\alpha }\phi )-\frac{M^2}{r^2}-\frac{\varepsilon ^2 B^2}{4}r^2+\varepsilon MB}\\ \dot{\theta }:=\frac{\,d\theta }{\,dt}=\frac{M}{r^2}-\varepsilon \frac{B}{2}.\\ \end{array} \right. \end{aligned}$$

This implies that

$$\begin{aligned} \frac{dt}{dr}&=\bigg [{2(E-\varepsilon ^{\alpha }\phi (r))-\frac{M^2}{r^2}-\frac{\varepsilon ^2 B^2}{4}r^2+\varepsilon MB}\bigg ]^{-1/2} \nonumber \\ \frac{d\theta }{dr}&= \frac{\frac{M}{r^2}-\frac{\varepsilon B}{2}}{\sqrt{2(E-\varepsilon ^{\alpha }\phi (r))-\frac{M^2}{r^2}-\frac{\varepsilon ^2 B^2}{4}r^2+\varepsilon MB}} . \end{aligned}$$

(A.1)

We now define the effective potential

$$\begin{aligned} \phi _{eff}( r)=\varepsilon ^{\alpha }\phi ( r)+\frac{M^2}{2r^2}+\frac{\varepsilon ^2 B^2}{8}r^2-\frac{\varepsilon MB}{2}. \end{aligned}$$

and we assume that the potential has a short range, i.e. $\phi (r):[0,1] \rightarrow \mathbb {R}$ and $\phi$ is continuous on [0, 1] and differentiable on (0, 1) .

Take the modulus of the initial velocity to be $| v|=1$. When the particle hits the obstacle of radius $r=1$ the conserved quantities read

$$\begin{aligned} \left\{ \begin{array}{l} E=\frac{1}{2}\\ M=\rho +\varepsilon \frac{B}{2}\\ \end{array} \right. \end{aligned}$$

being $\rho \in [0,1]$ is the impact parameter. The effective potential is

$$\begin{aligned} \phi _{eff}( r)= & {} \varepsilon ^{\alpha }\phi ( r)+\left( \rho +\varepsilon \frac{B}{2}\right) ^2\frac{1}{2r^2}+\frac{\varepsilon ^2 B^2}{8}r^2-\left( \rho +\varepsilon \frac{B}{2}\right) \frac{\varepsilon B}{2}\\= & {} \varepsilon ^{\alpha }\phi ( r) + \frac{1}{2}\bigg [ \frac{\rho }{r}-\frac{\varepsilon B}{2}\bigg (r-\frac{1}{r} \bigg ) \bigg ]^2. \end{aligned}$$

By integrating the equations of motion we obtain the collision time, namely the time spent inside the obstacle:

$$\begin{aligned} \tau =2\int _{r_{min}}^{1}dr \bigg [1-2\varepsilon ^{\alpha }\phi ( r)-\bigg ( \frac{\rho }{r}-\frac{\varepsilon B}{2}\bigg (r-\frac{1}{r} \bigg ) \bigg )^2 \bigg ]^{-1/2} \end{aligned}$$

(A.2)

where $r_{min}$ (the minimum distance from the centre) is the unique zero of the radicand, i.e.

$$\begin{aligned} 1=2\phi _{eff}(r_{min} ), \end{aligned}$$

so we can reformulate (A.2) as

$$\begin{aligned} \tau =\sqrt{2}\int _{r_{min}}^{1}\frac{dr}{\sqrt{2(\phi _{eff}(r_{min} )-\phi _{eff}(r ))}} \end{aligned}$$

where $2\phi _{eff}(r )\le 1$. The derivative of the effective potential reads

$$\begin{aligned} \phi '_{eff}( r)=\varepsilon ^{\alpha }\phi '( r)-\frac{\rho ^2}{r^3}-\frac{\varepsilon ^2 B^2}{4r^3}-\frac{\varepsilon B\rho }{r^3}+\frac{\varepsilon ^2 B^2}{4}r. \end{aligned}$$

By the mean value theorem we get

$$\begin{aligned} \vert \phi _{eff}(r_{min} )-\phi _{eff}(r )\vert= & {} \vert r-r_{min}\vert \vert -\phi '_{eff}(r^{*}) \vert \\\ge & {} \vert r-r_{min}\vert \bigg (\inf _{r \in (r_{min},1)}\vert -\phi '_{eff}(r) \vert \bigg ) , \qquad r^{*}\in (r_{min},r) \end{aligned}$$

and then

$$\begin{aligned} \tau \le \frac{\sqrt{2}}{(\inf _{r \in (r_{min},1)}\vert -\phi '_{eff}( r)\vert )^{1/2}}\int _{r_{min}}^{1}{\frac{1}{\sqrt{r-r_{min}}}\,dr}. \end{aligned}$$

Since $\phi '_{eff}( r) < 0$ for $r \in [0,1)$, then $\inf _{r \in (r_{min},1)}\vert -\phi '_{eff}( r)\vert =: \kappa >0$ and it follows easily that

$$\begin{aligned} \tau \le 2\bigg (\frac{2(1-r_{min})}{\kappa } \bigg )^{1/2} \le 2\bigg (\frac{2}{\kappa } \bigg )^{1/2}. \end{aligned}$$

For the corresponding rescaled problem the effective potential reads

$$\begin{aligned} \phi _{eff}^{(\varepsilon )}(r)= \varepsilon ^{\alpha }\phi (r/\varepsilon )+\frac{1}{2}\bigg [\frac{\varepsilon \rho }{r}+\frac{B}{2}\bigg (\frac{\varepsilon ^2}{r}-r \bigg ) \bigg ]^2 \end{aligned}$$

(A.3)

with $\rho \in [0,1)$. In this way one gets $- \phi _{eff}^{(\varepsilon )'}(r)=\frac{1}{\varepsilon }F(r/\varepsilon , \varepsilon )$ where

$$\begin{aligned} F(y, \varepsilon )=-\varepsilon ^{\alpha }\phi '(y)+(\rho + B)\rho y^{-3}+\frac{\varepsilon ^2 B^2}{4 y^3}(1-y^4) \end{aligned}$$

(A.4)

which is positive for $y < 1$ and uniformly in $\varepsilon$. The same argument as before yields the claimed estimate:

$$\begin{aligned} \tau _{\varepsilon } \le \frac{(2 \varepsilon )^{1/2}}{(\inf _{y \in (y_0,\varepsilon )} F( y,\varepsilon ))^{1/2}}\int _{y_0}^{\varepsilon }{\frac{dy}{\sqrt{y-y_{0}}}} \le C \varepsilon \end{aligned}$$

(A.5)

where $y_0=y_0(\varepsilon )$ is such that

$$\begin{aligned} 1=2 \varepsilon ^{\alpha }\phi (y_0)+ \bigg (\frac{\rho }{y_0}-\frac{\varepsilon ^2 By_0}{2} + \frac{B}{2y_0} \bigg )\,. \end{aligned}$$

We consider now the long range unrescaled potential defined in Assumption B1), i.e. $\psi _{\varepsilon }( r)=r^{-s}$ for $r < \varepsilon ^{\gamma -1}$ and $\psi _{\varepsilon } (r)=\varepsilon ^{-s(\gamma -1)}$ for $r \ge \varepsilon ^{\gamma -1}$. The same argument as for the short range case leads to the following estimate for the collision time after rescaling:

$$\begin{aligned} \tau \le \frac{(2 \varepsilon )^{1/2}}{(\inf _{y \in (y_0,\varepsilon ^{\gamma })} \tilde{F}( y,\varepsilon ))^{1/2}}\int _{y_0}^{\varepsilon ^{\gamma }}{\frac{dy}{\sqrt{y-y_{0}}}} \le C \varepsilon ^{\gamma } \end{aligned}$$

(A.6)

with

$$\begin{aligned} \tilde{F}(y,\varepsilon ):= & {} -\psi _{\varepsilon }'(y)+\varepsilon ^{2(\gamma -1)}\rho ^2 y^{-3} + B^2 \varepsilon ^{3 \gamma -2}\rho y^{-3}\\&+\, B^2 y^{-3}\varepsilon ^{4 \gamma -2}(1-y^4 \varepsilon ^{4(1-\gamma )})/4 > 0 \end{aligned}$$

for $y \in (y_0, \varepsilon ^{\gamma })$ where $y_0=y_0(\varepsilon )$ is such that $1= 2\psi _{\varepsilon }(y_0)+ \bigg [ \varepsilon ^{\gamma -1}\rho y_0^{-1}-\frac{B}{2}(\varepsilon ^{2\gamma -1}y_0^{-1}-\varepsilon y_0) \bigg ]^2$.

Appendix 2: Cross Section

Proposition B.1

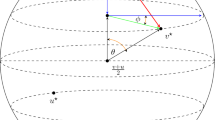
Consider the scattering angle $\theta (\rho , \varepsilon )$ of a particle with impact parameter $\rho$ due to a uniform magnetic field perpendicular to the plane with modulus $\varepsilon B$ and due to a radial potential $\varepsilon ^{\alpha }\phi$, where $\alpha > 0$ and $\phi$ satisfies assumptions A1, A2, A3. Consider also the scattering angle $\tilde{\theta }(\rho , \varepsilon )$ associated to the same radial potential as before, but without any magnetic field. Then, for $\varepsilon$ small enough one gets

$$\begin{aligned} \theta (\rho , \varepsilon ) = \tilde{\theta }(\rho , \varepsilon ) + O(\varepsilon )\,. \end{aligned}$$

(B.1)

Proof

Following [9, 16] we can write the exact formula for both of the scattering angles:

$$\begin{aligned} \tilde{\theta }(\rho , \varepsilon ) = \pi - 2\arcsin \rho - 2 \int ^{\tilde{u}_{max}(\rho , \varepsilon )}_{\rho } \frac{du}{\sqrt{1- u^2 - 2\varepsilon ^{\alpha }\phi (\rho u^{-1})}} \end{aligned}$$

(B.2)

where $\tilde{u}_{max}(\rho , \varepsilon )$ is the solution of the equation $\tilde{u}^2_{max}+ 2\varepsilon ^{\alpha }\phi (\rho \tilde{u}_{max}^{-1})=1$, while

$$\begin{aligned} \theta (\rho , \varepsilon ) = \pi - 2\arcsin \rho -2 \int ^{u_{max}(\rho , \varepsilon )}_{\rho }du \frac{1 + \frac{\varepsilon B}{2 \rho }(1 - \frac{\rho ^2}{u^2})}{\sqrt{1- 2\varepsilon ^{\alpha }\phi (\rho u^{-1})-u^2[1+\frac{\varepsilon B}{2 \rho }(1-\frac{\rho ^2}{u^2})]^2}} \end{aligned}$$

(B.3)

where ${u}_{max}(\rho , \varepsilon )$ is the solution of the equation $2\varepsilon ^{\alpha }\phi (\rho u_{max}^{-1})+u_{max}^2[1+\frac{\varepsilon B}{2 \rho }(1-\frac{\rho ^2}{u_{max}^2})]^2=1$.

Hence, an expansion of $\theta (\rho , \varepsilon )$ for $\varepsilon$ small enough yields the claimed asymptotic formula. $\square$

Proposition B.2

Let $\tilde{\theta }$ be the scattering angle associated to the long range potential $\Psi (r)=r^{-s}$ with $s>2$, $\theta _{\varepsilon , \gamma }$ the scattering angle due to a radial potential $\psi _{\varepsilon }$ defined in Assumption B1) and $\theta _{\varepsilon , \gamma }^{(B)}$ the scattering angle due to $\psi _{\varepsilon }$ and to a uniform, constant magnetic field perpendicular to the plane with modulus $\varepsilon B$. Then one has

• a) $\theta _{\varepsilon , \gamma }^{(B)} \rightarrow \tilde{\theta }$ as $\varepsilon \rightarrow 0$.

• b) $\Gamma ^{(B)}_{\varepsilon , \gamma }(\theta ) \rightarrow \Gamma (\theta )$ as $\varepsilon \rightarrow 0$, where $\Gamma ^{(B)}_{\varepsilon , \gamma }(\theta )$ is the differential cross section associated to the radial potential $\psi _{\varepsilon }$ and the magnetic field, while $\Gamma (\theta )$ is the one associated to the radial potential $\Psi$.

• c) $\Gamma ^{(B)}_{\varepsilon , \gamma }(\theta ) \le C \theta ^{-1-1/s}$ uniformly in $\varepsilon ,B$.

Proof

a) Let us now consider the truncated potential $\tilde{\Psi }=r^{-s}-A^{-s}$ with $s>2$ for $r \le A$ and $\tilde{\Psi }=0$ for $r> A$ with $A=\varepsilon ^{\gamma -1}$ and $\gamma \in (0,1)$. Take the modulus of the initial velocity of the light particle to be $|v|=1$.

We denote by $\rho$ the impact parameter (with $0\le \rho \le A$) while the scattering angle (that is the angle between the ingoing and the outgoing relative velocities) is

$$\begin{aligned} {\theta }_{\varepsilon ,\gamma }(\rho )=2\int _{\arcsin (\rho /A)}^{\pi /2}\bigg (1- \frac{\sin \beta }{v + s v^{s-1}} \bigg )d\beta . \end{aligned}$$

(B.4)

where $v=v(\beta )$ such that $v^2 + 2((v/\rho )^s - A^{-s}) = \sin ^2 \beta$ and $v=\rho / r$ (see Appendix in [8]). Following [8, 16], we can write the formula for the scattering angle associated to the potential $\tilde{\Psi }$ and with the uniform magnetic field. Due to its invariance under rescaling, the scattering angle associated to the equations of motion 2.4 reads

$$\begin{aligned} \theta ^{(B)}_{\varepsilon ,\gamma }(M)&= \pi -2\arcsin \left( \frac{M}{A}-\varepsilon \frac{B A^2}{2}\right) -2\int _{r_*}^{A}\frac{\frac{1}{r^2}(M-\varepsilon \frac{B}{2}r^2)\,dr}{\sqrt{1-2\tilde{\Psi }_{eff}(r)}} \nonumber \\&= 2 \int _{\arcsin (\frac{M}{A}-\frac{\varepsilon BA}{2})}^{\pi /2} d \beta \bigg [1-\frac{(1-\frac{\varepsilon BM}{2 u^2})\sin \beta }{u + su^{s-1}M^{-s} + \frac{\varepsilon ^2 B^2 M^2}{4 u^3}} \bigg ] \end{aligned}$$

(B.5)

where $\tilde{\Psi }_{eff}(r)=\tilde{\Psi }(r)+\frac{1}{2}\left( \frac{M}{r}-\frac{\varepsilon }{2}Br\right) ^2$, M is the value of the conserved momentum at the hitting time, i.e. $M=\rho +\varepsilon A^2\frac{B}{2}$, and $r_*$ is defined as the solution of the equation $2\tilde{\Psi }_{eff}(r_*)=1$. In the second line we made the change $r \rightarrow u \rightarrow \beta$ where $u=u(\beta ,M)=\frac{M}{r}$ and $\sin ^2 \beta = 2 \tilde{\Psi }(M/u)$. Note that the change of variable $u \rightarrow \beta$ is well defined because $\tilde{\Psi }(M/u)$ is non-decreasing when $u \in [M/A,M/r^*]$ for $\varepsilon$ small enough.

From (B.4) and (B.5) it is clear that ${\theta }_{\varepsilon ,\gamma }$ and $\theta _{\varepsilon ,\gamma }^{(B)}$ have the same asymptotic behaviour as $\varepsilon$ approaches 0. Since ${\theta }_{\varepsilon ,\gamma }\rightarrow \tilde{\theta }$, one gets the claim.

b) The inverse of the differential cross section associated to $\tilde{\theta }$ is

$$\begin{aligned} \bigg \vert \frac{d \theta _{\varepsilon ,\gamma }}{d \rho }\bigg \vert&= \frac{2}{\rho ^{s+1}}\int _{\arcsin (\rho /A)}^{\pi /2} \frac{d \beta \sin \beta s v^{s-1}}{(v + sv^{s-1}\rho ^{-s})^2} \bigg [s-\frac{1 + s(s-1) v^{s-2}\rho ^{-s}}{1+s v^{s-2} \rho ^{-s}} \bigg ]\nonumber \\&\quad + \frac{2 s \rho ^{-2} A^{2-s}}{1+2 s \rho ^{-2} A^{2-s}} \,. \end{aligned}$$

(B.6)

We want to study the limit of $d\theta _{\varepsilon ,\gamma }^{(B)}/d\rho$. For a mere computational convenience, we prefer to look at $d\theta _{\varepsilon ,\gamma }^{(B)}/dM$ which is related to $d\theta _{\varepsilon ,\gamma }^{(B)}/d\rho$ via

$$\begin{aligned} \frac{d\theta _{\varepsilon ,\gamma }^{(B)}}{dM}(M)=\frac{d\theta _{\varepsilon ,\gamma }^{(B)}}{d\rho }\left( \rho + \frac{\varepsilon BA^2}{2}\right) . \end{aligned}$$

(B.7)

From (B.5) one gets

$$\begin{aligned} \frac{d \theta _{\varepsilon ,\gamma }^{(B)}}{d M}= & {} -\frac{2}{A \sqrt{1-\left( \frac{M}{A}-\frac{\varepsilon BA}{2}\right) ^2}} \bigg [ \frac{s M^{-2}A^{2-s} + \varepsilon B A^2 M^{-1}}{1 + sM^{-2}A^{2-s} + \frac{\varepsilon ^2}{4} B^2 A^4 M^{-2}} \bigg ] \nonumber \\&- 2 \int _{\arcsin \left( \frac{M}{A}-\frac{\varepsilon BA}{2}\right) }^{\pi /2}\frac{d \beta \sin \beta }{\left( u + su^{s-1}M^{-s} + \frac{\varepsilon ^2 B^2 M^2}{4 u^3}\right) ^2}\nonumber \\&\times \big [ s^2 u^{s-1}M^{-s-1}-u'(1+s(s-1)u^{s-2}M^{-s}) \big ] \nonumber \\&-\, {\varepsilon B M} \int _{\arcsin (\frac{M}{A}-\frac{\varepsilon BA}{2})}^{\pi /2}\frac{d \beta \sin \beta }{u}\bigg [s(s+1)u^{s-2}M^{-s}(u'M-1) + 3 u'M \nonumber \\&+ \frac{5 \varepsilon ^2 B^2 M^3 u'}{4 u} + \frac{\varepsilon BM}{u^2} + \frac{3 \varepsilon B M^2}{2 u^3} -1 - \frac{3 \varepsilon ^2 B^2 M^2}{4 u^4} \bigg ] \end{aligned}$$

(B.8)

where

$$\begin{aligned} u' = \frac{du}{dM} = \frac{1}{M^{s+1}}\bigg (\frac{su^{s-1} + (1-\frac{\varepsilon BM}{2 u^2})\frac{\varepsilon B M^{s+1}}{2u}}{1+su^{s-2}M^{-s} - \frac{\varepsilon ^2 B^2 M^2}{4 u^4}}\bigg ) \,. \end{aligned}$$

(B.9)

As for item a), one realizes that $d\theta _{\varepsilon ,\gamma }^{(B)}/d\rho$ and $d\theta _{\varepsilon ,\gamma }/d\rho$ are asymptotically equivalent for any $\rho$, thus Proposition A.1 in [8] implies that $\Gamma _{\varepsilon , \gamma }^{(B)}(\theta ) \rightarrow \Gamma (\theta )$ for $\theta \in (-\pi , \pi )$ because its inverse map converges everywhere.

c) From (B.8) for $\varepsilon$ small enough a tedious expansion gives

$$\begin{aligned} \bigg \vert \frac{d \theta _{\varepsilon ,\gamma }^{(B)}}{d M} \bigg \vert \ge \bigg \vert \frac{d \theta _{\varepsilon ,\gamma }}{d \rho }\bigg \vert - \varepsilon \vert {\mathcal {R}}(B,M,\varepsilon )\vert \ge \frac{1}{C}\bigg \vert \frac{d {\theta }_{\varepsilon ,\gamma }}{d \rho }\bigg \vert \end{aligned}$$

(B.10)

where $C >1$ is a constant, $\mathcal {R}$ is bounded in $\varepsilon$. The claim follows thanks to Proposition A.1 in [8]. $\square$