1 Introduction

Recently, nanomaterials had great curiosity ever since their discovery to the scientific society due to their distinct properties and daily life applications in advanced technology. Researchers have been concerned in exploring materials in their nanoscale sizes because of their high surface area leading to improved properties in comparison with the bulk materials counterpart. Among various nanomaterials, ferrites are one of the important categories of nanomaterials, especially the transition metal-based ferrites are important materials due to their appealing properties such as structural, magnetic, electrical, and thermal properties [1]. the transition metal-based ferrites have very important applications as ferrofluids, photovoltaics, high-frequency devices (MHz to GHz) [2], and high-density recording media devices [3]. One of these interesting ferrites is cobalt ferrite which is widely studied because of its cubic structure, high coercivity, and superior chemical stability [4]. In addition to various technological applications were observed to relay on ferrites such as magnetic resonance imaging (MRI), sensors, motors, inductors, telecommunications, recording media, radar systems, electromagnetic interference (EMI), electronic circuits [5], memory cores, and biomedical applications [6]. The charming crystal structure of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) is inverse spinel structure, in which Co is a divalent atom that takes up half of the octahedral B-site, while Fe is a trivalent atom that occupies the other half of the octahedral B-site and all tetrahedral A site. The spinel ferrites exhibit high magnetic properties that are related to the exchange between A–B sublattice which is the more dominated one [7]. Doping ferrites with other metal ions such as (Zn, Cu, Ni, and Gd) is aimed to develop the physicochemical properties of nano-ferrite necessary for their purposes such as antibacterial agents [8], photocatalysis [9], and industrial applications [10]. Many studies confirmed that doping affected the structure, morphology, and related physical properties [11]. One of challenges in such applications the generation of a large amount of heat during the working of devices is the thermal management [12]. The discrepancy between the thermal properties of magnetic oxide materials and electrode substrate would be responsible for producing thermal stresses. If the thermal stress is large enough, it would lead to crack the materials during the cycling operation [13]. Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) nanomaterial is a good material for magnetic applications, so to improve its thermal properties, metal oxide phase such as \({\mathrm{Cu}}^{2+}\) and \({\mathrm{Zn}}^{2+}\) were doped in Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) matrix to enhance its thermal properties and overcome the thermal stress between the material and substrate.

Literature survey was made on recently published papers in cobalt ferrites and summarized as following. Rather et al. [5] have studied the effect aluminum ions on structural and magnetic properties of cobalt ferrites. X-ray diffraction, particle size analysis, thermogravimetric analysis, differential scanning calorimetry (DSC), scanning electron microscopy and energy-dispersive X-ray. Magnetic-Hysteresis (M–H) measured by vibrating sample magnetometry (VSM) and X-ray photoelectron spectroscopy (XPS) studies. Mahajan et al. [14] have synthesized series of cobalt ferrites-doped manganese. The single-phase spinel structure with cubic symmetry was assured by the XRD studies. The crystallite size lies in the nanoscale range of 35.4–43.6 nm. FTIR spectroscopy affirms the formation of spinel structure. FESEM micrographs reveal the presence of non-uniform grain Growth VSM study exhibits soft ferromagnetic nature due to the low coercivity value. Bajaj et al. [15] have used the sol–gel auto-combustion method to prepare a series of (In)-doped cobalt ferrites. XRD shows the formation of single-phase cubic spinel structure. The FE-SEM images of the typical samples show the well formation of spherical grains of average grain size 36 nm. The particle size determined from TEM histogram is found to be 35 to 32 nm. M–H plot reflects that the saturation magnetization overall decreases with doping due to the decreasing A–B interaction. The real and imaginary part of dielectric constant varies exponentially with frequency. The dielectric constant decreases with (In) doping. Jiang et al. [16] were synthesized the doped Zn–Cu–Co-ferrites by the sol–gel method. X-ray diffraction showed the cubic spinel structure of the sample. Fourier transform infrared revealed information about the functional groups of the sample chemical properties. The morphologies of the ferrite samples were observed as spherical and cubic shapes and the samples had polycrystalline structures by transmission electron microscopy and selected area electron diffraction patterns. energy-dispersive spectroscopy revealed the absence of other impurity elements. The magnetic properties of the samples were analyzed by hysteresis loops. The coercivity first decreased and then increased with the increase in doping amount. The coercivity showed that the samples were soft magnetic materials. They demonstrated that these materials are suitable for communication and high-frequency components.

However, it is strongly observed that the recent published papers gave focused on the structural and morphological associated with one or two physical properties. The full study of cobalt nanoferrites were absent in this literature. The need to full characterization of these cobalt ferrites doped with transition metals such as (copper and zinc) motivates us to do this task. The current full study aims to deal with all sides of property study of cobalt ferrites. The structural was investigated using XRD and FT-IR, the morphology was scrutinized by FESEM and HRTEM, the mechanical properties were evaluated, the dielectric characteristics were explained, the magnetic properties were determined using vibrating sample magnetometer, and the thermal features were assessed such as thermal diffusivity, thermal conductivity, and specific heat of our doped cobalt ferrites. The enthusiasm behind the choice of doping with Cu and Zn on Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) ferrite was: (1) Ferrites have very special properties where they have unique magnetic, dielectric, electrical, and structural features; (2) the electric and magnetic properties of cobalt ferrite are sensitive to Cu and Zn content, (3) few articles were discussed how the ferroelectric, thermal, and elastic properties changed by doping Zn and Cu on Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\). Therefore, a full study was carried out on the cobalt ferrite and its derivatives. The main idea was driven by carrying out a treatment of all limitations in such material as reported in the previous literature. The relationship between the crystal structure and physical properties of the doped cobalt ferrite was here presented. Structural, mechanical, thermal, electrical, and magnetic investigations were made. The novel obtaining findings were found to pave the route toward exploiting such material in different technological applications.

Here, in this work, according to our knowledge, there is a need to fully characterize a n nano-ferrite material and its derivatives utilizing in the electronic applications. So, we used the citrate auto-combustion technique to successfully prepare a series of ferrites: \({\mathrm{M}}_{x}{\mathrm{Co}}_{1-x}{\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\); [M: Zn or Cu and x = 0.5]. A set of complementary experiments were carried out to study these samples. The current work represents a systematic investigation of the impact of zinc and copper doping on the crystal structure nature, morphology, thermal, electric, and magnetic characteristics. Such new obtained data related to the crystal structure and its interrelationship with other properties are important in applications of cobalt ferrite-doped with zinc.

2 Experimental procedures

2.1 Materials

Iron nitrate Fe(N\({\mathrm{O}}_{3}{)}_{3}\)·9H2O (99%), cobalt nitrate Co(N\({\mathrm{O}}_{3}{)}_{2}\)·6\({\mathrm{H}}_{2}\)O, copper nitrate, Cu(N\({\mathrm{O}}_{3}{)}_{2}\)·6\({\mathrm{H}}_{2}\)O (99%), zinc nitrate [Zn(N\({\mathrm{O}}_{3}{)}_{2}\)·6\({\mathrm{H}}_{2}\)O] and citric acid (\({\mathrm{C}}_{6}{\mathrm{H}}_{8}{\mathrm{O}}_{7}\)) were purchased from Sigma-Aldrich and used as mineral precursors, without any purifications.

2.2 Nanoparticles preparation

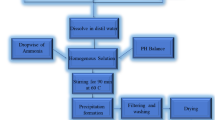
Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) nanoparticles were successfully prepared using the citrate spontaneous combustion technique as shown in Fig. 1. The required stoichiometric quantities of cobalt nitrate, copper nitrate, zinc nitrate, and iron nitrate as well as citric acid were dissolved in a small appropriate amount of distilled water, then harshly stirring was done. Then the pH value of the solution was adjusted to 7.0 and the solution’s temperature was increased to 250 °C to initiate the reaction and all fumes were gone. The final powder was annealed for 4 h at 800 °C at a rate of 4 °C/min. The resulting powder was ground in an agate mortar and preserved in a desiccator to prevent moisture from the air. The obtained samples, now, are appropriate for a set of characterization.

Fig. 1
figure 1

Flow chart for the synthesis of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) nanoparticles

Full size image

2.3 Nanoparticles characterization

The sample preparation in single-phase and without any impurities was confirmed through X-ray diffractometer type of analytical-x'pert pro, Netherlands. The diffractometer was fitted with Cu \({K}_{\alpha }\) x-ray radiation source with a wavelength of λ = 1.5404 Å. The operating conditions of x-ray tube were at 45 kV and 40 mA). The diffractograms were collected from 20° to 80° for all samples. Field emission scanning electron microscopy (FESEM) has a type of Sigma 300VP, operating at 15 kV, was exploited to study the surface topology of all prepared samples. High-resolution transmission electron microscope (HRTEM) has a type of JEM-ARM300F, operating at 200 kV, was utilized for examining the atomic lattices of all prepared nanoferrites. Fourier transform infrared (FT-IR) spectra were carried out in the wavenumber range of 4000–400 \({\mathrm{cm}}^{-1}\) through a FT-IR spectrometer (Perkin-Elmer 2000). A vibrating sample magnetometer (VSM) has a type of Lakeshore 7410S was exploited to measure the magnetic properties of prepared samples. The dielectric properties such as dielectric constant and electrical conductivity dependent frequencies at different temperatures of the prepared samples were measured by TH2826 (20 Hz–5 MHz) LCR meter. The thermal characteristics such as thermal conductivity, thermal diffusivity, and specific heat of all samples were measured at room temperature using TPS 2500 S, Hot Disk AB. Double nickel wire spirals implanted in KPF (i.e., Kapton polyimide film) were used as a hot disk sensor to generate heat during measurements. Between two cylindrical samples, the sensor was sandwiched with 20 mm of diameter and 10 mm of thickness and left for about 1 h for thermal stability with the surrounding atmosphere. In this study and as the present compositions represent a ceramic material, so the measurement time was set between 2 and 10 s, and the out power was set as 0.2 W while the radius of the sensor was selected to be 2.7 mm.

3 Results and discussion

3.1 Structural properties

The crystal structure of synthesized nanoparticles was confirmed by X-ray diffraction. Figure 2 depicts X-ray diffraction patterns of synthesized Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) nanoparticles. The XRD results confirmed the formation of the cubic ferrite spinel structure. All samples’ patterns indicated the formation of single-phase according to the ICDD cards [04-024-0072], [04-005-7078], [00-065-0376] and [04-002-0421] for \({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) respectively. All the investigated samples were found to belong to the space group (Fd-3m), and space group number (227).

Fig. 2
figure 2

XRD pattern (a) and Rietveld Analysis (b–d) of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) nano powder

Full size image

The crystallite size of the studied samples was computed through the X-ray line expansion method according to the Scherrer’s equation (Eq. 1) [17]:

$$D= \frac{0.9 \lambda }{\beta \mathrm{cos}\theta },$$
(1)

where λ is the radiation wavelength, θ is the diffraction angle, and β is the full width at half maximum (FWHM) of the diffraction peak. The crystallite size of the Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) nanoparticles was found to be 8, 15, and 14, respectively. The lattice constants were 8.4 nm, 8.39 nm, and 8.42 nm, respectively. All XRD patterns were examined using the Full-PROOF software, which is based on the Rietveld refinement process. The Rietveld fits were carried out utilizing the fundamental initial input parameters of cubic symmetry (with the Fd-3m space group) for Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\). At ambient temperature, the Rietveld refinement of an X-ray powder diffraction pattern for Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) ferrites is shown in Fig. 2b–d. A pseudo-Voigt function was applied to simulate the peak profile based on Fd-3m space group. The oxygen coordinates (x = y = z = u) were considered free parameters, but all other atomic fractional values were assumed to be fixed. A good agreement between the observed and calculated diffraction patterns is observed using the Rietveld analysis, which is verified by determining the difference pattern in the measured and calculated XRD patterns. A good agreement between the observed and calculated diffraction patterns is indicated using the Rietveld analysis, which is verified by determining the difference pattern in the measured and calculated XRD patterns. Table 1 presents the refinement fitting parameters, lattice parameter a (Å), amounts of different cations in A- and B-site for Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) ferrites. Cation distribution throughout the analyzed sample systems confirms the mixed spinel structure. Inhomogeneities inside the crystal are caused by the random distribution of cations across the two interstitial sites. These inhomogeneities, as well as the size discrepancy between host and dopant cations, are found to be responsible for the observed increase in lattice strain in doped samples, which is also caused by differing ionic radii in the lattice sites.

Table 1 Amounts of different cations in A- and B-site for Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) along with detailed Rietveld parameters
Full size table

Furthermore, structural details, the dislocation density (\(\delta )\) of such nanoparticles was calculated using the next relation [18]:

$$\delta =1/{D}^{2}$$
(2)

The obtained values of the crystallite size and dislocation density are listed in Table 3.

As well as the lattice parameters of the prepared specimens were computed using the diffraction planes by the following relation [18]:

$$\alpha =d\sqrt{{h}^{2}+{k}^{2}+{l}^{2}},$$
(3)

where \(\alpha\) represents the lattice constant, d is the inter-planar spacing, and the respective h, k, l are Miller indices. An additional informative parameter is the lattice strain. It was obtained using the Williamson–Hall (W–H) equation for peak broadening (β) as [18]:

$$\beta \mathrm{cos}\theta = \frac{0.9 \lambda }{D}+4 \varepsilon \mathrm{sin}\theta,$$
(4)

where \(\varepsilon\) is the lattice strain of all samples. Figure 3 displays the W–H plot of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\). The strain value (\(\varepsilon )\) was estimated from the slope of obtained fitted line [18] and listed in Table 3.

Fig. 3
figure 3

The Williamson–Hall (W–H) relation of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) nano-powder

Full size image

The X-ray density of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) nanoparticles was calculated using the following equation [19]:

$${\rho }_{\text{x}}= \frac{ZM}{{N}_{\text{A}}{a}^{3}},$$
(5)

where Z represents the number of formula units in a unit cell, M is the molecular weight, \({N}_{\text{A}}\) is the Avogadro’s number and a is the lattice constant. While the prepared nanoparticles’ bulk densities (\({\rho }_{\text{b}}\) = mass/volume) also were calculated and listed in Table 1, together with values of x-ray density. \({\rho }_{\text{x}}\) and \({\rho }_{\text{b}}\) values have been used to estimate the porosity (P) of the investigated samples using the relation [20]:

$$P=1- \frac{{\rho }_{\text{b}}}{{\rho }_{\text{x}}}$$
(6)

3.2 Elastic properties

FTIR transmittance spectra of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) nanoparticles recorded in the range of 4000–400 \({\mathrm{cm}}^{-1}\) is shown in Fig. 4. It is known in the spinel ferrites, the cations sharing the tetrahedral (A) and octahedral (B) sites, these two structural phases provide vibrational bands at \({\upnu }_{1}\) (tetrahedral) and \({\upnu }_{2}\) (octahedral) [20,21,22], as shown in Fig. 3a–d. The vibrational positions of these two bands are registered in Table 2. These two bands were found to peak at 235, 534, and 529 \({\mathrm{cm}}^{-1}\) for and 470, 429, and 420 \({\mathrm{cm}}^{-1}\) for Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), respectively. The positions of these two bands \({\upnu }_{1}\) and \({\upnu }_{2}\) are affected by the bond length in \({\mathrm{Fe}}^{3+}\)–\({\mathrm{O}}^{2-}\). Generally, the bond length modification is affected by the structural changes of the material. It is observed that the doping of Cu and Zn was found to shift the peaks of (A) and (B) sites towards the lower wavenumber. This may be due to a shorter bond length created by doping.

Fig. 4
figure 4

The FTIR spectra of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) nano-powder

Full size image
Table 2 The crystallite size, dislocation density, microstrain, lattice parameter, molecular mass, x-ray density, bulk density, porosity, and tetrahedral and octahedral vibrational band positions (\({\upnu }_{1}\)) and (\({\upnu }_{2}\)) for all samples
Full size table

The Debye temperature (\({\theta }_{\text{D}}\)) is the crystal’s highest typical vibration temperature, making heat capacity integration easier [23]. (\({\theta }_{\text{D}}\)) of the investigated crystals can be estimated using the \({\upnu }_{1}\) and \({\upnu }_{2}\) values [23] using the following equation:

$${\theta }_{\text{D}}= \frac{hc{\nu }_{\text{avg}}}{{k}_{\text{B}}},$$
(7)

where C is the speed of light, h is Planck’s constant, \({k}_{\text{B}}\) is Boltzmann’s constant and

$${\nu }_{\text{av}}= \frac{{\nu }_{1}+{\nu }_{2}}{2}$$
(8)

Elastic parameters usually reflect the interatomic bonds’ strength and stability. It undergoes the formation of crystalline structures. The elastic moduli are usually corresponding to the rearrangement of cubic crystal lattices in a solid material during a structural phase transition. For the investigated samples, a set of elastic parameters such as the force constants (\({K}_{\text{t}}\)), (\({K}_{\text{o}}\)), (\({K}_{\text{avg}}\)) [24] of the tetrahedral and octahedral sites, respectively, Poisson’s ratio (σ), stiffness constants \({C}_{11}\) and \({C}_{12}\) of longitudinal elastic wave velocity (\({V}_{\text{L}}\)) and transverse elastic wave velocity (\({V}_{\text{t}}\)), mean elastic velocity (\({V}_{\text{m}}\)), Young’s modulus (Y), Bulk’s modulus (B), and rigidity modulus (R), were calculated using the following relations [24,25,26,27]:

$${K}_{\mathrm{o}}=5.31*{10}^{-7} \times {M}_{\mathrm{B}} \times {v}_{2}^{2}$$
(9)
$${K}_{\mathrm{t}}=7.62*{10}^{-7} \times {M}_{\mathrm{A}} \times {v}_{1}^{2}$$
(10)
$${K}_{\mathrm{avg}}= \frac{{K}_{\mathrm{t}}+{K}_{\mathrm{o}}}{2}$$
(11)
$${C}_{11}= {K}_{\mathrm{avg}}/a$$
(12)
$${V}_{\mathrm{L}}= \sqrt{{C}_{11}/{\rho }_{\mathrm{x}}}$$
(13)
$${V}_{\text{t}}= \sqrt{{C}_{11}/3 {\rho }_{\text{x}}}$$
(14)
$$V_{{\text{m}}} = \left[ {\frac{1}{3}\left( {\frac{2}{{V_{t}^{3} }} + \frac{1}{{V_{l}^{3} }}} \right)} \right]^{{ - \frac{1}{3}}}$$
(15)
$$\sigma = 0.5 - \frac{0.5}{{\left( {\frac{{V_{{\text{L}}} }}{{V_{{\text{t}}} }}} \right)^{2} - 1}}$$
(16)
$${C}_{12}= \frac{{\sigma C}_{11}}{1-\sigma }$$
(17)
$$Y= \frac{({C}_{11}-{C}_{12})({C}_{11}+2{C}_{12})}{({C}_{11}+{C}_{12})}$$
(18)
$$B=\frac{1}{3} [{C}_{11}+2{C}_{12}]$$
(19)
$$R= {\rho }_{\text{x}} {V}_{\text{t}}^{2}$$
(20)
$$U_{{\text{L}}} = 3.108 \left( {MV_{{\text{m}}}^{2} } \right)10^{ - 5}$$
(21)

The obtained elastic parameters of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) are listed in Table 3.

Table 3 Elastic parameters of the prepared samples
Full size table

From Table 3, it can be observed that the incorporation of copper and Zinc in the Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) crystal has improved the crystal elastic properties of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) (i.e., the interatomic bonds strength of the cobalt ferrite was improved by doping). The highest values were obtained when Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) doped by copper. According to the Vegard's law [28], the Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) lattice parameter increased by the incorporation of copper and decreased by Zinc into the crystal. The similar oxidation state of \({\mathrm{Co}}^{2+}\), \({\mathrm{Zn}}^{2+}\) and \({\mathrm{Cu}}^{2+}\) made them have the same position in the structure. The variation of the ionic radii, \({\mathrm{Co}}^{2+}\) (0.58 Å for the A-site and 0.745 Å for B-site) [26, 27], \({\mathrm{Cu}}^{2+}\) is (0.57 Å for the A-site and 0.73 Å for B-site) and \({\mathrm{Zn}}^{2+}\) (0.74 Å for A site and 0.88 Å- for B-site) [29, 30]. In general, \({\mathrm{Cu}}^{2+}\) radius is slightly smaller than \({\mathrm{Co}}^{2+}\) makes interatomic bond strength larger, whilst \({\mathrm{Zn}}^{2+}\) radius is slightly greater than \({\mathrm{Co}}^{2+}\) makes interatomic bond strength smaller, explaining the observed variation in the lattice parameter. Also, it is observed that the force constant was increased by 45% and elastic moduli (Y and B) were improved by 46% when Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) crystal doped by \({\mathrm{Cu}}^{2+}\). Poisson's ratio is a quantity that measures the material deformation in a direction perpendicular to the applied force's direction. The magnitude of Poisson’s ratio (σ) of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) was found to increase as the crystal is doped by both copper and Zinc by 66%. This augmentation is likely due to the deformation that occurred in the crystal by the doping process. It is observed that the magnitude of (σ) for both Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) samples was fixed at (σ = 0.25), which is consistent with the isotropic elasticity theory.[28]. At the same time, Debye temperature θD was decreased by the addition of copper and Zinc, where the lowest value was obtained for Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) doped by zinc. In addition, Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) exhibits the smallest dislocation density (δ). An additional informative parameter is the lattice energy \({U}_{\text{L}}\). The obtained values of the lattice energy were increased by the doping process due to the augmentation of the interaction between ions. Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) exhibits the highest \({U}_{\text{L}}\) value because of it has the smallest radius. Consequently, the energy was released during the doping process depending on the change in the size of ions, the distance between their nuclei, and the attraction between them.

Finally, from Tables 2 and 3, Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) had the smallest values of dislocation density, lattice parameter, and porosity, and the largest microstrain, bulk density, and elastic properties. This behavior is related to the Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) strongest interatomic bonds decreased the dislocation density and porosity inside the unit cell and increased its elastic properties.

3.3 Morphological studies

The FESEM images of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) nanoparticles are shown in Fig. 5. The FESEM images reveal the formation of agglomerated clusters in all samples. The largest clusters size was observed for Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) sample, whilst the lowest of them were observed in Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) sample as shown in Fig. 5. These clusters sizes depend on the electrostatic forces between Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) and the dopant material (Cu or Zn). Figure 6 illustrates the HRTEM micrographs of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) samples. The HRTEM graphs reveal the cubic shape structure for all samples. The figure confirms the nanoscale of the nanoparticles with few agglomerations. HRTEM graphs show uniform diffraction fringes, indicating the crystalline properties of all investigated nanoparticles samples. Particle size histogram of the investigated samples estimated from HRTEM illustrated in Fig. 6.

Fig. 5
figure 5

FESEM micrographs and grain size error bars of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) nano-powder

Full size image
Fig. 6
figure 6

HRTEM micrographs of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) nano-powder

Full size image

3.4 Magnetic properties

magnetic-hysteresis loops (M–H) of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) samples at room temperature are shown in Fig. 7. Magnetic parameters such as saturation magnetization (\({M}_{\text{s}}\)), coercivity (\({H}_{\text{C}}\)), remanent magnetization, (Retentivity, \({M}_{\text{r}}\)), magnetic susceptibility (χ), flatness, and squareness were obtained from the measured hysteresis loop of samples. The obtained hysteresis loops of all investigated samples are of the typical ‘S’ type, indicating obvious ferrous magnetism. However, it is observed that the magnetization parameters varied by changing the doping material. As shown in Table 4, the substitution by (copper and Zinc) were lowered the magnetic parameters values of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\). In ferrite, the saturation values are belonging to the (A) site–(B) site anti-parallel coupling interaction. This interaction is sufficient to overcome any inclination for A–A or B–B pairings to disrupt the parallel orientation of all spins inside the A-site or B-site groups [31]. Based on the domain structure, critical diameter, and the crystal’s anisotropy [32,33,34], the replacement of \({\mathrm{Co}}^{2+}\) ions by \({\mathrm{Cu}}^{2+}\), and \({\mathrm{Zn}}^{2+}\) ions cause the super-exchange interaction between the A- and B-sites to be reduced.

Fig. 7
figure 7

magnetic-hysteresis loops (M–H) of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) at room temperature

Full size image
Table 4 The saturation magnetization (\({M}_{\text{s}}\)), coercivity (\({H}_{\text{C}}\)), remanent magnetization (\({M}_{\text{r}}\)), magnetic susceptibility (χ), flatness, and Squareness of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\)
Full size table

3.5 Thermal properties

The generated temperature of the hot disk sensor and as consequently the setting parameters are related to the thermal characterizations of the measured sample, and it can determine via the next equation [35]:

$$\Delta T \left(t\right)=\frac{\sqrt{\kappa t/{r}^{2}}}{K},$$
(22)

where K is the thermal conductivity, \(\kappa\) is the thermal diffusivity of the measured sample which refer to the diffusion energy to storage energy ratio and must be lower than 1 for ceramic materials, while the radius of the nickel sensor is r. Moreover, the thermal conductivity can correlate with the thermal diffusivity by the following equation [35]:

$$K=\uprho {C}_{\text{p}} \kappa,$$
(23)

where ρ is the sample density and \({C}_{\text{p}}\) is the specific heat of surrounding samples. The thermal conductivity, thermal diffusivity, and specific heat of the Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) samples were measured at room temperature and the data are listed in Table 5. The thermal conductivity of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) changed by the doping ions variation. The thermal conductivity and thermal diffusivity of pure Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) were enhanced by the incorporation of Zn and Cu ions as a result of the formation of conductive particle chains into the crystal lattice of pure Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) where the heat can flow more easily. The thermal conductivity and thermal diffusivity increased from 0.6 W/m k, 0.52 mm2/s for pure Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) to 0.82 W/m k, 0.6 mm2/s for Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\). Furthermore, the largest thermal conductivity (0.95 W/m k) and thermal diffusivity (0.75 mm2/s) were achieved for Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\). This could be due to the superior thermal properties of copper (398 W/m k) rather than zinc (113 W/m k). A similar result of thermal conductivity of pure Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) was reported by Ivan Djurek et. al. [36].

Table 5 The thermal conductivity, thermal diffusivity, and specific heat of all prepared nano-ferrites
Full size table

3.6 Electrical properties

Studying the electrical properties is an important topic in material science [37]. The real part of the AC conductivity for the three studied nanoparticle samples of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) was carried out in the frequency range from 20 Hz to 5 MHz at different temperatures from RT up to 250 °C. Figure 8 portrays the dependence of electrical conductivity on the frequency logarithm for (a) Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), (b) Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) and (c) Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\). It is well-known that ferrite consists of double superimpose layers. The first one is poorly conducting grain boundaries, while the second one is well-conducting grains. The poor conductive grains are initially active in the low frequency range, whereas the high conductive grains are initially active in the high-frequency [38]. Consequently, the electrical conductivity exhibits small values at low frequency, whilst it gives high values at high-frequency, as shown in Fig. 8. Additionally, the electrical conductivity of prepared samples shows a strong compositional dependence, it is observed that the values of electrical conductivity were found to be high for Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), then they shrink for Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), reaching to Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) which involved the lowest values, (i.e., the addition of Cu and Zn at the expense of Codiminishes the electrical conductivity, respectively). Also, as can be seen in Fig. 8, with increasing the temperature the electrical conductivity was increased. Generally, \({\mathrm{Fe}}^{3+}\) ions can exist at both A-sites and B-sites, favoring the B-sites [39]. The electrical conductivity of such ferrites is mainly due to the electron hopping between \({\mathrm{Fe}}^{2+}\) ↔ \({\mathrm{Fe}}^{3+}\) ions in the octahedral positions (i.e., B-sites). It is well-known that the \({\mathrm{Co}}^{2+}\) ions occupy the octahedral-coordinated sites, participating in the conduction process [39], with increasing the temperature, \({\mathrm{Co}}^{2+}\) ions oxidize to \({\mathrm{Co}}^{3+}\), creating the positive holes. So, electron hopping is accompanied by positive holes (\({\mathrm{Co}}^{2+}\) ↔\({\mathrm{Co}}^{3+}\)) enhances the electrical conductivity of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\). On the doping hand, \({\mathrm{Cu}}^{2+}\) ions have a strong predilection for octahedral locations, with an amount (~ 20%) residing at A-sites [39]. Therefore, \({\mathrm{Cu}}^{2+}\) ions may cause some \({\mathrm{Fe}}^{3+}\) ions to move from B-sites to A-sites, decreasing the electron hopping between \({\mathrm{Fe}}^{2+}\) ↔ \({\mathrm{Fe}}^{3+}\) ions at octahedral sites. So, the electrical conductivity mitigates. \({\mathrm{Zn}}^{2+}\) ions exhibit a strong predilection for tetrahedral sites. As zinc ions are embedded in A-sites, they do not take part in the conduction process. Observable mitigation in the conductivity results from the substitution of \({\mathrm{Co}}^{2+}\) by \({\mathrm{Zn}}^{2+}\) ions. This is due to the ionic size of the indicated \({\mathrm{Zn}}^{2+}\) cation. The ionic radius of the \({\mathrm{Zn}}^{2+}\) cation on octahedral coordination is bigger than that of \({\mathrm{Co}}^{2+}\) in the same coordination site. Such a size effect of the ionic radius causes harsh distortion of the crystal lattice, which in its turn hinders the electron hopping exchange, worsening the conductivity.

Fig. 8
figure 8

Electrical conductivity against the frequency logarithm at different temperatures of all prepared nano-ferrites

Full size image

It is well-known that the permittivity (\({\varepsilon }_{\mathrm{r}}\)) is the amount of energy that is transferred from an external electric field to the sample. The permittivity of the spinel ferrite depends on extrinsic and intrinsic factors. The extrinsic factors are related to the doping atom type and the morphology of the sample (i.e., grains and grain boundaries). Whereas the intrinsic factors are associated to the polarizability, the doping ionic radius, and the electric dipole moments [40, 41]. Generally, the spinel ferrites exhibit a usual behavior of permittivity that decreases with the frequency increasing. The variant of permittivity with frequency logarithm for the three studied nanoparticle samples of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) were also investigated in the temperature range from RT up to 250 °C. Figure 9 displays a similar behavior, it is observed that the permittivity is high at low frequencies and mitigates with the increase in frequency, at various temperatures. Additionally, it is noticed that the giant permittivity values were obtained at high temperatures. Such observed behavior is a general trend for such spinel ferrite. This behavior can be explained by the double-layer mechanism. Ferrites have grain boundaries, which are well conducted, and are separated by weak conducting grain boundaries. This superimpose structure supports space for charge agglomeration under the influence of an electric field, causing interfacial polarization (i.e., there is electric dipoles' inability to be convoyed with the frequency of the applied electric field) [40,41,42]. At low frequency, the polarization resulting from electron hopping between \({\mathrm{Fe}}^{3+}\) ↔ \({\mathrm{Fe}}^{2+}\) is high, and the permittivity increases. When the frequency of the alternating applied electric field increases, it is no longer followed by the charge carriers, shrinking the polarization then the permittivity worsens [43,44,45,46].

Fig. 9
figure 9

The reliance of permittivity on the frequency logarithm at different temperatures of all prepared nano-powder

Full size image

On the other hand, the Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) exhibits high values of permittivity with increasing the temperature due to the increasing number of \({\mathrm{Fe}}^{3+}\) ions at the octahedral sites.\({\mathrm{Cu}}^{2+}\) ions may decrease the electron hopping between \({\mathrm{Fe}}^{2+}\) ↔ \({\mathrm{Fe}}^{3+}\) ions at octahedral positions. So, the permittivity mitigates for Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) ferrite. The effect of ionic radius for \({\mathrm{Zn}}^{2+}\) cation on octahedral coordination causes harsh distortion of the crystal lattice, which in its turn hinders the electron hopping exchange, lowering the permittivity.

4 Conclusion

Nanoferrites of pure and doped M–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) (M=\({\mathrm{Cu}}^{2+}\) and \({\mathrm{Zn}}^{2+}\)) were prepared successfully by citrate auto-combustion technique. The impact of doping by \({\mathrm{Cu}}^{2+}\) and \({\mathrm{Zn}}^{2+}\) on cobalt ferrite were fully investigated. Decent findings were obtained contribute understanding the relationship between the crystal structure and the physical properties. The present study showed that the dopant ions affected the cobalt ferrite elastic properties, especially in the case of \({\mathrm{Cu}}^{2+}\) where its force constant increased by 45%, the elastic moduli by 46%, and its Poisson’s ratio by 66%. In general, the cobalt ferrite elastic properties were improved remarkably by doping process. The highest saturation magnetization was observed for virgin sample, Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), (56.1 emu/g) compared to it being 46.9 and 45 emu/g for Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), respectively. The highest magnetic susceptibility (0.639) was obtained for Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\). In addition to the incorporation by \({\mathrm{Cu}}^{2+}\) and \({\mathrm{Zn}}^{2+}\) improved the thermal features of Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\)-doped Zn and Cu rather than virgin Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), predicting required thermal stability in the working devices. The Cu–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) sample exhibits the highest value of thermal conductivity (0.95 W/m k, W/m k, increased to ~ 58%), thermal diffusivity (0.75 m \({\mathrm{m}}^{2}\)/s, increased to ~ 44%), and specific heat (0.85 Mj/\({\mathrm{m}}^{3}\) k) compared to (0.6 and 0.82 W/m k), (0.52 and 0.6 m \({\mathrm{m}}^{2}\)/s), and (0.62 and 0.72 Mj \({\mathrm{m}}^{3}\) k) for Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\) and Zn–Co\({\mathrm{Fe}}_{2}{\mathrm{O}}_{4}\), respectively. The present study offers well-completely characterization for virgin and doped cobalt ferrite material suitable as basic working materials for different applications.