Exploring the impact of nickel doping on the structure and low-temperature magnetic features of cobalt nano-spinel ferrite

Abstract

Tailoring the magnetic features of cobalt ferrite nanoparticles (NPs) has been achieved via varying the doping percent of nickel. The nickel-substituted cobalt ferrite NPs Ni_xCo_1-xFe₂O₄ (0 ≤ x ≤ 1.0) are constructed by the eco-friendly coprecipitation method. The formation of a nearly cubic single-phase spinel frame is assured by the analysis of XRD data. Moreover, the Rietveld analysis based on structure refinement is implemented in this study to precisely determine the microstructural parameters and estimate the cation distribution. A linear drop-in lattice constant with boosting the Ni²⁺ ion percent is acclaimed, in regard to Vegard's law. The creation of nanoparticles that are nearly spherical along with polyhedron shape and have a diameter of (about 39–45 nm) has been affirmed by utilizing high-resolution transmission electron microscopy (HRTEM). Also, the crystalline essence of the formed nanoparticles has been declared by selective area electron diffraction (SAED). The magnetic properties have been collected from the hysteresis loops and FC–ZFC curves. These curves have been tweaked as a function of low-temperature from 5 K up to 300 K and in the existence of an external magnetic field (± 70KOe). The magnetization curves revealed that CoFe₂O₄ (NPs) correspond to the hard ferrimagnetic material, whereas NiFe₂O₄ (NPs) matched well with identical soft ferrimagnetic material. Also, the divergence betwixt the theoretical and experimental values of the magnetic moment is well explained by the model of "Random Canting of Spins, (RCS)". In addition, a remarkable reduction is found in the recorded values of magnetic parameters by increasing Ni²⁺ content and decreasing the temperature towards 5 K. These findings imply the potential of Ni²⁺ ions doping in enhancing the magnetic properties of cobalt ferrite for vast magnetic applications.

1 Introduction

For decades, the applications of nanoparticle magnetic materials have drawn widespread attention in high-frequency devices, magnetic resonance imaging, recording media, ferrofluid, drug delivery, sensors/detectors, catalysts, and magneto-optical devices. These nano-materials have been influential due to their distinct electronic, optical, electrical, radiation shielding, magnetic properties, and low (NiFe₂O₄) or high (CoFe₂O₄) magnetic coercivity, which is typically altered bulk structure [1,2,3,4].

One of the major topics to be investigated in this field is the spinel ferrite materials that have the formula (M²⁺)[Fe³⁺]O₄, where M²⁺ is a divalent cation such as (Mn²⁺, Co²⁺, Ni²⁺, Mg²⁺, Zn²⁺, etc.). The M²⁺ and Fe³⁺ cations are doled out amongst the octahedral (B-) and tetrahedral (A-) interstitial positions in the FCC sub-lattice. Such distribution can be represented by: (M_1-λ²⁺ Fe _λ ³⁺) [M _λ ²⁺ Fe_{2- λ} ³⁺] O₄; where λ reveals the degree of inversion. Relying on the value of this inversion parameter ($\uplambda$), the cubic spinel ferrite structure has mainly three spinel systems. The regular spinel appears when λ = 0, while $\uplambda$ = 1 implies a reverse spinel, whereas $0<\uplambda <1$ involves the so-called mixed spinel.

Many prominent applications such as data recording and biomedical drug delivery applications depend mainly on the degree of softness or hardness of magnetic materials. Therefore, several studies have focused on combining soft and hard magnetic materials to synthesize valuable new materials with controllable functions. To tailor the magnetic features of ferrite nanoparticles, good control is required on both the percent between the soft (e.g. nickel) and hard (e.g. Cobalt) magnetic phases as well as the nanoparticle size in the prepared material [5, 6]. In addition, some features, such as cation distribution, microstructure, magnetic properties, size of particles, and optical parameters are greatly influenced by the synthesizing method. The recent development in the area of Nano-technological synthesis has stemmed from the evolutionary synthesize of ferrite by controlling its size, morphology, and chemical composition to allow tailoring its various properties for specific applications [7, 8]. Widely considered techniques include solid-state reaction [9], sol–gel [10], co-precipitation, combustion reaction synthesis, hydrothermal [11], and microemulsion methods [12]. Among the aforementioned techniques, the co-precipitation method is considered an ecofriendly and economical technique, which has a low-cost precursor and a relatively short reaction time [13]. With regard to the aforesaid information, the authors planned to make a deep investigation of tailoring the properties of a semi-hard magnetic material (cobalt ferrite (CoFe₂O₄)) by varying the doping concentration of one of the famous soft elements (nickel). This could enrich our current knowledge regards to this interesting material which enables the scientific community in exploiting it in several potential applications.

One of the fascinating spinel ferrites is the cobalt ferrite (CoFe₂O₄). The cobalt ferrite nano-sized materials are well proven as semi-hard magnetic materials that are influenced by the types of cations as well as their distribution among the interstitial sites in the lattice. This exhibits unique characteristics that enable scientists to use it in widespread applications for instance recording media, drug delivery, medical diagnostics, magneto-mechanical devices, magnetic refrigeration, light spin filter information storage, and ferrofluid technology [14,15,16]. Remarkable scientific studies have been conducted by researchers to fabricate and study Co ferrite NPs and their composites to enhance their physical properties. Despite several reports have investigated the magnetic features of spinel nickel and cobalt ferrites [17,18,19,20,21]. A lack of knowledge still exists with regard to the magnetic characteristics of Ni substituted CoFe₂O₄ NPs, especially at low temperatures [22, 23]. K. Maaz et al. synthesized the magnetic NPs of Ni-substituted Co ferrite (Ni_xCo_1-xFe₂O₄) by utilizing the co-precipitation route [6]. Their results based on the magnetic measurements demonstrated that the formed NPs at room temperature are vastly magnetic. Also, superparamagnetic blocking temperature revealed a lowering trend with the increment in the Ni-percent. Brajesh et al., [24] incorporated nanocrystalline Ni_1-xCo_xFe₂O₄ (x = 0.0, 0.4, 0.5, 0.6, 1.0) by utilizing the sol–gel approach. Both Rietveld and Raman spectroscopy techniques showed a very good agreement in the cation distributions in the synthesized materials. Adel Maher et al. [25] studied structural and magnetic features for Co_xFe_3-xO₄ nanoferrites (x = 0.5–1.2, with a step of 0.1) which were synthesized using the citrate-precursor auto combustion approach. They reported a forceful reliance of the magnetic characteristics on cation distribution.

From another point of view, the ferrite framework is marked by the FCC lattice of oxygen ions with octahedral and tetrahedral interstitial positions filled by trivalent and divalent metallic ions. Two sublattices are formed as a result of the two interstitial positions. There are three kinds of super-exchange interactions: A–A, B–B, and A–B. The A–B interaction is forceful among them [26]. Lassoued et al. [27] studied the magnetic properties of Ni–Co ferrite at room temperature. They indicated that the magnetic features such as coercivity and saturation magnetization of the compounds remarkably change with the concentration of Ni^2+‏.

It is worth mentioning that the fabrication of pure single-phase Ni–Co spinel ferrite NPs and investigating their low-temperature magnetic properties have not been covered properly in the literature. Hence, either development of traditional methods or exploring a novel approach for fabricating stoichiometric phase-pure spinel ferrites on wide-ranging presents an in dire need for scientists in this field. So, the main purpose of this work is to prepare the Ni–Co ferrite nano-spinel structure in a single-phase nanocrystalline form using the co-precipitation method. This method is considered an eco-friendly and economical technique. Where it is carried out without requiring hazardous organic solvents, or treatments under high pressure or temperature at a low-cost precursor [13]. In addition, this method helps in synthesizing monodispersed nanoparticles by regulating the nucleation and particle growth kinetics in a homogeneous solution". Moreover, we will try to fulfill the lack of knowledge regards to the low-temperature magnetic features of these fascinating nanoparticles. Further, integration of (Ni²⁺) ions into CoFe₂O₄ causes more control on the magnetization which means on the magneto-crystalline anisotropy, and the coercivity (H_c) for diverse implementation potential in magnetic recording. This study is considered a complementary work to our previous paper [28].

2 Experimental technique

2.1 Synthesis and characterization

The well-known co-precipitation technique has been utilized to synthesize the nanocrystalline ferrites Ni_xCo_1-xFe₂O₄, where x = 0.0, 0.3, 0.5, 0.7, and 1.0 by applying the approach used in our previous work [28]. Figure 1 depicts a schematic flowchart that implies a summary of the experimental work involved in this research. Furthermore, the spinel structure of the prepared samples was assured utilizing X-ray diffractometer (XRD) Philip model X’pert. Besides, the nano-sized nature of the investigated samples was inspected using the (HRTEM) (JEOLJEM-2100) which works at an accelerating voltage of 200 kV.

Fig. 1

A schematic flowchart that explains the experimental procedures applied in the research work

The magnetization has been recorded using a Superconducting Quantum Interference Device (SQUID) Magnetometer type MPMS-XL with magnetic field cycling ± 70 KOe in a range of temperature from 5 up to 300 K. To avoid any physical locomotion of the NPs through the experiments and to diminish the dipolar inter-particle interactions, a plastic tube has been exploited to compact samples. Also, in both the zero-field cooling (ZFC) and field cooling (FC) modes, the thermal variation of the dc susceptibility of each specimen has been recorded under applying a magnetic field of 50 Oe, 100 Oe, and 200 Oe in the temperature ambit 5–300 K.

3 Results and discussion

3.1 Rietveld refinement and lattice parameter determination

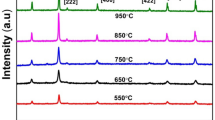
The XRD diffraction diagrams of the prepared Ni_xCo_1-xFe₂O₄ (x = 0.0, 0.3, 0.5, 0.7 and 1.0) compositions are shown in Fig. 2. The data confirm the single-phase nature of the spinel structure. All the diffraction peaks for the samples are indexed to the spinel ferrite with cubic structure and space group of Fd3m. XRD data are inspected by applying Rietveld analysis using the FullProf program. The fitting quality of the X-ray data is tested by the goodness of the fit $\left(\upchi ={R}_{\mathrm{wp}}/{R}_{\mathrm{exp}}\right)$, where (R_wp) stands for the weighted profile R-factor (R_wp), and (R_exp) is the expected R-factor [29]. Based on Rietveld's analysis, lattice parameter (a_R) is obtained.

Fig. 2

Rietveld refined XRD patterns of Ni_xCo_1-xFe₂O₄ specimens, where x = 0.0, 0.3, 0.5, 0.7 and 1.0

3.2 Cation distribution

To estimate the cation allocation in specimens under investigation, the theoretical lattice parameter is evaluated according to the expression [30]:

$$ {\raise0.7ex\hbox{$8$} \!\mathord{\left/ {\vphantom {8 {3\sqrt 3 }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3\sqrt 3 }$}}\left[ {\left( {r_{A} + R_{o} } \right) + \sqrt 3 \left( {r_{A} + R_{o} } \right)} \right], $$

(1)

where (r_A) and (r_B) are the radii of A-sites and B-positions, respectively. Based on the cation distribution [25],$\left({\mathrm{Ni}}_{\mathrm{\alpha }}^{2+} {\mathrm{Co}}_{\upbeta }^{2+} {\mathrm{Fe}}_{1-\mathrm{\alpha }-\upbeta }^{3+}\right)\left[{\mathrm{Ni}}_{\mathrm{x}-\mathrm{\alpha }}^{2+} {\mathrm{Co}}_{1-\mathrm{x}-\upbeta }^{2+}{\mathrm{Fe}}_{1+\mathrm{\alpha }+\upbeta }^{3+}\right]$, both (r_A) and (r_B) have been determined using the following relations [31]:

$$ r_{A} = \left[ { \left( {r_{{t{\text{etr Ni}}^{{2 + }} }} } \right) + \beta \left( {r_{{{\text{tetr Co}}^{{2 + }} }} } \right) + \left( {1 -\alpha - \beta } \right)\left( {r_{{{\text{tetr Fe}}^{{3 + }} }} } \right)} \right], $$

(2)

$$ r_{B} = \frac{1}{2}\left[ {\left( {x - } \right)\left( {r_{{octa Ni^{2 + } }} } \right) + \left( {1 - x - \beta } \right)\left( {r_{{octa Co^{2 + } }} } \right) + \left( {1 + + \beta } \right)\left( {r_{{octa Fe^{3 + } }} } \right)} \right], $$

(3)

where ${r}_{{Ni}^{2+}}$, ${r}_{{Co}^{2+}},$ and ${r}_{{Fe}^{3+}}$ are the ionic radii of Ni⁺², Co⁺², and Fe⁺³ ions. The subscripts (octa) and (tetr) refer to the location of the ions at B- and A-positions, respectively. All the values of ionic radii of the ions have been taken from the website of the "database of ionic radii" [31]. The calculated values of (r_A) and (r_B) are listed in Table 1.

Table 1 Rietveld refinement parameters of Ni_xCo_1-xFe₂O₄ ferrite samples

The best match between the theoretical (a_th), Reitveld (a_R), and lattice constants suggested an appropriate estimation of the cation distribution of the system (see Table 1). As a general trend, boosting the Ni²⁺ ion percent causes a linear diminution in lattice constant in the investigated ferrites (see Fig. 3). This may be understood in accordance with Vegard's law, where the ionic radius of Ni²⁺ ions is smaller than that of Co²⁺ either in A-sites or B-sites [32]. Considering the proposed cation distribution, Co²⁺ and Ni²⁺ ions fill strongly octahedral B-site. At higher substitution of Ni²⁺, ions occupy both octahedral B-position and tetrahedral A-position. Fe³⁺ ions are distributed between B- and A-positions. Similar results have been reported by other authors [33].

Fig. 3

Lattice parameters of Ni_xCo_1-xFe₂O₄ samples (x = 0.0, 0.3, 0.5, 0.7, and 1.0). a_R; from Rietveld, a_th; from cation distribution analysis and a_ref; reference data from Brajesh et al. [24]

3.3 X-ray, bulk densities, and percent porosity

The X-ray density (${\rho }_{x})$ has been estimated for all investigated materials utilizing the formula [28]:

$$ \rho_{x} = ZM/Na^{3} , $$

(4)

where ($Z$) presents the number of molecules in the unit cell of spinel lattice (Z = 8), ($\mathrm{a}$) is the lattice constant, ($M$) represents the sample molecular weight, and ($N$) is Avogadro’s number.

Also, the bulk density (${\rho }_{b}$) has been evaluated by the expression:

$$ \rho_{b} = \frac{m}{{\pi r^{2} h}}, $$

(5)

where m, r, and h refer to the mass, radius, and width of the samples. As observed from Fig. 4, an increase in X-ray and bulk densities by increasing Ni²⁺ concentration is expected as a result of replacing a higher density Ni⁺² ions (8.90 gm cm⁻³) with lower density Co⁺² ions (8.86 gm cm⁻³). The values of ${\uprho }_{\mathrm{b}}$ are lower than those of ${\rho }_{x}$ which may be interpreted to the formed pores in the preparation process [24]. Also, the percent porosity $\mathrm{p}$ has been specified using the formula:

$$ p = 100\left( {1 - \frac{{\rho_{b} }}{{\rho_{x} }}} \right). $$

(6)

Fig. 4

The dependence of X-ray (${\rho }_{x}$), bulk (${\rho }_{b}$) densities and percentage porosity (p%) on the Ni–Co ferrite samples (x = 0.0, 0.3, 0.5, 0.7, and 1.0)

The overall trend of the porosity decreases with increasing the concentration of Ni²⁺ ions, see Fig. 4. The recorded values of $p$ are decreased from 32.81% (for x = 0.0) to 27.80% (for x = 1.0).

3.4 Crystallite size determination

In regard to Scherrer’s equation, the plane (311) as the most intense peak at 2θ = 35.5° has been employed to calculate the crystallite size as follows [24, 34]:

$$ D_{{Sch}} = \frac{{k\lambda }}{{\beta \cos \theta }}, $$

(7)

where D_Sch stands for crystallite size; k (0.9) is the shape factor, λ is the wavelength of used radiation and β is the full width at half maximum (FWHM) (in radians). The magnitudes of crystallite size are found to be in the extent of 22–28 nm (Table 2).

Table 2 Micro-structural parameters of Ni_xCo_1-xFe₂O₄ ferrites

3.5 The Williamson–Hall analysis

The Williamson–Hall method is used to confirm our preceding calculation of the crystallite size and to determine the micro lattice strain. Nanoparticle materials, such as NixCo_1-xFe₂O₄ possess a pronouncing microstrain broadening within its XRD line profile. Such contribution is represented by the Gaussian part. While the crystallite size (${D}_{\mathrm{WH}}$) has a Lorentzian profile. The deconvolution of the line profile to calculate the contributing percentage for both profiles is estimated using the Williamson–Hall method [35].

$$ \beta = \frac{0.94\lambda }{{D_{WH} \cos \theta }} + 4\varepsilon \frac{{{\text{sin }}\theta }}{\cos \theta }. $$

(8)

In this formula, β is the FWHM of the most intensive peak in the recorded diagram, λ is the wavelength, ε is the micro-lattice strain, D_WH is the crystallite size, and 0.94 is the constant for FWHM of spherical crystals with cubic symmetry. The first part in Eq. (8) denotes the crystallite size lattice that depends on 1/cos(θ). While the other part represents the lattice strain which is a function of tan(θ). This indicates how the two parts interrelate differently to Bragg’s angle, θ. Finally, by reordering Eq. (8), it can be rewritten in the following form:

$$ \beta \frac{\cos \theta }{\lambda } = \frac{0.94}{{D_{WH} }} + 4\varepsilon \frac{sin\theta }{\lambda }. $$

(9)

A plot between β cos(θ)/λ (on the y-axis) versus 4 sin(θ)/λ (on the x-axis) can be drawn in light of assigning each point to its specific diffraction line, and estimating the β values using Voigt-pseudo profile. Applying a linear fit to the obtained data, both the lattice strain ε and the crystallite size D_WH can be determined from the slope and intercept, respectively. The obtained D_WH values are represented in Table 2. The table shows that D_WH ranges from about 25.67 nm to 33.23 nm using the Reitveld method and Scherrer’s equation. However, utilizing the Williamson–Hall approach, the average size is found to be 36 nm. This divergence is attributed to the contribution part of the micro-lattice stain factor that cannot be neglected in the aforementioned methods.

3.6 Transmission electron microscopy (TEM analysis)

The nanoscale frame of the Ni–Co ferrite specimens is inspected by High-Resolution transmission electron microscopy (HRTEM). Figure 5a, b implies the HRTEM micrographs that were utilized to evaluate the morphology and size of the studied samples. ImageJ program is exploited to estimate the particle size distribution, as shown in Fig. 5e. There is evidence of the formation of nearly spherical nanoparticles along with polyhedron-shaped that having a diameter of (about 39–45 nm). Indeed, the clear and uniform lattice fringes obtained from HRTEM proved the high crystallinity of the Ni-doped Co ferrite samples as seen in Fig. 5c. Moreover, Fig. 5d designates the regular distribution of bright spots detected in the SAED pattern of the ferrite samples. This is considered good evidence of the polycrystalline type of ferrite samples [36, 37].

Fig. 5

TEM and HR-TEM images of as-prepared pure and Ni substituted Co ferrite NPs a and b are TEM micrographs of various nanoparticles subjected to analysis at different magnifications, c HRTEM images of selected Ni–Co ferrite nanoparticles, d a SAED pattern obtained from numbers of NiCoFe₂O₄ NPs, e the particle size distribution of micrograph presented in (4-a) using ImageJ software

3.7 Surface area, dislocation density, and packing factor

The surface area ($\mathrm{S}$) is calculated using the relationship [38]:

$$ S = \frac{6000}{{D \rho_{x} }}.100. $$

(10)

Also, the dislocation density ($\delta$ in the samples is computed by applying the following equation:

$$ \delta = \frac{1}{{D^{2} }}. $$

(11)

Moreover, to clarify the difference in the strain and dislocation density, the packing factor (P) is estimated using the formula:

$$ P = \frac{D}{d} , $$

(12)

where ($d$) is the inter-planar spacing of the most intense peak (311). All the values calculated for surface area, $\mathrm{S}$ dislocation density, $\delta$ and packing factor, P, are listed in Table 2.

3.8 Hopping, bond lengths, and ionic radii calculations

Hopping lengths in the tetrahedral and octahedral positions are given, respectively, utilizing the expressions [39]:

$$ L_{A} = \frac{a\sqrt 3 }{4}, $$

(13)

$$ L_{B} = \frac{a\sqrt 2 }{4}. $$

(14)

The determined magnitudes of hopping lengths (L_A, L_B) are tabulated in Table 3. Both L_A and L_B are lowered by boosting the Ni²⁺ percent, which may be referred to the overall decrease in lattice constant. Tetrahedral $(\mathrm{A}-\mathrm{O})$ and octahedral ($\mathrm{B}-\mathrm{O})$ bond lengths are evaluated using the subsequent equations [39, 40]:

$$ A - O = a\sqrt 3 \left( {u - \frac{1}{4}} \right), $$

(15)

$$ B - O = a\sqrt 3 \left[ {3u^{2} - (11/4)u + 43/64} \right]^{1/2} . $$

(16)

Table 3 Hopping lengths, site radii and bond lengths of Ni_xCo_1-xFe₂O₄ ferrites

Since Ni²⁺ ions of a bit smaller radius replace Co²⁺ ions, the increment in Ni ions percent is not accompanied by a considerable change in the calculated bond lengths as represented in Table 3. The distance of the closest anion–anion approach is known as shared tetrahedral, d_AE, and octahedral edges, d_BE. Both parameters can be determined using the expressions:

$$ d_{{{\text{AE}}}} = a\sqrt 2 \left( {2u - \frac{1}{2}} \right), $$

(17)

$$ d_{{{\text{AB}}}} = a\sqrt 2 \left( {1 - 2u} \right). $$

(18)

Also, applying Standley’s equations [30], unshared octahedral edges, d_BEU, and the ionic radii of ions at tetrahedral and octahedral sites (${r}_{\mathrm{tetr}},{r}_{\mathrm{octa}}$) of investigated ferrites have been determined (see Table 3), from the XRD data based on the values of lattice and oxygen parameters as follows:

$$ d_{{{\text{BEU}}}} = a\left( {4u^{2} - 3u + \frac{11}{{16}}} \right)^{\frac{1}{2}} , $$

(19)

$$ r_{{{\text{tetr}}}} = \left( {u - \frac{1}{4}} \right)a\sqrt 3 - r\left( {O^{2 - } } \right), $$

(20)

$$ r_{{{\text{octa}}}} = \left( {\frac{5}{8} - u} \right)a - r\left( {O^{2 - } } \right). $$

(21)

3.9 Magnetic analysis

The magnetic behavior of Ni_xCo_1-xFe₂O₄ (x = 0, 0.5and 1.0) NPs has been implied in Fig. 6a–c at different selecting temperatures from 5 K up to 300 K. It is worth mentioning that the main factors that affect the magnetic behavior of spinel ferrites are crystallite size, chemical composition, and cation distribution [39]. Figure 6a–c illustrates the M–H curves for (a) CoFe₂O₄, (b) Ni_0⋅5Co_0⋅5Fe₂O_4, and (c) NiFe₂O₄ NPs at four different temperatures (5, 100, 200, and 300 K). The M–H loops reveal that the investigated nanoparticles have a ferrimagnetic nature. It is exciting to observe that the magnetization curves of CoFe₂O₄ NPs (Fig. 6a) agree well with hard ferrimagnetic substances, whilst the hysteresis loops of NiFe₂O₄ NPs (Fig. 5c) match well with identical soft ferrimagnetic material. These findings are in good agreement with earlier studies [41].

Fig. 6

a–c Hysteresis loops of the prepared ferrites at 5, 100, 200, and 300 K for a CoFe₂O₄, b Ni_0.5Co_0.5Fe₂O_4, and c NiFe₂O₄ samples

In addition, the different magnetic parameters of the investigated compositions are mentioned in Table 4. It is noticed that the saturation magnetization, M_s for (CoFe₂O₄) boosts from 56.5 emu/g to 58.7 emu/g as temperature declines from 300 to 5 K. The same trend has been observed for Ni_0.5Co_0.5Fe₂O₄ and NiFe₂O₄ wherever the saturation magnetization rises by falling in temperature. Commonly, in ferrite compositions, the magnetic moments of tetrahedral A-positions are aligned antiparallel to those of octahedral B-positions. Besides, the magnetic dipole orientation becomes disordered at room temperature. Hence, nickel-substituted Co ferrite NPs possess lower magnetization values at room temperature. Also, at 300 K, the hysteresis lineaments of the nanoparticles disappear. This affirms that the superparamagnetic behavior can be considered the dominant one. Lowering the temperature of the samples decreases the thermal effect which in turn explains the obtained values of magnetization. Such magnetization tendency was observed in other doped ferrite systems [42].

Table 4 Magnetic parameters for the Ni_xCo_1-xFe₂O₄ spinel ferrite system

To investigate the influence of Ni⁺² ions doping on the magnetization of the samples, M_s is calculated as a function of composition (x) at different selected temperatures (5, 100, 200, and 300 K). Referring to Table 4, the amount of M_s decreases with boosting the Ni²⁺ content. Such lowering tendency in the studied compositions may be explained due to the replacement of Co²⁺ ions (3µ_B) in B-sites by Ni²⁺ ions (2 µ_B) which reduces the saturation magnetization. From another point of view, the low magneto-crystalline nature of Ni²⁺ ions replacing Co²⁺ ions in octahedral (B-sites) has a direct effect on the measured saturation magnetization [43].

Considering the two sub-lattice models of ferrimagnetism [43, 44], Néels magnetic moment per formula unit, ${\mu }_{B}^{n}$, is given by:

$$ \mu_{B}^{n} = M_{B} - M_{A} $$

(22)

where M_B and M_A are the magnetic moments of both B- and A-sublattices, respectively. ${\mu }_{B}^{n}$ is the net theoretical magnetic moment that depends on the proposed cation distribution. The ${\mu }_{B}^{n}$ values are recorded in Table 5. Furthermore, the magnitudes of the experimental values of the magnetic moments (µ_B)_exp per formula unit in Bohr magneton are computed according to the following relationship [45]:

$$ \mu_{{B\left( {exp.} \right) = \frac{{M_{W} {\text{x}}M_{s} }}{5585}}} , $$

(23)

where M_W refers to the molecular weight of the studied ferrite and M_s stands for the saturation magnetization (emu/g). It is revealed that the theoretical and experimental magnetic moment values calculated at 100 K (for example) show a noticeable discrepancy. This could be explained in view of canting effect model. According to this model, the moments of B-sites are canted considerably. The substitution of some ions (in our study are Ni²⁺ ions) causes locally non-collinearity of the ferrimagnetic phase. Analogous results were reported in other ferrite systems [46]. Thus, the divergence between the experimental and theoretical results can be termed by the model of "Random Canting of Spins, (RCS)" [46]. Appling the RCS model, the magnetic ions on the B-positions can be canted with an average angle, θ_RCS. To correlate the relation between the n_B (μ_B) and the θ_RCS, the following formula has been applied:

$$ n_{B}^{N} \left( {\mu_{B} } \right) = M_{B} \cos \theta_{RCS} $$

(24)

Table 5 The magnetic moment, canting angles, and anisotropy constants of the ferrite system

The values of θ_RCS are calculated and listed in Table 5. They were found to be 45.57º, 44.77º, and 51.68º for x = 0.0, 0.5, and 1.0, respectively.

Our estimated magnetic parameters that recorded in Table 4 are compared with some reported values in Table 6. As seen in Table 6, the highest Hc values are recorded for CoFe₂O₄ at all selected temperatures. Whereas the NiFe₂O₄ possessed the smallest coercivity. Likewise, the coercivity amount of Ni_0.5Co_0.5Fe₂O₄ ferrite lies between those of Co and Ni- ferrite samples. Reduction in the coercivity by increasing Ni²⁺ content may result from the exchange anisotropy. Such exchange anisotropy is caused by the spin canting effect and spins disordered arrangements [50] in accordance with the Stoner Wolfforth model for nanoparticles (H_C ~ 2 K/M_S) [51]. In the case of (CoFe₂O₄), the observed higher values of coercivity in comparison with those previously published in [17, 20, 21] could be interpreted to the improved effective anisotropy constant (K_eff). This follows the expression (K_eff = K_bulk + (6/d) K_S), where K_S,is the surface anisotropy constant, and d is the particles size [52]. Moreover, considering Brawn relations (for simplicity), the magnetic anisotropy is given by [53]:

$$ H_{C} = \frac{2K}{{\mu_{o } M_{s} }}, $$

(25)

where K is the anisotropy constant. M_s and H_c are the saturation magnetization and coercivity obtained from the Hysteresis loops. The calculated anisotropy values are tabulated in Table 5.

Table 6 A comparison betwixt the magnetic parameters mentioned in the literature with the evaluated ones in the present study for CoFe₂O₄, NiFe₂O₄, and Co_0.5Ni_0.5Fe₂O₄ nanostructures at 300 K

Figure 7a–c displays the susceptibility–temperature curves recorded in FC and ZFC modes for the samples CoFe₂O₄, Ni_0.5Co_0.5Fe₂O_4, and NiFe₂O₄ in an external magnetic field of 50, 100, and 200 Oe. In ZFC mode, the investigated ferrite samples are cooled from 300 K down to 5 K in the absence of the measuring field. Later, measuring fields of 50, 100, and 200 Oe are applied, and the acquisition of magnetic measurements is performed in the warming up cycle. Whereas in FC mode the samples are cooled from 300 K down to 5 K in the existence of the magnetic field. Afterward, the measurements are taken as a function of increasing temperature. Figure 7a–c reveals a divergence between the FC and ZFC modes which could be interpreted to the magnetic relaxation of the nano-sized particles. Furthermore, it can be considered as good evidence of their super magnetic nature. The appearance of an obvious maximum at a critical temperature in the ZFC plots is a common behavior in ferrite materials. This temperature is known as the blocking temperature, T_B. The T_B represents the temperature at which a relaxation from the ferrimagnetic state to the superparamagnetic state occurs in nanoparticles. Also, it is clarified as the temperature above which the magnetic anisotropy barrier is stunned only by thermal activation energy. Below T_B, the nanoparticles exhibit ferrimagnetic behavior. In the investigated samples, it is observed that the blocking temperature did not change with the increase in the applied field. Where its value remains around (300 K) under the application of various magnetic fields. However, a strong split in the FC and ZFC curves under a higher applied field is observed instead. The same behavior was reported in many other ferrite systems [43, 44, 54,55,56].

Fig. 7

a–c ZFC and FC variations of the susceptibility versus the temperature at 50, 100, and 200 Oe for the CoFe₂O₄, Ni_0.5Co_0.5Fe₂O_4, and NiFe₂O₄ nanoparticles

4 Conclusion

The coprecipitation technique was used to successfully synthesize Ni-doped cobalt ferrite nanoparticles with the general formula Ni_xCo_1-xFe₂O₄ (x = 0.0, 0.3, 0.5, 0.7, and 1.0). XRD, TEM, and SQUID analyses were used to characterize the samples. The single-phase spinel cubic crystal structure is confirmed by XRD, and the crystallite size of all produced nanoparticles was computed using the Williamson–Hall analysis and was found to be in the range of 25.67 to 33.23 nm. The substitution of Ni²⁺ ions for Co²⁺ ions resulted in a reduction in lattice parameters, porosity, and hopping lengths in tetrahedral and octahedral sites. The cation distribution of the samples has been proposed using Rietveld refinement analysis. It was found that Co²⁺ and Ni²⁺ ions occupy strongly octahedral B-site. However, at higher concentrations of Ni²⁺ ions, they occupy both tetrahedral and octahedral sites. Also, Fe³⁺ ions are distributed among A- and B-positions. The sintered powders are found to be nearly spherical along with polyhedron shape and having a diameter of (about 39–45 nm) as revealed by the (HRTEM). The magnetic studies of Ni–Co ferrite NPs reveal a ferrimagnetic nature where the saturation magnetization, M_s is decreased remarkably as the temperature declines from 300 to 5 K. The magnetic data confirms the super-magnetic nature of the investigated samples. Generally, saturation magnetization, coercivity, and remanence all decrease with an increase in Ni²⁺. The room-temperature saturation magnetic moment of the Co_0.5Ni_0.5Fe₂O₄ NPs (15.00 emu/g) sits in the middle of the saturation magnetization of CoFe₂O₄ NPs (56.50 emu/g) and that of NiFe₂O₄ NPs (7.50 emu/g). Even though the room-temperature magnetic coercivity (H_c) of NiFe₂O₄ NPs is only 110 Oe. It boosts up to approximately 4 times (470 Oe) for Co_0.5Ni_0.5Fe₂O₄ and grows up to 10 times (1120 Oe) for CoFe₂O₄. For the current ferrite system, Yafet–Kittel angles were computed revealing a triangular spin configuration. Magnetic anisotropy of Ni–Co ferrite NPs decreases with the increase in Ni²⁺ concentration (x). Introducing Ni²⁺ ions as a dopant enhanced the magnetic properties of cobalt ferrite. Therefore, Ni-doped cobalt ferrites could be potential candidates for vast magnetic applications. The results indicate that the material is suitable for use in photodegradation and dye removal catalysis, which may be proposed as future applications for these interesting samples.