1 Introduction

When the speed of sound of a fluid in a certain domain of temperature and pressure is known and combined with data for the density and isobaric heat capacity along one isobar at a low pressure in this domain, the density and isobaric heat capacity at high pressures can be obtained from it by numerical integration of the differential relations between the thermodynamic properties with little computational effort [1].

We have recently applied the method of thermodynamic integration to determine the density and isobaric and isochoric heat capacity of isobutane from an accurate speed of sound data set, which was measured with a double-path-length pulse-echo apparatus in our laboratory [2]. In that work, it was shown that initial values of the isobaric heat capacity, which are often not available, can be derived from very accurate density data sets, which cover the temperature range of the speed of sound measurements at moderate pressures.

Here, we apply this method to toluene and n-butane, for which extensive and accurate speed of sound data sets were measured in our laboratory with the same apparatus. Meier and Kabelac [3] measured the speed of sound in liquid toluene between 240 K and 420 K up to 100 MPa with a relative uncertainty of 0.03 %. In this work, uncertainties are always given as expanded uncertainties (at the 0.95 confidence level), but simply referred to as uncertainties to retain conciseness. El Hawary and Meier [4] measured the speed of sound in liquid n-butane in the temperature range between 200 K and 420 K with pressures up to 100 MPa with a relative uncertainty of 0.016 %. McLinden and Splett [5] published accurate data for the density of toluene in the temperature range between 213.15 K and 473.15 K with pressures up to 35 MPa with a relative uncertainty of 0.01 %, and Glos et al. [6] provided an accurate data set for the density of n-butane with a relative uncertainty of 0.02 % in the temperature range between 95 K and 340 K with pressures up to 14 MPa. These data can be used in combination with the experimental speeds of sound for toluene and n-butane to derive values for the density and isobaric heat capacity on the initial isobar of the thermodynamic integration.

During the course of this work, three further experimental data sets for the speed of sound and derived properties of liquid toluene were published. Shchamialiou et al. [7] measured the speed of sound between 298.15 K and 433.15 K with pressures up to 100 MPa and a relative uncertainty of 0.05 %. In the work of Dhakal et al. [8], two data sets are reported. One was measured at the University of Western Australia in the temperature range from 306 K to 423 K at pressures up to 65 MPa with a relative uncertainty of 0.04 % to 0.08 %. The second was measured at Imperial College London and covers the temperature range between 283.15 K and 473.15 K with pressures up to 350 MPa and has a relative uncertainty of 0.12 %. Since our speed of sound data extend down to 240 K and are more accurate than these three data sets, it is worthwhile to explore the thermodynamic integration with our data as well.

This article is organized as follows. Section 2 describes the fundamentals of the thermodynamic integration, Sect. 3 presents correlations of our speed of sound data for toluene and n-butane, and Sect. 4 presents the results for the derived properties of toluene and n-butane. Our results are compared with experimental data and derived values of other authors from the literature in Sect. 5. Conclusions are presented in Sect. 6.

2 Method of Thermodynamic Integration

By numerical integration of the partial differential equations

$$\begin{aligned} \left( \dfrac{\partial \rho }{\partial p}\right) _T&= \dfrac{1}{c^2}+\dfrac{T}{\rho ^2\,c_p}\left( \dfrac{\partial \rho }{\partial T}\right) _p^2 \end{aligned}$$
(1)
$$\begin{aligned} \left( \dfrac{\partial c_p}{\partial p}\right) _T&= -\dfrac{T}{\rho ^3}\left[ 2\left( \dfrac{\partial \rho }{\partial T}\right) _p^2-\rho \left( \dfrac{\partial ^2 \rho }{\partial T^2}\right) _p\right] \end{aligned}$$
(2)

for the unknown functions \(\rho (T,p)\) and \(c_p(T,p)\), values for the density \(\rho\) and isobaric heat capacity \(c_p\) in the domain of the speed of sound measurements can be derived from the speed of sound data. In Eqs. 1 and 2, T denotes the temperature, p the pressure, and c the speed of sound. A well-posed initial value problem is obtained when Eqs. 1 and 2 are supplemented with values for the density and isobaric heat capacity at a low pressure isobar in the domain of the speed of sound measurements. The numerical integration of Eqs. 1 and 2 is performed on a regular grid in the pressure-temperature diagram. For the calculation of the speed of sound at the grid points, the speed of sound data are correlated as a function of temperature and pressure.

For the numerical integration of Eqs. 1 and 2, we apply the predictor-corrector method devised by Dàvila and Trusler [9]. Starting on the initial isobar \(p_0\), intermediate values for the density and isobaric heat capacity at the next pressure on the grid \(p_1\) are calculated by the predictor step

$$\begin{aligned} \rho (p_1)&= \rho (p_0)+\Delta p \left( \dfrac{\partial \rho }{\partial p}\right) _{T,p_0} \end{aligned}$$
(3)
$$\begin{aligned} c_p(p_1)&= c_p(p_0)+\Delta p \left( \dfrac{\partial c_p}{\partial p}\right) _{T,p_0}\quad , \end{aligned}$$
(4)

in which \(\Delta p\) denotes the pressure step size of the integration. The partial derivatives \((\partial \rho / \partial p)_{T,p_0}\) and \((\partial c_p/\partial p)_{T,p_0}\) on the initial isobar are calculated with Eqs. 1 and 2, which requires values for the derivatives \((\partial \rho /\partial T)_p\) and \((\partial ^2 \rho /\partial T^2)_p\) on the initial isobar. These values are obtained using the analytical derivatives of a polynomial fit to the initial values of the density as a function of temperature. The chosen order of the polynomial depends on the fluid and the temperature range, in which the thermodynamic integration is carried out.

The equations for the corrector step

$$\begin{aligned} \rho (p_1)&= \rho (p_0) + \frac{1}{2} \Delta p \left[ \left( \dfrac{\partial \rho }{\partial p}\right) _{T,p_0} + \left( \dfrac{\partial \rho }{\partial p}\right) _{T,p_1}\right] \end{aligned}$$
(5)
$$\begin{aligned} c_p(p_1)&= c_p(p_0) + \frac{1}{2} \Delta p \left[ \left( \dfrac{\partial c_p}{\partial p}\right) _{T,p_0} + \left( \dfrac{\partial c_p}{\partial p}\right) _{T,p_1}\right] \end{aligned}$$
(6)

contain the derivatives \((\partial \rho /\partial p)_T\) and \((\partial c_p/\partial p)_T\) at both isobars \(p_0\) and \(p_1\) and yield the final values for the density and isobaric heat capacity at the pressure \(p_1\). The partial derivatives \((\partial \rho /\partial p)_T\) and \((\partial c_p/\partial p)_T\) at \(p_1\) are calculated by Eqs. 1 and 2 using the speed of sound correlation and values for the density and isobaric heat capacity calculated by Eqs. 3 and 4 in the predictor step. Moreover, a polynomial of the same order as in the predictor step is fitted to the predicted values for the density at \(p_1\) as a function of temperature. Values for the derivatives \((\partial \rho / \partial T)_p\) and \((\partial ^2\rho / \partial T^2)_p\) at \(p_1\) are then again calculated using the analytical derivatives of the polynomial. After an integration step has been completed, the corrected densities and isobaric heat capacities at the isobar \(p_1\) serve as initial values for the next integration step. This procedure is repeated until the final pressure \(p_{\text{F}}\) is reached.

With a speed of sound correlation and the results of the thermodynamic integration for the density and its derivatives, further properties, such as the isochoric heat capacity, the thermal expansivity, or the isothermal and isentropic compressibility, can be calculated using well-known thermodynamic relations. In this work, we provide values for the isochoric heat capacity in addition to the density and isobaric heat capacity, which are calculated with the relation

$$\begin{aligned} c_v=c_p-\frac{T}{\rho ^2} \left( \frac{\partial \rho }{\partial T} \right) _p^2 \left( \frac{\partial \rho }{\partial p} \right) _T^{-1}. \end{aligned}$$
(7)

3 Speed of Sound Correlations

As an input for the thermodynamic integration, correlations of the speed of sound data for toluene and n-butane as a function of temperature and pressure in the domain of the integration are required. The functional form of the speed of sound correlations for toluene and n-butane was established by the linear structural optimization technique devised by Wagner [10]. The structural optimization is a statistical method that determines a functional representation of a given data set with a small number of terms, which represents the data set with the smallest sum of squared deviations, from a large initial set of terms, the so-called bank of terms. An implementation of the structural optimization technique, which was developed by Bischoff [11] at the University of Hannover in 1988, was translated into modern Fortran 90 code, and quadruple-precision 128-bit arithmetic was used throughout. The bank of terms consisted of 1281 polynomial terms of the reduced pressure \(p/p_\text {c}\), the reduced temperature \(T/T_\text {c}\), and products of both with integer and rational exponents between 0 and 15 in steps of 0.25 for temperature and between 0 and 4 in steps of 0.2 for pressure. The symbol \(p_\text {c}\) denotes the critical pressure and \(T_\text {c}\) the critical temperature of the fluid. It was observed that correlating the square of the speed of sound instead of the speed of sound yielded a somewhat more accurate representation of the experimental speeds of sound. Therefore, the square of the speed of sound was correlated as a double polynomial in reduced temperature and reduced pressure given by

$$\begin{aligned}{}[c(p,T)]^2= \sum _{i = 1}^N a_i \left( \dfrac{p}{p_\text {c}}\right) ^{m_i} \left( \dfrac{T}{T_\text {c}}\right) ^{n_i} \quad , \end{aligned}$$
(8)

where N is the number of terms in the polynomial. The coefficients \(a_i\) and exponents \(m_i\) and \(n_i\) of the correlations for toluene and n-butane are reported in Table 1. The correlation for toluene covers the complete temperature range of our measurements from 240 K to 420 K, whereas for n-butane the temperature range of the speed of sound correlation was chosen as large as the range, in which our speed of sound data and the density data of Glos et al. [6], which were used to determine the initial values for the thermodynamic integration, overlap, that is from 200 K to 340 K.

Relative deviations of the experimental data from the correlations are depicted in Fig. 1. Both correlations represent the data within 50 parts per million (ppm) or better with the exception of one state point for toluene at the lowest pressures on the highest isotherm, which deviates by 93 ppm from the correlation. At high pressures, the deviations decrease to 20 ppm. The uncertainty of the correlations is estimated by the sum of the uncertainty of the experimental data and their largest deviation from the correlation. It amounts to 0.04 % for toluene and 0.02 % for n-butane.

Table 1 Coefficients \(a_i\) and exponents \(m_i\) and \(n_i\), range of validity, and relative uncertainty \(U_\text {r,cor}\) of the speed of sound correlations for toluene and n-butane
Full size table
Fig. 1
figure 1

Relative deviations of the experimental speeds of sound in toluene of Meier and Kabelac [3] and in n-butane of El Hawary and Meier [4] from values calculated with the speed of sound correlations as a function of pressure and temperature. Experimental data: , 200 K; , 220 K; , 240 K; , 260 K; , 280 K; , 300 K; , 320 K; , 340 K; , 360 K; , 380 K; , 400 K; , 420 K

Full size image

4 Results for Derived Properties

4.1 Toluene

The thermodynamic integration for toluene was carried out in the temperature range between 238.15 K and 423.15 K, which is moderately larger than the range of the speed of sound measurements. At temperatures below 240 K and above 420 K, the speed of sound correlation was extrapolated beyond its range of validity. Since the extrapolation extends only modestly over the limits of the range of validity, it was assumed that the correlation predicts the speed of sound at 238.15 K and 423.15 K still within its uncertainty. The initial pressure for the thermodynamic integration was chosen as 1 MPa. With this choice, it is larger than the vapor pressure at the highest considered temperature of 423.15 K, so that the whole temperature range between 238.15 K and 423.15 K can be covered with the same initial pressure. Initial values for the density and isobaric heat capacity were derived in the range of the thermodynamic integration in steps of 5 K. This rather small step size was necessary to stabilize the polynomial fit at each pressure step of the integration.

The initial values for the density were derived from the data of McLinden and Splett [5]. In the range of the thermodynamic integration, the relative uncertainty of these data is between 60 ppm and 114 ppm. Since McLinden and Splett did not measure the density exactly at 1 MPa, but at slightly different pressures, values for the density at 1 MPa were interpolated from the experimental data with third- to sixth-order polynomials, which were fitted to the data at each measured isotherm. In the next step, a fifth-order polynomial in temperature was fitted to the interpolated values, from which the final initial values were calculated.

The isobaric heat capacity of liquid toluene at high pressures was measured by Akhundov and Eksaev [12, 13], Akhundov et al. [14], San José et al. [15], Nefedov and Filippov [16], Shulga et al. [17], and Segovia et al. [18]. Since only a few data of these seven data sets lie in the temperature range of the thermodynamic integration near or at the 1 MPa isobar and there are systematic differences between them, as will be shown in Sect. 5.1.2, the initial values for the isobaric heat capacity were derived from the density data of McLinden and Splett [5] and the speed of sound correlation for toluene by applying the procedure developed in our previous work on isobutane [2]. In this procedure, Eq. 1 is solved for the isobaric heat capacity to yield

$$\begin{aligned} c_p = \dfrac{T \left( \dfrac{\partial \rho }{\partial T}\right) _p^2}{\rho ^2\left[ \left( \dfrac{\partial \rho }{\partial p}\right) _T-\dfrac{1}{c^2}\right] } \end{aligned}$$
(9)

and applied to calculate values for the isobaric heat capacity on the initial isobar from initial values for the density, speed of sound, and the derivatives \((\partial \rho /\partial T)_p\) and \((\partial \rho /\partial p)_T\). The speed of sound on the initial isobar was obtained from the speed of sound correlation, Eq. 8, and the derivative \((\partial \rho /\partial T)_p\) at the initial pressure from the polynomial representation of the density. Initial values for \((\partial \rho /\partial p)_T\) on each isotherm were calculated with fifth-order polynomial fits to the isothermal density data of McLinden and Splett. Initial values for the derivative \((\partial ^2 \rho /\partial T^2)_p\), which are required in Eq. 2 to calculate the initial values for the derivative \((\partial c_p/\partial p)_T\), were also obtained from the polynomial representation of the density on the initial isobar.

With the calculated initial values, the thermodynamic integration was tentatively performed. First, the numerical stability of the algorithm was assessed by applying different pressure step sizes of 0.01 MPa, 0.1 MPa, and 1 MPa. Since the maximum differences in density and isobaric heat capacity between integrations with 0.01 MPa and 0.1 MPa were less than 0.1 ppm and 2 ppm, respectively, the pressure step size was chosen as 0.1 MPa. Second, the results for the derivatives of the density and \((\partial c_p/\partial p)_T\) were visually inspected after each run to check them for correct physical behavior. When the integration was performed with the initial values for the derivative \((\partial \rho /\partial p)_T\), it resulted in crossing isotherms of the derivative \((\partial c_p/\partial p)_T\), and the spacings between the isotherms were irregular and physically unreasonable. Moreover, the derived densities showed small deviations from the data of McLinden and Splett at high pressures. To improve the agreement, the initial values for the derivative \((\partial \rho /\partial p)_T\) were manually adjusted by a combination of trial and error and physical intuition until the data of McLinden and Splett were optimally matched, no intersections of the isotherms of the derivatives were observed, and the spacings between the isotherms of the derivatives were reasonable.

Fig. 2
figure 2

Derivatives \((\partial \rho / \partial T)_p\), \((\partial ^2 \rho / \partial T^2)_p\), \((\partial \rho / \partial p)_T\), and \((\partial c_p / \partial p)_T\) for toluene along isotherms between 238.15 K and 423.15 K in steps of 5 K as a function of pressure. The plots in the right column are enlargements of the grey-shaded areas in the plots in the left column

Full size image

The results for the derivatives after this optimization process are depicted in Fig. 2. Due to the low degree of the polynomial representation of the initial densities, the derivatives \((\partial \rho / \partial T)_p\) and \((\partial ^2 \rho / \partial T^2)_p\) are very stable and show reasonable behavior. The spacings between the isotherms of the derivative \((\partial ^2 \rho / \partial T^2)_p\) decrease with increasing temperature and do not intersect nor touch each other. Even during the optimization process of the initial values for \(\left( \partial \rho /\partial p\right) _T\), the isotherms of this derivative always remained physically correct. Therefore, the optimization focused on establishing the correct behavior of the derivative \((\partial c_p / \partial p)_T\). Since this derivative is mostly influenced by changes in \((\partial \rho / \partial p)_T\), the initial values for \((\partial \rho / \partial p)_T\) were adjusted until the behavior of \((\partial c_p / \partial p)_T\) was physically correct. The spacings between the lowest and highest isotherms 238.15 K and 423.15 K and their neighboring isotherms 243.15 K and 418.15 K are a little bit smaller than the spacings between the other isotherms. This is probably due to the application of the speed of sound correlation outside the range in which it was fitted to experimental data.

Figure 3 depicts relative deviations of the results for the initial values from the short fundamental equation of state (EOS) of Lemmon and Span [19] for toluene. The uncertainty of the EOS in density is 0.01 % in the vicinity of 300 K at ambient pressure and 0.05 % in the domain of the thermodynamic integration, and the uncertainty in the isobaric and isochoric heat capacity is 0.5 % in the domain of the thermodynamic integration. The initial values for the density agree with the EOS within 0.015 %, which is well within its uncertainty. The largest deviation of \(-0.015\) % is observed at 423.15 K. The deviations of the isobaric heat capacity at low temperatures are larger than the uncertainty of the EOS. Between 238.15 K and 298.15 K, they amount to between 0.78 % and 0.52 %. Above 298.15 K, they agree with the EOS within its uncertainty. The derivative \(\left( \partial \rho /\partial p\right) _T\) deviates between −0.71 % and 1.5 % from the EOS, while the deviations of the derivative \((\partial \rho / \partial T)_p\) change from −0.18 % at 238.15 K to 0.1 % at 393.15 K and decrease to \(-0.06\) % at 423.15 K.

Fig. 3
figure 3

Relative deviations in the optimized initial values for the density, isobaric heat capacity, and derivatives \((\partial \rho /\partial T)_p\) and \((\partial \rho /\partial p)_T\) of toluene from values calculated with the EOS of Lemmon and Span [19] as a function of temperature at the isobar 1 MPa. The error bars represent relative uncertainties in the initial values

Full size image

The results for the derived values are reported in Table 2. It is noted that the tabulated values for the density at pressures below 30 MPa resemble the experimental data of McLinden and Splett [5] and do not provide new information, but are included for the sake of completeness. The uncertainties in the derived values for the density and isobaric heat capacity were estimated by applying the Gaussian error-propagation law on each step of the predictor-corrector method using the uncertainties of the initial values as input. The relative uncertainties in density and isobaric heat capacity are plotted for all calculated isotherms as a function of pressure in Fig. 4. The relative uncertainty in the density decreases with pressure on each isotherm from 114 ppm at the initial isobar to 100 ppm at 423.15 K and 100 MPa and 109 ppm at 238.15 K and 100 MPa. This unexpected behavior is due to the fact that the absolute uncertainty increases less with pressure than the value of the density. The relative uncertainty in isobaric heat capacity increases with pressure on all isotherms because each integration step adds a larger contribution to its uncertainty than to the uncertainty in density. It varies from 0.28 % at 423.15 K and 1 MPa to 0.32 % at 238.15 K and 100 MPa. Since both uncertainties change only modestly with temperature and pressure, the relative uncertainties are generally estimated by their largest values to be 0.011 % in density and 0.32 % in isobaric heat capacity.

Fig. 4
figure 4

Relative uncertainties in the derived densities and isobaric heat capacities of toluene as a function of pressure for all calculated isotherms

Full size image
Table 2 Derived values for the density \(\rho\), the isobaric heat capacity \(c_p\), and the isochoric heat capacity \(c_v\) of toluene determined by thermodynamic integration as a function of temperature T and pressure p
Full size table

4.2 n-Butane

The temperature range of the density measurements of Glos et al. [6] overlaps with the range of the speed of sound measurements of El Hawary and Meier [4] between 200 K and 340 K. Since there are no further accurate density data available at higher temperatures in the liquid region, the thermodynamic integration was applied in this temperature range only. The initial isobar was chosen at 2 MPa. The initial values for the density and isobaric heat capacity were derived in the same way as described in Sect. 4.1 for toluene from the density data of Glos et al. and the speed of sound correlation for n-butane. This includes interpolation of densities at the initial isobar, the interpolation of density values at the isotherms 220 K and 240 K, which were not measured by Glos et al., and the determination of initial values for the isobaric heat capacity at 2 MPa by the procedure described in Sect. 4.1 for toluene and Ref. [2] for isobutane. Since the n-butane data of Glos et al. scatter somewhat more than their data for isobutane [6], it was more difficult to determine accurate initial values for the derivatives \(\left( \partial \rho /\partial T\right) _p\), \((\partial ^2 \rho /\partial T^2)_p\), and \((\partial \rho /\partial p)_T\). At 260 K, the density data at the lowest pressures scatter, so that a reliable initial value for the density could not be estimated at first instance. Furthermore, they published a wrong value for the pressure for the measurement at 280 K and 4 MPa, which made it more difficult to derive an accurate initial value for the derivative \((\partial \rho /\partial p)_T\) at 2 MPa at this isotherm. Since the isotherms 260 K and 280 K are in the center of the temperature range of the thermodynamic integration, inconsistent initial values have a large influence on the results for the density and heat capacities. Therefore, the measurements of Glos et al. [6] at the other isotherms were assigned a higher weight than the data at 260 K and 280 K.

Fig. 5
figure 5

Derivatives \((\partial \rho / \partial T)_p\), \((\partial ^2 \rho / \partial T^2)_p\), \((\partial \rho / \partial p)_T\), and \((\partial c_p / \partial p)_T\) for n-butane along isotherms between 200 K and 340 K in steps of 5 K as a function of pressure. The plots in the right column are enlargements of the grey-shaded areas in the plots in the left column

Full size image

As for toluene, the pressure step size was chosen as 0.1 MPa. In order to ensure correct physical behavior of the derivatives \((\partial \rho /\partial T)_p\), \((\partial ^2 \rho /\partial T^2)_p\), \((\partial \rho /\partial p)_T\), and \((\partial c_p/\partial p)_T\), the thermodynamic integration was tentatively performed with slightly different initial values for the derivative \((\partial \rho /\partial p)_T\), and the results for the derivatives were visually inspected for each run of the integration. The initial values for the derivative \((\partial \rho /\partial p)_T\) were manually adjusted until the Glos et al. data were optimally matched, no crossings of the isotherms of the derivatives \((\partial \rho /\partial T)_p\), \((\partial \rho /\partial p)_T\), and \((\partial c_p/\partial p)_T\) were observed, and the spacings between them were reasonable. Figure 5 depicts the results for the four derivatives. The isotherms of the derivatives \((\partial \rho / \partial T)_p\) and \((\partial \rho / \partial p)_T\) show the expected characteristic behavior and are well spaced. The isotherms of the derivative \((\partial ^2 \rho / \partial T^2)_p\) generally also show the correct physical behavior, but between 275 K and 340 K they are too close to each other. Moreover, the 200 K isotherm is too close to the 205 K isotherm. However, the influence of these deficiencies on the results for the isobaric heat capacity is small since the absolute values of the second derivative are small, especially at high pressures. The isotherms of the derivative \((\partial c_p/\partial p)_T\) do not cross each other and are overall reasonably spaced, except at the lower and upper limits of the temperature range of the integration. The two isotherms at 200 K and 340 K are a little bit to close to the 205 K and 335 K isotherms. The optimization of the initial values of the derivative \((\partial \rho /\partial p)_T\) is important because they have a large influence on the results for the isobaric heat capacity. In order to improve the behavior of the derivative \((\partial ^2\rho /\partial T^2)_p\) further, even more accurate density data would be required.

Fig. 6
figure 6

Relative deviations of the initial values for the density, isobaric heat capacity, and derivatives \((\partial \rho /\partial p)_T\) and \((\partial \rho /\partial T)_p\) of n-butane from values calculated with the EOS of Bücker and Wagner [20] as a function of temperature along the initial isobar 2 MPa. The error bars represent relative uncertainties in the initial values

Full size image

Figure 6 shows relative deviations of the optimized initial values for the density, isobaric heat capacity, and the derivatives \(\left( \partial \rho /\partial p\right) _T\) and \(\left( \partial \rho /\partial T\right) _p\) from the EOS of Bücker and Wagner [20]. The initial values for the density agree with the EOS within 60 ppm, whereas higher deviations of up to 1.3 % are observed for the isobaric heat capacity. The derivatives \((\partial \rho /\partial p)_T\) and \((\partial \rho /\partial T)_p\) deviate by up to 0.8 % and 0.16 %, respectively, from the EOS. The relative uncertainties in the initial values are estimated to be 0.02 % in density, between 0.50 % at 200 K and 0.27 % at 340 K in isobaric heat capacity, 0.05 % in the derivative \((\partial \rho /\partial p)_T\), and between 0.22 % at 200 K and 0.08 % at 340 K in \((\partial \rho /\partial T)_p\). As the density data of Glos et al. for n-butane scatter more than their data for isobutane, the maximum uncertainty of 0.02 % reported by Glos et al. was used as an estimate for the uncertainty of the initial values for the density. The initial values for the density and isobaric heat capacity agree with the EOS of Bücker and Wagner well within its uncertainty in both properties of 0.02 % and 1 % to 3 %, respectively.

Fig. 7
figure 7

Relative uncertainties in derived densities and isobaric heat capacities of n-butane as a function of pressure for all calculated isotherms

Full size image

The derived values for the density and isobaric and isochoric heat capacities are reported in Table 3. As for toluene, the uncertainties in the derived properties were estimated by applying the Gaussian error-propagation law on the predictor-corrector method with the uncertainty in the initial values for density, the isobaric heat capacity, the derivatives \((\partial \rho /\partial p)_T\) and \((\partial \rho /\partial T)_p\), and the speed of sound correlation as inputs. Relative uncertainties in the derived values for the density and isobaric heat capacity are shown in Fig. 7 as a function of pressure for all calculated isotherms. The uncertainties in both properties exhibit a similar behavior as for toluene. The relative uncertainties in the derived properties are conservatively estimated by the largest value on each isotherm to be 0.02 % for the density and between 0.52 % at 200 K and 0.30 % at 340 K for the isobaric heat capacity.

Table 3 Derived values for the density \(\rho\), the isobaric heat capacity \(c_p\), and the isochoric heat capacity \(c_v\) of n-butane determined by thermodynamic integration as a function of temperature T and pressure p
Full size table

5 Comparison of Derived Properties with Data from the Literature

In this section, our derived properties are compared to the fundamental EOSs of Lemmon and Span for toluene [19] and Bücker and Wagner for n-butane [20] and data of other authors from the literature. The literature search for experimental data sets for the properties of toluene and n-butane was carried out with the NIST TDE database [21].

5.1 Toluene

5.1.1 Density

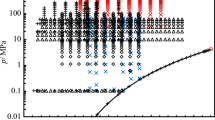
More than 750 data sets for the density are available in the NIST TDE database [21]. These data sets were filtered with regard to accuracy and extensiveness. Only data sets with data at pressures above ambient pressure, at temperatures in the region of thermodynamic integration, and which agree with the EOS of Lemmon and Span [19] within its uncertainty of less than 0.05 % were selected for the comparison. Especially single data were not considered. Table 4 summarizes details of the selected data sets for the density of toluene from the literature. Although many measurements of the density of toluene were carried out in the past, only the ten data sets of Akhundov and Abdullaev [22], Avelino et al. [23], Zéberg-Mikkelsen et al. [24], Moravkova et al. [25], Watson et al. [26], Segovia et al. [27], Valencia et al. [28], Rowane et al. [29], Tay and Trusler [30], and Shchamialiou et al. [7] extend into the high pressure liquid region above 35 MPa. The data of Rowane et al. have a rather large relative uncertainty of 0.8 % and are therefore not considered in the following discussion. Accurate data below 35 MPa were published by Sommer et al. [31], Glen and Johns [32], Zéberg-Mikkelsen and Andersen [33], Masui [34], Ihmels and Gmehling [35], Comuñas et al. [36], Magee and Bruno [37], Chyliński and Gregorowicz [38], and McGregor [39]. Besides these experimental data sets, Muringer et al. [40] and Dhakal et al. [8] obtained densities from speed of sound measurements by the method of thermodynamic integration in large parts of the liquid region. Shchamialiou et al. [7] applied a method of thermodynamic integration, which can be viewed as inverse to our method, to derive speeds of sound, isobaric and isochoric heat capacities and further properties from experimental density data. This version of thermodynamic integration uses a correlation of experimental density data as a function of temperature and pressure and initial values for the isobaric heat capacity derived from experimental data at atmospheric pressure as input. The distribution of the experimental data from the literature and the range of the thermodynamic integrations of this work, of Muringer et al., of Shchamialiou et al., and of Dhakal et al. is shown in a pressure-temperature diagram in Fig. 8.

Table 4 Summary of selected data sets for the density and isobaric as well as isochoric heat capacity of toluene from the literature
Full size table
Fig. 8
figure 8

Distribution of data from the literature for the density of toluene in the fluid region in a pressure-temperature diagram. The grey-shaded region denotes the region of thermodynamic integration. The dashed lines encircle the regions of thermodynamic integration of other authors: (red), Muringer et al. [40]; (blue), Shchamialiou et al. [7]; and (green), Dhakal et al. [8]. Experimental data: , Akhundov and Abdullaev [22]; , Avelino et al. [23]; , Chylinski and Gregorowicz [38]; , Comuñas et al. [36]; , Glen and Johns [32]; , Ihmels and Gmehling [35]; , Magee and Bruno [37]; , Masui [34]; , McGregor [39]; , McLinden and Splett [5]; , Morávková et al. [25]; , Segovia et al. [27]; , Shchamialiou et al. [7]; , Sommer et al. [31]; , Tay and Trusler [30]; , Valencia et al. [28]; , Watson et al. [26]; , Zéberg-Mikkelsen and Andersen [33]; and , Zéberg-Mikkelsen et al. [24]. , Triple point temperature, critical pressure, and , vapor pressure calculated with the EOS of Lemmon and Span [19]

Full size image

Relative deviations of the densities derived in this work, of the densities calculated by Muringer et al., Shchamialiou et al., and Dhakal et al., and the selected experimental data from the literature from the EOS of Lemmon and Span [19] are depicted in Figs. 9 and 10. Since the initial values of the density for the thermodynamic integration were derived from the data of McLinden and Splett [5], our derived densities agree with them within 3 ppm on all isotherms except at 323.15 K, where the deviations increase to 5 ppm at 19 MPa. The agreement with the EOS is within 0.016 % between 243.15 K and 323.15 K and within 0.01 % between 333.15 K and 373.15 K. Above 373.15 K, the deviations increase up to 0.03 % at the highest pressures measured by McLinden and Splett. The largest deviations are observed at 423.15 K near 35 MPa. At higher pressures, our derived densities agree with the EOS within 0.02 % between 243.15 K and 353.15 K, within 0.01 % between 333.15 K and 373.15 K, and at higher temperatures the deviations increase up to 0.04 % at 423.15 K.

Fig. 9
figure 9

Relative deviations of derived densities for toluene and data from the literature at nearby temperatures (\(T \pm 5\) K) from the EOS of Lemmon and Span [19] as a function of pressure. Derived values: , this work (, estimated uncertainty range); , Muringer et al. [40]; , Shchamialiou et al. [7]; and , Dhakal et al. [8]. Experimental data: , Akhundov and Abdullaev [22]; , Avelino et al. [23]; , Chylinski and Gregorowicz [38]; , Comuñas et al. [36]; , Glen and Johns [32]; , Ihmels and Gmehling [35]; , Magee and Bruno [37]; , Masui [34]; , McLinden and Splett [5]; , Shchamialiou et al. [7]; , Sommer et al. [31]; , Tay and Trusler [30]; , Valencia et al. [28]; , Watson et al. [26]; , Zéberg-Mikkelsen and Andersen [33]; and , Zéberg-Mikkelsen et al. [24]

Full size image
Fig. 10
figure 10

Relative deviations of derived densities for toluene and data from the literature at nearby temperatures (\(T \pm 5\) K) from the EOS of Lemmon and Span [19] as a function of pressure. Derived values: , this work (, estimated uncertainty range); , Shchamialiou et al. [7]; and , Dhakal et al. [8]. Experimental data: , Akhundov and Abdullaev [22]; , Glen and Johns [32]; , Ihmels and Gmehling [35]; , Masui [34]; , McGregor [39]; , McLinden and Splett [5]; , Shchamialiou et al. [7]; , Segovia et al. [27]; , Sommer et al. [31]; and , Tay and Trusler [30]

Full size image

Sommer et al. [31] measured the density between 233.15 K and 473.15 K up to 30 MPa in steps of 20 K with a single-sinker hydrostatic balance densimeter with a magnetic suspension coupling with a relative uncertainty of 0.015 %. Their results are very consistent and show the same pressure dependence as our derived densities and the McLinden and Splett data, but are systematically lower by up to 0.013 %. Unfortunately, Sommer et al. did not analyze the composition of their sample. However, at 293.15 K they carried out measurements with two further toluene samples in addition to the measurements with the sample with which all isotherms were measured to examine the influence of impurities. The measurements with the two additional samples agree better with the data of McLinden and Splett and our derived densities than the main body of measurements. Despite the systematic differences, the data of Sommer et al. agree with the data of McLinden and Splett and our derived densities within their uncertainty.

Except for the data of McLinden and Splett [5] and Sommer et al. [31], no other data set agrees with our derived densities completely within their uncertainty. However, in many cases mutual agreement within the uncertainties of our derived values and the data from the literature is found. Glen and Johns [32] also used a single-sinker densimeter for measurements of five isotherms between 293.14 K and 373.37 K in steps of 20 K up to 30 MPa and reported a relative uncertainty of 0.01 %. The deviations of their data from the data of McLinden and Splett and our values increase with temperature from +0.008 % at 293 K to +0.03 % at 373 K. Ihmels and Gmehling [35] measured the density between 273.15 K and 623.15 K up to 40 MPa with a vibrating-tube densimeter with an uncertainty of 0.03 %. Their data scatter somewhat more than the three single-sinker data sets, but also agree well with our derived densities and in large parts exhibit a similar pressure dependence as our derived densities. On some isotherms, for example at 373.15 K, 403.15 K, 413.15 K, and 423.15 K, they agree mostly with our values within their uncertainty. On the other isotherms, the deviations are larger and reach up to −0.04 % at 293.15 K. Shchamialiou et al. [7] also carried out measurements with a vibrating-tube densimeter. Their data cover the temperature range between 273.65 K and 473.15 K up to 140.1 MPa and have a relative uncertainty of 0.018 %. They show the same pressure dependence as our derived densities, the data of McLinden and Splett, and the data of Sommer et al., but are between 0.015 % and 0.05 % lower than our derived values and the data of McLinden and Splett. The data of Akhundov and Abdullaev [22], Avelino et al. [23], Zéberg-Mikkelsen et al. [24], Watson et al. [26], Segovia et al. [27], Valencia et al. [28], Zéberg-Mikkelsen and Andersen [33], Masui [34], Comuñas et al. [36], Magee and Bruno [37], Chylinski and Gregorowicz [38], and McGregor [39] scatter more and show larger deviations from our derived densities than the data of McLinden and Splett, Sommer et al., Glen and Johns, Shchamialiou et al., and Ihmels and Gmehling.

The densities derived by Muringer [40] also exhibit a similar dependence on pressure as our derived densities. At 243.15 K, they are by 0.02 % and, at 273.15 K, by about 0.01 % higher than our values. At 293.15 K and 323.15 K, they almost coincide with our values. The derived density values reported by Shchamialiou et al. [7] were calculated from a correlation, which was fitted to experimental data sets. They also exhibit a similar pressure dependence as our data. In large parts, they agree well with the data of Sommer et al., but at 313.15 K and 333.15 K they are systematically higher and coincide with the data of McLinden and Splett and our derived densities. The derived densities of Dhakal et al. [8] agree with our derived values and the data of McLinden and Splett near the initial isobars of thermodynamic integrations because their initial values for the density are also based on the data of McLinden and Splett. Between 283.15 K and 303.15 K, their data increase more strongly with pressure than our derived densities so that deviations up to 0.06 % are observed at 100 MPa. Nevertheless, the agreement of both data sets is within the uncertainty of 0.2 % of the densities derived by Dhakal et al. At higher temperatures, the derived densities of Dhakal et al. agree with our derived densities mostly within the uncertainty of our values.

5.1.2 Isobaric and Isochoric Heat Capacity

Fig. 11
figure 11

Distribution of data from the literature for the isobaric and isochoric heat capacity of toluene in a pressure-temperature diagram. The grey-shaded region represents the region of thermodynamic integration. The dashed lines encircle the regions of thermodynamic integration of other authors: (red), Sun et al. [44], (blue), Shchamialiou et al. [7] and (green), Dhakal et al. [8]. Black symbols denote isobaric heat capacities, green symbols denote isochoric heat capacities. Experimental isobaric heat capacities: , Akhundov and Eksaev [12, 13]; , Akhundov et al. [14]; , Holzhauer and Ziegler [41]; , San José et al. [15]; , Nefedov and Filippov [16]; , Shulga et al. [17]; and , Segovia et al. [18]. Experimental isochoric heat capacities: , Abdulagatov et al. [42]. , Triple point temperature, critical pressure, and , vapor pressure calculated with the EOS of Lemmon and Span [19]

Full size image

The NIST TDE database [21] contains 47 data sets for the isobaric heat capacity of toluene. Only Akhundov and Eksaev [12, 13], Akhundov et al. [14], Nefedov and Filippov [16], San José et al. [15], Segovia et al. [18], and Shulga et al. [17] reported data at pressures above ambient. Furthermore, Sun et al. [44], Shchamialiou et al. [7], and Dhakal et al. [8] derived values for the isobaric heat capacity by the method of thermodynamic integration from speed of sound data sets. The distribution of these eight data sets and the regions of thermodynamic integration of this work, Sun et al., Shchamialiou et al., and Dhakal et al. are shown in a pressure–temperature diagram in Fig. 11. The most comprehensive data set for the isobaric heat capacity was measured by Akhundov et al. [14]. They reported 774 data covering a large part of the liquid and supercritical regions between 298 K and 673 K with pressures up to 20 MPa. The two data sets of Akhundov and Eksaev [12, 13] cover a similar part of the liquid and superfluid regions from 310 K to 571 K and from 571 K to 672 K, respectively, up to 25 MPa. The data of Nefedov and Filippov [16] extend from 300 K to 620 K with pressures up to 30 MPa. Shulga et al. [17] performed measurements between 255 K and 402 K up to 993 MPa. San José et al. [15] reported data between 393 K and 503 K up to 2.5 MPa. Segovia et al. [18] measured four isotherms between 273.15 K and 333.15 K with pressures up to 20 MPa. Additionally, the data of Holzhauer and Ziegler [41] measured at ambient pressure between 162 K and 312 K are considered in the following discussion because there are only a few data at high pressures below 300 K for the isobaric heat capacity.

Fig. 12
figure 12

Relative deviations of derived isobaric heat capacities of toluene and data from the literature at nearby temperatures (\(T \pm 5\) K) from the EOS of Lemmon and Span [19] as a function of pressure. Derived values: , this work (, estimated uncertainty range); , Sun et al. [44]; and , Dhakal et al. [8]. Experimental data: , Akhundov and Eksaev [12, 13]; , Akhundov et al. [14]; , Holzhauer and Ziegler [41]; , Nefedov and Filippov [16]; and , Shulga et al. [17]

Full size image

Figure 12 depicts relative deviations of our derived isobaric heat capacities, the derived values of Dhakal et al. [8], and the selected data from the literature from the EOS of Lemmon and Span [19]. The experimental data of Segovia et al. [18] and the derived values of Shchamialiou et al. [7] are not included because they are only available at temperatures in the middle between the chosen isotherms in Fig. 12. The deviations of our derived values depend only little on pressure up to 303.15 K and decrease with pressure at higher temperatures. Overall, they change from +0.8 % at 243.15 K to \(-0.38\) % at 423.15 K. The deviations mainly result from the deviations of the initial values for the thermodynamic integration from the EOS. Above 303.15 K our values agree with the EOS within its uncertainty of 0.5 %, whereas at lower temperatures the deviations are somewhat larger than the uncertainty of the EOS, but the agreement is mostly within the mutual uncertainties.

The ambient pressure data of Holzhauer [41] agree with our derived values within the uncertainty of the derived values of about 0.32 % at 243.15 K and 263.15 K. At 283.15 K and 303.15 K, the deviations from our values are slightly larger than the uncertainty, but well within the mutual uncertainties. The extensive data of Akhundov et al. [14] agree well with our data at low pressure, but they exhibit a different dependence on pressure than our values, so that the deviations from our data increase with pressure. Up to 343.15 K, the deviations remain within the uncertainty of our values. On higher isotherms, the deviations from our values are larger than the uncertainty of our values, but they agree with them within their uncertainty of 0.8 %. The data of Akhundov and Eksaev [12, 13] show a similar dependence on pressure as the data of Akhundov et al. and agree with them within 0.3 %. The data of Nefedov and Filippov [16] and Shulga et al. [17] scatter more than the other data and agree only in parts with our values.

The values for the isobaric heat capacity derived by Dhakal et al. [8] agree with our derived values within the uncertainty of our values between 283.15 K and 343.15 K. At the higher isotherms, they are by up to 0.6 % lower than our derived values and lie moderately outside the uncertainty of our values, but well within the uncertainty of their data of 2.2 %. The derived values of Sun et al. [44] between 240 K and 300 K agree with our derived isobaric heat capacities with the uncertainty of our values with the exception of one value at 240 K and 100 MPa. Their values at 320 K are systematically lower than ours and lie moderately outside the uncertainty of our values.

Only two experimental data sets are available for the isochoric heat capacity of toluene. Their distribution in a pressure-temperature diagram is also shown in Fig. 11 using green symbols. Abdulagatov et al. [42] measured two isochors, but only one lies in the region of thermodynamic integration. The data of Polikhronidi et al. [43] are restricted to the vicinity of the critical point and, thus, lie outside the region of the thermodynamic integration. As for the isobaric heat capacity, Sun et al. [44], Shchamialiou et al. [7], and Dhakal et al. [8] provided values for the isobaric heat capacity, which were derived by the method of thermodynamic integration from speed of sound data sets.

Fig. 13
figure 13

Relative deviations of derived isochoric heat capacities of toluene and data from the literature from the EOS of Lemmon and Span [19] as a function of pressure. Derived values: this work (, estimated uncertainty range); , Sun et al. [44]; and , Dhakal et al. [8]. Experimental data: , Abdulagatov et al. [42]

Full size image

Figure 13 depicts relative deviations of our derived isochoric heat capacities, the derived values of Sun et al. [44] and Dhakal et al. [8], and the experimental data of Abdulagatov et al. [42] from the EOS of Lemmon and Span. The uncertainty of the EOS in the isochoric heat capacity amounts to 0.5 %. The deviations of our values increase slightly with pressure and decrease with temperature. The largest deviations of about 1 % are found at 243.15 K and 100 MPa, while on the 423.15 K isotherm they agree with the EOS within 0.3 %. Only one datum of Abdulagatov et al. [42] is shown in the plot for 403.15 K at 10 MPa, which deviates by about 0.9 % from our result. The rest of the data lies outside the scale of the plots. The derived values for the isochoric heat capacity of Dhakal et al. [8] agree with our values mostly within the uncertainty of our values. Moderately larger deviations are observed at above 363.15 K. Overall, the agreement is well within the uncertainty of the derived values of Dhakal et al. of 2.6 %. The derived values of Sun et al. [44] show a similar behavior as for the isobaric heat capacity. Between 240 K and 300 K, they agree with our values within the uncertainty of our values. Their values at 320 K are systematically lower than ours and lie somewhat outside the uncertainty of our values. We note that the deviations of the derived values of Dhakal et al. exhibit a shallow minimum at 10 MPa at the 283.15 K and 303.13 K isotherms. This effect is not observed for the derived values of Sun et al. and our derived values.

5.2 n-Butane

5.2.1 Density

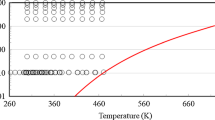
Data for the density and isobaric and isochoric heat capacity for liquid n-butane of other authors from the literature that were published until 2006 and used in the development of the EOS of Bücker and Wagner were reviewed in Ref. [20]. Since then, six further data sets for the density were published by Kumagai et al. [45], Miyamoto and Uematsu [46,47,48], Ito et al. [49], and Herrmann and Vogel [50]. Furthermore, independent of this work Meschkat and Meier [51] measured the density of n-butane on the two isotherms 300 K and 320 K up to 100 MPa with a vibrating-tube densimeter in our laboratory. These data have a relative uncertainty of 90 ppm. Details of selected data sets for the three properties from the literature are summarized in Table 5. The distribution of data sets for the density of n-butane from the literature in a pressure-temperature diagram is shown in Fig. 14. Additionally, the domain of the thermodynamic integration is indicated by the grey-shaded region.

Table 5 Summary of selected data sets for the density and isobaric and isochoric heat capacities of n-butane from the literature
Full size table
Fig. 14
figure 14

Distribution of data from the literature for the density of n-butane in the fluid region in a pressure-temperature diagram. The critical point is at (T = 425.13 K; p = 3.796 MPa). The grey-shaded region represents the region of thermodynamic integration. Experimental data: , Arve et al. [55]; , Glos et al. [6]; , Gupta and Eubank [53]; , Haynes [56]; , Herrmann and Vogel [50]; , Ito et al. [49]; , Kay [60]; , Kayukawa et al. [52]; , Kiran and Sen [54]; , Kumagai et al. [45]; , MacCallum and McKetta [57]; , Meschkat and Meier [51]; , Miyamoto and Uematsu [46]; , Miyamoto and Uematsu [48]; , Olds et al. [59]; , Petty and Smith [58]; and , Sage et al. [61]. , Critical pressure, critical temperature, and , vapor pressure calculated with the EOS of Bücker and Wagner [20]

Full size image

The relative deviations of the derived densities and data from the literature for the density from the EOS of Bücker and Wagner [20] are depicted in Figs. 15 and 16. The data of Glos et al. [6], Haynes [56], Ito et al. [49], Kayukawa et al. [52], Meschkat and Meier [51], Miyamoto and Uematsu [46], and Olds et al. [59] overlap with the region of the thermodynamic integration and were selected for the comparison. All other data from the literature either lie on the boiling line, in the temperature range below or above the domain of the thermodynamic integration, or their deviations from the EOS are mostly larger than the scale of the plots.

Fig. 15
figure 15

Relative deviations of derived densities for n-butane along isotherms and data from the literature at nearby temperatures (\(T \pm 2\) K) from the EOS of Bücker and Wagner [20] as a function of pressure. Derived values: , this work (, estimated uncertainty range). Experimental data: , Arve et al. [55]; , Glos et al. [6]; , Glos et al. [6] (interpolated); , Haynes [56]; , Kayukawa et al. [52]; , Miyamoto and Uematsu [46]. , Vapor pressure

Full size image
Fig. 16
figure 16

Relative deviations of derived densities for n-butane and data from the literature at nearby temperatures (\(T \pm 5\) K) from the EOS of Bücker and Wagner [20] as a function of pressure. Derived values: , this work (, estimated uncertainty range). Experimental data: , Arve et al. [55]; , Glos et al. [6]; , Haynes [56]; , Kayukawa et al. [52]; , Meschkat and Meier [51]; , Miyamoto and Uematsu [46]; and , Olds et al. [59]. , Vapor pressure

Full size image

Our derived densities agree with the data of Glos et al. [6] within 10 ppm on all isotherms, except for the initial value for the density at 340 K and 2 MPa, which deviates by −15 ppm. The largest deviations are observed at 200 K, 260 K, 280 K, and 340 K. These deviations are related to the behavior of the derivative \((\partial ^2 \rho /\partial T^2)_p\) at high pressure shown in Fig. 5, where the spacing of the isotherms is not as good as for toluene in Fig. 2. Up to 12 MPa, where the EOS was fitted to the data of Glos et al. [6], our derived densities and the Glos et al. data agree with the EOS within 60 ppm at 200 K, 40 ppm between 220 K and 320 K, and 0.013 % at 340 K. At higher pressures, the deviations of our derived densities increase up to −0.03 % between 200 K and 300 K and −0.06 % up to 340 K. Generally, the agreement is well within the uncertainty of the EOS, which is 0.02 % at pressures below 12 MPa and between 0.3 % and 0.5 % at higher pressures in the temperature range of the thermodynamic integration.

Arve et al. [55] performed measurements at pressures up to 1.13 MPa between 278.15 K and 338.15 K in steps of 20 K. Their data mostly agree with our derived values within the uncertainty of our derived values. Only their data at 338.15 K show somewhat larger deviations. Below 300 K, all other data sets show larger deviations from the EOS than our derived densities. The data of Miyamoto and Uematsu [46] have a similar pressure dependence as our derived values, but tend to scatter and are between 0.16 % and 0.18 % higher than our values. The data of Haynes [56] and Kayukawa et al. [52] agree with our derived values within 0.2 %, but exhibit a different pressure dependence. The data of Olds et al. [59] scatter more than the data of the other authors, but agree with the EOS within their uncertainty of 0.2 % and show the same pressure dependence as our derived densities and the data of Miyamoto and Uematsu. The data of Meschkat and Meier [51] agree with the derived densities and the data of Glos et al. [6] within 30 ppm at 300 K and within 60 ppm at 320 K, which confirms the high accuracy of our derived densities.

5.2.2 Isobaric and Isochoric Heat Capacity

For the isobaric heat capacity of n-butane, no data are available above ambient pressure. Aston and Messerly [65] published 23 data between 142 K and 268 K at ambient pressure, which can partly be compared with our derived isobaric heat capacities. The data of Beeck [67], Dailey and Felsing [63], Dobratz [64], Sage et al. [66], and Senftleben [62] lie in the gas region. Figure 17 depicts the distribution of these data sets and the region of thermodynamic integration in a pressure-temperature diagram.

Fig. 17
figure 17

Distribution of data from the literature for the isobaric and isochoric heat capacities of n-butane in a pressure-temperature diagram. The critical point is at (T = 425.13 K; p = 3.796 MPa). The grey-shaded region denotes the region of the thermodynamic integration. Black symbols denote isobaric heat capacities, green symbols isochoric heat capacities. Experimental isobaric heat capacities: , Aston and Messerly [65]; , Beeck [67]; , Dailey and Felsing [63]; , Dobratz [64]; , Sage et al. [66]; and , Senftleben [62]. Experimental isochoric heat capacities: , Magee and Lüddecke [68]. , Critical pressure, critical temperature; and , vapor pressure calculated with the EOS of Bücker and Wagner [20]

Full size image

Figure 18 shows relative deviations of our derived isobaric heat capacities and the data of Aston and Messerly [65] from the EOS of Bücker and Wagner [20]. Our derived values agree with the EOS within 0.9 %, which is within the uncertainty of the EOS of 1 % to 3 %. On all isotherms, the deviations are almost constant and change from +0.2 % at 200 K to \(-0.9\) % at 340 K. The data of Aston and Messerly [65] agree with our derived values within their uncertainty except for a single value at 240 K.

Fig. 18
figure 18

Relative deviations of derived isobaric heat capacities for n-butane along isotherms and data from the literature at nearby temperatures (\(T \pm 7.5\) K) from the EOS of Bücker and Wagner [20] as a function of pressure. Derived values: , this work (, estimated uncertainty range). Experimental data: , Aston and Messerly [65]. , Vapor pressure calculated with the EOS of Bücker and Wagner [20]

Full size image

Magee and Lüddecke [68] measured a comprehensive data set of the isochoric heat capacity of liquid n-butane between 150 K and 343 K up to 33.5 MPa with a relative uncertainty of 0.7 %. The distribution of these data in a pressure–temperature diagram is also shown in Fig. 17. Relative deviations of our derived isochoric heat capacities and the data of Magee and Lüddecke [68] from the EOS of Bücker and Wagner are shown in Fig. 19. Our derived isochoric heat capacities agree with the EOS within 1.1 % between 200 K and 240 K, within 1.5 % between 260 K and 280 K, and within 2.1 % between 300 K and 340 K. The uncertainty of the EOS in the isochoric heat capacity in the liquid region was estimated by Bücker and Wagner to be 1 % between 200 K and 300 K and 2 % to 3 % between 300 K and 340 K at pressures up to 33.5 MPa. At higher pressures, it amounts to 5 %. Thus, the agreement with the EOS is mostly within its uncertainty.

The data of Magee and Lüddecke generally tend to scatter. At 200 K and 220 K, they agree with our derived values within the uncertainty of our derived values. At 240 K, they lie partly outside the uncertainty. At low pressures on the 260 K isotherm, they agree within the uncertainty of the derived values, but at high pressures they are systematically higher by 1.3 %. Between 280 K and 340 K, the data of Magee and Lüddecke [68] show a similar pressure dependence as our derived values, but at 280 K and 300 K they are about 0.8 % higher. At 320 K, the deviations decrease to 0.5 % and at the highest isotherm 340 K the derived values and the data of Magee and Lüddecke [68] agree mostly within the uncertainty in the derived values. Generally, the agreement is mostly within the mutual uncertainties of the two data sets.

Fig. 19
figure 19

Relative deviations of derived isochoric heat capacities for n-butane along isotherms and data from the literature at nearby temperatures (\(T \pm 7.5\) K) from the EOS of Bücker and Wagner [20] as a function of pressure. Derived values: , this work (, estimated uncertainty range). Experimental data: , Magee and Lüddecke [68]. , Vapor pressure calculated with the EOS of Bücker and Wagner [20]

Full size image

6 Conclusions

Using the method of thermodynamic integration, accurate values for the density and isobaric and isochoric heat capacity of toluene and n-butane were derived from speed of sound data sets measured previously in our laboratory. Since no suitable data are available for the isobaric heat capacity on the initial isobars of the integration, a procedure developed by us in a previous work on isobutane, with which accurate values of the isobaric heat capacity can be derived from a speed of sound correlation and accurate experimental data for the density, has been applied to derive values for the isobaric heat capacity of toluene and n-butane on the initial isobar. Correlations of the experimental speeds of sound in toluene and n-butane as a function of temperature and pressure were developed using the method of structural optimization. Extensive comparisons of the derived properties with experimental data for the density and isobaric and isochoric heat capacity shows that our derived values are more accurate than most experimental data and values for these properties derived by other authors by the method of thermodynamic integration. Compared to recent works of other authors, our thermodynamic integration for toluene also covers the range of low temperatures between 240 K and 280 K. Especially valuable are the results for the isobaric heat capacity of n-butane at pressures above ambient because until now only data in the gas and liquid regions at ambient pressure have been published by other authors. Our derived values for the density and isobaric and isochoric heat capacity together with recent data from other authors can contribute to develop new improved EOSs for toluene and n-butane.