Recommended Values of the Viscosity in the Limit of Zero Density for R134a and Six Vapors of Aromatic Hydrocarbons as Well as of the Initial Density Dependence of Viscosity for R134a. Revisited from Experiment Between 297 K and 631 K

Abstract

Previously published experimental viscosity data at low density, originally obtained using all-quartz oscillating-disk viscometers for R134a and six vapors of aromatic hydrocarbons in the temperature range between 297 K and 631 K at most, were re-evaluated after an improved re-calibration. The relative combined expanded ($k=2$) uncertainty of the re-evaluated data are 0.2 % near room temperature and increases to 0.3 % at higher temperatures. The re-evaluated data for R134a as well as for the vapors of mesitylene, durene, diphenyl, fluorobenzene, chlorobenzene, and p-dichlorobenzene were arranged in approximately isothermal groups and converted into quasi-isothermal viscosity data using a first-order Taylor series in temperature. Then, the data for R134a were evaluated by means of a series expansion truncated at first order to obtain the zero density and initial density viscosity coefficients, $\eta ^{(0)}$ and $\eta ^{(1)}$. For the six aromatic vapors, the Rainwater–Friend theory for the initial density dependence of the viscosity was used to derive $\eta ^{(0)}$ values. Finally, reliable $\eta ^{(0)}$ and also $\eta ^{(1)}$ values for R134a were selected as reference values in the measured temperature range to be applied when generating a new viscosity formulation.

1 Introduction

Numerous studies dealing with the viscosity of gases and particularly of organic vapors were accomplished applying all-quartz oscillating-disk viscometers at the University of Rostock over four decades. For these studies reported by Vogel and co-workers, a large number of measurement series were performed using continuously renewed instruments of this viscometer type. Unfortunately, the viscosity values following from these studies were seriously affected by a calibration carried out for the relative measurements. In general, the calibration was based on experimental reference values for the viscosity of noble gases and of nitrogen at low densities and at room temperature. With regard to the six vapors of the aromatic hydrocarbons under discussion, the applied reference values were still older than those, which were used for the subsequent measurements concerning the initial density dependence of the viscosity of some other gases and vapors (see Ref. [1]). The old reference values for the viscosity of argon and nitrogen of Kestin and Leidenfrost [2] are nowadays considered as obsolete. Since accurate theoretically calculated viscosity values for argon at zero density [3] as well as improved experimentally based [4] and theoretical [5] viscosity values for nitrogen at low density became available and the information about the measurements with the previous all-quartz oscillating-disk viscometer still exists, the formerly measured data of Vogel and co-workers should be re-evaluated.

In this work, the re-evaluated results for the originally determined viscosity data of 1,1,1,2-tetrafluoroethane (R134a) [6] and of the vapors of 1,3,5-trimethylbenzene (mesitylene) [7], 1,2,4,5-tetramethylbenzene (durene) [7], biphenyl (diphenyl) [8], fluorobenzene [9], chlorobenzene [10], and 1,4-dichlorobenzene (p-dichlorobenzene) [8] are listed. Moreover, the re-evaluated viscosity data, concerning results at comparatively low and moderate densities between room temperature and at most 631 K, were employed to deduce the viscosity coefficients in the limit of zero density.

An analogous re-evaluation have already been discussed for argon [11], krypton [12], xenon [12], carbon dioxide [12], nitrogen [13], water vapor [14], ethane [15], propane [16], n-butane [17], and isobutane [18]. In the foregoing paper [1], the re-evaluated results for the viscosity of sulfur hexafluoride, methanol, n-pentane, n-hexane, n-heptane, neopentane, cyclohexane, benzene, toluene, p-xylene, phenol, and triethylamine were presented.

2 Oscillating-Disk Viscometer, Calibration, and Uncertainty

The primary measurements were performed applying two marginally dissimilar all-quartz oscillating-disk viscometers with small gaps (see Figs. 1 and 2 as well as Fig. 1 of Ref. [1]). The oscillating disk of the viscometer in Fig. 1 of the present paper had a radius $R=17.48\,{\text{mm}}$ and a thickness $d=1.55\,{\text{mm}}$. The moment of inertia amounted to $I=503.0\, {{\text{g}}\cdot {\text{mm}}}^2$, whereas the upper and lower gaps $b_1$ and $b_2$ between oscillating and fixed disks were 1.10 mm. The quartz-glass suspension strands of the viscometers had a length and a diameter of 170 mm and about (35–45) $\upmu$m, respectively, resulting in a period in vacuo $\tau _0$ at 298.15 K of 24.61 s and 24.33 s. The design principle for the viscometer was specified in Ref. [19]. Quartz glass was employed as the building material on account of its small thermal expansion coefficient so that changes in the dimensions of the viscometer could be neglected and measurements in a large temperature range became possible. In addition, the logarithmic decrement in vacuo $\Delta _0$ of a suspension strand made of fused quartz is negligibly small compared to that of a metal wire in the temperature range of the measurements [20]. Moreover, quartz glass is distinguished by a high chemical stability so that a possible decomposition of the organic vapors at higher temperature is only marginally influenced by a catalytic effect.

Fig. 1

Cross section of the first version of the all-quartz oscillating-disk viscometer

Fig. 2

Oscillating-disk system: (a) upper fixed disk, (b) oscillating disk, (c) lower fixed disk, (d) upper gap, (e) lower gap

In the case of the aromatic hydrocarbon vapors, the logarithmic decrement $\Delta$ of the damped harmonic oscillation was derived from length measurements applying the silicon-coated mirror at the lower end of the long thin rod which was fused underside the oscillating disk. The mirror was employed together with a high-precision scale and a telescope at a distance of 2 m from the axis of the viscometer to register the turning points of the damped oscillation. The second parameter, the period $\tau$ of the harmonic oscillation, was deduced from time measurements with a stop watch. For this, the crossing of the zero position was observed with the telescope. To reduce the uncertainty, the time was taken for at least ten full oscillations. For the measurements on R134a, $\tau$ and $\Delta$ were obtained only from time measurements applying, in connection with the viscometer shown in Fig. 1 of Ref. [1], an opto-electronic system which consists of a 1 mW helium-neon laser and two photoreceivers, stationarily located at fixed positions on an optical bench at the distance of 2 m from the viscometer (see Ref. [21]). Both procedures are distinguished by the same uncertainties with regard to $\Delta$ and $\tau$, because the movement of the disk is externally initiated by rotating a mechanical device through a small angle forward and reverse to the basic position. Five to 20 individual oscillations are taken after starting an oscillation run and passing some periods for the decay of perturbations. The relative uncertainty in $\Delta$ is $0.05\,\%$, while that in $\tau$ is $0.005\,\%$.

Unfortunately, an absolute measurement procedure is not feasible in the case of an all-quartz oscillating-disk viscometer. For absolute measurements, Newell [22] developed an appropriate theory, in which a so-called Newell constant $C_{\text{N}}$ has to be computed from the dimensions of the viscometer, which must be known with very high accuracy,

$$\begin{aligned} C_{\text{N}}= & {} 1 + \frac{8 p}{\pi }\left\{ \left( 1+u\right) \ln \left( 2+u\right) - \frac{1}{2} u \ln \left[ \left( 1+u\right) ^2 -1\right] \right\} + 2 p^2 \left[ 1+3u-N(u)\right] \quad \\ {\text{with}}&\quad p=\frac{b}{R}\,, \quad u=\frac{d}{2b}\,, \quad b=\frac{2b_1b_2}{b_1+b_2}\,. \end{aligned}$$

(1)

Here N(u) is a constant value for a considered viscometer [23]. Since all connections between the single parts of the all-quartz oscillating-disk viscometer have to be connected by fusing, the dimensions cannot be ascertained with an accuracy necessary for absolute measurements. For relative measurements, the working equation according to Newell is given as

$$\begin{aligned} C_{\text{N}}= & {} \left[ \frac{2I}{\pi \rho b R^4}\left( \frac{\Delta }{\theta }-\Delta _0\right) +a\frac{\Delta }{\theta }\right] \beta ^2 + f\frac{3\Delta ^2-1}{\theta ^2} \beta ^4 + h \frac{\Delta \left( \Delta ^2-1\right) }{\theta } \beta ^6 \\&{\text{with}} \quad \beta =\frac{b}{\delta }\,, \quad \delta =\left( \frac{\eta \tau _0}{2\pi \rho }\right) ^{1/2}\,, \quad \theta =\frac{\tau }{\tau _0}\,, \quad k= \frac{b_1}{b_2}\,, \\&{\text{and}}\quad a=\frac{2}{3} \,, \quad f=\frac{1}{45}\,, \quad h=\frac{8}{945}\quad {\text{for}} \quad k=1\,. \end{aligned}$$

(2)

This equation enables to calculate the Newell constant $C_{\text{N}}$ using one reliable reference viscosity value $\eta$ at an experimentally known low density $\rho$ of the calibration gas, especially at room temperature, including the measurement quantities $\Delta$ and $\tau$ (as well as $\Delta _0$ and $\tau _0$ in vacuo). The experimental density $\rho$ of the examined vapors was also comparatively small so that the contributions of the terms with f and h in Eq. 2 are entirely insignificant and even the term with a amounts to less than $0.1\,\%$ of the main contribution (see Ref. [24]). Hence, the Newell constant can properly be calculated from Eq. 2 using the only approximately established dimensions of the respective viscometer. This procedure makes it possible to calibrate the all-quartz oscillating-disk viscometer. To evaluate the actual measurements, the calculated Newell constant $C_{\text{N}}$ is employed and $\beta ^2$ is iteratively computed with Eq. 2. Finally, the boundary-layer thickness $\delta$ associated with $\eta$ and $\rho$ provides $\eta$.

The viscosity values needed for the calibration result from

$$\eta (T,\rho )= \eta ^{(0)}_{298.15} + (T-298.15) (\partial \eta /\partial T)_\rho + \rho (\partial \eta /\partial \rho )_T.$$

(3)

As already stated in Sec. 1, the experimental reference values of Kestin and Leidenfrost [2], used for the primary calibration of the all-quartz oscillating-disk viscometer, are out of date today. New theoretically calculated and experimentally determined reference viscosity values at 298.15 K have already been employed when the viscosities of argon [11], of methane and hydrogen sulfide [25], of nitrogen and carbon monoxide [13], and of acetic acid vapor [26] were newly measured with this type of viscometer. The previous outdated reference values for the viscosity of argon and nitrogen are compared with the new appropriate ones in Table 1, which shows that the difference consists essentially in the zero density viscosity coefficient $\eta ^{(0)}_{298.15}$ of the respective gas. Because the calibration measurements were not performed exactly at 298.15 K and of course not at zero density, the temperature derivative $(\partial \eta /\partial T)_\rho$ is required together with the density derivative $(\partial \eta /\partial \rho )_T$ in Eq. 3. To deduce the former derivative, one needs zero density viscosity values not only at 298.15 K but also at further temperatures. Since the impact of the density derivative $(\partial \eta /\partial \rho )_T$ on the reference viscosity value according to Eq. 3 is comparatively small, its values determined by Kestin et al. [27] were used for computing the new reference viscosity values for the re-calibration.

Table 1 Previous and new reference values for the calibration of the oscillating-disk viscometer

Two possibilities exist for the choice of a suitable $\eta ^{(0)}_{298.15}$ value for the re-calibration when the previous viscometer was calibrated with argon. Both a theoretically computed viscosity value and an experimentally based viscosity datum could be used. We preferred to apply a theoretical $\eta ^{(0)}_{298.15}$ value. Vogel et al. [28] used an ab initio potential energy curve for the argon atom pair (see Refs. [29, 30]) and the kinetic theory of dilute monatomic gases to calculate theoretical viscosity values in the limit of zero density. The relative uncertainty of the $\eta ^{(0)}_{298.15}$ value was supposed to be $<0.1\,\%$. Another theoretically computed viscosity value for argon at 298.15 K obtained by Mehl was compared with that by Vogel et al. in Figure 7.2b of Ref. [31]. This figure shows that the relative uncertainty of both theoretical values could actually be lowered to 0.07  %. The theoretical viscosity values for argon were originally listed by Vogel et al. with only five significant digits. Hellmann [3] repeated the calculations using one digit more. The obsolete experimentally based $\eta ^{(0)}_{298.15}$ value of Kestin and Leidenfrost [2] deviates from the new theoretical value of Hellmann at 298.15 K by $0.313\,\%$. The coefficient of the temperature dependence $(\partial \eta /\partial T)_\rho$ in Table 1 was derived using Ref. [3].

The new experimentally based viscosity datum $\eta ^{(0)}_{298.15}$ for argon recommended by Berg and Moldover [4] is distinguished by a very low value of the relative uncertainty: $u_{\text{r}}(\eta )=0.00\,027$. To obtain this value, Berg and Moldover critically assessed the results of viscosity measurements relative to helium using 18 instruments for 11 gases near 298.15 K, which were extrapolated to zero density. Then, they used a fitting process considering altogether 235 viscosity ratios, the values of which were anchored to the highly accurate, theoretically computed $\eta ^{(0)}_{298.15}$ value for helium reported by Cencek et al. [32]. In this way, similar to the improvement of a signal-to-noise ratio, the relative uncertainty of the $\eta ^{(0)}_{298.15}$ values for all 11 gases could be reduced. For an individual gas, the situation is somewhat inferior. Thus, Xiao et al. [33] re-evaluated previous measurements of May et al. [34] for argon carried out with a two-capillary viscometer to obtain viscosity ratios relative to helium between 200 K and 400 K. Applying again the $\eta ^{(0)}_{298.15}$ value for helium by Cencek et al., the relative uncertainty of the argon viscosity data increased to $u_{\text{r}}(\eta )=0.00\,038$. But, employing another measurement technique instead of the two-capillary viscometer (relative to helium), only an increased relative uncertainty can be achieved, probably twice as high. The difference between the theoretical viscosity value of Hellmann [3] and the experimentally based viscosity datum $\eta ^{(0)}_{298.15}$ of Berg and Moldover amounts to 0.058 % and is within the relative uncertainty of the theoretical value.

For nitrogen, Berg and Moldover [4] recommended the $\eta ^{(0)}_{298.15}$ datum of Table 1, which was determined by the same procedure already explained for argon. Note that the experimentally based $\eta ^{(0)}_{298.15}$ value of Kestin and Leidenfrost [2] deviates from the recommended value of Berg and Moldover at 298.15 K by $0.215\,\%$. In addition, the value of Berg and Moldover for nitrogen is distinguished by a deviation of $0.03\,\%$ from a theoretically based value $\eta ^{(0)}_{298.15}=17.701\,\upmu {{\text{Pa}}\cdot {\text{s}}}$, which was proposed by Hellmann [5]. Hellmann applied for his calculations an ab initio potential energy surface for the nitrogen molecule pair and the kinetic theory of molecular gases. Since the computed theoretical values are too low by about $0.3\,\%$ between 300 K and 700 K compared with the best experimental viscosity data, Hellmann suggested to increase his theoretical viscosity values by a factor 1.003. This was based on the finding that the temperature dependence of the theoretical values is in excellent agreement with that of the best experimental data. Therefore, the temperature derivative $(\partial \eta /\partial T)_\rho$ for nitrogen was derived from the theoretical values of Hellmann.

An uncertainty analysis applying the new $\eta ^{(0)}_{298.15}$ value for argon including the temperature and density derivatives $(\partial \eta /\partial T)_\rho$ and $(\partial \eta /\partial \rho )_T$, all given in Table 1, was performed in Ref. [1] and should not be repeated here. As a summary, the relative combined expanded ($k=2$) uncertainty of the experimental viscosity data for any gas or organic vapor results as $U_{\text{c,r}}(\eta )=0.002$ at room temperature and, assuming a slight increase with temperature, as $U_{\text{c,r}}(\eta )=0.003$ at higher temperatures.

The series of measurements on a certain gas or organic vapor were often supplemented by additional measurement series on the calibration gas. As long as no change of the Newell constant was detected, it was concluded that the suspension system of the viscometer did not undergo a change as a result of an alteration due to the measurements at high temperatures.

The investigation on R134a reported in 1996 was part of a round-robin project, in which a single source of supply should be applied. Thus, nine separate cylinders were filled and supplied by ICI Chemical and Polymers Ltd., UK, using special procedures for the cleanliness of the cylinders. The measurements extended over a larger density range up to somewhat more than $9\, {{\text{kg}}\cdot {\text{m}}^{-3}}$.

For the original measurements on the respective aromatic vapors, the evacuated oscillating-disk viscometer was filled by sublimation of the corresponding substance from ampules with the weighed samples. These small glass ampules were filled in turn by sublimation with the final purified samples after drying with molecular sieves as well as degassing by repeated freezing and evacuating. If applicable, the melting point of the substance was determined using the specifically designed filling apparatus. After freezing the substance at the bottom of the viscometer employing liquid nitrogen, the filling line was fused for the quasi-isochoric measurements. Note that the measurement densities of the aromatic hydrocarbon vapors were at least fifteen times smaller than the highest density for R134a.

3 Results of the Re-evaluated Measurements

Firstly, the temperatures of the original measurements were, apart from those for R134a, converted to the ITS-90 temperature scale. Secondly, the associated argon and nitrogen measurements were used to re-calibrate the employed oscillating-disk viscometer applying the revalued viscosity values of Table 1. Thirdly, the values of the improved Newell constants $C_{\text{N}}$ for a respective measurement series were applied for calculating the re-evaluated viscosity data using the directly obtained $\Delta$, $\tau$, $\tau _0$, and $\rho$ values.

Because this investigation is aimed at the identification of the viscosity in the limit of zero density, $\eta ^{(0)}$, and additionally for R134a of its initial density dependence, $\eta ^{(1)}$, isotherms should be considered. Since quasi-isothermal re-evaluated data are required for this analysis, the experimental re-evaluated points of the three (for five of the aromatic vapors), four (for p-dichlorobenzene), or six (for R134a) isochoric series were grouped such that approximated isotherms resulted. To have at least three isothermal values for the evaluation, we were forced to include actually data points at temperatures differing by $\pm 12\,{\text{K}}$. In addition, re-measurements were carried out at lower temperatures, after the highest temperature had been attained, to check for any thermal alteration or decomposition of the chemical substance. But it must be considered that the thermal alteration could be a reversible process. Then, a few experimental points at high temperatures or re-measured points had to be excluded owing to significantly increased viscosity values compared with other values of the quasi-isotherms. Hence, the isothermal groups could include a reduced number of data compared with the total number of series for a considered substance. For that reason, only one or two experimental data points could belong to an isotherm so that none or no trustworthy $\eta ^{(0)}$ and $\eta ^{(1)}$ (for R134a) values could be determined using the quasi-isothermal data. It should be restated that the density range of the isochores is rather restricted for the six aromatic vapors so that, in spite of the high reproducibility, small differences could particularly lead to unexpected values of the initial density dependence, $\eta ^{(1)}$.

The re-evaluated grouped results of the measured isochores are listed for R134a and the six aromatic vapors in Tables 2, 3, 4, 5, 6, 7, and 8. Each row of the different series consisting of filled and empty spaces represents a grouped isotherm. The table captions include the reference in which the measurements were originally described. In a footnote of the tables, the calibration gas and the purity of the measured samples are provided. Moreover, detailed information is indicated in further footnotes concerning individual experimental points which were included or excluded compared to the original publication.

Note that one experimental datum of Series 3 for chlorobenzene at the lowest temperature (see Table 7) should not directly be used, because this point was apparently measured at a density $\rho$ higher than that of the saturated vapor $\rho _{\text{sat}}$ at the measurement temperature.

Table 2 Re-evaluated viscosity data for 1,1,1,2-tetrafluoroethane (R134a)$^1$ of Wilhelm and Vogel [6]

Table 3 Re-evaluated viscosity data for 1,3,5-trimethylbenzene (mesitylene) vapor$^1$ of Vogel [7]

Table 4 Re-evaluated viscosity data for 1,2,4,5-tetramethylbenzene (durene) vapor$^1$ of Vogel [7]

Table 5 Re-evaluated viscosity data for biphenyl (diphenyl) vapor$^1$ of Vogel [8]

Table 6 Re-evaluated viscosity data for fluorobenzene vapor$^1$ of Kaussmann et al. [9]

Table 7 Re-evaluated viscosity data for chlorobenzene vapor$^1$ of Ahlmeyer et al. [10]

Table 8 Re-evaluated viscosity data for 1,4-dichlorobenzene (p-dichlorobenzene) vapor$^1$ of Vogel [8]

4 Validation of the Viscosity in the Limit of Zero Density and of Its Initial Density Dependence

As already discussed, the primary data points of the respective isochores were not measured at exactly identical temperatures for a certain substance. The same is true for the re-evaluated counterparts, which could only be compressed to approximate isotherms. Then, the re-evaluated data were converted into quasi-isothermal values applying a first-order Taylor series in temperature,

$$\eta (T_{\text{iso}}) = \eta (T_{\text{exp}}) + \left( \frac{\partial \eta }{\partial T}\right) _\rho (T_{\text{iso}} - T_{\text{exp}}) + R_{\text{N}}.$$

(4)

The temperature of the isotherms $T_{\text{iso}}$ conforms to the mean of the experimental temperatures $T_{\text{exp}}$ of the data for the distinct isochoric series measured at the respective approximate adjustment of the thermostat. The temperature derivative $(\partial \eta /\partial T)_\rho$ needed in Eq. 4 was deduced by means of the following equation,

$$\begin{aligned} \eta (T) = S \exp \left[ A \ln \left( T_{\text{R}}\right) +\frac{B}{T_{\text{R}}}+\frac{C}{T_{\text{R}}^2}+\frac{D}{T_{\text{R}}^3}+E\right] , \end{aligned}$$

(5)

where $T_{\text{R}} = T/(298.15\,{\text{K}})$ and $S=10\,\upmu {{\text{Pa}}\cdot {\text{s}}}$. The coefficients A, B, C, D, and E were derived in a fit of Eq. 5 to the experimental data of each isochoric series, in which the values of the re-measured experimental point or points of each isochore were also included, meaning that the influence of any reversible thermal alteration of the samples remained hidden. It was proven that the remainder $R_{\text{N}}$ in Eq. 4 is insignificant compared to the experimental uncertainty.

The only experimental point situated in the saturated vapor and reported for chlorobenzene in Table 7 does not correspond to the actual density at which the measurements of the isochore were carried out, but to the density of the saturated vapor $\rho _{\text{sat}}$ also given in that table. The small excess amount of the substance was adsorbed at the inner wall of the viscometer. The value of $\rho _{\text{sat}}$ was derived using a virial equation limited to the second virial coefficient B(T) according to

$$\begin{aligned} \rho _{\text{sat}} = \frac{1}{2 B(T)} - \left( \left[ \frac{1}{2 B(T)} \right] ^2 + \frac{p_{\text{sat}}}{B(T) R T} \right) ^{1/2}. \end{aligned}$$

(6)

Here, $p_{\text{sat}}$ is the saturation pressure, which was calculated for chlorobenzene with an Antoine equation recommended by NIST [35]. The second virial coefficient B(T) in turn was computed using a polynomial in 1/T given in Ref. [10].

The values of the zero density viscosity $\eta ^{(0)}$ and of the initial density dependence $\eta ^{(1)}$ were derived from a fit of the quasi-isothermal viscosity values at a certain temperature $T_{\text{iso}}$ as a function of density applying a series expansion truncated at first order,

$$\begin{aligned} \eta (T,\rho )= \eta ^{(0)}(T) + \eta ^{(1)}(T) \rho . \end{aligned}$$

(7)

It is clear that the density range for the aromatic vapors is badly restricted. Moreover, a fit using only three values, even though only two coefficients must be deduced, represents an invidious task. Already small uncertainties of the experimental data could have led to unreliable $\eta ^{(0)}$ and $\eta ^{(1)}$ values. In the case that only two experimental points were available for a grouped isotherm, $\eta ^{(0)}$ and $\eta ^{(1)}$ were directly calculated using Eq. 7. With one experimental point, it was not possible to derive $\eta ^{(0)}$ by means of Eq. 7. For R134a, it was distinctly easier to obtain appropriate $\eta ^{(0)}$ and $\eta ^{(1)}$ values applying Eq. 7, since the number of quasi-isothermal viscosity values was five or six and the density range was at least ten times larger compared to that of the aromatic vapors.

Therefore and particularly for the six aromatic vapors, the re-evaluated $\eta$ values of a quasi-isotherm were also rectified to the limit of zero density applying the Rainwater–Friend theory [36, 37], which describes the initial density dependence of the transport properties. For the viscosity, the second viscosity virial coefficient is defined as

$$B_\eta (T)= \frac{M \eta ^{(1)}(T)}{\eta ^{(0)}(T)}\,,$$

(8)

where M is the molar mass. Bich and Vogel [38, 39] published tables of the reduced second viscosity virial coefficient $B_\eta ^*$ as a function of the reduced temperature $T^*$. After that, Vogel et al. [40] proposed a reasonable correlation of $B^*_\eta (T^*)$, valid in the range $0.3\le T^*\le 100$,

$$\begin{aligned} B^*_\eta (T^*)= & {} \frac{B_\eta (T)}{N_{\text{A}}\sigma ^3} = \sum _{i=0}^{6}b_i {T^*}^{-i/4} +\, b_7 {T^*}^{-5/2} +\, b_8 {T^*}^{-11/2}\,, \end{aligned}$$

(9)

$$T^*= \frac{k_{\text{B}} T}{\varepsilon }.$$

(10)

In Eqs. 9 and 10, $N_{\text{A}}$ and $k_{\text{B}}$ are Avogadro’s and Boltzmann’s constants, respectively. The coefficients $b_i$ are listed in Table 9. The scaling factors $\varepsilon /k_{\text{B}}$ and $\sigma$ are usually the parameters for the Lennard-Jones 12-6 potential. Of course, none of the considered substances complies with the Lennard-Jones 12-6 potential so that the theoretical guidance for the representation of the initial density dependence of the viscosity is inadequate for them. But Eqs. 9 and 10 enable a secure extrapolation both to low and to high temperatures if appropriate values for the energy scaling factor $\varepsilon /k_{\text{B}}$ and the length scaling factor $\sigma$ can be derived from the measurements. At low temperatures T or better at low reduced temperatures $T^*$, negative values for $\eta ^{(1)}(T)$ and $B_\eta (T)$, respectively, are observed, which become less negative with increasing temperature, followed by a transition to positive values. After passing through a maximum, the values of $B_\eta (T)$ decrease monotonically and attain negative values at very high reduced temperatures, only proven experimentally for helium.

Table 9 Coefficients $b_i$ of Eq. 9 for the Rainwater–Friend theory

In principle, it is reasonable to derive optimized scaling factors $\varepsilon /k_{\text{B}}$ and $\sigma$ by fitting the theoretical results for the Rainwater–Friend theory, presented by Eqs. 9 and 10, to experimental $B_\eta (T)$ values of a selected substance resulting from Eq. 8. Typically, the $\eta ^{(0)}$ and $\eta ^{(1)}$ values following from the series expansion according to Eq. 7 should be employed to calculate the required experimental $B_\eta$ values. In Ref. [1], this was recently demonstrated for measurements on twelve gases and vapors, but those experiments extended over a distinctly larger density range and included more isochoric measurement series. When using a fit to three and four quasi-isothermal re-evaluated data points or a simple calculation from two re-evaluated data points, Eq. 7 may yield $B_\eta (T)$ values which are implausible and do not correspond to the pattern of the explained general behavior of second viscosity virial coefficients. Consequently, the fit of Eq. 9 to such values will not be satisfactory. In principle, only reliable $B_\eta (T)$ values should be included to determine the optimized scaling factors $\varepsilon /k_{\text{B}}$ and $\sigma$. For the aromatic vapors, less than half of the quasi-isotherms provided appropriate $B_\eta (T)$ values so that the derivation of the scaling factors was a complicated task and, aside from that, pretty subjective and arbitrary. The lastly taken selection of reasonably sensitive $B_\eta (T)$ values yielded the scaling factors for the aromatic vapors listed in Table 10 together with the information which isotherms could be or were not considered in the fit. Since the scaling factors for the aromatic vapors are rather insecure, the correction to the limit of zero density by means of the Rainwater–Friend theory was additionally performed using the scaling factors of similar substances. The rationale for this approach is that the density range over which the extrapolation has to be done is relatively small and the scaling factors for very similar substances are available. As an example, the molecular sizes and the electrostatic surface potentials of benzene and fluorobenzene, shown in Fig. 1b of Ref. [41], are not so different. In addition, the parameters of the 11-6-8 potential deduced from the measured viscosity coefficients (without extrapolation to the limit of zero density) and reported in 1982 (Ref. [42]) do not differ strongly (benzene: $\gamma =2.317$, $\sigma =0.4993\, {\text{nm}}$, $\varepsilon /k_{\text{B}}=582.9\,{\text{K}}$; fluorobenzene: $\gamma =2.447$, $\sigma =0.5102\,{\text{nm}}$, $\varepsilon /k_{\text{B}}=579.0\,{\text{K}}$). Hence, the scaling factors for benzene, toluene, p-xylene, and phenol, derived in Ref. [1] by employing $B_\eta$ values following from re-evaluated viscosity data measured in density ranges similar to R134a, are also given in Table 10. These scaling factors were partly applied in the next step as substitute for the scaling factors of the aromatic vapors considered in this paper. The scaling factors for R134a are also given in Table 10; they proved to be much more reliable.

Finally, the scaling factors were used to rectify the re-evaluated $\eta (T,\rho )$ values of each grouped isotherm to the limit of zero density. In doing so, the next relation following from Eqs. 7−10 was applied,

$$\begin{aligned} \eta ^{(0)}(T)= \frac{\eta (T,\rho )}{1 + N_{\text{A}}\sigma ^3 B^*_\eta (T^*) \rho / M}. \end{aligned}$$

(11)

Since data points from several isochoric series typically belonged to a quasi-isotherm, the $\eta ^{(0)}$ values resulted by averaging the corresponding values for each re-evaluated point of the quasi-isotherm. Furthermore, the $B_\eta$ values for all grouped isotherms computed via the fit were employed to deduce $\eta ^{(1)}$ values using the $\eta ^{(0)}$ values corrected with Eq. 11.

All of the resulting $\eta ^{(0)}$ and $\eta ^{(1)}$ values for R134a and for the respective aromatic vapors are summarized in Tables 11, 12, 13, 14, 15, 16, and 17. The number of quasi-isothermal experimental points considered for a grouped isotherm is specified in Column 2 of these tables. The results of the fit of Eq. 7 to the re-evaluated quasi-isothermal data are indicated in Columns 3−5: the $\eta ^{(0)}$ and $\eta ^{(1)}$ values are given together with their individual standard deviations ${\sigma }_{\eta ^{(0)}}$ and ${\sigma }_{\eta ^{(1)}}$ and with the standard deviation ${\sigma }_\eta$ for each isotherm. Footnotes concerning Column 1 clarify that re-measurements were performed or an experimental point in the saturated vapor was taken into account, whereas footnotes dealing with Column 2 state that only one or two data points had been considered. Finally, footnotes of Column 4 are related to the fact that an $\eta ^{(1)}$ value was implausible. In Columns 6 and 7 of Table 11 for R134a as well as in the respective columns of the first row of each quasi-isotherm of Tables 12, 13, 14, 15, 16, and 17, the $\eta ^{(0)}_{\text{RF}}$ values (including their standard deviations ${\sigma }_{\eta ^{(0)}_{\text{RF}}}$) following from Eq. 11 as well as the $\eta ^{(1)}_{\text{RF}}$ values, which resulted employing the scaling factors of Table 10 for the considered substance, are listed. In the second row and in some cases in the third row of Columns 6 and 7 for the respective quasi-isotherms of Tables 12, 13, 14, 15, 16, and 17, $\eta ^{(0)}_{\text{RF}}$ and $\eta ^{(1)}_{\text{RF}}$ values are provided which arose applying the scaling factors of selected substituted aromatic hydrocarbons, the measurements of which were quite recently re-evaluated [1], or even from scaling factors derived for other aromatic hydrocarbons considered in this paper. The respective substances are indicated in the table caption each.

The evaluation of the quasi-isothermal experimental data with the series expansion (Eq. 7) is discussed using the data for the second viscosity virial coefficient $B_\eta (T)$ computed from the $\eta ^{(0)}(T)$ and $\eta ^{(1)}(T)$ data with Eq. 8. In Figs. 3, 4, and 5, exemplarily for R134a, diphenyl, and chlorobenzene, the experimentally based $B_\eta (T)$ data are compared with the $B_\eta (T)$ values calculated applying the scaling factors $\varepsilon /k_{\text{B}}$ and $\sigma$, which were derived for the Rainwater–Friend theory by means of Eqs. 9 and 10.

Figure 3 for R134a shows that the $B_\eta (T)$ data of the experiments of Wilhelm and Vogel [6] nearly perfectly agree with the Rainwater–Friend theory and, in addition, that the $B_\eta (T)$ data for the re-measured isotherms at 317.54 K, 338.35 K, and 352.84 K only marginally deviate from those for the isotherms with increasing temperature. The reason for this agreement consists in the comparatively large experimentally probed density range.

Table 10 Optimized scaling factors for the Rainwater–Friend theory

Table 11 Values for the viscosity in the limit of zero density, $\eta ^{(0)}$, and for its initial density dependence, $\eta ^{(1)}$, resulting from the re-evaluated quasi-experimental isotherms of the measurements of Wilhelm and Vogel [6] on R134a

Table 12 Values for the viscosity in the limit of zero density, $\eta ^{(0)}$, and for its initial density dependence, $\eta ^{(1)}$, resulting from the re-evaluated quasi-experimental isotherms of the measurements of Vogel [7] on 1,3,5-trimethylbenzene (mesitylene) vapor. Values of $\eta ^{(0)}$ and $\eta ^{(1)}$ in the second row of each quasi-isotherm were derived with scaling factors of p-xylene given in Table 10

Table 13 Values for the viscosity in the limit of zero density, $\eta ^{(0)}$, and for its initial density dependence, $\eta ^{(1)}$, resulting from the re-evaluated quasi-experimental isotherms of the measurements of Vogel [7] on 1,2,4,5-tetramethylbenzene (durene) vapor. Values of $\eta ^{(0)}$ and $\eta ^{(1)}$ in the second row of each quasi-isotherm were derived with scaling factors of mesitylene given in Table 10

Table 14 Values for the viscosity in the limit of zero density, $\eta ^{(0)}$, and for its initial density dependence, $\eta ^{(1)}$, resulting from the re-evaluated quasi-experimental isotherms of the measurements of Vogel [8] on biphenyl (diphenyl) vapor. Values of $\eta ^{(0)}$ and $\eta ^{(1)}$ in the second and third rows of each quasi-isotherm were derived with scaling factors of mesitylene and durene, respectively, given in Table 10

Table 15 Values for the viscosity in the limit of zero density, $\eta ^{(0)}$, and for its initial density dependence, $\eta ^{(1)}$, resulting from the re-evaluated quasi-experimental isotherms of the measurements of Kaussmann et al. [9] on fluorobenzene vapor. Values of $\eta ^{(0)}$ and $\eta ^{(1)}$ in the second row of each quasi-isotherm were derived with scaling factors of benzene given in Table 10

Table 16 Values for the viscosity in the limit of zero density, $\eta ^{(0)}$, and for its initial density dependence, $\eta ^{(1)}$, resulting from the re-evaluated quasi-experimental isotherms of the measurements of Ahlmeyer et al. [10] on chlorobenzene vapor. Values of $\eta ^{(0)}$ and $\eta ^{(1)}$ in the second and third rows of each quasi-isotherm were derived with scaling factors of toluene and phenol, respectively, given in Table 10

Table 17 Values for the viscosity in the limit of zero density, $\eta ^{(0)}$, and for its initial density dependence, $\eta ^{(1)}$, resulting from the re-evaluated quasi-experimental isotherms of the measurements of Vogel [8] on 1,4-dichlorobenzene (p-dichlorobenzene) vapor. Values of $\eta ^{(0)}$ and $\eta ^{(1)}$ in the second row of each quasi-isotherm were derived with scaling factors of p-xylene given in Table 10

Fig. 3

Comparison of calculated values of the second viscosity virial coefficient $B_\eta (T)$ with experimental data for R134a, as a function of temperature T. Experimental data of Wilhelm and Vogel [6]: $\blacksquare$, isotherms included in the fit of Eq. 9; $\square$, re-measured isotherms excluded from the fit of Eq. 9. Values calculated with the optimized scaling factors $\sigma =0.48499\,{\text{nm}}$ and $\varepsilon /k_{\text{B}}= 277.99\,{\text{K}}$ using the theoretical $B^*_\eta$ function of the Rainwater–Friend theory corresponding to Eq (9): ———

Fig. 4

Comparison of calculated values of the second viscosity virial coefficient $B_\eta (T)$ with experimental data for diphenyl, as a function of temperature T. Experimental data of Vogel [8]: $\blacksquare$, isotherms included in the fit of Eq. 9; $\square$, isotherms excluded from the fit of Eq. 9. Values calculated with the scaling factors $\sigma =1.33\,380\,{\text{nm}}$ and $\varepsilon /k_{\text{B}}= 499.56\,{\text{K}}$ using the theoretical $B^*_\eta$ function of the Rainwater–Friend theory corresponding to Eq (9): ———. Values calculated using the scaling factors of mesitylene given in Table 10: – – – – –, according to the range of the quasi-isotherms; $\cdot \cdot \cdot \cdot \cdot \cdot \cdot$, extrapolated down to 298 K and up to 1073 K. Values calculated using the scaling factors of durene given in Table 10: — — —, according to the range of the quasi-isotherms; $\cdot \cdot \cdot \cdot \cdot \cdot \cdot$, extrapolated down to 298 K and up to 1073 K

Fig. 5

Comparison of calculated values of the second viscosity virial coefficient $B_\eta (T)$ with experimental data for chlorobenzene, as a function of temperature T. Experimental data of Ahlmeyer et al. [10]: $\blacksquare$, isotherms included in the fit of Eq. 9; $\boxplus$, fictitious value at 408.75 K included in the fit of Eq. 9; $\square$, isotherms excluded from the fit of Eq. 9. Values calculated with the scaling factors $\sigma =1.13\,855\,{\text{nm}}$ and $\varepsilon /k_{\text{B}}= 365.35\,{\text{K}}$ using the theoretical $B^*_\eta$ function of the Rainwater–Friend theory corresponding to Eq (9): ———. Values calculated using the scaling factors of toluene given in Table 10: – – – – –, according to the range of the quasi-isotherms; $\cdot \cdot \cdot \cdot \cdot \cdot \cdot$, extrapolated down to 298 K and up to 1073 K. Values calculated using the scaling factors of phenol given in Table 10: — — —, according to the range of the quasi-isotherms; $\cdot \cdot \cdot \cdot \cdot \cdot \cdot$, extrapolated down to 298 K and up to 1073 K

Figure 4 demonstrates that, in the case of diphenyl, only four of eight experimentally based $B_\eta$ data are in some degree suitable to derive acceptable scaling factors. Apart from chlorobenzene, the situation is similar for the other aromatic vapors meaning that about half of the experimental $B_\eta$ data points conforms to the Rainwater–Friend theory. Furthermore, the subsequent calculations of $B_\eta$ values with scaling factors of the substituted and/or of the aromatic hydrocarbon vapors discussed in this paper prove that the choice of the aromatic hydrocarbon vapor can be somewhat arbitrary as long as a certain similarity is met. In Fig. 4 for diphenyl, the scaling factors of mesitylene are less appropriate, whereas the scaling factors of durene yield a $B_\eta (T)$ curve whose trend is roughly like that resulting from the scaling factors of diphenyl itself. Whereas the differences between the corresponding curves (here obtained with the scaling factors of durene and diphenyl itself) are comparatively large at low temperatures, they decrease with increasing temperature T. Analogous statements can be made for mesitylene, durene, fluorobenzene, and p-dichlorobenzene, respectively.

Figure 5 illustrates that only two experimental $B_\eta$ data points are appropriate for chlorobenzene, whereas most of the $B_\eta$ data completely differ with the temperature function $B_\eta (T)$ of the Rainwater–Friend theory. Therefore, a fictitious $B_\eta (T)$ datum at 408.75 K that corresponds to $\eta ^{(1)}=-6.00\,\upmu {{\text{Pa}}\cdot {\text{s}}\cdot {\text{L}}\cdot {\text{mol}}}^{-1}$ was selected. This choice seems to be quite reasonable when the computed $B_\eta$ curve, resulting with the deduced scaling factors for chlorobenzene, is compared with the $B_\eta$ curves following from the scaling factors for toluene and phenol.

Table 18 Coefficients of Eq. 13 for the respective substances

Fig. 6

Extrapolation behavior of the correlations according to Eqs. 12 and 13 at low temperatures. Experimentally based correlation: ————–, R134a. Correlations based on the Rainwater–Friend theory: — – – — – –, fluorobenzene; — $\cdot \cdot$ — $\cdot \cdot$ — $\cdot \cdot$, chlorobenzene; — – — – — –, p-dichlorobenzene; — — — —, mesitylene; – – – – – – –, durene; — $\cdot$ — $\cdot$ — $\cdot$, diphenyl. Extrapolation down to low temperatures: $\cdot \cdot \cdot \cdot \cdot \cdot \cdot$; R134a and fluorobenzene (down to 1 K), chlorobenzene and p-dichlorobenzene (down to 150 K), mesitylene (down to 70 K), durene and diphenyl (down to 200 K)

Fig. 7

Extrapolation behavior of the correlations according to Eqs. 12 and 13 at high temperatures. Experimentally based correlation: ————, R134a. Correlations based on the Rainwater–Friend theory: — – – — – –, fluorobenzene; — $\cdot \cdot$ — $\cdot \cdot$ — $\cdot \cdot$, chlorobenzene; — – — – — –, p-dichlorobenzene; — — — —, mesitylene; – – – – – – –, durene; — $\cdot$ — $\cdot$ — $\cdot$, diphenyl. Extrapolation up to 1500 K for all seven substances: $\cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot \cdot$

5 Recommended Values for the Viscosity in the Limit of Zero Density and of Its Initial Density Dependence

As already explained, this report aims at providing reliable values for the viscosity in the limit of zero density, $\eta ^{(0)}(T)$, and, if possible, for its initial density dependence, $\eta ^{(1)}(T)$. In principle, the $\eta ^{(0)}$ data of Columns 3 of Tables 11, 12, 13, 14, 15, 16, and 17, resulting from the fit of Eq. 7 to the quasi-isothermal viscosity data, should be preferred and the $\eta ^{(0)}_{\text{RF}}$ values of Columns 6 at the same temperatures should not be considered. This is certainly valid for R134a and holds in general when $\eta ^{(0)}(T)$ and $\eta ^{(1)}(T)$ data can reliably be derived with Eq. 7 from quasi-isotherms, whose corresponding measurements extend over a comparatively large density range. This was the case for the substances considered in Ref. [1]. However, for the aromatic vapors considered in this paper, the density range of the experiments is so small that a reasonable evaluation of the quasi-isotherms is generally hindered. In addition, when the $\eta ^{(0)}$ data of Columns 3 arose from only two experimental points and the $\eta ^{(1)}(T)$ values and accordingly the $B_\eta (T)$ values are implausible, the $\eta ^{(0)}$ data had to be substituted by the $\eta ^{(0)}_{\text{RF}}$ values of Columns 6 at the corresponding temperatures. Furthermore, if only one quasi-experimental viscosity datum was available and only $\eta ^{(0)}_{\text{RF}}$ values could be deduced by means of the Rainwater–Friend theory, the respective values of the Columns 6 had to be applied in any case.

In conclusion, the experimentally based $\eta ^{(0)}(T)$ and $\eta ^{(1)}(T)$ data deduced from the series expansion of Eq. 7 are recommended for R134a, but not for the aromatic hydrocarbon vapors considered in this paper. For these substances, the $\eta ^{(0)}_{\text{RF}}(T)$ values of Column 6, given in the first row of each quasi-isotherm and following from the Rainwater–Friend theory with the determined scaling factors for the respective substance, should be preferred. This is further based on the fact that the use of Eq. 11 is only connected with a change in the viscosity of $-(0.35\,{\text{to}}\,0.56)\,\%$ at the lowest temperatures up to $(-0.05\,{\text{to}}\,+0.12)\,\%$ at the highest temperatures, when the highest measured density is corrected to zero density. Then, the $\eta ^{(0)}$ data for R134a and the respective $\eta ^{(0)}_{\text{RF}}$ values were correlated applying the following equations which appropriately extrapolate both to low and to high temperatures:

$$\begin{aligned} \eta ^{(0)}(T)= & {} \frac{T^{1/2}}{{\mathfrak{S}}_\eta (T)}\,, \end{aligned}$$

(12)

$$\begin{aligned} {\mathfrak{S}}_\eta (T)= & {} f_1 T \exp (-2 T^{1/3}) + \frac{f_2+ f_3 \exp (-T^{1/3})}{T^{1/3}} + f_4 \exp \left( -\frac{1}{T^{1/3}}\right) \,. \end{aligned}$$

(13)

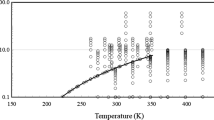
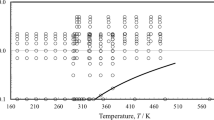
In Eq. 12, $\eta ^{(0)}$ is in $\upmu {{\text{Pa}}\cdot {\text{s}}}$ and T in K. The functional form of ${\mathfrak{S}}_\eta (T)$ was chosen by using symbolic regression [43], implemented in the Eureqa software package, along the lines of Laesecke and Muzny [44, 45], correlating the dilute gas viscosities for carbon dioxide and methane, as well as of Hellmann [46], who correlated the dilute gas viscosity for ethane. The coefficients $f_i$ ($i=1,...,4$) obtained by fitting Eqs. 12 and 13 to the $\eta ^{(0)}$ data for R134a and to the $\eta ^{(0)}_{\text{RF}}$ values of the aromatic hydrocarbon vapors are listed in Table 18. The functional form of Eq. 13 has no physical relevance and, consequently, the parameters $f_1$ to $f_4$ have no physical significance for the different chemical species. The extrapolation behavior of these correlations is illustrated in Figs. 6 and 7. Figure 6 shows that the correlations for R134a and for fluorobenzene appropriately extrapolate down to 1 K. But the correlations for the other hydrocarbon vapors do not adequately extrapolate to such a low temperature. Thus, the correlations for chlorobenzene and p-dichlorobenzene yield reasonable $\eta ^{(0)}$ viscosity values down to 150 K, whereas the correlation for mesitylene provides meaningful values down to 70 K and those for durene and diphenyl down to 200 K. This is also demonstrated in this figure and certainly sufficient for all practical purposes. Figure 7 shows that the correlations for all seven substances reliably extrapolate up to 1500 K.

The $\eta ^{(0)}_{\text{cal}}$ values calculated with Eqs. 12 and 13 are exemplarily compared for diphenyl in Fig. 8 and for chlorobenzene in Fig. 9 with corresponding $\eta ^{(0)}$ data and $\eta ^{(0)}$ values of Tables 14 and 16, that means with the experimentally based $\eta ^{(0)}$ data of Columns 3, deduced by means of a fit with Eq. 7, and with $\eta ^{(0)}_{\text{RF}}$ values of Columns 6, derived using Eq. 11 and the scaling factors of different aromatic vapors. The relative deviations $\Delta$ in these figures are marked in the majority of cases with error bars calculated from the standard deviations $\sigma _\eta$ given in Columns 3 and 6. Note that in the case of only one experimentally based datum, no values for $\sigma _\eta$ were derived and no error bars could be plotted. Figure 8 shows that the four $\eta ^{(0)}$ data points of those quasi-isotherms, to which Eq. 9 was fitted to determine the scaling factors of diphenyl, deviate from the $\eta ^{(0)}_{\text{cal}}$ values, which were calculated applying Eqs. 12 and 13 with the respective coefficients of Table 18, by $<\pm 0.03\,\%$, whereas the excluded four $\eta ^{(0)}$ data points differ by up to $+0.50\,\%$. The $\eta ^{(0)}_{\text{RF}}$ values which were obtained with the scaling factors of diphenyl itself and were employed to derive the coefficients of Table 18, are represented by Eqs. 12 and 13 within $\pm 0.04\,\%$. In contrast, the $\eta ^{(0)}_{\text{RF}}$ values which are based on the scaling factors of mesitylene deviate by $-0.26\,\%$ to $+0.02\,\%$, while those obtained with the scaling factors of durene differed by $-0.15\,\%$ to $-0.01\,\%$, each systematically increasing with temperature. Figure 9 illustrates that the two $\eta ^{(0)}$ data points at 320 K and 342 K, to which Eq. 9 including a third fictitious datum was fitted to determine the scaling factors of chlorobenzene, differ from the $\eta ^{(0)}_{\text{cal}}$ values, which were calculated applying Eqs. 12 and 13 with the respective coefficients of Table 18, by $<\pm 0.11\,\%$, whereas the excluded eight $\eta ^{(0)}$ data points deviate by up to $+0.90\,\%$. The $\eta ^{(0)}_{\text{RF}}$ values which were obtained with the scaling factors of chlorobenzene and were applied to determine the coefficients of Table 18 are represented by Eqs. 12 and 13 within $\pm 0.09\,\%$. In contrast, the $\eta ^{(0)}_{\text{RF}}$ values which resulted with the scaling factors of toluene differ by $-0.12\,\%$ to $+0.10\,\%$, while those obtained with the scaling factors of phenol deviate by $-0.02\,\%$ to $+0.17\,\%$, each to a large extent systematically increasing with temperature. However, the differences following for the $\eta ^{(0)}_{\text{RF}}$ values with the scaling factors of the different aromatic hydrocarbons are comparatively small. Similar evidence could be given for the remaining four aromatic hydrocarbon vapors.

It has already been demonstrated in Figs. 4 and 5 that there exists a large uncertainty in the $B_\eta (T)$ data. The reason for this is the fact that some of the $\eta ^{(1)}(T)$ data points in Columns 4 of Tables 14 and 16 are implausible and sometimes are actually characterized by the wrong sign. Moreover, the $\eta ^{(1)}_{\text{RF}}$ values of the Columns 7 differ strongly when the first row of a quasi-isotherm is compared with the second and/or third row of Table 14 (obtained by employing the scaling factors of other aromatic hydrocarbon vapors of this paper) and of Table 16 (derived by applying the scaling factors of substituted aromatic hydrocarbon vapors of Ref. [1]). Consequently, the reliability of the $\eta ^{(1)}_{\text{RF}}$ values of the first row of any quasi-isotherm is not sufficient to recommend these values. The $\eta ^{(1)}_{\text{RF}}$ values of mesitylene listed in Table 12 should be judged in the same way, even if the differences to those $\eta ^{(1)}_{\text{RF}}$ values resulting with the scaling factors for p-xylene are extremely small.

Fig. 8

Representation of the zero density viscosity $\eta ^{(0)}_{\text{cal}}$ for diphenyl calculated by means of Eqs. 12 and 13, based on experimental $B_\eta$ data, which were obtained by the serious expansion (Eq. 7), and on the Rainwater–Friend theory using Eq. 11 and the scaling factors of Table 10, as a function of temperature T. Relative deviations of the experimentally based data $\eta ^{(0)}_{\text{exp}}$, of the $\eta ^{(0)}_{\text{RF}}$ values for the Rainwater–Friend theory, and for the Rainwater–Friend theory with scaling factors of Table 10 for mesitylene and durene, each from the calculated values $\eta ^{(0)}_{\text{cal}}$: $\Delta = 100 (\eta ^{(0)}_{\text{exp}}-\eta ^{(0)}_{\text{cal}})/\eta ^{(0)}_{\text{cal}}$, $\Delta = 100 (\eta ^{(0)}_{\text{RF}}-\eta ^{(0)}_{\text{cal}})/\eta ^{(0)}_{\text{cal}}$, $\Delta = 100 (\eta ^{(0)}_{\text{RF,Mes}}-\eta ^{(0)}_{\text{cal}})/\eta ^{(0)}_{\text{cal}}$, and $\Delta = 100 (\eta ^{(0)}_{\text{RF,Dur}}-\eta ^{(0)}_{\text{cal}})/\eta ^{(0)}_{\text{cal}}$. Experimental data of Vogel [8]: $\blacksquare$, $B_\eta$ data from isotherms included in the fit of Eq. 9; $\square$, $B_\eta$ data from isotherms excluded from the fit of Eq. 9. $\bigcirc$, values for the Rainwater–Friend theory with scaling factors for diphenyl; $\vartriangle$, values for the Rainwater–Friend theory with scaling factors for mesitylene; $\triangledown$, values for the Rainwater–Friend theory with scaling factors for durene

Fig. 9

Representation of the zero density viscosity $\eta ^{(0)}_{\text{cal}}$ for chlorobenzene calculated by means of Eqs. 12 and 13, based on experimental $B_\eta$ data, which were obtained by the serious expansion (Eq. 7), and on the Rainwater–Friend theory using Eq. 11 and the scaling factors of Table 10, as a function of temperature T. Relative deviations of the experimentally based data $\eta ^{(0)}_{\text{exp}}$, of the $\eta ^{(0)}_{\text{RF}}$ values for the Rainwater–Friend theory, and for the Rainwater–Friend theory with scaling factors of Table 10 for toluene and phenol, each from the calculated values $\eta ^{(0)}_{\text{cal}}$: $\Delta = 100 (\eta ^{(0)}_{\text{exp}}-\eta ^{(0)}_{\text{cal}})/\eta ^{(0)}_{\text{cal}}$, $\Delta = 100 (\eta ^{(0)}_{\text{RF}}-\eta ^{(0)}_{\text{cal}})/\eta ^{(0)}_{\text{cal}}$, $\Delta = 100 (\eta ^{(0)}_{\text{RF,Tol}}-\eta ^{(0)}_{\text{cal}})/\eta ^{(0)}_{\text{cal}}$, and $\Delta = 100 (\eta ^{(0)}_{\text{RF,Phe}}-\eta ^{(0)}_{\text{cal}})/\eta ^{(0)}_{\text{cal}}$. Experimental data of Ahlmeyer et al. [10]: $\blacksquare$, $B_\eta$ data from isotherms included in the fit of Eq. 9; $\square$, $B_\eta$ data from isotherms excluded from the fit of Eq. 9. $\bigcirc$, values for the Rainwater–Friend theory with scaling factors for chlorobenzene; $\vartriangle$, values for the Rainwater–Friend theory with scaling factors for toluene; $\triangledown$, values for the Rainwater–Friend theory with scaling factors for phenol

6 Concluding Remarks

Using all-quartz oscillating-disk viscometers for relative measurements at the University of Rostock, the viscosities of several organic vapors have been measured and reported by Vogel and co-workers about forty years ago. In this work, measurements on six aromatic hydrocarbon vapors together with later ones on R134a (Ref. [6]) were re-evaluated after re-calibrating the employed viscometers. The originally determined viscosity data were published in Refs. [7] (mesitylene and durene), [8] (diphenyl and p-dichlorobenzene), [9] (fluorobenzene), and [10] (chlorobenzene). For the re-evaluation, up-to-date reference viscosity values for argon and nitrogen at room temperature and zero density were applied, which were theoretically computed and in the case of nitrogen also experimentally based. Whereas the measurements on R134a were performed between 297 K and 438 K over an extended range of moderate densities, the research on the aromatic hydrocarbon vapors concerned comparatively restricted low densities at temperatures between 304 K and 631 K. The relative combined expanded ($k=2$) uncertainty of the re-evaluated results for all seven compounds amounts to 0.2 % near room temperature increasing to 0.3 % at higher temperatures.

Quasi-isothermal data are needed to determine reliable values for the viscosity in the limit of zero density, $\eta ^{(0)}$, and possibly for its initial density dependence, $\eta ^{(1)}$, which was a further aim of this work. For this, approximately isothermal groups of the re-evaluated data of the isochoric measurement series were listed for each substance. To obtain as much as possible quasi-isothermal values for the evaluation, we were forced to summarize data points at temperatures differing by up to $\pm 12\,{\text{K}}$. In doing so, the experimental re-evaluated points of three (five of the aromatic hydrocarbon vapors), of four (p-dichlorobenzene), and of six (R134a) isochoric series were grouped such that approximated isotherms followed. Then, the re-evaluated data of the quasi-isothermal groups were converted into isothermal values using a first-order Taylor series in temperature.

A series expansion in density truncated at first order was applied to derive $\eta ^{(0)}$ and $\eta ^{(1)}$ data from the isothermal viscosity data. This procedure could appropriately be employed to deduce $\eta ^{(0)}$ and $\eta ^{(1)}$ data for R134a. Since the density range of the measurements on the six aromatic hydrocarbon vapors was insufficiently large, the resulting $\eta ^{(0)}$ and primarily the obtained $\eta ^{(1)}$ data had such large uncertainties that half of them had to be refused. In particular, if only two experimental data points belonged to an isotherm, the reliability of the $\eta ^{(0)}$ and $\eta ^{(1)}$ data was distinctly reduced. Hence, the Rainwater–Friend theory for the initial density dependence of the viscosity was applied to determine $\eta ^{(0)}$ and $\eta ^{(1)}$ values. For this, optimized scaling factors of length and energy were deduced by means of a fit of theoretical second viscosity virial coefficients, $B_\eta (T)$, to the comparatively reliable experimentally based $B_\eta (T)$ data, which were obtained from the $\eta ^{(0)}$ and $\eta ^{(1)}$ data deduced with the series expansion in density. Furthermore, $\eta ^{(0)}$ and $\eta ^{(1)}$ values were deduced applying scaling factors for similar aromatic hydrocarbon vapors dealt with in this paper and for aromatic hydrocarbon vapors re-evaluated in Ref. [1]. All resulting $\eta ^{(0)}$ and $\eta ^{(1)}$ values are summarized in tables for the respective substance.

In principle, the $\eta ^{(0)}$ and $\eta ^{(1)}$ data resulting from the series expansion in density should be preferred. This holds for R134a, for which, apart from the re-measurements, all $\eta ^{(0)}$ and $\eta ^{(1)}$ data of Columns 3 and 4 of Table 11 are recommended. For the six aromatic hydrocarbon vapors, only the $\eta ^{(0)}$ values derived with the Rainwater–Friend theory applying the optimized scaling factors of energy and length of the respective vapor can be recommended, while the $\eta ^{(1)}$ values are somewhat doubtful. The selected $\eta ^{(0)}$ values are once more summarized in Table 19. The relative combined expanded ($k=2$) uncertainty is estimated to be $U_{\text{c,r}}(\eta )=0.003$ at all temperatures. The reason for this judgement consists in that the re-evaluated experimental data are characterized by $U_{\text{c,r}}(\eta )=0.002$ near room temperature and by an increase to $U_{\text{c,r}}(\eta )=0.003$ at higher measurement temperatures, while the shift to the limit of zero density amounts to at most $-0.5\,\%$ at the lowest temperatures decreasing to $\pm 0.1\,\%$ at the highest ones.

Table 19 Recommended viscosity values in the limit of zero density for six aromatic hydrocarbons$^1$