Relating matrix stress to local stress on a hard microstructural inclusion for understanding cleavage fracture in high strength steel

Abstract

Macroscale cleavage fracture toughness of high strength steels is strongly related to the fracture of hard microstructural inclusions. Therefore, an accurate determination of the local stress on these inclusions based on the matrix stress is necessary for the statistical modelling of macroscale cleavage fracture. This paper presents analytical equations to quantitatively estimate the stress of the microstructural inclusions from the far-field stress of the matrix. The analytical equations account for the inclusion shape, the inclusion orientation, the far-field stress state and matrix material properties. Finite element modelling of a representative volume element containing a hard inclusion shows that the equations provide an accurate representation of the local stress state. The equations are implemented into a multi-barrier model and compared with CTOD experiments with two different levels of constraint.

1 Introduction

Mechanical integrity assessment of steel structures frequently requires knowledge of their resistance to catastrophic failure by fast, unstable crack growth, expressed as fracture toughness. Ferritic steels exhibit a transition from ductile fracture modes at higher temperatures to brittle fracture at lower temperatures. Toughness at lower temperatures and the transition temperature region are related to transgranular quasi-cleavage fracture, which will be called cleavage in this paper. Many material requirements, for example Charpy test results, are related to the prevention of cleavage. The need for more accurate cleavage modelling is particularly acute for a new generation of high- and very high-strength steels (yield strength of 500 to 1000 MPa) because they generally have lower toughness, and therefore, a lower safety margin. Furthermore, these classes of steels obtain their favorable properties through their complex, multi-phase microstructures, which complicates microstructural modelling of cleavage-driven failure.

As a highly localized phenomenon, cleavage fracture exhibits strong sensitivity to material characteristics at the microstructural level, dependent on material and structure fabrication, and it is coupled with a constraint effect originating from the macroscopic stress state. It is generally accepted that the micromechanism of cleavage fracture can be described by three critical events: particle fracture, propagation of a particle-size crack and the propagation of a grain-size crack (Lin et al. 1986; Martín-Meizoso et al. 1994; Pineau 2008; Chen et al. 2010; Pineau et al. 2016; Namegawa et al. 2019). A summary of the models describing micromechanisms of cleavage fracture can be found in Jiang et al. (2019). Table 1 shows a schematic representation of these three critical events and the corresponding parameters to define cleavage criteria. As the first in the chain of events that leads to cleavage, fracture of the hard particle requires special attention.

Table 1 Micromechanisms of cleavage fracture

Second-phase particles are particles which do not belong to the matrix phases. They are present because of the alloying elements that are added for hardenability, yield strength, and other properties. Carbides, brittle inclusions, and M-A constituent are examples of second phase particles that are widely reported as being detrimental for cleavage fracture in steels (Ray et al. 2012; Chen and Cao 2015; Jia et al. 2017; Tankoua et al. 2018). Although steels also have soft inclusions like MnS, they mostly affect the ductile failure mode and are not the focus in this paper. It has been observed that larger inclusions and inclusion clusters act as weakest features in the microstructure, allowing brittle crack initiation and propagation (Ghosh et al. 2013; Popovich and Richardson 2015; Pallaspuro 2018; Bertolo et al. 2020). The probability that cracks initiate in a given particle depends on the particle size, shape, volume fraction and orientation of the elongated particles with respect to the applied stress (Lindley et al. 1970; Ray et al. 1995; Bordet et al. 2005; Chen et al. 2010; Miao and Knott 2016). Therefore, it is important to be able to estimate the local stresses on hard inclusions based on the global loading in order to be able to capture the first stage of cleavage fracture, especially in high-strength steels.

Studies on the stress distributions within or around inclusions have been performed extensively (Huang 1972; Lee and Smivri 1981; Wilner 1988; Ramakrishnan 1996; Lee and Mear 1999; Lauke and Schüller 2002; Huang and Li 2005; Gao 2008). These works contributed to a good understanding of the stress distribution within or around a hard inclusion embedded in an elastic–plastic matrix. It is found that there is a critical aspect ratio at which interface debonding changes to particle fracture, and the remote stress triaxiality has a significant effect on this transition (Lee and Mear 1999).

However, methods that can directly determine the local stress on a hard inclusion from the remote stress still need development. For linear elastic problems, the Eshelby solution (1957) is available for the calculation of the stress on a spheroidal inclusion. For nonlinear problems, the classic Eshelby solution has been modified to incremental approaches with the mean-field (MF) homogenization method making use of equivalent tangent operators (e.g. Mori and Tanaka 1973; Doghri and Ouaar 2003). Corresponding validations (Pierard et al. 2006) showed that the MF method can give accurate predictions of the effective properties of a composite at continuum level, but this does not guarantee the same accuracy at the microstructural phase level. The accuracy of the MF method at the phase level (especially for the inclusions), or other methods using Eshelby tensors, relies on the assumptions of a homogeneous stress inside the inclusion and a homogeneous equivalent tangent operator of the matrix. Violation of the basic assumptions leads to inaccuracy or even failure of the Eshelby tensor based methods. To improve the average stress calculation of individual phases, Delannay et al. (2007) proposed including fitting parameters for the MF method. Because this modified method remains heuristic and is not predictive a priori for other composite materials, Brassart et al. (2010) presented an extended MF method which is fully coupled with a nonlinear finite element analysis (FEA) of the inclusion problem to avoid the use of Eshelby tensors. Thus, the calculation of the inclusion stress has to be performed with numerical simulations (e.g. FEA).

Determination of the inclusion stress using FEA can be computationally costly because the microstructures (both matrix and inclusions) of metals can vary widely. The material may contain hard inclusions that have various shapes, orientations and material properties. Under different loading patterns, the constraint effect may also vary locally and lead to various stress states. Lambert-Perlade (2004), Hardenacke et al. (2010), and Shibanuma et al. (2016) developed empirical equations to relate the far-field stress to the local stress on a hard inclusion for a specific material. A more detailed summary of the available empirical equations will be given in the “Discussion” section of the present paper. An empirical equation that can account for multiple parameters and can be used for a general case will require extensive simulations and suffer from an ambiguous fitting process. Thus, this paper aims to propose an analytical solution that can be used for the calculation of local stress on a hard inclusion based on the far-field stress on the matrix.

2 Development of analytical solution of the local stress on inclusions

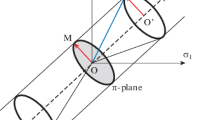
For elastic problems, the Eshelby solution (1957) is available for the calculation of the stress on a spheroidal inclusion. The detailed calculation of the Eshelby solution involves determination of the Eshelby tensor from inclusion geometry and the formulation of equilibrium equations, which can be found in Mura (1987). However, the Eshelby solution is not valid during plastic deformation for the dilute inclusion problem. A simplified analytical equation is established in this paper to quantitatively determine the stress on the inclusion from the far-field stress on the macroscale. The geometric representation of this problem is illustrated in Fig. 1 as an elastic hard inclusion embedded in an infinite volume of elastic–plastic matrix. In this paper, the inclusion is assumed to be an ellipsoid characterized by the principal semi-axes (R₁ ≠ R₂ = R₃). The remote load is modelled as two principal stresses σ₁ and σ₂, which are normal to R₃. The angle between inclusion’s principal semi-axis R₁ and the remote first principal stress σ₁ is noted as θ. For the third principal direction, the remote deformation is considered to be zero, which corresponds to a plane strain condition on macroscopic scale for the matrix.

Fig. 1

A schematic representation of a microstructural inclusion embedded in an infinite matrix under a general remote load and b remote deviatoric (pure shear) stress

2.1 Key assumptions

The following five assumptions are used in the derivation of the analytical solution:

• (1) There is perfect cohesion between the inclusion and the matrix.

• (2) The matrix has low-hardening behaviour after yielding.

• (3) The average first principal stress over the mid-section of the inclusion is the representative stress (${\sigma }_{1,inclu}$).

• (4) If ${\sigma }_{1,matrix}$ is the remote first principal stress of the matrix, then the stress difference (${\sigma }_{1,inclu}-{ \sigma }_{1,matrix}$) is only related to the deviatoric part of the remote stress field (the maximum shear stress) when remote plastic deformation is pronounced. The derivation of the analytical solution is based on a formulation with remote shear stress, while the hydrostatic pressure of the remote stress field is not considered. This assumption is further validated with FEA in Sect. 3.

• (5) The tensile stress induced by shear deformation vanishes in the matrix close to the inclusion, and the entire reduced stress is taken by the inclusion. This assumption is further illustrated in Sect. 2.2 and validated with FEA in Sect. 3.

Assumption (1) comes from the observation that cleavage fracture is mostly transgranular failure initiated rather by particle cracking than by boundary decohesion. Assumption (2) corresponds to a characteristic of high strength steels. For example, Bannister (2000) reported on the plasticity properties of hundreds of structural steels. Almost all of the steels with a yield strength greater than 500 MPa had an ultimate strength that is less than 25% greater than the yield strength. Assumption (3) is due to the fact that the maximum tensile stress within the inclusion is largely influenced by the imperfect morphology which cannot to be reflected by analytical derivation, and the average tensile stress over the mid-section can reflect the driving force to break an inclusion. Assumption (4) is based on the argument that the stress difference caused by hydrostatic pressure is due to the compatible deformation under volume change, and when the matrix remains elastic, extra uniform strain is generated inside the inclusion to satisfy the compatibility of deformation. However, when the matrix enters the plastic stage, large deviatoric deformation can be generated in the matrix near the inclusion allowing the condition of compatible deformation to be satisfied. The extra strain inside the inclusion will no longer remain uniform, and the influence of hydrostatic pressure is negligible. Assumption (5) is due to the effect that the inclusion gives extra constraint to the nearby matrix and the matrix cannot deform freely along the slip plane. As a consequence, larger shear stress is generated along the inclusion/matrix interface rather than along the remote shear direction. The tensile stress associated with the shear deformation is also redistributed from the matrix to the inclusion.

2.2 Two dimensional analysis

The analytical expression of the inclusion problem is first formulated in 2D based on a plane-strain condition by Fig. 2. When only considering the remote deviatoric stress, the general case will reduce to Fig. 1b, where τ = σ₁ =  − σ₂. In Fig. 2, the principal stress coordinate system is used, where the y axis is parallel to the remote maximum principal stress and the x axis is parallel to the remote minimum principal stress. The inclusion outline is visualized by the solid lines in Fig. 2 and is defined as an ellipse by:

Fig. 2

a Parameters for the analytical expression of an inclusion in a 2D coordinate and b free body diagram of half the inclusion and the matrix in its vicinity

$$\left(\frac{\left(\mathrm{cos}\left(\theta \right)x-\mathrm{sin}\left(\theta \right)y\right)}{1}\right){}^{2}+\left(\frac{\left(\mathrm{cos}\left(\theta \right)y+\mathrm{sin}\left(\theta \right)x\right)}{{R}_{1}/{R}_{2}}\right){}^{2}=1.$$

(1)

In Eq. 1, x and y are lengths normalized by the minor axis of the ellipse and are dimensionless. There are four planes parallel to the remote principal shear directions, which are visualized by the dashed lines in Fig. 2a, forming a rectangle around the inclusion. According to slip-line theory, only the matrix between the inclusion and the rectangle is assumed to be influenced by the presence of the inclusion, and the shear field outside the rectangle will be uniform. The parameters c₁, c₂, c₃, and c₄ shown in Fig. 2 can be found from geometry.

Figure 2b shows the free body diagram of half the inclusion and the matrix in its vicinity. The outline of the isolated body is visualized by the solid lines. There are five straight boundaries of this free body noted as ${l}_{1}$ to ${l}_{5}$. The forces acting on these boundaries are noted as ${F}_{1}$ to ${F}_{5}$ respectively. When the inclusion has the same material properties as the matrix, the isolated body behaves like a homogeneous matrix material. Boundaries ${l}_{1}$ and ${l}_{2}$ are parallel to the remote principal shear directions and thus ${F}_{1}$ and ${F}_{2}$ are pure shear forces. Boundaries ${l}_{3}$ and ${l}_{5}$ are normal to the remote first principal stress and thus ${F}_{3}$ and ${F}_{5}$ are parallel to the y axis.

The force equilibrium in the y direction is:

$${F}_{1}\mathrm{cos}45^\circ +{F}_{2}\mathrm{cos}45^\circ ={F}_{3}+{F}_{4,y}+{F}_{5},$$

(2)

where ${F}_{1}=\tau {l}_{1}$, ${F}_{2}=\tau {l}_{2}$ and ${F}_{3}={F}_{5}=\tau {l}_{3}$.

When the inclusion is of a much stronger material than the matrix (e.g. the inclusion remains in elastic stage when the matrix is yielding), there is an extra constraint for plastic deformation of the matrix in the vicinity. The shear stress along the inclusion/matrix interface is generally increased. In order to maintain force equilibrium, the normal stress at the horizontal boundaries ${l}_{3}$ and ${l}_{5}$ is reduced. Consequently, the matrix in the vicinity of the inclusion has a much smaller stress in the principal direction, and the reduced stress is taken by the inclusion. The force F_4,y is further decomposed into the force that it would otherwise have in a homogenous system, F_4h,y and the added force that it has because it takes stresses from the unstressed surroundings, F_4Δ,y.

$${F}_{4,\mathrm{y}}={F}_{4\mathrm{h},\mathrm{y}}+{F}_{4\Delta ,y}.$$

(3)

The forces ${F}_{3}$ and ${F}_{5}$ are assumed to become zero and will lead to the following force equilibrium in the y direction:

$${F}_{1}\mathrm{cos}45^\circ +{F}_{2}\mathrm{cos}45^\circ ={F}_{4\mathrm{h},\mathrm{y}}+{F}_{4\Delta ,y}.$$

(4)

The extra force taken in the y-direction by the inclusion can be calculated as ${F}_{4\Delta ,y}=2\tau \left(\frac{{c}_{1}-{c}_{2}}{2}-{c}_{3}\right)$. If this force is averaged at the inclusion mid-section normal to the y direction, the averaged extra stress is:

$${\sigma }_{1,inclu}-{\sigma }_{1,matrix}=\frac{\Delta {F}_{4,y}}{2{c}_{4}}=\tau \frac{{(c}_{1}-{c}_{2})/2-{c}_{3}}{{c}_{4}}=\frac{{\sigma }_{eq,matrix}}{\sqrt{3}}\frac{{(c}_{1}-{c}_{2})/2-{c}_{3}}{{c}_{4}}.$$

(5)

2.3 Formulation

As result of the 2D analysis, the representative stress of the inclusion (${\sigma }_{1,inclu}$) can be calculated with:

$${\sigma }_{1,inclu}={\sigma }_{1,matrix}+f\left(\frac{{R}_{1}}{{R}_{2}},\theta \right){\sigma }_{eq,matrix},$$

(6)

where ${\sigma }_{1,matrix}$ is the first principal stress on the far field, and ${\sigma }_{eq,matrix}$ is the remote Von-Mises stress of the matrix; $f\left(\frac{{R}_{1}}{{R}_{2}},\theta \right)$ is given as:

$$f\left(\frac{{R}_{1}}{{R}_{2}},\frac{{R}_{3}}{{R}_{2}},\theta \right)=(\frac{({c}_{1}-{c}_{2})/2-{c}_{3}}{{c}_{4}})/\sqrt{3},$$

(7)

where ${c}_{1}$, ${c}_{2}$, ${c}_{3}$ and ${c}_{4}$ can be determined with Eqs. 8 to 16.

$${c}_{1}={x}_{1}+\frac{p{x}_{1}+\sqrt{q{x}_{1}^{2}+4h}}{2h},$$

(8)

$${c}_{2}=-{x}_{2}+\frac{p{x}_{2}-\sqrt{q{x}_{2}^{2}+4h}}{2h},$$

(9)

$${c}_{3}=\frac{ph\left({c}_{1}+{c}_{1}\right)+\sqrt{q{h}^{2}{\left({c}_{1}+{c}_{2}\right)}^{2}+{4(p}^{2}-q)h}}{{p}^{2}-q},$$

(10)

$${c}_{4}=\sqrt{1/\left[{\left(\frac{\mathrm{cos}\theta }{1}\right)}^{2}+{\left(\frac{\mathrm{sin}\theta }{{R}_{1}/{R}_{2}}\right)}^{2}\right]},$$

(11)

$${x}_{1}=\sqrt{\frac{16{h}^{3}+4h{p}^{2}+16p{h}^{2}}{{q}^{2}-\left(4{h}^{2}+{p}^{2}+4ph\right)q}},$$

(12)

$${x}_{2}=\sqrt{\frac{16{h}^{3}+4h{p}^{2}-16p{h}^{2}}{{q}^{2}-\left(4{h}^{2}+{p}^{2}-4ph\right)q}},$$

(13)

$$h={\mathrm{sin}}^{2}\theta +\frac{{\mathrm{cos}}^{2}\theta }{{{(R}_{1}/{R}_{2})}^{2}},$$

(14)

$$p=2\mathrm{cos}\theta \mathrm{sin}\theta \left(1-\frac{1}{{{(R}_{1}/{R}_{2})}^{2}}\right),$$

(15)

$$q=4{\mathrm{cos}}^{2}\theta {\mathrm{sin}}^{2}\theta {\left(\frac{1}{{{(R}_{1}/{R}_{2})}^{2}}-1\right)}^{2}-4\left({\mathrm{sin}}^{2}\theta +\frac{{\mathrm{cos}}^{2}\theta }{{{(R}_{1}/{R}_{2})}^{2}}\right)\left({\mathrm{cos}}^{2}\theta +\frac{{\mathrm{sin}}^{2}\theta }{{{(R}_{1}/{R}_{2})}^{2}}\right).$$

(16)

The above equations are based on a 2D formulation, assuming the 3-D ellipsoidal inclusion to have a symmetric geometry. In that case, the result remains even if the local shear direction deviates from remote shear direction. When the symmetric axis of the inclusion lies parallel to the remote first principal stress, the above assumption is satisfied and the derivation does not require correction. When the symmetric axis of the inclusion has an angle to the remote first principal stress, the 2D geometric characterization of the inclusion may differ along the third direction (when the 2D derivation is at the xy plane, the third direction perpendicular to the xy plane is denoted by z axis), and a correction term should be applied. The correction term is heuristically assumed to be proportional to the geometry asymmetry with shear stress as a weight factor:

$$\frac{{{(\sigma }_{1,inclu}-{\sigma }_{1,matrix})}_{corrected}}{{{(\sigma }_{1,inclu}-{\sigma }_{1,matrix})}_{xy}}=\left(1-\frac{{\tau }_{yz,max}}{{\tau }_{xy, max}}\right)+\frac{{\tau }_{yz,max}}{{\tau }_{xy, max}}\times \frac{{\left(\frac{{(c}_{1}-{c}_{2})/2-{c}_{3}}{{c}_{4}} \right)}_{yz}}{{\left(\frac{{(c}_{1}-{c}_{2})/2-{c}_{3}}{{c}_{4}} \right)}_{xy}},$$

(17)

where ${\tau }_{yz,max}$ and ${\tau }_{xy, max}$ are the maximum shear stresses in yz plane and in xy plane respectively, ${\left(\frac{{(c}_{1}-{c}_{2})/2-{c}_{3}}{{c}_{4}} \right)}_{yz}$ and ${\left(\frac{{(c}_{1}-{c}_{2})/2-{c}_{3}}{{c}_{4}} \right)}_{xy}$ are geometry calculations based on yz plane and xy plane respectively. For plane strain condition, the correction term is approximated as a function of ${c}_{4}$:

$$\frac{{{(\sigma }_{1,inclu}-{\sigma }_{1,matrix})}_{corrected}}{{{(\sigma }_{1,inclu}-{\sigma }_{1,matrix})}_{xy}}=0.3+0.7\times {c}_{4}.$$

(18)

If the matrix is in the elastic stage, the inclusion stress can be calculated by analytical equations following Eshelby’s solution. The effects of remote stress triaxiality and inclusion modulus can be included. If the matrix has developed significant plasticity, the inclusion stress is only related to the shear components in the remote loading condition as stated in Assumption (4). In such a situation, the effects of remote stress triaxiality and inclusion modulus can be neglected, and the inclusion stress is calculated by the present analytical equations involving the inclusion geometry, orientation and the remote matrix stress. When the matrix starts to yield but has not reached a threshold plastic strain (${\varepsilon }_{p,th}$), the inclusion stress is calculated by a linear interpolation with respect to plastic strain from the stress calculated by Eshelby’s solution in the elastic range to the stress calculated by Eqs. 6 to 17 when the plastic strain is equal to ε_p,th. The exact value of ${\varepsilon }_{p,th}$ to define the transition can be regarded as the plastic strain at which the strain hardening rate $d\sigma /d{\varepsilon }_{p}$ of the steel is less than 0.5% of the Young’s modulus.

3 Validation with numerical simulations

In order to validate the analytical solution (Eqs. 6 to 17) that predicts the representative stress on a hard inclusion, numerical simulations with nonlinear FEA are performed. The FEA model is first described. After that, the assumption of the shear regions formed around the inclusion is validated. The effect of the remote stress triaxiality, the remote plastic strain, and the Young’s modulus of the inclusion are evaluated. Comparison between analytical solution and numerical simulations is presented on the geometry of the inclusion with first the aspect ratio (ratio of major to minor axis) and thereafter the orientation. Finally, the effect of the stress–strain curve of the matrix is considered.

3.1 Description of FEA model

The FEA solutions are performed with Abaqus 2017 (Dassault Systemes 2017) for an elastic hard inclusion embedded in an elastic–plastic matrix. The stress–strain relationship of the steel is characterized by Ludwik’s law, which is defined with the flow stress ($\sigma$) and the effective plastic strain (${\varepsilon }_{p}$) as:

$$\sigma ={\sigma }_{y}+K{\varepsilon }_{p}^{{n}_{L}},$$

(19)

where K and n_L are material parameters. For the reference study, ${\sigma }_{y}$ is 690 MPa, K is 234 MPa, and n_L is 0.17, which are determined from a tensile test of S690 QL steel at room temperature. The inclusion is a linearly elastic material with a Young’s modulus of 300 GPa and a Poisson’s ratio of 0.3. According to several authors (e.g. Lamagnere et al. 1996; Chen et al. 2017; Gu et al. 2019), typical hard inclusion moduli vary from 250 to 380 GPa. A sensitivity study is performed for various aspect ratios of the spheroidal inclusion (R₁/R₂), stress triaxiality of the remote load (η), angle between inclusion’s major axis and remote principal stress (θ), and material properties of the inclusion and the matrix.

For the case where θ = 0°, one eighth of the entire $40\, \upmu {\mathrm m}\times 40\, \upmu \mathrm{m}\times 40\, \upmu{\mathrm m}$ cubic volume is modelled with the use of symmetry as shown in Fig. 3a. The longer axis of the inclusion is 4 μm, resulting in a volume fraction of inclusions of approximately 0.04% and a length fraction of 10%. The boundary conditions of the inclusion problem is referred as the far-field state, which represents the plastic strain and stress triaxiality on a macroscopic level. The boundary conditions of the cubic volume correspond to a plane-strain condition on the macroscopic scale. Normal traction is applied uniformly in two principal directions (axis 1 and 2), and normal displacement is constrained to zero in the third principal direction (axis 3). Displacement control is used to apply deformation at the boundary surfaces to generate a final plastic strain of approximately 0.05. The displacement along axis 1 (u₁) is the major tensile traction and the displacement along axis 2 (u₂) is set as a ratio to u₁ to generate a constant stress triaxiality. The C3D20R (20-node hexahedron with reduced integration) element is used to mesh both the inclusion and the matrix. The average element of the inclusion has a length of 0.01 $\upmu{\mathrm m}$. The average element of the matrix has a length of 1 $\upmu {\mathrm m}$. The matrix in the vicinity of the inclusion has a linearly biased mesh to transition to a larger element size. For the case where θ > 0° (Fig. 3b), half of the entire cubic volume is modelled with the use of symmetry. The size of the inclusion, cubic volume, element density and the loading conditions are the same as for θ = 0°.

Fig. 3

3D model of an inclusion (in colour green) embedded in a cubic volume matrix a θ = 0° one eighth of the cube and b θ > 0° half the cube

The full Newton–Raphson algorithm is used to solve the geometric and material nonlinearity. The representative inclusion stress is defined as the average tensile stress acting on the mid-section of the inclusion. The mid-section lays normal to the tensile loading direction (axis 1 in Fig. 3), through the centroid, and separates the inclusion into two anti-symmetrical parts. The average stress is computed as the normal component of the total force acting on the mid-section divided by the area of the mid-section. The total force accounts for both tensile and compressive components, while since the remote load long axis 1 is in tension the average stress on mid-section would also be in tension. A convergence study on element size has been conducted. Re-running the same model with twice the inclusion size was checked, yielding the same results. The check of element size and inclusion size is not included in the manuscript for brevity.

3.2 Validation of shear plane hypothesis

Figure 4 shows the distribution of first principal stress near the inclusion for the case of a spherical inclusion (R₁ = R₂), under η = 2. It confirms the assumption that a shear plane is formed at the inclusion/matrix interface, following the principal shear direction. Between the shear plane and the inclusion, the matrix undergoes significant stress variation. The principal stress directions in the vicinity of the inclusion have been distorted due to the constraint of the inclusion. Consequently, the first principal stress inside the inclusion is higher than the remote first principal stress.

Fig. 4

Distribution of first principal stress around the inclusion (stress is given in MPa)

3.3 Validation of assumption on plastic strain and stress triaxiality

The stress is computed using the solution for shear only. The remote pressure does not play a role when matrix deformed plastically. Figure 5 shows the inclusion stress under various stress triaxiality values, which supports the assumption. Although the stress depends on the stress triaxiality in the elastic and the early yielding stage, the dependence vanishes when a certain level of plastic deformation has been developed in the matrix. It is observed that the influence of the hydrostatic pressure on the stress difference between inclusion and matrix is decreasing if the remote plastic strain is greater than 0.01 and fully vanishes if remote plastic strain is greater than 0.03. It should be mentioned that it is straightforward to notice this phenomenon when the stress is plotted with the absolute difference between inclusion stress and matrix stress, as in Fig. 5a. If the stress is plotted as a normalized value (as in Fig. 5b), it can be compared with the results in the literature (Lee and Mear 1999; Thomson and Hancock 1984; Wilner 1988) but does not show the above conclusion.

Fig. 5

Stress of the inclusion vs remote plastic strain under various stress triaxialities (η) a plotted as absolute difference and b plotted as normalized value

3.4 Effect of inclusion elastic modulus

A similar effect is observed in the sensitivity study of the inclusion modulus. Figure 6 shows that the influence of the inclusion modulus is decreasing with increasing remote plastic strain and fully vanishes for remote plastic strain greater than 0.02. If the matrix has developed significant plasticity, the effects of inclusion modulus can be neglected, as stated in the development of the analytical solution.

Fig. 6

Stress difference vs. plastic strain for various inclusion moduli (R₁/R₂ = 1)

3.5 Effect of inclusion shape

To assess the influence of the shape of the inclusion, the aspect ratio was first varied parametrically while the stress triaxiality was held constant at η = 2. Based on the matrix elasto-plastic properties, ${\varepsilon }_{p,th}$ in the analytical solution is determined as 0.02. Figure 7 shows the results of this study. It is observed that the inclusion stress is higher for larger values of R₁/R₂. This effect occurs for all levels of remote plastic strain.

Fig. 7

Stress difference vs plastic strain for various aspect ratios (θ = 0°)

Next, the effect of orientation was assessed. Figure 8 shows an inclusion of R₁/R₂ = 2 under the same remote loading condition, but the major axis (R₁) has an angle (θ) with the direction of the remote first principal stress. It is observed that as θ increases, the stress at an elongated inclusion is reduced. This effect exists for all levels of remote plastic strain. By comparing the curve θ = 90° in Fig. 8 with the curve R₁/R₂ = 0.5 in Fig. 7, it can be noticed that the stress is less pronounced for the inclusion of R₁ = 0.5R₂ = 0.5R₃. This indicates that the effect of inclusion geometry is related to its three-dimensional morphology, even if the remote loading condition is plane strain.

Fig. 8

Stress difference vs. plastic strain for various inclusion orientations (R₁/R₂ = 2)

3.6 Effect of the shape of the stress–strain curve

The analytical solution has been compared with FEA models of various matrix properties other than the reference study. The yield strength and Ludwik’s parameters K and n_L, given in Eq. 19, have been varied to determine the influence. Figure 9a shows the stress–strain curves of steels A–D. Figure 9b shows the parameters to define steels A–D. Steels A–D are all high strength steels with ${\sigma }_{y}\ge 690$ MPa and relatively low-hardening behaviour. The varied parameter values are hypothetical, while the resulting curves can be compared with stress–strain curves for commonly used high strength steels, for example as reported by Wuertemberger (2016). The analysis is performed with an arbitrary case R₁/R₂ = 2 and θ = 45°. According to Fig. 9c, the analytical solution shows good performance independently of yield strength and n_L values. However, for a higher K value (pronounced hardening in the early yielding stage), the analytical solution is seen to give a less accurate prediction of the stress. This phenomenon can be explained by its violation of the assumption of the low-hardening condition. Thus, the analytical solution should be used carefully on materials that have pronounced hardening behavior.

Fig. 9

a Hardening behaviour for various matrix materials, b material parameters of steels A–D, and c stress difference vs. plastic strain for steels A–D

3.7 Summary of validation studies

The analytical model has been systematically compared with FEA to assess the underlying assumptions and accuracy over a range of parameters. It was first demonstrated that shear regions around the inclusion do form as a tangent to the hard inclusion, with a 45° angle relative to the first principal stress. It was shown in Figs. 5 and 6 that the fully plastic solution is independent of stress triaxiality and the Young’s modulus of the inclusion. It was shown in Figs. 7, 8 and 9 that the analytical model was able to accommodate the shape (aspect ratio and orientation) of the inclusion and various stress–strain curves. Materials that show a high level of hardening show less correlation with the analytical solution. This is to be expected based on the assumptions used in developing the solution and based on the observations that high-strength steels (the focus of this study) tend to have low hardening rate.

The analytical model is able to capture important input parameters within approximately 25% when full plasticity is developed. The Eshelby solution remains a good method of assessing linear-elastic conclusions. We present and validate a solution for fully plastic behavior. We have shown that linear interpolation between the elastic condition and the fully plastic behavior can provide an acceptable accuracy. In the validations,${ \varepsilon }_{p,th}$ is set as 0.02, where the strain hardening rate $d\sigma /d{\varepsilon }_{p}$ of the steel is less than 0.5% of the Young’s modulus. The linear interpolation and criterion to define ${ \varepsilon }_{p,th}$ is demonstrated and validated in Figs. 7, 8, and 9. The method is developed and validated for plane strain conditions, but the assumptions and deviations are maintained for plane stress conditions.

4 Application to cleavage fracture modelling

The developed solution has been applied on fracture test data to demonstrate the relevance for cleavage fracture modelling. The data sets include specimens taken from the top quarter section and middle section of the S690 QL steel plate. All specimens are fractured at − 100 $\mathrm{^\circ{\rm C} }$ and have a brittle fracture mode.

4.1 Description of the materials and mechanical tests

A commercially available 80 mm thick quenched and tempered S690 high strength steel plate is used in this paper for illustration and validation. Materials are extracted from the top quarter section and the middle section of plate. The materials have been previously characterized in Bertolo et al. (2020). The chemical composition of the steel plate is shown in Table 2.

Table 2 Chemical composition of S690QL

The microstructure of the plate varies through the thickness from a fully tempered martensitic structure in the regions close to the surfaces to a mixed tempered martensitic–bainitic structure in the central section of the plate. Spherical inclusions and second-phase particles ranging from 1 to 5 µm were observed through the full thickness, including oxides and nitrides of rather complex chemical composition such as (Mg, Ti)(O, N), (Mg, Al, Ca)(O, N) and (Mg, Al, Ca, Ti)(O, N). In the middle position, in addition to the spherical inclusions, cubic and elongated inclusions with dimensions ranging from 1 to 11 µm were observed. Niobium-rich carbides and nitrides such as (Ti, Nb)(N), (Ti, Nb)(C), Nb(C), and (Nb, Ti)(C,N) are present in the middle position. Figure 10 shows representative morphology of the inclusions observed in the S690QL steel plate at top quarter section and middle section.

Fig. 10

SEM micrograph of inclusions in the S690QL steel plate (RD rolling direction, ND normal direction) a a (Mg, Al, Ca)(O,N) inclusion and b a Nb enriched inclusion

Prior austenite grains (PAG) at three locations in each section were reconstructed based on EBSD data and ARPGE software. Figure 11 shows the statistical distribution of grain size in each section, with the Least Square fitting. It is apparent that the middle section specimens have larger average grain size and a greater portion of extremely large grains (major axis larger than 50 µm).

Fig. 11

Statistical distribution of grain size at top quarter and middle section

The parameters of Ludwik’s law are determined for top quarter and middle section by tensile tests at − 100 °C. The values of the parameters are summarized in Table 3.

Table 3 Material parameters of S690 QT steel determined by tensile test at − 100 °C

Fracture toughness tests were performed according to ISO 12135 at − 100 °C using sub-sized single edge notched bending (SENB) specimens, with three geometries (a₀/W equal to 0.5, 0.25 and 0.1). For top quarter section specimens, geometries of a₀/W = 0.5 and 0.25 are considered as high and low constraint conditions, respectively. For middle section specimen, geometries of a₀/W = 0.5 and 0.1 are considered as high and low constraint conditions, respectively. The geometry of the SENB specimens is specified in Fig. 12 and Table 4. Fractographic examinations reveal that the microstructural hard inclusions play an important role in the cleavage fracture process (Bertolo et al. 2020).

Fig. 12

Geometry information of the SENB specimen (Z direction coincides to ND of the plate)

Table 4 Geometric information of the initial crack length

4.2 Statistical modelling of cleavage fracture

In this paper, the modelling of cleavage fracture considers crack nucleation in hard particles and crack propagation through grain boundaries. Observation of the fracture surface reveals that the tested specimens are fractured by crack initiated from oxides and Nb inclusions. The inclusions are relatively large compared to commonly observed hard particles, like carbides, and the cracks initiated by the large inclusions can easily propagate through the inclusion/grain interface. Thus, the dominant barrier of crack propagation is assumed to be the grain boundary instead of the inclusion/grain interface. The modelling approach is adapted from a double-barrier model proposed by Lambert-Perlade (2004), assuming the initiated microcrack to be always large enough to propagate through the inclusion/grain interface.

In the model, FEA of a macroscopic specimen gives the result of stress/strain distribution under a certain global load level (represented as a CTOD). The process zone (PZ) is taken to be the plastic zone. Cleavage probability of each element within the process zone is calculated based on its stress and strain condition. By accounting for the cleavage probability of all elements over the process zone, the total failure probability of the specimen can be calculated.

Prior to the cleavage modelling, the stress concentration factor of inclusion,${f}_{\alpha }$, is calculated using the developed analytical solution based on the material properties and inclusion geometry. The cleavage probability of a single potential cracking nucleus in element j under load level i, ${P}_{f,ij}$, is calculated based on the following steps:

• (1) Calculate the inclusion stress ${\sigma }_{1,inclu}$ from Eq. 6 and check if the inclusion stress exceeds the critical value ${\sigma }_{H}^{C}$. A micro-crack is initiated in the inclusions if ${\sigma }_{1,inclu}>{ \sigma }_{H}^{C}$, and ${P}_{f,ij}$ would be calculated by steps (2)–(3). Otherwise, it is assumed that no micro-crack is initiated and ${P}_{f,ij}=0.$

• (2) If the inclusion stress exceeds the critical value to nucleate a crack, a minimum grain size ${D}_{c}$ is calculated by Griffith-like criteria as for the first principal stress within the grain (${\sigma }_{1,matrix}$) to propagate the crack across the grain boundary, by

  $${{D}_{c}=(K}_{Ia}^{mm}{/{\sigma }_{1,matrix})}^{2},$$

  (20)

  where ${K}_{Ia}^{mm}$ is the crack arrest parameter of grain boundary.

• (3) A cleavage probability ${P}_{f,ij}$ is calculated for the possibility that a grain has the major axis greater than ${D}_{c}$. ${P}_{f,ij}$ can be calculated by

  $${P}_{f,ij} ={\int }_{{D}_{c}}^{+\infty }{f}_{g}(D)dD=\frac{\alpha }{{D}_{c}^{\beta }},$$

  (21)

  where ${f}_{g}(D)$ is the distribution density function of the grain major axis. In this paper, ${\int }_{{D}_{c}}^{+\infty }{f}_{g}(D)dD$ is measured from microscopy and fitted as a power-law function with parameters α and β.

The total fracture probability ${P}_{f,i}$ at load step i is then updated based on the weakest-link mechanism. ${P}_{f,i}$ is calculated from a Weibull-like formulation that accounts for the total cleavage probability of all potential cracking nuclei within the process zone (PZ):

$${P}_{f,i}=1-\mathrm{exp}(-\underset{PZ}{\overset{}{\int }}N{P}_{f,ij}dV),$$

(22)

where N is the average number of potential cracking nuclei (inclusion) per unit volume.

After looping over all elements, the calculation will be performed for the next load step until all the load steps are evaluated. When the computation is finished, the output is the fracture probability of each load step, in terms of CTOD value.

4.3 Finite element modelling of the fracture test

SENB specimens with the geometry specified in Table 4 are modelled in Abaqus 2017 (Dassault Systemes 2017). In total, four analyses are performed to consider the variety of initial crack length and material properties. For each analysis, a quarter of the specimen ($L/2\times B/2\times W$) is modelled as a 3D deformable solid by using symmetry. The support and load roller are modelled as analytical rigid surfaces. The contact surface between rollers and the specimen is frictionless. Figure 13a shows the 3D model of a quarter of the specimen and two rollers. Figure 13b shows the mesh near the crack tip. The initial prefatigued crack tip is modeled as a finite notch that is 0.005 mm in radius. According to Andrieu (2012), this finite notch is small enough to model the near-crack-tip-field for the CTOD value considered in this study. C3D20R element is used for the mesh. The smallest element near the crack tip has a length of 0.001 mm. Displacement control is used to apply a total deflection of 1 mm. A full Newton–Raphson algorithm is used to solve the geometric and material nonlinearity. The material parameters of the top quarter section and the middle section are taken as the values in Table 3.

Fig. 13

a 3D model of the three-point-bending test and b mesh near the crack tip

4.4 Cleavage fracture modelling assuming spherical inclusions

The inclusions of both the top quarter section and the middle section are assumed to be spherical for the purposes of calculating ${f}_{\alpha }$. The material parameters of the matrix are taken as in Table 3. The remaining input parameters are listed in Table 5.

Table 5 Value of the input parameters for the cleavage model

There are two major differences in the microstructures between the top quarter specimens and the middle section specimens: the grain size distribution and the existence of the elongated inclusions. With the assumption that the grain boundary is the barrier to arrest micro-cracks, the inverse modelling will result in two fitted parameters ${K}_{Ia}^{mm}$ (crack arrest parameter of grain boundary) and ${\sigma }_{H}^{C}$ (critical stress of hard inclusion). Determination of these two parameters uses two constraint conditions. The fitted parameter values are listed in Table 6.

Table 6 Parameter values from inverse modelling

The fitting on the top quarter specimens and middle quarter specimens results in similar values of ${K}_{Ia}^{mm}$ but significantly different values of ${\sigma }_{H}^{C}$, which corresponds to the microstructural observation that there are similar grain boundaries but distinct inclusions through the thickness. The inclusions in the middle section are computed to have lower strength, which means they are more prone to fracture. Figure 14 shows the resulting P_f-CTOD curves from the modelling in comparison with experimental data.

Fig. 14

P_f-CTOD curve of top quarter section in comparison with experimental data (dots are the experimental data and curves are the model predictions)

4.5 Fracture modelling considering the inclusion geometry

The above modelling of cleavage fracture with the assumption of spherical inclusions shows that the inclusions in the middle section are computed to have lower strength. One of the potential causes of the lower inclusion strength in the middle section can be related to the elongated inclusion shape. In order to explain the variety of inclusion strength determined in the cleavage fracture modelling, the developed analytical solution is used to calculate inclusion stress with (a) oblate and (b) prolate as shown in Fig. 15.

Fig. 15

a Oblate (R₁/R₂ = 1, R₂/R₃ = 2 or 3), and b prolate inclusions (R₁/R₂ = 2 or 3, R₂/R₃ = 1) with remote loading in plane strain

It has been observed that the inclusions in the middle section tend to have a longer axis along the RD and a shorter axis along the ND, as shown in Fig. 10. The aspect ratio of individual inclusions varies significantly. In this study, an assumption of aspect ratio of 2 and 3 is used to estimate the effect. For both the oblate and prolate shapes, the minor axis lies along the ND, which is the out of plane direction of the SENB specimens, and the major axis lies perpendicular to the crack (θ = 0°). Table 7 shows the results of cleavage parameter determination considering the variety of inclusion geometry.

Table 7 Parameter values from inverse modelling considering inclusion geometry

This example shows that the inclusion strength strongly depends on the inclusion shape, while the crack arrest parameter of the grain boundary is independent of inclusion features. Compared with Table 6, when the inclusions are modelled with shapes that are prone to cracking, a higher critical stress of hard inclusion is determined, as the stress concentration effect is considered in the calculation of inclusion stress.

Table 7 shows the critical inclusion stresses obtained from the cases oblate (R₁/R₂ = 1, R₂/R₃ = 3) and prolate (R₁/R₂ = 2, R₂/R₃ = 1) are closer to the values determined for the top quarter section. The prolate geometry would lead to anisotropy in the rolling direction and the longitudinal direction, while the oblate geometry does not. Since the microscopic observation and fracture tests only reveal anisotropy between the rolling direction and the normal direction, but not for the longitudinal direction, the oblate assumption is more sensible for the investigated material. Although the present example only shows the trend of critical inclusion stress versus inclusion shape, it proves the strong correlation between fracture modelling and the microstructural feature of inclusions. If the inclusion geometry and orientation can be determined in a statistical format, the developed solution is capable of exploring its effect on cleavage fracture with more detail.

5 Discussion

5.1 Capabilities of the model

In the above validations and applications, the analytical solution reflects the influence of several factors on the inclusion stress, which corresponds to the observations of hard inclusion behaviour in cleavage fracture that have been reported in literature. The following factors have been reflected:

• (1) The stress level depends on the shape and orientation of the inclusion. The tensile stress on the inclusion is much more pronounced when the inclusion has its major axis along the remote first principal stress. This difference can explain the observation that particle fracture is often reported for elongated inclusions when loaded along their length (Pineau et al. 2016).

• (2) The representative inclusion stress increases with remote plastic strain when matrix hardening is considered. It agrees with the observation that plastic deformation is necessary for cleavage initiation even if the cleavage is stress-controlled (Bordet et al. 2005).

• (3) Various matrix plasticity parameters have been used to validate the solution. It is found that the inclusion stress increases with the yield stress of the matrix. It explains the observation that particle cracking is preferred in a hard matrix and a soft matrix favours particle decohesion (Chen and Cao 2015).

5.2 Comparison with existing solutions

The analytical solution developed in this paper can also be compared with empirical equations. The empirical equations for the stress in an inclusion that have been used by other researchers are in a format similar to Eq. 6. Shibanuma et al. (2016) calculated the maximum principal stress at a cementite particle by:

$${\sigma }_{1,inclu}=\frac{{E}_{inclu}}{{E}_{matrix}}{\sigma }_{1,matrix}+0.179{\sigma }_{y}\left(\frac{{\varepsilon }_{p,matrix}}{{\varepsilon }_{y}}\right)^{0.627}.$$

(23)

Lambert-Perlade (2004) calculated the maximum principal stress in the M-A particle by:

$${\sigma }_{1,inclu}={\sigma }_{1,\mathrm{matrix}}+1.8({\sigma }_{eq,matrix}-{\sigma }_{y,matrix}).$$

(24)

Hardenacke et al. (2010) proposed an equation to calculate the particle stress and attempted to account for particle geometry and orientation with four empirical parameters:

$${\sigma }_{1,inclu}={c}_{I}{\sigma }_{1,\mathrm{matrix}}+{c}_{M}{c}_{II}{({\varepsilon }_{1})}^{{c}_{III}},$$

(25)

while the determination of the c parameters is not explicit in the publication.

The proposed analytical solution Eq. 6 can be written as an empirical equation fitted with the present results of FEA:

$${\sigma }_{1,inclu}={\sigma }_{1,matrix}+{{c}_{F}\sigma }_{eq,matrix},$$

(26)

where ${c}_{F}$ is a fitted parameter related to the aspect ratio and orientation of the inclusion. For the case θ = 0°, the fitted relationship is:

$${c}_{F}=0.3026\frac{{R}_{2}}{{R}_{1}}.$$

(27)

As introduced at the beginning of this paper, methods based on Eshelby tensors have been used to calculate the stress of inclusions. Beremin ductile fracture model provides equations in a similar format of Eq. 6 (Beremin 1981):

$${\sigma }_{1,inclu}={\sigma }_{1,\mathrm{matrix}}+{c}_{B}({\sigma }_{eq,matrix}-{\sigma }_{y}),$$

(28)

where parameter ${c}_{B}$ is determined analytically with the usage of Eshelby tensors. In the following discussion, Eq. 28 is used as the representative of Eshelby tensor based equations to be compared with the present analytical solution.

Figure 16 shows the performance of the developed analytical solution (Eqs. 6 to 17), the fitted empirical equation (Eqs. 26 and 27), and the solutions provided by other researchers (Eqs. 23, 24 and 28), by comparing with FEA results. The comparison is in terms of the ratio ${({\sigma }_{1,inclu}-\sigma }_{1,matrix})/{\sigma }_{eq,matrix}$. The matrix material is material A in Fig. 9 and comparison is at ${\varepsilon }_{p,matrix}=0.05$. The comparison is based on spheroidal inclusions of various aspect ratios (R₁/R₂ = 0.5, 1, 1.5, and 2) with θ = 0°. Among the considered equations, only the Shibanuma formula (Eq. 23) always accounts for the elastic mismatch, which is not supported by the FE results. Equations 23 and 24 have the shortcoming of not reflecting the influence of particle geometry and orientation (which results in a single data point representing a spherical inclusion in Fig. 16). Equation 25 attempts to reflect the particle geometry, but deviates from FEA results. Both the fitted empirical equation (Eqs. 26 and 27) and the analytical solution (Eqs. 6 to 17) in the present article give good predictions in terms of particle geometry. However, the empirical equations 26 and 27 are unable to take account of the orientation of the inclusion.

Fig. 16

Performance of the current developed analytical solution and empirical equations

As described in Part 1, mean-field method has been widely used in multi-scale material modelling. Figure 17 shows the results by using the MF method in Abaqus 2017 (Dassault Systemes 2017), which was adapted from Doghri and Ouaar (2003), to analyse the inclusion problem (with R₁/R₂ = 1, η = 0, matrix material A). Both the general method and the spectral method (Doghri and Ouaar 2003) have been tested for the isotropization of the matrix material. The result shows that the two isotropization methods can well predict the matrix behaviour (which is equivalent to the macroscale behaviour in a dilute inclusion problem), but fail to predict the inclusion stress when the matrix material enters nonlinearity. It requires calibration from FEA to predict the stress concentration of inclusions in the case of highly nonlinear constituent materials.

Fig. 17

Result of using mean-field method on the inclusion problem

5.3 Limitations

In general, the analytical equations derived in the present paper are able to involve several features as the inclusion geometry, the inclusion orientation, the far-field stress state and different matrix material properties. It should be noticed that the analytical solution is only suitable for the following situations:

• (1) The inclusions are distributed sparsely in the matrix. The space between inclusions should be at least five times the inclusion diameter. Otherwise, there will be interaction between inclusions, which the developed solution does not account for.

• (2) The matrix material has low-hardening behaviour after yielding. The presence of an inclusion will result in high local plastic strain in the matrix. If the matrix material has pronounced hardening behaviour after yielding, the local stress state in the matrix near the inclusion will be much higher than assumed. The stress in the inclusion will be underestimated by the analytical solution.

• (3) The inclusion can be assumed as an ellipsoid. The analytical solution estimates the representative stress of the inclusion, which is an average stress over the midsection. If the inclusion has a very irregular shape, the average stress may not represent the stress level within the inclusion and the analytical solution should not to be used.

6 Conclusions

This paper presents analytical equations to quantitatively calculate the stress on a hard inclusion from far-field stress on a matrix. The solution has been derived based on the assumption of shear-dominated behaviour in fully-formed plasticity. Validation was performed by numerical modelling of a microscopic hard inclusion in a high strength steel. The simulation validates the assumptions on which the analytical solution is based and estimates the performance of the analytical solution. Finally, the solution was demonstrated by using it in an existing statistical framework to model cleavage fracture in CTOD specimens.

The main conclusions are highlighted as the following:

• (1) A set of analytical equations is established to quantitatively estimate the inclusion stress from far-field matrix stress. The analytical equations together with the classic Eshelby’s solution are able to take account of the interaction of the far-field hydrostatic pressure and deviatoric stress.

• (2) The analytical equations are able to take account of features such as the inclusion shape and the inclusion orientation. The prediction corresponds to the FEA results that the inclusion stress is much more pronounced for the inclusion that has its major axis along the remote first principal stress.

• (3) The analytical equations give an approximate solution for the inclusion stress that is asymptotically approached in plastic deformation of low-hardening materials. The maximum error of σ_1,inclu − σ_1,matrix is 25% for the studied cases. For materials with more pronounced hardening behaviour, the analytical solution is less satisfying.

The analytical solution to quantitatively determine the stress on a microstructural hard inclusion can be used for the statistical characterization of macroscale cleavage fracture, and on the identification of anisotropic fracture behavior. It avoids costly numerical simulations when the features of microstructural inclusions vary widely in the steel and provides an efficient estimation of inclusion fractures in the cleavage process. Because the solution can account for multiple parameters, it can be used not only for a particular material but in general for high strength steels containing heterogeneous microstructures and under various loading patterns. The ductile damage mode is often modeled based on the assumption that hard particles separate from the surrounding matrix material. While it was not the purpose of this study, such a failure model may also benefit from the current developments if a failure model is applied to determine when decohesion occurs between the hard particle and the surrounding matrix.