Evaluation of Flow and Failure Properties of Treated 4130 Steel

Abstract

In numerical modeling of material behavior, deformation is calculated with analytical constitutive equations. When joined with a failure criterion, simulations can predict plastic stress–strain behavior and eventual fracture of the material. The Air Force Institute of Technology (AFIT) uses the Johnson–Cook empirical constitutive equation and damage criterion to model high speed wear. The Johnson–Cook equations employ material parameters which must be characterized experimentally for each material being simulated for accurate results. This paper describes the testing and analytics used to determine the Johnson–Cook constitutive and damage material coefficients for treated 4130 steel. The flow and damage coefficients are calculated and the results are used to construct a finite element model in ABAQUS. This model is compared against the experimental data for final validation.

Introduction

Holloman Air Force Base (HAFB) is home to the 10-mile long Holloman High Speed Test Track (HHSTT) rocket sled testing grounds. During test runs, rocket stages attached to the back of the sled propel the main sled forward at tremendous speeds. An example of one such rocket sled is shown below in Fig. 1.

Fig. 1

Picture of a June 2014 HHSTT sled featuring treated 4130 steel slippers on a 1080 steel track rail, obtained from correspondence with HAFB

The slipper, a component that connects rocket sleds to the test track rails, is subjected to extreme conditions during test runs. High strain rates, high temperatures, micro impact events, friction, and bouncing generated from rocket propulsion all contribute to material loss of the slipper contact surface by melting and mechanical wear. After test runs, the slippers are discarded. It is of interest to accurately model how much of the slipper material is lost during test runs, which requires being able to trace the failure of the material.

Over the years, AFIT has spearheaded modeling the complex deformation of the slipper by utilizing metallurgical examination and various finite element and hydrocode modeling programs [1–4]. Much progress has been made in developing a robust model that accounts for temperature, strain rate, the contact surface bouncing, friction, and micro surface impacts. The finite element model uses the Johnson–Cook constitutive and damage equations to characterize flow stress and failure. These equations are emperically-based and driven by experimentally determined material parameters. AFIT is now attempting to model the wear of a HHSTT run where the slipper material is a heat treated 4130 steel, which has not yet been characterized for the constitutive and damage model. Thus, new characterization is required to obtain the material constants.

There are several examples of previous characterizations of steels for the Johnson–Cook model. Armox 500T and 600T, 1010 steel, Mild and DP590 steel, DH-36, and RHA are a few of the similar materials with published fittings for the strength portion [5–9]. Full model characterizations including the damage criteria are more sparse, but there are publications for HY-80, HY-100, and HY-130 steels, Weldox 460 and 4140 steel [10–13]. Each study follows a similar solving structure, but differ in small ways in approaching the solving sequence. Some are able to incorporate significantly higher strain rates and others only characterize at room temperature, but generally the approach is the same.

Though there are many studies characterizing the Johnson–Cook flow equation for other materials, none exist for 4130 steel with or without a heat treatment. The presentation of the solving methods of both strength and damage equations with newly generated experimental data for comparison makes this work unique.

Mathematical Motivation

Recall that stress–strain curves can be divided into two portions: an initial, linear, elastic region followed by a non-linear, plastic region. These segments are divided by the yield point, where the yield stress and strain ceases to behave linearly.

Thus, to describe strain occurring at a point within a model, one can use the definition:

$$\epsilon = \epsilon _{e}+\epsilon _{p}$$

(1)

And similarly for strain rate:

$$\dot{\epsilon } = \dot{\epsilon }_e+\dot{\epsilon }_p$$

(2)

where $\epsilon _{e}$ is elastic strain, $\dot{\epsilon }_e$ is elastic strain rate, $\epsilon _{p}$ is plastic strain, and $\dot{\epsilon }_p$ is plastic strain rate.

The elastic region of strain can be represented one-dimensionally as $\frac{\sigma }{E}$, which models recoverable deformation. The plastic region can be modeled using any number of constitutive equations that have been developed over the years describing non-recoverable deformation. The transition point between the regions (yield point) is determined numerically by the von Mises yield criterion. Once the second deviatoric stress invariant ($J_2$) reaches a critical value, usually the predefined yield strength of the material, the model transitions from using elastic relations for stress and strain calculations to the constitutive flow relations [14, 15].

The Johnson–Cook Constitutive Model

AFIT has been using the experimentally-based Johnson–Cook viscoplastic constitutive equation for its research. The model is popular due to its versatility, simplicity, and the ease with which the material parameters can be obtained [16]. It has the form:

$$\hat{\sigma }_y = (A+B\epsilon _{p}^{n})\left(1+C\ln \frac{\dot{\epsilon _p}}{\dot{\epsilon _o}}\right)(1-T^{*m})$$

(3)

where $\hat{\sigma }_y$ is the vonMises or equivalent flow stress, A is the yield stress, B is the plastic strain coefficient, $\epsilon _p$ is the plastic strain, n is the strain hardening coefficient, C is the plastic strain rate coefficient, $\dot{\epsilon _p}$ is the plastic strain rate, $\dot{\epsilon _0}$ is a normalizing strain rate, and m is the thermal coefficient. $T^*$ is the homologous temperature, defined as

$$\begin{aligned} T^* = \frac{T-T_{ref}}{T_{melt}-T_{ref}} \end{aligned}$$

(4)

where T is the sample temperature, $T_{ref}$ is a reference temperature (23 °C for this study), and $T_{melt}$ is the melting temperature of the sample material, for 4130 steel 1432 °C.

A strength (or flow) equation dictates stress–strain behavior beyond the elastic limit. The first set of parenthesis are static stress contributions which include the yield stress and strain hardening behavior [16]. It is based on Ludwiks equation:

$$\sigma _{flow}= \sigma _{yield}+B\epsilon _p^n$$

(5)

where $\sigma _{flow}$ is the post-yield stress, $\sigma _{yield}$ is the yield stress, and B and n are strain hardening coefficients [17, 18].

The second set of parenthesis describes the strain rate behavior. It is based on a simple logarithmic model proposed by Ludwik and used by Lindholm [19].

$$\sigma =\sigma _{yield}(1+C\log \dot{\epsilon _p})$$

(6)

The third set of brackets describes temperature effects, where increasing temperatures causes the flow stress to decrease. The homologous temperature is used to normalize the material temperature against a reference temperature. Thermal contributions are quite important for AFIT’s research since the rocket sled wear event being modeled experiences extreme temperature fluctuations. Furthermore, it allows the model to include the effects of heat generated internally by the deformation process.

Authors have noted it is more likely that the three behaviors (static stress, strain rate, and temperature) are more interrelated than how the model currently is formulated, but it has been shown to give reasonably accurate prediction for low-mid strain rate material impacts [18, 20, 21].

Johnson–Cook Failure Criterion

The flow equation dictates the stress–strain behavior of a material beyond the elastic limit, but does nothing to predict when the material will fail. For this reason, a damage criterion is needed to flag at what point the fracture will occur. The Johnson–Cook damage criterion is shown below:

$$D=\sum \frac{\Delta \epsilon ^{p}}{\epsilon _f}$$

(7)

where D is the accumulating damage, $\Delta \epsilon ^{p}$ is an increment of accumulating equivalent plastic strain, and $\epsilon _f$ is the equivalent strain to fracture at the current strain, strain rate, and temperature conditions. Once damage accumulates so that the value of D is equal to 1, failure of the material has occurred. In simulations the failed element is phased out by setting the stress tensors equal to zero [22]. The criterion is based on calculating the critical failure strain, shown in Eq. 8 [22].

$$\epsilon _f=[D1+D2 e^{-D3Q}] \left[1+D4 \ln \frac{\dot{\epsilon _p}}{\dot{\epsilon _0}}\right][1+D5T^*]$$

(8)

where $\epsilon _f$ is the equivalent strain at failure, D1-D5 are all experimentally determined coefficients, and Q is the triaxiality factor.

The formulation of the failure strain Eq. 8 is similar compared to the strength Eq. 3. D1–D3 are stress state coefficients related to void formation in the metal, D4 is correlated with rate sensitivity, and D5 accounts for temperature effects. The first bracketed set in the equation, $[D1+D2 e^{-D3Q}]$, is based off a model from Hancock and Mackenzie:

$$\bar{e}^f= \bar{e}_n+\alpha e^{\frac{-3\sigma _m}{2\sigma }}$$

(9)

where $\bar{e}_n$ is the void nucleation strain and $\alpha$ is a material dependent hole growth rate [23].

The triaxiality factor is the ratio of mean stress to equivalent stress, which fluctuates throughout deformation. It serves as a measure of ductility.

$$Q = \frac{\sigma _{m}}{\bar{\sigma }_{eq}}$$

(10)

The mean stress is defined as the average of the three principal stresses:

$$\sigma _{m} = \frac{\sigma _{11}+\sigma _{22}+\sigma _{33}}{3}$$

(11)

The equivalent stress, or vonMises stress, is defined as:

$$\bar{\sigma }_{eq} = \sqrt{\frac{3\sigma _{ij}\sigma _{ij}}{2}}$$

(12)

One can make an observation based on the formulation of Q: that when a problem is uniaxial, all stress tensors but $\sigma _{11}$ cancel, leaving a constant Q value. Thus, one-dimensionally, the equivalent strain at fracture is equal to the failure strain. However for all other cases, the two are not necessarily equal.

It should be noted that in the original Johnson–Cook development, D3Q is actually a positive term in Eq. 8. Also, Johnson and Cook note that this equation is only valid for triaxiality values up to 1.5, and beyond that a different equation must be used [22].

Experimental Testing Program

Material Treatment and Composition

The material of interest is 4130 steel that has undergone a heat treatment. Annealed 4130 steel is first manipulated to drawing specifications, heated above its critical austenitizing temperature, 1675 °F (910 °C), quenched, and then tempered at 1050 °F (566 °C) until it reaches a strength of 120–140 ksi (827–965 MPa). The chemical composition of 4130 steel is listed below in Table 1.

Table 1 Percent composition of alloying elements of 4130 steel [25]

Sample Manufacturing

Experiments were carried out at the University of Dayton Research Institute (UDRI) with samples supplied by Holloman AFB. Samples were machined from the same treated AISI 4130 steel used for rocket sled slippers. Two types of samples were manufactured: notched specimens for triaxiality determination, seen in Fig. 2, and smooth, ASTM sub-size E8 dogbone samples for tensile testing seen in Fig. 3. Prior to experimentation, measurements of the diameters and lengths of the all samples were recorded.

Fig. 2

Diagram of notched triaxiality determination sample, shown with the 0.8 mm radius (Dimensions are in English units)

Fig. 3

Sub-size ASTM E8 threaded dogbone specimen diagram (Dimensions are in English Units) [24]

The notched triaxiality test samples are 2 inches (50.8 mm) in length with a diameter of 0.325 inches (8.255 mm) and are machined with one of 3 different notch sizes: 0.4, 0.8, and 2.36 mm. Five samples of each notch radius were fabricated. However, tolerances were unable to be met on the notch sizes and they were manually turned into the samples. This left a rough surface finish and uneven radii. To account for this, the radius of each sample was measured using digital comparator. Each sample was measured 3 times, rotating the sample by approximately 120 degrees for each measurement. The radii for 0.4 mm radius varied between 0.503 and 0.448 mm, the 0.8 mm radius varied between 0.812 and 0.889 mm, and the 2.36 mm notch varied between 2.55 and 2.49 mm. Results of these measurements were averaged. The nominal radii measured at 0.48 ± 0.02, 0.87 ± 0.03, and 2.52  ± 0.03 mm, and they were used for calculations and modeling. These samples were all tested on the servo-hydraulic test stand.

The other specimens for this program are smooth cylindrical dogbones for tension tests. They are 1.15 inches (29.21 mm) in total length with a gage length of 0.35 inches (8.89 mm) and a minimum diameter of 0.125 inches (3.175 mm). Again there were issues with the surface finish of the samples - jitter marks were noted and are seen in Fig. 4. These specimens were tested on both the Servo-Hydraulic test stand, and in a Split-Hopkinson Bar apparatus. The test program for the dogbone specimens is outlined in Table 2.

Fig. 4

Sub-size ASTM E8 threaded dogbone specimens. Rough machining visible in jitter marks on the threads of the specimen and the turning marks on the gage length. Photo credit to Ron Hoffman

Table 2 Test Program carried out at the University of Dayton Research Institute including the target strain rates and temperatures, and the number of specimens tested for each strain rate—temperature combination

Low Strain Rate Tension Test Equipment: Servo-Hydraulic Test Stand

An MTS servo-hydraulic station (#5), with a load frame capacity of 89.0 kN equipped with a 44.4 kN actuator is operated at room temperature for tension tests at lower strain rates. Load is measured using a load cell calibrated through 22.2 kN full-scale, and actuator displacement was measured using a linear variable differential transformer. The full-scale for the stroke was 1 inch (25.4 mm) and a slack adapter was used to allow the actuator time to ramp up to speed before applying the test load. A mechanical extensometer (Epsilon Model 3443-0025-100-HT2) calibrated to 5.1 mm (0.2 inches) full-scale with a measuring range of +100 %/−5 % was used to measure strain [26].

The servo-hydraulic test stand was run at two different strain rates: 0.01/s (quasistatic) and 0.5/s (reference). Normally the reference strain rate is 1/s, however limitations on the testing equipment available at UDRI resulted in a lower testing rate.

High Strain Rate Tension Test Equipment: Split-Hopkinson Bar

The Split-Hopkinson Bar (SHB), or Kolsky Bar apparatus in a tension configuration is used to generate appropriately high strain rates for the experiments. A schematic of the set-up is shown in Fig. 5.

Fig. 5

Schematic of Split-Hopkinson Bar experiment. The striker bar impacts the incident bar, sending a stress pulse through the specimen and the transmitter bar. Strain gages record the incident, transmitted, and reflected pulse signals

The assembly consists of a striker bar, an incident bar, a material sample, a transmitter bar, and two strain gages placed on the incident and transmitter bars to collect data. The bars and projectiles are all made of 0.5 inch (12.7 mm) diameter Inconel 718. The strain gages are Constantan foil, type Micro-Measurements type CEA-06-250UW-10C with a gage length of 6.35 mm and a strain limit of ±5 %. They are wired as half-bridge and mounted diametrically to one another, with one on the incident bar and the other on the transmitter bar. The gage factor is 2.130 ± 0.5 %, and the specimen-to-gage distance is 6 feet (1.83m) for each gage. This distance is chosen based on the time needed to measure strain in a specimen, which is determined by the striker bar length. The distance chosen allows strain measurements in the specimen of ≥60 %.

Samples are heated via a Lindbergh Cycle Dyne induction unit, Model A-50 (9.2KVA). The induction coil surrounds the collar with the sample inside. The collar has a hole drilled out to allow the insertion of a thermocouple to monitor the sample temperature. Heating was achieved in ~20 min for the 223 °C samples, ~30 min for the 466 °C samples, and ~20 min for the 707 °C samples. For the 223 and 466 °C samples, the heating rate was held constant until the target temperature was reached, with no holding time. For the 707 °C samples, heating rate was increased while ramping up initially, and then slowed significantly for the final minutes while approaching 707 °C.

Split-Hopkinson Bar set-ups are extremely useful for dynamic, high strain rate experiments and can create strain rates ranging from 100 to 10000/s through the gage length of the material sample [27]. In this experiment, the projectile bar is propelled into an incident bar by a gas gun at velocities ranging from 7 to 19 m/s generating strain rates from 500 to 1800/s. Depending on the particular set-up of SHB used, stress waves generated in the sample can either be compressive or tensile. This study uses a tensile set-up devised by Nicolas in 1981 whereby a collar is placed around the specimen so a compressive wave travels over the specimen and then is reflected back as a tensile wave, breaking the specimen in tension during the reflection [28].

Split-Hopkinson Bar Stress and Strain

The engineering stress and strain of the experiment can be obtained by utilizing elastic wave relations and the stress pulses measured by the strain gages on the incident and transmitter bars [27]. The relevant equations used are:

$$\epsilon _s= \frac{2C_o}{L}\int _{0}^{t} (\epsilon _R)dt$$

(13)

and

$$\sigma _s=\frac{A_H}{A_s} E\epsilon _t$$

(14)

where $\epsilon _s$ is the sample strain, $C_o$ is the elastic wave speed of the striker bar (4968 m/s), L is the starting gage length of the sample (8.89 mm), $\epsilon _R$ is the reflected strain wave, $\sigma _s$ is the sample stress, $A_H$ is the cross-sectional area of the Hopkinson bars (1.27E−7 m³) and $A_s$ is the cross-sectional area of the gage section of the sample. (7.92E−9 m³). The full derivation of these equations can be found in Chen and Song’s work for compression, or Cinnamon’s dissertation for tension [27, 29].

A spectrum of strain rates is needed to demonstrate the effect of strain rate on flow stress. For this specific SHB set-up, 500/s is on the low end of strains that can be generated and 1800/s is on the high end. Similarly, the plastic behavior in a variety of thermal environments needs to be observed. The range of temperatures are room temperature (23 °C) and then $\frac{1}{6}$, $\frac{1}{3}$, and $\frac{1}{2}$ of the melting temperature based on English units. In SI units, they are (223 °C), (466 °C), and (707 °C).

Data Reduction

For brittle materials, it is relatively simple to convert engineering stress and strain to true stress and strain using Eqs. 15 and 16.

$$\sigma _{true}=\sigma _{eng}(1+\epsilon _{eng})$$

(15)

$$\epsilon _{true}=\ln {(1+\epsilon _{eng})}$$

(16)

where $\sigma _{eng}$ and $\epsilon _{eng}$ are engineering stress and strain.

These equations are only reliable until the cross-sectional area begins to shrink during the necking process of failure [30]. This makes Eqs. 15 and 16 ideal for brittle materials which exhibit little to no necking. For ductile materials that exhibit significant necking, the only way to obtain true stress–strain curves is to use Eqs. 17 and 18, which require having continuous measurement of the changing cross-sectional area.

$$\sigma _{true}=\sigma _{eng}\frac{A_o}{A_i}$$

(17)

$$\epsilon _{true}=\ln {\frac{A_o}{A_i}}$$

(18)

where $A_i$ is the current area and $A_o$ is the original starting area.

The changing area can be measured using high speed cameras or digital image correlation. Since our specimens in the Split-Hopkinson Bar device were enclosed in a metal collar during test runs, neither of these options were viable. Sasso has presented an area change approximation method correcting for necking present in high strain rate tension Hopkinson bar experiments [31]. This was applied to the engineering stress and strain to obtain true stress and strain data for the Split-Hopkinson data. The correction used was:

$$\left( \frac{A_0}{A}\right) _{linear} = 4\left( \sqrt{\frac{3(3-\epsilon _{eng})}{1+\epsilon _{eng}}}-1\right) ^{-2}$$

(19)

By approximating the changing area and assuming the radial and tangential stresses are equal due to isotropy, the stress obtained by substituting Eqs. 19 in 17 results in the measurement of average axial stress. It is only the axial stress because it is assumed that the area reduction is constant and does not take any curvature into account. The Bridgman correction factor, seen in Eq. 20, provides a method of estimating the additional contributions from the progressing curvature in the sample as failure is taking place [32].

$$\sigma _{eqv} = \frac{\sigma _{axial}}{(1+2R/a)\ln (a/2R)}$$

(20)

The Bridgman correction factor is regularly used to account for the additional hoop stresses generated from necking. It is a geometry-based measurement which again requires continuous measurement of the necking area dimensions during failure, or straining a sample beyond necking but not to failure to obtain curvature measurements [32] [33]. For steels, there is a popular function that approximates these measurements and it is used in this work [30, 32].

$$B = 0.0684x^3+0.0461x^2-0.205x+0.825$$

(21)

$$\sigma _{B} = B\sigma _{true}$$

(22)

where $x = \log _{10}\epsilon _{true}$ and is true for valid for strain values $0.12\le \epsilon _{true}\le 3$. Correction is not required for strains below 0.12. These corrections will allow an axial curve to represent the overall response of a 3D effect.

Experimental Results

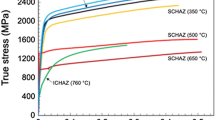
The following figures show the experimental curves obtained from the experiments. Figure 6 shows the averaged quasistatic and 0.5/s data, performed on the MTS servo-hydraulic test stand at room temperature. The results in Figs. 7, 8, and 9 were carried out on the SHB test stand at strain rates ranging from 500/s to 1800/s and temperatures ranging from room temperature to 707 °C. Figure 7 shows the 500/s curves, Fig. 8 shows the 1000/s curves, and Figure 9 shows the 1800/s curves.

Fig. 6

Averaged experimental data for the 0.01/s (quasistatic) and 0.5/s (reference) strain rates

Fig. 7

Averaged experimental data for the 500/s strain rates

In the 500/s experimental data, there is an unusual trend that continues throughout all of the results, where the fracture strain decreases with increasing temperature up until the highest temperature. There is some strain softening that becomes more pronounced with increasing temperature, until the highest temperature where there actually appears to be strain hardening.

Fig. 8

Averaged experimental data for the 1000/s strain rates

The 1000/s results again show unusual failure strain behavior. The increased strain rate reduces the yield strain for the room temperature and 223 °C experiments, and the thermal softening appears to be more pronounced for the 223 and 466 °C curves. The difference in flow stress between the two is decreasing. Conversely, the 707 °C results have a more pronounced increase in flow stress with increasing strain. There is noise in these results particularly. Testing performed on the same test stand after the data collection for this project confirmed this is mostly due to alignment issues.

Fig. 9

Averaged experimental data for the 1800/s strain rates

The 1800/s curves still keep with the same unusual failure strain pattern as with the 500 and 1000/s curves. In general, the thermal data is showing a lot more noise than the previous strain rates. The effects from thermal softening are minimal, and again the 707 °C shows no signs of it. The 223 and 466 °C curves are now overlapping.

Coefficient Determination

Johnson–Cook Strength Coefficient Determination

Determining the Johnson–Cook strength coefficients is a fairly straight-forward process of isolating a portion of the strength equation through normalization, plotting it against the experimental data, and performing a curve fit. The Johnson–Cook strength equation is again stated:

$$\hat{\sigma }_y = (A+B\epsilon _{p}^{n})\left(1+C\ln \frac{\dot{\epsilon _p}}{\dot{\epsilon _o}}\right)(1-T^{*m})$$

(23)

The static stress terms, yield stress (A) and isothermal strain (B and n), are found using data from the averaged 0.5/s strain rate tensile experiments. A is determined by the 0.2 % offset method. First the elastic modulus (E) is determined by calculating the slope of the linear portion of the stress–strain curve, and then the slope is offset by 0.2 %. The intersection of the experimental curve and the 0.2 % offset line is the yield stress of the material. This is shown in Fig. 10. The curve is a typical one for a low-alloy carbon steel, and we are able to determine a yield stress of 673 MPa and an elastic modulus of 160 GPa.

B and n are found by plotting the logarithmic reference 0.5/s plastic stress and strain, isolated using Eqs. 24 and 25 below.

Fig. 10

0.2 % offset fit for treated 4130 using averaged 0.5/s tension data. The calculated Young’s Modulus and yield stress are 160,000 MPa and 673 MPa respectively

$$\sigma _{plastic} = \sigma _{true}-A$$

(24)

$$\epsilon _{plastic}= \epsilon _{true}-\frac{A}{E}$$

(25)

The logarithmic plastic stress is plotted against the logarithmic plastic strain while the curve exhibits hardening. The data is then fit linearly to obtain the slope (n) and the intercept, which is used to find the B coefficient by raising 10 to the power of the intercept. This is shown in Fig. 11. The region of plastic hardening was small, and it was found that this fitting portion was subjective to how much data was included or excluded. B was calculated to be 190 MPa and n, 0.1538.

Fig. 11

Curve fit for Johnson Cook strain rate coefficients B and n of treated 4130 steel. The plastic portion of the quasistatic curve that exhibits strain hardening is isolated and fit linearly. B is 10 raised to the power of the intercept, found here to be 190 MPa, and n is the slope of the line, 0.1538

To continue, a dynamic reference strain ($\epsilon _{ref}$) must be defined. It is used as a reference point for comparing dynamic stress values when calculating C and m. The value is chosen from the reference data, and must be large enough that the stress is in the flow region, but not so large as to be greater than the ultimate tensile strength of the material where failure or necking has begun to occur. In other studies, the value has ranged between 5 and 10 % [3, 20]. For this study, the reference strain is found by plotting the experimental 0.5/s plastic stress–strain curve against the solved $\sigma = (A+B\epsilon _p^n)$ curve. The point when the two curves meet is taken as the reference strain, found to be 4% of the total strain for our data, as seen below in Fig. 12.

Fig. 12

0.5/s average reference stress–strain curve plotted against the solved $\sigma = (A+B\epsilon _p^n)$ curve. The two curves come together between 0.03 and 0.04 of the total strain. The reference strain 0.04 was chosen as it produced the best fitting results

Room temperature 0.01, 0.5, 500, 1000, and 1800/s tensile data is used to calculate the strain rate coefficient C. To isolate the strain rate effects, the flow equation is normalized against the static stress and thermal stresses:

$$\frac{\hat{\sigma }_y }{(A+B\epsilon _{ref}^{n})(1-T^{*m})}=\left(1+C\ln \frac{\dot{\epsilon }_p}{\dot{\epsilon }_o}\right)$$

(26)

Since only room temperature data is used, the thermal term cancels.

$$\frac{\hat{\sigma }_y }{(A+B\epsilon _{p}^{n})}=\left(1+C\ln \frac{\dot{\epsilon }_p}{\dot{\epsilon }_o}\right)$$

(27)

A, B, and n are the constants solved for previously, and here $\epsilon _{ref}$ is the dynamic reference strain 0.04. The $\hat{\sigma }_y$ term is the dynamic stress found from the experimental true stress–strain curve at 0.04 strain.

The normalized stresses for each strain rate are plotted against the natural log of their strain rates producing a plot that can be linearly fitted to obtain the value for C, found to be 0.017. This is shown in Fig. 13.

Fig. 13

Curve fit for the strain rate coefficient Johnson Cook C for treated 4130 steel. The stress at a reference strain (in this study, 0.03) is normalized against the 0.5/s stress and plotted at the natural log of each room temperature strain rate (0.01, 0.5, 500, 1000, and 1800/s). The points are linearly fit, and the slope is the value of C, 0.017

The fit shows good correlation with other Johnson–Cook fits for metals, and indicates that the 4130 steel flow stress does have a response dependence on strain rate [3, 20].

When fitting the for the thermal coefficient, the low strain rate data is excluded (0.01, 0.5/s) as is any room temperature data. The 500, 1000, and 1800/s strain-stress curves for 223, 466, and 707 °C temperatures (approximately 1/6, 1/3, and 1/2 the melting temperature) are all used. As before, the dynamic stress obtained at the reference strain is normalized to isolate the thermal portion of the curve. This is done by dividing the experimental stress at the reference strain by the room temperature stress portions as seen in Eq. 28.

$$\begin{aligned} \frac{\hat{\sigma _y}}{(A+B\epsilon _{p}^{n})(1+C\ln \frac{\dot{\epsilon _p}}{\dot{\epsilon _o}})}=(1-T^{*m}) \end{aligned}$$

(28)

The logarithms of the normalized stress and the homologous temperature are plotted against each other, and the slope of the linear fit of the data represents m as in Fig. 14.

Fig. 14

Curve fitting for the Johnson Cook thermal coefficient m of treated 4130 steel. The stress at the same reference strain is found for each strain rate (500, 1000, 1800/s) and at each temperature (223, 466, 707 °C) and normalized against their respective room temperature counterparts. Then the normalized strains are subtracted from one and plotted against the natural log of the homologous temperature and fit linearly for each of the strain rate resulting in three separate linear fits. Each slope is an m value, and in this study the final chosen value of m is 1.07

Each strain rate is plotted and fitted individually, resulting in a spread of m values. The value of m is chosen based on which one gives the best analytical results when compared to the experimental data.

Damage Coefficients

A similar process is undertaken to calculate the Johnson–Cook damage coefficients. Recall the damage equation:

$$\epsilon _f=[D1+D2 e^{-D3Q}] \left[1+D4 \ln \frac{\dot{\epsilon _p}}{\dot{\epsilon _0}}\right][1+D5T^*]$$

(29)

where $\epsilon _f$ is the equivalent plastic strain at fracture, Q is the stress triaxiality factor, $\epsilon _0$ is the reference strain rate (0.5/s), $\dot{\epsilon }_p$ is the plastic strain rate, $T^*$ is the homologous temperature, and D1–D5 are the damage coefficients.

The first step is calculating the triaxiality-dependent factors D1–D3. The notched specimens’ geometry and failure strains are used to calculate initial triaxiality and coefficient values using an equation developed by Bridgman and used by Hopperstad and Borvik:

$$Q_0 = \frac{1}{3}+\ln {\left(1+\frac{a_0}{2R_0}\right)}$$

(30)

where $a_0$ is radius of the initial cross-sectional area of the notched specimen and $R_0$ is the radius of the specimen notch [34, 36].

The equation uses the same ($\frac{a}{R})$ ratio developed by Bridgman for smooth necking specimens, but here is applied to predict plastic conditions of pre-strained, notched specimens.

Recall, the triaxiality value is always fluctuating throughout deformation. But for a mathematical simplification for the purpose of this coefficient fitting, one can assume that during straining the hydrostatic stress ($\sigma _m$) and equivalent stress ($\hat{\sigma }$) change at the same rate and and the plastic strain is constant across the necking cross section [23, 34]. This creates a constant triaxiality value. In an investigation by Mackenzie et al., it was found that using the initial triaxiality as the constant value results in an under-prediction of stress triaxiality in large notches by as much as 20 % for large a/R ratios, but the difference decreases as the notch size decreases [35]. Thus it is shown to provide a good conservative value for ductility measurement [36].

The initial triaxiality results from Eq. 30 and failure strains of the notched specimens are used to calculate the first coefficients, D1–D3. The failure strains from the tension tests of the notched specimens are plotted against the triaxialities. The curve is fitted in MATLAB using the Levenberg–Marquardt numerical solving method, a standard method for solving non-linear least squares problems.

For those unfamiliar with the algorithm, the Levenberg–Marquardt method fits a set of data points to a parameterized function by minimizing the sum of squares of the errors between the data points and the function [37]. It is one of the most popular optimization method used for solving nonlinear problems, and combines two different solving algorithms: the method of steepest descent and the Gauss–Newton method. The Method of Steepest Descent (or Gradient Descent Method) finds a minimum moving point to point by calculating a slope gradient until the value is within a small amount of error. However, depending on the particular function, this can be a time-consuming process hence the method has a poor rate of convergence. The Gauss–Newton Method assumes the function is locally quadratic, and minimizes the sum of squares errors by finding the minimum of the quadratic. As the errors become smaller, the algorithm switches from behaving like the steepest descent method to the Gauss–Newton method [37]. By combining the two methods, the rate of convergence and the overall fit is improved.

The resulting D1–D3 fit is seen in Fig. 15.The fit looks good, and the coefficient value compares well to other similar metals.

Fig. 15

Curve fit for the Johnson–Cook damage ductile metal failure void coeffieicnts D1, D2, and D3 for treated 4130 steel. The failure strains of the triaxiality specimens are plotted against their calculated triaxiality Eq. 9. These points are fit using the Levenburg–Marquardt algorithm, and found to be −0.1895, 0.7324, and 0.6633

For D4 and D5, the solving process mirrors that of C and m in that a reference point is used, though rather than a dynamic reference strain it is a triaxiality value [20]. This triaxiality is selected from the range of triaxialities used in the notch fitting, and is chosen based on which produces the best fit when compared to the experimental data. In this study it was found to be the largest triaxiality: 1.33. The resulting normalized equations are seen in Eqs. 31 and 32. The fits for D4 and D5 are seen in Figs. 16 and 17.

$$\frac{\epsilon _f}{[D1+D2 e^{-D3Q_{ref}}]}= \left[1+D4 \ln \frac{\dot{\epsilon }_p}{\dot{\epsilon }_0}\right]$$

(31)

$$\frac{\epsilon _f}{[D1+D2 e^{-D3Q_{ref}}] \left[1+D4 \ln \frac{\dot{\epsilon }_p}{\dot{\epsilon }_0}\right]}=[1+D5T^*]$$

(32)

Fig. 16

The failure strains of treated 4130 steel are found at each room temperature strain rate (0.01, 0.5, 500, 1000, 1800/s) and normalized against the triaxiality data at a calibrated reference triaxiality (1.33). These are plotted against the natural log of each of the strain rates and fit linearly. There are three different fits for each of the three triaxialities that are being calibrated. The slope of the line is D4, and the calibrated value is 0.0291

Fig. 17

The failure strains of treated 4130 steel are found at each strain rate (500, 1000, 1800/s) for each temperature (23, 223, 466, 707 °C) and normalized against the triaxiality data at the chosen reference triaxiality. These are plotted against the correlating homologous temperature and fit linearly. As in the thermal m fitting, each strain rate is plotted separately to allow for calibration. The slope of the line is D5, and the calibrated value is 0.7162

Figure 16’s trend is along the lines of what is seen in other documentation, however the slope for the smaller triaxiality values are higher than other metals’ reported values [20]. Figure 17 is a departure from what is expected. While it is not unusual for increasing strain rates to cause earlier fracture strains, typically the increase of temperature would induce more ductile behavior and thus larger fracture strains. The decrease in failure strain with increasing temperature until the final highest temperature is odd. However the value of D5 does fall within other reported values, despite the linear fit not matching the data well.

Results

A finite element model was created in ABAQUS to validate the calculated coefficients. ABAQUS explicit mode is used as opposed to implicit mode. Explicit mode is geared for involved wave mechanics problems, which is ideal for a high strain rate deformation problem. The step time used was 1e−6 s to ensure enough data points were collected to form a smooth curve. Material properties used for modeling can be found in Tables 3 and 4.

The model is an axisymmetric representation of the sub-size E8 dogbone specimen with a clamped boundary condition on one end and a positive displacement boundary condition on the other, resulting in the creation of a tensile stress within the gage section, as seen in Fig. 18. The dimensions match those of the sub-size E8 specimens used, with minor simplifications (omitting the threads and approximating the radius of curvature as a straight line). It is composed of 405 quadrilateral linear axisymmetric elements (CAX4R in ABAQUS notation) with 492 nodes. A predefined temperature field is used to apply the different temperature states. The displacement boundary condition is applied using a tabular amplitude based on target strain rate calculations. Strain rate can be expressed:

$$\dot{\epsilon } = \frac{d\epsilon }{dt}$$

(33)

where a change in strain $d\epsilon$ is occurring over a time step dt. The strain expanded is:

$$\epsilon = \frac{L-L_0}{L_0}$$

(34)

where L is the current length of the gage section and $L_0$ is the original gage length. By substituting Eq. 34 and a time step into Eq. 33, one can solve for a change in displacement in the gage section.

$${L-L_0}=\dot{\epsilon }L_0dt$$

(35)

A tabular time-amplitude table was created By solving the equation for 1000/s for a series of increasing time steps. By adjusting the value of the U2 displacement, one could scale the strain rate to a different strain rate (0.5 = 500/s, 1 = 1000/s, 1.8 = 1800/s).

The experimental and simulation results are plotted against each other in Figs. 19, 20, and 21. Each figure features all temperatures (23, 223, 466, and 707 °C) run at the same strain rate. Figure 19 shows the 500/s curves, Fig. 20 shows the 1000/s curves, and Fig. 21 shows the 1800/s curves. Dashed lines indicate the simulated runs, and solid lines indicate averaged experimental curves.

Fig. 18

ABAQUS Explicit finite element model of an approximated sub-size E8 dogbone specimen in tension subjected to the same temperatures and strain rates the Split Hopkinson Bar specimens experienced

Table 3 Mechanical, elastic, and thermal material properties of 4130 steel used for ABAQUS finite element simulation

Table 4 Summary of Johnson–Cook Strength and damage coefficients calculated for treated 4130 steel

Fig. 19

Stress–strain curve for 500/s impacts at various temperatures. Dashed lines are experimental data, and solid lines are analytically obtained through finite element analysis

The 500/s curves all show good agreement between experimental and simulated flow stresses at all temperatures. The flow stress decreases as the run temperature increases, which matches what is seen in experiments and what is simulated. The simulated failure strains are larger than what occurred experimentally for the 223 and 466 °C runs, but are fairly close to the 23 and 707 °C experimental curves. The simulations does show some thermal softening, which becomes more prominent as the temperature increases.

Fig. 20

Stress–strain curve for 1000/s impacts at various temperatures. Dashed lines are experimental data, and solid lines are analytically obtained through finite element analysis

In the 1000/s curves, the flow stress shows good agreement between simulated and experimental 223, 466, and 707 °C curves, and the 23 °C curve is improves over the 500/s runs. Again the failure strain is over-predicted in simulations for 23 and 707 °C, but is very close to the 23 and 707 °C experimental runs.

Fig. 21

Stress–strain curve for 1800/s impacts at various temperatures. Dashed lines are experimental data, and solid lines are analytically obtained through finite element analysis

The 1800/s flow stresses are spot on for the 23 and 707 °C curves. The noise in the 223 °C curves and the 466 °C curves makes it difficult to differentiate where exactly they land, but the predicted flow stresses do give reasonable predictions. As in the other cases, the failure strain is still over-predicted for the mid-range temperatures, but is a little under-predicted for the 23 °C experimental failure strain, and ever more so for the 707 °C experimental failure strain.

Discussion

The Johnson–Cook constitutive and damage coefficients can be compared to other characterizations for similar materials. Table 5 contains a few materials regularly used in aerodynamic applications that have been characterized.

Table 5 Comparison of Johnson–Cook strength and damage coefficients for various metals

Comparing the strength coefficients, the yield strength A is a bit low, but is expected as per the specifications of the the heat treatment. The strain hardening coefficients B and n are lower than those compared, but match more closely with materials like Tungsten or VascoMax 300 [3, 16]. The strain rate coefficient C matches well with the other materials, which all show little strain rate dependence on flow stress. The thermal coefficient m is on the low side, but is still reasonable.

Comparing the damage coefficients, void formation coefficients D1, D2, and D3 are all within expected ranges. The strain rate coefficient D4 is higher than the other reported materials, indicating a stronger influence of strain rate on the fracture strain. The thermal coefficient D5 is also within the expected ranges, but is suspect since the experimental fitting was not linear.

The values of the coefficients themselves are within the expected ranges. When actually using them in the Johnson–Cook model, it generally gives good results, but it is better at some temperatures (room, 707 °C) than others (223 and 466 °C) for failure strains. Consider Table 6 for a comparison. The flow equation does give good results, though the results at room temperature ares under-predicted.

Table 6 Failure Strains of 4130 steel as measured experimentally and as predicted using the Johnson–Cook failure equation, with calculated percent differences

Note that the first three temperatures, 23, 223, and 466 °C actually show a decrease in failure strain, then it more than doubles at 707 °C. This could be for a number of reasons. Steel is an allotropic material, and at raised temperatures will undergo phase transformations altering its structure and material behavior, notably ductility. The highest temperature run in the experiment, 707 °C, is close to the transformation temperature point of steel (732 °C). The steel may be undergoing a phase change which increases the ductility.

Published thermal properties of 4130 steel seem to support this idea. Right around 700 °C, the specific heat capacity begins to deviate from it’s previously linear trend and starts to spike [40]. Figure 22 shows that right around the highest experimental temperature, the behavior deviates significantly. This most likely explains the sudden uptake in ductility at 707 °C.

Fig. 22

Variation of 4130 specific heat capacity C with temperature. Behavior of $\alpha$ and C begins differing right around 1300 °F, or roughly 700 °C [40]. Where the specific heat capacity suddenly peaks, the thermal diffusivity dramatically dips

To attempt to improve the failure strain predictions, the damage coefficients were calculated a second time excluding the 707 °C data shown in Fig. 23. This changed D5 from 0.7162 to −0.8053. The failure results are compared in Table 7.

Fig. 23

The failure strains of treated 4130 steel are found at each strain rate (500, 1000, 1800/s) for each temperature (23, 223, 466 °C) and normalized against the triaxiality data at the chosen reference triaxiality. These are plotted against the correlating homologous temperature and fit linearly. As in the thermal m fitting, each strain rate is plotted separately to allow for calibration. The slope of the line is D5, and the calibrated value is −0.8503

Table 7 Failure Strains of 4130 steel as measured experimentally and as predicted using the Johnson–Cook failure equation refit with D5 equal to −0.8503, with calculated percent errors

The failure strains are closer to the experimental values and significantly more precise. This solution is only viable for a the 23–466 °C temperature range though, so for AFIT’s modeling efforts where the temperature reaches the melting point, it is less than ideal for use.

There is another curiosity in addition to the non-linear failure strains. At 466 °C the material exhibits high strain rate sensitivity, raising the flow stress almost to the level of the 223 °C curve. This is not seen as dramatically at any other temperature.

Most likely this is a result of atomic interplay between strain rate and thermal factors that the model is not built to take into account. Fundamentally, plastic deformation is caused by atomic movement driven by dislocation shifting in a material’s microstructure. Predicting dislocation movement is acknowledged to be extremely challenging, as there are many different competing factors that may be causing the shifts. Which factor is dominating is dependent on the structural arrangement of the material and the conditions the material is subjected to. However, knowledge of the primary drivers can be critical to forming an accurate model. For example, Couque showed in his research that at strain rates over 1000/s, dislocation movement switched from being thermally activated to viscously activated. He was able to compensate for this in his model and improve his results [41].

Figuring out the dislocation intricacies happening during deformation, while extremely interesting, will be time consuming and may not be the quickest approach for addressing AFIT’s present modeling challenges. If the fracture details are not of interest, the flow model does do a good job and would be acceptable for modeling. However, if the failure of the material is of interest, the damage model does not seem to be a reliable option. This is especially true considering that the material being model at AFIT is at temperatures much higher than the ones run in these experiments and the fracture does not occur in a consistent manner.

The fact that the fracture behavior does not have a consistent trend may mean that the Johnson–Cook model may not be the best choice of a damage criterion for high temperature applications. It may be worth investigating other materials-based damage models for simulation purposes, or doing additional characterization work at higher temperatures to get an improved fit for a larger temperature range. Another idea is to simply modify the Johnson–Cook equation to fit the experimental results for this particular material. This is a common practice, and a published example can be found in Couque’s work [41].

Conclusions

This paper has shown the methodology used in determining the parameters of a plastic strain rate formulation (Johnson–Cook Constitutive and Damage models). Results from the coefficient solving are then used in a finite element model and compared directly against experimental data. The modeled curves are shown to generally have good strength comparison over a large range of strain rates and temperatures, however the results become less accurate at lower temperatures. The damage model over-predicts mid-temperature failure strains and does not track with the non-linear failure strain behavior observed experimentally. The Johnson–Cook damage criterion may need modifications to more accurately predict failure of this particular steel.