Development of an image-based numerical model for predicting the microstructure–property relationship in alumina trihydrate (ATH) filled poly(methyl methacrylate) (PMMA)

Abstract

Particulate composites are found in a wide range of applications. Their heterogeneous microstructure affects their bulk behavior and structural performance, however tools for predicting this important structure-property relationship are still lacking. In this study, a numerical method that can provide predictions of the mechanical response of a particulate polymeric matrix composite as a function of volume fraction and particle mean diameter is presented. The work is derived for an alumina trihydrate filled poly(methyl methacrylate) but the methodology is generic and can be used for any particulate composite. Representative Volume elements are determined through images obtained from scanning electron microscopy. The model takes into account the possibility of failure through interface debonding as well as cracks through the matrix. The model predictions for the modulus and fracture strength of the composites are validated through independent experiments on the composite. The numerical results are also used to qualitatively explain the trends measured regarding the fracture toughness of the composites. Compared to other literature on particulate composites, our study is the first to report accurate stress–strain distributions as well as fracture predictions whilst all the necessary model parameters defining the failure criteria are all derived through independent experiments. This paves the way for a relatively simple methodology for determining structure-property relationships in composites design, enabling smarter material utilization and optimal mechanical properties.

1 Introduction

Particle reinforced polymeric composites appear in a very wide range of applications, e.g. paints, consumer products, automotive parts, explosives and biological systems such as foods. A specific example is the material being investigated in this study, which is alumina trihydrate (ATH) filled poly methyl methacrylate (PMMA) (lightly crosslinked) used in countertop/bench top surfaces with the ATH acting as a flame retardant and smoke suppressant filler to enhance fire safety. At the macro-scale, random arrangements allow such composites to be treated as homogeneous and isotropic. However, at the micro-scale, the heterogeneous structure plays a key role in influencing the mechanical properties of the filled polymers. Understanding how the microstructure impacts the bulk properties is still an active field of research. Specifically, predictive modelling tools for this structure-bulk property relationship are needed such that composite design may be rationalised and made more efficient, replacing costly, trial-and-error experimental approaches.

Well-dispersed non-adhering particles essentially act as a large number of voids and leads to a lower modulus. During the deformation of a polymeric matrix with limited extensibility (e.g. PMMA, which is the matrix used in this study), these voids become cracks and extend to a critical size that causes brittle failure (Lange 1970; Spanoudakis and Young 1984a, b). If particles are well bonded to a brittle matrix, larger strains are required for debonding and the formation of voids (Fu et al. 2008; Hsueh 1989; Young and Beaumont 1977; Zhu et al. 1999). However, research has also indicated that strong adhesion between fillers and matrix may decrease the strength of the resulting composite (Ranade et al. 2006).

For a constant volume fraction, smaller particle size means larger interface, which leads to a higher reinforcement efficiency. However, at high filler volume fractions, the possible agglomeration of smaller particles can lead to non-uniform distributions, and thereby, creating weak regions which cause a decrease in mechanical properties (Dasari et al. 2006; Finnigan 2005).

The effects of the volume fraction on the strength of particle-filled composites have also been investigated (Baptista et al. 2016; Ferreira et al. 1997; Hanumantha-Rao et al. 1998; Wang et al. 2013) with inconclusive results; as the filler content increases, the strength of the composites may increase, decrease or fluctuate. On the other hand, the decrease in particle size can increase the strength as long as the particles are well dispersed (Nakamura et al. 1992; Pukanszky and Vörös 1993; Radford 1971).

At low volume fraction of added particles, a moderate increase in fracture toughness, $G_{IC}$, can be observed as volume fraction increases (Evans et al. 1985; Hussain et al. 1996; Moloney et al. 1984; Spanoudakis and Young 1984a). At high volume fraction ($>40\%$), a further increase in volume fraction could lead to a decrease in $G_{IC}$ values (Gunel and Basaran 2013b; Stapountzi et al. 2009). This was explained by the fact that the particles tend to agglomerate and cause stress concentrations leading to premature failure (Ferreira et al. 1997). In addition, particle size has been reported to affect the $G_{IC}$ of composites. However, the trends with particle size vary widely for different materials (Nakamura et al. 1991; Spanoudakis and Young 1984a; Williams 2010). For example, when the particle radius exceeded 10 $\upmu \hbox {m}$, the addition of larger silica particles in epoxy matrix led to a higher $G_{IC}$ (Nakamura et al. 1991) while increasing particle radius in the case of glass particles led to a decrease in $G_{IC}$ for the same matrix (Spanoudakis and Young 1984a).

In an effort to explain such contradictory experimental observations, a number of modelling studies have been reported. Historically, these are based on analytical models for predicting the deformation properties (e.g. modulus) of the composites. The models are based on the description of the strain field inside and around a rigid particle embedded in an infinite matrix (Eshelby 1957; Hashin and Shtrikman 1963; Mori and Tanaka 1973; Teng 2010) as derived by Eshelby (1957) for linear elasticity. Eshelby’s work provided the basis for several micromechanical models that followed, resulting in the well-known Mori and Tanaka method (Mori and Tanaka 1973), several bounding methods such as the Hashin and Shtrikman (1963), Weng (1992) and Lielens et al. (1998). For a comprehensive review of such models the reader is referred to Stapountzi et al. (2009).

Taking the imperfect interface into consideration, Teng (2010) developed a three-phase model derived from the Mori–Tanaka solution whereas Benveniste (1987) and Nie and Basaran (2005) have used spring elements to model this imperfect interface. Williams (2010) derived an analytical model for the prediction of the debonding process in a particle filled composite based on a unit cell. More recently, Jiang (2016) reviewed several analytical micro-mechanics-based models and proposed a model taking into account matrix cracking and debonding, the latter through a Weibull distribution function for the cumulative probability of particle debonding.

Several studies have used the cohesive zone approach (Xu and Needleman 1993) to model the filler/matrix interfacial behaviour. The latter has been largely facilitated through the large increase in available computational power. Hashemi et al. (2015) used a potential based cohesive model to characterize interfacial debonding in composite materials containing multi-coated particles. Ponnusami et al. (2015) studied the interaction between an approaching crack and a particle as a function of the mismatch in elastic and fracture properties. Cohesive zone models have also been used in the metal matrix composite (MMC) community; for example Charles et al. (2010) studied the competition between interface debonding and particle fracture whereas Qing (2014) studied the influence of particle arrangement and interface strength on the mechanical behaviour of MMCs. Using a multi-particle unit cell model, Basaran and Gunel (2013) and Gunel and Basaran (2013b) studied the influence of interphase properties and interparticle distance on large deformation micromechanics of PMMA/ATH composites. However, the assumptions of the fillers being perfect spheres and equally spaced in all directions, limit the application of this approach to real composites (Tarleton et al. 2013). The majority of the numerical modelling studies have used simulated microstructures or ideal, regular unit cell geometries. However, another implication of the advancement in finite element model simulations and computational power is that real microstructures as measured from microscopic studies may be used instead (Arora et al. 2015; Dastgerdi et al. 2016; Mcwilliams et al. 2013). These lead to more accurate predictions of the mechanical properties (Tarleton et al. 2013).

Though an immense amount of work, as summarised above, is reported in the literature on structure–property relationships for particulate composites, there is still a lack of relatively simple and cost-efficient predictive micromechanical models that can deliver predictions for the mechanical response and in particular the fracture properties of these materials. This work sets out a methodology to achieve this aim. Numerical simulations from previous studies (e.g. Arora et al. 2015; Basaran and Gunel 2013; Gunel and Basaran 2013a) only accounted for composite failure by interface debonding. In this work and for the first time, composite failure by both interface debonding and matrix cracking was incorporated. A real microstructure-based FEA approach for predicting the mechanical behaviour and fracture patterns in ATH filled PMMA composites is presented. The usage of real scanning electron microscopy (SEM) microstructural images in defining the representative volume elements (RVEs) for the modelling study, enables the simulation of agglomeration-induced stress concentrations. The numerical predictions are compared and validated against experimental data measured in this study. Most importantly, the common problem regarding the difficulty of experimental calibration of the associated damage models is addressed through direct experimental identification. The suggested methodology is relatively simple and generic such that it could form a powerful design tool in particulate composite design.

2 Materials and experimental methods

All materials were supplied by E.I. DuPont Nemours & Co. (Inc) (Dupont 2014). Particles with a mean diameter of 15 $\upmu \hbox {m}$ were used for the manufacture of materials denoted here as composites A, C and E at volume fractions of 34.7, 39.4 and 44.4 vol%, respectively. At 39.4 vol%, 8 $\upmu \hbox {m}$ (mean diameter) particles were used in material denoted as B whilst 25 $\upmu \hbox {m}$ (mean diameter) particles were used in material D. A summary of material information and notation is shown in Table 1.

Table 1 Particle size and volume fraction of the ATH/PMMA composites (Dupont 2014)

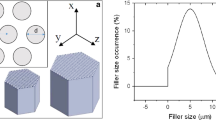
The particle diameters quoted above are mean diameters. Indeed, the ATH fillers used in this work had a wide size distribution. Figure 1 shows the size distribution of the ATH fillers, where clear monomodal distributions are displayed for all three sizes. These data were obtained using laser light diffraction.

Fig. 1

Distribution of particle size in the composite B (average size $=$ 8 $\upmu \hbox {m}$), composites A, C and E (average size $=$ 15 $\upmu \hbox {m}$), and composite D (average size $=$ 25 $\upmu \hbox {m}$) (Dupont 2014)

Tensile tests were performed on unfilled PMMA for determining its elastic modulus and fracture strength. Type M-I (ASTM 1998) ‘bone-shaped’ tensile specimens were provided by the material supplier. The width, gauge length and thickness of each specimen were 10, 50 and 10 mm, respectively. An Instron 3369 system with a 5 kN load cell was used for conducting the tests. The crosshead motion rate was set at 5 mm/min.

Flexural tests and single edge notched bending (SENB) tests were performed to investigate the mechanical properties of the composites. Both tests were performed using an Instron 4466 system (5 kN load cell) and the deflection was measured using digital image correlation (DIC) software DaVis (LaVision 2006). The flexural tests were performed according to ASTM D790M-10 standard (ASTM 2010). The length, width and thickness of the rectangular specimens were 125, 10 and 6 mm, respectively. The loading span was set as 96 mm, while the crosshead motion rate was 2.1 mm/min. The tests were performed up to failure to determine the strength of the composites.

The SENB tests were performed according to ISO 13586 (ISO 2000) on both the composites and unfilled PMMA using the Instron 4466 system with a 5 kN load cell. The dimensions of the SENB specimens were $50\times 10\times 5$ (mm$^{3}$), where 5 mm was the thickness of the samples. A notch of 5 mm in length was cut along the centre of each specimen using a horizontal milling machine. In addition, to avoid the overestimation of the fracture toughness, the tip of each notch was tapped using a new liquid-nitrogen-cooled razor blade to introduce a sharp crack. The loading span was set at 40 mm. The tests were performed at a cross-head motion rate of 1 mm/min, whilst the compliance correction test was performed at 0.1 mm/min.

A Talysurf/Hobson Series 2 machine was used to measure the roughness of the fracture surface of the tested SENB specimens. A stylus was moved vertically to contact the sample surfaces and then moved laterally across the surface for 8 mm at 0.5 mm/s. By measuring the vertical stylus displacement as a function of position, the surface profile was recorded. The arithmetic average of the absolute values of the profile height deviations from the mean line, Ra, and the mean width of the roughness profile elements, RSm, were calculated.

Fig. 2

Typical a SEM image of the polished composite surface and b corresponding RVE

A Hitachi S-3400N scanning electron microscope was used to observe the fracture surfaces near the crack tips of the tested SENB samples. The images were captured using the back scattered electrons (BSE) mode. In addition, fifteen images of the polished surface of each composite were taken using the secondary electron (SE) mode and were processed using ImageJ (Rasband 2016) in order to define the RVEs employed in the numerical simulations (see Sect. 3).

In addition to the experiments outlined above, compact tension tests were also performed in order to characterise the properties of the interface between the ATH particle and the PMMA matrix in accordance of the method proposed by Tan et al. (2005b). Since the same coupling agent was used in all the composites, CT tests were only performed on three replicates of composite C. The tests were performed according to the ISO 13586 standard (ISO 2000) on an Instron 3369 system fitted with a 5 kN load cell, at a crosshead motion rate of 10 mm/min. To ensure the crack propagated along the centre line of each specimen, a shallow side groove (radius $\approx 1\,\hbox {mm}$) was machined on the back surface of the sample; the front surface was left flat so that DIC could be performed. DIC was performed on the images captured using a $\hbox {Phantom}^\circledR$ Miro M/R/LC310 high speed camera at 500 frames per second in order to obtain the strain field around the crack tip. The size of the field of view was 22.4 mm $\times$ 20 mm and the resolution was 448 pixels by 400 pixels. Therefore, the resolution of the images was $0.05 \times 0.05\,\hbox {mm}^{2}/\hbox {pixel}$. According to Vendroux and Knauss (1998), the DIC technique can measure the displacement in the order of 0.005 pixel, which was about 0.25 $\upmu \hbox {m}$ in the present work.

3 Numerical model details

In order to derive predictions of the modulus and strength of the composite as a function of its microstructure, numerical simulations were performed using RVEs derived from the SEM micrographs of the polished composite surfaces. The commercial finite element analysis software Abaqus with the explicit solver (Dassault 2016a) was used for all analyses.

3.1 Model geometry and boundary conditions

Due to the difficulty of generation and the associated high computational cost of 3D FE geometries, 2D plane strain geometries were used in this study. The usage of the 2D geometries was also justified by its proven satisfactory accuracy (Arora et al. 2015) and the low aspect ratio of the fillers (approximately 1.2, see Sect. 4.2).

Using image processing and reconstruction algorithms developed by Tarleton et al. (2012), the SEM images of the polished composite surfaces were converted into 2D geometries. Once a particle was approximated as a polygon, the particle/matrix interfacial region is produced by offsetting the boundary a small distance inwards. The interfacial region is then assigned as a single layer of cohesive elements.

A typical example of the SEM image conversion to the RVE modelled in FEA is shown in Fig. 2. For each composite, fifteen SEM images taken from random positions on the sample were reconstructed into RVEs. The reconstructed 2-dimensional RVEs were rectangular. Three different RVE sizes, i.e. horizontal $\times$ vertical: $120 \, \upmu \hbox {m} \times 90 \,\upmu \hbox {m},\, 200 \, \upmu \hbox {m} \times 150 \, \upmu \hbox {m}$ and $300 \, \upmu \hbox {m} \times 225 \, \upmu \hbox {m}$, were compared for studying the effect of the RVE size on the predictions. In addition, the mesh dependence of the FE prediction was investigated by using three different mesh sizes (0.75, 1.5 and 3 $\upmu \hbox {m}$). For the FE prediction to be comparable with the experimental results, plane strain was assumed. Therefore, the matrix and filler were meshed using 4-node bilinear elements CPE4R (reduced integration with hourglass control), whilst the interface was meshed using cohesive elements COH2D4.

A simple uniaxial tensile deformation was applied as the boundary condition despite flexural tests being performed to experimentally investigate the modulus and strength of the ATH/PMMA composites. During bending of a sample, zero stress prevails at the neutral axis whereas tensile and compressive stresses build up at either side of the neutral axis. Once the material fails, the corresponding load is taken for calculation of the flexural strength. Since the material fails in the portion under tension, the flexural strength should be theoretically the same as the tensile strength. However, in reality there are defects present in the specimens. In the tensile test, the defects affect the strength uniformly, whilst in flexure, defects near the top or the bottom surfaces will have a larger effect than the same type of defects located near or on the neutral axis. Therefore, the value of the flexural strength is approximately 1.5–2.1 times higher than that of the tensile strength (Sahagian and Proussevitch 1998). The effects of the defects are not simulated directly in the FE simulation, which means the strength prediction obtained using tensile and flexural boundary conditions would be the same. Therefore, a tensile boundary condition in the form of a 5% deformation on the top surface was applied to each RVE in the vertical direction (Fig. 2). The bottom surface was constrained in the vertical direction with one node on the bottom left corner constrained in both directions. The two side edges were left free which according to Arora et al. 2015) gives results which are as accurate as periodic boundary conditions. Also it is worth noting that periodic boundary conditions are applicable for repeatable RVEs, while the present RVEs of the composites are random and not repeatable.

3.2 Damage models and material definition

Both the constituents were treated as linear elastic isotropic materials. Note that the structure of ATH particles is graphitic in nature, so modelling the correct anisotropy would increase the complexity significantly. In addition, the orientation of the graphitic planes of each particle embedded in the composite is unknown and modelling such effects would be computationally prohibitive. It is therefore assumed here that failure in the composites is primarily due to interface debonding and matrix cracking; this led to the simplifying assumption that the filler is an isotropic, elastic material with no need to model inter-particle fracture. The elastic properties of the matrix and filler were taken from the experiments described in Sect. 2 or from literature (also summarised later in Table 3).

Debonding along the filler/matrix interface is one of the main failure mechanisms of composites. A bilinear traction separation law was used for simulating the interfacial debonding through the cohesive elements placed along the boundaries of the particles (Dassault-Systèmes 2016b). After the onset of damage, the cohesive elements soften and fail, at which point their stiffness is degraded to zero. The determination of the interfacial properties, i.e. interfacial linear stiffness, interfacial cohesive strength and interfacial cohesive fracture energy are presented in Sect. 4.5. The same cohesive zone properties were assumed for mode I and mode II whereas the mixed mode failure locus was taken to be linear.

In addition to the debonding failure mode at the particle-matrix interface, the numerical simulations accounted for possible fracture propagating in the matrix. PMMA fails by crazing (Döll 1983; Saad-Gouider et al. 2006) and its failure mechanism can be determined from inverse analysis (Elices et al. 2002) or crack tip field analysis (Réthoré and Estevez 2013). However, a brittle cracking model was used for simulating this matrix failure in the current study. This is mainly because in particle-filled composites, the toughening effects of the fillers prevent crazing of the polymer matrix (Chee et al. 2012). Meanwhile, as shown by Nie et al. (2006), the failure of ATH/PMMA composites is initiated by the debonding between filler/matrix and the damage of the PMMA matrix is caused by the growth of the cavity, which happens so fast that crazing cannot be observed. In addition, to simulate the crazing of PMMA, cohesive elements need to be used over the entire RVE (Tijssens et al. 2000), which may complicate the model significantly and increase the computational cost. Therefore, in this study, crack initiation is detected using a simple Rankine criterion, which means that a crack is formed when the principal tensile stress reaches the crack initiation stress of the brittle material. Once the criterion has been met, a first crack is assumed to have formed. The crack growth direction is controlled using a fixed, orthogonal model, which means the crack grows in a direction normal to the direction of maximum tensile principal stress at the time of crack initiation. Little experimental data of the crack initiation stress of PMMA is available. Therefore, a theoretical value, $E_m /10$, is first assumed. However, this value is related to the cohesive forces between atoms (Lawn 1993), which means that for brittle solid such as the PMMA matrix studied here, the value $E_m /10$ may lead to overestimation of the composite strength. Therefore, lower values of the crack initiation stress, i.e. $E_m /20, E_m /30{\ldots }$, are also used in a parametric study in order to investigate the influence of this value on the model’s predictions. Note that these values will be later compared to the failure strength of PMMA.

To simulate the post-crack behaviour of the brittle PMMA matrix, both the tensile (Mode I) and the shear (Mode II) softening behaviours are considered. In Mode I, the post-crack tensile behaviour is illustrated in Fig. 3, where the area under the linear softening relationship is equal to the fracture toughness, $G_{IC}$, of PMMA. The latter was determined through the SENB tests described above.

Fig. 3

Mode I softening behaviour for the brittle cracking model

For the effect on the Mode II fracture, a shear retention model was used, in which the post-crack shear modulus, $\mu _m^{cr}$ is defined as a function of the crack opening displacement:

$$\begin{aligned} \mu _m^{cr} =\rho \mu _m \end{aligned}$$

(1)

where $\mu _m$ is the shear modulus of the uncracked matrix and $\rho$ is the traditional shear retention factor dependent on the normal strain across the crack, $e^{cr}$. This dependence is modelled by a power law form (Dassault 2016c):

$$\begin{aligned} \rho =\left( {1-\frac{e^{cr}}{e_{max}^{cr} }} \right) ^{P} \end{aligned}$$

(2)

where p and $e_{max}^{cr}$ are material parameters.

For simplicity the value of p was chosen as 1, whereas $e_{max}^{cr}$ was set to 1%. The latter is the typical failure strain of PMMA (Kaplan 1999).

4 Experimental results

4.1 Experimental results for PMMA matrix

The modulus and strength of unfilled PMMA matrix is measured as $3.02\pm 0.03 \, \hbox {GPa}$ and $76\pm 3\, \hbox {MPa}$, respectively. The fracture energy of unfilled PMMA obtained using SENB tests is $395.1\pm 27.1 \, \hbox {N/m}$. The results agree with reported data in literature (Kaplan 1999) and were used as input in the numerical simulations.

4.2 SEM microstructures of composites

The SEM images of the polished surfaces are shown in Fig. 4. It can be seen that the ATH particles were well dispersed in the PMMA. The images were converted into binary images and the particle analysis function of ImageJ (Rasband 2016) was used to obtain the particle volume fraction. According to Stapountzi et al. (2009), who tested samples from the same manufacturer using laser light scattering, the aspect ratio of the particles is approximately 1.2. Sahagian (Sahagian and Proussevitch 1998) indicates that if the aspect ratio of the particles is close to unity, the 2-D area fraction of fillers can be assumed to be equal to the 3-D volume fraction. The derived volume fraction results were very repeatable for each composite, as shown in Table 2. The standard deviations obtained from analysing five images were in the order of 2%–3%. The mean values correlated very well with the values obtained from the manufacturer (compare Table 1 and Table 2). The volume weighted mean D[4,3] of the particles was also determined independently using Laser Light Scattering in order to confirm the manufacturer data. The results are also shown in Table 2.

Fig. 4

SEM images ($\times 300$) of polished surfaces of ATH/PMMA composite at mean particle size and filler volume fraction of a 15 $\upmu \hbox {m}$, 34.7%, b 8 $\upmu \hbox {m}$, 39.4%, c 15 $\upmu \hbox {m}$, 39.4%, d 25 $\upmu \hbox {m}$, 39.4% and e 15 $\upmu \hbox {m}$, 44.4%

4.3 Composite flexural test results

Five specimens were tested for each composite. The experimental results are reported in Table 2; note that the moduli and the strength data will also be plotted together with the model predictions to enable comparisons in Sect. 6. A 39% increase in Young’s modulus is shown in Table 2 for the same particle size when the volume fraction increases from 34.7 to 44.4% (composites A and E). This implies that the two constituents were strongly bonded together. As the particle size increases from 8 to $15 \,\upmu \hbox {m}$ for the same volume fraction (composites B and C), the modulus shows a 1.3% increase, while a further increase from 15 to $25\, \upmu \hbox {m}$ leads to a 2.6% increase (composites C and D). The difference is not large enough to conclude an influence of particle size on the composite’s modulus. The latter is in agreement with other observations in the literature (Fu et al. 2008; Stapountzi et al. 2009).

Table 2 Modulus and strength of the ATH/PMMA composites obtained using flexural tests

Fig. 5

Effect of filler volume fraction on the fracture toughness of ATH/PMMA composites

In Table 2, the flexural strength of the composites is shown to initially decrease as the filler loading increases (composites A, C and E). The decrease is less than 8%, which is not statistically high enough to point to an effect of filler volume fraction on strength. This may be caused by the balance between the strengthening effect of the rigid particles acting as barriers to crack growth and the weakening effect of particle agglomerations.

On the other hand, the flexural strength of the composites decreased as the mean particle diameter increased (composites, B, C and D) with values of 82.4–66.4 MPa for 8–25 $\upmu \hbox {m}$ respectively. This can be explained by the larger particle/matrix interface area of the smaller particles for a given volume fraction, which can transfer the stress from the matrix into the fillers more efficiently.

Fig. 6

Effect of mean particle diameter on the fracture toughness of ATH/PMMA composites

4.4 Fracture toughness of the composites

Figure 5 shows the effect of filler content on the values of $K_{IC}$ and $G_{IC}$ of ATH/PMMA composites. It can be seen that the value of $G_{IC}$ decreased as the volume fraction increased, while the value of $K_{IC}$ remained constant. The addition of rigid particles may cause an increase in $K_{IC}$ values of polymers, because as the particles are pinned in the matrix, higher loads are required for the cracks to grow within the material. However, due to the high filler content used in this work, an increase in the volume fraction can cause particle agglomeration and hence, induce stress concentrations, which can initiate and extend cracks until the critical crack size is reached and the material fails. Therefore, the balance between the toughening effects of the rigid particles and the weakening effects of the particle agglomeration could be the main reason of the constant $K_{IC}$ values as the filler content varies.

On the other hand, the $G_{IC}$ values decrease as the volume fraction increases. This decrease could be caused by the restraining effects of the rigid particles on the polymeric matrix, i.e. the deformation of the matrix around the crack tip is more limited as filler content increases and therefore less energy can be absorbed during crack propagation. In addition, the decrease in the $G_{IC}$ values can be explained by the following calculation. Using the simple rule of mixtures, the Poisson’s ratio of the composite, $v_c$, is:

$$\begin{aligned} v_c =\phi _f v_f +\phi _m v_m \end{aligned}$$

(3)

where the Poison’s ratio of the ATH particle and PMMA are $v_f =0.24$ and $v_m =0.38$, respectively (Stapountzi et al. 2009) and $\phi _f,\phi _m$ are the volume fractions of the filler and the matrix respectively. As the volume fraction increased from 34.7 to 44.4 vol%, the values of $K_{IC}$ stayed constant, and the change in Poisson’s ratio is around 4% (0.289–0.302) (Eq. 3). Therefore, according to the relationship between $K_{IC}$ and $G_{IC}$:

$$\begin{aligned} G_{IC} =\frac{\left( {1-v^{2} } \right) }{E}K_{IC} \end{aligned}$$

(4)

as the volume fraction increased, the increase in elastic modulus led to a decrease in the values of $G_{IC}$.

The effect of particle diameter on $K_{IC}$ and $G_{IC}$ values of ATH/PMMA composites is shown in Fig. 6. With increasing particle diameter, both $K_{IC}$ and $G_{IC}$ values display increasing trends. It is suggested here that this phenomenon is due to the higher probability of particle agglomeration taking place for the smaller particles at the high volume fractions studied hence leading to lower $K_{IC}$ and $G_{IC}$ values.

Nakamura et al. (1991) suggested that in brittle polymers filled with small particles, the crack tip is sharp but slightly deflected by the particles. However, in composites filled with big particles, the crack tip is blunt and extensively deflected by the particles, which means greater energy is required for crack initiation in bigger particle filled polymers. This argument is supported from the fracture surface SEM observations shown in Fig. 7 and the fracture surface roughness measurements (see Fig. 8). As shown in Fig. 7, similar fracture surfaces were observed in composites with different filler content (Fig. 7a, c, e), whilst the fracture surface became rougher as the particle size increased (Fig. 7b–d). This agrees with the roughness measurements in Fig. 8, in which the Ra and RSm values seem to be independent of the volume fraction but increased with increasing particle diameter.

Fig. 7

SEM images ($\times 1000$, BSE mode) of fracture surfaces of ATH/PMMA composite at mean particle size and filler volume fraction of a 15 $\upmu \hbox {m}$, 34.7%, b 8 $\upmu \hbox {m}$, 39.4%, c 15 $\upmu \hbox {m}$, 39.4%, d 25 $\upmu \hbox {m}$, 39.4% and e 15 $\upmu \hbox {m}$, 44.4%

Fig. 8

The roughness of the SENB fracture surface as function of a volume fraction and b particle diameter

4.5 Experimental determination of interfacial properties for the CZM law

The parameters needed in the cohesive zone model have been determined experimentally using the methodology outlined in Tan et al.’s work (Tan et al. 2005b). For the definition of the interface behaviour in the numerical simulation, the initial linear stiffness of the interface, $k_\sigma$, the cohesive strength, $\sigma _{max}^{int}$ and the cohesive fracture energy release rate, $\gamma _{int}$, need to be determined. Using the DIC technique, the displacement and stress around a macroscopic crack tip were obtained. An extended Mori–Tanaka method (which takes into consideration the effect of interface debonding) and the equivalence of cohesive energy on the macroscopic and microscopic scale were used to link the macroscale compact tension experiment to the microscale cohesive law for particle/matrix interfaces (Tan et al. 2005a, b). Firstly Eqs. (5) and (6) below enable the calculation of the value of $k_\sigma$:

$$\begin{aligned} K_c= & {} \frac{1}{\frac{1}{K_m }+\frac{9\left( {1-v_m } \right) }{2E_m }\frac{f-\sum \phi _{fN} \alpha _N }{1-f+\sum \phi _{fN} \alpha _N }} \end{aligned}$$

(5)

$$\begin{aligned} \alpha _N= & {} \frac{3\left( {1-v_m } \right) }{2E_m \left( {\frac{1}{k_\sigma R_{fN} }+\frac{1}{3K_P }+\frac{1}{4\upmu _m }} \right) } \end{aligned}$$

(6)

where $K_c =E_c /\left[ {3\left( {1-2v_c } \right) } \right]$ is the bulk modulus of the composite, $K_m$ is the bulk modulus of the matrix, $K_P$ is the bulk modulus of the particle and $\alpha _N$ is the ratio of the average stress in the particles of radius $R_{fN}$, $\sigma _{fN}$, to the average stress in the matrix, $\sigma _m$. With the mechanical properties obtained from experiments and literature (see Sects. 4.1 and 4.3), the value of $\sum \phi _{fN} \alpha _N$ can be calculated as 0.5 using Eq. 5. The value of $k_\sigma$ is then calculated using the corresponding values of $R_{fN}$ and $\phi _{fN}$ obtained from the particle size distribution in Fig. 1. The linear modulus of the interface was therefore found to be $k_\sigma =3.61\,\hbox {GPa}/\upmu \hbox {m}$. However, it is known that there is no significant effect of $k_\sigma$ on the results as long as it is large enough to avoid introducing artificial compliance to the system, nor too high such that it causes numerical convergence problems (Arora et al. 2015).

Fig. 9

Horizontal (u-), vertical (v-) and normal strain perpendicular to the fracture plane ($\varepsilon _{yy})$ measured using DIC with the raw image as the background at the point of crack initiation

Figure 9 shows the horizontal (u-), vertical (v-) and normal strain perpendicular to the fracture plane ($\varepsilon _{yy} )$ measured using DIC with the raw image as the background at the point of crack initiation. From the macroscopic strain field around the crack tip (see Fig. 9c), the macroscopic cohesive law of the ATH/PMMA composite (Fig. 10) was obtained by plotting the cohesive stress (i.e. the value of $E_c \varepsilon _{yy}$ as close to the crack tip as possible, see position indicated by a red ‘X’ mark in Fig. 9) against the crack opening width (i.e. the difference between the v- displacements just above and under the fracture plane at the crack tip). As shown in Fig. 10, the macroscopic cohesive strength is 54.5 MPa, whilst the critical crack opening width is 0.015 mm. These values give a macroscopic cohesive energy of $\sim$ 410 N/m which agrees with the fracture energy of composite C obtained using SENB tests ($\sim$ 400 N/m, see Fig. 5b).

Using the calculated value of $\sum \phi _{fN} \alpha _N$ as 0.5, the value of the macroscopic cohesive stress, $\sigma$, is given by (Tan et al. 2005b):

$$\begin{aligned} \sigma= & {} \left( {1-\phi _f } \right) \sigma _m +\sum \phi _{fN} \sigma _{fN} \nonumber \\= & {} \left[ {\left( {1-\phi _f } \right) +\sum \phi _{fN} \alpha _N } \right] \sigma _m =1.1\sigma _m \end{aligned}$$

(7)

Therefore, the value of $\sigma _m$ is 49.6 MPa, so the value of $\sigma _{fN}$ can be calculated from:

$$\begin{aligned} \sigma _{fN} =\alpha _N \sigma _m \end{aligned}$$

(8)

According to Tan et al. (2005b), the normal traction stress on the interface equals the value of $\sigma _{fN}$. Since the relatively bigger particles debond first (Jung et al. 2000) and the values of $\alpha _N$ converge to the value $\alpha _N \approx 2.4$ at large particle diameter (see Fig. 11), the interface cohesive strength, $\sigma _{max}^{int}$, is calculated from Eq. (8) at 119 MPa.

Table 3 A summary of the material properties used as input in the numerical simulations

Fig. 10

Cohesive law of the PMMA/ATH composite obtained using DIC

Fig. 11

The effect of particle diameter on the value of $\alpha _N$

During the crack process, the total cohesive energy, $U_{coh}$, is given by:

$$\begin{aligned} U_{coh} =\mathop \int \limits _0^{\delta _c^{cr} } \sigma \; d\delta ^{cr} \cdot A \end{aligned}$$

(9)

where $\delta _c^{cr}$ is the critical crack opening width and A is the area of the crack surface. The value of $U_{coh}$ is found from the area under the cohesive law shown in Fig. 10. It can also be expressed as:

$$\begin{aligned} U_{coh}= & {} U_{interface} +U_{matrix}\nonumber \\ U_{interface}= & {} \gamma _{int} A_{interface}\nonumber \\ U_{matrix}= & {} \gamma _m A_{matrix} \end{aligned}$$

(10)

where $\gamma _{int}$ and $\gamma _m$ are the energy per unit area consumed during the interface debonding and matrix fracture (395.1 N/m from SENB tests, see Sect. 4.1) respectively. $A_{interface}$ is the area of the particle/matrix interface, $A_{matrix}$ is the area of the torn matrix calculated from:

$$\begin{aligned}&\frac{A_{interface} }{A}\approx \phi _f\nonumber \\&\quad \frac{A_{matrix} }{A}=1-\phi _f \end{aligned}$$

(11)

Combining Eqs. 9, 10 and 11, the value of $\gamma _{int}$ is finally calculated as $\sim$ 430 N/m. As calculated above, the interface cohesive strength is 119 MPa, which gives a critical interface opening of approximately 7 $\upmu \hbox {m}$. Note that the critical opening here is defined as the crack opening when the interface stress drops to zero. The debonding process should have already started before this critical opening is reached and in fact starts at approximately 0.03 $\upmu \hbox {m}$ (using the initial stiffness of 3.61 $\hbox {GPa}/\upmu \hbox {m}$).

Even though the CZM parameters obtained above seemed reasonable in terms of magnitude, the accuracy of the DIC-obtained strain field around the crack tip may be limited due to the tiny crack opening in brittle materials such as for the composites studied here (Roux and Hild 2006). Therefore, a further check on the accuracy was performed by using an analytical model by Williams (Stapountzi et al. 2011; Williams 2010). The latter provides estimates for the fracture toughness of particle reinforced composites as a function of volume fraction. The model assumes a value for the interface strength, $\sigma _{max}^{int}$. In this study, it was used in an inverse fashion, i.e. the latter value was determined by fitting the model to the experimentally derived fracture toughness—volume fraction data (i.e. data from composites A, C and E). The model calculations are outlined in the Appendix and the interfacial strength was estimated at approximately 200 MPa. This is the same order of magnitude as the value of 119 MPa obtained using the method by Tan et al. (2005b). Williams’s model assumes the composites are only toughened by the debonding of the particles, whilst in reality, there are other toughening mechanisms including crack pinning, deflection and blunting. The results indicate that the interfacial strength obtained using Tan et al.’s method (Tan et al. 2005b) is a reasonable estimation.

Fig. 12

RVE size study for determining the effect of RVE size on the FE prediction

Fig. 13

The effect of mesh size on the predicted stress–strain response (composite D: 25 $\upmu \hbox {m}$, 39.4 vol%)

Fig. 14

Crack path obtained using FE simulations with different mesh density (composite D: 25 $\upmu \hbox {m}$, 39.4 vol%)

Fig. 15

Elastic modulus of ATH/PMMA composites as function of a filler volume fraction and b particle diameter: comparison of the experimental data and the FE prediction

5 Results from the numerical simulations

This section presents the results from the numerical simulations of the RVEs being subjected to tensile deformations. The predictions are compared to the experimentally derived values of modulus and fracture strength as a function of volume fraction and particle size. The material property parameters used in the simulations are summarised in Table 3.

5.1 Effect of the RVE size

The model predictions obtained corresponding to the three RVE sizes showed that the modulus and strength were in agreement (within 6 and 3% respectively). Despite a small effect on the global load-displacement response, the change in RVE size was found to affect the crack path (see Fig. 12). The application of a bigger RVE size may provide a crack path in higher compliance with the actual situation. Therefore, the RVE size of $200 \,\upmu \hbox {m} \times 120\,\upmu \hbox {m}$ was selected for further study.

5.2 Mesh dependence study

Figure 13 shows the effect of the mesh density on the stress–strain curves obtained using the FE simulation. The numerically predicted values for elastic modulus and fracture strength are not affected by the mesh size. However, it is shown that the mesh density affects the post-crack behaviour of the composite. This indicates a mesh dependency of the post-crack FE prediction, however it is small. The mesh dependency was also observed in the predicted crack path (see Fig. 14). In a more finely meshed RVE, micro-cracks existed besides the main crack, which could be more realistic (Tarleton et al. 2012). Therefore, despite the higher computational cost, a finer mesh ($\hbox {mesh size }= 0.75 \, \upmu \hbox {m}$) was selected for subsequent investigations.

5.3 Elastic modulus of the composites

As a validation of the microstructural image based modelling technique, the elastic modulus obtained from the FE models and the experiments are compared. The results are also compared to the micromechanical model by Lielens for extra verification (Lielens et al. 1998).

Figure 15 shows the modulus obtained from the model along with the experimental data as function of volume fraction and particle diameter, respectively. It is seen that the FE prediction is lower than the experimental data. This divergence was expected since the particles with diameter less than $1~\upmu \hbox {m}$ were ignored during the SEM image-RVE conversion to enable a reasonable mesh density. Indeed, the volume fraction of the RVEs obtained using ImageJ (Rasband 2016), was around 2–3 vol% lower than the actual volume fraction due to the finer particles being lost during the SEM image-RVE conversion.

Fig. 16

FE prediction of the elastic modulus of ATH/PMMA composites as a function of the actual RVE volume fraction; comparison with the Lielens et al. (1998) micromechanical prediction

Fig. 17

Elastic Strength of ATH/PMMA composites as function of a filler volume fraction and b mean particle diameter: comparison of the experimental data and the FE prediction

The micromechanical Lielens model (Lielens et al. 1998) was next employed to provide a comparison with the experimental and numerical predictions. The numerical predictions for the composite’s modulus are plotted against the actual RVE volume fraction and compared with the Lielens predictions in Fig. 16 as well as with the experimental data. It is now observed that the numerical and analytical Lielens predictions are both very close to the experimental data. The omission of the finer particles in the models is not thought to be adversely affecting the accuracy of the predictions for fracture strength as debonding of the larger particles occurs first and therefore limits critically the composite’s strength (Jung et al. 2000).

5.4 Elastic strength and fracture toughness of the composites

Figure 17 shows the FE predictions of the elastic strength as functions of the filler volume fraction and the mean particle diameter. Encouragingly, the numerical trend agrees extremely well with the experimentally observed trend. In both cases, however, when the value $E_m /10$ is used as the crack initiation stress, significant overestimation of the strength is observed in each of the two plots, while the value $E_m /20$ seems to be a more appropriate choice. Only flexural tests were performed in the present work due to a limitation in the material supply. As already mentioned, the value of the flexural strength is approximately 1.5–2.1 times higher than that of the tensile strength (Wypych 2016). In fact, specifically for PMMA/ATH composites, Nie et al. (2006) performed flexural and tensile tests and the strength obtained from these tests were 76 and 48 MPa, respectively. Therefore, $E_m /30$ may be better choice when predicting the tensile strength. Using a value of $E_m =3.02$ GPa (see Sect. 4.1), $E_m /30$ is equal to approximately 100 MPa which is comparable to the cohesive stress of PMMA (100 MPa according to (Döll 1983; Döll and Könczöl 1990)). Therefore it is concluded that using the failure strength of the polymer as the crack initiation stress is appropriate. It is also worth noting here that for this 100 MPa strength and the $G_{ICm}$ of 395.1 $\hbox {J/m}^{2}$, a value of approximately 8 $\upmu \hbox {m}$ is calculated as the critical opening displacement (the value of the crack opening at zero post-crack stress in Fig. 3).

Fig. 18

Maximum principal stress and maximum principle strain distribution contours at a strain of 1.5% of a composite A: 15 $\upmu \hbox {m}$, 34.7 vol%, b composite B: 8 $\upmu \hbox {m}$, 39.4 vol%, c composite C: 15 $\upmu \hbox {m}$, 39.4 vol%, d composite D: 25 $\upmu \hbox {m}$, 39.4 vol% and e composite E: 15 $\upmu \hbox {m}$, 44.4 vol%

Fig. 19

Particle debonding at strain of 1.5% in a composite A: 15 $\upmu \hbox {m}$, 34.7 vol%, b composite B: 8 $\upmu \hbox {m}$, 39.4 vol%, c composite C: 15  $\upmu \hbox {m}$, 39.4 vol%, d composite D: 25 $\upmu \hbox {m}$, 39.4 vol% and e composite E: 15 $\upmu \hbox {m}$, 44.4 vol%

From the output stress contours shown in Fig. 18, the stress inside the particles was found to be higher than the stress distributed in the matrix. In addition, the bigger the particle, the higher the stress the particle is bearing. Therefore, the failure of the composites generally starts with the debonding of the relatively big particles, which may also be observed more clearly when the stress degradation factor (SDEG)contours are plotted in Fig. 19; SDEG values of 1 signify fully debonded regions (red contour) and values of SDEG $=$ 0 show undamaged surfaces (blue contours). Therefore, the small effect of the volume fraction on the elastic strength shown in Fig. 17a can be explained by the similar particle size distribution in composites A, C and E (see Fig. 1). It is also worth noting here that even though the stress in the particles is higher than the matrix, its magnitude is only about 300 MPa. This is smaller than the typical strength of engineering ceramics. Therefore, the assumption that there is no failure in the particles is in fact justified by the numerical results.

The composite strength is negatively correlated to the mean particle diameter (see Fig. 17b). This may be explained by the larger particle/matrix interface area of the smaller particles for a given volume fraction, which can transfer the stress from the matrix into the fillers more efficiently. However, according to the stress distribution in composites with different mean particle diameters (Fig. 18), the stress is more uniformly distributed in the composite filled with smaller particles due to its narrower particle size distribution (see Fig. 1). In other words, in composites filled with relatively big particles (with a wider particle size distribution), the stress is concentrated in the big particles and causes earlier debonding (see Fig. 19d), hence a lower composite strength. Therefore, despite the seemingly negative correlation between the mean particle diameter and the strength of the composites, the change in particle diameter may not necessarily be the main factor affecting the strength. The particle size distribution also plays a role on the stress concentrations observed.

Fig. 20

An example of crack initiation due to matrix failure; this is caused by particle agglomeration and associated stress concentration

The numerical simulations can also be used to further support the arguments made in Sect. 4.4 regarding the effect of the particle size on the fracture toughness of the composites. In some of the FE simulations, it was observed that the crack was initiated by agglomeration-induced matrix failure which was then followed by particle debonding. An example is shown in Fig. 20. For the fifteen simulations performed per composite, the frequency of this type of failure occurring in composite B (mean diameter of $8 \upmu \hbox {m}$) was 8 times (rate of 8/15). This was higher than the occurrence of this type of failure in that observed in composite C (mean diameter $15 \, \upmu \hbox {m}$) which was 4/15, whereas composite D with the largest mean diameter of 25 mm showed the lowest number of such failures with only 2/15. This may indicate a higher agglomeration degree for the smaller mean particle diameter as expected and could explain the lower fracture toughness observed in Fig. 6 at the smaller particle diameters. However, further work is required to confirm this theory statistically, using a larger number of separate simulations for each composite. Furthermore, from the FE predictions of the crack path, it can be seen that the growth can be blocked/deflected by the relatively big particles (red circles in Fig. 21), which then led to the higher values of $K_{IC}$ and $G_{IC}$ values with increasing particle diameter.

Fig. 21

Crack path in a composite A: 15 $\upmu \hbox {m}$, 34.7 vol%, b composite B: 8 $\upmu \hbox {m}$, 39.4 vol%, c composite C: 15 $\upmu \hbox {m}$, 39.4 vol%, d composite D: 25 $\upmu \hbox {m}$, 39.4 vol% and e composite E: 15 $\upmu \hbox {m}$, 44.4 vol%

Finally, determining a methodology such that the values of $K_{IC}$ and $G_{IC}$ can also be predicted through the numerical method, in addition to the modulus and strength of the composite, is a current aim and work is underway towards achieving this.

6 Conclusions

A combined experimental-numerical study was conducted in order to highlight the effect of the microstructure on the global response of ATH/PMMA particulate composites. The interface behaviour is characterised via a cohesive traction-separation model while the damage of the matrix is defined using a brittle cracking model. The parameters used in the FE simulation were obtained through appropriate experiments. The comparison between the experimental results and FE predictions indicates that the SEM image-converted RVE FE model can provide accurate predictions of the elastic modulus as well as the failure strength of particle filled composite. For the failure strength, the numerical trends with particle diameter and volume fraction were extremely close to the trends observed experimentally, giving confidence in the developed models. The fracture strength of the composites increased with decreasing particle size. This was caused by the more uniformly distributed stress due to the narrower particle size distribution of the composites filled with smaller particles. In addition, the effect of filler content on the composite strength is insignificant due to the similar filler size distribution. For the fracture toughness, it was shown that increasing particle size led to higher $K_{IC}$ and $G_{IC}$ values due to the blocking/deflecting effect of the bigger particles. Furthermore, according to the strain map obtained from the SEM image-converted geometry, the FE predictions indicate a higher likelihood of agglomeration-induced cracks initiating in the matrix in the composites with a smaller mean particle diameter. On the other hand, as the volume fraction increased, the $G_{IC}$ values decreased due to the restraining effects of the rigid particles on the matrix deformation, but the $K_{IC}$ values showed little change due to the balance between the toughening effect of the rigid particles and the weakening effect of particle agglomeration.

The methodology presented here can be applied to any particulate composite. The important results highlighted above were enabled due to the novelty of our method over related studies reported in the literature. Specifically the main advantages are: (i) the complex real microstructure of the composite is taken into account, (ii) both matrix and interface fracture mechanisms are addressed, and (iii) all the parameters needed as inputs for the simulation of matrix and interface damage are extracted from independent experiments (they are not fitted parameters). The accuracy of the model in predicting accurate trends with both volume fraction and particle mean diameter was remarkable (within 4% for fracture stress) and therefore it forms a significant step towards the design of particulate composites. The developed models lend themselves for parametric studies to readily and cost-efficiently quantify the effect of various quantities related to the material (e.g. interface strength) or microstructural features (e.g. particle size) so as to inform the material designer on how to tune the various parameters to meet the demands of a specific application.

Appendix

Williams (2010) model is based on one spherical particle with a radius of $R_f$ embedded in a unit cell with a side length of l. The toughening of the composite is assumed to be only caused by the debonding of the particle around the crack tip under a sufficient hydrostatic stress. The debonding process leads to an increase in the plastic work in a zone around the particle. The model takes into account the inter-particle interaction (Stapountzi et al. 2011) and the relationship between the volume fraction and fracture toughness of composites, $G_{ICc}$, is given by:

$$\begin{aligned} Y= & {} \frac{\frac{G_{ICc} }{G_{ICm} }-\phi _a }{1-\phi _a }=\frac{4\left( {1-v_m } \right) }{3\pi }\left( {\frac{R_f }{r_m }} \right) x^{2}\nonumber \\&\left( \frac{1}{x\phi _f }-\left( {\frac{5v_m -1}{2\left( {1+v_m } \right) }} \right) \right) \end{aligned}$$

(1)

where $R_f$ is the diameter of the particle (here taken as the mean particle diameter), $G_{ICm}$ and $v_m$ are the fracture toughness of the matrix (obtained using SENB tests) and Poisson’s ratio of the matrix [$v_m$= 0.38 (Stapountzi et al. 2009)], respectively. $r_m$ is the radius of the matrix plastic zone given by:

$$\begin{aligned} r_m =E_m G_m /2\pi \sigma _y^2 \end{aligned}$$

(2)

with $\sigma _y$ being the tensile yield stress of the matrix [in the range of 52–71 MPa (Kaplan 1999)]. The area fraction of the matrix on a plane through the equator of the particle, $\phi _a$ and the value of parameter, x, are given by:

$$\begin{aligned}&\phi _a =1-\pi \left( {\frac{R_f }{l}} \right) ^{2}=1-\pi \left( {\frac{3\phi _f }{4\pi }} \right) ^{2/3}\nonumber \\&\quad =1-1.21\phi _f ^{2/3} \end{aligned}$$

(3)

$$\begin{aligned}&x=\frac{1}{2}\left( {\frac{1+v_m }{1-v_m }} \right) \frac{\sigma _{max}^{int} }{\sigma _y } \end{aligned}$$

(4)

where $\sigma _{max}^{int}$ is the interfacial strength at the interface $r=R_f$ and l is the side length of the unit cell. Equation 1 can be expressed as:

$$\begin{aligned} Y=m\phi _f ^{-1}+c \end{aligned}$$

(5)

The effect of volume fraction on fracture toughness can then be determined via plotting Y versus $\phi _f ^{-1}$ and approximating the data with a linear relationship. For $v_m =0.38$, the values of m and c become:

$$\begin{aligned} m=0.26\left( {\frac{r_0 }{r_m }} \right) x \;\ and \;\ c=-0.089\left( {\frac{r_0 }{r_m }} \right) x^{2} \end{aligned}$$

(6)

Note that if the values of m and c are derived from fitting Eq. 5 to experimental data, the interface strength, $\sigma _{max}^{int}$, can be calculated. The model was used to fit the fracture toughness data as a function of volume fraction (fit not shown). The correlation coefficient was approximately 0.95, indicating a good linear fit of the data though it should be pointed out that the fit was performed on a limited number of available data, i.e. three data points only. With the obtained values of m (0.99) and c ($-1.4$), the ratio of the interfacial strength and the matrix yield strength was calculated as $\sim$ 3. Taking the yield stress value to be approximately equal to the fracture strength measured as 76 MPa in Sect. 4.1, the interfacial strength is estimated at approximately 200 MPa, which is the same order of magnitude as the value of 119 MPa obtained using Tan et al.’s method (Tan et al. 2005b).