Methods for studying allometry in geometric morphometrics: a comparison of performance

Abstract

Allometry has been the focus of growing interest in studies using geometric morphometric methods to address a wide range of research questions at the interface of ecology and evolution. This study uses computer simulations to compare four methods for estimating allometric vectors from landmark data: the multivariate regression of shape on a measure of size, the first principal component (PC1) of shape, the PC1 in conformation space, and a recently proposed method, the PC1 of Boas coordinates. Simulations with no residual variation around the allometric relationship showed that all four methods are logically consistent with one another, up to minor nonlinearities in the mapping between conformation space and shape tangent space. In simulations that included residual variation, either isotropic or with a pattern independent of allometry, regression of shape on size performed consistently better than the PC1 of shape. The PC1s of conformation and of Boas coordinates were very similar and very close to the simulated allometric vectors under all conditions. An extra series of simulations to elucidate the relation between conformation and Boas coordinates indicated that they are almost identical, with a marginal advantage for conformation. Empirical examples of ontogenetic allometry in rat skulls and rockfish body shape illustrate simple biological applications of the methods. The paper concludes with recommendations how these methods for estimating allometry can be used in studies of evolution and ecology.

Introduction

Allometry is an important factor to consider in many branches of biology because body size pervasively influences physiological and developmental processes in animals and plants (Calder 1984; Schmidt-Nielsen 1984; LaBarbera 1989). Most obviously, growth is an increase in body size of an organism. Through their association with other life history features, growth and development are also intimately tied into the ecological and evolutionary context of the organism (Roff 1992; Gilbert and Epel 2008). Morphological traits can be viewed as the cumulative product of growth and development of an organism up to the time when traits are observed, and many of them are involved in functions such as foraging and reproduction and are therefore undergoing adaptive evolution. Accordingly, allometry has been of long-standing interest for ecology and evolutionary biology (Huxley 1932; Jolicoeur 1963; Cock 1966; Gould 1966a; Mosimann 1970; LaBarbera 1989; Klingenberg 1996) and in recent decades the advent of new disciplines and approaches such as evo-devo and geometric morphometrics has reinvigorated the field (Loy et al. 1998; Monteiro 1999; Sidlauskas et al. 2011; Mitteroecker et al. 2013; Klingenberg 2016; Outomuro and Johansson 2017; Bookstein 2021).

Historically, the study of allometry started with the observation that log-transformed values of different linear measurements of growing animals, when plotted against one another, tended to fall along straight lines (i.e., the original measurements were related by a power function) and by the insight that this can be interpreted in terms of relative growth ratios of the traits (Huxley 1924; Teissier 1926; Gayon 2000). For the situation when multiple measurements are considered simultaneously, Jolicoeur (1963) proposed a multivariate generalization of a best-fitting line in a scatter plot using the first principal component of log-transformed measurements. This approach was extended by methods for size correction (e.g., Burnaby 1966) and has been widely used since then (Cheverud 1982; Shea 1985; Klingenberg 1996). By contrast, Gould (1966a, p. 587, p. 629) explicitly defined allometry as the study of proportion changes correlated with variation in size of either the whole organism or the part of interest, and emphasized that the term was not limited to any specific mathematical expression, such as the power function. He also repeatedly highlighted geometric similarity as an important criterion in allometric studies (Gould 1966b, 1968, 1971, 1975, 1977). Mosimann (1970) formalized this approach for multiple linear measurements: shape is a vector of ratios, each measurement divided by a general size variable computed from the measurements jointly. Allometry is a correlation between shape vectors and the size variable (Mosimann 1970; Mosimann and James 1979). These two different approaches have been distinguished as two “schools” of thought: the Huxley–Jolicoeur school that characterizes allometry as the covariation among two or more traits in response to variation of size, where each of the traits contains its own size information, and the Gould–Mosimann school that is based on separating size and shape into separate components according to the criterion of geometric similarity and defines allometry as the covariation between them (Klingenberg 1998, 2016). Whereas both frameworks were initially developed for traditional morphometric studies of sets of distance measures, both also apply to studies using the methods of geometric morphometrics (Klingenberg 2016).

This paper uses computer simulations of landmark configurations to compare the performance of two methods within each of the two major allometric frameworks in the context of geometric morphometrics. For the Gould–Mosimann school, the simulations include the multivariate regression of shape on centroid size, the most widely used method for analyzing allometry in geometric morphometrics (Loy et al. 1998; Monteiro 1999; Rosas and Bastir 2002; Drake and Klingenberg 2008; Rodríguez-Mendoza et al. 2011; Springolo et al. 2021), and the estimation of an allometric vector using the first principal component (PC1) in the shape tangent space (O'Higgins and Jones 1998; Cobb and O'Higgins 2004; Sardi and Ramírez Rozzi 2012; Watanabe and Slice 2014). For the Huxley–Jolicoeur school, the comparisons cover the PC1 in the conformation space, where position and orientation of landmark configurations are standardized but not size (also known as size-and-shape space; Bensmihen et al. 2008; Feng et al. 2009; Milne and O'Higgins 2012; O'Higgins and Milne 2013; Mydlová et al. 2015), and a recently proposed method using the PC1 of Boas coordinates (Bookstein 2018, 2021).

Because the spaces in which morphologies are represented and analyzed are important for understanding morphometric methods (Kendall 1984; Small 1996; Kendall et al. 1999; Rohlf 2000; Dryden and Mardia 2016; Klingenberg 2016), I briefly present Kendall’s shape space and conformation space, as well as the respective tangent spaces, before explaining the set-up of the models for allometry used in the simulations. A first set of simulations uses models in which allometry is the only variation, with no residual scatter around the allometric relationships at all. These simulations test the logical compatibility between methods: if the methods are logically consistent with each other, they are expected to provide corresponding results for such deterministic allometric relations. Two more sets of simulations add residual noise that is either isotropic or has a random but anisotropic structure. These simulations examine the statistical performance of the methods for analyzing allometry in the presence of noise that is either completely homogeneous in every available direction or that has a pattern different from that induced by the allometry. Some additional analyses examine the relationship between the conformation space and Boas coordinates (Bookstein 2018, 2021). Finally, two contrasting examples demonstrate the application of the different frameworks to empirical growth data from rats (Moss et al. 1981; Bookstein 1991) and rockfish (Rodríguez-Mendoza et al. 2011).

Shape space, conformation space and methods for analyzing allometry

For understanding and comparing morphometric methods, including those used to study allometry, it is helpful to consider the underlying shape or form spaces (Rohlf 2000; Klingenberg 2016). For the comparison of the Gould–Mosimann and Huxley–Jolicoeur approaches to allometry in the context of geometric morphometrics, the key point is that they use different spaces. The Gould–Mosimann school separates size and shape according to the criterion of geometric similarity, and therefore uses shape spaces. Because size is external to shape spaces, analyses of allometry then are based on regressions of shape on size or similar methods. The Huxley–Jolicoeur school characterizes allometry as covariation among traits without separating size and shape, and therefore finds allometric trajectories by fitting lines to the scatter of data points in conformation space. In practice, analyses of morphometric data are using some form of Procrustes superimposition algorithm and a projection to the tangent spaces to the shape or conformation spaces (Kendall 1984; Rohlf and Slice 1990; Goodall 1991; Dryden and Mardia 2016). It is therefore useful to consider those as well.

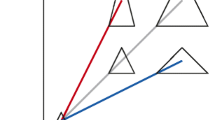
Kendall’s shape space is familiar to morphometricians, especially the one for triangles in two dimensions, which is the surface of a sphere (Fig. 1a; e.g., Rohlf 1999; Klingenberg 2020). The points in a shape space represent every possible shape for a given number of landmarks and dimensionality, and the pairwise distances between points correspond to the Procrustes distances between the respective shapes. Shape spaces for more than three landmarks are difficult to understand because they are curved multidimensional spaces (Small 1996; Kendall et al. 1999; Dryden and Mardia 2016; Klingenberg 2020). For that reason, practical shape analyses normally use tangent spaces. Just as maps provide a flat representation of the curved surface of the Earth, a shape tangent space gives a local linear approximation of the shape space in the vicinity of the tangent point (Fig. 1c). In practice, the usual choice for the tangent point is the mean shape. Because the tangent space is linear, the standard methods of multivariate statistics can be used within it. For biological data, shape variation is usually sufficiently limited for the tangent approximation to be good enough for practical shape analyses (Rohlf 1999; Marcus et al. 2000; Klingenberg 2020).

Fig. 1

Shape space, conformation space, and the respective tangent spaces. (a) Kendall’s shape space for triangles, one hemisphere viewed from a direction so that an equilateral triangle forms the pole (center; the other half of the sphere is hidden and holds mirror images of the visible triangles in corresponding positions). The circle at the periphery of the diagram (equator of the sphere) corresponds to the collinear triangles, in which all three vertices lie on a single straight line. (b) The conformation space for collinear triangles. It is a cone, with each cross-section corresponding to a scaled copy of the respective shape space (here the circle of collinear triangles that forms the equator of the shape space for all triangles). A straight line from any point to the tip of the cone represents conformations that have the same shape but different sizes. (c) A tangent space to the shape space for triangles. It is a linear (flat) approximation to the surface of the sphere in the vicinity of the point where the tangent plane touches the shape space (dot), but there are distortions with increasing distance from the tangent point. (d) A tangent space to the conformation space for collinear triangles. Note that the line from the tangent point to the tip of the cone (dashed line) runs within the tangent space. Rectangular boundaries have been added to the tangent spaces in the diagrams (c, d) to facilitate visual interpretation. Diagrams (a–c) from Klingenberg (2016)

Two types of analysis of allometry that are in widespread use are based on the shape (tangent) space: the regression of shape on centroid size and the correlation of the PC1 of shape with centroid size. Both these types of analysis are firmly in the Gould–Mosimann school because the size measure (usually centroid size or sometimes log-transformed centroid size) is external to the shape space. For both these types of analysis, the first step is a generalized Procrustes superimposition and tangent projection (Table 1, left two columns; this paper focuses entirely on partial Procrustes superimposition, e.g. Dryden and Mardia 2016). This procedure starts with centering the landmark configurations so that the center of gravity of each configuration is located at the origin of the coordinate system (step 1) and scaling to unit centroid size (step 2). The subsequent steps iteratively rotate the landmark configurations to fit them optimally to a consensus configuration, updating the consensus to converge to the mean shape of the sample (steps 3–6). In essence, the rotation step consists of successive ordinary Procrustes fits of all landmark configurations to the consensus, and the aligned configurations are then averaged to find the consensus for the next iteration. Finally, once changes in the consensus are negligible, the aligned landmark configurations are projected onto the shape tangent space at the sample mean shape (step 7). The resulting shape coordinates can then be used for analyzing allometry.

Table 1 An outline of the superimposition algorithms used by the different methods for analyzing allometry with landmark coordinates

In this framework, allometry is an association of shape with size. The most straightforward way to characterize this association is by a multivariate regression of shape on a measure of size, such as centroid size or log-transformed centroid size (e.g., Loy et al. 1996, 1998; Monteiro 1999; Rosas and Bastir 2002; Drake and Klingenberg 2008; Rodríguez-Mendoza et al. 2011; Sidlauskas et al. 2011; Weisensee and Jantz 2011; Klingenberg et al. 2012; Strelin et al. 2016, 2018; Sansalone et al. 2020; Simons 2021; Springolo et al. 2021). Using log-transformed centroid size is often advantageous if size variation is large, as it can render the relationship to size more linear and reflects the multiplicative nature of growth, but for data with relatively small ranges of size, untransformed centroid tends to be easier to interpret. For this method, the regression vector contains information about the pattern and strength of allometry because it is the expected shape change for an increase in centroid size (or log-transformed centroid size) by one unit. The strength of allometry can be quantified as the length of the regression vector (square root of the sum of its squared elements). In the limiting case of perfect isometry, when there is no allometry at all, the regression vector consists of only zeros. This method can also be used for size correction (Sidlauskas et al. 2011; Klingenberg 2016). Analyses of allometry using multivariate regression make no assumptions whether allometry is the only or the main effect on shape in a dataset, and they can therefore also be used in the presence of other factors influencing shape variation.

An alternative method for characterizing allometry within the Gould–Mosimann framework is to use regression or correlation to assess the relation between the PC1 of shape and a size measure such as centroid size (e.g., O’Higgins and Jones 1998; Sardi and Ramírez Rozzi 2012; Watanabe and Slice 2014; Bastir et al. 2017; Nishimura et al. 2019). The direction of the PC1 provides the pattern of allometry and the correlation or covariance with the size measure are indications of the strength of the relationship. If there is no allometry, correlation and covariance are expected to be zero and the direction of the PC1 is unrelated to allometry. The crucial assumption implicit in this approach is that allometry is the only factor having a major influence on shape. If this assumption is not met, the analysis can be misleading because no PC or multiple PCs may be correlated with the size measure (Singleton 2002; Sardi et al. 2007; Watanabe and Slice 2014).

Whereas most analyses in geometric morphometrics focus on shape variation, far fewer studies have used the Huxley–Jolicoeur framework. A fundamental characteristic of this approach is that it does not divide the form of objects into the separate aspects of size and shape, but it considers form jointly as a single coherent feature. Whereas the shape of an object is all its geometric features except its size, position and orientation, the form includes all the geometric features except position and orientation—size is an integral component of form. In analogy to Procrustes distance, a measure of distance between the forms of two landmark configurations can be defined: after one configuration is aligned with the other by translating and rotating so that the sum of squared distances between corresponding landmarks is minimal, the distance measure is computed as the square root of that sum. I call this distance measure conformation distance (Klingenberg 2016). This distance measure has been proposed several times independently in different contexts and under different names: first for comparing human skulls (Boas 1905), and later in the field of statistical shape analysis under the names “figure” (Ziezold 1977, 1994), “size-and-shape” (Kendall 1989; Le 1995; Kendall et al. 1999; Dryden and Mardia 2016), and “form” (Goodall 1991; but note that several very different concepts have also been called “form”). A closely related measure of distance, root mean square deviation (RMSD), differs only by a constant factor and has long been a standard measure of difference between conformations of proteins in structural biology (Kabsch 1976; Cohen and Sternberg 1980).

Conformation space (also known as “size-and-shape space”; Kendall et al. 1999; Dryden and Mardia 2016) is the space in which each point represents one of the possible conformations for a given number of landmarks and dimensionality, and pairwise distances between points in this space are the conformation distances between the corresponding pairs of conformations. By comparison to shape spaces, conformation spaces are more complex because they include size as an additional dimension. It is possible to imagine that differently scaled copies of the corresponding shape space are “stacked up” along this additional dimension of size. As a result, conformation spaces are hard to visualize; the only one that can be visualized in no more than three dimensions is the conformation space for collinear triangles (Fig. 1b; Klingenberg 2016; the conformation space for all triangles requires four dimensions). It considers only those triangles for which all three vertices lie on a straight line, and for which the shape space is a circle (the ‘equator’ of the shape space for all triangles, visible as the outer circle in the diagram of Fig. 1a). It is easy to imagine stacking up increasingly larger circles along a size axis, and it follows that this conformation space is a cone emanating from an apex corresponding to the conformation with size zero, for which all three landmarks are exactly in the same point. In Fig. 1b, the cone is cut off at a cross-section to make the diagram clearer to understand, but in reality, the conformation space has no such boundary and would continue indefinitely. Each cross-section of this cone is a circle corresponding to the shape space of collinear triangles (Fig. 1b; the “equator” of the shape space for all triangles, outer circle in Fig. 1a). These circles are oriented consistently, so that each straight line running from the apex of the cone along its side represents the set of conformations that all have the same shape, but different sizes. This kind of lines therefore can be interpreted as vectors of isometric variation of form (note that they are locally orthogonal to the circles corresponding to the scaled shape spaces). Further, the distance of a point from the apex of the cone is the centroid size of the respective conformation.

The tangent space to the conformation space of collinear triangles is a plane (Fig. 1d). It is defined by the tangent to the circular cross-section of the space at the tangent point and by the isometric line from the tangent point to the apex. The tangent space touches the conformation not only at a single tangent point, but along the entire isometric line passing through that point (dashed line in Fig. 1d). This has an implication that is important for the study of allometry: whereas the usual concerns about small variation and the quality of the tangent approximation apply for the shape of configurations (and are usually manageable; Rohlf 1999; Marcus et al. 2000; Klingenberg 2020), the fact that a vector for isometric variation of size is runs within the conformation tangent space means that no such concerns exist for size, no matter how large its variation is. Therefore, even large disparities in size do not lead to severe distortion when projecting conformations to the tangent space. This is especially relevant for analyses of ontogenetic and evolutionary allometry, where size ranges regularly extend over more than an order of magnitude. Other conformation spaces cannot be easily visualized, but it is true in general that the tangent space contains the isometric vector that passes through the tangent point, and therefore that size variation can be arbitrarily large without affecting the quality of the fit to conformation tangent space.

The standard procedure for finding mean conformations in empirical data and fitting the data to tangent space is a Procrustes superimposition that omits the scaling step (Table 1, third column). The resulting mean conformation has a minimal sum of squared distances to the conformations of the landmark configurations from which it was obtained (for proofs, see Ziezold 1994; Le 1995). This means that this procedure provides a least-squares estimate for the mean conformation, as the complete Procrustes procedure does for the mean shape. No extra projection to tangent space is necessary because the centering and rotation steps in the Procrustes procedure fulfil the relevant constraints of the conformation tangent space (for analyses of shape, the tangent projection only deals with the tangent constraint concerning size; Kent 1995). The superimposed landmark configurations resulting from the procedure can be used for analyses of variation of conformation in the sample. For instance, for the analysis of allometry, a PCA using the covariance matrix of the aligned landmark coordinates and then using the resulting PC1 as an estimate of the allometric vector. In empirical examples, the PC1 scores tend to be highly correlated with centroid size or other size measures (e.g., Langlade et al. 2005; Hsu et al. 2020).

Boas coordinates have recently been proposed as an alternative approach for analyzing allometry (Bookstein 2018, 2021). The starting point for this method is the first proposal by Boas (1905) of the least-squares 3D superimposition of one landmark configuration onto another by centering and rotation to an optimal fit, but without scaling. This criterion for optimal superimposition of two configurations is the same as for the conformation approach, and the resulting measure of pairwise distances between configurations is therefore also the same. As a further consequence, the space these distances define must be the same as conformation space (Fig. 1b). Boas (1905) focuses entirely on the comparison of two configurations and a time, and so did Bookstein (2018, 2021) in most of his discussion. About the generalized superimposition of multiple specimens, Bookstein (2018, 2021) did not provide much detail but repeatedly specified that Boas coordinates are obtained by multiplying each configuration of Procrustes shape coordinates by its own centroid size. The complete superimposition algorithm (fourth column of Table 1) therefore consists of a standard generalized Procrustes fit and an extra step (step 8 in Table 1) that multiplies the shape coordinates by centroid size to undo the scaling step (step 2). For this un-scaling to restore centroid sizes successfully, the procedure must use a partial and not a full Procrustes superimposition and there must be no projection to shape tangent space, because both those procedures would change the centroid size (Dryden and Mardia 2016) and thus would produce incorrect results in the un-scaling step (step 8). Boas coordinates are distinct from the analysis of conformations because the superimposition algorithms differ (Table 1, third and fourth columns). As pointed out by Bookstein (2021), the rotation step (step 4) is the same for a given target M and centered landmark configuration, regardless of whether that configuration is in the scale of original measurements (${{\varvec{X}}}_{i}^{\text{C}}$) or whether it is scaled to the corresponding preshape (${{\varvec{Z}}}_{i}$). The scale information does not enter the rotation, no matter whether the rotation is computed by singular value decomposition (for 2D or 3D data, step 4 in Table 1; the matrix L takes up all the scale information, but is not used in computing the rotation matrix) or by complex regression (for 2D data; Appendix A2 in Bookstein 2021). The difference between the algorithms is in how they compute the consensus M to which configurations are fitted in each iteration (step 5): for the analysis of conformation, the centered and rotated landmark configurations are used in their original scale, whereas for Boas coordinates (as for Procrustes analyses of shape) it is the rotated preshapes (all centered and scaled to unit centroid size). As a result, the consensus M for the conformation procedure can be interpreted as being proportional to a weighted average of the shapes of configurations in the sample, with centroid size as the weighting factor, whereas the M for Boas coordinates is an unweighted average of those shapes. Bookstein (2018, 2021) and O'Higgins et al. (2019) mention this difference between the two approaches. The difference between weighted and unweighted averages implies that the consensus matrices M for the two methods will differ by more than just scaling and sampling error particularly if there is a systematic association between shape and size, that is, if there is allometry. For this reason, it will be useful to explore the relative performance of the methods using conformations and Boas coordinates in more detail in simulations of allometric variation.

Models used in the simulations

Allometric models

An inherent problem for comparing the Gould–Mosimann and Huxley–Jolicoeur frameworks is that the relation between shape space and conformation space is slightly nonlinear. The problem is that a model of linear allometry in one space is expected to yield a subtly nonlinear response in the other space. For instance, if the point P in Fig. 2b moves from M upwards and to the right along the allometric vector repeatedly by equal shifts, the corresponding steps of point P′ in shape tangent space become progressively smaller (this is also true for the projection into shape space). Such nonlinearities may produce deviations from predictions based on local linear approximations, such as the enumeration of constraints on tangent spaces (Klingenberg 2020) or the matrix J of Bookstein (2018, 2021). To avoid bias in favor of either of the two approaches, this study uses two parallel sets of simulations, one situated in conformation space and the other in shape tangent space (Fig. 2).

Fig. 2

Diagrammatic representation of the setup of simulation models. (a) Simulation model situated in conformation space. This model includes displacements Δ from the mean conformation M along the allometric vector, and some simulations also include residual variation around P (dashed circle), drawn either from an isotropic or anisotropic distribution with total variance var(ε). (b) Simulation model situated in shape tangent space. This model simulates allometric displacements from the mean shape M′ along the vector α and possibly residual variation, both within the shape tangent space, and subsequently computes landmark configurations by scaling to the appropriate centroid size. For further details, see the main text

One set of simulations was conducted using a model situated in the configuration space (Fig. 2a), with different numbers of landmarks (k = 6, 8, 10, 15, 20, 30, 40, 50, 100) in both 2D and 3D. For each simulation run, a mean configuration M was chosen with a centroid size set arbitrarily to 5 units and a shape M′ drawn randomly from a uniform shape distribution with the appropriate number of landmarks and dimensions. The line from the origin O of the coordinate system through M′ and M is a vector of isometric variation because variation along this direction only changes the scaling of the resulting configurations (Klingenberg 2020). There are two ways in which allometric effects can become stronger or weaker: the angle β between the allometric trajectory and the isometric vector can change (and accordingly the amount of shape change per unit of size increase) or the displacements Δ along the allometric trajectory can increase or diminish. Variation of Δ is closely related to size variation of P, but variation in the centroid size of P (the distance between points O and P in Fig. 2a) is a trigonometric function of both β and Δ and is therefore a nonlinear function of both. The simulations varied the angle β from 0° to 30° in steps of 5°, corresponding to a spectrum from completely isometric variation to clear allometric variation. The pattern of allometric changes was generated by a random shape vector α orthogonal to the vector of the mean shape. The vector α and angle β together determine the direction of the allometric vector in conformation space (oblique red line in Fig. 2a). The magnitudes of displacements Δ from the mean M along the allometric vector were modelled in two different ways: as a normal distribution and as a lognormal distribution, each with mean zero and variances of 0.4, 0.6, 0.8 or 1.0 squared units of size.

The second set of simulations used a model situated in shape tangent space (Fig. 2b). This model was the same as above, but instead of modelling displacements Δ along the allometric vector in conformation space, the model included deviations Δs of centroid size from the mean, drawn from the same set of distributions as Δ. To compute the magnitude of the allometric displacement along the vector α in shape tangent space Δs was divided by the mean size and multiplied by sin(β). Finally, the resulting shapes were scaled to the appropriate centroid size for each landmark configuration (mean size plus Δs).

Residual error structure

A first series of simulations used these two models with no residual noise at all to examine whether the four different methods to analyze allometry (Table 1) are logically compatible with one another. The remaining simulations included an additional component of residual noise that was either isotropic or had a pattern of its own (dashed circles labeled ε in Fig. 2). This noise was added in the space in which the respective model was situated (with appropriate scaling to make the amounts of noise compatible between the two sets of simulations). Isotropic noise, without any pattern and equal amounts of variation in all directions of the space of landmark coordinates, was simulated as independent and normally distributed random variables with equal variances. In a separate set of simulations, patterned noise was simulated as multivariate normal vectors with zero mean and a covariance structure according to the model of exponential decrease of eigenvalues (Varón-González et al. 2020). In this model, the successive eigenvalues diminish by a constant factor, chosen to be 0.7 in this case, producing a decline in eigenvalues that is steep initially and then tapers off, as it is seen in many empirical datasets. The set of eigenvectors for each such simulation run was simulated as a random rotation matrix (using the QR decomposition; Press et al. 2007). As a result, the pattern of the residual variation is completely independent of the allometric vector. For both isotropic and anisotropic noise, residuals were drawn from a multivariate normal distribution with mean zero and a total variance var(ε) of 0, 0.2, 0.4, 0.6, 0.8, 1.0, or 1.2 squared units of size. Because the residual component was applied to the entire space of landmark coordinates, it contributed variation that included translations and rotations in addition to variation of form.

Evaluation of results

Each simulation generated data for a sample of 100 individuals. The allometry in the data was analyzed with all four methods presented in Table 1. The outcome was quantified as the angle between the estimated allometric vector from the respective method and the expected allometric vector, either the allometric vector in conformation space or the vector α in the shape tangent space at M′ (Fig. 2). This angle (here called “error angle”) is a consistent way to compare the performance of all four methods. For the two methods from the Gould–Mosimann approach, which are based on shape space, comparisons to the expected direction of the allometric vector do not apply for the case of isometry: the expected regression vector entirely consists of zeros and its direction is therefore undefined, whereas the PC1 is entirely determined by residual noise (in the absence of noise, there is no shape variation at all, and therefore no PCs exist). Therefore, comparisons with these two methods were only evaluated for values of the angle β > 0. For each combination of parameter values, 100 simulations were run, and the resulting error angles were averaged for presentation.

Simulations were run in R, version 4.1.0 (R Core Team 2021). The code used for the simulations and analyses is included in the Supplementary Information.

Simulations with no residual variation

Most of the simulations for allometry without residual noise showed close agreement between the expected allometric vectors and those estimated from the simulated data (Figs. 3, 4, S1–S6). Error angles were small or very small for the majority of simulations, with the only exceptions occurring in simulations using lognormal distributions of the Δ or Δs values and particularly for simulations situated in shape tangent space (Figs. S1, S3, S4, S6). Throughout all simulations, there was a consistent trend for error angles to be smaller for the estimation methods that used the same space in which the simulation model was situated. For simulations using normal distributions of the Δ or Δs values, the error angles for the methods in which the model was situated were in the order of 1° or less (often substantially less) and ranged to a few degrees for the estimation methods based on the other space. For the simulations using lognormal distributions of the Δ or Δs values, error angles mostly were small in the space in which the model was situated, whereas they tended to be substantially bigger in the other space. There were also trends for error angles to increase with higher angle β between the allometric and isometric vectors and with the variances of the Δ or Δs values, that is, when allometry in the model was stronger, and to decline with increasing numbers of landmarks. By contrast, the results were very similar for 2D and 3D data. Finally, there appeared no noticeable differences in the error angles produced by alternative estimation methods that used the same space (panels a vs. b and c vs. d in Figs. 3, 4, S1–S6).

Fig. 3

Performance of methods for estimating allometry without any residual noise for 2D data, from simulations situated in the conformation space and with allometric displacements Δ along the allometric vector drawn from a normal distribution. The plots show the error angles, averaged over sets of 100 simulation runs for each combination of parameters, as functions of the angle β between the allometric and isometric vectors, for different numbers of landmarks, k. In each plot curves are color-coded according to the variance of the Δ values, the deviations from the mean conformation along the allometric vector

Fig. 4

Performance of methods for estimating allometry without any residual noise for 2D data, from simulations situated in the shape tangent space and with deviations from the mean size drawn from a normal distribution. The plots show the error angles, averaged over sets of 100 simulation runs for each combination of parameters, as functions of the angle β between the allometric and isometric vectors, for different numbers of landmarks, k. In each plot curves are color-coded according to the variance of the Δs values, the deviations from the mean centroid size

These observations are consistent with an interpretation that the observed discrepancies arise from the nonlinearities in the mapping functions between the allometric trajectories in conformation and shape tangent space. Those nonlinearities are more accentuated for larger displacements from the mean size or conformation and for larger angles between allometric and isometric vectors. Also, the greater discrepancies found for the lognormal than for the normal distributions, particularly in the models situated in shape space (Figs. S4, S6), most likely can be explained as consequences of large deviations in Δ or Δs values, which are expected with higher frequency under the lognormal distribution, and may produce unrealistic effects in the models. These extreme effects suggest some caution may be required in interpreting the results particularly from simulations using lognormal distributions of Δ or Δs values.

That estimation methods using the same space in which the simulation models is situated yield smaller error angles than the methods using the other space indicates that both approaches are logically consistent with one another, and neither is inherently superior over the other. Up to the subtle nonlinearity in the mapping between the conformation space and shape tangent space and possible pathological effects of extreme deviations in the simulation models, the logic that underlies each of the different estimation methods is mutually compatible with any of the others. In addition, for most types of simulations, the effects of nonlinear mapping are negligible by comparison to the effects of residual error (compare the top row of blocks to the other rows in Figs. 5, 6, 7 and 8, S7–S12). Further assessment of the relative merits of methods for estimating allometry therefore is a question of statistical performance and needs to examine how well they do in the presence of residual noise.

Fig. 5

Performance of methods for estimating allometry in the presence of isotropic residual noise for 2D data, from simulations situated in the conformation space and with displacements along the allometric vector following a normal distribution. The heatmaps show the error angle in response to the angle β between the allometric and isometric vectors and to the variance of the deviations Δ from the mean conformation along the allometric vectors. Isotropic residual noise was added in different amounts, with total variances var(ε) ranging from 0 to 1.2 units of squared size (no residual variation to slightly more than the maximum of the variance of Δ)

Fig. 6

Performance of methods for estimating allometry in the presence of isotropic residual noise for 2D data, from simulations situated in the shape tangent space and with deviations from the mean size drawn from a normal distribution. The heatmaps show the error angle in response to the angle β between the allometric and isometric vectors and to the variance of the Δs values, the deviations from the mean centroid size. Isotropic residual noise was added in different amounts, with total variances var(ε) ranging from 0 to 1.2 units of squared size (no residual variation to slightly more than the maximum of the variance of Δs)

Fig. 7

Performance of methods for estimating allometry in the presence of patterned residual noise for 2D data, from simulations situated in the conformation space and with displacements along the allometric vector following a normal distribution. The heatmaps show the error angle in response to the angle β between the allometric and isometric vectors and to the variance of the deviations Δ from the mean conformation along the allometric vectors. Non-isotropic residual noise was added in different amounts, with total variances var(ε) ranging from 0 to 1.2 units of squared size (no residual variation to slightly more than the maximum of the variance of Δ)

Fig. 8

Performance of methods for estimating allometry in the presence of patterned residual noise for 2D data, from simulations situated in the shape tangent space and with deviations from the mean size drawn from a normal distribution. The heatmaps show the error angle in response to the angle β between the allometric and isometric vectors and to the variance of the Δs values, the deviations from the mean centroid size. Non-isotropic residual noise was added in different amounts, with total variances var(ε) ranging from 0 to 1.2 units of squared size (set to match those used in the model situated in conformation space by a linear approximation)

Simulations with isotropic residuals

In the presence of isotropic residual noise, the two methods using shape space were clearly affected and the error angles reflect the amount of residual variation in the model (colors are darker in the lower blocks of heat maps in parts a and b of Figs. 5, 6, S7–S9, S11; the exception to this pattern are the simulations situated in shape tangent space using lognormal distributions of Δs values, Figs. S10, S12). Both regression of shape on size and the PC1 of shape recovered the allometric vector better when the angle β between the allometric and isometric vectors was relatively large. Presumably this is a consequence of the fact that variation is nearly isometric with small β, and the residual noise therefore contributes a bigger proportion of the total shape variation. The regression of shape on centroid size performed consistently as well or better than the PC1 of shape in the same simulations (compare parts a vs. b of Figs. 5, 6, S7–S12). Also, it is immediately apparent that the two methods using conformation space universally performed well, with very small error angles, almost regardless of how strong the allometry was or how much residual noise was present (parts c and d of Figs. 5, 6, S7–S9, S11). The exceptions to this pattern were the simulations situated in shape tangent space using lognormal distributions of Δs values (Figs. S10, S12), where the two methods using the conformation space performed consistently poorly, even in the absence of residual error (i.e., with var(ε) = 0), whereas the regression of shape on size and PC1 of shape did unusually well. It is likely that these results were consequences of extreme values in the simulations. In all scenarios, there was little difference between the simulations in two dimensions and those in three dimensions.

Simulations with patterned residuals

When the simulations included residual variation that was itself structured, with patterns of variation independent of allometry, the contrast in performance between methods was more accentuated (Figs. 7, 8, S14, S17; slightly less so for simulations using lognormal distributions of Δ or Δs values, Figs. S13, S15, S16, S18). The differences to the simulations with isotropic noise were most striking for the two methods using the shape space (compare parts a vs. b in Figs. 7, 8, S14, S17). The regression method produced slightly larger error angles for models with patterned residual variation than for the corresponding models with isotropic residuals (e.g., compare Fig. 7a vs. Fig. 5a, Fig. 8a vs. Fig. 6a, etc.). By contrast, the performance of the PC1 of shape dropped drastically from models with isotropic noise to the corresponding models with anisotropic residual variation (e.g., compare Fig. 7b vs. Fig. 5b, Fig. 8b vs. Fig. 6b, etc.). The two methods using conformation space continued to perform very well, but with high levels of residual variation (total variance var(ε) of 1.0 or 1.2) and the highest level of the var(Δ), even these two methods produced larger error angles (top rows of the heatmaps, especially for k ≥ 15, in the bottom two blocks of Fig. 5c, d). The effects of anisotropic residual noise on the performance of all four methods tended to be slightly less drastic in simulations with few landmarks and to become more accentuated with increasing numbers of landmarks. Again, the results for 3D data were very similar for those for 2D data (e.g. compare Fig. 7 vs. Fig. S14, Fig. 8 vs. Fig. S17).

How do Boas coordinates differ from conformation?

The close and consistent similarity between the results for the methods using the PC1 of conformation and of Boas coordinates raises the question how the two methods differ, and whether there is a way to choose between them. A separate series of simulations addressed this question, based on the allometric model situated in conformation space (Fig. 2a) with normally distributed deviations along the allometric vector and anisotropic residual variation at a fixed level of var(ε) = 0.6. The strength of allometry was varied through the angle β between the allometric and isometric vectors, which ranged from 0° (isometry) to 30°, and through the variance of the deviations Δ from the mean conformation along the allometric vector, ranging from 0.4 to 1 squared units of size. The number of landmarks was set to 6, 8, 10, 15, 20, 30, 40, 50 and 100 in different simulation runs and separate simulations were conducted for 2D and 3D data. In each simulation run, a sample of 100 landmark configurations was generated and conformation and Boas coordinates were computed using the respective superimposition algorithms (Table 1). For each combination of parameter values, 100 separate simulations were run.

Because superimposition algorithms for both the analyses of conformation (Ziezold 1994; Le 1995; Dryden and Mardia 2016) and Boas coordinates (Bookstein 2018, 2021) use a least-squares criterion, a suitable measure for comparison are the total sums of squares of the superimposed landmark configurations, or equivalently their total variances (differing only by a constant factor). Differences are presented here as percentage differences of the total variance of Boas coordinates minus the total variance of conformation, with the value for conformation set to 100% (i.e. positive percentages mean Boas coordinates have larger total variance or sums of squares than conformation). The differences were computed for all simulation runs separately and percentage differences averaged over the 100 runs for each set of parameter values.

Consistent with the close match of estimated allometric vectors, the percentage differences of total variances between the two methods were all very small (Fig. 9). All the average percentage differences were positive, indicating that the total variances of Boas coordinates slightly exceeded those for conformation. This is not surprising, given that the generalized Procrustes algorithm for conformation has been proven to yield a least-squares superimposition (Ziezold 1994; Le 1995). The differences were nearly zero under an isometric model (i.e., if the angle β was zero) and tended to become larger when allometry was stronger (i.e., with increasing angle β and variance of shifts Δ along the allometric vector). The differences between the two methods were largest for small numbers of landmarks and diminished for configurations with very many landmarks. Also, the differences were greater for analyses in three than in two dimensions (note that the plots in parts a and b of Fig. 9 are not scaled equally).

Fig. 9

Differences in the quality of superimpositions between conformation and Boas coordinates. (a) Comparisons for 2D data. (b) Comparisons for 3D data. The plotted values were computed as the percentage differences of total variance of Boas coordinates minus the total variance of conformation, with the total variance of conformation set as 100%, and averaged over 100 simulations per combination of parameters. The plots show the averaged percentage differences as functions of the angle β between the allometric and isometric vectors, for different numbers of landmarks, k. In each plot curves are color-coded according to the variance of the Δ values, the deviations from the mean conformation along the allometric vector

Does it matter? Applying the methods to empirical examples

To put the preceding simulations into perspective, I present two applications of the various methods in two examples of ontogenetic data: the Vilmann rat data, from a laboratory experiment following individual rats from 7 to 150 days of postnatal age (Moss et al. 1981, 1983; Bookstein 1991, 2018, 2021), and an example of growth in a marine fish, the rockfish (Helicolenus dactylopterus, also called bluemouth or blackbelly rosefish), with specimens obtained from bottom trawl surveys on the continental shelf off the coast of Galicia (Spain; Rodríguez-Mendoza et al. 2011). These two examples differ in the sampling designs of the respective studies as well as in the growth characteristics of the two species, which are in turn related to their life histories and ecologies. Therefore, they illustrate different features that can be encountered in studies of ontogenetic allometry.

Rat data

For the rat example, landmarks were digitized from lateral radiographs taken at the ages of 7, 14, 21, 30, 40, 60, 90, and 150 days (Moss et al. 1981, 1983). The data, including eight midsagittal landmarks of the braincase, are publicly available (http://sbmorphometrics.org/data/Book-VilmannRat.txt; as published in Bookstein 1991, appendix A.4.5). The dataset used here included just those 18 rats with complete records of all eight landmarks at eight ages (as in the analyses in Bookstein 2018, 2021).

The multivariate regression of shape on centroid size for the rat data accounted for 76.3% of the total shape variation. The shape change associated with the regression (Fig. 10a) was a combination of a stretching of the ventral row of landmarks and a dorsoventral compression that is particularly accentuated in the region of the parietal and interparietal bones (upper-left region of the grids), turning the braincase from a rounded to an elongated box-like shape. The scatter of the regression scores (the shape variable in the direction of the regression vector in shape tangent space; Drake and Klingenberg 2008) against centroid size showed a clear linear trend, except for the data points at the age of 7 days, which were slightly offset from the overall trend and were separated from those of the other age groups by a distinct gap in size (Fig. 10b). The PC1 of the shape data accounted for 82.2% of the total variance of shape. It produced an estimate of allometry that was very similar to the regression estimate, as the angle between the shape PC1 and regression vector was only 1.55° (shape change not shown here, but a transformation grid is presented in Fig. 1b of Bookstein 2021).

Fig. 10

Allometry in the example of the Vilmann rat data (Bookstein 1991). (a) Allometric analysis by multivariate regression of shape on size. The two transformation grids show the shape changes from the average shape to the shapes expected for changes in centroid size by − 350 units (left) and + 350 units (right) from the average size. The two grids are scaled to equal centroid sizes. (b) The scatter plot of the regressions scores (vertical axis, in units of Procrustes distance) against centroid size (units of measurement not specified in the original source, Bookstein 1991). (c) Allometric analysis for the rat data using the PC1 in the conformation space. The two transformation grids show the change to the conformations along the PC1 with scores − 400 units (left) and + 350 units (right), including the changes in size. (d) Scatter plot of the scores of PC1 versus PC2 in the conformation space (in units of length measurements, not specified in the original source)

The PC1 of conformation for the rat data accounted for 95.2% of the total variance of conformation. The conformation changes along the PC1 (Fig. 10c), from the left to the right grid, featured an expansion that was clearly stronger in the horizontal than in the vertical direction, and was particularly pronounced for the stretching of the ventral part of the braincase. In addition, the upper-left corner of the transformation grid was clearly “pulled out” toward the upper left in the right transformation grid by comparison to the left grid, corresponding to a marked vertical expansion of the occipital to form a sharper angle with the interparietal bone. The result was an overall expansion from a rounded to a more box-like form of the braincase. The scatter of the PC1 scores of the conformations (horizontal direction in Fig. 10d) closely corresponded to centroid size (horizontal axis of Fig. 10b).

The PC1s of conformation and of Boas coordinates corresponded very closely to each other: the angle between them is only 0.0076°. This close similarity is also apparent from the graphs of the PC1 of conformation (Figs. 10c, d) to those that Bookstein (2021) obtained for the PC1 of Boas coordinates from the same data: the transformation grids seemed identical except for the spacing of grid lines and scaling of the degree of change (cf. Fig. 10c vs. Fig. 2b of Bookstein 2021); the scatters of PC1 versus PC2 scores matched closely, up to changes in sign (but signs are arbitrary for PCs; cf. Fig. 10d vs. Fig. 3b of Bookstein 2021); and finally, the PC1 of both conformation and Boas coordinates correlated tightly with centroid size (compare the spacing of points along the horizontal axes in Figs. 10b, d; cf. Fig. 7a of Bookstein 2021).

The angle between the estimated allometric vector and the isometric vector in conformation space (corresponding to the angle β in the simulation models; Fig. 2a) was 22.36° regardless of whether the PC1 of conformation or Boas coordinates was used as the estimate. To examine how compatible the Gould–Mosimann and Huxley–Jolicoeur approaches are for this example, I obtained the projection of the conformation PC1 onto the shape tangent space and computed the angles between this and the PC1 for shape and the allometric regression vector. The angle between the projected conformation PC1 and the shape PC1 was 1.60° and the angle between the projected conformation PC1 and the regression vector of shape on centroid size was 2.74°. It seems that all allometric methods yield compatible results in this example, likely because there appear to be no substantial sources of variation except for allometry, which is quite strong and therefore produces a clear pattern in both conformation space and shape tangent space that is easily recovered by all methods.

Rockfish data

The rockfish example uses a sample of 191 specimens, from Galicia, taken from a larger study of allometry in this species (Rodríguez-Mendoza et al. 2011). For each fish, 13 landmarks were digitized to characterize its overall body shape (for further details, see Rodríguez-Mendoza et al. 2011).

In this dataset, centroid size ranged from 5.2 to 34.5 cm, a nearly sevenfold difference, and correlated very strongly with the total length of the fish (Fig. 3 in Rodríguez-Mendoza et al. 2011). The multivariate regression of shape on centroid size accounted for 8.99% of total shape variation, and a permutation test rejected the null hypothesis of independence (P < 0.0001). This indicates that allometry is clearly present but is not the dominant source of shape variation. The shape changes over the observed range of body sizes were fairly subtle (Fig. 11a), with overall body shape changing from more triangular (with the apex above the head, at the insertion of the first dorsal fin spine) to more elliptical. This change involved the posterior body becoming relatively higher, the pectoral and pelvic fins shifting posteriorly and downward relative to nearby structures, and the maxilla relatively shortening and rotating to a steeper angle. The plot of regression scores against centroid size (Fig. 11b) shows a clear allometric trend, but also a substantial amount of residual scatter. The PCA of shape produced a dominant PC1 accounting for 44.7% of the total variance of shape, which shared some aspects of the associated shape change with the regression vector, but which also contained other prominent features of variation (not shown). The angle between the PC1 of shape and the allometric regression vector in shape space was 52.4°. This relatively poor correspondence indicates that the PC1 included other sources of variation in addition to (or instead of) allometry, and therefore would be ineffective as an estimator of allometry.

Fig. 11

Allometry in the rockfish data (Rodríguez-Mendoza et al. 2011). (a) Allometric analysis by multivariate regression of shape on size. The warped outline drawings show the average shape plus allometric shape changes expected for a decrease in centroid size by 10 cm (left) and an increase by 20 cm (right). Both diagrams are scaled to equal centroid size. (b) The scatter plot of the regressions scores (vertical axis, in units of Procrustes distance) against centroid size (horizontal axis, in cm). (c) Allometric analysis using the PC1 in the conformation space. The two warped outline drawings show the conformations along the PC1 with scores − 10 cm (above) and + 20 cm (below). The two diagrams are scaled proportionately to represent the complete changes in conformation. (d) Scatter plot of PC1 versus PC2 in the conformation space for the rockfish data (both PCs are in cm)

The PC1 of conformation accounted for 98.4% of the total variance in the rockfish example. The conformation change associated with this PC1 involved a large difference in size (Fig. 11c) and more subtle changes in shape that correspond to the change found in the regression vector (cf. Fig. 11a, c): a slightly disproportionate expansion of the height of the posterior part of the body, expansion of the region posterior to the operculum and pectoral and pelvic fins, and slightly less drastic expansion of the maxilla along with the rotation to a slightly steeper orientation. Together, these changes amounted to an overall appearance that was more triangular for small individuals and more elliptic for large ones. The dominance of the conformation PC1 is also very clear from the plot of PC1 versus PC2 (Fig. 11d). The scores of the conformation PC1 corresponded closely to centroid size (compare the scatters along the horizontal axes in Fig. 11b, d).

The PC1s of conformation and of Boas coordinates were virtually identical: the angle between the two PC1s was only 0.00019°. The angles between both these estimates of the allometric vector and the isometric vector in conformation space were 2.38°, indicating that the rockfish example was much closer to isometry than the rat example. The projection of the conformation PC1 onto the shape tangent space made an angle of 15.2° with the regression vector of shape on centroid size and an angle of 42.5° with the PC1 of shape. This indicates that the correspondence between estimates of allometry based on the Huxley–Jolicoeur framework (in conformation space) and on the Gould–Mosimann framework (in shape space) is moderately good, and it reinforces the result above that the PC1 of shape is a poor estimator of allometry in this example.

Discussion

The computer simulations and the two contrasting examples reported in this paper have yielded some consistent conclusions relevant to practical analyses of allometry in the context of morphometric studies concerning the evolution, ontogeny, or ecology of diverse organisms. The simulations without residual error (Figs. 3, 4, S1–S6) established that, up to minor nonlinearities of the mapping between the shape tangent space and conformation space, the Gould–Mosimann and Huxley–Jolicoeur frameworks for analyzing allometry are logically compatible with each other. Among the four alternative methods for analyzing allometry compared here, two belong to the Gould–Mosimann framework: the multivariate regression of shape on size and the PC1 of shape (and possibly relating PC1 scores to a measure of size by correlation or regression). The regression approach performed clearly better in some simulation experiments (cf. Figs. 5, 6, 7, 8, 9, parts a vs. b) and the PC1 of shape also seemed to do poorly in the rockfish example. The two methods belonging to the Huxley–Jolicoeur framework, the PC1 in conformation space and the PC1 of Boas coordinates, performed well in the simulation experiments and also appeared to do so for both empirical examples. These two methods consistently yielded results that were nearly identical—a finding that is somewhat unexpected because they use different variants of superimposition algorithm (Table 1) and previous discussions have alluded to the potential for differences (Bookstein 2018, 2021; O’Higgins et al. 2019). Whereas it is reassuring that the two main frameworks of allometry are logically compatible with each other, this also raises the question how investigators should choose between them for actual empirical studies.

Allometry within the Gould–Mosimann framework

Among the methods using shape space, multivariate regression of shape on centroid size performed consistently better than the PC1 of shape in the presence of residual noise. The difference in performance was dramatic if the residual noise had a pattern itself that was independent of allometry and the Δ or Δs values were drawn from a normal distribution (Figs. 7, 8, S14, S17), somewhat less so if the Δ or Δs values were from a lognormal distribution (Figs. S13, S15, S16, S18). The reason why the PC1of shape performed poorly as an estimate of an allometric vector was that its main assumption, that patterns of the shape variation originate exclusively from allometry, was violated in these simulations. Yet even when the residual noise was isotropic and therefore had no pattern of its own, the PC1 did not perform as well as an estimator of allometry as the regression method (Figs. 5, 6, S7–S9, S11). It seems that just adding non-allometric variation, even though it was completely unstructured, was sufficient to affect the precision of PC1 estimates detrimentally, at least accentuating the problems that the regression approach also faced. In all the simulations, there appears to be no situation where the PC1 of shape outperformed the multivariate regression of shape on size as an estimator of allometry. Even if the aim is just to provide a score that can subsequently be related to measures of size, there seems to be no benefit in estimating a vector of allometry without considering the available information on size.

The two examples provide different perspectives on this issue. For the rat example, both methods using the shape space produced similar estimates of allometry, which were also compatible with the estimates based on the Huxley–Jolicoeur framework. With an angle of 22.36° between the isometric and allometric vectors in conformation space, this example is in the upper third of the range of the angle β used in the simulation models, where all estimation methods perform well if the amount of residual variation is not too large. Evidence that residual variation was modest by comparison to allometry were the high proportions of total variance for which the multivariate regression or PC1s accounted in all analyses: there seemed to be a good fit of the allometric model regardless of the analytical framework used. Therefore, the rat example appears to have properties that make it similarly permissive to all methods for estimating allometry.

By contrast, the rockfish example has an angle of just 2.38° between the isometric and allometric vectors in conformation space, which is less than the minimum angle of 5° used in the simulation models (apart from the situation of perfect isometry, with β = 0). In addition, residual shape variation is substantial—because variation is close to isometric, the non-allometric part takes up by far the largest share of the total shape variation. Despite the very large scale of size variation, this situation is challenging. With this combination of parameters (at the left margin of the heat maps in Figs. 5, 6, 7 and 8, S7–S18), simulation results indicate that the PC1 of shape performs poorly and even the multivariate regression of shape on size displays some instability in the simulation experiments. The higher degree of incongruence among methods for the rockfish example likely reflects this instability.

What are the consequences of this type of problem in estimating allometry? It is important to keep in mind that the regression method does not use exclusively the direction of the regression vector. As a result of the almost isometric variation, the magnitudes of the regression coefficients will be near zero, which is correct in this situation. Any use of the regression vector, for instance for size correction (Klingenberg 2016), will have little effect because the predicted changes also will be small. Therefore, even in this challenging situation, the regression method is not expected to lead to misleading inferences or erroneous size corrections.

Allometry within the Huxley–Jolicoeur framework

The two methods belonging to the Huxley–Jolicoeur framework performed very well in the simulation experiments, and a key insight is that they produce very similar results despite the difference in the superimposition algorithms they use (last two columns of Table 1). The algorithm omitting the scaling step altogether (third column of Table 1) yields the mean conformation that is optimal in a least-squares sense (Ziezold 1994; Le 1995), and therefore also the optimal superimposition. The simulations presented here show that superimpositions from both methods differ remarkably little in their quality and that Boas coordinates are therefore a close approximation to the optimal solution. Differences are larger when allometry is stronger (greater angle β and larger displacements along the allometric vector), as expected, and diminish with increasing numbers of landmarks (Fig. 9). Because both methods produce nearly the same results under all the conditions considered here, the difference is unlikely to matter in practice. This close similarity in the superimpositions is the reason why estimates of allometry based on these two methods also consistently performed similarly (Figs. 3, 4, 5, S1–S9).

It is less clear why the two methods from the Huxley–Jolicoeur framework performed better than those from the Gould–Mosimann framework (except for simulations situated in shape tangent space and using a lognormal distribution of Δ or Δs values, in which there seemed to be problems because of extreme effects; Figs. S4, S6, S10, S12, S16, S18). There are some explanations for specific situations: for instance, for simulations with near-isometric variation (very small angle β; left margins of the heat maps in Figs. 5, 6, 7 and 8) the methods based on shape space yield poor estimates because there is little allometric shape variation and therefore the directions of allometric vectors are poorly defined, so that residual variation can easily affect the estimates. Also, size usually takes up a substantial proportion of the variation in the data (including in all simulations of this study) and is a component of allometric vectors in conformation space, which are therefore inevitably aligned to some extent with the isometric vector in conformation space. For shape, by contrast, the proportions of allometric versus residual variation are usually much more variable and there is no a-priori expectation at all about the direction of allometric vectors in shape tangent space. Therefore, estimating the directions of allometric vectors in conformation space may be easier than in shape tangent space. Using those directions (or error angles) in comparing performance may therefore give a systematic advantage to estimation methods using conformation space.

A further problem is related to the scaling of residual variation between spaces. The models used residual variation around the allometric relationship that was homoscedastic, with equal amounts and patterns of residual variation at every position along the allometric vector. Because of the scaling by size that is involved in projecting from conformation space to shape (tangent) space or vice versa, variation that is homoscedastic in one space will be heteroscedastic after projection into the other space. It is not possible for the residual variation to be homoscedastic in both the conformation and shape (tangent) space. Heteroscedasticity is problematic for statistical procedures such as regression and therefore may explain some of the poorer performance of the methods using shape tangent space in the presence of residual noise for the simulations situated in conformation space. Nevertheless, because results did not substantially differ between corresponding simulations situated in the two spaces (e.g., Fig. 5 vs. Fig. 6, Fig. 7 vs. Fig. 8), this effect appears not to be an important cause for the performance difference in these simulations. Yet, such a pattern of heteroscedasticity does appear to be present for the rockfish example, where the degree of scatter of PC2 scores in conformation space rises from left to right (Fig. 11d; a hint of it may also be apparent for the rat example, Fig. 10d, but note that the allometric relation here is markedly nonlinear). It is unclear what effect this may have in this example or generally in empirical data.

Which method should I choose?

The key question for investigators is which method to choose for empirical studies of allometry. The choice is easy once the investigator has decided whether to use the shape space (the Gould–Mosimann framework) or the conformation space (Huxley–Jolicoeur framework) for the study. For studies using shape space, allometry should be analyzed by multivariate regression of shape on a suitable measure of size (e.g., centroid size or log-transformed centroid size; Monteiro 1999; Klingenberg 2016) because the simulations have shown that this method consistently outperforms the alternative method of computing the PC1 of shape, especially when the residual variation is structured itself (Figs. 5, 6, 7 and 8, S7–S18). For studies focusing on form without separating size from shape, the two methods using conformation space perform similarly well, so that the choice between them does not make much of a difference. In favor of the algorithm using conformation (third column in Table 1), it can be argued that it is slightly simpler (no scaling and un-scaling steps), that it results in a superimposition that is equal to or marginally better than Boas coordinates (Fig. 9), and that not even Bookstein (2018, 2021) or O'Higgins et al. (2019) have pointed out any direct advantages of Boas coordinates over conformations. In practice, a potential advantage of Boas coordinates is that they are simple to obtain even if only software for shape analysis is available (but investigators must ensure that it uses a partial and not a full Procrustes superimposition and that it does not perform a projection to shape tangent space, because either of those would invalidate the procedure).

A more difficult choice is whether to use the Gould–Mosimann or the Huxley–Jolicoeur framework for a given study. To answer this question, the investigator needs to consider not only the analysis of allometry, but the research question that the study is addressing overall. Are size and shape relevant per se for this question, or is it more appropriate to treat morphology as a single, coherent (albeit multidimensional) feature without separating size from shape? Considering these questions may lead to a choice that is optimal in the broader context of a particular study. Also, because the two frameworks are mutually compatible, both are likely to yield similar conclusions for any given study. If a clear allometric pattern is present (as in the rat example, Fig. 10), both frameworks will show related patterns differing mainly in the respective styles of presentation; alternatively, if variation is nearly isometric (as in the rockfish example, Fig. 11) or if there is no clear allometric pattern because of limited variation in size, both approaches provide indicators that this is the case (e.g., information about the absolute scale or relative amount of variation for which allometry accounts).

Both the Gould–Mosimann and the Huxley–Jolicoeur approaches apply to all levels of allometry: static, ontogenetic, and evolutionary allometry (e.g., Cock 1966; Gould 1966a; Cheverud 1982; Klingenberg and Zimmermann 1992; Klingenberg 1996, 2014). Whereas static and ontogenetic data can be used in allometric analyses without further adjustments, appropriate phylogenetic comparative methods such as independent contrasts or PGLS should be used for evolutionary allometry (e.g., Klingenberg and Marugán-Lobón 2013; Adams 2014). The quantity each of the approaches uses to characterize morphological variation, that is, shape in the Gould–Mosimann approach or conformation in the Huxley–Jolicoeur approach, can be used as a “common currency” to relate the different levels of allometry with each other (e.g., Weisensee and Jantz 2011; Klingenberg et al. 2012; Mydlová et al. 2015; Hipsley and Müller 2017; Springolo et al. 2021). This perspective holds considerable promise for characterizing different levels of allometry in studies designed to combine multiple levels of variation, so that the contributions of multiple factors and their interactions can be analyzed jointly. Such multilevel studies, based on rigorous and flexible quantification of morphological variation by geometric morphometrics, are likely to provide major new insights into processes at the interface of development, ecology, and evolution.