1 Introduction

Antiauthoritarianism is present in many trends in mathematics education, such as cooperative learning approaches and constructivist pedagogies (Amit & Fried, 2005, p. 145). In Sweden, however, antiauthoritarianism is often characterised by the use of self-regulatory, individualized ways of working (Carlgren, Klette, Myrdal, Schnack, & Simola, 2006; Skolverket, 2004), and these have increased at the expense of collective modes of working (Lindblad & Sahlström, 1999). Education has been transformed into a private and individualistic mission rather than a public mission (Englund, 1993). Since the 1990s, both the structure of the system and the meaning and content of schooling have changed from traditional ways of teaching based on the class to work based on the individual, where “the idea of the educated citizen seemed to have been replaced by the separated individual responsible for his/her own life” (Carlgren et al., 2006, p. 303). In the current National Curriculum in Sweden (Läroplan för det obligatoriska skolväsendet, 1994), the idea that students construct their own knowledge has been replaced by the idea that students should be responsible for their own learning. This change to less teacher responsibility for knowledge construction, together with societal changes, has formed the basis of the instructional mode labelled ‘student's independent work’, which is characterised by students planning and working on their own with different tasks independent of other students (Ståhle, 2006; Vinterek, 2006; Österlind, 1998).

In the context of mathematics classroom practice, both students and teachers are engaged in the construction of mathematics knowledge. When knowledge is to be constructed by students themselves, it could be discussed where the responsibility for offering valid conditions for this construction is to be placed. The responsibility could either be at an institutional level, in the form of instructional responsibility, or at an individual level, in the form of student's responsibility. In the National Curriculum in Sweden, the student's responsibility is emphasised. The individualized ways of working, e.g. the instructional mode labelled ‘student's independent work’, represent a low level of instructional responsibility in that students are supposed to take a large part of the responsibility for motivating themselves and for planning and accomplishing their own mathematics learning.

The subject of the present study is the classroom practice of mathematics instruction, and the main aim is to investigate how teachers practise instructional responsibility. Teacher responsibility, which embraces both form and content, thus expresses how the mathematics instruction takes its responsibility for students' mathematics knowledge construction.

In accordance with the trends described above, mathematics education in Sweden has become more and more individualized in the last two decades (Skolverket, 2004; Skolverkets Rapport nr. 323, 2008), and mathematics education has become formally non-tracked. However, despite the fact that mathematics education is formally untracked, test results in Sweden are similar to the pattern observed in countries with an early differentiation of schooling, which is characterised by a low average and a large dispersion (Hanushek & Wössmann, 2006). This calls for research about effects of changes in the mathematics classroom practice towards more individualization and diminishing instructional responsibility. Increased attendance of multilingual students in the classes and increased socioeconomic, linguistic and ethnical segregation in the schools (Gustafsson, 2006) are further reasons for investigating effects of these changes in instructional modes, with a focus on differential effects. For this reason, a model is needed to describe and analyse mathematics instructional practice that has the potential to highlight dimensions of instructional responsibility for knowledge construction and how this responsibility is expressed by different aspects of teacher responsibilities in the instructional practice.

From a Vygotskian holistic point of view, learning is understood as a process where more complex structures of knowledge, present in the surrounding world, can be attained through interaction with other people (Vygotsky, 1978). The social action is to be viewed as a precondition for the individual action. The way participants in the mathematics classroom use different tools, such as language, for interpersonal and intrapersonal communication will affect the knowledge construction (Vygotsky, 1986). In the classroom, teachers obviously have the responsibility for arranging the instructional practice in order to enable this communication and thinking.

Research in the field of socio-cultural studies close to the context of the research objects has provided empirical evidence of the importance of instruction based on interaction between participants, where communication and teachers' responsibility for knowledge construction are essential (e.g. Barwell, 2003; Moschkovich, 2007). Previous research based on survey data concerning the effectiveness of different teaching patterns does not show such an unambiguous picture (Seidel & Shavelson, 2007). Analyses of video-data from the Third International Mathematics and Science Study (TIMSS 1995) describe different country-specific teaching patterns with different effects on achievements (e.g. Stigler & Hiebert, 1999), but in later empirical studies the complexity of these national characteristics is problematized. Huang and Leung (2002) compared how the same mathematical content was taught in the Czech Republic, Hong Kong and Shanghai and found that there are similarities between the teachings although the national characteristics vary. Another study that supports the unclear meaning of teaching patterns is presented by Hugener, Pauli, Reusser, Lipowsky, Rakoczy and Klieme (2009) who found complex relations between previous knowledge, teaching patterns and different qualities of outcomes. If students believe that they are capable of successfully mastering tasks, they are also more willing to take their own responsibility for the learning process, the authors' state. This shows the importance of teachers imparting self-reliance to the students in a way that enables them to take responsibility for their own learning process.

This study aims to investigate how the traditional division of mathematics teaching into teacher- and student-centred instructional practises overlaps the instructional responsibility for students' mathematics knowledge construction. A main aim is to develop a model that makes this instructional responsibility visible. Related to Vygotskys' theory of learning, this responsibility could be viewed as a prerequisite for interaction, communication and individual reasoning, which in this theory is meant to be necessary for students' own knowledge construction. Finally, the validity of this model for instructional responsibility will be examined by investigating its correspondence with Swedish data from TIMSS 2003, 8th grade.

2 How to conceptualise and define mathematics classroom practise

The term Instructional mode is used here as a label to depict what implicit pedagogical principles underlie classroom practises of instruction and instructional responsibility for mathematics knowledge construction. They are viewed as potentially important for students' opportunities to learn mathematics; ‘...differences in mathematical achievements among groups do not rest solely upon students' cultural/mathematical backgrounds, but also in the socio-political organization of mathematics classrooms’ (Lester, 2007, p. 407). This necessitates the development of a model for description and analysis of these modes. Conceptualisation of dimensions of classroom practise supportive of students’ mathematical progress will constitute the theoretical starting points when developing such a model. From previous research, several important underlying dimensions of implicit pedagogical principles in the mathematics instructional practise can be identified. In the following, some of these dimensions that deal with instructional responsibility and its consequences will be discussed.

It has been argued that instructional modes affording opportunities for interaction and talking are more supportive of students' mathematical progress than modes sustaining students' individual work. Moschkovich (2002) writes that all manners of talking can contribute in their own way to the mathematical discussion and bring resources to the conversation. That conversation is an important dimension of instructional modes for student’s mathematical progress is maintained by many researchers (Brown & Palincsar, 1989; King, 1992; Saxe, Gearhart, Note, & Paduano, 1993; Webb, 1991; Yackel, Cobb, Wood, Wheatley, & Merkel, 1990). Furthermore, different qualitative aspects of talking and interaction are problematized in previous studies, for example, how the mathematical content is treated. Clarke and Xu (2008) focused on the nature of the content of the talking, i.e. whether it is mathematical or more private, and emphasised this as important for students' mathematical progress. In the same study, the responsibility for how knowledge construction is distributed between teacher and students was emphasised and the importance of letting the students participate and take responsibility for their knowledge construction was stressed. Another qualitative aspect of interaction and talking concerns how teachers make use of the variation between students and how they take charge of the peer effects (Barwell & Clarkson, 2004; Hanushek & Wössmann, 2006; Moschkovich, 2002; Shayer & Adhami, 2007). Results from these studies indicate that teachers need to take responsibility both for emphasising and preparing the mathematics content and for making students' experiences and reasoning about the content visible in a way that enables students to take responsibility for their learning process. In other studies too, this is meant to be essential for mathematical learning (Bentley, 2003; Marton & Säljö, 1976, 1997; Stigler & Hiebert, 1997).

A frequently used way of categorising mathematics education is to distinguish between teacher- and student-centred modes of instruction. The ‘traditional instructional mode’ is characterised by teacher-centred instruction where the teacher is supposed mainly to explain procedures and give directions (Hiebert, Gallimore, Garnier, Givvin, Hollingsworth, & Jacobs, 2003; Porter, 1989; Silver & Smith, 1996; Stigler & Hiebert, 1997). The students are expected to listen and remember what the teacher says and very little time is spent on letting the students explain thoughts and reach a consensus on mathematical ideas. Interaction and communication are not supposed to be important. The teacher is expected to take the responsibility for emphasising and preparing the mathematics content, but not for making students' experiences and reasoning about the content visible in a way that enables them to take responsibility for their learning process. Thus, in this instructional mode, a dimension of instructional responsibility concerning teachers initiating students to construct their own knowledge is absent.

This way of conceptualising and defining classroom practice as teacher-centred has, however, been challenged by many researchers. In East Asian regions, it has been shown that descriptions of mathematics classrooms cannot easily be made in this way. Mok and Morris (2001) argue: “... these descriptions fail to capture many salient features of pedagogy”. In spite of the fact that the instructional mode was teacher-centred, the authors argued that the instructional practice could be viewed as a ‘social constructivist/Vygotskian model’. The lessons were characterised by interaction between participants and by active participation of the pupils. Classroom contexts were characterised by a combination of whole-class teacher–pupil interactions and highly structured group/pair work. A later study by Mok (2003) showed that teacher-centred instruction in East Asian regions was characterised by a conscious teacher intervention together with students' active thinking moments. The common stereotype view of teacher-centred modes has also been problematised by other researchers. For example, Clarke (2006) and Häggström (2008) both argue that underlying dimensions of teacher-centred instruction could be more complex than the traditional definition assumes.

Student-centred instruction is characterised more by interaction and communication in learning, which is intended to develop the mathematical identity of the student (Ball & Bass, 2000; Boaler & Greeno, 2000; Cobb, Wood, & Yackel, 1993; Lampert, 2001; Yackel et al., 1990). In this instructional mode, the teacher is viewed as vital for initiating interaction between participants and for striving for high quality in the conversation (Yackel et al., 1990), i.e. for initiating students' process of constructing their own mathematics knowledge. Thus, the results indicate that student-centred instruction supports students' mathematical learning when there is interaction and communication among participants, and when the teacher takes the responsibility for knowledge construction by both emphasising the mathematics content and giving the students opportunities to give their perspective on this content. This largely corresponds with what is emphasised in much research as important pedagogical principles in instructional practise. However, a dimension of instructional responsibility concerning teachers' support for students to construct their own knowledge is not that prominent in the student-centred instructional mode.

The student-centred way of defining classroom practise has not been problematised by researchers to the same degree as the teacher-centred mode. As was discussed earlier, a high degree of student-centring is traditionally seen as the more desirable instructional mode and a lower degree of student-centring is seen as less desirable. To characterise classroom practise as student-centred could, however, be misleading, if a dimension of instructional responsibility concerning in what way teachers are offering valid conditions for students' mathematics knowledge construction is lacking. Similarly, it could be misleading to characterise classroom practise as teacher-centred, as the dimension concerning in what way teachers are initiating students to construct their own knowledge would then not be noticed. Taken together, instructional responsibility could be present in both the teacher- and the student-centred instructional modes. These modes are, however, covered by different dimensions of responsibility, and no mode of those mentioned simultaneously covers both a dimension of responsibility for teaching, emphasising and preparing the mathematics content and a dimension for initiating students to construct their own knowledge.

Comprehensive school in Sweden is often characterised by the student-centred mode since the instructional mode “student's independent work” is predominant. However, in the student-centred mode, the teacher is supposed to be vital for initiating students' processes of knowledge construction and the instructional practice is supposed to be characterised by interaction and conversation. In contrast, the ‘student's independent work’ is characterised by modest teacher intervention and by little interaction and communication between participants (Skolverkets Rapport nr. 323, 2008; Vinterek, 2006).

Previous research indicates that this oft-occurring mode of instruction in Sweden may treat some students unfairly, as the responsibility for mathematics knowledge construction is handed over to the students:

If a large part of the constitution of the mathematical content in the classroom is handed over to the students there is a risk that less resourceful students will not be given the opportunity to discern critical aspect of the content. This means that students that have less previous experience rely more on the actual teaching and how the content is handled in the classroom by initiative from the teacher. (Häggström, 2008, p. 225)

The dominance in Sweden of ‘student's independent work’ has become apparent since 1994 when tracking was excluded from the curricula,Footnote 1 and during a period of a declining level of achievement and an increasing dispersion in mathematics performance, the presence of ‘student's independent work’ has continuously increased (Skolverkets Rapport nr. 323, 2008). It is thus important to further problematise the traditional way of characterising mathematics education in teacher- or student-centred modes. Instructional responsibility cannot be taken for granted when categorising instructional modes in the Swedish mathematics education. Thus, it is appropriate to simultaneously identify dimensions of instructional responsibility concerning the conditions supplied for students' mathematics knowledge construction and the responsibility for initiating students to construct this knowledge. Neither the student- nor the teacher-centred instructional mode is appropriate here. An alternative model for depicting mathematics instruction is thus needed.

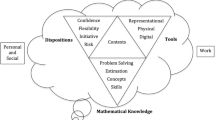
Such an alternative model has been developed in a theory by Brousseau (1986, 1997), the theory of didactic situation. Here, three parts are viewed as involved in a didactic situation, the teacher, the student and the academic subject. The relations between these parts could be described by a triangle where the corners represent the three parts and the axis the internal relations, see Fig. 1.

Fig. 1
figure 1

The didactical triangle by Brousseau

Full size image

This didactic situation is a model for explaining the interaction in a learning environment involving some mathematics, Brousseau argues. Beyond the student and the teacher, an additional instance, ‘the silent actor’ should be noted. This refers to rules, most often tacit, activated through the didactical contract. According to these roles, interaction comes up in the didactic situation. The social axis in Fig. 1 represents the negotiation between teachers and students that constitutes the roles. The didactical contract explains the rules that regulate the interaction between actors in the learning context in terms of responsibility of students and the teacher regarding what they could, should or should not do regarding mathematical knowledge (Brousseau, 1986, 1997).

Brousseau's model is neither teacher- nor student-centred but content-centred. The learning environment, however, is regarded as an important condition for students' construction of knowledge. In this model, the teacher does not have the power to make the students learn, this is the responsibility of the students, but the teacher must offer the conditions for them to access the knowledge. In the figure, this is represented in the didactical axis. The learning environment is, however, also supposed to be a-didactic in the sense that the teacher does not make known to the students their intention regarding the knowledge they have to construct, see the third axis in Fig. 1. The teacher must, however, verify that the students understand the task they have to solve and what is expected in the situation. The knowledge is constructed through interaction in the learning environment in the form of action and feedback. Thus, the teacher is not absent, he interacts with both the students and the system constructed by the students and the learning environment. Accordingly, this model considers how teachers both practise instructional responsibility and offer valid conditions for students' construction of their knowledge.

In the following review of previous research, some studies dealing with different aspects of responsibility will be discussed. One example is the study by Clarke and Xu (2008) mentioned above, in which the theoretical framework concerned the distribution of responsibility for knowledge construction between the teacher and the students. The focus in this study was not if, or in what way, teachers act to initiate students' processes of constructing their own knowledge. The focus, rather, was on the student's construction of knowledge. An essential concept in the study is ‘agency’, and the focus is on students' agency in the learning process, which could be regarded as an outcome of instructional responsibility. It is, however, only the dimension expressing teacher responsibility for initiating students' process of generating their own knowledge that is problematised, not the dimension expressing the responsibility for offering valid conditions for generating knowledge.

Amit and Fried (2005) and Fried and Amit (2003) discuss responsibility in terms of authority. They conclude that teachers in mathematics education have tremendous authority, and that this authority may have an impact on how students interact with the teacher and how they approach mathematics. The authors suggest that teachers use their authority to link together the private domain, which is distinguished by reflections and deliberations, and the public domain, which is more distinguished by precise use of standard notations and representations. This is called ‘revised authority’ in the study. Authority is mirrored in students' opinions about mathematics teachers and it is stated that students regard the teacher as the holder of knowledge and expertise. However, having tremendous authority does not automatically imply that this authority is used by the teacher in the instructional practice. This authority could be viewed as an appropriate means for teachers when creating opportunities for mathematics knowledge construction and foremost when initiating students' processes of constructing their own knowledge. In relation to the concept instructional responsibility discussed in this study, authority could thus be viewed as one quality of requirements for performing and maintaining this responsibility.

Mok, Cai and Fong Fung (2008) do not use the expression ‘responsibility’, but it is clear from this study that instructional responsibility should provide sufficient support for students' mathematical explorations, but not so much support that the teacher takes over the process of thinking from his students. Mok et al. (2008) argue that the opportunity for learning depends significantly on the nature of interaction generated in the classroom discourse, and that it is the teacher's choice to orchestrate the classroom discourse in that way. This pinpoints the two dimensions discussed above concerning how teachers practise instructional responsibility, namely, by both initiating students' processes of constructing their own knowledge and offering valid conditions for this construction of their knowledge.

Boaler and Greeno (2000) talk about traditional and reform-oriented teaching in terms of different qualitative outcomes of knowledge. The practise of learning forms the knowledge that is produced, they argue. Students in traditional teaching, which the authors name didactic teaching, may find it difficult to use their mathematics in new and varied situations. Students in reform-oriented teaching, which Boaler and Greeno (2000) call discussion-based teaching, are supposed to be more able to use their mathematical knowledge in new situations. Didactic teaching is characterised by students working with textbooks and the teachers presenting procedures, and these students are supposed to learn to perform. However, in discussion-based teaching, students should be active agents in their classes and their role is to contribute to the shared understanding of ideas developed in the class. In relation to the instructional responsibility, didactic- and discussion-based teachings represent two qualitatively different modes of instruction rather than two dimensions that simultaneously could be present in the same mathematics classroom.

Morgan, Tsatsaroni and Lerman (2002) have developed a model describing assessment practises, which consists of opposing forms according to the strength of power relations (examiner/teacher) and control relations (adviser/advocate). According to Morgan et al. (2002), the pedagogical discourse could serve to reproduce power and control relations or to change them. What is focused on by Morgan et al. is the strength of power relations, while what is focused on in the present study is the instructional responsibility mediated by teachers' and students' actions in the instructional practice.

To conclude, Clarke and Xu (2008) talk about students' responsibility for their knowledge generation as an outcome of an instructional responsibility, while Amit and Fried (2005) and Fried and Amit (2003) talk about authority which could be viewed as an appropriate means for teachers to initiate opportunities for this knowledge construction of students themselves, i.e. a quality of requirements for performing and maintaining responsibility. Mok et al. (2008) do not, however, explicitly talk about responsibility, but state that teachers in the instructional practice should provide sufficient support for students’ mathematical progress, but also hand over responsibility to the students for managing their own processes of thinking. Boaler and Greeno (2000) also talk about these two dimensions, not as interacting in the same mathematics classroom but rather as two qualitatively different modes of instruction labelled didactic- and discussion-based teaching. Finally, the reproduction of power and control relations is discussed by Morgan et al. (2002). These studies all touch on different dimensions of responsibility for mathematics knowledge construction. However, to describe and analyse consequences of Swedish mathematics education, a broad spectrum of essential dimensions of instructional responsibility for students' mathematics knowledge construction should simultaneously be elucidated. Although such dimensions have been discussed by others, none of those mentioned above, with the exception of Brousseau's theory, has discussed them simultaneously in terms of instructional responsibility, and that is what I intend to do in this study.

The aim of this study is to develop a model for description and analysis of classroom practices of mathematics instruction. In doing this, it has been hypothesised that instructional responsibility is important for students' chances of learning mathematics during mathematics lessons, and further that instructional responsibility is multidimensional. One of these dimensions is the teacher's responsibility for offering valid conditions for students' construction of their own knowledge and another is the teacher's responsibility for initiating students' processes of constructing their own knowledge. Finally, to emphasise the content and not just the modes of working, a dimension capturing the mathematics content is also needed. This hypothesised model relates in some respects to Brousseau's theory (1986, 1997), which focuses on the entire set of dimensions. However, here a large-scale empirical approach is adopted to characterise variation between classrooms along the three hypothesised dimensions. Other authors cited above, do not simultaneously focus on all dimensions of instructional responsibility, but their findings have nonetheless inspired the design of the present model. Mok et al. (2008) deal with the two above-mentioned dimensions of teacher responsibility, even though they are conceptualised in another way. In this study, the hypothesis will be tested by investigating how the three-dimensional construct instructional responsibility is reflected in an empirical data set, TIMSS 2003.

3 Research settings and method

The empirical study was conducted as a secondary analysis of TIMSS data from 2003 focusing on mathematics for Swedish students in 8th grade. A latent variable analysis was conducted in order to identify descriptive dimensions of instructional modes concerning both teacher responsibility and mathematics content that could support students' mathematical progress.

3.1 Data sources

The data source for the empirical study was the TIMSS 2003 study, focusing on mathematics for Swedish students in 8th grade, with 4,256 students from 274 classes in 160 schools. The contextual variables were derived from teacher and student questionnaires. In the data subset used, only those classes with one mathematics teacher were included (253 classes). After listwise deletion, there were 3,288 observations left in 217 classes with an average cluster size of 15.15. For items used in the analysis, see Table 1.

Table 1 List of items used in the CFA, within(individual)- and between(class)-level
Full size table

3.2 Latent variable analysis through multilevel confirmatory factor analysis, M-CFA

Because of the design effect in survey research using cluster samples, it was necessary to take into account the hierarchical structure of the data (Hox, 2002). Accordingly, Multilevel Confirmatory Factor Analysis (M-CFA) was used as the method of analysis. CFA requires a strong empirical or conceptual foundation to guide the specification and evaluation of the factor model (Brown, 2006). Factor analysis is an analytical approach intended to recognise underlying dimensions of a construct, in this study the ‘instructional mode’. A latent variable (an unobserved variable), or a factor, represents the theoretical construct which is measured by a number of observed (manifest) variables, indicating the construct. The connection between the indicators and the latent variable is expressed by the factor loadings, the magnitude of the relations between indicators and the latent variable (Brown, 2006). The multilevel approach refers to the hierarchical structure of the data. In this study there is such a relation between individuals, representing the student level, and the educational group, representing the class level. Students, thus, are nested within classes. To avoid both measurement and conceptual problems, standard analysis methods should not be used (Hox, 2002). The method used in this analysis, M-CFA, separates the variation between the students from the variation between the classes, and offers estimated model parameters separately for the student and the class levels. Because of the multilevel approach, observed variables obtained from both the student and the teacher questionnaires are allowed to indicate the construct at the class level. For the student level, however, only observed variables obtained from the student questionnaire could be used.

A two-level structural equation model approach with three factors was adopted for the measurement model and the Mplus (Muthén & Muthén, 1998) and STREAMS (Gustafsson & Stahl, 2004) software was applied in the analyses. The Within-level represents individual students within the classes and the Between-level represents classes and concerns differences between classes. The latent factors were indicated by ten items from the student questionnaire and seven from the teacher questionnaire, see Table 1. Students in the TIMSS study responded to the questions ‘In math lessons, how often do you do...?’ Responses were indicated on a 4-point Likert scale, which ranged from 1 (Every or almost every lesson) to 4 (Never). Teachers either responded to the questions ‘In math lessons, how often do you ask students to...’ or to ‘Which part of the lesson time in mathematics do students...?’ Responses were noted on a 4-point Likert scale, which ranged from 1 (Every or almost every lesson) to 4 (Never), or by supplying a percentage estimate.

Several indices were used to assess model fit: chi-square test, root mean-square error of approximation (RMSEA) and the standardised root mean-square residual (SRMR) (Brown, 2006). RMSEA values of less than 0.05 represent a ‘close fit’, and models with values above 0.1 should be rejected. The SRMR was used as an absolute fit index. The SRMR value should be 0.08 or less. Because the chi-square statistic is very sensitive to sample size, chi-square/df ratio was examined to check fit (Kline, 1998). A goodness-of-fit index, Comparative Fit Index, CFI, shows a good performance overall (Hox, 2002). Usually a value of at least 0.95 is required to accept a model.

3.3 Hypothesised measurement model for instructional modes

The research question in this study concerns how to frame a model for description and analysis of mathematics instruction important for students' performances. It is hypothesised that instructional responsibility is important for student's chances of learning mathematics during the mathematic lessons, and further that instructional responsibility is multidimensional. In order to develop a measurement model for the construct instructional responsibility, the theoretical starting points for formulation of latent factors and selection of appropriate indicators were made explicit. One of the dimensions was hypothesised to be the teacher's responsibility for offering valid conditions for students' construction of their own knowledge, for example, by emphasising and preparing the mathematics content. Another dimension was hypothesised to be the teacher's responsibility for initiating students' processes of constructing their own knowledge, for example, by making their experiences and reasoning about the content visible. Finally, a third dimension, representing the specific mathematics content, was hypothesised to be essential when modelling instructional responsibility.

The first dimension of instructional responsibility was hypothesised to be represented by the latent factor labelled Teacher Responsibility for offering valid Conditions for students' mathematics learning (TRC). The second dimension was hypothesised to be represented by the latent factor labelled Teacher Responsibility for initiating Students to construct their own mathematics knowledge (TRS). Finally the third dimension of underlying important instructional responsibility was represented by the latent factor labelled Specific Mathematics Content (SMC). In order to highlight the presence of relevant mathematics content in the mathematics classrooms, this dimension was hypothesised to represent teacher responsibility for emphasising the mathematics content and not just working modes, which are captured by the two previous latent factors.

The elaborated construct instructional responsibility was tested by TIMSS data from 2003 focusing on mathematics for Swedish students in 8th grade. Beyond performance on the mathematics test, this data set also contains information about background variables and the mathematics teaching. TIMSS data makes analysis at both student- and class-level possible. For the present study with a focus on mathematics instruction, the TIMSS data thus constitutes a relevant basis. However, with these data it is not possible to investigate how the instruction is manifested in the classroom, just how it manifests itself in students' and teachers' own experiences of mathematics lessons, as evidenced by their responses in questionnaires. This thus constitutes a restriction when interpreting the validity of the construct. However, the TIMSS data offer a lot of information and the quality is excellent in many respects (Gustafsson, 2008), although the complexity, the lack of control of the data and the loss of key variables should be taken into account when performing secondary analysis (Bryman, 2004).

Teacher responsibility for offering valid conditions for students' construction of their own knowledge could be indicated by observed variables regarding both students' and teachers' opinions about how the mathematics content is being emphasised and prepared by the teacher. The teacher's responsibility for initiating students' processes of constructing their own knowledge could similarly be indicated by observed variables regarding both students' and teachers' opinions about how it is made possible for students to construct their own knowledge, for example by using their experiences and reasoning about the content. Finally, observed variables regarding the students' opinions about the instruction in terms of specific mathematics content could indicate the third dimension in the construct.

When related to Swedish conditions, the dimension concerning teacher responsibility for offering valid conditions for students' mathematics learning, TRC, was hypothesised to be an important underlying pedagogical principle. As has already been mentioned, in Sweden the instructional mode ‘student's independent work' is heavily relied upon in mathematics education and this practice is characterised by students both planning and working on their own with different tasks independent of other students, with responsibility laid on students' individual responsibility for mathematics learning (Ståhle, 2006; Vinterek, 2006; Österlind, 1998). The TRC dimension could be viewed as a prerequisite for the mathematics content to be emphasised and prepared and for interaction and talking to be realised, which in this study was hypothesised to be characteristics of approaches influencing students' mathematical progress.

Observed variables from both the student and the teacher questionnaires in the TIMSS data were selected for indicating the latent factor TRC, see Table 1. From the student questionnaire, three observed variables were chosen to capture this latent factor, namely, BSBMHLSP (In your math lessons, how often do you listen to the teacher giving a lecture-style presentation?), BSBMHHQT (In your math lessons, how often do you have a quiz or test?) and BSBMHWPO (In your math lessons, how often do you work on problems on your own?). From the teacher questionnaire it was hypothesised that four observed variables have the capacity to reflect this latent factor, namely, BTBMASWF (In teaching mathematics to the students in the TIMSS class, how often do you usually ask them to work with fractions and decimals?), BTBMPTLS (In a typical week of mathematics lessons for the TIMSS class, what percentage of time do students spend listening to lecture-style presentations?), BTBMPTTQ (In a typical week of mathematics lessons for the TIMSS class, what percentage of time do students spend taking tests or quizzes?) and BTBMASPC (In teaching mathematics to the students in the TIMSS class, how often do you usually ask them to practise computational skills?). All the selected observed variables depict a classroom in which the teacher emphasises and prepares the mathematics content. The manifest variable BSBMHWPO should be viewed as an indicator of the individual student's experiences of working with the mathematics content itself, rather than an indicator of his/her experiences of working autonomously. However, it was hypothesised that this manifest variable should not be included at the class level because it probably does not distinguish between classes, depending on the customary presence of individually working in the classes. To sum up, this latent factor was included in the model aiming to show the extent to which the responsibility for offering valid conditions for students' construction of their own knowledge by emphasising and preparing the mathematics content is focused on the teacher. From the student and teacher questionnaires in the TIMSS data, seven observed variables were hypothesised to have the capacity to reflect this latent factor.

For the second latent factor, TRS, indicators were selected that reflect to what extent teachers take the responsibility for initiating students' processes of constructing their own knowledge by e.g. making their experiences and reasoning about the content visible, see Table 1. From the student questionnaire in the TIMSS data, four observed variables were hypothesised to have the capacity to indicate this latent factor, namely, BSBMHMDL (In your math lessons, how often do you relate what you are learning in mathematics to your daily life?), BSBMHROH (In your math lessons, how often do you review your homework?), BSBMHEXP (In your math lessons, how often do you explain your answers to the class?) and BSBMHSCP (In your math lessons, how often do you decide on your own procedures for solving complex problems?). These observed variables mirror a classroom where student’s experiences and ways of reasoning about mathematical issues are made visible, i.e. teachers who use their responsibility for giving the students opportunities to relate to their everyday life, to their experiences and to their work with mathematical issues. From the teacher questionnaire, the indicators BTBMASDL (In teaching mathematics to the students in the TIMSS class, how often do you usually ask them to relate what they are learning in mathematics to their daily lives?), BTBMHDAD, (How often do you use the homework as a basis for class discussion about the mathematics homework assignments?) and BTBMASEA (In teaching mathematics to the students in the TIMSS class, how often do you usually ask them to explain their answers?) were selected. For the same reasons as those stated above for BSBMHWPO, BSBMHSCP should be viewed as an indicator depicting diversity among students within classes but not between classes. To sum up, this latent factor, TRS, was included in the model aiming to show how teachers take the responsibility for initiating students' processes of constructing their own knowledge by e.g. making their experiences and reasoning about the content visible. From the student and teacher questionnaires in the TIMSS data, seven observed variables were hypothesised to have the capacity to reflect this latent factor.

Finally, the latent factor labelled SMC, concerning the presence of relevant mathematics content in the mathematics classroom, was included in the model. In the student questionnaire in the TIMSS data, only four observed variables contained information about specific mathematics content. Other items were about forms of education. Three of these four variables have been used as indicators of this latent factor, while one has been disregarded in this study. The observed variables hypothesised to have the capacity to depict this latent factor were BSBMHASM (In your math lessons, how often do you practise adding, subtracting, multiplying, and dividing without using a calculator?), BSBMHWFD (In your lessons, how often do you work with fractions and decimals?) and BSBMHEFR (In your math lessons, how often do you write equations and functions to represent relationships?). The topics mirrored by these variables emphasise mathematics content with relevance for the mathematics teaching for grade 8. Students with high scores on these questions are able to regard their instruction in terms of specific mathematics content. They show awareness of the occurrence of this specific content in the mathematics lessons. The observed variable BSMHGCT (In your math lessons, how often do you interpret data in tables, charts or graphs?) was excluded because it represents such a frequent topic in Swedish mathematics teaching that when used as an indicator for SMC it does not contribute to distinguishing between the different classrooms in the dataset. The other three variables do, however, have this capacity.

4 Results

In order to evaluate the potential for this hypothesised model to account for observed relations in empirical data, an examination of the correspondence between the model and Swedish data from TIMSS 2003, 8th grade, was made. The results are shown in Fig. 2, with factor loadings and variances for the indicators, both for the Within- and the Between-levels. The intra-class correlation, ICC, suggested sizeable class effects, the ICCs ranging between 0.051 and 0.291. The model showed a reasonably good fit. The comparative fit index, CFI, was 0.863 and the root mean-square error of approximation, RMSEA, was 0.036. There was an appropriate model fit at the student level, where the standardised root mean-square residual, SRMR, was 0.027. The fit at the class level was, however, a bit harder to interpret, the SRMR measure being somewhat higher (0.126) than the suggested criterion. As the modification indices on the Between-level showed no indications of local misfit, the impressions of poor model fit signalled by the SRMR index may be due to limitations of this index when applied in multilevel structural equation models (Brown, 2006). The substantial meaningfulness of the model, and the possibilities of interpretation, also contribute to the evaluation of the fit.

Fig. 2
figure 2

Factor loadings for within(individual)- and between(class)-level estimates. (Two-tailed Est./SE < 2.0, p value >0.05)

Full size image

The latent variables were all positively correlated, but no correlation was higher than 0.8, which supports the hypothesis that the latent factors represent different constructs (Brown, 2006). See Table 2.

Table 2 Factor correlation, within- and between-level
Full size table

All factor loadings in the model were statistically significant. Substantially they also correspond to the underlying theoretical starting points for the model. For the latent factor Teacher Responsibility for offering valid Conditions for students' mathematics learning (TRC), which was hypothesised to be indicated by items mirroring to what extent teachers take the responsibility for offering valid conditions for students' construction of their own knowledge by e.g. emphasising and preparing the mathematics content, most factor loadings for the selected indicators were significant and medium-high, both at the Within- and at the Between-level. Two factor loadings at the Between-level were, however, negatively loaded, although one of them was scarcely significant. These indicators could still be interpreted as utterances from teachers who are taking the responsibility for knowledge construction. If the teacher during the mathematics lessons feels that there is insufficient time for both traditional lectures, tests and other pedagogical practices, then negative relations between these different categories of indicators could arise. The scaling for the two negatively loaded indicators is also different from the scaling used for all other indicators in the model. These items ask for the percentage of the lesson time during one normal week (In a typical week of mathematics lessons for the TIMSS class, what percentage of time do students spend listening to lecture-style presentations?/BTBMPTLS and In a typical week of mathematics lessons for the TIMSS class, what percentage of time do students spend taking tests or quizzes?/BTBMPTTQ). Teachers who take the responsibility for offering valid conditions for students' construction of their own knowledge in the instructional practice could also feel that the time for traditional lectures and tests is limited, and this could be because these teachers prioritise more time for other activities than traditional ‘teachers-desk instruction’. The students, on the other hand, at the same time answer that they often listen to long briefings and having tests, but they do not take into account how large a part of the lesson time these take. Factor loadings for the indicators from the student questionnaire, unlike those from the teacher questionnaire, thus are positive, but express the same conditions, namely teachers taking responsibility for emphasising and preparing the mathematics content. These results suggest that it is possible to distinguish variation between individuals within and between classes concerning teacher responsibility for emphasising and preparing the mathematics content.

For the latent factor Teacher Responsibility for initiating Students to construct their own mathematics knowledge (TRS), all factor loadings were found to be significant and somewhat higher. This latent factor is thus well indicated by the present subset of items concerning students' opinions about and opportunities for taking responsibility for their own learning process. The indicators BTBMASEA (In teaching mathematics to the students in the TIMSS class, how often do you usually ask them to explain their answers?) and BTBMASDL (In teaching mathematics to the students in the TIMSS class, how often do you usually ask them to relate what they are learning in mathematics to their daily lives?) had weaker factor loadings than other indicators. A common characteristic of all indicators depicting this latent factor is teacher responsibility for initiating students' processes of constructing their own knowledge, for example, by making their experiences and reasoning about the content visible.

Finally, the latent factor Specific Mathematics Content (SMC) was found to be well captured by the current set of indicators with fairly high factor loadings. This latent factor mirrors the extent to which students experience the presence of specific mathematics content in the mathematics classrooms. The observed variable BSBMHASM (In your math lessons, how often do you practise adding, subtracting, multiplying, and dividing without using a calculator?) indicates work with arithmetic without a calculator, BSBMHWFD (In your lessons, how often do you work on fractions and decimals?) indicates work with fractions and decimals corresponding with the aims of the curriculum. Finally, the observed variable BSBMHEFR (In your math lessons, how often do you write equations and functions to represent relationships?) indicates work with equations and functions that also corresponds with the aims of the curriculum.

To sum up, the investigation of the correspondence between the model and data from TIMSS 2003 shows a satisfactory result. The model demonstrates the potential to describe Swedish mathematics education among 8th graders along the lines of the dimensions in the model. This is, however, shown to be easier between students within the classes than between the classes. The substantial meaningfulness of the model contributes to the assessment of model fit.

5 Discussion

In this study, a model is suggested for analysing classroom practises of mathematics instruction that challenges the traditional division into teacher- versus student-centred modes. It is hypothesised that instructional responsibility is important for students' chances of learning mathematics during the lessons and, further, that instructional responsibility is multidimensional. One dimension is characterised by the teachers taking the responsibility for offering students valid conditions for constructing their own knowledge, and another by responsibility for initiating students’ processes of knowledge construction. These two, together with a third dimension concerning the presence of specific mathematics content in the mathematics classroom, constitute the theoretical basis of the model for instructional mode developed in this study. For Swedish conditions, with the heavy use of self-regulatory and individualized ways of working in mathematics education, the instructional responsibility for knowledge construction cannot be taken for granted. By making this responsibility clear by means of a model for description and analysis of mathematics instructional practises, a tool for analysing and changing the practice is obtained.

By means of two-level confirmatory factor analysis, it has also been investigated whether this model agrees with Swedish 8th grade data from TIMSS 2003. The results show that the model can account for the interrelations at both individual and classroom levels among questionnaire items hypothesised to represent the proposed dimensions of instructional responsibility. The TIMSS data thus support the model, even though this empirical support is not without complications.

The first dimension in the model is represented by the latent factor labelled Teacher Responsibility for offering valid Conditions for students' mathematics learning. This dimension captures one important aspect of the traditional teacher-centred instruction, namely, whether the teacher takes the responsibility for emphasising and preparing the mathematics content or not. Teacher-centred instruction is, however, conceptualised in a more normative way, where teachers are mainly supposed to explain procedures and give directions, which is believed to be sufficient in the learning process. Interaction and communication are thus not prominent in that mode, while in TRC they are an essential aspect of the dimension. The selected items from the student and the teacher questionnaires contributed to the validation of this dimension. However, the lack of items indicating the presence of talking and communication makes the representation of this dimension less than perfect. Also, the limited variation among the observed variables derived from the teacher questionnaire limits the possible selection of indicators. Nevertheless, it is still judged that the TIMSS data have the quality to validate the dimension TRC in the construct instructional responsibility.

The second dimension in the construct is labelled Teacher Responsibility for initiating Students to construct their own mathematics knowledge. This dimension captures essential aspects of the mode student-centred instruction, but from the instructional point of view. Items reflecting students' and teachers' opinions concerning their own experiences of mathematics lessons indicate opportunities for students' reasoning, for using their experiences, for constructing mathematics knowledge, etc. It would, however, be desirable to have access to variables with more power to characterise the mathematics classrooms. Some of the variables used in this study represent vague questions with possibilities for students and teachers to make broad interpretations, possibly resulting in biased answers and validity problems. For example, teachers could in general be willing to answer ‘yes’ to the question of whether they ask students to relate what they learn to everyday life or not. Some indicators may thus lack the capacity to discern different instructional modes. However, the data used provides a sufficiently good foundation for validating the dimension TRS.

Finally, the dimension Specific Mathematics Content makes it possible to highlight the presence of relevant mathematics content in the mathematics classrooms, depicting the extent to which the teacher takes the responsibility for emphasising the content and not just the forms of working that are represented in the two previous latent factors. This dimension is well captured by the current set of indicators but it should be noted that only variables from the student level are used due to a lack of variation in the teachers' answers.

The use of TIMSS data as the basis of the construction of the model is justified by its potential to capture general structures within educational practise. The high quality of the data and its representation of different levels within the educational system make it possible to conduct powerful analyses. The size of the dataset, with a broad range of classes represented, is a requirement when analysing differences. However, besides a lack of observed variables to fully represent the dimensions in the model, some limitations with respect to the validity of the observed variables have been mentioned earlier. The questions asked could lose in precision because of their general nature and insufficient national adaptations. They also run the risk of capturing a superficial level of the instructional practise instead of underlying essential dimensions. However, bearing in mind the many merits of the data, these shortcomings do not repudiate their capacity to test the hypothesised model in this study.

The correspondence of this model with data from TIMSS 2003 is good, which supports the appropriateness to adopt the model to yield alternative perspectives on modes of instruction. It should be noted, though, that at the class level, there are some weak factor loadings and that some dimensions in the model would benefit from better indicators. There is thus room to improve the model and to refine the validation by using other data.

An essential implication of the results from this study is the potential of the model developed to further examine effects of the commonly occurring instructional mode ‘student's independent work’ in Swedish mathematics education, with a focus on differential effects on different groups of students. In contrast to more traditional models for mathematics instruction but in line with Brousseau's theory of the didactic situation, the model developed in this study makes it possible to simultaneously focus on different dimensions of instructional responsibility for knowledge construction, which could provide useful conceptual tools for analysing classroom practises. However, the model also demonstrates how the three dimensions may be identified through combining information from teachers and students about their perceptions of the teaching, which makes it possible to use the model in further empirical research on antecedents and consequences of the dimensions of instructional responsibility.