Skip to main content
SpringerLink
Log in

Every unsuccessful problem solver is unsuccessful in his or her own way: affective and cognitive factors in proving

  • Published:
Educational Studies in Mathematics Aims and scope Submit manuscript

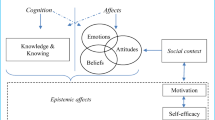
Abstract

It is widely recognized that purely cognitive behavior is extremely rare in performing mathematical activity: other factors, such as the affective ones, play a crucial role. In light of this observation, we present a reflection on the presence of affective and cognitive factors in the process of proving. Proof is considered as a special case of problem solving and the proving process is studied adopting a perspective according to which both affective and cognitive factors influence it. To carry out our study, we set up a framework where theoretical tools coming from research on problem solving, proof and affect are present. The study is performed within a university course in mathematics education, where students were given a statement in elementary number theory to be proved and were asked to write down their proving process and the thoughts that accompanied this process. We scrutinize the written protocols of two unsuccessful students, with the aim of disentangling the intertwining between affect and cognition. In particular, we seize the moments in which beliefs about self and beliefs about mathematical activity shape the performance of our students.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. The full text of the questionnaire is reported as an appendix in (Hadamard 1954).

  2. There is evidence that already in 1914 Hadamard and Polya worked together.

  3. It is well known that there is a problem of terminology, see the discussion in the book (Leder et al. 2002). We adopt the view of McLeod (1992), who claims that “the affective domain refers to a wide range of beliefs, feelings, and moods that are generally regarded as going beyond the domain of cognition. H. A. Simon (1982), in discussing the terminology used to describe the affective domain, suggests that we use affect as a more general term; other terms (for example, beliefs, attitudes, and emotions) [are] used as more specific descriptors of subsets of the affective domain.” (p. 576)

  4. We underline the difference between the representational systems cited before (affective system, cognitive system, ...) and the representations as semiotic resources (symbols, graphs, ...).

  5. In (Harel & Sowder 1998) a person’s proof scheme consists of what constitutes ascertaining and persuading for that person. These schemes are grouped in three main classes: external (ritual, authoritarian, symbolic), empirical (inductive, perceptual), analytical (transformational, axiomatic). In this study we will be concerned with ritual proof scheme (mathematical arguments are judged only on the basis of their surface appearance) and symbolic proof scheme (proof is carried out using symbols without reference to their meaning).

  6. Cognitive units are defined by Barnard and Tall (1997, p. 41) as “a piece of cognitive structure that can be held in the focus of attention all at one time”.

  7. These students follow a curriculum which is oriented to the profession of mathematics teacher in secondary school. To become a mathematics teacher it is necessary to have a degree in scientific or technological disciplines and afterwards to follow a two years training program.

  8. Two proofs are reported in the Appendix.

  9. The case study of Frank is performed through the analysis of different sets of data: questionnaire on beliefs, on-line motivation questionnaire on the problem, video of the think aloud solving process, video based stimulated recall interview.

  10. We point out that when we mention panic, we do not refer to an attitude towards mathematics in general, rather we refer to a state of feeling confined to the moment of resolution of the given problem.

  11. We note that Booh uses the term least rather than greatest, but he refers to divisors and not to multiples.

  12. Indeed, the definition of coprime numbers requires also the fact that 1 is the only common factor (this means that it is the greatest common factor, and not the least!).

  13. Leo Tolstoy, Anna Karenina (1877; trans. Constance Garnett).

References

  • Barnard, T., & Tall, D. (1997). Cognitive units, connections and mathematical proof. In E. Pehkonen (Ed.) Proceedings of PME 21 (Vol. 2, pp. 41–48). Lahti - Helsinki: University of Helsinki – Lahti Research and Training Centre.

    Google Scholar 

  • Berger, P. (1998). Exploring mathematical beliefs – the naturalistic approach. In M. Ahtee, & E. Pehkonen (Eds.), Research methods in mathematics and science education (pp. 25–40). Helsinki: Department of Teacher Education, Research Report 185.

    Google Scholar 

  • Boaler, J. (1997). Experiencing school mathematics: Teaching styles, sex and setting. Buckingham, (Bucks): Open University Press. As quoted in (Burton, 1999).

  • Boaler, J., Wiliam, D., & Brown, M. (1998). Students’ experiences of ability grouping-disaffection, polarisation and the construction of failure. Paper given to the Mathematics Education and Society Conference (Measi1), Nottingham, September. As quoted in (Burton, 1999).

  • Boero, P. (2001). Transformation and anticipation as key processes in algebraic problem solving. In R. Sutherland, T. Rojano, A. Bell, & R. Lins (Eds.), Perspectives on school algebra (pp. 99–119). Dordrecht: Kluwer.

    Google Scholar 

  • Brousseau, G. (1997). Theory of didactical situations in mathematics, Didactique des mathématiques 1970–1990. Dordrecht: Kluwer.

    Google Scholar 

  • Burton, L. (1999). Why is intuition so important to mathematicians but missing from mathematics education? For the Learning of Mathematics, 19(3), 27–32.

    Google Scholar 

  • Carlson, M., & Bloom, I. (2005). The cyclic nature of problem solving: an emergent multidimensional problem-solving framework. Educational Studies in Mathematics, 58, 45–75.

    Article  Google Scholar 

  • Clarkson, P., & Leder, G. C. (1984). Causal attributions for success and failure in mathematics: a cross cultural perspective. Educational Studies in Mathematics, 15, 413–422.

    Article  Google Scholar 

  • Crawford, K., Gordon S., Nicholas, J., & Prosser, M. (1994). Conceptions of mathematics and it is learning: The perspectives of students entering university. Learning and Instruction, 4, 331–345. As quoted in (Burton, 1999).

    Article  Google Scholar 

  • DeBellis, V. A., & Goldin, G. A. (1997). The affective domain in mathematical problem solving. In E. Pehkonen (Ed.) Proceedings of PME 21 (Vol. 2, pp. 209–216). Lahti - Helsinki: University of Helsinki–Lahti Research and Training Centre.

  • DeBellis, V. A., & Goldin, G. A. (2006). Affect and meta-affect in mathematical problem solving: a representational perspective. Educational Studies in Mathematics, 63, 131–147.

    Article  Google Scholar 

  • Evans, J., Hannula, M. S., Zan, R., & Brown, L. C. (Guests eds.) (2006a). Affect in Mathematics Education: exploring theoretical frameworks. A PME special issue. Educational Studies in Mathematics, 63(2).

  • Evans, J., Morgan, C., & Tsatsaroni, A. (2006b). Discursive positioning and emotion in school mathematics practices. Educational Studies in Mathematics, 63, 209–226.

    Article  Google Scholar 

  • Frank, M. L. (1985). What myths about mathematics are held and conveyed by teachers? Arithmetic Teacher, 37, 10–12.

    Google Scholar 

  • Furinghetti, F., & Morselli, F. (2007). For whom the frog jumps: the case of a good problem solver. For the Learning of Mathematics, 27(2), 22–27.

    Google Scholar 

  • Garofalo, J. (1989). Beliefs and their influence on mathematical performance. Mathematics Teacher, 82, 502–505.

    Google Scholar 

  • Gholamazad, S., Liljedahl, & P., Zazkis, R. (2003). One line proof: what can go wrong? In N. A. Pateman, B. J. Dougherty, & J. T. Zilliox (Eds.), Proceedings of PME 27 and PMENA (Vol. 2, pp. 429–435). Honolulu: University of Hawai’i.

    Google Scholar 

  • Goldin, G. A. (2002). Affect, meta-affect, and mathematical belief structures. In G. C. Leder, E. Pehkonen, & G. Törner (Eds.), Beliefs: A hidden variable in mathematics education? (pp. 59–72). Dordrecht: Kluwer.

    Google Scholar 

  • Gómez-Chacón, I. N. (2000). Affective influence in the knowledge of mathematics. Educational Studies in Mathematics, 43, 149–168.

    Article  Google Scholar 

  • Hadamard, J. (1954). An essay on the psychology of invention in the mathematical field. New York: Dover, (First published by PUP in 1945).

    Google Scholar 

  • Harel, G., & Sowder, L. (1998). Students’ proof schemes: Results from exploratory studies. In A. H. Schoenfeld, J. Kaput, & E. Dubinsky (Eds.), Research in Collegiate Mathematics Education (Vol. 3, pp. 234–283). Providence, RI: American Mathematical Society.

    Google Scholar 

  • Haylock, D. W. (1987). A framework for assessing mathematical creativity in schoolchildren. Educational Studies in Mathematics, 18, 59–74.

    Article  Google Scholar 

  • Hazin, I., & da Rocha Falcâo, T. (2001). Self-esteem and performance in school mathematics: a contribution to the debate about the relationship between cognition and affect. In M. van den Heuvel-Panhuizen (Ed.), Proceedings of PME 25 (Vol. 3, pp. 121–128). Utrecht: Freudenthal Institute.

    Google Scholar 

  • Heath, T. L. (1956). The thirteen books of Euclid’s Elements translated from the text of Heiberg with introduction and commentary. New York, NY: Dover Publications.

    Google Scholar 

  • Imai, T. (2000). The influence of overcoming fixation in mathematics towards divergent thinking in open-ended mathematics problems on Japanese junior high school students. International Journal of Mathematical Education in Science and Technology, 31, 187–193.

    Article  Google Scholar 

  • Lampert, M. (1990). When the problem is not the question and the solution is not the answer: mathematical knowing and teaching. American Educational Research Journal, 27, 29–63.

    Google Scholar 

  • Leder, G. C., Pehkonen, E., & Törner, G. (2002). Beliefs: A hidden variable in mathematics education? Dordrecht: Kluwer.

    Google Scholar 

  • Leron, U., & Hazzan, O. (1997). The world according to Johnny: a coping perspective in mathematics education. Educational Studies in Mathematics, 32, 265–292.

    Article  Google Scholar 

  • Lithner, J. (2000). Mathematical reasoning in school tasks. Educational Studies in Mathematics, 41, 165–190.

    Article  Google Scholar 

  • Mason, J., & Pimm, D. (1984). Generic examples: seeing the general in the particular. Educational Studies in Mathematics, 15, 277–289.

    Article  Google Scholar 

  • McLeod, D. B. (1992). Research on affect in mathematics education: a reconceptualization. In D. A. Grouws (Ed.), Handbook of research on mathematics learning and teaching (pp. 575–596). New York, NY: Macmillan.

    Google Scholar 

  • McLeod, D. B. (1994). Research on affect and mathematics learning in the JRME: 1970 to the present. Journal for Research in Mathematics Education, 25, 637–647.

    Article  Google Scholar 

  • Morselli, F. (2002). Analisi di processi dimostrativi in ambito algebrico, Unpublished Dissertation, Dipartimento di Matematica dell’Università di Genova.

  • Morselli, F. (2006). Use of examples in conjecturing and proving: an exploratory study. In J. Novotná, H. Moraová, M. Krátká, & N. Stehlíková (Eds.), Proceedings of PME 30 (Vol. 4, pp. 185–192). Prague: Charles University.

    Google Scholar 

  • Op’T Eynde, P., & Hannula, M. (2006). The case study of Frank. Educational Studies in Mathematics, 63, 123–129.

    Article  Google Scholar 

  • Pehkonen, E., & Pietilä, A. (2003). On relationships between beliefs and knowledge in mathematics education. In M.A.Mariotti (Ed.), Proceedings of CERME 3, CD-Rom.

  • Poincaré, H. (1908). L’invention mathématique. L’Enseignement Mathématique, 10, 357–371.

    Google Scholar 

  • Polya, G. (1931). Comment chercher la solution d’un problème de mathématiques? L’Enseignement Mathématique, 30, 275–276.

    Google Scholar 

  • Polya, G. (1945). How to solve it, A new aspect of mathematical method. Princeton: PUP.

    Google Scholar 

  • Radford, L. (1996). La résolution des problèmes: comprendre puis résoudre. Bulletin AMQ, XXXVI(3), 19–30.

    Google Scholar 

  • Schoenfeld, A. H. (1983). Beyond the purely cognitive: Beliefs systems, social cognitions, and metacognitions as driving forces in intellectual performance. Cognitive Science, 7, 329–363.

    Article  Google Scholar 

  • Schoenfeld, A. H. (1987). Confessions of an accidental theorist. For the Learning of Mathematics, 7(1), 30–38.

    Google Scholar 

  • Schoenfeld, A. H. (1989). Exploration of students’ mathematical beliefs and behavior. Journal for Research in Mathematics Education, 20, 338–355.

    Article  Google Scholar 

  • Schoenfeld, A. H. (1992). Learning to think mathematically: problem solving, metacognition and sense making in mathematics. In D. A. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 334–370). New York, NY: Macmillan.

    Google Scholar 

  • Simon, H. A. (1982). Comments. In M. S. Clark, & S. T. Fiske (Eds.), Affect and cognition (pp. 333–342). Hillsdale, NJ: L. Erlbaum, as quoted in (McLeod, 1992).

    Google Scholar 

  • Simon, M. A. (1996). Beyond inductive and deductive reasoning: the search for a sense of knowing. Educational Studies in Mathematics, 30, 197–210.

    Article  Google Scholar 

  • Walen, S. B., & Williams, S. R. (2002). A matter of time: Emotional responses to timed mathematics tests. Educational Studies in Mathematics, 49, 361–378.

    Article  Google Scholar 

  • Weber, K. (2001). Student difficulty in constructing proof: The need for strategic knowledge. Educational Studies in Mathematics, 48, 101–119.

    Article  Google Scholar 

  • Weber, K. S., & Alcock, L. (2004). Semantic and syntactic proof productions. Educational Studies in Mathematics, 56, 209–234.

    Article  Google Scholar 

  • Weiner, B. (1972). Theories of motivation. Chicago, IL: Rand McNally.

    Google Scholar 

  • Weiner, B. (1980). The order of affect in rational (attributional) approaches to human motivation. Educational Researcher, 19, 4–11.

    Google Scholar 

  • Yackel, E., & Cobb, P. (1996). Sociomathematical norms, argumentation, and autonomy in mathematics. Journal for Research in Mathematics Education, 27, 458–477.

    Article  Google Scholar 

  • Zan, R., Brown, L., Evans, J., & Hannula, M. S. (2006). Affect in mathematics education: an introduction. Educational Studies in Mathematics, 60, 113–121.

    Article  Google Scholar 

  • Zazkis, R., & Liljedahl, P. (2004). Understanding primes: The role of representation. International Journal for Research in Mathematics Education, 35, 164–186.

    Article  Google Scholar 

Download references

Acknowledgements

Research program supported by MIUR (PRIN 2005019721_002 ‘Meanings, conjectures, proofs: from basic research in mathematics education to curricular implications’).

Author information

Authors and Affiliations

  1. Dipartimento di Matematica dell’Università di Genova, via Dodecaneso 35, 16146, Genoa, Italy

    Fulvia Furinghetti & Francesca Morselli

Authors
  1. Fulvia Furinghetti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Francesca Morselli
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Fulvia Furinghetti.

Appendix: Two proofs of the statement

Appendix: Two proofs of the statement

Proof by contradiction:

Let m and n be two coprime numbers.

suppose that m and m  +  n are not coprime. Then there exist a  ∈  N, a  ≠  1, p, q  ∈  N such that m  =  ap, \(m + n = aq\). Since m  +  n  >  m it is q  >  p.

Then \(m + n = ap + n = aq\)

$$\begin{array}{*{20}l} {aq - ap = n} \hfill \\ {a\left( {q - p} \right) = n.\,{\text{Since}}\,q > p,\,q - p\,{\text{is}}\,{\text{a}}\,{\text{natural}}\,{\text{number}}{\text{.}}} \hfill \\ \end{array} $$

Hence m, n are not coprime, which contradicts the hypothesis.

Direct proof:

Let m and n be two coprime numbers.

Let a∈ N be a common factor of m and m  +  n

Then, there exist p, q ∈ N such that m  =  ap, \(m + n = aq\). Since m  +  n  >  m it is q  >  p.

Hence \(m + n = ap + n = aq\)

$$\begin{array}{*{20}c} {aq - ap = n} \\ {a\left( {q - p} \right) = n.} \\ \end{array} $$

Since q  >  p, q−p is a natural number. Thus, a is a common factor of m and n.

Since m, n are coprime, a must be 1.

Then, if a is a common factor of m and m  +  n, a is 1, that is to say m and m  +  n are coprime.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Furinghetti, F., Morselli, F. Every unsuccessful problem solver is unsuccessful in his or her own way: affective and cognitive factors in proving. Educ Stud Math 70, 71–90 (2009). https://doi.org/10.1007/s10649-008-9134-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10649-008-9134-4

Keywords

Search

Navigation