Central configurations in planar n-body problem with equal masses for $n=5,6,7$

Abstract

We give a computer-assisted proof of the full listing of central configuration for n-body problem for Newtonian potential on the plane for $n=5,6,7$ with equal masses. We show all these central configurations have a reflective symmetry with respect to some line. For $n=8,9,10$, we establish the existence of central configurations without any reflectional symmetry.

1 Introduction

A central configuration, denoted as CC, is an initial configuration $(q_1, \ldots , q_n)$ in the Newtonian n-body problem, such that if the particles were all released with zero velocity, they would collapse toward the center of mass c at the same time. In the planar case, CCs are initial positions for periodic solutions which preserve the shape of the configuration. CCs play also an important role in the study of the topology of integral manifolds in the n-body problem (see Moeckel and the references given there).

In this paper, for $n=4,5,6,7$, we consider two questions:

• finding all CCs in the n-body problem on the plane ($d = 2$) with equal masses and

• showing that each CC has a line of reflection symmetry.

For $n=8,9,10$, we establish the existence of some non-symmetric CCs previously found numerically in Moeckel, Ferrario (2002) and Simo (2018).

1.1 The state of the art

The listing (apparently full for $n \leqslant 9$ ) of central configurations with equal masses was given by Ferrario (2002) in unpublished notes for $n \in \{3,\ldots ,10\}$ and by Moeckel for $n \leqslant 8$. For $n=4$, it was shown by Albouy (1995) that all CCs have some reflectional symmetry and later in Albouy (1996) with computer assistance the full list of central configurations was given. From numerical simulations (see for example Moeckel; Ferrario 2002), it is apparent that all CCs with equal masses have some reflectional symmetry for $n=5,6,7$. Moeckel has found numerically some CCs without any symmetry for $n=8$. Also for $n=9$ Simo (2018) has found 2 families, non-equivalent, and without any symmetry. Some CCs without symmetry for $n=10$ can be found also in Ferrario (2002).

The investigations of central configurations for equal masses are a subcase of more general problem of central configurations with arbitrary positive masses. The general conjecture of finiteness of central configurations (relative equilibria) in the n-body problem is stated in Wintner (1941) and appears as the sixth problem of Smale’s eighteen problems for the 21st century (Smale 1998). There are many works on the existence of some particular central configurations. Here we discuss only those papers which aim to more general statement about all CCs. The two most important works are Hampton and Moeckel (2005) and Albouy and Kaloshin (2012). In Hampton and Moeckel (2005), the finiteness of CC for $n=4$ for any system of positive masses was proved with computer assistance. In Albouy and Kaloshin (2012), for $n=4$ problem the finiteness of CC was proven without computer assistance. In the same paper, the finiteness for $n=5$ was proven for arbitrary positive masses, except perhaps if the 5-tuple of positive masses belongs to a given codimension 2 subvariety of the mass space. It is interesting to notice that the equal masses case treated in our paper belongs to this subvariety. For the spatial 5-body problem, Moeckel (2001) established the generic finiteness of Dziobek’s CCs (CCs which are not planar). A computer-assisted work by Hampton and Jensen (2011) strengthens this result by giving an explicit list of conditions for exceptional values of masses. A common feature of these works is that they give a quite poor estimate for the maximum number of central configurations. In this context, it is worth to mention the work of Simo, based on extensive numerical studies. In Simo (1978), he gives the number of CCs for all possible masses for $n=4$.

In Lee and Santoprete (2009), the spatial 5-body problem with equal masses was considered. A complete classification of the isolated central configurations of the 5-body problem was given (this includes also planar isolated CCs). The approach has a numerical component; hence, it cannot be claimed to be fully rigorous. Also the proof does not exclude the possibility that a higher-dimensional set of solutions exists. On the other hand, the existence of identified isolated CC has been proven using the Krawczyk’s operator, i.e., a tool from interval arithmetic we also use. Kotsireas (see Kotsireas 2000 and references given there) considers the 5-body problem with equal masses. He gives computer-assisted proof of a full list of all such configurations and shows that each of them posses some reflectional symmetry.

The above-mentioned works study the polynomial equations derived from the equations for CC using the (real or complex) algebraic geometry tools. In contrast, we take a different approach: we use standard interval arithmetic tools; hence, in principle we can treat also other potentials which cannot be reduced to polynomial equations.

1.2 The main results

Theorem 1

There exist only a finite number of various types of CCs, for $n=5,6,7$ the planar n-body Newtonian problem with equal masses. They are listed in Supplementary Material. Any CC can be obtained from one of them by suitable composition of translation, rescaling, rotation, reflection and permutation of bodies. Moreover, each of these central configurations has some reflectional symmetry.

Theorem 2

For $n=8,9,10$ in the planar n-body Newtonian problem with equal masses, there exist CCs without any line of reflectional symmetry. They are listed in Supplementary Material.

In the case of equal masses, one can consider equivalences in two different ways: either one passes from a solution to another one by rotation (scaling is already taken into account) or one can also add permutations and reflections. For instance, for 4 bodies in the first criterion of equivalence there are 50 classes [see numerical work by Simo (1978)], while in the second only 4 classes. In this paper, we use this second criterion for equivalence.

Let us briefly describe our method. This is basically a brute force approach using standard interval arithmetic tools. Throughout the paper, we will use often box or $cube$ to describe a set which is a product of intervals (some of them can be degenerated). The interval arithmetic allows to evaluate elementary functions on the box in a single call, i.e., the box is returned containing the true result for all points in the argument box (see for example Moore 1966; Neumeier 1990). When looking for CCs, we explore the whole configuration space (modulo some a priori bounds), and it is surprising that the most demanding part is to exclude the possibility of the existence of CC in a given box. Once we are ‘very close’ to an isolated CC, it is relatively easy to establish its existence and local uniqueness using the Krawczyk (1969) operator. The additional difficulty is that the potential contains singularity, which introduces some non-compactness in the domain to be covered. Our algorithm, which is more or less a binary search algorithm, scales poorly with n — this is the dimensionality curse (see Traub et al. 1988), which means that the complexity of our algorithm grows exponentially with n. For example, assume that we can decide if a box in the configuration space contains some CC, only when its diameter is less than $10^{-2}$ in each direction. Then adding a new body in $[-1,1]\times [-1,1]$ multiplies the number of boxes to be examined by $(2/10^{-2})^2 = 4\cdot 10^4$. For this reason, we were not able to obtain a rigorous listing of CCs for $n=8$. Note that for $n=5$ the computations were done in 24 seconds, for $n=6$ it took about one hour to get the result, while for $n=7$ we needed almost a hundred hours (see Sect. 7.3 for more technical data).

For any CC from the listing in Moeckel or Ferrario (2002) for $n\geqslant 8$ we have found no difficulty proving its existence and local uniqueness. In particular, we confirmed the existence of non-symmetric planar CCs for $n=8,9,10$ (see Theorem 2).

The paper is organized as follows. In Sect. 2 we recall the equations for the central configurations and their basic properties. In Sect. 3, we derive several a priori bounds for CC, so that we obtain a compact domain for our search algorithm. In Sect. 4, we discuss various tests which are used to show that a given box does not contain any CC. In Sect. 5, we derive a reduced set of equations for CC. This is necessary because to apply the Krawczyk’s method we need to ensure that the system of equations does not contain any degeneracies, which are due to symmetries of the original system of equations for CCs. In Sect. 6, we give assumptions and basic ideas concerning the computer-assisted proofs of main Theorems 1 and 2 and we explain the Krawczyk’s method. Details of the algorithm are described in Sect. 7. In Sect. 8, we present an attempt to minimize the dependency problem in interval arithmetic in the evaluation of the gravitational force. In electronic supplementary material, we give an output of the program establishing Theorems 1 and 2 (also for $n= 3,4$) and pictures of all CCs found.

2 Equations for central configurations

In the paper by |z|, where $z=(z_1,\ldots ,z_d) \in \mathbb {R}^d$, we will denote the euclidean norm of z, i.e., $|z|=\left( \sum _{i=1}^d z_i^2\right) ^{1/2}$ and by (x, y), where $x,y \in \mathbb {R}^d$, we will denote the standard scalar product, i.e., $(x|y)=\sum _{i=1}^d x_iy_i$. We will often use $z^2:=(z|z)$.

Let $q_i \in \mathbb {R}^d$, $i=1,\ldots ,n$ and $d\geqslant 1$ (the physically interesting cases are $d=1,2,3$), where $q_i$ is a position of i-th body with mass $m_i \in \mathbb {R}_+$. Let us set

$$\begin{aligned} M=\sum _{i=1}^n m_i. \end{aligned}$$

(1)

Central configurations are solutions of the following system of equations (see Moeckel):

$$\begin{aligned} \lambda (q_i-c) = \sum _{\begin{array}{c} j=1\\ j\ne i \end{array}}^n \frac{m_j}{r_{ij}^3}(q_i - q_j)=:\frac{1}{m_i}f_i(q_1,\ldots ,q_n), \quad i=1,\ldots ,n, \end{aligned}$$

(2)

where $\lambda \in \mathbb {R}$ is a constant, $c=\left( \sum _{i=1}^n m_i q_i\right) /M$ is center of mass, $r_{ij}=r_{ji}=|q_i - q_j|$ is the Euclidean distance between i-th and j-th bodies and $(-f_i)$ is the force which acts on i-th body resulting from the gravitational pull of other bodies. The system of Eq. (2) has the same symmetries as the n-body problem. It is invariant with respect to group of isometries of $\mathbb {R}^d$ and the scaling of variables.

In the planar case if we consider the bodies in a rotating system (with the center of mass at the origin) with constant angular velocity $\omega =\sqrt{\lambda }$, the physical meaning of (2) is obvious: the gravitational attraction is compensated by the centrifugal force and the central configurations are fixed points in the rotating frame (see  Moeckel and the references given there).

The system (2) has dn equations and $dn + 1$ unknowns: $q_i \in \mathbb {R}^d$ for $i = 1, \ldots , n$ and $\lambda \in \mathbb {R}_+$. The system has a O(d) and scaling symmetry (with respect to $q_i$’s and $m_i$’s). If we demand that $c=0$ (which is obtained by a suitable translation) and $\lambda =1$ (which can be obtained by rescaling $q_i$’s or $m_i$’s), we obtain the equations (compare Moeckel; Moeckel 2014; Albouy and Kaloshin 2012)

$$\begin{aligned} q_i= \sum _{j,j\ne i} \frac{m_j}{r_{ij}^3}(q_i - q_j)=:\frac{1}{m_i}f_i(q_1,\ldots ,q_n), \quad i=1,\ldots ,n. \end{aligned}$$

(3)

It is easy to see that if (3) is satisfied, then $c=0$ (see Sect. 2.1) and (2) also holds for $\lambda =1$. A $q = (q_1,\ldots ,q_n) \in \left( \mathbb {R}^d\right) ^n$ is called a configuration. If q satisfies (3) then it is called a normalized central configuration (abbreviated as CC). For the future use, we introduce the function $F:\Pi _{i=1}^n\mathbb {R}^{d } \rightarrow \Pi _{i=1}^n\mathbb {R}^{d }$ given by

$$\begin{aligned} F_i(q_1,\ldots ,q_n) = q_i - \sum _{j,j\ne i} \frac{m_j}{r_{ij}^3}(q_i - q_j), \quad i=1,\ldots ,n. \end{aligned}$$

(4)

Then the system (3) becomes

$$\begin{aligned} F(q_1,\ldots ,q_n)=0. \end{aligned}$$

(5)

2.1 Some identities and conservation laws

It is well know that for any $(q_1,q_2,q_3,\ldots ,q_n)\in (\mathbb {R}^d)^n$ holds

$$\begin{aligned}&\sum _{i=1}^n f_i = 0, \end{aligned}$$

(6)

$$\begin{aligned}&\sum _{i=1}^n f_i \wedge q_i = 0, \end{aligned}$$

(7)

where $v \wedge w$ is the exterior product of vectors, the result being an element of exterior algebra. If $d=2,3$ it can be interpreted as the vector product of v and w in dimension 3. The identities (6) and (7) are easy consequences of the third Newton’s law (the action equals reaction) and the requirement that the mutual forces between bodies are in direction of the other body.

But (6) and (7) can be seen also as the consequences of the symmetries of Newtonian n-body problem. According to Noether’s Theorem, by the translational symmetry we have a conservation of momentum, which is equivalent to (6), while the rotational symmetry implies the conservation of angular momentum, which is implied by (7).

Note that the components of $v \wedge w$ are given by determinants. In any dimension in the presence of the rotational symmetry, for any direction of rotation identified by $v_1 \wedge v_2$ ( $v_1$ and $v_2$ are perpendicular unit vectors) the following quantity must be zero (as a consequence of the Noether Theorem and the invariance with respect to the rotation in the plane $v_1,v_2$)

$$\begin{aligned} \sum _{i=1}^{n} \det \left[ \begin{array}{cc} (f_i|v_1) &{} (q_i|v_1) \\ (f_i|v_2) &{} (q_i|v_2) \end{array} \right] =0. \end{aligned}$$

(8)

Consider system (3). After multiplication of i-th equation by $m_i$ and addition of all equations using (6), we obtain (or rather recover) the center of mass equation

$$\begin{aligned} \left( \sum _{i=1}^n m_i\right) c=\sum _i m_i q_i = 0. \end{aligned}$$

(9)

We can take the equations for n-th body and replace it with (9) to obtain an equivalent system.

$$\begin{aligned} q_i= & {} \sum _{j,j\ne i} \frac{m_j}{r_{ij}^3}(q_i - q_j)=:\frac{1}{m_i}f_i(q_1,\ldots ,q_n), \quad i=1,\ldots ,n-1, \end{aligned}$$

(10)

$$\begin{aligned} q_n= & {} -\frac{1}{m_n}\sum _{i=1}^{n-1} m_i q_i. \end{aligned}$$

(11)

Later in Sect. 5, we will use (7) to define a reduced system of equations for CCs which will not have the degeneracies present in system (3).

2.2 Moment of inertia of central configurations

The important role of the moment of inertia in the investigation of central configurations is well known. In our context, it plays a crucial role in stating some a priori bounds for central configurations. We present, with proofs, some well-known results on moment of inertia taken from the notes by Moeckel (2014) and the paper of Albouy and Kaloshin (2012).

Definition 1

For a configuration q let the moment of inertia I(q) and the potential function U(q) be given by

$$\begin{aligned} I(q)=\sum _i m_i q_i^2, \quad U(q)=\sum _{i<j} \frac{m_i m_j}{r_{ij}}. \end{aligned}$$

(12)

Lemma 3

Assume that $\sum _i m_i q_i=0$ and $M=1$. Then

$$\begin{aligned} I(q)= \sum _{i<j}m_i m_j (q_i - q_j)^2. \end{aligned}$$

(13)

Proof

Let us denote $q_{i,j}=q_i - q_j$. Since

$$\begin{aligned} q_i^2 = (q_i|q_i)= & {} \left( \left( q_i - \sum _j m_j q_j \right) |q_i\right) \qquad \qquad \qquad \qquad \qquad (\hbox {since} \sum _i m_i q_i=0)\\= & {} \left( \left( q_i\sum _j m_j - \sum _j m_j q_j\right) |q_i\right) \qquad \qquad \qquad (\hbox {since} \sum _j m_j = 1)\\= & {} \left( \left( \sum _j m_j(q_i - q_j)\right) |q_i\right) = \sum _j m_j \left( q_{i, j}|q_i\right) , \end{aligned}$$

we have,

$$\begin{aligned} I(q)=\sum _i m_i q_i^2= \sum _{i,j} m_i m_j \left( q_{i,j}|q_{i} \right) . \end{aligned}$$

Observe that

$$\begin{aligned} \sum _{i,j} m_i m_j \left( q_{i,j}|q_{i} \right) = - \sum _{i,j} m_i m_j \left( q_{i,j}|q_{j} \right) , \end{aligned}$$

hence

$$\begin{aligned} I(q)=\frac{1}{2}\left( \sum _{i,j} m_i m_j \left( q_{i,j}|q_{i} \right) - \sum _{i,j} m_i m_j \left( q_{i,j}|q_{j} \right) \right) = \frac{1}{2}\sum _{i,j} m_i m_j (q_{i,j}|q_{i,j}). \end{aligned}$$

$\square$

Lemma 4

If $q \in \left( \mathbb {R}^d\right) ^n$ is a (normalized) central configuration, then

$$\begin{aligned} I(q)=U(q). \end{aligned}$$

(14)

Proof

We take the scalar product of i-th equation in (3) by $m_i q_i$ and add these equations to obtain

$$\begin{aligned} I(q)= & {} \sum _{i} m_i q_i^2 = \sum _{i,j; i \ne j} \frac{m_i m_j}{r_{ij}^3}(q_i - q_j|q_i)\\= & {} \sum _{i<j} \frac{m_i m_j}{r_{ij}^3}(q_i - q_j|q_i-q_j)= \sum _{i<j} \frac{m_i m_j}{r_{ij}}=U(q). \end{aligned}$$

$\square$

3 A priori bounds for central configurations

From the point of view of CAP (computer-assisted proofs) in the problem of finding and counting all CCs, the issue of compactness of the search domain is fundamental. The lack of compactness arises for the following two reasons:

• two or more bodies might be arbitrary close to a collision,

• some bodies might be arbitrary far from the origin.

The goal of this section is to deal with these issues. We will give a priori bounds (depending on $m_i$’s) on the minimal distance of the closest bodies and for the size of the central configuration.

3.1 Lower bound on the distances

It is well known that central configurations are away from the collision set (see Shub 1970 or Moeckel 2014, Prop. 15). However, in these works no quantitative statement directly applicable to system (3) has been given. Here we develop explicit a priori bounds.

The main idea is to use $I(q)=U(q)$ (see Lemma 4) to show that some term(s) $m_im_j/r_{ij}$ entering U(q) dominate and cannot be balanced, when bodies are very close. Observe that using $I(q)=U(q)$ and positivity of all terms entering U(q) allows us to escape the discussion of large terms on the rhs in the system (3), which might cancel out or not etc. This is not the case in the framework of Albouy and Kaloshin (2012), where complex configurations and even complex masses have been considered, hence the positivity of I and U is lost.

Lemma 5

Assume that a (normalized) central configuration $q \in \left( \mathbb {R}^d\right) ^n$ satisfies $|q_i| \leqslant R$ for $i=1,\ldots ,n$. Then

$$\begin{aligned} I(q) \leqslant MR^2. \end{aligned}$$

Proof

Since for any $1 \leqslant i \leqslant n:|q_i| \leqslant R$, thus $I(q) = \sum _{i} m_iq_i^2 \leqslant \sum _{i} m_iR^2 = MR^2.$ $\square$

Theorem 6

Assume that a (normalized) central configuration $q \in \left( \mathbb {R}^d\right) ^n$ satisfies $|q_i| \leqslant R$ for $i=1,\ldots ,n$. Then

$$\begin{aligned} r_{ij} > \frac{m_i m_j}{M R^2}, \quad 1\leqslant i < j \leqslant n. \end{aligned}$$

(15)

Proof

From Lemmas 4 and 5, for any $1\leqslant i < j \leqslant n$, we have

$$\begin{aligned} M R^2 \geqslant I(q) = U(q) = \sum _{i < j}\frac{m_i m_j}{r_{ij}} > \frac{m_i m_j}{r_{ij}}. \end{aligned}$$

$\square$

Below we establish a lower bound on the radius of ball centered at 0 and containing a central configuration in the case of equal masses.

Theorem 7

Assume that all masses are equal and q is a normalized central configuration such that $|q_i| \leqslant R$. Then

$$\begin{aligned} R^3 \geqslant \frac{n-1}{4n}M. \end{aligned}$$

(16)

Proof

Let $m=\frac{M}{n}$. Since for any $1 \leqslant i \leqslant n:|q_i| \leqslant R$, thus $r_{ij}\leqslant 2R$ and we obtain the following bound

$$\begin{aligned} U(q)= & {} \sum _{i< j} \frac{m_i m_j}{r_{ij}} \geqslant \sum _{i < j} \frac{m^2}{2R} \\= & {} \frac{m^2}{2R}\cdot \frac{n(n-1)}{2} =\frac{(n-1)M^2}{4nR}. \end{aligned}$$

Hence from Lemmas 4 and 5, we obtain

$$\begin{aligned} \frac{(n-1)M^2}{4nR} \leqslant U(q)=I(q) \leqslant M R^2. \end{aligned}$$

$\square$

If $M=1$, then $\lim _{n\rightarrow \infty } \root 3 \of {\frac{n-1}{4n}} = 4^{-1/3}\approx 0.629961$. This estimate appears to be reasonably good, as shown in Table 1.

Table 1 The size of a minimal ball containing all normalized central configurations with $M=1$ for several n’s for equal masses case

In the next theorem, we do not assume that all masses are equal.

Theorem 8

Assume $M=1$ and q is a normalized central configuration. Then there exists a pair $i \ne j$ such that

$$\begin{aligned} r_{ij} \geqslant 1. \end{aligned}$$

(17)

Proof

For the proof by contradiction, assume that $r_{ij} <1$ for all pairs of bodies. Hence we have $r_{ij}^2 < 1/r_{ij}$ for all pairs. From Lemma 3, it follows

$$\begin{aligned} I(q)=\sum _{i<j} m_i m_j r_{ij}^2< \sum _{i<j} m_i m_j \frac{1}{r_{ij}}=U(q). \end{aligned}$$

From Lemma 4, it follows that q is not a central configuration. $\square$

Observe that the above estimate is optimal, because it is realized for the equilateral triangle for $n=3$ and a tetrahedron (non planar CC) for $n=4$. From the above theorem, we obtain the following lower bound for the size of a central configuration. Contrary to Theorem 7, we do not assume that all masses are equal.

Theorem 9

Assume that $M=1$ and q is a normalized central configuration and $|q_i| \leqslant R$ for $i=1,\ldots ,n$. Then $R \geqslant 1/2$.

Proof

For the proof by contradiction assume that $R < 1/2$. Then for all pairs $r_{ij} <1$. From Theorem 8, it follows that q is not central configuration. $\square$

3.2 The upper bound on the size of central configuration

The goal of this section is to give the upper bounds for the size of the central configuration. This time we exploit the fact that if the forces are bounded, then large $q_i$’s on the left hand side of the system (3) cannot be balanced. The obvious difficulty with the realization of this idea is: we can have a group of bodies with large norms which are close to each other in the central configuration, which produce large terms on rhs of the system (3). To overcome this, we consider clusters of points far from the origin and the resulting force on it. In such situation, mutual interactions between bodies in the cluster cancel out.

Lemma 10

Assume $q \in \left( \mathbb {R}^d\right) ^n$ is a normalized central configuration. Let $R=|q_{i_0}|=\max _{i=1,\ldots ,n} |q_i|$. Then for all $\varepsilon \in \left( 0,R/(n-1)\right)$ holds

$$\begin{aligned} R - (n-2) \varepsilon < \frac{M}{\varepsilon ^2}. \end{aligned}$$

(18)

Proof

For simplicity let’s assume that $d = 2$ and $q_i = (x_i, y_i)$. Let us fix any $\varepsilon \in \left( 0,R/(n-1)\right)$. After a suitable rotation of coordinate system, we can assume that

$$\begin{aligned} q_{i_0}=(R,0). \end{aligned}$$

(19)

Let $\mathcal {C}$ be a minimal subset (cluster) of indices of bodies satisfying the following conditions

• $i_0 \in \mathcal {C}$

• if $j \in \mathcal {C}$ and $|q_k - q_j| \leqslant \varepsilon$, then $k \in \mathcal {C}$.

The cluster $\mathcal {C}$ can be constructed as follows: We start with $i_0 \in \mathcal {C}$. Then we add all bodies which are not farther than $\varepsilon$ from the bodies already in $\mathcal {C}$. We repeat this until the set $\mathcal {C}$ stabilizes, which will happen after at most $n-1$ steps. From assumption about $\varepsilon$ and R, it follows that

$$\begin{aligned} R > (n-1)\varepsilon . \end{aligned}$$

(20)

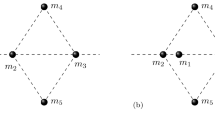
Observe that (20) implies that $\mathcal {C} \ne \{1,\ldots ,n\}$. Indeed (20) and (19) imply that $x_i >0$ for all $i \in \mathcal {C}$. This and the center of mass condition (9) implies that $\mathcal {C}$ cannot contain all bodies. This implies that the process of building $\mathcal {C}$ must stop after at most $n-2$ steps. Therefore, we obtained a cluster $\mathcal {C}$ with the following properties (Fig. 1)

$$\begin{aligned} q_i\in & {} \overline{B(q_{i_0},(n-2)\varepsilon )}, \quad \forall i \in \mathcal {C}, \end{aligned}$$

(21)

$$\begin{aligned} |q_i - q_j|> & {} \varepsilon , \quad i \in \mathcal {C}, j \notin \mathcal {C}. \end{aligned}$$

(22)

Fig. 1

$R > (n-1)\varepsilon$ and $r = (n-2)\varepsilon$; the darkened area is the region where all the bodies from cluster are located

Without any loss of the generality, we can assume that $i_0=1$ and $\mathcal {C}=\{1,\ldots ,s\}$. Note that for any $k\geqslant 2$ there is [compare (6)]

$$\begin{aligned} \sum _{i = 1}^k\sum _{j = 1, j\ne i}^k \frac{m_im_j}{r_{ij}^3}(q_i - q_j) = 0, \end{aligned}$$

thus by adding Eq. (3) multiplied by $m_i$ for $i=1,\ldots ,s$ we obtain

$$\begin{aligned} m_1 q_1 + \cdots + m_s q_s= & {} \sum _{\begin{array}{c} i=1,\ldots ,s,\\ j=1,\ldots , s,\\ j\ne i \end{array}}\frac{m_i m_j (q_i - q_j)}{r_{ij}^3}\ + \sum _{\begin{array}{c} i=1,\ldots ,s,\\ j=s+1,\ldots ,n \end{array}}\frac{m_i m_j (q_i - q_j)}{r_{ij}^3}\nonumber \\= & {} \sum _{\begin{array}{c} i=1,\ldots ,s,\\ j=s+1,\ldots ,n \end{array}}\frac{m_i m_j (q_i - q_j)}{r_{ij}^3}. \end{aligned}$$

(23)

Let

$$\begin{aligned} M_s= & {} \sum _{i=1}^s m_i,\\ c_{s}= & {} \frac{1}{M_s}\sum _{i=1}^s m_i q_i, \\ F_{s}= & {} \frac{1}{M_s}\sum _{i\in \mathcal {C}; j \notin \mathcal {C}} \frac{m_i m_j (q_i - q_j)}{r_{ij}^3}. \end{aligned}$$

Observe that (23) could be now rewritten as

$$\begin{aligned} c_s=F_s. \end{aligned}$$

(24)

It is easy to see [cf. (21)] that for $i\in \mathcal {C}$: $x_i \geqslant R - (n-2) \varepsilon > 0$, hence

$$\begin{aligned} |c_s|= & {} \frac{1}{M_s}\left| \sum _{i=1}^s m_i q_i\right| \geqslant \frac{1}{M_s}\left| \sum _{i=1}^s m_i(R - (n-2)\varepsilon , y_i)\right| \nonumber \\\geqslant & {} \frac{1}{M_s}(R - (n-2)\varepsilon )\sum _{i=1}^s m_i\nonumber \\= & {} R - (n-2) \varepsilon , \end{aligned}$$

and

$$\begin{aligned} |F_s|\leqslant & {} \frac{1}{M_s}\sum _{i\in \mathcal {C}; j \notin \mathcal {C}} \frac{m_i m_j }{r_{ij}^2} \leqslant \frac{1}{\varepsilon ^2} \frac{1}{M_s}\sum _{i\in \mathcal {C}; j \notin \mathcal {C}} m_i m_j\\= & {} \frac{1}{\varepsilon ^2} \frac{1}{M_s}\left( \sum _{i\in \mathcal {C}} m_i \right) \cdot \left( \sum _{j \notin \mathcal {C}} m_j \right) = \frac{1}{\varepsilon ^2} \sum _{j \notin \mathcal {C}} m_j < \frac{M}{\varepsilon ^2}. \end{aligned}$$

Hence from the above and (24), we obtain

$$\begin{aligned} R - (n-2) \varepsilon \leqslant |c_s| = |F_{s}| < \frac{M}{\varepsilon ^2}. \end{aligned}$$

$\square$

From Lemma 10, we obtain the following estimate on the size of any central configuration.

Theorem 11

Assume that $M=1$ and $q \in \left( \mathbb {R}^d\right) ^n$ is a normalized central configuration. Then

$$\begin{aligned} \max _{i} |q_i| \leqslant \left\{ \begin{array}{ll} n-1, &{} n\geqslant 2;\\ \left( 2^{1/3}+2^{-2/3} \right) (n-2)^{2/3}, &{} n\geqslant 4. \end{array} \right. \end{aligned}$$

(25)

Proof

Let $R=\max _{i=1,\ldots ,n} |q_i|$. From Lemma 10 it follows that for any $\varepsilon > 0$ holds

$$\begin{aligned} R \leqslant \max \left( (n-1)\varepsilon , (n-2)\varepsilon + \frac{1}{\varepsilon ^2} \right) . \end{aligned}$$

(26)

Indeed, if $\varepsilon < R/(n-1)$ then we apply Lemma 10, otherwise we have $R \leqslant (n-1)\varepsilon$. Let us optimize the bound (26) with respect to $\varepsilon$.

Let us denote by

$$\begin{aligned} B(\varepsilon )=\max \left( (n-1)\varepsilon , (n-2)\varepsilon + \frac{1}{\varepsilon ^2} \right) . \end{aligned}$$

(27)

It is easy to see that

$$\begin{aligned} (n-1)\varepsilon< & {} (n-2)\varepsilon + \frac{1}{\varepsilon ^2}, \quad \hbox {for} \, \varepsilon < 1, \\ (n-1)\varepsilon= & {} (n-2)\varepsilon + \frac{1}{\varepsilon ^2}, \quad \hbox {for} \, \varepsilon = 1, \\ (n-1)\varepsilon> & {} (n-2)\varepsilon + \frac{1}{\varepsilon ^2}, \quad \hbox {for} \, \varepsilon > 1. \end{aligned}$$

Hence

$$\begin{aligned} B(\varepsilon ) = \left\{ \begin{array}{ll} (n-2)\varepsilon + \frac{1}{\varepsilon ^2}, &{} \hbox {for} \, \varepsilon < 1, \\ (n-1)\varepsilon , &{} \hbox {for} \, \varepsilon \geqslant 1. \end{array} \right. \end{aligned}$$

Therefore,

$$\begin{aligned} \inf _{\varepsilon >0} B(\varepsilon )= \inf _{\varepsilon \in (0,1]}\left( (n-2)\varepsilon + \frac{1}{\varepsilon ^2}\right) . \end{aligned}$$

The function $g(\varepsilon )=(n-2)\varepsilon + 1/\varepsilon ^2$ is decreasing for $\varepsilon < \varepsilon _0=\left( \frac{2}{n-2}\right) ^{1/3}$ and is increasing for $\varepsilon > \varepsilon _0$. Observe that $\varepsilon _0 \in (0,1]$ iff $n \geqslant 4$. Therefore, we obtain

$$\begin{aligned} \inf _{\varepsilon >0} B(\varepsilon )=\left\{ \begin{array}{ll} n-1, &{} n\leqslant 4; \\ g(\varepsilon _0), &{} n\geqslant 4. \end{array} \right. \end{aligned}$$

(28)

We have

$$\begin{aligned} g(\varepsilon _0) = (n-2)\left( \frac{2}{n-2}\right) ^{1/3} + \left( \frac{n-2}{2}\right) ^{2/3}=\left( 2^{1/3}+2^{-2/3} \right) (n-2)^{2/3}. \end{aligned}$$

$\square$

For $n\leqslant 10$ and the equal masses, the above estimate appears to be an overestimation. The largest possible size of CC found was slightly above 1 and is considerably smaller than the one established in the above theorem.

4 Exclusion tests for CCs

Assume that we have an interval set D (i.e., a box, a product of intervals) in which we would like to exclude the existence of CC. We do not assume that $D \subset \,\mathrm{dom}\,F$ [see (5)] and this is an important point. The a priori estimates discussed in Sect. 3 allow to exclude D iff there is no point in D which satisfies the obtained bounds.

In the following, we discuss other exclusion tests.

4.1 Checking for zeros

One obvious test is to check whether in the interval evaluation of F(D) [see (5)] at least one of the component does not contain zero. Observe that a partial tests of this type are possible even if D admits the collision, i.e., formally it is not contained in $\,\mathrm{dom}\,F$, but we can do this verification whenever $D \subset \,\mathrm{dom}\,F_i$. The test takes the following form:

• 0. given box D in the configuration space, such that $D \subset \,\mathrm{dom}\,F_i$ (i.e., the i-th does not have a collision with other bodies). Let $D_i=\{q_i \,|\, q \in D\}$.

• 1. compute the interval enclosure of $f_i(q)$ for $q \in D$, denoted by $\langle f_i(D)\rangle$,

• 2. if $D_i \cap \frac{1}{m_i}\langle f_i(D)\rangle =\emptyset$ [compare Eq. (3)], then D does not contain any normalized central configuration

• 3. if $D_i \cap \frac{1}{m_i}\langle f_i(D)\rangle \ne \emptyset$, then we define $D^{\mathrm {ref}}=\{q \in D\, |\, q_i \in \frac{1}{m_i}\langle f_i(D)\rangle \}$.

Observe that point 2 allows us exclude the box D, but if this is impossible then we can replace D by $D^{\mathrm {ref}}$ obtained in point 3, as any CC contained in D must belong to $D^{\mathrm {ref}}$. This is one of several places in our algorithm, where we attempt to do better than doing naive binary subdivision in order to relieve the curse of dimensionality.

4.2 The cluster of bodies—checking for zeros test

In the case of colliding bodies or a cluster of close bodies, say with indices $i=1,\ldots , s$, after adding first s equations multiplied by $m_i$ we obtain

$$\begin{aligned} \sum _{i=1}^s m_i q_i = \sum _{i=1}^s \sum _{j=s+1}^n \frac{m_i m_j}{r_{ij}^3}(q_i - q_j). \end{aligned}$$

Therefore, for the cluster of bodies $\mathcal {C} \subset \{1,\ldots ,n\}$ we will check whether

$$\begin{aligned} (0,0) \in \sum _{i \in \mathcal {C}}^s m_i q_i - \sum _{i\in \mathcal {C}}^s \sum _{j\notin \mathcal {C}}^n \frac{m_i m_j}{r_{ij}^3}(q_i - q_j), \end{aligned}$$

(29)

where the expression on the rhs of (29) is evaluated in the interval arithmetic on D.

If it is not satisfied, then we conclude that D does not contain any CC. Again let us stress that the set D might contain some collisions, and this test is still applicable.

4.3 The cluster of bodies—test based on moment of inertia and potential

We will exploit $I(q)=U(q)$ for CC (compare Lemma 4), but our focus will be on the subsets (clusters) of bodies. Let us fix $\mathcal {C} \subset \{1,2,\ldots ,n\}$ and $Z \subset \left( \mathbb {R}^d\right) ^n$. Let us define

$$\begin{aligned} U_{\mathcal {C},Z}= & {} \inf _{q \in Z} \sum _{i<j, i,j \in \mathcal {C}} \frac{m_i m_j}{r_{ij}}, \\ I_{\mathcal {C},Z}= & {} \sup _{q \in Z} \sum _{i \in \mathcal {C}} m_i q_i^2, \\ F_{\mathcal {C},Z}= & {} \inf _{q \in Z} \sum _{ i \in \mathcal {C}, k \notin \mathcal {C}} \frac{m_i m_k}{r_{ik}^3} (q_i-q_k| q_i). \end{aligned}$$

In the case when $\mathcal {C}=\{1,\ldots ,n\}$ we set $F_{\mathcal {C},Z}=0$.

The important point is that we can compute the infimum in $U_{\mathcal {C},Z}$ even if the set Z contains collisions. It makes sense to take as $\mathcal {C}$ a cluster of close points (containing possible collisions and near collisions), so that there is no collision between bodies in $\mathcal {C}$ and its complement. In such case, $F_{\mathcal {C},Z}$ will be finite.

We have the following criterion for nonexistence of CC in Z:

Lemma 12

Assume that $U_{\mathcal {C},Z}, I_{\mathcal {C},Z}, F_{\mathcal {C},Z} \in \mathbb {R}$ and

$$\begin{aligned} I_{\mathcal {C},Z} < U_{\mathcal {C},Z} + F_{\mathcal {C},Z}, \end{aligned}$$

then there is NO central configuration in Z.

Proof

Without any loss of the generality we can assume that $\mathcal {C}=\{1,\ldots ,s\}$ for some $1 \leqslant s \leqslant n$. Consider system (3). We multiply i-th equation by $m_i q_i$ and we add first s equations. We obtain (compare the proof of Lemma 4)

$$\begin{aligned} \sum _{i=1}^s m_i q_i^2 = \sum _{1\leqslant i< j \leqslant s} \frac{m_i m_j}{r_{ij}} + \sum _{i=1}^s \sum _{j>s} \frac{m_i m_j (q_i - q_j|q_i)}{r_{ij}^3}. \end{aligned}$$

(30)

Let us stress that (30) must hold for any central configuration. Now for $q \in Z$ holds

$$\begin{aligned}&\sum _{1\leqslant i< j \leqslant s} \frac{m_i m_j}{r_{ij}} + \sum _{i=1}^s \sum _{j>s} \frac{m_i m_j (q_i - q_j|q_i)}{r_{ij}^3}\\&\quad \geqslant U_{\mathcal {C},Z} + F_{\mathcal {C},Z} > I_{\mathcal {C},Z} = \sum _{i=1}^s m_i q_i^2. \end{aligned}$$

Hence (30) is not satisfied. Therefore, we do not have any central configuration in Z. $\square$

Observe that if $\mathcal {C}=\{1,\ldots ,n\}$ the above lemma is reduced to checking whether $\inf _{q \in Z} U(q) > \sup _{q \in Z} I(q)$.

5 The reduced system of equations for CC on the plane

5.1 Non-degenerate solutions of full and reduced systems of equations

Following Moeckel (2014), we state the definition.

Definition 2

We will say that a normalized central configuration $q=(q_1,\ldots ,q_n)$ is non-degenerate if the rank of $D\!F(q)$ is equal to $dn-\dim SO(d)$. Otherwise the configuration will be called degenerate.

The idea of the above notion of degeneracy is to allow only for the degeneracy related to the rotational symmetry of the problem, because by setting $\lambda =1$ in (2) and keeping the masses fixed we removed the scaling symmetry.

The system (10–11) obtained from (5) after removing the n-th body using the center of mass [condition (9)] we write as

$$\begin{aligned} F_{\mathrm {red}}(q_1,\ldots ,q_{n-1})=0, \end{aligned}$$

(31)

where $F_{\mathrm {red}}: \Pi _{i=1}^{n-1}\mathbb {R}^{d} \rightarrow \Pi _{i=1}^{n-1}\mathbb {R}^{d}$. Then it is easy to see that $q=(q_1,\ldots ,q_{n-1},q_n)$ is a non-degenerate central configuration iff the rank of $D\! F_{\mathrm {red}}(q_1,\ldots ,q_{n-1})$ is $d(n-1)-\dim SO(d)$.

5.2 The reduced system on the plane

We consider a planar case here, i.e., $d=2$. The fact that the system of Eq. (3) is degenerate (each solution give rise to a circle of solutions) make this system not amenable for the use of standard interval arithmetic methods (see for example the Krawczyk operator discussed in Sect. 6.3) to rigorously count all possible solutions. We need to kill the SO(2)-symmetry and then hope that all solutions will be non-degenerate. In this section, we show how to reduce the system (3) to an equivalent system amenable to the interval analysis tools.

Let us fix $k \in \{1,\ldots ,n-1\}$ and consider the following set of equations

$$\begin{aligned} q_i= & {} \frac{1}{m_i}f_i(q_1,\ldots ,q_n(q_1,\ldots ,q_{n-1})), \quad i\in \{1,\ldots ,n-1\}, i \ne k \qquad \end{aligned}$$

(32)

$$\begin{aligned} x_k= & {} \frac{1}{m_k}f_{k,x}(q_1,\ldots ,q_n(q_1,\ldots ,q_{n-1})), \end{aligned}$$

(33)

$$\begin{aligned} q_n(q_1,\ldots ,q_{n-1})= & {} -\frac{1}{m_n}\sum _{i=1}^{n-1} m_i q_i, \end{aligned}$$

(34)

where $f_i = (f_{i,x}, f_{i, y})$. Observe that the system (32–34) coincides with the system (10–11) with the equation for $y_k$ dropped.

The next theorem addresses the question: whether from the reduced system (32–34) we obtain the solution of (3)?

Theorem 13

Assume $d = 2$. If $(q_1,\ldots ,q_{n-1},q_n(q_1,\ldots ,q_{n-1}))$ is a solution of the reduced system (32–34) and $x_k \ne x_n$, then it is a normalized central configuration, i.e., it satisfies (3).

Proof

Let $q_i$ be as in our assumptions. We need to show that $m_k y_k=f_{k,y}$. From (34), (6) and (7), it follows that

$$\begin{aligned} 0= & {} \sum _{i=1}^n f_i \wedge q_i = \sum _{i=1}^{n-1}f_i \wedge q_i + \left( -\sum _{i=1}^{n-1}f_i \right) \wedge \left( \frac{-\sum _{i=1}^{n-1}m_i q_i}{m_n} \right) \\= & {} \sum _{i=1}^{n-1}f_i \wedge q_i \left( 1 + \frac{m_i}{m_n} \right) + \frac{1}{m_n} \sum _{i,j=1, i\ne j}^{n-1}m_j f_i \wedge q_j. \end{aligned}$$

Since from (32)

$$\begin{aligned} q_i \wedge f_i= & {} 0, \quad i=1,\ldots ,n-1; \quad i \ne k, \end{aligned}$$

we obtain

$$\begin{aligned} 0= f_k \wedge q_k \left( 1 + \frac{m_k}{m_n} \right) + \frac{1}{m_n} \sum _{i,j=1, i\ne j}^{n-1}m_j f_i \wedge q_j. \end{aligned}$$

(35)

Let us take the look at $\sum _{i,j=1, i\ne j}^{n-1}m_j f_i \wedge q_j$. We have from (32)

$$\begin{aligned} \sum _{i,j=1, i\ne j, i \ne k, j\ne k}^{n-1}m_j f_i \wedge q_j = \sum _{i,j=1, i\ne j, i \ne k, j\ne k}^{n-1} f_i \wedge f_j =0, \end{aligned}$$

hence again from (32), it follows that

$$\begin{aligned} \sum _{i,j=1, i\ne j}^{n-1}m_j f_i \wedge q_j= & {} \sum _{i=1,i \ne k}^{n-1} \left( m_k f_i \wedge q_k + m_i f_k \wedge q_i\right) \\= & {} \sum _{i=1,i \ne k}^{n-1} \left( m_k m_i q_i \wedge q_k - m_i q_i \wedge f_k\right) \\= & {} \left( \sum _{i=1,i \ne k}^{n-1} m_i q_i \right) \wedge \left( m_k q_k - f_k\right) . \end{aligned}$$

From the above and (35), we obtain

$$\begin{aligned} 0= f_k \wedge q_k \left( 1 + \frac{m_k}{m_n} \right) + \frac{1}{m_n}\left( \sum _{i=1,i \ne k}^{n-1} m_i q_i \right) \wedge \left( m_k q_k - f_k\right) . \end{aligned}$$

From (33), we have

$$\begin{aligned} 0= & {} f_k \wedge q_k \left( 1 + \frac{m_k}{m_n} \right) + \frac{1}{m_n}\left( \sum _{i=1,i \ne k}^{n-1} m_i q_i \right) \wedge \left( m_k q_k - f_k\right) \\= & {} (f_{k,x}y_k - f_{k,y}x_k)\left( 1 + \frac{m_k}{m_n} \right) + \frac{1}{m_n}\left( \sum _{i=1,i \ne k}^{n-1} m_i x_i \right) \left( m_k y_k - f_{k,y}\right) \\= & {} (m_k x_k y_k - f_{k,y}x_k)\left( 1 + \frac{m_k}{m_n} \right) + \frac{1}{m_n}\left( \sum _{i=1,i \ne k}^{n-1} m_i x_i \right) \left( m_k y_k - f_{k,y}\right) \\= & {} \left( m_k y_k - f_{k,y}\right) \left( x_k\left( 1 + \frac{m_k}{m_n} \right) + \frac{1}{m_n}\left( \sum _{i=1,i \ne k}^{n-1} m_i x_i \right) \right) \\= & {} \frac{1}{m_n} \left( m_k y_k - f_{k,y}\right) \left( m_n x_k + \left( \sum _{i=1}^{n-1} m_i x_i \right) \right) \\= & {} \frac{1}{m_n} \left( m_k y_k - f_{k,y}\right) \left( m_n x_k -m_n x_n \right) = \left( m_k y_k - f_{k,y}\right) \left( x_k - x_n \right) . \end{aligned}$$

Now if $x_k - x_n \ne 0$, then $m_k y_k = f_{k,y}$. $\square$

The system (32–33) contains $2(n-1)-1$ equations in $2(n-1)$ variables and has O(2) symmetry (i.e., rotations around origin and reflection symmetries with respect to lines passing through the origin map solutions of this system into itself). In order to obtain a system with the same number of equations and variables, we can impose additional condition leading to the removal of $y_k$ variable, so that the rotational symmetry will be broken. Obviously in the above setting we could drop the equation for $x_k$ and we will obtain an analogous result.

We can think of a general reduced system as follows:

• we fix some hyperplane H, in the reduced (by the center of mass condition) configuration space $\mathbb {R}^{2(n-1)}$, so that H is transversal to the action SO(2) and k is such that $v_k \in \{x_k,y_k\}$ can be computed in terms of other variables. This will induce an embedding, $J_{k}:\mathbb {R}^{2(n-1)-\dim SO(2)} \rightarrow H$.

• in the system (10–11) we remove the equation for $v_{k}$. Then the reduced system can be written as

  $$\begin{aligned} R_{k} F_{\mathrm {red}} (J_{k}z)=0, \end{aligned}$$

  (36)

  where $R_k$ is a projection which removes $v_k$ variable in the image.

The system (32–34) supplemented by substitution $y_k=y_k(\ldots )$ is an example of (36). We present the following obvious result

Theorem 14

Assume for simplicity that H is given by

$$\begin{aligned} y_{k}=\sum _{i \ne k, i\leqslant n-1} a_i y_i + \sum _{i\leqslant n-1} b_i y_i. \end{aligned}$$

(37)

Assume that q is a solution of reduced system (36) with a substitution (37), such that $x_k\ne x_n$. Then q is a normalized central configuration. If q is non-degenerate solution of the reduced system, then this is non-degenerate solution of (3).

Proof

The first part is obvious in view of Theorem 13 and condition $x_k \ne x_n$ implies that it is a central configuration. The maximum rank in the reduced system gives the non-degeneracy of the configuration in the sense of Definition 2. $\square$

Following Albouy and Kaloshin (2012), we have tried two possibilities

• we set $k=2$ and we eliminate variable $y_2$ by setting

  $$\begin{aligned} y_2=y_1, \end{aligned}$$

  (38)

• we set $k=n-1$ and we eliminate variable $y_{n-1}$ by setting

  $$\begin{aligned} y_{n-1}=0. \end{aligned}$$

  (39)

Observe that for both normalizations defined above for any CC q there is a rotation R such that Rq satisfies this normalization. Hence we can safely impose any of those conditions without losing any CC. In both cases, we will need

$$\begin{aligned} x_k \ne x_n. \end{aligned}$$

(40)

First consider (38). Condition (40) does not hold for some CC in the case of equal masses. For example, for $n=4$ and an equilateral rectangle, such that $x_2=x_4$ we obtained numerically (and also symbolically using Mathematica) that the jacobian matrix for the reduced system has a zero eigenvalue. Hence the solution is degenerate for the reduced system.

Now, consider the condition (39). If we setup our computations so that $q_{n-1}$ body maximizes the distance from the origin for all bodies, then we have (40) satisfied, otherwise $q_n$ will be further from zero. This observation does not prove that if q is a non-degenerate CC in the sense of Definition 2, then it is also a non-degenerate solution of the reduced system, but this appears to happen in our rigorous computation of central configurations so far.

In our proof, since we apply the Krawczyk method (see Sect. 6.3) to obtain the solutions of the reduced system, all CCs whose existence we establish are non-degenerate in the sense of Definition 2.

6 On the computer-assisted proof

We normalized masses so that $M=\sum _i m_i=1$. In this section, we index bodies from 0 to $n-1$ to be in the agreement with our program. In the sequel, we study the following reduced system

$$\begin{aligned} q_i= & {} \frac{1}{m_i}f_i(q_0,\ldots ,q_{n-2},q_{n-1}(q_0,\ldots ,q_{n-2})), \quad i\in \{0,\ldots ,n-3\}, \end{aligned}$$

(41)

$$\begin{aligned} x_{n-2}= & {} \frac{1}{m_{n-2}}f_{n-2,x}(q_0,\ldots ,q_{n-2},q_{n-1}(q_0,\ldots ,q_{n-2})), \end{aligned}$$

(42)

where we set

$$\begin{aligned} y_{n-2}= & {} 0, \end{aligned}$$

(43)

$$\begin{aligned} q_{n-1}(q_0,\ldots ,q_{n-2})= & {} -\frac{1}{m_{n-1}}\sum _{i=0}^{n-2} m_i q_i . \end{aligned}$$

(44)

6.1 Equal masses case, the reduction in the configuration space for CCs

In the case of equal masses, after a suitable rotation and permutation of the bodies, we can assume that

$$\begin{aligned} |x_{n-2}| \geqslant |q_i| , \quad i=0,\ldots ,n-1. \end{aligned}$$

(45)

Condition (45) guarantees that $x_{n-2} \ne x_{n-1}$, hence by Theorem 13 the solution of a reduced system (41–42) is CC. In view of symmetry and Lemma 9, we impose some more conditions

$$\begin{aligned} n-1 \geqslant x_{n-2} \geqslant 0.5. \end{aligned}$$

(46)

After a suitable permutation of bodies and a reflection with respect to 0X-axis, it is easy to see that each CC has its equivalent in the set of the configurations satisfying the following conditions

• $q_{n-2}=(R,0)$ is the furthermost body from the origin

• $q_0$ is the leftmost with non-negative y-coordinate

• $q_1$ has the smallest y coordinate

• all other bodies have their x coordinates in the order of increasing/decreasing indices.

This, combined with Lemma 10, shows that it is enough to consider the following set in which we look for the central configuration

$$\begin{aligned}&\displaystyle 0.5 \leqslant x_{n-2} \leqslant (n-1), \end{aligned}$$

(47)

$$\begin{aligned}&\displaystyle -(n-1) \leqslant x_0 <0, \end{aligned}$$

(48)

$$\begin{aligned}&\displaystyle x_0 \leqslant x_i \leqslant x_{n-2}, \quad i=0,\ldots ,n-1, \end{aligned}$$

(49)

$$\begin{aligned}&\displaystyle y_0 \geqslant 0, \end{aligned}$$

(50)

$$\begin{aligned}&\displaystyle -(n-1) \leqslant y_1 \leqslant 0, \end{aligned}$$

(51)

$$\begin{aligned}&\displaystyle y_1 \leqslant y_i \leqslant (n-1) , \quad i=0,\ldots ,n-1 \end{aligned}$$

(52)

$$\begin{aligned}&\displaystyle x_2 \leqslant x_3 \leqslant \cdots \leqslant x_{n-3} \leqslant x_{n-1}. \end{aligned}$$

(53)

We call this order increasing due to the requirement (53). In the computation, we use analogous decreasing ordering in which we state the opposite, i.e.,

$$\begin{aligned} x_2 \geqslant x_3 \geqslant \cdots \geqslant x_{n-3} \geqslant x_{n-1}. \end{aligned}$$

(54)

For now, we do not know why it is better to use the decreasing order, but the difference is significant (see Table 2).

Table 2 Times of asynchronous computations in minutes for different orderings (the computations were carried out on the computer Intel Core i7-5500U CPU @ 2.40 GHz $\times$ 4 with 8 GB RAM; a single thread was used)

6.2 Outline of the approach

In the algorithm, we look for all zeros of the reduced system (41, 42), which under assumption $x_{n-1}\ne x_{n-2}$ by Theorem 13 is equivalent to (3). For our algorithm, proving an existence of locally unique solution in some box is as important as proving that in a given box there is no solution.

For proving of the existence of the locally unique solution, we use the Krawczyk operator applied to the system (41, 42). To rule out the existence of solution, we use the exclusion tests discussed in Sect. 4 and also the Krawczyk operator.

The symmetry of CCs is established by proving the uniqueness in a suitable symmetric box (see Sect. 7.2).

6.3 The Krawczyk operator

The Krawczyk operator (Alefeld 1994; Krawczyk 1969; Neumeier 1990) is an interval analysis tool to establish the existence of unique zero for the system of n nonlinear equations in n variables. Below we briefly explain how the Krawczyk operator is derived, as it appears mysterious and little known outside the interval arithmetic community.

6.3.1 Motivation, heuristic derivation

Let $F: \mathbb {R}^n \rightarrow \mathbb {R}^n$ be a $C^1$-function. We would like to solve the equation

$$\begin{aligned} F(x)=0. \end{aligned}$$

(55)

We begin by explaining the basic idea of the Krawczyk method. The Newton method is given by

$$\begin{aligned} N(x)=x - dF(x)^{-1}F(x). \end{aligned}$$

(56)

It is well known that if $F(x^*)=0$ and $dF(x^*)$ is nonsingular, then $x^*$ is an attracting fixed point for N(x). It turns out that the same is true if we replace $dF(x)^{-1}$ by a fixed matrix C, which is sufficiently close to $dF(x^*)^{-1}$. The modified Newton operator is given by

$$\begin{aligned} N_m (x)= x - C F(x). \end{aligned}$$

(57)

Now let us turn the things around and ask how can we use $N_m$ as a way to prove the existence of solution of (55). This is quite obvious. Namely, if U is homeomorphic to a closed finite-dimensional ball and if

$$\begin{aligned} N_m(U) \subset U, \end{aligned}$$

(58)

then from the Brouwer theorem it follows, that there exists $x_0 \in U$ such that $N_m(x_0)=x_0$. Since C is invertible, we obtain that $F(x_0)=0$. To obtain the uniqueness, it is enough show that $N_m$ is a contraction on U. Observe that it is impossible to verify in a single interval evaluation of the formula (57), that for some interval set [x] holds $N_m([x]) \subset [x]$, because the computed diameter of $[x] - CF[x]$ is greater than or equal to $\,\mathrm{diam}\,([x]) + \,\mathrm{diam}\,(CF([x]))$. It turns out the mean value form of $N_m$ can cure this deficiency. If $x_0 \in [x]$, then

$$\begin{aligned}&N_m([x]) \subset N_m(x_0) + [d N_m([x])]_I \cdot ([x] - x_0)\\&\quad =x_0 - C F(x_0) + (Id - C [df([X])]_I)([x] - x_0)=K(x_0,[x],F). \end{aligned}$$

This explains why the requirement $K(x_0,[x],F) \subset [x]$ has something to do with zeros of F(x).

6.3.2 The Krawczyk method

A method proposed by Krawczyk for finding zero’s of F:

• $[x] \subset \mathbb {R}^n$ be an interval set (i.e., product of intervals),

• $x_0 \in [x]$. Typically $x_0$ is chosen to be midpoint of [x], we will denote this by $x_0=mid([x])$.

• $C \in \mathbb {R}^{n \times n}$ be a linear isomorphism.

The Krawczyk operator is given by

$$\begin{aligned} K(x_0,[x],F):= x_0 - C F(x_0) + (Id - C \left[ dF([x]) \right] _I)([x] - x_0). \end{aligned}$$

(59)

Theorem 15

• 1. If $x^* \in [x]$ and $F(x^*) =0$, then $x^* \in K(x_0,[x],F)$.

• 2. If $K(x_0,[x],F) \subset \mathrm{int}\,[x]$, then there exists in [x] exactly one solution of equation $F(x)=0$. This solution is non-degenerate, i.e., dF(x) is an isomormophism.

• 3. If $K(x_0,[x],F) \cap [x]=\emptyset$, then for all $x \in [x]$ $F(x) \ne 0$.

Observe that point 2. in the above theorem gives us the way to establish the existence of unique zero of F in [x], while point 3. rules out the existence of zero in [x], i.e., in the terminology of previous section this is the exclusion test. When [x] is close to a zero of F then ${<}F([x]){>}$ the evaluation of F([x]) in the interval arithmetic might produce such overestimates that $0 \in {<}F([x]){>}$, while the Krawczyk operator will rule out the existence of 0 of F in [x]. This is in fact quite common phenomenon.

The Krawczyk operator is used as a part of iteration process

• 0. given $[x]_0 \subset \mathbb {R}^n$

• 1. compute $[y] = K(mid([x]_k),[x]_k,F)$

• 2. if $[y] \subset \mathrm{int}\,[x]_k$, then return success, a unique solution in $[x]_0$ was found

  elseif $[x]_k \subset [y]$, then return failure

  elseif set $[x]_{k+1}:=[y] \cap [x]_k$ and goto 1.

The above loop can be executed several times and even if no success is obtained the last computed [y] may give us useful information, because we know from Theorem 15 that all possible zeros are contained in [y]. This set, instead of $[x]_0$, can be used in further computations, while $[x]_0 {\setminus } [y]$ can be discarded. In the next section, we will discuss what is essentially a binary search algorithm, which scales poorly with the number of bodies due to the curse of dimensionality (Traub et al. 1988) and the reduction obtained by the Krawczyk method, i.e., replacing $[x]_0$ by [y] for further subdivision leads to significant speed improvements, because the Krawczyk method on sufficiently small scales appear to work in time polynomial with respect to the number of bodies.

In our context, the only weakness of the Krawczyk operator is that it requires the sets of the diameter in each coordinate directions to be smaller than $10^{-2}$ to give us something. Above that threshold, we usually have $[x] \subset K(mid([x]),[x],F)$ and the Krawczyk method is useless.

7 The algorithm

The algorithm runs in the reduced configuration space which is a subset of $\mathbb {R}^{2(n-1)-1}$, i.e., a configuration is represented by a point $(x_0, y_0,\ldots , x_{n-3}, y_{n-3}, x_{n-2})$. Physically, we interpret such a configuration as $n-1$ bodies with $q_i=(x_i, y_i)$ for $i = 0, \ldots , n-3$ and $q_{n-2}=(x_{n-2},0)$. From (44) we obtain $q_{n-1}$ the position of the last body.

Input: The input of the algorithm consists of

• 1. n—the number of bodies

• 2. some cube in the reduced configuration space.

Output: All different (up to reflections and rotations) central configurations in the full system for a given input cube. Since we use interval arithmetic for calculations, central configurations are also cubes containing the exact solution in their interior.

The program is divided into two stages: searching finds solutions and testing tests them to distinguish different CC and to find the kind of symmetry (if any exists).

7.1 Searching stage

In this stage, we cover the configuration space with cubes. To fulfill requirements of Krawczyk’s method (see Theorem 15), we must ensure that every point is in the interior of some cube. The algorithm runs for any initial cube; however, if our goal is to find all the central configurations (for fixed n and equal masses) the reasonable cube is as follows (compare Sect. 6.1):

$$\begin{aligned} x_0\in & {} [-(n-1), 0]\\ y_0\in & {} [0, n-1]\\ x_1, \ldots , x_{n-3}\in & {} [-(n-1), n-1]\\ y_1\in & {} [-(n-1), 0]\\ y_2, \ldots , y_{n-3}\in & {} [-(n-1), n-1]\\ x_{n-2}\in & {} [0.5, n-1] \end{aligned}$$

Simple recursive algorithm works as follows:

• (I) if there is no solution in the cube return 0;

• (II) if there is unique solution in the cube return 1;

• (III) otherwise bisect the longest edge and recursively run the procedure for both parts;

• (IV) return result.

In the more detailed version of the algorithm, the cube is represented by a vector of bodies. The class Bodies contains this vector and some methods to manipulate these bodies. An instance of Bodies is a cube bodies with some additional information (Fig. 2).

Fig. 2

Two steps a ${\mathop {\longrightarrow }\limits ^{1}}$ b ${\mathop {\longrightarrow }\limits ^{2}}$ c of the algorithm on the cube with each wall projected on the plane: the longest edge is divided and new coordinates of the last body, $q_2$, are calculated. Notice that after subdivision the new cubes have an intersection with non-empty interior

7.1.1 Details and optimizations

The crucial function thereIsNoSolution(bodies) contains a series of tests (the exclusion tests); if these tests are not satisfied, then we know that there is no solution in bodies:

• 1. checkAprioriBounds(bodies)—tests if bodies satisfy a priori bounds (see Theorem 11);

• 2. checkUEqI(bodies)—if there is no collision in bodies, tests if $U(q) == I(q)$ (see Lemma 4);

• 3. clusterTest(bodies)—see Lemma 12 and Subsec. 4.2

• 4. distanceTest(bodies)—tests the order of bodies (see conditions (47)–(53))

• 5. checkZero(bodies, i)—computes functions of vector field [see Eq. (4)] and tests if it is possible to have $F(q_0, \ldots , q_{N-1}) = 0$ as discussed in Sect. 4.1.

To break (or to rather to relieve) the dimensionality curse, we are looking for the possibility of restricting bodies before bisecting them (line 16). First place we are able to do this is the function thereIsNoSolution(bodies) (see Sect. 4.1). Another place is in krawczykMethod(bodies). If Krawczyk’s method fails (line 5), bodies will have been restricted by intersection with the operator. Hence it is now (from line 17 onwards) the restricted cube that is being processed. This gives a large growth of efficiency.

Since the Krawczyk’s method is costly and usually fails for large sets, we introduced a parameter bias. If the size (diameter) of all variables is not greater than bias then the Krawczyk’s method is run. There is a big difference in execution time of the program depending on the value of the bias parameter; in Table 3 we present computation times for 5 bodies . For the same initial data, the program finds 8 solutions (some of them are later identified to be the same solutions), but numbers of failed and ‘no-zero-inside’ cubes differ.

Table 3 Comparison of execution times for 5 bodies for different thresholds, where we start Krawczyk’s method (the computations were carried out on the computer Intel Core i7-5500U CPU @ 2.40 GHz $\times$ 4 with 8 GB RAM; a single thread was used)

7.2 Testing stage

The main goal of this stage is to identify distinct solutions. Additionally, we check the symmetry of solutions. In this stage, we consider solutions in the full system.

The solutions obtained in the search stage are given as a list of boxes in which we have a unique solution. Some of these boxes may overlap and can in fact contain the same solution. Because we consider the equal masses case we also do not want to distinguish solutions which differ by the indexes of the bodies. Hence two solutions produced in the searching stage can in fact be equivalent for two reasons:

• (1) the only difference is the ordering of the bodies,

• (2) the boxes defining them have non-empty intersection, having been obtained in different series of partitions.

Fig. 3

Reasons for two solutions (projected onto the plane) to be equivalent: the exact unique central configuration (marked with dots) is inside both. Interval hull of these solutions is marked by dashed boxes

For any pair of solutions, we treat the first one as a ‘model’, while bodies in the second solution are permuted in an attempt to match the model. When trying to match the solutions, we create a set containing both of them (an interval hull) and we prove the uniqueness within it. The rough idea is shown below (Fig. 3):

It may happen that there exists a solution in the set unionBodies, but the set is too small to prove this using the Krawczyk operator, thus we ‘inflate’ it and retry the proof in the bigger set (the function blowUp(unionBodies)).

Establishing a (reflectional) symmetry of CC is very similar to testing the uniqueness of solutions. However, it requires an additional step to calculate a symmetric image. We take an interval hull of CC and its symmetric image. The possible lines of reflection are an axis OX or the bisector of the angle with the vertex at (0, 0) and the rays passing through $q_{n-2}$ (the body furthest from (0, 0)) and through $q_i$ (different bodies are tested). The sketch of the function establishing this symmetry is given below.

In line 2, we calculate the parameters of the possible reflection symmetry line, but the symmetry tested contains also a permutation of bodies, we construct a configuration symBodies considering all possible permutations of bodies. Note that lines 5–12 in the function checkSym are identical, up to the variable names, to lines 3–11 in theSameSolutions.

7.3 Technical data

The main computations were carried out in parallel using the template function std::async (from the standard C++ library) which runs the function asynchronously (potentially in a separate thread which may be part of a thread pool) on Dell R930 4x Intel Xeon E7-8867 v3 (2,5GHz, 45MB), 1024 GB RAM. The compiler is gcc version 4.9.2 (Debian 4.9.2-10+deb8u2). The best obtained times for different number of bodies with $\mathtt{bias}=10^{-2}$ are presented in Table 4.

Table 4 Comparison of execution times for different number of bodies

8 Minimizing dependency problem in gravitational force evaluation

In this section, we describe a method of calculations of functions and their derivatives used in the program. Let us denote $F_i = (f_i^1, f_i^2)$, $r_{ij} = \sqrt{(x_i - x_j)^2 + (y_i - y_j)^2}$. Then functions $f_i^{[1,2]}$ and their derivatives are (with analogs for y’s):

$$\begin{aligned} \displaystyle {f_i^1}= & {} \displaystyle {x_i - \sum _{\begin{array}{c} j = 1,\\ j\ne i \end{array}}^{N} m_j \frac{x_i - x_j}{r_{ij}^{3}}}\nonumber \\ \displaystyle {f_i^2}= & {} \displaystyle {y_i - \sum _{\begin{array}{c} j = 1,\\ j\ne i \end{array}}^{N} m_j \frac{y_i - y_j}{r_{ij}^3}}\nonumber \\ \displaystyle {\frac{\partial }{\partial x_k}f_i^1}= & {} \displaystyle {-m_k \left( 3\frac{(x_i - x_k)^2}{r_{ik}^5} - \frac{1}{r_{ik}^3}\right) + m_k\left( 3\frac{(x_i - x_N)^2}{r_{iN}^5} - \frac{1}{r_{iN}^3}\right) } \quad \text{ for } k\ne i\nonumber \\ \displaystyle {\frac{\partial }{\partial x_i}f_i^1}= & {} \displaystyle {1 + \sum _{\begin{array}{c} j = 1,\\ j\ne i \end{array}}^{N-1} m_j \left( 3\frac{(x_i - x_j)^2}{r_{ij}^5} - \frac{1}{r_{ij}^3}\right) + m_N\left( 1 + \frac{m_i}{m_N}\right) \left( 3\frac{(x_i - x_N)^2}{r_{iN}^5} - \frac{1}{r_{iN}^3}\right) } \nonumber \\ \displaystyle {\frac{\partial }{\partial x_k}f_i^2}= & {} \displaystyle {-3m_k \frac{(x_i - x_k)(y_i - y_k)}{r_{ik}^5} + 3m_k\frac{(x_i - x_N)(y_i - y_N)}{r_{iN}^5}} \end{aligned}$$

(60)

$$\begin{aligned} \displaystyle {\frac{\partial }{\partial x_i}f_i^2}= & {} \displaystyle { 3\sum _{\begin{array}{c} j = 1,\\ j\ne i \end{array}}^{N-1} m_j \frac{(x_i - x_j)(y_i - y_j)}{r_{ij}^5} + 3m_N\left( 1+\frac{m_i}{m_N}\right) \frac{(x_i - x_N)(y_i - y_N)}{r_{iN}^5}} \\ \displaystyle {\frac{\partial }{\partial y_k}f_i^1}= & {} \displaystyle {\frac{\partial }{\partial x_k}f_i^2}\quad \hbox {for all } k.\nonumber \end{aligned}$$

(61)

In the program, we have to evaluate $f_i^{[1,2]}$ on a box D in configurations space. The naive interval evaluation of $f_i^{[1,2]}$, where we just plug-in the interval arguments, might lead to severe overestimation due to the dependency problem (Moore 1966; Neumeier 1990). The best solution would be a cheap but rigorous estimate of $\sup$ and $\inf$ of $f_{i}^1$ and $f_{i}^2$ over D; this however appears to be a difficult and costly task. For the Krawczyk method, we also need good estimates for $\frac{\partial f_i}{\partial x_j}$ and $\frac{\partial f_i}{\partial y_j}$ and we face the same problem. Thus we decided to optimize the computation of the following expressions

$$\begin{aligned} \frac{(x_j - x_i)^a}{r_{ij}^b}\quad \hbox {and}\quad \frac{(y_j - y_i)^a}{r_{ij}^b} \end{aligned}$$

over $q = (x,y) = (x_j - x_i, y_j - y_i)\in D \subset \mathbb {R}^2$, since such components appear in all above equations. In Eqs. (60) and (61), we evaluate expressions in the form $xy/r^5$ as a product of $x/r^3$ and $y/r^2$ which are treated as separate expressions.

8.1 Estimates for $x^a / r^b$ and $y^a / r^b$

Assume we want to calculate

$$\begin{aligned} f_x(x,y)= & {} \frac{x^a}{r^b} = \frac{x^a}{(x^2 + y^2)^\frac{b}{2}}\end{aligned}$$

(62)

$$\begin{aligned} f_y(x,y)= & {} \frac{y^a}{r^b} = \frac{y^a}{(x^2 + y^2)^\frac{b}{2}}, \end{aligned}$$

(63)

where $a < b$, $(x,y) = (x_j - x_i, y_j - y_i)$. Let us define $D = (x_L, x_R)\times (y_L,y_R)$. We want to estimate $f_x$ and $f_y$ on D. We always assume that $(0,0)\not \in D$. To minimize the overestimation of these calculations, we look for the possible local extrema in D.

Fig. 4

Calculated lines and location of critical points

Let us consider the function $f_x$; the second case of $f_y$ is symmetrical. First notice that by solving the system of equations

$$\begin{aligned} \frac{\partial }{\partial x} f_x(x,y)= & {} \frac{x^{a-1}(x^2(a-b) + ay^2)}{r^{b+2}} = 0\end{aligned}$$

(64)

$$\begin{aligned} \frac{\partial }{\partial y} f_x(x,y)= & {} - \frac{bx^ay}{r^{b+2}} = 0, \end{aligned}$$

(65)

we obtain $(x,y) = (0,0)$, which is impossible in our settings. Since there is no local extremum inside D thus it is attained on the edge of D. Te determine the specific points, where this extremum can be, we explore Eqs. (64) and (65) and analogical for $f_y$, and we obtain:

• border points on the lines $y =\, \pm \,x\sqrt{\frac{b-a}{a}}$ and $x = \,\pm \, y\sqrt{\frac{b-a}{a}}$ (blue points in Fig. 4)

• border points for $x = 0$ and for $y = 0$ (black points in Fig. 4)

Additionally we consider corners of D (red points in Fig. 4). Next we examine all these point to establish the maximum and the minimum value of $f_x$ and $f_y$.

Note, that there is still a lot of room for further optimization, but for now only this version is implemented in the program.