Long-term passive distance-bounded relative motion in the presence of $J_2$ perturbations

Abstract

This paper presents closed-form solutions for the problem of long-term satellite relative motion in the presence of $J_2$ perturbations, and introduces a design methodology for long-term passive distance-bounded relative motion. There are two key ingredients of closed-form solutions.One is the model of relative motion; the other is the Hamiltonian model and its canonical solution of the $J_2$-perturbed absolute motion. The model of relative motion makes no assumptions on the eccentricity of the reference orbit or on the magnitude of the relative distances. Besides, the relative motion model is concise with straightforward physical insight, and consistent with the Hamiltonian model. The Hamiltonian model takes into account the secular, long-periodic and short-periodic effects of the $J_2$ perturbation. It also remains separable in terms of spherical coordinates to ensure the application of the Hamilton–Jacobi theory to derive the canonical solution. When deriving the canonical solution, pseudo-circular and pseudo-elliptical orbits are treated separately and Carlson’s method is employed to calculate elliptic integrals, which takes advantage of the symmetry of the integrand. These symmetry properties hold physical insights of the $J_2$-perturbed absolute motion. To design the long-term distance-bounded relative motion, the nodal period and the drift of right ascension of the ascending node (RAAN) per nodal period are, respectively, matched non-instantaneously. Even though the nodal period and the drift of RAAN per nodal period can be obtained via the canonical solution, action-angle variables are used to obtain the frequency of the system without finding the complete solution to the perturbed orbital motion.

1 Introduction

Non-traditional space mission attributes such as responsiveness, in contrast to traditional attributes such as cost and mass, add a new impetus to the advance of space systems, in particular to systems of small satellites. Especially, space architectures using fractionated spacecraft hold an immense potential to meet non-traditional requirements (Brown et al. 2006). With modules in the fractionated system being physically separated, yet functionally linked via wireless networks, the architecture enhances space assets’ flexibility, robustness and responsiveness. Requirements on the fractionated cluster are at least fourfold. First, the wireless network shall be maintained in the cluster. Second, collision avoidance or safe operational distances between any two modules in the cluster shall be considered. The first and second requirements imply that the cluster shall be distance bounded. Third, the cluster shall be scalable and allow for adding or removing modules. Fourth, the cluster keeping shall ideally be passive to avoid continuous consumption of onboard propellant even in the presence of perturbations. In order to design the cluster that meets all aforementioned requirements, new approaches must be developed to accurately predict and analyze the long-term behavior of the relative motion between two satellites.

To study the long-term behavior of satellites flying in low Earth orbits (LEO), the orbital motion can no longer be treated as Keplerian. The most dominant perturbation is the Earth’s oblateness, which is primarily characterized by the $J_2$ term from the spherical harmonic expansion of the Earth’s gravity field. Reported research on the relative motion of two or more satellites in the presence of the $J_2$ perturbation is mainly following either an analytical or a numerical approach. The analytical approach proposed first by Schaub and Alfriend (2001) addressed the problem of $J_2$-invariant relative orbits for formation flying. Taking $J_2$ perturbations into account for the design of formation flying, the resulting drifts need to be cancelled to ensure station keeping of the satellites in the formation. Basically, there are two ways to achieve that. One is to zero the drifts of all the individual satellites in the formation which, in general, is not possible. The other matches the relative drifts between two individual orbits which is the methodology to design $J_2$-invariant relative orbits. $J_2$-invariant relative orbits are designed based on mean orbital elements and the constraints imposed on the mean relative orbital elements are derived based on the first-order approximation. It is noted that the energies of the orbits that constitute $J_2$-invariant relative orbits are generally not equal to each other. Instead, the energy difference depends on the semi-major axis, the eccentricity and the inclination (Schaub and Junkins 2003).

However, the cluster flight of modules in a fractionated space system is different from formation flying of multiple satellites, as there is no requirement of the precise station keeping between two modules. Thus, there is no need to match the drifts between two individual orbits instantaneously. In addition, when considering the effect caused by the $J_2$ perturbation, the long-term passive distance-bound relative motion is most relevant for the establishment of a cluster. In such a context, the first-order approximation of the $J_2$-invariant relative orbits may not be valid anymore. Furthermore, the establishment of the cluster should include the cases where relative distances between two modules are on the order of tens or even hundreds of kilometers. Therefore, most existing methodologies are not applicable anymore. For example, Schweighart and Sedwick had derived a high-fidelity linearized $J_2$ model for satellite formation flying (Schweighart and Sedwick 2002). In order to linearize the relative motion in the presence of $J_2$ perturbations, both the $J_2$ potential and its gradient are approximated by their time averages. Besides, those averages are taken under the assumption of a constant-radius reference orbit. Even though a general linearization of the $J_2$ potential is performed, it is only valid when the relative distance between two satellites is small. In their research the relative distance is less than 1km.

To study $J_2$-perturbed long-term relative motion, an analytical approach is preferred. Analytical approaches are also referred to as closed-form solutions, where the solutions of relative motion are derived based on the integrable solutions of the absolute motion. The super-integrability of absolute motion in the equatorial plane is used by Martinusi and Gurfil (2011) and by means of elliptic integrals the closed-form solutions were obtained, which lead to exact periodicity conditions of relative motion. However, for inclined orbits the dynamics are no longer integrable.

Another closed-form solution of relative motion was obtained under the integrable approximation of the $J_2$ perturbation (Lara and Gurfil 2012). The intermediary Hamiltonian model of absolute motion is established via canonical polar-nodal variables. However, only the secular term of the $J_2$ perturbation is taken into account and the resulting drifts are matched instantaneously. In addition, the energies of different orbits in bounded relative motion are identical, which are different from the general cases of $J_2$-invariant relative orbits. Their research can be analyzed from a different perspective. It is well known that if two satellites have the same orbital elements except RAAN, the difference of RAAN as well as the other five orbital elements remains the same even in the presence of the $J_2$ perturbation (Mazal and Gurfil 2013). When such a closed-form solution of the relative motion is used to design bounded relative orbits and only secular effects of the $J_2$ perturbation are considered, since the derived Hamiltonian does not contain the argument of perigee explicitly, the argument of perigee can be chosen as the design parameter for bounded relative motion. However, if the argument of perigee is explicitly countered for in the Hamiltonian and the instantaneous matching of drifts is required at the same time, then bounded relative motion can only be achieved through a difference in RAAN (with the exception of cases involving the critical inclination).

As a counterpart, numerical approaches are also often conducted to study the long-term behavior of $J_2$-perturbed relative motion. One numerical method takes advantage of a genetic strategy which is refined by means of nonlinear programming (Sabatini et al. 2008). Since the global optimization technique is used, the computational load is huge and a physical interpretation of the results is not straightforward. However, the resulting drifts are not matched instantaneously and only a couple of special inclinations exist for passive bounded relative motion in the presence of the $J_2$ perturbation.

Another important numerical approach is based on the Poincaré surface of section from the dynamical system point of view (Xu et al. 2012). The $J_2$ perturbation is fully included in the Hamiltonian and the resulting drifts are not matched instantaneously. The Poincaré surface of section is located on the equatorial plane to obtain the nodal period and the drift of RAAN per nodal period numerically. The numerical representation is ergodic and thus the computational load is inevitably huge. Numerical proof shows that different orbits can share an identical nodal period and the drift of RAAN per nodal period in the presence of the $J_2$ perturbation. This means that for a given chief orbit there exists a large number of deputy orbits that can establish a long-term passive relative motion. However, the periodicity of those relative motion has not been studied.

The literature review can be summarized as follows which is made mainly based on (Xu et al. 2012) and (Broucke 1994). Satellites’ orbits under the $J_2$ perturbation can be classified as pseudo-circular or pseudo-elliptical (without consideration of the chaotic phenomena). For pseudo-circular orbits, the time derivative of the orbit radius is zero, and the radius differs from different combinations of the obit energy and the polar component of the angular momentum. Moreover, the nodal period and the drift of RAAN per nodal period of pseudo-circular orbits remain constant in the presence of the $J_2$ perturbation. However, for pseudo-elliptical orbits both the nodal period and the drift of RAAN per nodal period change periodically with respect to the orbit period. Therefore, the mean nodal period and the drift of RAAN per nodal period, rather than the instantaneous one, can be used to establish the long-term passive distance-bounded relative motion. It is noted that pseudo-circular and pseudo-elliptical orbits can be grouped together if they have the same combination of the orbit energy and the polar component of the orbit angular momentum. However, in the same group all the orbits don’t share identical nodal period and the drift of RAAN per nodal period except in the case where two orbits have the same orbital elements except RAAN. This therefore indicates that those orbits can’t be employed to establish the long-term distance-bounded relative motion.

In this paper an analytical method is presented to find the closed-form solutions of satellite relative motion in the presence of $J_2$ perturbations. First, a model of satellite relative motion is derived based on the geometrical relationship between two satellite orbits, where no assumption regarding to the magnitude of the relative distance or eccentricity of the reference orbit has been made. In order to design the long-term passive distance-bounded relative motion in the presence of $J_2$ perturbations, the parameters that characterize relative motion need to be studied and analyzed accounting for $J_2$ perturbations. This leads to a design methodology for the desired relative motion. The spherical coordinates, i.e., radius, azimuth angle and latitude, are employed to model the orbital motion in the presence of $J_2$ perturbations and the Hamilton–Jacobi theory is exploited to obtain the canonical solutions. The approximated $J_2$ perturbed gravitational potential is incorporated in the Hamiltonian such that not only the secular, short-periodic and long-periodic disturbances are accounted for, but also the Hamiltonian is still separable, which means that canonical solutions exist. Essentially, however, it is the nodal period and the drift of RAAN per nodal period that play key roles in the design. Moreover, the periods of the latitude and the azimuth angle correspond to the nodal period and the period of RAAN, respectively. Therefore, the periods of the latitude and the azimuth angle are of utmost importance as well. As a consequence, the action-angle variables can be taken advantage of to obtain the frequency of the system without finding the complete solution of the orbital motion that is disturbed by the approximated gravitational potential. Ultimately, to design the long-term passive distance-bounded relative motion, the nodal period and the drift of RAAN per nodal period are, respectively, matched non-instantaneously.

This paper is organized as follows. In Sect. 2, a model of relative motion between two satellites is derived including a model of the relative motion for small relative orbital elements and the nearly circular chief orbit. After that, in order to study the characteristics of the parameters in the model of relative motion, the canonical solutions of the $J_2$-perturbed orbital motion are presented in Sect. 3, where the approximated Hamiltonian are derived first and then the standard procedure of the Hamilton–Jacobi theory is followed to obtain the canonical solutions. In Sect. 4, the nodal period and the drift of RAAN per nodal period are derived, followed by the design methodology of the long-term distance-bounded relative motion in the presence of the $J_2$ perturbation. Finally, conclusions are drawn and an analysis to future research is provided.

2 Model of the relative motion

A model of the relative motion is derived in this section to lay the foundation for the closed-form solutions. The presented model is derived based on the geometrical relationship between two satellites, and features a kinematic property. Compared with the model in terms of orbit element differences (Schaub and Junkins 2003), there is neither linearization nor assumption of small differences between orbit elements required. Therefore, the derived model is valid for eccentric reference orbits as well as relative distances of large magnitude (on the order of tens or even hundreds of kilometers). The model of relative motion is also concise, i.e., as simple as possible, to ensure that the characteristics of the relative motion can be analyzed via the closed-form solution. In addition, the model of relative motion provides physical insights to the problem.

2.1 Model of the relative motion

The geometric relationship between two satellites, i.e., chief and deputy, is shown in Fig. 1. The subscript $C$ and $D$ stand for the chief and deputy satellite, respectively. As shown in Fig. 1, the orbits of two satellites are projected on a celestial sphere, the origin of which is the center of the Earth. The ascending nodes of the chief and deputy satellites are denoted by $N_C$ and $N_D$, respectively. The chief’s RAAN is $\varOmega _C$, while the one of the deputy is $\varOmega _D$, and the difference between $\varOmega _D$ and $\varOmega _C$ is defined as $\Delta \varOmega$, i.e., $\Delta \varOmega \triangleq \varOmega _D -\varOmega _C$. Denote by $\delta i$ the angle between the two orbital planes. The inclination difference $\Delta i$ is defined as $\Delta i\triangleq i_D -i_C$. The perigee of the chief satellite is marked as the point $P_C$. One intersection point of those two projected orbits on the surface of the celestial sphere is $I$.The arc lengths between $I$ and the ascending nodes $N_C$ and $N_D$ are $\varphi _C$ and $\varphi _D$, respectively. The relative angular positions of the chief and deputy satellite with respect to $I$ are denoted as $\theta _C$ and $\theta _D$, respectively. The relative angular position of the deputy with respect to the chief is represented via the azimuth angle, $\alpha$, and the elevation angle, $\delta$. The azimuth angle is measured counterclockwise as seen from the pole of the chief orbit and covers all the values between 0 and $2\pi$. The elevation angle is restricted to $-\pi /2$ to $\pi /2$.

Fig. 1

Geometric relationship between two satellites

The inertial reference frame $\left\{ {{\mathbf {X}}_I, {\mathbf {Y}}_I, {\mathbf {Z}}_I } \right\}$, and the local vertical and local horizontal (LVLH) reference frame, $\left\{ {{\mathbf {o}}_r, {\mathbf {o}}_\theta , {\mathbf {o}}_h } \right\}$, are defined to describe the absolute orbital motion and the relative motion, respectively. The inertial reference frame is defined as follows. The origin, $O$, is located at the center of the Earth. The axis $OX_I$, points towards the vernal equinox. The axis $OZ_I$, is along the Earth’s rotation axis, perpendicular to the Earth’s equatorial plane. The axis $OY_I$ lies in the Earth’s equatorial plane and completes the right-hand reference frame. The LVLH reference frame $\left\{ {{\mathbf {o}}_r, {\mathbf {o}}_\theta , {\mathbf {o}}_h } \right\}$ is defined as follows. The origin of the frame is centered on the center of mass (CM) of the chief satellite. The vector ${\mathbf {o}}_r$ points radially outward, while the vector ${\mathbf {o}}_h$ is parallel to the orbit momentum vector of the chief satellite in the orbit normal direction. The vector ${\mathbf {o}}_\theta$ completes the right-hand reference frame (positive in the velocity direction of the chief spacecraft).

For the derivation of the relative motion model, the relative position vector is firstly represented in terms of the azimuth and elevation angles, which are then geometrically interpreted by projecting those two orbits on the celestial sphere. In such a way, the relative motion is modeled based on the geometric relationship with respect to the intersection point $I$. The relative position of the deputy with respect to the chief in the LVLH reference frame can be written as the functions of $\alpha$ and $\delta$

$$\begin{aligned} \left\{ {\begin{array}{l} x=r_D \cos \delta \cos \alpha -r_C \\ y=r_D \cos \delta \sin \alpha \\ z=r_D \sin \delta \\ \end{array}} \right. \end{aligned}$$

(1)

where $r_C$ and $r_D$ are the radius of the chief and deputy satellite, respectively. Based on the geometric relationship between two satellites, the angles $\alpha$ and $\delta$ are expressed as

$$\begin{aligned} \left\{ {\begin{array}{l} \alpha =\arctan (\cos \delta i\tan \theta _D )-\theta _C \\ \delta =\arcsin (\sin \delta i\sin \theta _D ) \\ \end{array}} \right. \end{aligned}$$

(2)

Substituting (2) into (1), the relative motion between the chief and the deputy can be expressed in the LVLH reference frame based on the geometric relationship.

$$\begin{aligned} \left\{ {\begin{array}{l} x=\frac{r_D }{2}\left[ {\left( {1+\cos \delta i} \right) \cos (\theta _C -\theta _D )+\left( {1-\cos \delta i} \right) \cos (\theta _C +\theta _D )} \right] -r_C \\ y=\frac{r_D }{2}\left[ {\left( {1+\cos \delta i} \right) \sin (\theta _C -\theta _D )+\left( {1-\cos \delta i} \right) \sin (\theta _C +\theta _D )} \right] \\ z=r_D \sin \delta i\sin \theta _D \\ \end{array}} \right. \end{aligned}$$

(3)

Furthermore, the angular distance between the satellites and the intersection point in Eq. (3) can be related to the orbital elements via

$$\begin{aligned} \theta _i =\omega _i +f_i -\varphi _i =f_i -\phi _i, {i=C,D} \end{aligned}$$

(4)

where $\omega$ is the argument of the perigee, $f$ is the true anomaly, and $\phi$ is the arc length between the intersection point and the perigee of the satellite, i.e., $\phi \triangleq \varphi -\omega$. $\varphi _C$ and $\varphi _D$ can be calculated as follows.

$$\begin{aligned} \left\{ {\begin{array}{l} \sin \varphi _C =\frac{\sin \Delta \varOmega }{\sin \delta i}\sin i_D \\ \sin \varphi _D =\frac{\sin \Delta \varOmega }{\sin \delta i}\sin i_C \\ \end{array}} \right. \end{aligned}$$

(5)

Note that $\varphi _C$ and $\varphi _D$ are ill-defined when $\delta i=0$, which indicates that those two orbits are in the same plane. Such a particular case is not discussed in this paper. The angle $\delta i$ between two orbital planes can be written in terms of the inclinations of two orbits and $\Delta \varOmega$

$$\begin{aligned} \cos \delta i=\cos i_C \cos i_D +\sin i_C \sin i_D \cos \Delta \varOmega \end{aligned}$$

(6)

2.2 Approximation of the model of relative motion

If all the relative orbital elements are small and the chief orbit is near circular (Schaub and Junkins 2003), i.e.,

$$\begin{aligned} \left\{ {\begin{array}{l} e_C \approx 0 \\ f_C \approx M_C +2e_C \sin M_C \\ \sin \delta i\approx \sqrt{\Delta i^{2}+\sin ^{2}i_C \Delta \varOmega ^{2}} \\ \end{array}} \right. \end{aligned}$$

(7)

where $M$ is the mean anomaly and $e$ is the eccentricity, then the model of the relative motion can be approximated as

$$\begin{aligned} \left\{ {\begin{array}{l} x=\Delta a-a_C \Delta e\cos (n_C t+\xi ) \\ y=a_C (\cos i_C \Delta \varOmega +\Delta \omega +\Delta M_0 )+2a_C \Delta e\sin (n_C t+\xi ) \\ z=a_C \sqrt{\Delta i^{2}+\sin ^{2}i_c \Delta \varOmega ^{2}}\sin [(n_C t+\xi )+(\phi _C -\xi )] \\ \end{array}} \right. \end{aligned}$$

(8)

where $a_c$ is the semi-major axis of the chief satellite, $\Delta a$ is the difference of the semi-major axis, $\Delta e$ is the difference of the eccentricity, $n_c$ is the mean angular velocity of the chief orbit, $\Delta M$ is the difference of mean anomaly, $\xi$ is the phase angle defined as $\xi =\tan ^{-1}(e_C \Delta M/\Delta e)$. Note that this approximated model of the relative motion is only valid in the case of unperturbed orbital motion. According to (8), the relative motion can be interpreted as the intersection curve between an elliptical cylinder and a plane as shown in (9).

$$\begin{aligned} \left\{ {\begin{array}{l} \left( {\frac{x-\Delta a}{-a_C \Delta e}} \right) ^{2}+\left[ {\frac{y-a_C (\cos i_C \Delta \varOmega +\Delta \omega +\Delta {M}_0 )}{2a_C \Delta e}} \right] ^{2}=1 \\ \\ z=\frac{1}{2}\sqrt{\Delta i^{2}+\sin ^{2}i_c \Delta \varOmega ^{2}}\cos (\phi _C -\xi )\frac{y-a_C (\cos i_C \Delta \varOmega +\Delta \omega +\Delta {M}_0 )}{a_C \Delta e} \\ {\begin{array}{ll} &{} \quad {-\sqrt{\Delta i^{2}+\sin ^{2}i_c \Delta \varOmega ^{2}}\sin (\phi _C -\xi )\frac{x-\Delta a}{a_C \Delta e}} \\ \end{array} } \\ \end{array}} \right. \end{aligned}$$

(9)

3 Canonical solution

In this section the canonical solution of the $J_2$-perturbed orbital motion is derived. Firstly, the generalized coordinates, i.e., the spherical coordinates, are introduced, and then the most separable form of the potential based on the spherical coordinates is given. Then, the approximated separable Hamiltonian of the $J_2$-perturbed orbital motion is obtained by applying the most separable form of the potential. After that, the canonical solution is presented. Since two polynomials play very important role in the canonical solution, they are analyzed respectively. To follow, the elliptic integrals in the canonical solution are calculated via the Carlson’s methods. In the end, action-angle variables are defined to derive the nodal period and the drift of RAAN per nodal period.

3.1 Generalized coordinates and the most separable form of the potential

Consider the orbital motion of a satellite in the central force field of the Earth, using spherical coordinates $(r, \lambda , \gamma )$ shown in Fig. 2 for the generalized coordinates. $r$ is the radius, $\lambda$ is the azimuth angle (for example, the longitude), and $\upgamma$ is the latitude. Denote by $\Psi _i (i=1,2,3)$ the three orthogonal curves and by $s_i \;(i=1,2,3)$ the arc lengths corresponding to these curves. Then,

$$\begin{aligned} \left\{ {\begin{array}{l} s_1 =r \\ s_2 =r\lambda \cos \gamma \\ s_3 =r\gamma \\ \end{array}} \right. \end{aligned}$$

(10)

and the metric coefficients are

$$\begin{aligned} \left\{ {\begin{array}{l} h_1 =1 \\ h_2 =r\cos \gamma \\ h_3 =r \\ \end{array}} \right. \end{aligned}$$

(11)

Then the kinetic energy is

$$\begin{aligned} T=\frac{1}{2}\sum _{i=1}^3 {\frac{p_i^2}{h_i^2}} =\frac{1}{2}\left( {p_r^2 +\frac{p_\lambda ^2 }{r^{2}\cos ^{2}\gamma }+\frac{p_\gamma ^2}{r^{2}}} \right) \end{aligned}$$

(12)

where $p_r, p_\lambda \hbox { and } p_\gamma$ are the conjugate momenta.

Fig. 2

Spherical coordinates

Assume the potential energy is $U$, then the Hamiltonian is

$$\begin{aligned} H\left( {r,\lambda , \gamma , p_r, p_\lambda , p_\gamma } \right) =\frac{1}{2}\left( {p_r^2 +\frac{p_\lambda ^2 }{r^{2}\cos ^{2}\gamma }+\frac{p_\gamma ^2 }{r^{2}}} \right) +U \end{aligned}$$

(13)

In order to yield the canonical solutions of the Hamiltonian in (13), full separation of the variables can be guaranteed if $U$ has the following form.

$$\begin{aligned} U=U_1 (r)+\frac{1}{r^{2}}U_2 (\gamma )+\frac{U_3 (\lambda )}{r^{2}\sin ^{2}\gamma } \end{aligned}$$

(14)

The most general separable form of the gravitational potential in (14) can be derived based on the Staeckel conditions (Goldstein 1981). It is easy to verify directly by substitution of (14) into (13) that the Hamiltonian is completely separable. Furthermore, if only the $J_2$ perturbation is considered, then the general separable form can even be simplified further.

The gravitational potential including the $J_2$ perturbation is

$$\begin{aligned} U=-\frac{\mu }{r}+\frac{J_2 \mu R_E^2 }{2r^{3}}(3\sin ^{2}\gamma -1) \end{aligned}$$

(15)

where $\mu$ is the gravitational constant of the Earth, $J_2$ is the second-order zonal harmonics, $R_E$ is the Earth’s mean equatorial radius. The first part on the right of Eq. (15) leads to the classic Keplerian orbits, while the second part can be considered as the $J_2$ perturbation.

Since $\lambda$ is absent in the gravitational potential shown in Eq. (15) and hence in the Hamiltonian shown in Eq. (13), $\lambda$ shall be also cyclic in the most general separable form of the gravitational potential in Eq. (14), which leads to the simplified separable form of the potential

$$\begin{aligned} U=U_1 (r)+\frac{1}{r^{2}}U_2 (\gamma ) \end{aligned}$$

(16)

3.2 The separable Hamiltonian

Since (15) doesn’t have the form (16), an approximation of the gravitational potential is required, which must include the secular effects caused by the $J_2$ perturbation. The latitude $\gamma$ is related to the orbital elements by the relation

$$\begin{aligned} \sin \gamma =\sin i\sin (\omega +f) \end{aligned}$$

(17)

Substituting (17) into (15), $U$ becomes

$$\begin{aligned} U=-\frac{\mu }{r}+\frac{J_2 \mu R_E^2 }{2r^{3}}[3\sin ^{2}i\sin ^{2}(\omega +f)-1] \end{aligned}$$

(18)

Since $r$ and $f$ are periodic functions of the mean anomaly $M$, there are three types of terms on the right side of (18). Terms that depend on $M$ are short-period; terms depending on $\omega$ but not on $M$ are long-period, while those depending neither on $\omega$ nor $M$ are secular (Roy 1988). According to (Roy 1988), the secular and short-periodic terms are identified as follows.

$$\begin{aligned} \left\{ \begin{array}{l} U_{secular} =-\frac{3}{2}\frac{\mu J_2 R_E^2 }{a^{3}}\left( {\frac{1}{3}-\frac{1}{2}\sin ^{2}i} \right) \left( {1-e^{2}} \right) ^{-3/2} \\ U_{short} =-\frac{3}{2}\frac{\mu J_2 R_E^2 }{a^{3}}\left( {\frac{a}{r}} \right) ^{3}\left\{ \underbrace{\left( {\frac{1}{3}-\frac{1}{2}\sin ^{2}i} \right) \left[ {1-\left( {\frac{r}{a}} \right) ^{3}\left( {1-e^{2}} \right) ^{-3/2}} \right] }_{part1}\right. \\ \left. \qquad \qquad \qquad \qquad \qquad \quad \qquad \quad +\underbrace{\frac{1}{2}\sin ^{2}i\cos 2(f+\omega )}_{part2} \right\} \\ \end{array} \right. \end{aligned}$$

(19)

The secular terms and the first part of the short-periodic terms are combined together to yield

$$\begin{aligned} U_{1} =-\frac{J_2 \mu R_E^2 }{2r^{3}}\left( {1-\frac{3}{2}\sin ^{2}i} \right) \end{aligned}$$

(20)

which is consistent with the full separation form. In other words, if only the secular terms and the first part of the short-periodic terms are retained in the Hamiltonian, there exist canonical solutions for the system. By subtracting (20) in the $J_2$-perturbed potential, the terms related to remaining short-period and long-period effects are

$$\begin{aligned} U_{\mathrm{left}} =\frac{3J_2 \mu R_E^2 }{2r^{3}}\left( {\sin ^{2}\gamma -\frac{1}{2}\sin ^{2}i} \right) \end{aligned}$$

(21)

which is not consistent with the full separation form in (16) due to $r$ cubed in the denominator. In order to make (21) consistent with the full separation form, for long-term orbital motion $1/r$ may be approximated by its time average with respect to the true anomaly $f$.

$$\begin{aligned} \left( {\frac{1}{r}} \right) _{ average} =\frac{1}{2\pi }\int _0^{2\pi } {\frac{1}{r}df=\frac{1}{a(1-e^{2})}} =\frac{1}{2}\left( {\frac{1}{r_a }+\frac{1}{r_p }} \right) \end{aligned}$$

(22)

where $r_p$ and $r_a$ are the radius at the perigee and apogee, respectively. Then, the approximation of the gravitational potential including the $J_2$ perturbation is expressed as

$$\begin{aligned} U=-\frac{\mu }{r}\left[ {1+\frac{J_2 R_E^2 }{2r^{2}}\left( {1-\frac{3}{2}\sin ^{2}i} \right) -\frac{3J_2 R_E^2 }{2ra\left( {1-e^{2}} \right) }\left( {\sin ^{2}\gamma -\frac{1}{2}\sin ^{2}i} \right) } \right] \end{aligned}$$

(23)

Therefore, the full separable Hamiltonian is

$$\begin{aligned} H\left( {r,\lambda , \gamma , p_r, p_\lambda , p_\gamma } \right)&= \frac{1}{2}\left( {p_r^2 +\frac{p_\lambda ^2 }{r^{2}\cos ^{2}\gamma }+\frac{p_\gamma ^2 }{r^{2}}} \right) -\frac{\mu }{r}\left[ 1+\frac{J_2 R_E^2 }{2r^{2}}\left( {1-\frac{3}{2}\sin ^{2}i} \right) \right. \nonumber \\&\quad \left. -\,\frac{3J_2 R_E^2 }{2ra(1-e^{2})}\left( {\sin ^{2}\gamma -\frac{1}{2}\sin ^{2}i} \right) \right] \end{aligned}$$

(24)

which includes the secular, short-periodic and long-periodic terms. Even though the Hamiltonian in (24) is the same as the one proposed by Sterne (1958), the derivation presented here starts from the most general separable Hamiltonian in spherical coordinates. Moreover, the revealed approximation made in (22) plays a key role to analyze the nodal period and the drift of RAAN per nodal period, and thus certainly has impacts on the design of the long-term passive distance-bounded relative motion. If only the secular effects are considered, then in the Hamiltonian both the azimuth angle $\lambda$ and the latitude $\upgamma$ are cyclic, which leads to the conservation of the angular momentum and its polar component (i.e. a constant inclination). Hamiltonians that include only secular terms ignore the effects of the short-periodic and long-periodic terms, such as the precession of the angular momentum vector, which will ignore the long-periodic change of the inclination. In addition to (20), there are several other ways to include the secular effects caused by the perturbation in the Hamiltonian, such as the first and third combinations presented in (Garfinkel 1958). However, when the secular terms are not included, there will be an extra term involving $1/r$ in the perturbing Hamiltonian, which is consistent with the fully separable form, and therefore should be an avoidable cost for the separable Hamiltonian.

3.3 Canonical solutions

The Hamilton–Jacobi theory is exploited to derive the canonical solutions for the Hamiltonian (24). Because the Hamiltonian is fully separable, the Hamilton’s characteristic function has the following form

$$\begin{aligned} W=W_r (r)+W_\lambda (\lambda )+W_\gamma (\gamma ) \end{aligned}$$

(25)

The azimuth angle, $\lambda$, is cyclic in the Hamilton and hence

$$\begin{aligned} W_\lambda (\lambda )=\alpha _\lambda \lambda \end{aligned}$$

(26)

where $\alpha _\lambda$ is a constant of integration. Since the Hamiltonian is not explicit in time, $H$ is constant and equals to the energy of the system. Then, the Hamilton–Jacobi equation is

$$\begin{aligned} \frac{1}{2}\left[ {\left( {\frac{\partial W_r }{\partial r}} \right) ^{2}+\frac{\alpha _\lambda ^2 }{r^{2}\cos ^{2}\gamma }+\frac{1}{r^{2}}\left( {\frac{\partial W_\gamma }{\partial \gamma }} \right) ^{2}} \right] +U_1 (r)+\frac{1}{r^{2}}U_2 (\gamma )=E \end{aligned}$$

(27)

By segregating all the terms that depend only on $\lambda$, and if another constant of integration related to $\gamma$ is denoted as $\alpha _\gamma$, then

$$\begin{aligned} \left( {\frac{\partial W_\gamma }{\partial \gamma }} \right) ^{2}+\frac{\alpha _\lambda ^2 }{\cos ^{2}\gamma }+2U_2 (\gamma )=\alpha _\gamma ^2 \end{aligned}$$

(28)

Finally, the dependence of $W$ on $r$ is given by

$$\begin{aligned} \left( {\frac{\partial W_r }{\partial r}} \right) ^{2}+\frac{\alpha _\gamma ^2 }{r^{2}}+2U_1 (r)=2\alpha _r \end{aligned}$$

(29)

where $\alpha _r$ is the third constant that equals to the energy, i.e., $\alpha _r =E$. Combining (26), (28) and (29), the Hamilton’s characteristic function is

$$\begin{aligned} W=\int \limits _r {\frac{\sqrt{2r^{2}\alpha _r -2r^{2}U_1 (r)-\alpha _\gamma ^2 }}{r}{d}r} +\int \limits _\gamma {\sqrt{\alpha _\gamma ^2 -\alpha _\lambda ^2 \sec ^{2}(\gamma )-2U_2 (\gamma )}d\gamma } +\alpha _\lambda \lambda \end{aligned}$$

(30)

In the following the units of length and time are non-dimensionalized by the characteristic length $R_E$ and the characteristic time $\sqrt{R_E^3 /\mu }$, respectively. Then the gravitational constant of the Earth equals to one. Based on the integration constants defined before, the conjugate momenta can be written as

$$\begin{aligned} \left\{ \begin{array}{l} p_r =\dot{r}=\dfrac{\partial W}{\partial r}=\frac{\sqrt{2r^{2}\alpha _r -2r^{2}U_1 (r)-\alpha _\gamma ^2 }}{r}=\sqrt{2\alpha _r +2\frac{1}{r}+\frac{J_2 }{r^{3}}(1-\frac{3}{2}\sin ^{2}i)-\frac{\alpha _\gamma ^2 }{r^{2}}} \\ p_\lambda =r^{2}\dot{\lambda }\cos ^{2}\gamma =\dfrac{\partial W}{\partial \lambda }=\alpha _\lambda \\ p_\gamma =r^{2}\dot{\gamma }=\dfrac{\partial W}{\partial \gamma }=\sqrt{\alpha _\gamma ^2 -\alpha _\lambda ^2 \sec ^{2}(\gamma )-2U_2 (\gamma )}\\ \qquad \qquad \qquad \qquad \qquad =\sqrt{\alpha _\gamma ^2 -\alpha _\lambda ^2 \sec ^{2}(\gamma )-\frac{3J_2 }{a(1-e^{2})}(\sin ^{2}\gamma -\frac{1}{2}\sin ^{2}i)} \\ \end{array} \right. \end{aligned}$$

(31)

Then the canonical solution of the Hamilton–Jacobi equation are

$$\begin{aligned} \left\{ {\begin{array}{l} \beta _r +t=\displaystyle \frac{\partial W}{\partial \alpha _r }=\int \limits _r {\frac{{d}r}{p_r }} \\ \beta _\lambda =\displaystyle \frac{\partial W}{\partial \alpha _\lambda }=\lambda -\int \limits _\gamma {\frac{\alpha _\lambda \sec ^{2}(\gamma ){d}\gamma }{p_\gamma }} \\ \beta _\gamma =\displaystyle \frac{\partial W}{\partial \alpha _\gamma }=-\int \limits _r {\frac{\alpha _\gamma {d}r}{r^{2}\cdot p_r }} +\int \limits _\gamma {\frac{\alpha _\gamma {d}\gamma }{p_\gamma }} \\ \end{array}} \right. \end{aligned}$$

(32)

It is worth noting the physical meanings of the canonical constants. As mentioned before, $\alpha _r$ is the total energy, and $\beta _r$ is a quantity that is minus the time of the passage of the radius defined in the lower limit of the integral. For example, if the lower limit is the radius at the perigee, then $\beta _r$ is minus the time of the pericentric passage. The constant $\alpha _\lambda$ is the polar component of the angular momentum and $\beta _\lambda$ is the RAAN. If $U_2 (\gamma )$ is zero, then $\alpha _\gamma$ is the angular momentum and $\beta _\gamma$ is the inclination (Sterne 1958).

3.4 Analysis of polynomials

One of the striking features of the four integrals in (32) is the fact that the behavior of the integrals depends not so much on the nature of the integrand as on the nature of $p_r$ and $p_\gamma$. In other words, the curves represented by $p_r$ in the phase plane $(r,\dot{r})$ and by $p_\gamma$ in the phase plane $(\upgamma ,\dot{\upgamma })$ determine the behavior of the four integrals in (32). The first polynomial, which is related to $p_r$, is used to classify the orbits under the $J_2$ perturbation into pseudo-circular and pseudo-elliptical orbits. The second polynomial, which is related to $p_\gamma$, is used to derive the maximum declination (inclination) of the satellite with respect to the equatorial plane. Those two polynomials are studied in this subsection. Note that the chaotic phenomena near the critical inclination (Broucke 1994) is not considered in this paper.

3.4.1 Pseudo-circular and pseudo-elliptical orbits

The first important polynomial is related to $p_r$, which is listed again for further reference.

$$\begin{aligned} p_r =\dot{r}=\sqrt{2\alpha _r +2\frac{1}{r}+\frac{J_2 }{r^{3}}\left( {1-\frac{3}{2}\sin ^{2}i} \right) -\frac{\alpha _\gamma ^2 }{r^{2}}} \end{aligned}$$

(33)

As shown in (33), the motion in the phase plane $(r,\dot{r})$ is made of closed curves, and thus $r$ is a periodic function, which is shown in Fig. 3.

Fig. 3

Pseudo-circular and pseudo-elliptical orbit in the phase plane

For pseudo circular orbits and the apogee and perigee of the pseudo elliptical orbits, the time derivative of the radius, namely $p_r$, should be zero.

$$\begin{aligned} p_r =\dot{r}=\sqrt{2\alpha _r +2\frac{1}{r}+\frac{J_2}{r^{3}}\left( {1-\frac{3}{2}\sin ^{2}i} \right) -\frac{\alpha _\gamma ^2 }{r^{2}}}=0 \end{aligned}$$

(34)

The cubic function derived from (34) is

$$\begin{aligned} f(r)=r^{3}+\frac{1}{\alpha _r }r^{2}-\frac{\alpha _\gamma ^2 }{2\alpha _r }r+\frac{J_2 }{2\alpha _r }\left( {1-\frac{3}{2}\sin ^{2}i} \right) \end{aligned}$$

(35)

Note that $f(r)$, multiplied by $2\alpha _r$ (negative) and then divided by $r^{3}$ to get the radicand in (34), shall be negative to make (33) and (34) well defined.

The related cubic equation is

$$\begin{aligned} r^{3}+\frac{1}{\alpha _r }r^{2}-\frac{\alpha _\gamma ^2 }{2\alpha _r }r+\frac{J_2 }{2\alpha _r }\left( {1-\frac{3}{2}\sin ^{2}i} \right) =0 \end{aligned}$$

(36)

which, as a cubic equation with real coefficients, has at least one real root. Moreover, for bounded orbital motion the cubic equation shall have at least two real roots corresponding to the radius at the apogee as well as at the perigee, and thus, based on the nature of the roots of cubic equations, (36) shall have three real roots. The roots of (36) can be calculated as follows (Press et al. 2007).

First compute

$$\begin{aligned} Q=\frac{2+3\alpha _r \alpha _\gamma ^2 }{18\alpha _r^2 },R=\frac{4+9\alpha _r \alpha _\gamma ^2 +27J_2 \alpha _r^2 \left( 1-\frac{3}{2}\sin ^{2}i\right) }{108\alpha _r^3 } \end{aligned}$$

(37)

If $R^{2}<Q^{3}$, then Eq. (36) has three distinct real roots, which corresponds to the case where the orbit is pseudo-elliptical and two of the roots are the radius of the apogee and perigee, respectively. If $R^{2}=Q^{3}$, then Eq. (36) has a multiple root, which corresponds to the case where the orbit is pseudo-circular and the multiple root is its radius. If $R^{2}>Q^{3}$, Eq. (36) has one real root and two complex conjugate roots, which should not be the case for the bounded orbital motion. The comparison between $R^{2}$ and $Q^{3}$ can be achieved by evaluating the value of $\alpha _r \alpha _\gamma ^\mathbf{2}$ when $1-1.5\sin ^{2}i$ is positive, negative or equals to zero. For Keplerian orbits with units such that $\mu$ equals to one, the value of $\alpha _r \alpha _\gamma ^\mathbf{2}$ is

$$\begin{aligned} -\frac{1}{2}\le \alpha _r \alpha _\gamma ^2 =-\frac{1}{2a}\times a(1-e^{2})=-\frac{1-e^{2}}{2}<0 \end{aligned}$$

(38)

Note that $\alpha _r \alpha _\gamma ^\mathbf{2}$ meets the lower bound when the Keplerian orbits are circular. However, when the orbits are perturbed by $J_2$ as defined in (24), the lower bound of $\alpha _r \alpha _\gamma ^\mathbf{2}$ is slightly less than $-0.5$ if $1-1.5\sin ^{2}i<0$, and slightly greater than $-0.5$ if $1-1.5\sin ^{2}i>0$, and equals to $-0.5$ if $1-1.5\sin ^{2}i=0$. The reason is that the osculating semi-major axis is defined in terms of the energy without the perturbing part of the gravitational potential, but $\alpha _r$ is the total energy that is different from the energy of the osculating orbit. Therefore, $\alpha _r$ does not equal to $1/-2a$ all the time; instead, it depends on the value of $1-1.5\hbox {sin}^{2}i$ as well. For $J_2$ perturbed orbits, the lower bound of $\alpha _r \alpha _\gamma ^2$ are met by pseudo circular orbits. The comparison between $R^{2}$ and $Q^{3}$ is shown in Table 1. In Table 1, $r_1, r_2$ and $r_3$ are the roots of Eq. (36). When comparing $\hbox {R}^{2}$ with $\hbox {Q}^{3}$, the following expression (39), instead of (37), is employed.

$$\begin{aligned} \begin{aligned} Q^{{\prime }3}&=46{,}656\alpha _r^6 \times Q^{3}=(4+6\alpha _r \alpha _\gamma ^2 )^{3} \\ R^{{\prime }2}&=46{,}656\alpha _r^6 \times R^{2}=[8+18\alpha _r \alpha _\gamma ^2 +54J_2 \alpha _r^2 (1-1.5\sin ^{2}i)]^{2} \\ \end{aligned} \end{aligned}$$

(39)

As an example, the relationship between $\hbox {R}^{\prime 2}$ and $\hbox {Q}^{{\prime }3}$ is shown in Fig. 4 when $1-1.5\hbox {sin}^{2}i=0$. Note that $c_1, c_2$ and $c_3$ in Table 1 are very small positive numbers, which can be calculated based on the horizontal coordinates of the intersection points of curves of $Q^{\prime 3}$ and $R^{\prime 2}$. For example, when $i=50.7831^{^{\circ }}$ and $\alpha _r =-0.4$, $c_1 =0.00003451$ and $c_2 =0.01173245$; when $i=60^{^{\circ }}$ and $\alpha _r =-0.4$, $c_3 =0.0000433$.

Table 1 Orbit classification based on $i,\alpha _r$ and $\alpha _\gamma ^2$

Fig. 4

Relationship between $\mathbf{R}^{{\prime }2}$ and $\mathbf{Q}^{{\prime }3}$ for $1-\frac{3}{2}\mathbf{sin}^{2}i=0$

After computing $Q$ and $R$, all three roots can be computed via the parameter $\theta$

$$\begin{aligned} \theta =\arccos \left( R/\sqrt{Q^{3}}\right) \end{aligned}$$

(40)

Then the three roots of Eq. (36) are

$$\begin{aligned} \left\{ {\begin{array}{l} r_1 =-2\sqrt{Q}\cos \left( {\frac{\theta }{3}} \right) -\frac{1}{3\alpha _r } \\ r_2 =-2\sqrt{Q}\cos \left( {\frac{\theta -2\pi }{3}} \right) -\frac{1}{3\alpha _r } \\ r_3 =-2\sqrt{Q}\cos \left( {\frac{\theta +2\pi }{3}} \right) -\frac{1}{3\alpha _r } \\ \end{array}} \right. \end{aligned}$$

(41)

Note that $r_1 \le r_2 \le r_3$. Besides, based on the convexity and concavity as well as the characteristics of those two local extremes of $f(r)$, the first root $r_1$ is negative when $1-1.5\hbox {sin}^{2}i<0$, and vice versa. When $\theta =0$, i.e., $R^{2}=Q^{3}$, the orbits are pseudo-circular and the radii are

$$\begin{aligned} r_2 =r_3 =\sqrt{Q}-\frac{1}{3\alpha _r }=\sqrt{\frac{2+3\alpha _r \alpha _\gamma ^2 }{18\alpha _r^2 }}-\frac{1}{3\alpha _r } \end{aligned}$$

(42)

When $R^{2}<Q^{3}$, the orbits are pseudo-elliptical and the radius at the perigee and apogee are $r_2$ and $r_3$, respectively. The semimajor axis and the eccentricity of the pseudo-elliptical orbit are

$$\begin{aligned} a=\frac{r_3 +r_2 }{2}, \quad e=\frac{r_3 -r_2 }{r_3 +r_2 } \end{aligned}$$

(43)

It should be pointed out that since $f(r)$ shall be negative, the integration region of those two integrals related to $r$ in (32) shall be limited to the region below the horizontal axis, i.e. $r_2 \le r\le r_3$.

3.4.2 Maximum declination with respect to the equatorial plane

The second important polynomial is related to $p_\gamma$, i.e.,

$$\begin{aligned} p_\gamma =\sqrt{\alpha _\gamma ^2 -\alpha _\lambda ^2 \sec ^{2}(\gamma )-\frac{3J_2 }{a(1-e^{2})}\left( {\sin ^{2}\gamma -\frac{1}{2}\sin ^{2}i} \right) } \end{aligned}$$

(44)

Note that $\gamma$ is the latitude of the satellite, i.e., $-\frac{\pi }{2}\le \gamma \le \frac{\pi }{2}$, and thus $\cos \gamma$ is always not negative. The second polynomial can be written by the substitution $x=\sin \gamma$

$$\begin{aligned} g(x)=\frac{3J_2}{a(1-e^{2})}x^{4}-\left[ {\alpha _\gamma ^2 +\frac{3J_2 }{a(1-e^{2})}\left( {1+\frac{1}{2}\sin ^{2}i} \right) } \right] x^{2}+\alpha _\gamma ^2 -\alpha _\lambda ^2 +\frac{3J_2}{2a(1-e^{2})}\sin ^{2}i \end{aligned}$$

(45)

Assume that $x_1^2$ and $x_2^2$ are the roots of the following quadratic equation

$$\begin{aligned} \frac{3J_2 }{a(1-e^{2})}x^{4}-\left[ {\alpha _\gamma ^2 +\frac{3J_2 }{a(1-e^{2})}\left( {1+\frac{1}{2}\sin ^{2}i} \right) } \right] x^{2}+\alpha _\gamma ^2 -\alpha _\lambda ^2 +\frac{3J_2}{2a(1-e^{2})}\sin ^{2}i=0 \end{aligned}$$

(46)

To show that $0\le \hbox {x}_1^2 \le 1, \hbox {x}_2^2 \ge 1$ and $\hbox {x}_1^2 <\hbox {x}_2^2$, note that

$$\begin{aligned} \begin{array}{l} g(0)=\alpha _\gamma ^2 -\alpha _\lambda ^2 +\frac{3J_2 }{2a(1-e^{2})}\sin ^{2}i\ge 0, \\ g(1)=-\alpha _\lambda ^2 \le 0 \\ \end{array} \end{aligned}$$

(47)

Therefore, $x$ shall oscillate between the bounds $\pm x_1$, i.e., $-\hbox {asin }x_1 \le \gamma \le \hbox {asin }x_1$, to make the radicand in (44) well defined, i.e.,

$$\begin{aligned} p_\gamma =\sqrt{\frac{3J_2}{a(1-e^{2})}\frac{(x_1^2 -x^{2})(x_2^2-x^{2})}{1-x^{2}}} \end{aligned}$$

(48)

Thus, the sine value of the positive maximum declination of the perturbed satellite orbit is $x_1$. Note that when $\gamma$ reaches its maximum, $\dot{\gamma }$ equals to zero and $\gamma$ equals to the inclination. Therefore, $p_\gamma$ in (31) can be simplified to the following equation that can be exploited to derive the inclination.

$$\begin{aligned} \frac{3J_2 }{2a(1-e^{2})}x_1^4 -\left[ {\alpha _\gamma ^2 +\frac{3J_2 }{2a(1-e^{2})}} \right] x_1^2 +\alpha _\gamma ^2 -\alpha _\lambda ^2 =0 \end{aligned}$$

(49)

3.5 Calculation of elliptic integrals

The four elliptic integrals in (32) can be interpreted as cubic cases and solved by using Carlson’s method (Carlson 1977, 1987, 1988, 1989). There are three main reasons for this approach. The first one is that Carlson’s functions allow arbitrary ranges of integration and arbitrary positions of the branch points of the integrand with respect to the interval of integration. Thus, unlike other standard methods which require one of the limits of the integration be a zero of the polynomial, Carlson’s method is suitable for computing the parameters in (3). The second reason is that the zeros of $f(r)$ in (35) and $g(x)$ in (45) are determined a priori and embrace straightforward physical meanings. The symmetry of the zeros can be taken advantage of by the Carlson’s method, which, in contrast, is concealed in other methods such as Legendre’s notation. Last but not the least, the symmetry of the method allows the expansion of the elliptic integral in a series of elementary symmetric functions that gives high precision with relatively few terms and provides the most efficient method of computing the incomplete integral of the third kind (Olver et al. 2010), which gives a substantial edge to implement the method in this paper onboard a satellite. Since $p_r$ equals zero, for pseudo circular orbits the two integrals related to $r$ are not valid any more. Thus, in this subsection following the introduction of Carlson’s method, the calculation of elliptical integrals is divided into the cases of pseudo circular and pseudo elliptical orbits.

3.5.1 Carlson’s method of elliptic integrals

Denote elliptic integrals in cubic cases as

$$\begin{aligned}{}[p]_{m,n} =[p_1, \ldots ,p_4 ]_{m,n} =\int _m^n {\prod _{i=1}^4 {(a_i +b_i t)^{p_i /2}} dt} \end{aligned}$$

(50)

where $p_i$’s are nonzero integers. The upper and lower limits of the integration are $n$ and $m$, respectively. The integrand is real and the integral shall be well defined. If both limits of the integration are zeros of the integrand, the integral is complete; otherwise, it is incomplete. According to Carlson’s method, the elliptic integrals in (50) may be expressed in terms of the following symmetric and homogeneous R-functions

$$\begin{aligned} R_F (x,y,z)&= \frac{1}{2}\int _0^\infty {[(t+x)(t+y)(t+z)]^{-1/2}dt}\end{aligned}$$

(51)

$$\begin{aligned} R_J (x,y,z,w)&= \frac{3}{2}\int _0^\infty {[(t+x)(t+y)(t+z)]^{-1/2}(t+w)^{-1}dt} \end{aligned}$$

(52)

and their two special cases

$$\begin{aligned} R_D (x,y,z)&= R_J (x,y,z,z)\end{aligned}$$

(53)

$$\begin{aligned} R_C (x,y)&= R_F (x,y,y) \end{aligned}$$

(54)

The functions $R_F, R_D$ and $R_J$ replace Legendre’s integrals of the first, second, and third kinds, respectively, while $R_C$ includes the inverse circular and inverse hyperbolic functions. Generally, the R-functions can be calculated based on the duplication theorem. Take $R_F$ as an example.

$$\begin{aligned} R_F (x,y,z)=R_F \left( {\frac{x+\lambda }{4},\frac{y+\lambda }{4},\frac{z+\lambda }{4}} \right) \end{aligned}$$

(55)

with

$$\begin{aligned} \lambda =\sqrt{xy}+\sqrt{xz}+\sqrt{yz} \end{aligned}$$

(56)

Equation (55) is iterated until the arguments of $R_F$ are nearly equal, then the following equation can be made use of

$$\begin{aligned} R_F (x,x,x)=x^{-1/2} \end{aligned}$$

(57)

It is worth noting that typically only two or three iterations are required and the error deceases by a factor of $4^{6}=4{,}096$ for each iteration (Press et al. 2007).

3.5.2 Pseudo circular orbits

For pseudo circular orbits, the Hamiltonian is reduced to

$$\begin{aligned} H_C \left( {r,\lambda , \gamma , p_r, p_\lambda , p_\gamma } \right) =\frac{1}{2}\left( {\frac{p_\lambda ^2 }{r^{2}\cos ^{2}\gamma }+\frac{p_\gamma ^2 }{r^{2}}} \right) -\frac{1}{r}\left[ {1-\frac{J_2 }{2r^{2}}(3\sin ^{2}\gamma -1)} \right] \end{aligned}$$

(58)

Note that $r$ is constant and there is no approximation of the gravitational potential in (58). Since $p_r$ equals zero, $W(r)$ in (25) is a constant. However, due to the fact that only the partial derivatives of $W$ are involved in the solution, the constant $W(r)$ is irrelevant. Then the characteristic function of pseudo circular orbits becomes

$$\begin{aligned} W=\int \limits _\gamma {\sqrt{[\alpha _\gamma ^2 -\alpha _\lambda ^2 \sec ^{2}(\gamma )-2U_2 (\gamma )]}d\gamma } +\alpha _\lambda \lambda \end{aligned}$$

(59)

• 1. Solution of $\beta _\lambda$ Even though $a(1-e^{2})$ can be replaced by $r$ for pseudo-circular orbits, $a(1-e^{2})$ is still retained in the following equations. For pseudo-circular orbits, the solution of $\beta _\lambda$ is

  $$\begin{aligned} \frac{\partial W}{\partial \alpha _\lambda }=\lambda -\int \limits _\gamma {\frac{\alpha _\lambda \sec ^{2}(\gamma )d\gamma }{p_\gamma }} =\lambda -\int \limits _x {\frac{\alpha _\lambda dx}{(1-x^{2})\sqrt{\frac{3J_2 }{a(1-e^{2})}(x_1^2 -x^{2})(x_2^2 -x^{2})}}} \end{aligned}$$

  (60)

  If the specified domain $[m,n]$ of the integral in (60) satisfies $0\le m<n\le x_1$, then by the substitution $z=x^{2}$ the integral can be reduced to an elliptic integral

  $$\begin{aligned} \begin{aligned} \frac{\partial W}{\partial \alpha _\lambda }&=\lambda -\frac{\alpha _\lambda }{2}\sqrt{\frac{a(1-e^{2})}{3J_2 }}\int _{m^{2}}^{n^{2}} {z^{-1/2}(x_1^2 -z)^{-1/2}(x_2^2 -z)^{-1/2}(1-z)^{-1}{d}z} \\&=\lambda -\frac{\alpha _\lambda }{2}\sqrt{\frac{a(1-e^{2})}{3J_2 }}[-1,-1,-1,-2]_{m^{2},n^{2}} \end{aligned} \end{aligned}$$

  (61)

  which is an elliptic integral of the cubic case. The complete integral is

  $$\begin{aligned} \begin{aligned} \frac{\partial W}{\partial \alpha _\lambda }&=\lambda -2\int _0^{x_1 } {\frac{\alpha _\lambda {d}x}{\left( {1-x^{2}} \right) \sqrt{\frac{3J_2 }{a\left( {1-e^{2}} \right) }\left( {x_1^2 -x^{2}} \right) \left( {x_2^2 -x^{2}} \right) }}} \\&=\!\lambda \!-\!2\alpha _\lambda \sqrt{\frac{a(1\!-\!e^{2})}{3J_2 }}\left[ {R_F \left( {0,x_2^2 -x_1^2, x_2^2 } \right) +\frac{1}{3}x_1^2 x_2^2 R_J \left( {0,x_2^2 -x_1^2, x_2^2, x_2^2 -x_1^2 x_2^2 } \right) } \right] \\ \end{aligned} \end{aligned}$$

  (62)

  If the specified domain $[m,n]$ of the integral in (60) satisfies $-x_1 \le m<n\le 0$, then the integral reduces to

  $$\begin{aligned} \begin{aligned} \frac{\partial W}{\partial \alpha _\lambda }&=\lambda +\frac{\alpha _\lambda }{2}\sqrt{\frac{a(1-e^{2})}{3J_2 }}\int _{m^{2}}^{n^{2}} {z^{-1/2}(x_1^2 -z)^{-1/2}(x_2^2 -z)^{-1/2}(1-z)^{-1}{d}z} \\&=\lambda +\frac{\alpha _\lambda }{2}\sqrt{\frac{a(1-e^{2})}{3J_2 }}[-1,-1,-1,-2]_{m^{2},n^{2}} \end{aligned} \end{aligned}$$

  (63)

  If the specified domain $[m,n]$ of the integral in (60) satisfies $-x_1 \le m\le 0<n\le x_1$, then the integral reduces to

  $$\begin{aligned} \begin{aligned} \frac{\partial W}{\partial \alpha _\lambda }&=\lambda -\frac{\alpha _\lambda }{2}\sqrt{\frac{a(1-e^{2})}{3J_2 }}\left( {-\int _{m^{2}}^0 {(z)^{-1/2}(x_1^2 -z)^{-1/2}(x_2^2 -z)^{-1/2}(1-z)^{-1}{d}z} } \right. \\&\quad \left. {+\int _0^{n^{2}} {z^{-1/2}(x_1^2 -z)^{-1/2}(x_2^2 -z)^{-1/2}(1-z)^{-1}{d}z} } \right) \\&=\lambda -\frac{\alpha _\lambda }{2}\sqrt{\frac{a(1-e^{2})}{3J_2 }}\left( {-[-1,-1,-1,-2]_{m^{2},0} +[-1,-1,-1,-2]_{0,n^{2}} } \right) \\ \end{aligned} \end{aligned}$$

  (64)

• 2. Solution of $\beta _{\upgamma }$

  $$\begin{aligned} \frac{\partial W}{\partial \alpha _\gamma }&= \int \limits _\gamma \! {\frac{\alpha _\gamma d\gamma }{p_\gamma }} \!=\!\alpha _\gamma \sqrt{\frac{a(1-e^{2})}{3J_2 }}\int _x {(x_1 -x)^{-1/2}(x_1 \!+\!x)^{-1/2}(x_2 \!-\!x)^{-1/2}(x_2 \!+\!x)^{-1/2}{d}x} \nonumber \\&= \alpha _\gamma \sqrt{\frac{a\left( {1-e^{2}} \right) }{3J_2 }}[-1,-1,-1,-1] \end{aligned}$$

  (65)

  which is an elliptic integral of the first kind defined by Carlson. For the complete integral with the interval $[-x_1, x_1 ]$, it follows

  $$\begin{aligned} \frac{\partial W}{\partial \alpha _\gamma }&= \alpha _\gamma \sqrt{\frac{a(1-e^{2})}{3J_2 }}[-1,-1,-1,-1]_{-x_1, x_1 }\nonumber \\&= 2\alpha _\gamma \sqrt{\frac{a(1-e^{2})}{3J_2 }}R_F \left( {0,(x_1 +x_2 )^{2},(x_2 -x_1 )^{2}} \right) \end{aligned}$$

  (66)

3.5.3 Pseudo elliptical orbits

• 1. Solution of $\beta _r +t$

  $$\begin{aligned} \begin{aligned} \frac{\partial W}{\partial \alpha _r}&=\int _r {\frac{dr}{p_r }} =\int _r {\frac{r^{3/2}dr}{\sqrt{2\alpha _r r^{3}+2r^{2}-\alpha _\gamma ^2 r+J_2 (1-\frac{3}{2}\sin ^{2}i)}}} \\&=(-2\alpha _r )^{-1/2}\int _r {(r_3 -r)^{-1/2}(r-r_2 )^{-1/2}(r-r_1 )^{-1/2}r^{-1/2}r^{2}dr}\\&=(-2\alpha _r )^{-1/2}[-1,-1,-1,-1,4] \end{aligned} \end{aligned}$$

  (67)

  It is an elliptic integral of the third kind. Note that, instead of using the integral $[3,-1,-1,-1]$, $[-1,-1,-1,-1,4]$ is employed to avoid the singularity of the integration when exploiting Carlson’s method. For the complete integral within the interval $[r_2, r_3]$, $\beta _r +t$ becomes

  $$\begin{aligned} \begin{aligned} \frac{\partial W}{\partial \alpha _r}&=(-2\alpha _r )^{-1/2}[-1,-1,-1,-1,4]_{r_2, r_3 } \\&=-\frac{1}{2}(-2\alpha _r )^{-1/2}\left\{ {(r_1 +r_2 +r_3 )I_3^{\prime } +r_1 r_2 I_2 +[(r_3 -r_2 )(r_3 -r_1 )-2r_3^2 ]I_1 } \right\} \end{aligned} \end{aligned}$$

  (68)

  where

  $$\begin{aligned} \left\{ {\begin{array}{l} I_1 =2R_F (0,r_3 (r_2 -r_1 ),r_2 (r_3 -r_1 ))\\ I_2 =\frac{2}{3}(r_3 -r_2 )(r_3 -r_1 )R_D (0,r_3 (r_2 -r_1 ),r_2 (r_3 -r_1 )) \\ I_3^{\prime } =\frac{2}{3}r_3 (r_3 -r_2 )(r_3 -r_1 )R_J (0,r_3 (r_2 -r_1 ),r_2 (r_3 -r_1 ),r_3 (r_3 -r_1 )) \\ \end{array}} \right. \end{aligned}$$

  (69)

• 2. Solution of $\beta _\lambda$

  The solution of $\beta _\lambda$ for pseudo-elliptical has been given in (60), (61), (62), (63) and (64).

• 3. Solution of $\beta _\upgamma$

  $$\begin{aligned} \begin{aligned} \frac{\partial W}{\partial \alpha _\gamma }&=-\int \limits _r {\frac{\alpha _\gamma dr}{r^{2}\cdot p_r }} +\int \limits _\gamma {\frac{\alpha _\gamma d\gamma }{p_\gamma }} =-\alpha _\gamma (-2\alpha _r )^{-1/2}\\&\quad \times \int \limits _r {r^{-1/2}(r-r_1 )^{-1/2}(r-r_2 )^{-1/2}(r_3 -r)^{-1/2}dr} \\&\quad +\alpha _\gamma \sqrt{\frac{a(1-e^{2})}{3J_2 }}\int \limits _x {(x_1 -x)^{-1/2}(x_1 +x)^{-1/2}(x_2 -x)^{-1/2}(x_2 +x)^{-1/2}dx} \\&=-\alpha _\gamma (-2\alpha _r )^{-1/2}[-1,-1,-1,-1]+\alpha _\gamma \sqrt{\frac{a(1-e^{2})}{3J_2 }}[-1,-1,-1,-1] \end{aligned} \end{aligned}$$

  (70)

  The complete integrals of the two individual parts in (70) are of the first cases, and can be calculated as follows

  $$\begin{aligned} -\int _{r_2 }^{r_3 } {\frac{\alpha _\gamma dr}{r^{2}\cdot p_r }} =-2\alpha _\gamma (-2\alpha _r )^{-1/2}R_F (0,r_3 (r_2 -r_1 ),r_2 (r_3 -r_1 )) \end{aligned}$$

  (71)

  and

  $$\begin{aligned} \int _{-\sin ^{-1}x_1 }^{\sin ^{-1}x_1 } {\frac{\alpha _\gamma d\gamma }{p_\gamma }} =2\alpha _\gamma \sqrt{\frac{a(1-e^{2})}{3J_2 }}R_F (0,(x_1 +x_2 )^{2},(x_2 -x_1 )^{2}) \end{aligned}$$

  (72)

3.6 Action-angle variables

Essentially, the nodal period and the drift of RAAN per nodal period play key roles for the design of distance-bounded relative motion. Since the Hamiltonian is fully separable, the action-angle variables can be taken advantage of to obtain the frequencies of the system without finding the complete solution of the orbital motion that is disturbed by the approximated gravitational potential.

The action variables are defined as

$$\begin{aligned} \left\{ {\begin{array}{l} J_r =\oint {\frac{\partial W}{\partial r}dr} =\oint {\sqrt{2\alpha _r +2\frac{1}{r}+\frac{J_2 }{r^{3}}(1-\frac{3}{2}\sin ^{2}i)-\frac{\alpha _\gamma ^2 }{r^{2}}}dr} \\ J_\lambda =\oint {\frac{\partial W}{\partial \lambda }d\lambda } =\oint {\alpha _\lambda d\lambda } \\ J_\gamma =\oint {\frac{\partial W}{\partial \gamma }d\gamma } =\oint {\sqrt{\alpha _\gamma ^2 -\alpha _\lambda ^2 \sec ^{2}(\gamma )-\frac{3J_2 }{a(1-e^{2})}(\sin ^{2}\gamma -\frac{1}{2}\sin ^{2}i)}d\gamma } \\ \end{array}} \right. \end{aligned}$$

(73)

and the angle variables are defined as

$$\begin{aligned} \left\{ {\begin{array}{l} w_r =\frac{\partial W}{\partial r}=p_r \\ w_\lambda =\frac{\partial W}{\partial \lambda }=p_\lambda \\ w_\gamma =\frac{\partial W}{\partial \gamma }=p_\gamma \\ \end{array}} \right. \end{aligned}$$

(74)

Once the Hamiltonian is determined as a function of the action variables

$$\begin{aligned} H=H(J_r, J_\lambda , J_\gamma ) \end{aligned}$$

(75)

the frequencies of the system can be derived as the derivatives of $H$ with respect to the action variables.

$$\begin{aligned} \left\{ {\begin{array}{l} \nu _r =\frac{\partial H(J_r, J_\lambda , J_\gamma )}{\partial J_r } \\ \nu _\lambda =\frac{\partial H(J_r, J_\lambda , J_\gamma )}{\partial J_\lambda } \\ \nu _\gamma =\frac{\partial H(J_r, J_\lambda , J_\gamma )}{\partial J_\gamma } \\ \end{array}} \right. \end{aligned}$$

(76)

3.6.1 Anomalistic, nodal and sidereal periods

Instead of performing the contour integration in (73) and then deriving the Hamiltonian in terms of the action variables, the Jacobian matrix and its inverse are taken advantage of to derive the anomalistic, sidereal and nodal periods.

The second integral in (73) is simple

$$\begin{aligned} J_\lambda =2\pi \alpha _\lambda =2\pi p_\lambda \end{aligned}$$

(77)

Then the Jacobian matrix of the action variables with respect to $\alpha _r, \alpha _\lambda$ and $\alpha _\gamma$ can be written as

$$\begin{aligned} \left[ {{\begin{array}{l} {J_r } \\ {J_\lambda } \\ {J_\gamma } \\ \end{array} }} \right] =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {\frac{\delta J_r }{\delta \alpha _r }}&{} {\frac{\delta J_r }{\delta \alpha _\lambda }}&{} {\frac{\delta J_r }{\delta \alpha _\gamma }} \\ {\frac{\delta J_\lambda }{\delta \alpha _r }}&{} {\frac{\delta J_\lambda }{\delta \alpha _\lambda }}&{} {\frac{\delta J_\lambda }{\delta \alpha _\gamma }} \\ {\frac{\delta J_\gamma }{\delta \alpha _r }}&{} {\frac{\delta J_\gamma }{\delta \alpha _\lambda }}&{} {\frac{\delta J_\gamma }{\delta \alpha _\gamma }} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\alpha _r } \\ {\alpha _\lambda } \\ {\alpha _\gamma } \\ \end{array} }} \right] =\left[ {{\begin{array}{lll} A&{} 0&{} B \\ 0&{} {2\pi }&{} 0 \\ 0&{} C&{} D \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\alpha _r } \\ {\alpha _\lambda } \\ {\alpha _\gamma } \\ \end{array} }} \right] \end{aligned}$$

(78)

where

$$\begin{aligned} A&= -(-2\alpha _r )^{-1/2}\left\{ {(r_1 +r_2 +r_3 )I_3^{\prime } +r_1 r_2 I_2 +[(r_3 -r_2 )(r_3 -r_1 )-2r_3^2 ]I_1 } \right\} \end{aligned}$$

(79)

$$\begin{aligned} B&= -2\alpha _\gamma (-2\alpha _r )^{-1/2}I_1\end{aligned}$$

(80)

$$\begin{aligned} C&= -4\alpha _\lambda \sqrt{\frac{a(1-e^{2})}{3J_2 }}\left[ {R_F \left( {0,x_2^2 -x_1^2, x_2^2 } \right) +\frac{1}{3}x_1^2 x_2^2 R_J \left( {0,x_2^2 -x_1^2, x_2^2, x_2^2 -x_1^2 x_2^2 } \right) } \right] \end{aligned}$$

(81)

$$\begin{aligned} D&= 4\alpha _\gamma \sqrt{\frac{a(1-e^{2})}{3J_2 }}R_F (0,(x_1 +x_2 )^{2},(x_2 -x_1 )^{2}) \end{aligned}$$

(82)

and $I_3^{\prime }, I_2$ and $I_1$ are given in (69). Compared with the canonical solutions shown in Sect. 3.5, $A$ is twice of the complete solution of $\beta _r +t, B$ is associated with the former part of the solution of $\beta _\gamma , C$ is related to the solution of $\beta _\lambda$, and $D$ corresponds to the latter part of the solution of $\beta _\gamma$. For pseudo-circular orbits, because $r_2$ and $r_3$ are multiple roots, both $I_3^{\prime }$ and $I_2$ equal to zero. Hence, $A$ and $B$ can be further simplified

$$\begin{aligned} A&= \frac{1}{\sqrt{-2\alpha _r }}\frac{2\pi r}{\sqrt{1-r_1 }}\end{aligned}$$

(83)

$$\begin{aligned} B&= \frac{-2\alpha _\gamma }{\sqrt{-2\alpha _r }}\frac{\pi }{r\sqrt{1-r_1 }} \end{aligned}$$

(84)

The Jacobian matrix is inverted to yield the anomalistic, sidereal and nodal frequencies

$$\begin{aligned} \left\{ {\begin{array}{l} \nu _r =\frac{\partial \alpha _r }{\partial J_r }=\frac{1}{A} \\ \nu _\lambda =\frac{\partial \alpha _r }{\partial J_\lambda }=\frac{BC}{2\pi AD} \\ \nu _\gamma =\frac{\partial \alpha _r }{\partial J_\gamma }=-\frac{B}{AD} \\ \end{array}} \right. \end{aligned}$$

(85)

The anomalistic, sidereal and nodal periods are therefore

$$\begin{aligned} \left\{ {\begin{array}{l} P_r =A \\ P_\lambda =\frac{2\pi AD}{BC} \\ P_\gamma =-\frac{AD}{B} \\ \end{array}} \right. \end{aligned}$$

(86)

Note that since $2\pi$ is not included in the definition of the action variables, the conventional angular velocities of the anomalistic, sidereal and nodal motion are

$$\begin{aligned} n_i =2\pi \nu _i, \quad i=r,\lambda , \gamma \end{aligned}$$

(87)

As shown in (86), when the approximated $J_2$ perturbation in (23) is taken into account, the orbital motion is non-degenerate, which is different from the completely degenerate Keplerian orbit motion. The anomalistic period depends on the energy of the orbit and three roots of the cubic function (36). Both the sidereal and nodal periods are associated with the anomalistic period and the roots of the Eq. (46).

3.6.2 Drift of RAAN per nodal period

The drift of RAAN per nodal period $D_\varOmega$ can be calculated based on the sidereal frequency and the nodal period as follows.

$$\begin{aligned} D_\varOmega =2\pi \nu _\lambda P_\gamma -2\pi =-C-2\pi \end{aligned}$$

(88)

Furthermore, thanks to the standard form of (81), (88) can be expressed by the series expansion

$$\begin{aligned} D_\varOmega \!=\!\frac{2\alpha _\lambda \pi }{x_2 }\sqrt{\frac{a(1-e^{2})}{3J_2 }}\left( {\sum _{n=0}^\infty {\left[ {\frac{(2n)!}{2^{2n}(n)!}} \right] ^{2}\left( {\frac{x_1^2 }{x_2^2 }} \right) ^{n}} \!+\!\sum _{n=0}^\infty {\frac{(2n)!x_1^{2n} }{2^{2n}(n)!}\sum _{m=0}^n {\frac{(2m)!}{2^{2m}(m)!x_2^{2m} }} } } \right) -2\pi \end{aligned}$$

(89)

Finally, as key ingredients to the design of the long-term distance-bounded relative motion, the nodal period and the drift of RAAN per nodal period are listed in (90) for future reference. Note that the nodal period depends on both the solution of $\beta _r +t$ and $\beta _\gamma$, while the drift of RAAN per nodal period depends only on $\beta _\lambda$. Therefore, the matched $P_\gamma$ constrains both the anomalistic and nodal motion, while the matched $D_\varOmega$ constrains the sidereal motion.

$$\begin{aligned} \left\{ {\begin{array}{l} P_\gamma =-\frac{AD}{B} \\ D_\varOmega =-C-2\pi \\ \end{array}} \right. \end{aligned}$$

(90)

4 Long-term distance-bounded relative motion

In this section, a methodology to design the long-term distance-bounded relative motion is presented, i.e., to find the orbits with matched nodal period as well as matched drift of RAAN per nodal period. In essence this requires to match the nodal period $P_\gamma$ and the drift of RAAN $D_\varOmega$. The characteristics of $P_\gamma$ and $D_\varOmega$ are presented first by expressing $P_\gamma$ as a function of $D_\varOmega$. In such a way, the intersection points between two different curves represent the matched cases, which can be exploited to design the long-term distance-bounded relative motion. Subsequently, an algorithm for generating the long-term distance-bounded relative motion is presented. Finally, one design example of the long-term distance-bounded relative motion is shown as verification.

4.1 Nodal period $P_\gamma$ and drift of RAAN per nodal period $D_\varOmega$

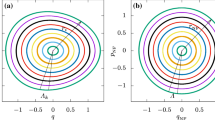
As shown in Table 1, for a given inclination $i$ and orbit energy $\alpha _r$, there is only one choice of $\alpha _\gamma$ to generate a pseudo-circular orbit. Hence, the pair $(\alpha _r, \quad \alpha _\gamma )$ corresponds to a pseudo-circular orbit with radius $r$ and inclination $i$. For pseudo-circular orbits with the same inclination, a higher orbit energy leads to a longer nodal period and a slightly slower drift of RAAN per nodal period, which is shown in Fig. 5 by the dashed curves from the bottom to the up, such as AB. For pseudo-circular orbits with the same orbital energy, a larger inclination angle results in a slightly longer nodal period and slower drift of RAAN per nodal period, which is shown in Fig. 5 by the dashed curves from the left to the right, such as CD. The dashed curves from the right to the left together with those from the bottom to the top form a reference grid to design the long-term distance-bounded relative motion, which can also be used as the search domain to match the nodal period and the drift of RAAN per nodal period. Note that since the Hamiltonian of the pseudo-circular orbits in Eq. (58) takes into account the full $J_2$ perturbation, there is no approximation made to derive both the nodal periods and the drift of RAAN per nodal periods of pseudo-circular orbits. Note also that since the time derivative of the radius of pseudo-circular orbits equals to zero, the time average of the radius in Eq. (22) is the radius itself, which is the essential reason why there is no approximation in (24) for pseudo-circular orbits.

Fig. 5

Nodal period and drift of RAAN per nodal period

Pseudo-elliptical orbits can be categorized based on the pseudo-circular orbits. As discussed before, the pair $(\alpha _r, \alpha _\gamma , i)$ defines a pseudo-circular orbit uniquely, and then $(\alpha _r, i)$ together with different $\alpha _\gamma$’s defines different pseudo-elliptical orbits with different eccentricities. For example, the solid curve EF in Fig. 5 defines a group of pseudo-elliptical orbits associated with the pseudo-circular orbit $(\alpha _r =-0.3995, i=50.6^{\circ })$. The point F denotes the pseudo-circular orbit, and as $\alpha _\gamma$ decreases, the nodal period increases slightly while the drift of RAAN per nodal period becomes faster. The point E denotes the pseudo-elliptical orbit with eccentricity of 0.196. As shown in Fig. 5, there are in total four groups of pseudo-elliptical orbits denoted by four solid curves, and for each pseudo-elliptical orbit both the nodal period and the drift of RAAN per nodal period are constant. However, it is worth mentioning that when the $J_2$ perturbation is fully taken into account to derive the nodal period and the drift of RAAN per nodal period of the pseudo-elliptical orbit, $P_\gamma$ and $D_\varOmega$ is periodic rather than constant with respect to the orbital resolutions. In (Xu et al. 2012), the periodic nodal periods and the drifts of RAAN per nodal period are averaged, respectively, to represent $P_\gamma$ and $D_\varOmega$ of pseudo-elliptical orbits. In this paper, for long-term orbital motion one $1/r$ in (21) is approximated by its time average with respect to the true anomaly $f$, and hence the nodal period and the drift of RAAN per nodal period of the pseudo-elliptical orbit are constant. However, compared with the ergodic representation of the nodal period and the drift of RAAN per nodal period based on the Poincaré surface of section in (Xu et al. 2012), the representation in this paper is based on an analytical solution. Therefore, the computational load of the algorithm is much less.

The most interesting characteristic of the nodal period and the drift of RAAN per nodal period shown in Fig. 5 is that the pseudo-circular orbit and the pseudo-elliptical orbit can share the same nodal period as well as the drift of RAAN per nodal period, which is represented by the intersection points between the solid curves and the dashed curves. For example, the intersection point P between AB and EF corresponds to the pseudo-circular orbit along the dashed curve AB and also associated with the pseudo-elliptical orbit along the solid curve EF; the nodal period and the drift of RAAN per nodal period of those two orbits are matched. Therefore, the point P can be exploited to design the long-term distance-bounded relative motion. In addition to that, pseudo-elliptical orbits may share the same nodal period and the drift of RAAN as well, such as in the example of point $P_e$ shown in Fig. 6. However, both the nodal period and the drift of RAAN per nodal period of the pseudo-circular orbit are unique, and can’t be identical with those of other pseudo-circular orbits. In other words, the intersection points between two different dashed curves represent the same pseudo-circular orbit.

Fig. 6

Pseudo-elliptical orbits with matched nodal period and drift of RAAN

4.2 Long-term distance-bounded relative motion

In this subsection a methodology is presented to establish the long-term distance-bounded relative motion. First of all, in order to calculate the nodal period and the drift of RAAN per nodal period, the initial states $(r, \lambda , \gamma , \dot{r}, r\dot{\lambda }, r\dot{\gamma })$ are transformed to canonical constants $(\alpha _r, \alpha _\lambda , \alpha _\gamma )$, and all other necessary complementary parameters, such as $r_1, r_2$, and $r_3$, are calculated. Subsequently, the algorithm of establishing the orbit with matched $P_\gamma$ and $D_\varOmega$ is presented.

4.2.1 Transformation from spherical coordinates to canonical constants

The algorithm to transform spherical coordinates to canonical constants is presented in Table 2. In the algorithm the spherical coordinates are transformed first to osculating orbital elements to obtain the starting value of $a, e$, and $i$. Then the algorithm iterates to obtain the final canonical constants $(\alpha _r, \alpha _\lambda , \alpha _\gamma )$ and complementary parameters. The algorithm converges very fast, typically with less than three iterations.

Table 2 Algorithm to Transform Spherical Coordinates to Canonical Constants

4.2.2 Matching nodal period and the drift of RAAN per nodal period

Given the initial spherical coordinates, the nodal period and the drift of RAAN per nodal period of the orbit can be matched based on the algorithm in Table 3.

Table 3 Matching nodal period and the drift of RAAN per nodal period

4.3 Sample case and verification

Given the initial spherical coordinates $(r=1.0504624, \lambda =0, \gamma =0, \dot{r}=0, r\dot{\lambda }=0.7130711, r\dot{\gamma }=0.7130711$, based on the Algorithm 1 in Table 2 the canonical constants and the complementary parameters are computed and calculated in Table 4. After that, the reference pseudo-circular orbit can be found as shown in Table 4 as well. Then the reference grid and the database can be generated, which is shown in Fig. 7. The dashed curves from the right to the left are generated every $0.01^{\circ }$, and those from the bottom to the up are generated every $0.000005$. By searching the nodal period and the drift of RAAN per nodal period of the sample orbit in the database, the pseudo-circular orbit with the matched nodal period and the drift of RAAN per nodal period is $\alpha _r =-0.443930177, i=44.435988754^{\circ }$ and $\alpha _\gamma ^2 =1.126557759$.

Table 4 Results of the sample orbit

Fig. 7

Matched pseudo-circular orbit with sample pseudo-elliptical orbit

4.4 Analysis of the proposed methodology

4.4.1 Effects of the atmospheric drag

The atmospheric drag does play a role on the orbital motion of a satellite. The secular perturbations caused by the atmospheric drag mainly affect the semimajor axis and the eccentricity of the orbit. Neither RAAN nor the inclination of the orbital plane is affected by the atmospheric drag. The change of the orbital period due to the atmospheric drag for circular orbits is approximately (Wertz and Larson 1999)

$$\begin{aligned} \Delta P=\frac{-6\pi ^{2}C_D A\rho a^{2}}{mV} \end{aligned}$$

(91)

where $P$ is the orbital period, $C_D$ is the drag coefficient, $\rho$ is the air density, $a$ is the semimajor axis, $V, A$, and $m$ are the satellite’s velocity, effective area, and mass, respectively.

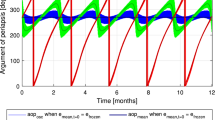
This paper studies the relative motion between modules of fractionated spacecraft. Suppose the fractionated architecture is exploited to establish a space infrastructure which supports various Earth observation payloads (Chu et al. 2014). The orbit altitude of most Earth observation missions is around 800km. Thus, our following analysis is related to the orbits of 800km altitude. This paper focuses on the establishment of distance-bounded relative motion, which is achieved by matching the nodal period and the drift of RAAN per nodal period, respectively. Therefore, the nodal period and the drift of RAAN per nodal period are of most importance. Roughly speaking, the atmospheric drag has no effect on the drift of RAAN, and for the circular orbit with 800 km altitude the change of orbital period is approximately $-3\times 10^{-5}s$ according to (91). To compare, the change of the period due to $J_2$ perturbations can be calculated as follows (Wertz and Larson 1999).

$$\begin{aligned} \Delta P=\frac{2\pi \times \sqrt{{a^{3}}/\mu }}{\left[ {\frac{3}{2}\frac{J_2 R_E^2 }{p^{2}}\left( 1-\frac{3}{2}\sin ^{2}i\right) (1-e^{2})^{1/2}} \right] } \end{aligned}$$

(92)

For the circular orbit of the same altitude with $i=0$ and $e=0$ the change of period due to $J_2$ perturbations is approximately $-8s$, which is on the order of $10^{5}$ higher than the change of period caused by the atmospheric drag. On the other hand, the propellant cost to maintain the 800km altitude in the presence of the atmospheric drag is roughly 0.863m/s/yr (Wertz and Larson 1999). Therefore, it is reasonable to assume that the altitude is maintained in the presence of atmospheric drag, and hence the methodology presented in this paper to achieve distance-bounded relative motion is still applicable.

Apart from the establishment of distance-bounded relative motion, this paper also presents the closed-form solutions of the $J_2$-perturbed relative motion, which is based on an approximated separable Hamiltonian. Our research only focuses on the impacts of the $J_2$ perturbation on the distance-bounded relative motion. The atmospheric drag is not included in the Hamiltonian, because if the atmospheric drag is considered then the Hamiltonian won’t keep the separable form, and thus the analytical solutions cannot be derived. In the literature the use of two separate theories (one for the atmospheric drag and one for gravitational field perturbations) is typical to derive the analytical solutions. However, it is very interesting to develop an analytical theory that embodies both oblateness and the atmospheric drag effects at the same time, which is still open for our feature research.

4.4.2 Fidelity of the approximated Hamiltonian

A full comparison of the approximated Hamiltonian against the STK HPOP is performed. The orbital information in the sample case is used. The initial position vector of the orbit is $(6699996, 0, 0)$m, and the initial velocity vector is $(0, 5637.0865, 5637.0865)$ m/s. The full comparison is performed along all the three directions for orbit propagation in one day. The motion in the $X$ direction is shown in Fig. 8a and the enlarged view is shown in Fig. 8b. The motion in the $Y$ direction is shown in Fig. 8c and the enlarged view is shown in Fig. 8d. The motion in the $Z$ direction is shown in Fig. 8e and the enlarged view is shown in Fig. 8f. The differences along the $X, Y$ and $Z$ directions are tens of kilometers.

Fig. 8

Comparison of the approximated Hamiltonian with STK HPOP. a Comparison of the approximated Hamiltonian with STK HPOP along the $\mathbf{X}$ direction. b Enlarged view of comparison of the approximated Hamiltonian with STK HPOP along the $\mathbf{X}$ direction. c Comparison of the approximated Hamiltonian with STK HPOP along the $\mathbf{Y}$ direction. d Enlarged view of comparison of the approximated Hamiltonian with STK HPOP along the $Y$ direction. e Comparison of the approximated Hamiltonian with STK HPOP along the Z direction. f Enlarged view of comparison of the approximated Hamiltonian with STK HPOP along the Z direction

4.4.3 An example of distance-bounded relative motion

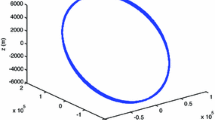
The closed-form solutions presented in our paper can be applied to a much larger range of relative motion. Since the relative motion is modelled based on the geometric relationship between two orbits, there is no assumption neither on the eccentricity of the reference orbit nor on the relative distances. Our closed-form solutions are applicable to the relative motion with relative distances of hundreds of kilometers. For example, the distance-bounded relative motion is established between the following two orbits in the sample case: the deputy is $(r=1.0504624,\lambda =0, \gamma =0, p_r =0, p_\lambda =0.7490544, p_{\upgamma } =0.7490544)$ and the chief is $(r=1.12617597,\lambda =0, \gamma =0, p_r =0, p_\lambda =0.7576328, p_{\gamma } =0.7438125)$. The matched nodal period and the drift of RAAN per nodal period are $P_\upgamma =7.5029568$ and $D_{\Omega } =-0.328757$, respectively. The relative distance of the relative motion is shown in Fig. 9a, which is greater than 400km. The distance-bounded relative motion is shown in Fig. 9b.

Fig. 9

Example of distance-bounded relative motion. a Relative distances of distance-bounded relative motion over one period. b Relative motion of distance-bounded relative motion over one period

5 Conclusion

The long-term distance-bounded relative motion of satellites in the presence of $J_2$ perturbations is studied in this paper. The presented method allows to find the closed-form solutions analytically. There are two key ingredients of the closed-form solutions. One is the model of the satellite relative motion; the other is the Hamiltonian model and its canonical solutions of the $J_2$-perturbed absolute motion. The model of relative motion is based on the geometric relationship between two satellites, and makes neither assumption on the eccentricity of the reference orbit nor on the magnitude of the relative distances. Besides, the relative motion model is concise with straightforward physical insights, and consistent with the Hamiltonian model.

With respect to the $J_2$-perturbed orbital motion, a Hamiltonian model is developed, which accounts for the secular, long period and short period effects of the $J_2$ perturbation, such that it remains separable in terms of the spherical coordinates. This ensures the application of the Hamilton–Jacobi theory and the action-angle variables. The only approximation made in the Hamiltonian is that one item of the orbit radius in the $J_2$-perturbed gravitational potential is approximated by its time average with respect to the true anomaly, which seems appropriate for the research of the long-term orbital motion. The consequences of the approximation are that for pseudo-elliptical orbits both the nodal period and the drift of RAAN per nodal period remain constant rather than periodic. However, this approximation has no impact on the pseudo-circular orbits. The canonical solutions of the system are found using Carlson’s method, which provides straightforward physical insights for both the pseudo-circular and pseudo-elliptical orbits. It turns out that huge momentum for the design of distance-bounded relative motion can really be gained by the analytical classification of pseudo-circular and pseudo-elliptical orbits.

One important contribution of this paper is to derive the analytical expression of the nodal period and the drift of RAAN per nodal period by means of the action-angle variables. The methodology even can be applied without finding the complete solution of the $J_2$-perturbed orbital motion. Based on the nodal period and the drift of RAAN per nodal period of pseudo-circular orbits, a reference grid can be established to study the nodal periods and the drift of RAAN of pseudo-elliptical orbits, and, moreover, to design a suitable long-term distance-bounded relative motion. The long-term distance-bounded relative motion is established without making assumptions on the eccentricity or on the magnitude of the relative distance. A new and efficient algorithm is developed to transform the spherical coordinates to the canonical constants, which typically requires less than three iterations. Furthermore, the algorithm for matching the nodal period and the drift of RAAN per nodal period is efficient as well with little computational load. The developed methodology is thus highly relevant for mission analysis and on-board implementations of distributed space architectures, such as formations, swarms or fractionated spacecraft.

We believe that the ideas and methodology we present constitute a starting point toward a more complete analytical understanding of the long-term orbital motion in the presence of the $J_2$ perturbation, as well as the design of the long-term passive distance-bounded relative motion.