1 Introduction

Coronavirus disease 2019 (COVID-19) is a major life-threatening global epidemic (pandemic) that the world is still battling with its ongoing outbreaks. The disease is caused by a highly virulent new strain of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) (Ahmad et al. 2021). COVID-19, which emerged from Wuhan city of China in December 2019, was first reported to the World Health Organization (WHO) in late December, 2019 (Chen et al. 2021). Following its rapid spread across the globe within short time, the disease was declared as a pandemic on March 11, 2020 (Chatterjee et al. 2022; Ariffin et al. 2021).

The pandemic has affected the world in many ways; it overwhelmed health systems, caused socioeconomic disruptions and a significant number of death tolls in many countries including the United State of America (USA), Italy, India, Brazil and Malaysia. As at May 10, 2022, the number of confirmed cases of COVID-19 around the world was estimated at 517,816,860, including 38,907,718 active cases and 6,280,681 deaths (Worldometer 2022). The pandemic became the most important public health challenge mankind ever faced since the 1918 Spanish flu pandemic (Gumel et al. 2021). This led most governments all over the world to put forth important steps in preventing and stemming the spread of the disease. SARS-CoV-2 is an RNA virus belonging to the family Coronaviridae and genus Betacoronavirus. Epidemiological investigations have shown that RNA viruses have high mutation rate (Abidemi et al. 2021). Like many other viruses, it is no longer news that COVID-19 mutates particularly during the high transmission periods (Birch et al. 2021). For instance, on September 7, 2020, the Delta variant of SARS-CoV-2 was first detected in India (Kang et al. 2022). It became a variant of concern (VOC), as classified by WHO on May 11, 2021. This variant rapidly outcompeted other variants of SARS-CoV-2 and became the predominant variant worldwide in November 2021 (Kang et al. 2022). Early 2022, the threat of a new COVID-19 surge with the spread of Omicron variant was faced worldwide (The Lancet Regional Health 2022). Different variants can trigger different degrees of infection, symptoms, rate of transmission and susceptibility. Furthermore, it is evident that treatment for one variant does not necessarily work for another (Birch et al. 2021). Hence, to increase the population’s protection against COVID-19, the rich countries have endorsed booster doses due to emergence of a new variant with suggestive immune escape and potentials for reinfection (The Lancet Regional Health 2022). The main transmission route of COVID-19 includes direct spread, contact spread and aerosol spread (Chang et al. 2021). Direct transmission of COVID-19 through respiratory droplets from coughing or sneezing. People who are in close contact with a suspected or confirmed COVID-19 patient can be infected by the virus (Akkilic et al. 2022; Chatterjee et al. 2022). Indirect transmission may take place in individuals by contacting either eyes, nose or mouth while contacting contaminated objects or surfaces (Akkilic et al. 2022; Chatterjee et al. 2022). Epidemiological studies have shown that the most common symptoms shown by patients are viral pneumonia, fever, dry cough, sore throat, myalgia and fatigue at the onset of COVID-19 (Anggriani and Beay 2022). However, there are other symptoms such as nasal congestion, runny nose, sore throat, myalgia and diarrhea (Chen et al. 2021). The incubation period of COVID-19 is generally between 2 days to 14 days (Anggriani and Beay 2022; Ariffin et al. 2021), or longer with 5 days on average (Ariffin et al. 2021). It has been reported that presymptomatic transmission contributes majorly to the spread of COVID-19 (Alleman et al. 2021). It has been observed that after recovery from primary COVID-19 infection, the same person can be infected with another variant of COVID-19 (Atifa et al. 2022).

As attaining the recovery phase for COVID-19 becomes the main hope for government and the public, every country implemented a standard operating procedure (SOP) to prevent and control COVID-19 outbreaks when pharmaceutical intervention in the form of vaccination was not yet available. The non-pharmaceutical interventions (precautionary measures) enforced by various countries to halt the chain of COVID-19 transmission include social distancing, wearing masks, regular hand washing, a ban on air traffic, bans on social gatherings in different areas, lockdowns, isolation, social distance, quarantine, awareness programs, and personal hygiene, such as wearing a mask and washing hands regularly (Chatterjee et al. 2022; Ali et al. 2022) and PCR testing for case detection (Baker et al. 2021). From late 2020, USA, United Kingdom (UK) and European countries among many other countries have deployed different vaccination campaigns (González-Parra et al. 2022; Biswas et al. 2021). This approval of vaccines for public use marked the commencement of a slow recovery (The Lancet Regional Health 2022).

On the 25th of January 2020, Malaysia reported the first confirmed cases of COVID-19 involving three tourists with immediate travel history from China who had entered Malaysia through Johor from Singapore on January 23, 2020 (Ariffin et al. 2021). Since then, the country has experienced different waves of the global epidemic. As at May 10, 2022, the cumulative number of confirmed cases of COVID-19 has risen to 4,463,740 including 22,953 active cases and 35,590 deaths (Ministry of Health Malaysia 2022; Worldometer 2022).

Before the licensure of COVID-19 vaccines, different non-pharmaceutical intervention strategies were deployed by the Malaysian government in order to curb the community spread of the disease in the country. These include imposition of movement control order (which first came to implementation on March 18, 2020 (Ariffin et al. 2021; TheStar, Malaysia announces movement control order 2022), social distancing, lockdown, advancement from a targeted PCR testing approach to a widespread PCR testing for case detection, self-quarantine and wearing of facemasks (Abidemi et al. 2021). In Malaysia, the public vaccine administration commenced in February 2021 (Ministry of Health Malaysia 2022). As of May 10, 2022, Malaysia has a high percentage of vaccinated people to be 84.86% of the population, including 2.99% and 81.87% of who have received the first and second dose of vaccine, respectively (Our World in Data, Coronavirus 2022).

Since late 2019 when COVID-19 emerged, many mathematical models have been constructed by researchers to facilitate understanding of the dynamical spread and control of the pandemic in different countries (Atifa et al. 2022; Abro et al. 2021; Anggriani and Beay 2022; Gumel et al. 2021; Ojo and Goufo 2023; Alleman et al. 2021; Dass et al. 2021; Abidemi et al. 2021; Olaniyi et al. 2020; Okuonghae and Omame 2020; Abioye et al. 2021; Peter et al. 2021b; Betti et al. 2021; Ojo et al. 2022b; Ali et al. 2022a, b; Algehyne and Ibrahim 2021; Peter et al. 2021a; Bandekar and Ghosh 2022; Omame et al. 2021). For instance, Atifa et al. (2022) developed and analysed a compartmental model for COVID-19 transmission dynamics by taking into consideration the effect of reinfection of individuals after recovery using Pakistan reported cases. A mathematical model based on Lotka-Volterra equations to gain insights into the impact of lockdown on COVID-19 spread by examining the difference in the growth rate of COVID-19 patients before and after the imposition of lockdown in Pakistan and Malaysia was presented by Abro et al. (2021).

In another study, Anggriani and Beay (2022) proposed a newly formulated non-linear deterministic model to explore the roles of self-isolation at home and hospitalization on the population dynamics of COVID-19. In their study, Gumel et al. (2021) proposed and analysed three non-linear mathematical models for different aspects of COVID-19. Alleman et al. (2021) proposed and calibrated an appropriate non-linear deterministic model to describe the impacts of non-pharmaceutical interventions on COVID-19 transmission based on publicly available epidemiological data for Belgium.

In an attempt to gain insights into the transmission dynamics of COVID-19 before and after movement control order implementation in Malaysia, Dass et al. (2021) proposed and calibrated a non-linear mathematical model including asymptomatic class using the actual observed cases in Malaysia. Abidemi et al. (2021) developed an appropriate non-linear mathematical model taking into consideration the impact of different pharmaceutical and non-pharmaceutical control interventions for the dynamics of COVID-19. The model was parametrized using the publicly available cumulative number of reported cases for Malaysia.

Olaniyi et al. (2020) formulated and analysed a compartmental COVID-19 epidemic model taking into account the disease transmission routes from asymptomatic, symptomatic and hospitalized individuals to gain insightful information about the transmission dynamics of COVID-19 using Nigeria’s cumulative number of active cases data. Okuonghae and Omame (2020) used a non-linear mathematical model to assess the impacts of non-pharmaceutical interventions on the population dynamics of COVID-19 based on the cumulative number of reported and active cases in Lagos State, Nigeria. Abioye et al. (2021) proposed non-optimal and optimal control mathematical models to describe the dynamics of transmission and optimal control of COVID-19 in Nigeria.

Peter et al. (2021b) developed and analysed a non-linear mathematical model to describe the transmission dynamics of COVID-19. The model was fitted to the observed data for Pakistan. To estimate the time at which a mutant variant is able to take over a wild-type strain during COVID-19 outbreak, Betti et al. (2021) proposed and analysed a two-strain COVID-19 mathematical model featuring a wild-type and mutant-type viral populations by using the available cumulative case data for Ontario in parametrizing the model.

Ali et al. (2022b) investigated the transmission dynamics of COVID-19 by constructing a non-linear deterministic model with fractal fractional derivative. Ali et al. (2022a) developed and analysed a non-linear fractional derivative compartmental model to examine the effect of asymptomatic and symptomatic transmissions on COVID-19 outbreak. Algehyne and Ibrahim (2021) used a fractal-fractional dimensional nonlinear mathematical model taking into account the impact of lockdown to analyse the dynamical behaviour of COVID-19 in Santos, Campinas and São Paulo cities of Brazil. Peter et al. (2021a) used a fractional-order deterministic compartmental model to examine the community spread and control mechanism of COVID-19 in Nigeria. In some other mathematical studies, many authors have studied non-linear mathematical co-infection models of COVID-19 with other infections, such as tuberculosis, dengue and malaria among others (Bandekar and Ghosh 2022; Omame et al. 2021).

Recent epidemiological models of COVID-19 have introduced a compartment related to the vaccinated population (Aguilar-Canto et al. 2022; Chatterjee et al. 2022; Choi et al. 2021; Demongeot et al. 2022; González-Parra et al. 2022). Specifically, Aguilar-Canto et al. (2022) proposed and analysed a mathematical model with multiple types of vaccines and trained the model with COVID-19 data from six different countries including Germany and Italy. The model was analysed by employing sensitivity theorems. Moreover, Chatterjee et al. (2022) presented and analysed a fractional-order nonlinear mathematical model, which includes a vaccination compartment and captures the effects of fear on the rates of transmission of the disease and reinfection of vaccinated individuals.

Choi et al. (2021) proposed and calibrated an age-structured non-linear mathematical model taking into consideration vaccination and precautionary interventions (particularly, social distancing) for describing COVID-19 transmission dynamics based on the actual epidemiological data for Korea. In the work of Demongeot et al. (2022), a deterministic compartmental model taking into consideration a variable vaccination in terms of effectiveness for COVID-19 transmission dynamics based on the reported cases and vaccination data of New York City was studied. Furthermore, González-Parra et al. (2022) constructed and parametrized an age-structured non-linear mathematical vaccination model for COVID-19 to assess the optimal vaccination strategy under different scenarios based on data related to USA. In view of the new development in the control of community spread of COVID-19 pandemic in different countries, and Malaysia in particular, this paper aims to construct and analyse a non-linear mathematical model that explicitly includes different compartmental classes for the populations of vaccinated individual with first and second doses for the global epidemic and to investigate the impact of transmission rate, the rate of first vaccine dose, the second dose vaccination rate and the recovery rate due to the second dose of vaccination on the dynamics of the disease outbreak. The new model is parameterized using the cumulative number of daily cases reported for Malaysia. The subsequent part of this paper is structured as follows: Sect. 2 discusses the description, formulation, and theoretical analysis of the proposed COVID-19 vaccination model. This is followed up by parameter estimation and model fitting in Sect. 3. The sensitivity analysis of each parameter with respect to the threshold quantities is presented in Sect. 4, while the numerical simulations of the dynamics of the proposed model are reported in Sect. 5. The concluding remark is given in Sect. 6.

2 Model Formulation and Analysis

In this section, we develop and analyze a deterministic mathematical model to effectively study the transmission and control of COVID-19 in a population. Before the simulation of the dynamics of the model, we investigate the qualitative properties of the model by theoretically analyzing the positivity and boundedness of solutions, computation of the threshold quantity and the stability of the equilibrium.

2.1 Model Formulation

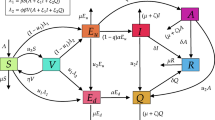
The COVID-19 model at a given time t is derived by dividing the total human population into the mutually-exclusive compartments of susceptible, S(t), vaccinated with first dose, \(V_{1}(t)\), vaccinated with second dose, \(V_{2}(t)\), exposed, E(t), asymptomatically-infectious, A(t), symptomatically-infectious, I(t), hospitalized H(t), and recovered, R(t) individuals. Therefore, the total human population denoted by N(t), is given as

$$\begin{aligned} S(t)+V_{1}(t)+ V_{2}(t)+E(t)+ A(t)+ I(t)+ H(t)+ R(t) \end{aligned}$$

It should be noted that the asymptomatically-infectious, A(t), are individuals who have exceeded the incubation period but are showing mild or no clinical symptoms of the disease, while the symptomatically-infectious, I(t), are the individuals who have passed the peak of the incubation period and are showing moderate or severe symptoms of COVID-19. In addition, the hospitalized population, H(t), contains the group of individuals that exhibit a clinical symptom of COVID-19 and are hospitalized or self-isolated for treatment. The asymptomatically infectious, symptomatically infectious, and hospitalized individuals are infectious and capable of transmitting the infection to susceptible individuals after an effective contact.

Recruitment into susceptible class is assumed to be through immigration or birth at a rate \(\theta\), susceptible individuals moves to vaccinated class after receiving the first dose of COVID-19 vaccine at a rate \(\phi\), the first dose of vaccinated individuals moves to the susceptible compartment at a rate \(\tau\) due to the fact that, the first dose of the vaccine is imperfect to protect against COVID-19 and the rest of the population moves to second dose of vaccinated class at a rate \(\sigma\). It is assume that individuals in the second dose of vaccinated population moves to recovered class at a rate \(\eta\). The force of infection \(\lambda =\frac{\alpha (\beta _{A} A+\beta _{I} I+\beta _{H} H)}{N(t)}\), where \(\alpha\) is the effective transmission rate,\(\beta _{A}\) is the reduction rate in disease transmission for asymptomatic individuals, \(\beta _{I}\) is the reduction rate in disease transmission for symptomatic individuals and \(\beta _{H}\) is the reduction rate in disease transmission for hospitalized individuals. The parameter \(\varepsilon\) represents the movement rate from the exposed class while a fraction k develops infection and moves to symptomatic class, the rest of \((1-k)\) become asymptomatic. Let \(\psi\) represents movement or exit rate from asymptomatic class A(t), then fraction \(\rho\) may recover naturally from asymptomatic infection and the rest of \((1-\rho )\) becomes symptomatic. We assume that disease induced death in asymptomatic individuals, A(t), is negligible. The exit rate from symptomatic infected class is \(\omega\), where the fraction b recovered and the rest of \((1-b)\) are hospitalized. \(\mu\) is the per-capita natural death rate in all the classes. We assume additional death rate due to COVID-19 in symptomatic and hospitalized class at rate d.

The model used in studying the transmission dynamics of COVID-19 in this study is given by the following system of the nonlinear differential equation. The state variables and parameters of the model are given in Table 1, while the flow diagram is depicted in Fig. 1.

$$\begin{aligned} \begin{aligned} \frac{dS}{dt} =&\ \theta -\lambda S -(\mu +\phi )S + \tau V_{1}, \\ \frac{dV_1}{dt} =&\ \phi S-(\tau +\sigma +\mu )V_{1}, \\ \frac{dV_2}{dt} =&\ \sigma V_{1} -(\eta +\mu )V_{2}, \\ \frac{dE}{dt} =&\ \lambda S - (\varepsilon +\mu )E, \\ \frac{dA}{dt} =&\ \varepsilon (1-\kappa )E -(\mu +\psi )A, \\ \frac{dI}{dt} =&\ \varepsilon \kappa E + \psi (1-\rho )A -(\mu +\delta +\omega )I, \\ \frac{dH}{dt} =&\ \omega (1-b)I - (\mu +\delta +d)H, \\ \frac{dR}{dt} =&\ \omega bI+\psi \rho A+ d H +\eta V_{2}-\mu R, \end{aligned} \end{aligned}$$
(1)

with the initial conditions \(S(0)>0, V_{1}(0) \ge 0, V_{2}(0) \ge 0, E(0)\ge 0, A \ge 0, I(0) \ge 0\), \(H \ge 0\), and \(R\ge 0\). where \(\alpha\) is the effective transmission rate, \(\beta _{A}\) is the reduction rate in disease transmission for asymptomatic individuals, \(\beta _{I}\) is the reduction rate in disease transmission for symptomatic individuals, and \(\beta _{H}\) is the reduction rate in disease transmission for hospitalized individuals.

Fig. 1
figure 1

Flow chart of the COVID-19 model (1)

Full size image
Table 1 Description of the model’s variables and parameters
Full size table

2.2 Positivity and Boundedness of Solutions

It is important to show that the presented model (1) is epidemiologically meaningful in the feasible and bounded in the region \(\mathcal {D}\), such that the state variables of the model are non-negative for all given time \(t>0\). Thus, we state the following result.

Theorem 1

The initial data for the model satisfies \(S(0)>0, V_{1}(0)\ge 0\), \(V_{2}(0)\ge 0\), \(E(0) \ge 0, A(0) \ge 0, I(0) \ge 0,\) \(H(0)\ge 0\) and \(R(0) \ge 0\) such that the solutions of the model represented by \((S(t), V_{1}(t)\), \(V_{2}(t), E(t), A(t)\), I(t), H(t), R(t)) with non-negative initial data remain non-negative for all time \(t > 0\).

Proof

We let \(T=\sup \{t>0: S(t)>0, V_{1}(t)>0, V_{2}(t)>0, E(t)>0, A(t)>0, I(t)>0, H(t)>0, R(t)>0 \in [0,t] \}\), for all time \(T>0\). From the first equation of the set of equations in (1), it follows that

$$\begin{aligned} \frac{dS}{dt} = \theta + \tau V_{1} - \lambda S -(\mu +\phi )S \ge \theta -\lambda S - (\mu +\phi )S \end{aligned}$$
(2)

By using the integrating factor method, the above differential equation (2) is further written as

$$\begin{aligned} \frac{d}{dt}\left( S(t)exp\left[ (\mu +\phi )t+\int _{0}^{t}\lambda (x)dx\right] \right) \ge \theta exp\left[ (\mu +\phi )t+\int _{0}^{t}\lambda (x)dx\right] . \end{aligned}$$

Therefore,

$$\begin{aligned} S(T)exp\left[ (\mu +\phi )T+\int _{0}^{T}\lambda (x)dx\right] -S(0)\ge \int _{0}^{T}\theta \left( exp\left[ (\mu +\phi )y+\int _{0}^{y}\lambda (x)dx\right] \right) dy \end{aligned}$$

so that,

$$\begin{aligned} \begin{aligned} S(T) \ge&\ S(0) exp\left[ -(\mu +\phi )T-\int _{0}^{T}\lambda (x)dx\right] \\&\ + exp\left[ -(\mu +\phi )T-\int _{0}^{T}\lambda (x)dx\right] \times \int _{0}^{T}\theta \left( exp\left[ (\mu +\phi )y+\int _{0}^{y}\lambda (x)dx\right] \right) dy >0. \end{aligned} \end{aligned}$$
(3)

It is trivial that the inequality \(S(T)\ge 0\) is positive. In a similar way, the remaining state variables can be shown to be positive for all time \(t>0\). Therefore, all the solutions of model (1) remain non-negative for all non-negative initial conditions. \(\square\)

To show that the presented COVID-19 model is mathematically and epidemiologically meaningful, we consider the analysis of the model (1) in the feasible region \(\mathcal {D} \subset \mathcal {R}_{+}^{8}\) such that

$$\begin{aligned} \mathcal {D} =\left\{ \left( S, V_{1}, V_{2}, E, A, I, H, R \right) \in \mathcal {R}_{+}^{8}: S+V_{1}+ V_{2}+E+ A+ I+ H+ R \le \frac{\theta }{\mu } \right\} \end{aligned}$$
(4)

By following the standard technique method given in Ojo and Akinpelu (2017) and Ojo et al. (2021), the feasible region \(\mathcal {D}\) can be shown to be positively invariant. Hence, all the solutions \((S(t), V_{1}(t), V_{2}(t), E(t), A(t), I(t), H(t), R(t))\) remain in the region \(\mathcal {D}\) where the model is said to be mathematically and epidemiologically well-posed (Ojo and Goufo 2021; Peter et al. 2018a). Thus, we claim the following result.

Theorem 2

The feasible region \(\mathcal {D} \subset \mathcal {R}_{+}^{8}\) of the COVID-19 model is positively invariant with positive initial conditions in \(\mathcal {R}_{+}^{8}\).

2.3 Existence and Stability of the COVID-Free Equilibrium (CFE)

The disease-free equilibrium steady state henceforth refer to as COVID-free equilibrium steady state (CFE) is obtained by equating the right hand side of all the equations in (1), and the variables (E, A, I) to zero. Thus, the COVID-free equilibrium, denoted by \(\mathcal {E}_{0}\), is obtained as \(\mathcal {E}_{0}=(S^{*}, V_{1}^{*}, V_{2}^{*}, E^{*}, A^{*}, I^{*}, H^{*}, R^{*})\) where \(E^{*}=A^{*}= I^{*}=H^{*}=0\) and

$$\begin{aligned} \begin{aligned} S^{*} =&\ \frac{\theta (\tau +\sigma +\mu )}{\mu \tau +(\sigma +\mu )(\mu +\phi )}, \\ V_{1}^{*} =&\ \frac{\theta \phi }{\mu \tau +(\sigma +\mu )(\mu +\phi )}, \\ V_{2}^{*} =&\ \frac{\theta \phi \sigma }{(\eta +\mu )\left[ \mu \tau +(\sigma +\mu )(\mu +\phi )\right] },\\ R^{*} =&\ \frac{\theta \phi \sigma \eta }{\mu (\eta +\mu )\left[ \mu \tau +(\sigma +\mu )(\mu +\phi )\right] }. \end{aligned} \end{aligned}$$
(5)

The next-generation matrix method (Diekmann et al. 1990; Peter et al. 2017, 2020; James Peter et al. 2022; Ojo et al. 2022a; Peter et al. 2022, 2018b, 2018c) is used to analyse the stability of the COVID-free equilibrium. Particularly, using the notation in Oke et al. (2020), the Jacobian matrix of the new infection terms (F) and the remaining transfer terms (V) are obtained as

$$\begin{aligned} F= \left[ \begin{array}{cccc} 0 &{} \frac{\alpha S^{*}\beta _{A}}{N^{*}} &{} \frac{\alpha S^{*}\beta _{I}}{N^{*}} &{} \frac{\alpha S^{*}\beta _{H}}{N^{*}} \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \end{array} \right] \text { and } V=\left[ \begin{array}{cccc} k_{4} &{} 0 &{} 0 &{} 0 \\ -\varepsilon k_{5} &{} k_{6} &{} 0 &{} 0 \\ -\varepsilon \kappa &{} -\psi k_{7} &{} k_{8} &{} 0 \\ 0 &{} 0 &{} -\omega k_{9} &{} k_{10} \end{array} \right] \end{aligned}$$

where \(k_{4}=\varepsilon +\mu\), \(k_{5}=1-\kappa\), \(k_{6}=\mu +\psi\), \(k_{7}=1-\rho\), \(k_{8}=\mu +\delta +\omega\), \(k_{9}=1-b\) and \(k_{10}=\mu +\delta +d\). Following Ojo and Akinpelu (2017), the threshold quantity given by \(\mathcal {R}_{0}=\varpi (FV^{-1})\) (with \(\varpi\) being the spectral radius) is obtained as

$$\begin{aligned} \mathcal {R}_{0}=\varpi (FV^{-1})=\mathcal {R}_{A}+\mathcal {R}_{I}+\mathcal {R}_{H} \end{aligned}$$
(6)

where,

$$\begin{aligned} \mathcal {R}_{A}= \frac{\alpha S^{*}\beta _{A}\varepsilon k_{5}}{N^{*}k_{4}k_{6}}, \quad \mathcal {R}_{I}= \frac{\alpha S^{*}\beta _{I}\varepsilon (\psi k_{5}k_{7}+\kappa k_{6})}{N^{*}k_{4}k_{6}k_{8}}, \quad \mathcal {R}_{H}= \frac{\alpha S^{*}\beta _{H}\varepsilon \omega k_{9}(\psi k_{5}k_{7}+\kappa k_{6})}{N^{*}k_{4}k_{6}k_{8}k_{10}}. \end{aligned}$$

The threshold quantity \(\mathcal {R}_{0}\) is the control reproduction number (also known as effective reproduction number) of the model (1). This quantity measures the average number of new COVID-19 cases that a single typical infectious individual can generate in a population that is susceptible with a certain fraction that are vaccinated individuals. As seen in (6), \(\mathcal {R}_{0}\) is the sum of the reproduction numbers associated with the number of new cases generated by asymptomatically infectious humans \((\mathcal {R}_{A})\), symptomatically infectious humans \((\mathcal {R}_{I})\) and hospitalized individuals \((\mathcal {R}_{H})\). Now, following Theorem 2 of Van den Driessche and Watmough (2002), we use the control reproduction number \(\mathcal {R}_{0}\) to establish the local stability of the COVID-free equilibrium (CFE) \(\mathcal {E}_{0}\), and the result is given in the Theorem below.

Theorem 3

The CFE \(\mathcal {E}_{0}\) of the model (1) is locally asymptotically stable in the biological feasible region \(\mathcal {D}\) if \(\mathcal {R}_{0}<1\), and unstable otherwise.

Proof

To prove Theorem 3, we obtained the Jacobian matrix of system (1) at the CFE \(\mathcal {E}_{0}\) as

$$\begin{aligned} \mathcal {J}_0(\mathcal {E}_{0})= \left[ \begin{array}{cccccccc} -k_{1} &{} \tau &{} 0 &{}0 &{} -\frac{\alpha S^{*}\beta _{A}}{N^{*}} &{}-\frac{\alpha S^{*}\beta _{I}}{N^{*}} &{} -\frac{\alpha S^{*}\beta _{H}}{N^{*}}&{} 0 \\ \phi &{} -k_{2} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} \sigma &{} -k_{3} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -k_{4} &{} \frac{\alpha S^{*}\beta _{A}}{N^{*}} &{} \frac{\alpha S^{*}\beta _{I}}{N^{*}} &{} \frac{\alpha S^{*}\beta _{H}}{N^{*}} &{}0 \\ 0 &{} 0 &{} 0 &{} \varepsilon k_{5} &{} -k_{6} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} \varepsilon \kappa &{} \psi k_{7} &{} -k_{8} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{}0 &{} 0 &{} \omega k_{9} &{} -k_{10} &{} 0 \\ 0 &{} 0 &{} \eta &{} 0 &{} \psi \rho &{} b \omega &{} d &{} -\mu \end{array} \right] , \end{aligned}$$
(7)

where \(k_{1}=\mu +\phi\), \(k_{2}=\tau +\sigma +\mu\), \(k_{3}=\eta +\mu\), \(k_{4}=\varepsilon +\mu\), \(k_{5}=1-\kappa\), \(k_{6}=\mu +\psi\), \(k_{7}=1-\rho\), \(k_{8}=\mu +\delta +\omega\), \(k_{9}=1-b\), and \(k_{10}=\mu +\delta +d\), while \(S^{*}\) and \(N^{*}=S^{*}+V_{1}^{*}+V_{2}^{*}+R^{*}\) are steady states given in (5). To establish the stability of the COVID-free equilibrium, it is necessary to show that the eigenvalues of the Jacobian matrix \(\mathcal {J}_0(\mathcal {E}_{0})\) are all negative. From (7), the first two eigenvalues are obtained as \(-\mu\) and \(-k_{3}\). The remaining six eigenvalues are obtained by using the sub-matrix \(\mathcal {J}_1(\mathcal {E}_{0})\) given below as

$$\begin{aligned} \mathcal {J}_1(\mathcal {E}_{0})= \left[ \begin{array}{cccccccc} -k_{1} &{} \tau &{} 0 &{} -\frac{\alpha S^{*}\beta _{A}}{N^{*}} &{} -\frac{\alpha S^{*}\beta _{I}}{N^{*}} &{} -\frac{\alpha S^{*}\beta _{H}}{N^{*}} \\ \phi &{} -k_{2} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} -k_{4} &{} \frac{\alpha S^{*}\beta _{A}}{N^{*}} &{} \frac{\alpha S^{*}\beta _{I}}{N^{*}} &{} \frac{\alpha S^{*}\beta _{H}}{N^{*}} \\ 0 &{} 0 &{} \varepsilon k_{5} &{} -k_{6} &{} 0 &{} \\ 0 &{} 0 &{} \varepsilon \kappa &{} \psi k_{7} &{} -k_{8} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} \omega k_{9} &{} -k_{10} \end{array} \right] \end{aligned}$$
(8)

Following the standards of the Routh–Hurwitz criterion (Paul and Kuddus 2022), all the eigenvalues of the sub-matrix \(\mathcal {J}_1(\mathcal {E}_{0})\) will be real and negative if the following holds:

  1. (i)

    Tr \((\mathcal {J}_1(\mathcal {E}_{0}))<0\)

  2. (ii)

    Det \((\mathcal {J}_1(\mathcal {E}_{0}))>0\)

  3. (iii)

    The product of Tr \((\mathcal {J}_1(\mathcal {E}_{0}))\) and the sum of all principal minors of \(\mathcal {J}_1(\mathcal {E}_{0})\) is equal to Det \((\mathcal {J}_1(\mathcal {E}_{0}))\).

Using the sub-matrix (8), we obtain the following

$$\begin{aligned} Tr(\mathcal {J}_1(\mathcal {E}_{0}))=-(k_{1}+k_{2}+k_{4}+k_{6}+k_{8}+k_{10})<0 \end{aligned}$$

and

$$\begin{aligned} Det(\mathcal {J}_1(\mathcal {E}_{0}))=k_{4}k_{6}k_{8}k_{10}(k_{1}(\sigma +\mu )+\mu \tau )(1-\mathcal {R}_{0})>0. \end{aligned}$$

From the above inequalities, we show that the first two Routh-Hurwitz conditions hold. Thus, to establish the third condition, we obtain the sum of all the \(5 \times 5\) principal minors of \(\mathcal {J}_1(\mathcal {E}_{0})\) represented by \(\mathcal {M}\) as

$$\begin{aligned} \mathcal {M}=k_{4}k_{6}k_{8}k_{10}(\phi \tau -k_{1}k_{2})(k_{1}+k_{2})(1-\mathcal {R}_{0})(Z_{1}+Z_{2})>0. \end{aligned}$$

Where \(Z_{1}=\varepsilon \left[ \kappa \omega k_{9}k_{12}+k_{11}(\psi k_{5}k_{7}+\kappa k_{6}+\kappa k_{10})+k_{5}k_{13}(k_{8}+k_{10})\right]\), \(Z_{2}=k_{4}k_{6}(k_{8}+k_{10})+k_{8}k_{10}(k_{4}+k_{6})\), \(k_{11}=\frac{\alpha S^{*}\beta _{I}}{N^{*}}\), \(k_{12}=\frac{\alpha S^{*}\beta _{H}}{N^{*}}\), and \(k_{13}=\frac{\alpha S^{*}\beta _{A}}{N^{*}}\). For the above inequality \(\mathcal {M}>0\) to hold, then \(k_{1}k_{2}<\phi \tau\) and \(\mathcal {R}_{0}<1\) must be satisfied. To establish the Routh- Hurwitz criterion, the third condition must be satisfied such that \(\mathcal {M}\) \(\times\) Tr\((\mathcal {J}_1(\mathcal {E}_{0}))\) \(=\) Det\((\mathcal {J}_1(\mathcal {E}_{0}))\), thus all the eigenvalues of the sub-matrix (7) are negative real part if \(\mathcal {R}_{0}<1\). Hence, the CFE \(\mathcal {E}_{0}\) is said to be locally asymptotically stable and unstable otherwise. \(\square\)

A simple interpretation and epidemiological implication of Theorem 3 is that a small inflow of COVID-infected individuals will not generate an outbreak of the disease in the population if the threshold quantity \(\mathcal {R}_{0}\) is less than unity. In other words, the disease will rapidly dies out when the control reproduction number \(\mathcal {R}_{0}<1\) if the initial sizes of the infected individuals is in the basin of attraction of \(\mathcal {E}_{0}\).

3 Parameter Estimation and Model Fitting

Table 2 Values of parameters of model (1)
Full size table
Fig. 2
figure 2

Fitting of the cumulative number of daily reported cases to model (1)

Full size image
Fig. 3
figure 3

PRCC results and contour plots for the parameters of \(\mathcal {R}_A\)

Full size image
Fig. 4
figure 4

PRCC results and contour plots for the parameters of \(\mathcal {R}_I\)

Full size image
Fig. 5
figure 5

PRCC results and contour plots for the parameters of \(\mathcal {R}_H\)

Full size image
Fig. 6
figure 6

PRCC results and contour plots for the parameters of \(\mathcal {R}_0\)

Full size image
Fig. 7
figure 7

The histogram of PRCC results for the parameters respect to each compartments

Full size image
Fig. 8
figure 8

The contour plot of PRCC results for the parameters respect to each compartments

Full size image
Fig. 9
figure 9

Bifurcation diagram of model (1) driven by the effective transmission rate \((\alpha )\)

Full size image
Fig. 10
figure 10

Time series of model (1) with \(\alpha =0.25,0.5,0.75,0.95\)

Full size image
Fig. 11
figure 11

Bifurcation diagram of model (1) driven by the rate of first vaccine dose \((\phi )\)

Full size image
Fig. 12
figure 12

Time series of model (1) with \(\phi =0.01,\ 0.02,\ 0.03,\ 0.04\)

Full size image
Fig. 13
figure 13

Bifurcation diagram of model (1) driven by the second dose vaccination rate \((\sigma )\)

Full size image
Fig. 14
figure 14

Time series of model (1) with \(\sigma =0.1,\ 0.3,\ 0.7,\ 0.9\)

Full size image
Fig. 15
figure 15

Bifurcation diagram of model (1) driven by the recovery rate due to second dose vaccination \((\eta )\)

Full size image
Fig. 16
figure 16

Time series of model (1) with \(\eta =0.05,\ 0.1,\ 0.15,\ 0.2\)

Full size image

Estimation of parameters of model (1) based on the data from reported cases of COVID-19 in Malaysia is explored in this section. To be specific, the model is parameterized to investigate the disease burden with effect of vaccination control in terms of the cumulative number of daily reported cases in Malaysia from February 24, 2021 up to February 15, 2022 (that is, from the beginning of vaccination program implementation in Malaysia). In this work, the values for parameters such as the recruitment rate of susceptible compartment, \(\theta\), human natural death rate, \(\mu\), disease-induced death rate, \(\delta\), progression rate from exposed class, \(\varepsilon\), fraction of exposed individuals that progress to infectious state, \(\kappa\), rate of migration from asymptomatic infected compartment, \(\psi\), rate of migration from symptomatic infectious class, \(\omega\), treatment (or recovery) rate of hospitalized individuals, d, rate of reduction in disease transmission for asymptomatic individuals, \(\beta _A\) and rate of reduction in disease transmission for symptomatic infectious individuals, \(\beta _I\), are either chosen or estimated from well-established literature as discussed below: As of 2021, the average life expectancy of Malaysian people is 75.6 years (Department of Statistics Malaysia 2022), so that \(\mu =1/(75.6\times 365)\) per day. Further, keeping in mind that the total population of Malaysia in 2021 is estimated at 32.7 million (Department of Statistics Malaysia 2021), we set \(N(0)=32700000\) so that \(\theta /{\mu }=N(0)=32700000\) is assumed as the limiting total human population in the absence of the disease. Thus, \(\theta\) is estimated as \(\theta =1185\). The incubation period for COVID-19 is estimated to average 5.2 days (Okuonghae and Omame 2020; Olaniyi et al. 2020; Rothan and Byrareddy 2020), with a range of 3 to 14 days (Okuonghae and Omame 2020), so that we set \(\varepsilon =1/5.2\). The relative infectiousness of asymptomatic infected individuals when compared to symptomatic individuals is still unknown; however, several studies have assumed that asymptomatic infection transmissibility was 0.5 times that of symptomatic infections (Okuonghae and Omame 2020; Olaniyi et al. 2020; Chen et al. 2020), hence we set \(\beta _I=1\) and \(\beta _A=0.5\beta _I\). The fraction of infectious cases that are asymptomatic is uncertain; however some studies have suggested setting this to 0.5 (Okuonghae and Omame 2020; Olaniyi et al. 2020), hence we set \(\kappa =0.5\). The average recovery period is about 15 days (Okuonghae and Omame 2020; Cauchemez et al. 2014; Chen et al. 2020), so that we set \(\psi =\omega =1/15\). There were 12 deaths out of the total number COVID-19 cases of 3545 reported on February 24, 2021 (Ministry of Health Malaysia 2022), so the disease induced death rate is estimated as \(\delta =12/3545=0.0034\). The treatment (or recovery) rate for hospitalized individuals is set to \(d=0.0667\), following the works in Olaniyi et al. (2020) and Chen et al. (2020)). Whereas the values of the remaining parameters of model (1) (rate of first vaccine dose, \(\phi\), rate of movement from \(V_1\) class to S class, \(\tau\), effective transmission rate, \(\alpha\), recovery rate due to second dose of vaccine, \(\eta\), rate of second dose vaccination, \(\sigma\), proportion of symptomatic infected individuals that recovered, b, proportion of asymptomatic individuals that recovered, \(\rho\), and rate of reduction in disease transmission for hospitalized individuals, \(\beta _H\)) are estimated by fitting the model to the reported COVID-19 cases. In many previous studies (Okuonghae and Omame 2020; Olaniyi et al. 2020; Abidemi et al. 2021; Abidemi and Aziz 2020, 2022), it has been shown that deterministic models fit well to cumulative number of reported cases. Thus, model (1) is fitted with the cumulative number of daily reported COVID-19 cases. Following Olaniyi et al. (2020) and Abidemi and Aziz (2022), the parameter estimation is conducted based on the least squares method implemented in MATLAB with ode45 routine with a view to minimizing the sum of squared-errors defined as \(\sum \left( Y(t, \Phi )-X_{{data}}\right) ^2\) constrained by the COVID-19 model (1), where \(X_{{data}}\) denotes the real reported data, and \(Y(t, \Phi )\) is the solution of the model associated with the cumulative number of daily reported cases over time t with the estimated parameters set \(\Phi\), where \(\Phi \in \left\{ \phi ,\tau ,\alpha ,\eta ,\sigma ,b,\rho ,\beta _H\right\}\).

Furthermore, the initial conditions are estimated according to the demographic data of Malaysia and the reported COVID-19 cases by the Ministry of Health Malaysia (Ministry of Health Malaysia 2022) and Our Wold in Data (Our World in Data, Coronavirus 2022) between February 24 2021 and February 15 2022. The total population of Malaysia in 2021 is estimated at 32.7 million as at 2021 (Department of Statistics Malaysia 2021). Thus, the initial total population is fixed at \(N(0)=32700000\). As at February 24, 2021, 3 people had received the first dose of vaccine, while 60 people had received the second dose of vaccine, so we set \(V_1(0)=3\) and \(V_2(0)=60\). On this day, there were 3545, 30568 and 3331 numbers of new, active and recovered cases, respectively, so \(I(0)=3545\), \(H(0)=30568\) and \(R(0)=3331\). In Altahir et al. (2020) and Wang et al. (2020), it was assumed that the number exposed individuals is 20 times the number of symptomatic infected individuals, so \(E(0)=20\times I(0)=70900\). We further make a similar assumption that the number of asymptomatic infected individuals is assumed to be 10 times the number of symptomatic individuals, thus \(A(0)=10\times I(0)=35450\). Finally, the initial size of the susceptible individual subpopulation is easily determined from \(S(0)=N(0)-(V_1(0)+V_2(0)+E(0)+A(0)+I(0)+H(0)+R(0))\) as \(S(0)=32556143\). Figure 2 demonstrates the results obtained from the model fitting with reported cumulative number of daily cases, while Table 2 provides the estimated model parameter values.

4 Sensitivity Analysis

In this section, the global sensitivity analysis of model (1) is provided. The Partial Rank Correlation Coefficient (PRCC) is used to identificate the most influential parameters of a given function (Marino et al. 2008). To generate the random data that used in PRCC, the Saltelli sampling given is employed (Saltelli 2002; Saltelli et al. 2010). In this phase, the open-source Python library called SALib developed by Herman and User is applied to construct the random data using Saltelli sampling (Herman and Usher 2017). The probability intervals are obeyed for the parameter values random sampling. All parameters are included except the recruitment rate of susceptible class \((\theta )\) and natural death rate \((\mu )\) which previously estimated. Two epidemiological aspects becomes the aims as follows.

  1. 1.

    The value of reproduction numbers \(\mathcal {R}_A\), \(\mathcal {R}_I\), \(\mathcal {R}_H\), and \(\mathcal {R}_0\) of model (1).

  2. 2.

    The value of each compartment density of model (1).

The PRCC results for the reproduction number associated with the number of new cases generated by asymptotically infectious humans \((\mathcal {R}_A)\) show that there are four most influential parameters namely the effective transmission rate \((\alpha )\) and the reduction rate in disease transmission for asymptomatic individuals \((\beta _A)\) which have positive relationship with \((\mathcal {R}_A)\), and the fraction of exposed individuals who have been infected \((\kappa )\) and the movement rate from asymptimatic infected class \((\psi )\) which have negative relationship with \((\mathcal {R}_A)\). This PRCC results are given in Fig. 3a and the relation between \(\beta _A\) with \(\psi\) and \(\alpha\) are given in Fig. 3b, c.

The next PRCC results given by Fig. 4a show that the effective transmission rate \((\alpha )\) and the reduction rate in disease transmission for symptomatic individuals \((\beta _I)\) are the most influential parameters which have positive relationship with the reproduction number associated with the number of new cases generated by symptotically infectious humans \((\mathcal {R}_I)\). The contour plots in \(\left( \omega ,\beta _I\right)\) and \(\left( \kappa ,\beta _I\right) -\)planes are given on Fig. 4b, c to show that \(\kappa\) and \(\omega\) are also in take effect to \((\mathcal {R}_I)\).

When the PRCC results for the reproduction number associated with the number of new cases generated by hospitalized individuals \((\mathcal {R}_H)\) are investigated, we obtain that three parameters becomes the most influential given by the effective transmission rate \((\alpha )\), the proportion of symptomatic infected individual who recovered (b), and the reduction rate in disease transmission for hospitalized individuals \(\beta _H\), see Fig. 5a. \(\alpha\) and \(\beta _H\) have positive relationship with \((\mathcal {R}_H)\) while b has the different sign. The second place is given by the disease induced death rate. To show the influence of those parameters, the contour plots are portrayed in Fig. 5b, c.

Now, the most influential parameter for control reproduction number \((\mathcal {R}_0)\) is identified. The PRCC results given by Fig. 6a indicate that the effective transmission rate \((\alpha )\) plays the important role in increasing \(\mathcal {R}_0\). The relation of \(\alpha\) with \(\phi\) and \(\tau\) are presented in Fig. 6b, c to show that those two parameters are also have impact to \(\mathcal {R}_0\).

Table 3 Most influenced parameter for each variable
Full size table

Furthermore, the most influential parameters for the value of each compartment density of model (1) are investigated. To obtain the solution, the fourth-order Runge–Kutta numerical scheme is employed. By neglecting the recruitment rate of susceptible class \((\theta )\) and natural death rate \((\mu )\) we compute the solution for 200, 400, 600, and 800 days and obtain PRCC results as in Figs. 7 and 8 and most influential parameters for each compartment as in Table 3. The rate of first vaccine dose \((\phi )\) becomes the most influential parameter for susceptible class (S). For those who received the first dose of vaccine \((V_1)\) and the second dose of vaccine \((V_2)\), the second dose vaccination rate \((\sigma )\) and the recovery rate due to second dose of vaccination \((\eta\)) have respectively become the dominating parameters. For the exposed class (E), asymptomatic infected class (A), symptomatic infected class (I), and hospitalized class (H), the rate of first vaccine dose is the most influential parameters. Finally, the PRCC results indicate that the disease induced death rate \((\delta )\) is the most influential parameter for for the recovered class (R).

5 Numerical Simulations

In this section, some numerical simulations are demonstrated. Fourth-order Runge–Kutta scheme is used to compute the numerical solution. Based on the PRCC results, the influence of four parameters namely, the effective transmission rate \((\alpha )\), the rate of first vaccine dose \((\phi )\), the second dose vaccination rate \((\sigma )\), and the recovery rate due to second dose vaccination \((\eta )\) are studied. All parameters values can be found in Table 2 and the dynamical behaviors are observed when a parameter is varied. For each case, two types simulations are given namely the bifurcation diagram and the appropriate time-series. The proposed bifurcation diagram is presented to show the change in stability of CFE and the occurrence of COVID-endemic equilibrium point (CEE) when the bifurcation parameter is varied. To support the circumstance, the time-series are given for several values of the parameters. From biological point a view, this simulations exhibit how big is the role of each parameter in suppressing the spread of COVID-19.

5.1 The Influence of the Effective Transmission Rate \((\alpha )\)

Using the parameter values in Table 2 by varying \(\alpha\) in interval [0.86, 1], the bifurcation diagram driven by the influence of the effective transmission rate \((\alpha )\) is portrayed in Fig. 9. We show that the CFE is locally asymptotically stable for \(0.86\le \alpha <\alpha ^*\) where \(\alpha ^*\approx 0.9287\). When \(\alpha\) crosses \(\alpha ^*\), CFE losses its stability and a locally asymptotically stable CEE occurs via forward bifurcation. When \(\alpha\) increases after crosses \(\alpha ^*\), the CEE also increases. Now, by setting \(\alpha =0.25,0.5,0.75,0.95\), the time-series is simulated, see Fig. 10. When the effective transmission rate \((\alpha )\) increases, the peak of exposed (E), asymptomatic (A), symptomatic (S) and hospitalized (H) individuals increases. The convergence rate to the equilibrium point for each compartments also increase. This means, we need to suppress the effective transmission rate by applying the health protocols such as social distancing, hand hygiene, and the use of health masks.

5.2 The Influence of the Rate of First Vaccine Dose \((\phi )\)

In these simulations, the rate of first vaccine dose \((\phi )\) is varied in interval \(0\le \phi \le 0.04\) to show its impact to the population densities of compartments. The forward bifurcation also occurs when \(\phi\) crosses \(\phi ^*\approx 0.0212\), see Fig. 11. When \(\phi <\phi ^*\), we have a locally asymptotically stable CFE and CEE does not exist. CFE becomes unstable and CEE is locally asymptoticaly stable when \(\phi\) passes through \(\phi ^*\). Although CEE increase, but the peak for E, A, I, and H decreases when \(\phi\) increase as we show in Fig. 12. The recovered individual (R) also increase due to the proportion of \(\phi\). This means, the first vaccine dose has great contribution to reduce the number of infected individuals.

5.3 The Influence of the Second Dose Vaccination Rate \((\sigma )\)

To show the impact of the second dose vaccination rate \((\sigma )\) to the spread of COVID-19, we vary \(\sigma\) in interval \([0,6]\times 10^{-5}\). It is shown from Fig. 13 that for \(0\le \sigma <\sigma ^*\), \(\sigma ^*=3.2252\times 10^{-5}\), both CFE and CEE exist where CFE is unstable while CEE is locally asymptotically stable. The CEE decreases when \(\sigma\) increases and finally disappears when \(\sigma\) crosses \(\sigma ^*\). The stablity of CFE also changes sign, becomes a locally asymptotically stable point for \(\sigma >\sigma ^*\). This phenomenon is called forward bifurcation where \(\sigma\) is the bifurcation parameter and \(\sigma ^*\) is the bifurcation point. For example, we plot the time-series for \(\sigma =0.1,0.3,0.7,0.9\) and obtain Fig. 14. The peak point of E, A, I, H decreases when the value of \(\sigma\) increases. From biological explanation, when the second dose vaccination rate \((\sigma )\) increases, we can hold down the spread of COVID-19 and suppress the endemic condition. For some values of \(\sigma\), the existence of COVID-19 may extincts.

5.4 The Influence of the Recovery Rate Due to Second Dose Vaccination \((\eta )\)

From PRCC results, the recovery rate due to second dose vaccination \((\eta )\) is the most influential parameter for the recovered class. We plot this condition in Fig. 15 for \(0.05\le \eta \le 0.2\) and show that \(\eta\) is directly proportional to the density of recovery class (R) and inversely proportional to the density of the second dose of vaccine individuals \((V_2)\). We have not found the bifurcation in this interval. The interesting phenomena is given by Fig. 16 where although this parameter is the most influential for R, the great leverage occurs only on the decrease of \(V_2\). This condition describes that the recovery rate to the second dose only has direct impact on the density of \(V_2\) and small impact in R which makes sense since all individuals moves to R.

6 Conclusion

Since the severe acute respiratory syndrome coronavirus 2 (SAR-CoV-2) was first reported in Wuhan China, the disease remains a global public health challenge that has taken many human lives. To mitigate the impact of this deadly disease, several control measures have been implemented to reduce its burden on the population. Among many other preventive measures that were implemented is vaccination. The use of the vaccine has helped in reducing the number of reported cases all over the world. The effectiveness of this preventative measure requires an initiation of multiple doses of vaccine to effectively contain the infection by fully developing the human immunity against the virus.

In this work, a non-linear mathematical model was developed and analyzed to study the impact of vaccination status on the dynamics spread of COVID-19 in the population. The COVID-19 model presented explicitly includes different compartmental classes for the population of vaccinated individuals with first and second doses. Following the development of the model, the threshold quantities were obtained to investigate the conditions for attaining a disease-free environment. We show that when the threshold quantity \(\mathcal {R}_{0}\) is less than unity, then the COVID-free equilibrium is said to be locally asymptotically stable and unstable otherwise. To identify the most influential parameters on the threshold quantities, we performed a global sensitivity analysis by using the Partial Rank Correlation Coefficient (PRCC). The result from this analysis informs us of the most impactful parameters that contribute most to the spread and control of the disease. These parameters are effective transmission rate \((\alpha )\), the rate of first vaccine dose \((\phi )\), the second dose vaccination rate \((\sigma )\), and the recovery rate due to second dose of vaccination \((\eta )\).

Using the resulting parameters, a numerical simulation was performed to first illustrate the bifurcation phenomenon, which shows the change in stability of COVID-free equilibrium point and the occurrence of COVID- endemic equilibrium point under some parameter variation. In addition, the time series of the dynamical behavior of the system is presented under different values of the most influential parameters. The result shows that adhering to the preventive measures has a huge impact on reducing the spread of the disease in the population. For instance, our numerical simulation shows that an increase in the effective transmission rate \((\alpha )\) directly increases the peak of the exposed, asymptomatic, symptomatic, and hospitalized individuals. This implies that to reduce the spread and burden of COVID-19 in the population, the effective transmission rate must be curbed. This can be achieved by applying the health protocols such as social distancing, good personal hygiene, and the use of face masks. Furthermore, the impact of the rate of the first vaccine dose and second vaccine dose were illustrated. As expected, increasing vaccination rates decreases the population of infected individuals. Particularly, an increase in the second dose vaccination rate shows to hold down the spread of COVID-19 and suppress the endemic condition.

Although, following the implementation of both the first and second dose of the vaccine, COVID-19 remains a threat to the human community. As a result, it is important to inform the public of the significant impact of the second dose and boosters to better provide the level of protection needed to eradicate the disease in the population. Therefore, to attain a high level of herd immunity to the disease, mass vaccination exercises should be encouraged to cover most of the population to prevent another outbreak of COVID-19.