Introduction

Fractured-rock aquifers serve as an important source of groundwater in various parts of the world. The relationship between hydrogeochemical processes and groundwater chemistry is particularly important when studying fractured rock aquifers due to the complex hydrogeology. Specifically, basalt aquifer systems have chemical characteristics that can reveal how these flow systems evolve over time (Bath 2007). Groundwater is mainly stored within the vesicles, fractures and sedimentary interflow beds found throughout the lithological framework of these aquifer types (Möller et al. 2016).

Hydrochemistry and isotopic analysis are increasingly used to improve understanding of the composition of groundwater in these types of aquifers (Duan et al. 2022; He et al. 2022; Li et al. 2018). Hydrochemistry can help define the chemical reactions occurring as groundwater interacts with the host rock (Nagaiah et al. 2017). Understanding the variation in hydrochemistry can therefore aid in identifying the hydrogeochemical processes that influence the groundwater′s hydrochemical facies (e.g., Akpataku et al. 2019; Flores Avilés et al. 2022; Gastmans et al. 2016; Owoyemi et al. 2019; Shanyengana et al. 2004; Teramoto et al. 2020; Wagh et al. 2016). It is important to understand the controlling factors on water chemistry in order to preserve groundwater resources.

Stable isotope geochemistry in hydrogeology studies is commonly used to complement hydrochemical data. As an isotopic signature can reflect the processes that are occurring throughout the hydrologic cycle, important information can be obtained from the analysis of groundwater isotopic ratios. Stable isotopes have been used as tracers of groundwater origin, recharge conditions, flow patterns, mixing of waters, and (paleo-)climatic effects in many complex groundwater flow systems (e.g., Awaleh et al. 2017; Birks et al. 2019; Deiana et al. 2018; Gao et al. 2022; Petelet-Giraud et al. 2018; Schubert et al. 2021; Wang et al. 2022). Groundwater flow and storage in fractured-rock systems in particular is poorly understood due to strong heterogeneity and anisotropy; however, stable isotopes are proving to be an effective tracer for determining recharge and transport processes in recent fractured-rock investigations (e.g., Rathay et al. 2018; Rohde et al. 2015; Wright and Novakowski 2019).

There are various graphical and statistical techniques available for interpretating groundwater quality data. The application of chemometric methods such as hierarchical cluster analysis (HCA), principal components analysis (PCA) and factor analysis (FA), are used in groundwater studies to develop conclusions based on statistically important factors in water-quality-data variability (e.g., Astel et al. 2006; Loganathan et al. 2015; Sreedhar and Nagaraju 2017; Wu et al. 2020). Therefore, when investigating variations in hydrogeochemical data, not only will analytical results and geographical data play an informative role in understanding trends, but also along with the application of chemometric methods, a deeper and more complete understanding can be achieved. The combination of these techniques has proven to provide further insight into these aquifer types and the data will reflect the geochemical evolution of these complex settings (Morales-Casique et al. 2016; Pandey et al. 2020; Sunkari et al. 2021).

Chemical data availability and quality is a major problem that is commonly highlighted in global groundwater assessments (Giordano 2009); thus, there is considerable scope for further investigation into the hydrogeochemical processes that control the chemistry of groundwater within basalt aquifers found in Australia, as well as the application of hydrogeochemical and statistical techniques in such research. Although there have been investigations into Australian basaltic aquifers, such as the Newer Volcanic Province (e.g., Raiber et al. 2009), many localised areas of the remnants of the Cenozoic magmatic activity like Tamborine Mountain, Queensland have been largely overlooked. To date there is no intensive research on the controls on the hydrogeochemical evolution, nor seasonal and spatial variations in groundwater chemistry at this location. Hence, Tamborine Mountain represents a noticeable knowledge gap regarding groundwater dynamics in an Australian basalt aquifer system. The current study investigates the aquifers located in the Tertiary basalt formation at Tamborine Mountain and aims to use the combination of analytical and multivariate analysis of hydrogeochemical data to aid in the understanding of the controlling factors of the hydrogeochemical evolution in fractured rock aquifer systems. This is a method which can be applied to other groundwater resources, including other fractured rock systems with multiple aquifers.

Study area and hydrogeological setting

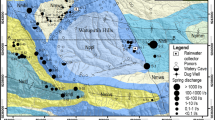
The investigation area is located in the Gold Coast hinterland, ~50 km south of Brisbane, South-East Queensland (Fig. 1). Tamborine Mountain is an elevated plateau that is ~12 km long by up to 6 km wide and was formed as a remnant of the northern flanks of the Tweed Volcano that is centred over Mount Warning, New South Wales. It is a rural area that has no reticulated water supply or sewerage system. The community relies on septic tanks, bores and rainwater. Land uses include urban development, farming, commercial horticulture and vegetation conservation areas.

Fig. 1
figure 1

a–b Location and c geological map of Tamborine Mountain, Queensland, Australia

Full size image

Tamborine Mountain is ~500–550 m above sea level and experiences a subtropical climate with warmer summers and cooler winters. The highest annual rainfall recorded was in 1974 (3643 mm) and the lowest annual rainfall recorded was in 2002 (756 mm). In 2020, the area had a total rainfall of 1,704.7 mm and 2021 had a total of 2,234.3 mm (BOM 2021). Periods of prolonged rainfall are usually most frequent during the wet season.

Geology

The elevated plateau is carved on several horizontal flows of deeply weathered Tertiary basalt lava in which surface geology falls away steeply around the periphery of the area. Over time, the rock formations have become exposed due to weathering and erosion and has produced a gently undulating surface (Willmott et al. 2010).

As described by Willmott et al. (2010), the geological history of the plateau begins with a long period of stability with no significant geological activity occurring during the late Jurassic and Cretaceous period. Due to erosional processes, the older surrounding rocks in the Gold Coast hinterland were mainly worn down. These older rock formations include Neranleigh-Fernvale beds, Chillingham Volcanics, Ipswich Coal Measures and the Woogaroo Subgroup (Fig. 1). During this time, an ancient erosional surface formed upon which basaltic lavas were later deposited. These basaltic lavas were emplaced during tertiary volcanism at ~23 million years ago. The eruption of these basalts is thought to have resulted from subcrustal processes (Ball et al. 2021). Subsequently, numerous periods of volcanism occurred, separated by periods of weathering and erosion.

The Albert Basalt is the first and lowermost basaltic flow of the plateau. It originates from the Focal Peak volcanic centre near Mount Barney to the southwest of Tamborine. The remaining basalt comes from the old Tweed Volcano that is centred over Mount Warning, NSW, and is known as the Beechmont Basalt where several subunits have been identified. Units A, C and E are described as several thin basalt flows interbedded with sediments. Unit B, the Cameron Falls member, and unit D, the Eagle Heights member, consist of single massive flows with localized fracturing.

Hydrogeology

It should first be noted that Tamborine Mountain is recharged primarily from local rainfall that infiltrates the soils and moves towards the saturated zone. Irrigated crops contribute on a smaller scale to recharge as well. Unfortunately, there is not much known about the aquifer structure at Tamborine Mountain. However, based on Willmott’s et al. (2010) findings, it is apparent that the highly fractured and vesicular horizontal basalt beds, particularly units A and C, play an important role for groundwater storage on Tamborine Mountain. These sequences appear to be permeable and direct groundwater laterally outwards to the mountain benches where they form spring zones. Connectivity pathways are likely provided from jointing and fractures between aquifers where there are thick and less-permeable basalt layers allowing water to move progressively downwards and laterally to the water table (Willmott et al. 2010).

Groundwater on Tamborine Mountain is utilised for a diverse range of reasons such as domestic gardens and drinking supply, commercial crop irrigation, and commercial extraction for both local and off-mountain markets. Groundwater is extracted from several hundred private bores across the study area which draw from multiple horizons within the Beechmont basalt sequence.

Methods

Field methods

Field sampling included the collection of rainwater, surface water and groundwater at 20 sites across the mountain (Fig. 1). When selecting the sampling sites, accessibility and site condition had to be taken into consideration. Rainfall samples were collected from one site on the mountain using an installed rainfall gauge. In total, six surface-water sites and 13 groundwater bores were selected for sampling and monitoring. The bore sites selected will be classified as either “deep” (>30 m to water table) or shallow (<30 m to water table). It is acknowledged that bores with depth to water table larger than 30 m are not generally considered as deep; however, this classification is made based on the scale of the bores studied at Tamborine Mountain which range from ~12 to ~103 m. Surface-water sites that are located near the bores being studied were chosen to investigate surface-water/groundwater interactions. A 12-month sampling program was created with bimonthly field work across 2 days to ensure both wet and dry seasons were included in the data collection. During the wetter season, an extra field trip was undertaken to encompass all changes in groundwater chemistry; therefore, a total of seven sampling trips were carried out from September 2020 to August 2021.

Water levels of all bore sites were monitored with automatic pressure transducers with measurements every 10–30 min. Additionally, a barometric pressure transducer was installed near one of the monitoring bores, which was central to the study area. A barometric pressure correction factor is used to remove the barometric pressure from the recorded pressure in the water level loggers.

Groundwater samples were collected using a flow-through cell connected by a flexible plastic sampling hose to extract samples from the bores′ pumps. Before sampling, the bores were purged until the physico-chemical parameters stabilised so that the most accurate representation of the aquifer water was collected. Water quality measurements including temperature (°C), pH, electrical conductivity (EC μS/cm), redox potential (ORP mV) and dissolved oxygen (DO mg/L) were measured using a WTW Multimeter with the attached respective probes via the flow through cell. Washed polypropylene bottles were used for all sample collection and then stored in a cooler box at refrigerated temperatures (<4 °C) containing ice bricks for their transport to Brisbane and placed in cold-room refrigeration. Bottles collected for cation analysis were first washed with 2% nitric acid.

Laboratory methods

The chemical analysis conducted on the samples collected was completed at the Central Analytical Research Facility (CARF) located at QUT Gardens Point Campus. Analysis of major cations, including but not limited to Na+, K+, Ca2+ and Mg2+, was undertaken using inductively coupled plasma optical emission spectroscopy (Perkin Elmer ICP-OES 8300DV). Sample preparation included filtering samples through a 0.45-μm filter membrane and then acidifying them with 200 μL of double distilled nitric acid.

Analysis of major anions, including but not limited to Cl–, NO3– and SO42–, was undertaken using ion chromatography (Thermo Scientific Dionex ICS-2100 IC). Sample preparation included filtering the samples with a 0.45-μm filter membrane. HCO3– was measured via alkalinity analysis using a Mettler Toledo Auto-Titrator on unfiltered samples. During major ion analysis quality control measures were incorporated through various dilutions of certified reference material (CRM), sample duplicates and laboratory blanks

Stable water isotope analysis of δ2H and δ18O was conducted using a Los Gatos Liquid Water Isotope Analyser. Sample preparation included filtering samples through a 0.45-μm filter membrane into 2-ml clear glass vials. Isotope data is reported in per mill (‰) relative to Standard Mean Ocean Water (SMOW), and the measurement precision was ±0.8‰ (1σ) for δ2H and ±0.2‰ (1σ) for δ18O.

Statistical methods

Minitab statistical software was used to undertake all statistical analytical procedures and 12 variables were analysed including Na+, K+, Mg2+, Ca2+, Cl–, SO42–, HCO3–, NO3–, pH, electrical conductivity, dissolved oxygen, redox potential and water level. Where there were missing values, the mean for that variable was used. Descriptive statistics including mean, standard deviation, minimum and maximum value were first determined. For data reduction, principal component analysis (PCA) and factor analysis (FA) was used. The data was standardized to prevent the influence of differing scales. PCA was chosen for factor extraction. Components with eigenvalues greater than 1 were then evaluated. For FA, in order to find factors that are explained more easily in regard to hydrogeochemical processes, varimax rotation was applied as it maximises the variance of a component. Hierarchical cluster analysis (HCA) was then applied to the data to classify the variables and samples into similar groupings. As the linkage rule, Ward’s method was used, and the Euclidian distance was applied as the measure of similarity.

Results

Multivariate analysis

The hydrogeochemical compositions in surface-water samples varied moderately (Table 1). The concentration of Na+, K+, Mg2+ and Ca2+ had mean values of 12.14, 0.58, 2.23 and 2.35 mg/L, respectively. The concentration of Cl−, SO42−, HCO3− and NO3− had mean values of 18.82, 2.44, 12.11 and 7.06 mg/L, respectively. The physicochemical parameters of pH, EC, DO and had mean values of 5.60, 99.24 μS/cm, 5.87 mg/L and 162.54 mV, respectively. Water level had a mean level of 0.23 m.

Table 1 Descriptive statistics of surface water and groundwater hydrogeochemistry. SD standard deviation
Full size table

The groundwater chemistry in groundwater samples varied on a larger scale as seen in Table 1. Na+, K+, Mg2+ and Ca2+ concentrations had a mean of 21.62, 1.72, 6.18 and 14.28 mg/L, respectively. Cl−, SO42−, HCO3− and NO3− concentrations had a mean of 14.94, 24.13, 86.53 and 3.50 mg/L, respectively. pH, EC, DO and redox had a mean of 6.32, 233.44 μS/cm, 2.46 mg/L and 115.43 mV, respectively. Water level (depth to groundwater had a mean of 24.78 m.

Dendrograms produced by hierarchical cluster analysis were used to determine if seasonal trends exist as well grouping sites together based on their chemical similarities and dissimilarities. The hydrogeochemical data has been grouped into either wet season (Jan 2021, February 2021 and April 2021) or dry season (September 2020, November 2020, June 2021 and September 2021). Two clusters have been generated for both wet and dry season (Fig. 2). The first cluster consists of all deep groundwater bores (bores with depth >30m) except for B5. The second cluster consists of all shallow bores (bores with depth <30m) and surface-water sites. The order of cation abundance was Na > Ca > Mg > K for cluster 1 and 2 in both the wet and dry season. The order of anion abundance for cluster 1 was HCO3 > SO4 > Cl > NO3 for both wet and dry season. For cluster 2 it was HCO3 > Cl > NO3 > SO4 for both wet and dry season also. Sites do not change from their main clusters from wet to dry season. This indicates seasonal variation in groundwater chemistry is very limited. Due to the limited seasonal variability in the hydrochemistry data, the following analysis was conducted on data that was averaged across the entirety of the sampling programme.

Fig. 2
figure 2

Dendrogram of hierarchical cluster analysis for samples collected during a wet season and b dry season

Full size image

To compare the hydrochemistry between the two main clusters for each data set, the mean chemical parameters is shown in Table 2 for the averaged data. The samples grouped by cluster 1 are dominant in Na, K, Mg, Ca, Cl, SO4, HCO3, pH, EC and water level. Cluster 2 instead is characterised by higher NO3 and DO levels.

Table 2 Average hydrogeochemical data of each cluster
Full size table

To identify the processes affecting water quality, chemical associations defined by factor analysis based on the loadings onto variables were examined. Factor analysis generates two matrices which includes a principal component matrix and a rotated factor matrix. Only eigenvalues greater than 1 are retained based on the Kaiser criterion. PCA and FA of this data set yielded three components, as seen in Table 3. More than 80% of the variance is explained by the first three components, with respective percentages of 60.37, 12.01, and 8.78% of the total variance. PC1 has high loadings on Na, K, Mg, Ca, HCO3, pH, EC, DO, redox and water level. Both PC2 and PC3 are evidently secondary factors due to the low percentages of total variance. PC2 has no strong loadings with any variable. PC3 has high loading on only Cl.

Table 3 PCA and FA (varimax rotated) results for hydrogeochemical data
Full size table

After rotation, the first three factors account for 36.50, 34.90 and 9.80% of the total variance, respectively. Factor 1 has high loading on Na, Ca, SO4, pH, EC and water level. Factor 2 has high loading on K, Mg, HCO3, DO and redox. NO3 does not highly correlate with any factor; however, it is moderately loaded with factor 2. Factor 3 has high loading on only Cl.

The FA scores and loadings for the sites plotted along the principal axes are presented in Fig. 3, grouped by the HCA results. Clusters 1 and 2 are represented by different shaped points. Scores obtained from FA are indicative of how the factors influence each site. The degree of continuity and clustering of the sites can be further investigated using this method. There is clear differentiation between the two clusters based on the distribution of points.

Fig. 3
figure 3

Varimax-rotated biplot of hydrogeochemical data

Full size image

Hydrogeochemical analysis

The Piper diagram indicates that various water types exist at Tamborine Mountain based on the major ions present (Fig. 4). The two deepest bores (B1 and B2) in the study area have mixed water type and all other deep bores are characterised by a Ca–or–Na–HCO3 water type. All shallow bores, most surface-water sites, and rainfall are of a Na–Cl water type. Pond and Guanaba Creek show a mixed water type for some of the sampling dates.

Fig. 4
figure 4

Major ion chemistry for all sites across the whole sampling programme, plotted on the Piper diagram

Full size image

Water level data in all sampled bore and surface-water sites over the whole sampling period is compared with rainfall data collected from a Bureau of Meteorology station known as Mt Tamborine Fern St, station number: 040197 (BOM 2021) in Fig. 5. Some bores had systematic errors with the water level loggers and therefore water level could not be measured for the whole sampling programme in these instances. Fluctuation in response to rainfall events for most sites is evident. Na–Cl type bores (shallow bores) show a relatively fast response to rainfall events as well as water level decline after rainfall stops. In bores that are moderately deeper (Ca– or Na– HCO3 type bores), rainfall response is delayed. In bores that are of mixed type (deepest bores), there is little to no response to rainfall events. Instead, they show very slow marginal response over long periods.

Fig. 5
figure 5

Change from average water level for each sampled bore over the sampling programme and Mt Tamborine Fern St average monthly rainfall data. Black diamonds represent sampling date

Full size image

The physicochemistry has been averaged over the 12-month sampling programme for each sampling site to show their relationship with bore depth. Electrical conductivity is higher in bores that have greater depth, excluding bore B5 (Fig. 6a). Thus, TDS will also be higher within the deeper bores. Surface-water sites display a similar electrical conductivity and therefore TDS to the shallow bores. Generally, pH is more basic in bores that have greater depth (Fig. 6b). Dissolved oxygen levels are highest in both surface-water sites and shallow groundwaters (Fig. 6c); however, B8 and B1 show similar dissolved oxygen levels to shallow groundwater sites. As for redox (Fig. 6d), only bores B7, B6, B4 and B3 contain reducing conditions, while all other sites show oxidizing conditions.

Fig. 6
figure 6

Physicochemistry at each sampling site over the 12-month sampling programme: a electrical conductivity, b pH, c dissolved oxygen and d redox potential

Full size image

The controlling mechanisms of groundwater composition can be assessed via the Gibbs diagram (Gibbs 1970). This relates water composition with its dominant sources by defining three distinct zones—evaporation dominance, rock weathering dominance and precipitation dominance. Therefore, by plotting the weight ratio of major cations, Na+/(Na++Ca2+) and major anions, Cl–/(Cl–+HCO3–) as a function of total dissolved solids, the source of the major ions can be defined. Figure 7 presenting the Gibbs diagrams indicates that rock weathering is the main factor controlling water composition for all sites; however, deep groundwater sites clearly plot away from the surface-water and shallow groundwater sites which group much closer together and fall outside the boomerang-shaped boundary. This suggests rock dominance extends towards lower TDS concentrations at higher Na+/(Na+ + Ca2+) ratios as a result of rock weathering. Rainfall samples as expected fall in the precipitation dominance region.

Fig. 7
figure 7

Gibbs diagrams indicating the dominant geochemical processes controlling water composition

Full size image

To understand the changes in chemical composition of groundwater, the geochemical variations in the ionic concentrations should be investigated—for example, determining the ionic ratios by plotting data along an X–Y coordinate can provide valuable information (Varol and Davraz 2014). Figure 8a depicts the (Ca2+ + Mg2+)/(HCO3– + SO42–) ratio. When samples are plotted above the equiline into the Ca2+ + Mg2+ side then it is evident that carbonate weathering is the dominant hydrogeochemical process occurring. The other side (HCO3– + SO42) indicates the dominance of silicate weathering (Sonkamble et al. 2012). The sampling points fall below the 1:1 equiline, owing to the high concentrations of HCO3– and SO42–. These high concentrations indicate silicate weathering as the dominant hydrogeochemical process.

Fig. 8
figure 8

Scatter plots of a (Ca2+ + Mg2+)/(HCO3– + SO42–) ratio, b (Na++K+), and c (Ca2+ + Mg2+) against total cations

Full size image

As silicate weathering is a key hydrogeochemical process that controls groundwater composition within this type of aquifer, estimating the ratio between Na+ + K+ and total cations can give greater insight into this process. If samples are plotted above the Na+ + K+ = 0.5 total cation line, then it can be assumed that silicate weathering is not occurring as much. Whereas if samples plot below and closer to the 1:1 equiline, silicate weathering is the dominant geochemical process (Sonkamble et al. 2012). As can be seen in Fig. 8b, surface water and shallow groundwaters fall above the 0.5 total cations; however, most deep groundwaters plot below this line, closer to the 1:1 equiline. This indicates that mainly deeper groundwaters are provided with sodium and potassium ions via silicate weathering. Feldspar minerals such as albite may be a major contributing source for the Na+ + K+ ions.

Furthermore, estimating the ratio between Ca2+ + Mg2+ and total cations can also help with understanding the impact of silicate weathering. If samples plot close to the 1:1 equiline then the weathering of minerals that are rich in calcium and magnesium is dominant. Plagioclase (anorthite) or pyroxene (augite) could be the source of this. If samples are plotted above the Ca2+ + Mg2+ = 0.5 total cation line, then it can be assumed, as correlated with Fig. 8b, that the weathering of feldspar (albite) is dominant. As can be seen in Fig. 8c, surface water and shallow groundwaters plot below the 0.5 total cations line and deep groundwaters fall above this line.

Stable isotope analysis

Tracing the variations in stable isotopic composition aids in understanding possible sources and the geochemical evolution of groundwater. The global meteoric water line (GMWL) given by the equation of δ2H = 8δ18O + 10 (Craig 1961) and the closest local meteoric water line was plotted (Brisbane, Australia, LMWL) in Fig. 9 as reference lines. The LMWL is given by the equation of δ2H = 7.53δ18O + 12.12 using LSR (IAEA 2014); however, Tamborine Mountain rainfall data does not conform to the Brisbane’s LMWL and therefore may not reflect the actual isotope composition of the regional precipitation, which is likely a result of latitude and altitude effects on isotopic composition (Araguás-Araguás et al. 2000). An estimated MWL has therefore been made for Tamborine Mountain based on the rainfall samples collected and is given by the equation of δ2H = 6.4518O + 11.7 and has an R2 of 0.91. However, this is based on a very limited data set and should not be considered as the accurate MWL for the local area.

Fig. 9
figure 9

δ18O versus δ2H plot a highlighting rainfall, surface water, shallow and deep bores, b highlighting collection in wet and dry season. The estimated Tamborine Meteoric Water Line (Tamborine MWL), Brisbane Meteoric Water Line (Brisbane MWL), and the Global Meteoric Water Line (GMWL) are shown

Full size image

The δ2H(SMOW) and δ18O(SMOW) values of rainwater range from ca. –35.6 to –5.5‰ and –7.2 to –2.8‰, respectively. Surface-water ranges from ca. –24.8 to –1.0‰ and –5.4 to –1.1‰, respectively. Groundwater ranges from ca. –25.1 to –17.7‰ and –5.8 to –3.1‰, respectively. It is clear that rainfall samples are more enriched in δ2H and δ18O, except for rainfall samples collected in April 2021 and June 2021, which are the two lower points on the graph (Fig. 9a). Overall, surface-water samples show more δ2H and δ18O enrichment than shallow groundwater and finally deep groundwater samples plot towards values that are more depleted. Also, samples collected in the wet season generally show more depletion in δ2H and δ18O than the dry season (Fig. 9b).

Deuterium excess (d-excess) can also be used to assess the sources of water vapour. This is defined by Dansgaard (1964) as d = δD – 8 δ18O and averages 10‰ for precipitation. However, the d-excess values for precipitation may differ depending on the geographic location and climatic conditions (Abu Jabal et al. 2018). The d-excess of groundwater, surface water and rainfall during the dry and wet season are given in Table 4. Mean d-excess values for all samples exceed the d-excess value for global precipitation (GMWL) of 10‰. The d-excess values of groundwater and surface water are significantly lower than the local precipitation d-excess measured. There is also a clear increase in d-excess values for deep, shallow bores and surface water from the dry to the wet season.

Table 4 Results of deuterium excess (d-excess) analysis for dry and wet season. SD standard deviation
Full size table

Discussion

Hydrogeological zones

Groundwater chemistry may differ spatially and temporally as a result of aquifer characteristics, water infiltration and land use; thus, monitoring is required over periods to ensure sufficient understanding and management of the groundwater resource (Yenigun et al. 2021). The chemical and statistical analysis conducted can provide insight into the spatial and temporal chemical patterns and their geochemical processes in the Tamborine Mountain aquifers.

Based on the HCA results (Fig. 2), there was an insignificant effect of seasonal variation on groundwater chemistry from wet to dry season. Clearly, a 1-year sampling programme has limited the ability to discover seasonal effects. Although seasonal trends do not exist, spatial variations were identified across the mountain. These spatial variations in hydrogeochemistry are strong and can be attributed to depth in the lithological framework of Tamborine Mountain. Statistical analysis has shown for example that there are large chemical variations in the groundwater sites studied (Table 1). Both HCA and FA (Fig. 3) have shown that on a simplistic level there are two main zones that exist in this hydrogeological system based on the spatial distribution of the two clusters. Cluster 1 sites include all deep groundwater bores except for B5, whereas cluster 2 consists of B5, all shallow bores and surface-water sites. Hence, these clusters evidently exist due to the hydrogeochemical controls at deep versus shallow depths in this groundwater resource.

Hydrogeochemical classification

It is possible to determine the geochemical evolution pattern by identifying water chemistry types (Pradhan et al. 2022). Piper diagrams are widely used as a graphical means of showing linear trends of major ions within a groundwater system (Piper 1944); therefore, it is important to first define the hydrochemical facies before attempting to determine the hydrogeochemical controls on groundwater. From this, it is possible to then draw conclusions about the geochemical processes that are occurring within the lithological environment, and hence the flow patterns. The piper plot (Fig. 4) suggests four main geochemical facies, a calcium bicarbonate facies (four sites from C1 and one site from C2), sodium bicarbonate facies (one site from C1), mixed facies (two sites from C1), and a sodium chloride facies (all sites from C2). Based on these different chemical facies, there is clearly not as high of a level of connectivity between aquifers as previously thought by Willmott et al. (2010).

Ca– and Na–HCO3 waters

These sites contain higher EC levels, more alkaline pH levels and low DO levels. B3 (only site that is Na–HCO3 water type), B4, B6 and B7 have reducing conditions and, B5 and B8 have oxidising conditions (Fig. 6). These reducing conditions are associated with depth, dissolved oxygen levels and hydrogen ion concentrations (Neumann 2012). Dissolved oxygen levels are the lowest in these reducing bores out of all sites due to the deep nature of these bores. In addition, the pH is very alkaline in these bores as bicarbonate is the dominant ion and in fact, they have the highest bicarbonate levels out of all sites. The two bores that on the contrary are experiencing oxidising conditions, still have very similar chemical properties to the other three, but instead have moderate DO levels, which may be a result of the hydraulic regime. In any type of bedrock, large hydraulic gradients as well as high hydraulic conductivity will rapidly introduce waters into depth (Wikberg 1992). Higher hydraulic connectivity in this type of bedrock is likely the result of a more highly fractured system as also suggested by Lachassagne et al. (2011), Love et al. (2002) and Mastrorillo et al. (2020). Thus, increased water flow may be allowing oxygen to dissolve more readily into the water and consequently producing an oxic environment.

These bores generally show a delayed response to the intense rainfall events. This ‘lag effect’ causes the water level to gradually increase over a longer period of time. Water level decline is also slow, indicating a lower connectivity to other aquifers and discharge areas. Groundwater level rise is therefore a likely result of water leakage from above aquifers. The slower responses in deeper aquifers indicate limited connectivity with the shallow aquifer, which may be due to the presence of lower permeability layers such as clays which restrict vertical groundwater movement. Similar findings were also noted by Chou (2021), whose study determined that often groundwater recharge does not occur continuously nor rapidly, but rather, there is a considerable time delay between rainfall and its contribution to deeper aquifers based on lithological composition and matrix storage features.

Mixed waters

Mixed waters include bores B1 and B2 which are the deepest bores in this study. It should be noted that B8 also shows mixed water type for two of the sampling dates. The disparity between the bores, however, is that B2 and B8 contain elevated SO4 concentrations in addition to high HCO3 concentrations compared to B1. All other parameters are similar in all bores. They contain high EC levels, more alkaline pH levels, moderate DO levels and are undergoing oxidising conditions. Due to the shallower bore depth of B8 compared to the other two bores and the fact that B1 has dissimilar SO4 concentrations, there is clearly complex hydrology in this area. As stated earlier, B8 is likely drawing from an aquifer within Unit C; however, is likely more confined in this area due to the minimal rainfall response. This bore also shows similar SO4 concentrations as B2. Due to the deep nature of bore B2 and the little response to rainfall, it is likely intersecting a deeper aquifer than the Ca– or Na–HCO3 water types, such as an aquifer that is situated within unit B and is recharged from the leakage of the above aquifer. The source of SO4 is clearly not affecting B1; therefore, this bore is likely drawing from a localised aquifer.

Na–Cl waters

Na–Cl waters contain all shallow bores and surface-water sites. These sites have the most similar ion chemistry to the rainfall samples. Compared to all other water types, these have lower EC levels, more acidic pH levels, high DO levels and are undergoing oxidising conditions. The oxidising conditions reflect waters that are in proximity to the surface and are, therefore, interacting with atmospheric oxygen. As seen in Fig. 5, these shallow bores show a relatively fast response to rainfall events suggesting high connectivity to the surface. Water levels then decline as a result of lateral and vertical groundwater flow. Based on the hydrogeochemical data collected, it is therefore evident that these bores are accessing an aquifer that is relatively shallow and unconfined that has good connectivity with the surface. Shallow groundwater and surface water are characterised by the same water type. This is consistent with the results of other groundwater/surface-water studies such as Martinez et al. (2015) who determined that similarities in the hydrochemistry of neighbouring groundwater and surface-water sites indicated interaction. However, shallow groundwaters have higher electrical conductivity values, indicating evaporation before recharge and/or water-rock interactions; hence, the groundwater moves towards deeper depths where it becomes higher in dissolved ions.

Hydrogeochemical processes

Groundwater chemistry can be influenced by various factors including the original composition of recharge waters which in this case is precipitation, the mineralogical composition of the reservoir rock, groundwater residence times, and other properties of the groundwater flow path (Cao et al. 2018; Fenta et al. 2020). As seen in Fig. 7, the Gibbs diagram plots the samples where rock weathering dominates as the process controlling groundwater ion chemistry. However, shallow groundwater and surface-water sites plot very close to the boundary between rock weathering dominance and precipitation dominance, providing further evidence that groundwater/surface-water interaction is occurring. Rainfall samples plotted in the precipitation dominant zone as expected. These findings are consistent with previous studies that have used Gibbs diagram plots as these studies have also shown that groundwater ion chemistry is controlled by rock weathering processes in basaltic aquifers (e.g., Locsey et al. 2011; Lu et al. 2015; Nagaiah et al. 2017).

As water–rock interaction is the controlling process that influences groundwater composition, it is important to identify what type of rock weathering processes are occurring. Investigating the relationship between major ions can help in understanding the changes in groundwater composition and the origin of these ions (Zhang et al. 2020; Kale et al. 2021). Silicate weathering in basalt aquifers is one of the main geochemical processes governing the major ions chemistry of groundwater (Sonkamble et al. 2012). Silicate weathering can be understood by determining the ratio between Ca + Mg versus HCO3 + SO4 (Fig. 8a). It was determined that the samples were placed below the 1:1 line, which indicated the prevalence of silicate weathering in these groundwater systems.

Silicate weathering can be further understood by assessing the ratio between total cations and Na + K as well as Ca + Mg (Fig. 8b,c). Both ratios suggest that silicate weathering is the driving process in cation production due to the dissolution of silicate minerals. Similarly, Subramani et al. (2009) have correlated high relative proportions of Na + K and Ca + Mg to total cations as indicators of rapid release of ions from Na–K–Ca–Mg bearing silicate minerals. As the deeper bores have high proportions of these ions in comparison to shallow bores and surface waters, they have experienced greater weathering. Therefore, the dissolution of specific silicate minerals will be further investigated to understand the evolution of groundwater at Tamborine Mountain.

As basalt contains considerable amounts of primary silicate minerals which are thermodynamically unstable, they weather or dissolve to secondary minerals such as kaolinite and Fe–Al–oxides when in contact with water (Baker and Owen Kelly 2017; Hadnott et al. 2017). Basalt primary minerals commonly include pyroxene, plagioclase feldspar and olivine (Möller et al. 2016). According to Ewart et al. (1977), all these minerals are present in the magmas of the Tertiary volcanic province of the Tweed Volcano; therefore, the CO2 from the atmosphere contained in rainwater permeates the soil zone and interacts with the basalt. Then mineral dissolution reactions consume CO2 which releases cations and bicarbonate as water encounters silicate minerals that are soluble (Pawar et al. 2008). The dissolution reaction of these minerals is presented in the following:

$${\displaystyle \begin{array}{cc}\mathrm{Albite}\ \left(\mathrm{Alkalic}\ \mathrm{Plagioclase}\right)\kern6.75em & \mathrm{Kaolinite}\kern17em \\ {}2\mathrm{Na}\left({\mathrm{Al}\mathrm{Si}}_3\right)\mathrm{O}8+2{\mathrm{H}}^{+}+9{\mathrm{H}}_2\mathrm{O}+2{\mathrm{CO}}_2\kern0.75em \to & {\mathrm{Al}}_2{\mathrm{Si}}_2{\mathrm{O}}_5{\left(\mathrm{OH}\right)}_4+2{\mathrm{Na}}^{+}+4{\mathrm{H}}_44{\mathrm{Si}\mathrm{O}}_2+2{\mathrm{H}\mathrm{CO}}_{3^{-}}\end{array}}$$
(1)
$${\displaystyle \begin{array}{cc}\mathrm{Anorthite}\ \left(\mathrm{Calcic}\ \mathrm{Plagioclase}\right)\kern4.75em & \mathrm{Kaolinite}\kern11.5em \\ {}\mathrm{Ca}\left({\mathrm{Al}}_2{\mathrm{Si}}_2\right){\mathrm{O}}_8+2{\mathrm{H}}^{+}+3{\mathrm{H}}_2\mathrm{O}+2{\mathrm{CO}}_2\kern0.5em \to & \begin{array}{c}\kern-0.4em {}{\mathrm{Al}}_2{\mathrm{Si}}_2{\mathrm{O}}_5{\left(\mathrm{OH}\right)}_4+{\mathrm{Ca}}^{2+}+2{\mathrm{H}\mathrm{CO}}_{3^{-}}\end{array}\end{array}}$$
(2)
$${\displaystyle \begin{array}{cc}\mathrm{Augite}\ \left(\mathrm{Pyroxene}\right)\kern14em & \mathrm{Kaolinite}\kern19em \\ {}{\mathrm{Mg}}_{0.7}\left.{\mathrm{Ca}\mathrm{Al}}_{0.3}\right)\left({\mathrm{Al}}_{0.3}{\mathrm{Si}}_{1.7}\right){\mathrm{O}}_6+3.4{\mathrm{H}}^{+}+1.1{\mathrm{H}}_2\mathrm{O}\kern0.75em \to & 0.3{\mathrm{Al}}_2{\mathrm{Si}}_2{\mathrm{O}}_5{\left(\mathrm{OH}\right)}_4+{\mathrm{Ca}}^{2+}+0.7{\mathrm{Mg}}^{2+}+1.1\mathrm{H}4\mathrm{SiO}4\end{array}}$$
(3)
$${\displaystyle \begin{array}{cc}\mathrm{Al}\mathrm{bite}\ \left(\mathrm{Alkalic}\ \mathrm{Plagioclase}\right)\kern1.75em &\ \mathrm{Gibbsite}\ \left(\mathrm{Aluminium}\ \mathrm{oxide}\right)\\ {}\mathrm{Na}\left({\mathrm{AlSi}}_3\right){\mathrm{O}}_8+{\mathrm{H}}^{+}+7{\mathrm{H}}_2\mathrm{O}\kern0.5em \to & \begin{array}{c}\kern-0.1em {}\mathrm{Al}{\left(\mathrm{OH}\right)}_3+3{\mathrm{H}}_4{\mathrm{SiO}}_4+{\mathrm{Na}}^{+}\end{array}\ \end{array}}$$
(4)
$${\displaystyle \begin{array}{cc}\mathrm{Forsterite}\ \left(\mathrm{Olivine}\right)\kern4.25em & \mathrm{Silicic}\ \mathrm{Acid}\kern7em \\ {}{\mathrm{Mg}}_2{\mathrm{SiO}}_4+4{\mathrm{CO}}_2+4{\mathrm{H}}_2\mathrm{O}\kern0.5em \to & 2{\mathrm{Mg}}_{2^{+}}+{\mathrm{H}}_4{\mathrm{SiO}}_4+4{\mathrm{H}\mathrm{CO}}_3\end{array}}$$
(5)

These processes are particularly prevalent in the deeper aquifers as a result of the water having more time to interact with surrounding lithology and therefore longer residence times. This is observed in previous studies of basaltic groundwaters (e.g., Gastmans et al. 2016); furthermore, PC1 (Table 3) has strong positive loadings on Na, K, Mg, Ca, HCO3, pH, EC and water level. It is strongly negatively loaded with DO and redox. This can therefore be regarded as water–rock interaction as these ions are a large part of weathered basalt groundwaters due to high rates of silicate weathering. It is also clear that alkaline environments with high EC values (i.e., larger concentrations of ions) are highly correlated with groundwaters that are at deeper depths. As a result of this, these sites have reducing conditions where there is lower DO; therefore, PC1 represents natural processes, whereas PC2 does not show any strong correlations between variables.

Factor analysis however is not completely consistent with PCA. Factor 1 (Table 3) loaded with Na, Ca, SO4, pH, EC and water level. Na and Ca are important indices contributing to basalt groundwaters and can be attributed to the dissolution of Na–Ca bearing minerals such as albite and anorthite. This can be regarded as water–rock interaction. SO4 was only found relatively high in two sites (B2 and B8). Hydrochemical and geological evidence indicates that the lithology in this area is prevalently basaltic; therefore, SO4 likely comes from an anthropogenic point source such as sulphate-rich chemical fertilizers. Factor 1 as a result represents a mixture of natural and anthropogenic processes, while factor 2 shows strong positive loading of K, Mg and HCO3. This can also therefore be regarded as water–rock interaction attributed to the weathering of silicate minerals such as augite and/or fosterite. Factor 2 is also strongly negatively loaded with DO and redox. Thus, factor 2 represents natural processes. The hydrogeochemical evolution of Tamborine Mountain is summarised in Fig. 10. It is clear that both PCA and FA can both be used to determine the main factors controlling groundwater hydrogeochemistry; however, it seems that FA is the most accurate method in this case based on the interpretation of the results.

Fig. 10
figure 10

Schematic cross section detailing groundwater flow and hydrogeochemical processes at Tamborine Mountain

Full size image

Stable isotopes

The stable isotopes of H2O can be used to determine the sources of groundwater. Many hydrological studies have specifically used the oxygen and hydrogen isotopes (δ2H and δ18O) in precipitation as a tracer for groundwater (e.g. Chen et al. 2011; Gastmans et al. 2016; El-Sayed et al. 2018). As groundwater moves along its flow paths, its isotopic composition can be altered and therefore will reflect the origin and history of the water (i.e., recharge and discharge processes, salinization and evaporation before recharging).

Based on the estimated Tamborine Mountain MWL, there are some samples that plot along or very close to the MWL, thereby indicating a meteoric origin for the recharge of these waters. However, many samples shift to more positive values due to the enrichment of heavy isotopes, an enrichment that is prevalent in the samples collected during the dry season when less rainfall occurred, which can be attributed to the evaporation of rainfall during infiltration. This occurs due to the discrimination of heavy isotopes (2H and 18O) versus light (2H and 16O), whereby light isotopes evaporate more efficiently and therefore vapor is more enriched in light water molecules and the residual water becomes more enriched in heavy isotopes (Mazor 2004). When rainwater infiltrates slowly into the ground, there may be significant evaporation before infiltration can occur (Alemayehu et al. 2011); thus, there was slower groundwater infiltration through the subsurface into the aquifers when less rainfall had occurred.

A correlation has been observed between the depletion of heavy isotopes and rainfall intensity. Raindrops that are small fall slowly and are quickly equilibrated with ambient vapor. Large raindrops, on the other hand, are less equilibrated with the ambient vapor during intense rainfall as they transit through the atmosphere more quickly than small raindrops do; hence, as rainfall intensity increases, the 18O becomes further depleted (Xi 2014). Due to these reasons, samples collected in the dry season are more enriched as they are instead affected by higher evaporation rates that are not hindered by intense rainfall events (Alemayehu et al. 2011).

The d-excess values for the dry and wet season (Table 4) further support these findings. The lower mean d-excess values in both groundwater and surface-water sites compared to the local precipitation suggests an evaporative loss of rainwater before it flows through creeks and reaches the aquifers. Surface-water sites during the wet season have lower d-excess values than groundwater sites, indicating that they tend to experience a higher degree of evaporation compared to groundwater. However, during the dry season some groundwater sites show a lower d-excess than surface-water sites, a trend similar to the one observed by Bedaso and Wu (2021). They ascribed this to two possible reasons: the isotopic exchange with aquifers or the existence of water originating from a different climatic regime. Nonetheless, the predominant trend is that all sites have mean d-excess values that are higher in the wet season compared to the dry season, thereby indicating and further supporting that groundwater and surface water undergo more evaporation prior to infiltration when there are dryer conditions, and hence fewer rainfall events.

Conclusion

Both analytical and multivariate analysis were used to identify the hydrogeological processes and to characterise the water cycle at Tamborine Mountain for the first time. The findings reveal the spatial and seasonal variation of the hydrochemistry in groundwater, surface water and rainfall. The conclusions of the study are as follows:

  1. 1.

    Groundwater recharge and mineral weathering processes are the main geochemical processes controlling groundwater evolution.

  2. 2.

    As rainwater reaches the surface of the Earth, permeates the soil zone, and travels from shallow groundwaters to deep groundwater, the chemical character of the water changes from Na–Cl to Ca– and Na–HCO3 to mixed. Hence spatial variations across the mountain are controlled by the variations in depth of the groundwater bores.

  3. 3.

    Rainwater infiltrating the soil and bedrock is low in dissolved solids as a result of being undersaturated with most, if not all, minerals. As this rainfall hits the ground surface and travels through the creeks, there is an increase in dissolved solids. Direct recharge into the aquifer that is likely unconfined and close to the surface, causes groundwater to have very similar chemistries to surface waters and rapid water level response to rainfall.

  4. 4.

    As water moves along its flow path through joints and fractures towards deeper aquifers where there may be confining conditions, water evolves to those higher in calcium, sodium and bicarbonate concentrations leading to higher pH levels and electrical conductivities as well as lower dissolved oxygen and redox values. These aquifers have a much slower response to rainfall events.

  5. 5.

    Seasonal variations are only evident in the stable isotopic data and are related to the frequency of intense rainfall events.

These findings and methods of assessment can be applied as a reference in studying similar groundwater resources in fractured-rock aquifers. In particular, the contribution of this study may prove significant to the region as the basaltic plateau investigated is part of many localised areas of the remnants of Cenozoic magmatic activity along the eastern seaboard of Australia. Improvements to this study are related to the limitations of a 1-year sampling programme. Further investigations, including an annual sampling programme, would benefit this groundwater resource to understand any longer-term trends.