Eigenvalues of truncated unitary matrices: disk counting statistics

Abstract

Let T be an $n\times n$ truncation of an $(n+\alpha )\times (n+\alpha )$ Haar distributed unitary matrix. We consider the disk counting statistics of the eigenvalues of T. We prove that as $n\rightarrow + \infty$ with $\alpha$ fixed, the associated moment generating function enjoys asymptotics of the form

$$\begin{aligned} \exp \big ( C_{1} n + C_{2} + o(1) \big ), \end{aligned}$$

where the constants $C_{1}$ and $C_{2}$ are given in terms of the incomplete Gamma function. Our proof uses the uniform asymptotics of the incomplete Beta function.

1 Introduction

Let $n \in {\mathbb {N}}_{>0}$, $\alpha >0$, and consider the joint probability measure

$$\begin{aligned} \frac{1}{n!Z_{n}}\prod _{1 \le j<k \le n}|z_{k}-z_{j}|^{2} \prod _{j=1}^{n} (1-|z_{j}|^{2})^{\alpha -1} d^{2}z_{j}, \qquad |z_{j}| \le 1, \end{aligned}$$

(1.1)

where $Z_{n}$ is the normalization constant. Note that the $z_{j}$’s are constrained to lie in the unit disk ${\mathbb {D}}:=\{z\in {\mathbb {C}}:|z|\le 1\}$. A main motivation for studying this point process stems from its connection with random matrices: it is shown in [19] that for $\alpha \in {\mathbb {N}}_{>0}$, (1.1) is the law of the eigenvalues of an $n\times n$ truncated unitary matrix T, i.e. T is the upper-left $n\times n$ submatrix of a Haar distributed unitary matrix of size $(n+\alpha )\times (n+\alpha )$. By rewriting (1.1) in the form

$$\begin{aligned} \frac{1}{n!Z_{n}}\prod _{1 \le j<k \le n}|z_{k}-z_{j}|^{2} \prod _{j=1}^{n} e^{-nQ(z_{j})} d^{2}z_{j}, \qquad Q(z) := {\left\{ \begin{array}{ll} -\frac{\alpha -1}{n}\ln (1-|z|^{2}), &{} \text{ if } |z|< 1, \\ +\infty , &{} \text{ if } |z| \ge 1, \end{array}\right. } \end{aligned}$$

we infer that for general $\alpha >0$ (not necessarily $\alpha \in {\mathbb {N}}_{>0}$), (1.1) is also the law of a Coulomb gas with n particles at inverse temperature $\beta = 2$ associated with the potential Q [11].

We emphasize that (1.1) is a probability measure only for $\alpha >0$. If $\alpha =0$, the above matrix T is an $n\times n$ Haar distributed unitary matrix, for which the n eigenvalues $\textrm{z}_{1},\ldots ,\textrm{z}_{n}$ lie exactly on the unit circle according to the probability measure proportional to

$$\begin{aligned} \prod _{1 \le j<k \le n}|\textrm{z}_{k}-\textrm{z}_{j}|^{2} \prod _{j=1}^{n} d\theta _{j}, \qquad \textrm{z}_{j} = e^{i\theta _{j}}, \; \theta _{j}\in [0,2\pi ). \end{aligned}$$

(1.2)

As is well-known, the equilibrium measure associated with (1.2) is the uniform measure on the unit circle.

This work focuses on the point process (1.1) as $n\rightarrow +\infty$ with $\alpha >0$ fixed. In this regime, $Q(z) = \mathcal{O}(n^{-1})$ for any fixed $z\in {\mathbb {D}}$, and the associated equilibrium measure $\mu$ is defined as the unique measure minimizing the following energy functional

$$\begin{aligned} \nu \mapsto I[\nu ] = \iint \ln \frac{1}{|z-w|}\nu (d^{2}z)\nu (d^{2}w) \end{aligned}$$

among all Borel probability measures $\nu$ supported on ${\mathbb {D}}$. This problem is a so-called classical (or unweighted) electrostatics problem, and as such the support of $\mu$ must be the boundary of ${\mathbb {D}}$ [16] (and this, despite the fact that the point process (1.1) is two-dimensional). Because the density of (1.1) is invariant under rotation, we conclude that $\mu$ is the uniform measure on the unit circle $\partial {\mathbb {D}}$.

Fig. 1

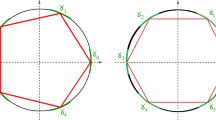
Illustration of the point process (1.1) with $n=500$ and $\alpha =2$ (left), $\alpha =5$ (middle) and $\alpha =10$ (right). The unit circle is represented in red (color figure online)

In the language of random matrix theory, $\partial {\mathbb {D}}$ is a “hard wall” of (1.1). For two-dimensional Coulomb gases, it is a standard fact that along a hard wall the equilibrium measure is singular with respect to the two-dimensional Lebesgue measure; moreover, a non-zero percentage of the points are expected to accumulate (as $n \rightarrow + \infty$) in a very small interface of width 1/n around the hard wall, see e.g. [3, 16, 17]. Following [3], we call this small interface “the hard edge regime”. A particular feature of (1.1) is that the associated equilibrium measure $\mu$ is purely singular (i.e. $\mu$ has no absolutely continuous component and $\int _{\partial {\mathbb {D}}} d\mu =1$). Hence, for large n and $\alpha$ fixed, most of the points $z_{1},\ldots ,z_{n}$ of (1.1) are expected to lie in a 1/n-neighborhood of $\partial {\mathbb {D}}$, see also Fig. 1.

There already exists a fairly rich literature on truncated unitary matrices. For example, the convergence of the distribution of the maximal modulus $\max _{j}|z_{j}|$ to the Weibull distribution has been studied in [13, 14, 17], several characterizations in terms of Painlevé transcendents for expectations of powers of the characteristic polynomial are established in [9], and results on the eigenvectors can be found in [10]. Also, besides (1.1), other two-dimensional point processes whose points are distributed within a narrow interface (or “band”) have been considered, see e.g. [2, 7, 12]; however, the point processes considered in these works only feature “soft edges”, and are thus very different from (1.1).

Let $\textrm{N}({r}):=\#\{z_{j}: |z_{j}| < {r}\}{\in \{0,1,\ldots ,n\}}$ be the random variable that counts the number of points of (1.1) in the disk centered at 0 of radius r. The goal of this paper is to understand the large n behavior of the multivariate moment generating function

$$\begin{aligned} {\mathbb {E}}\bigg [ \prod _{j=1}^{m} e^{u_{j}\textrm{N}(r_{j})} \bigg ] \end{aligned}$$

(1.3)

where $m \in {\mathbb {N}}_{>0}$ is arbitrary (but fixed), $u_{1},\dots ,u_{m} \in {\mathbb {R}}$ and $r_{1}< \dots <r_{m}$. We consider the hard edge regime, i.e. the radii $r_{1},\dots ,r_{m}$ are merging near 1 at the critical speed $1-r_{j} \asymp n^{-1}$ (we also allow $r_{m}=1$), see also Fig. 2. More precisely, we define

$$\begin{aligned}&r_{\ell } = \Big ( 1-\frac{t_{\ell }}{n} \Big )^{1/2},{} & {} t_{1}> \ldots > t_{m} \ge 0. \end{aligned}$$

(1.4)

Note that if $t_{m}=0$, then $r_{m}=1$ and trivially $\textrm{N}(r_{m})=n$ with probability one.

Fig. 2

Left: two circles (in black) merging near the unit circle (in red). Right: a zoom is taken around i. For both pictures, $\alpha =10$ and $n=500$

In Theorem 1.2 below, we prove that

$$\begin{aligned} {\mathbb {E}}\bigg [ \prod _{j=1}^{m} e^{u_{j}\textrm{N}(r_{j})} \bigg ] = \exp \bigg ( C_{1} n + C_{2} + o(1) \bigg ), \qquad \text{ as } n \rightarrow + \infty , \end{aligned}$$

and we give explicit expressions for the constants $C_{1}$ and $C_{2}$ in terms of the following functions

$$\begin{aligned} {\mathcal {H}}_{\alpha }(x;\vec {t},\vec {u})&:= 1 + \sum _{\ell =1}^{m} (e^{u_{\ell }}-1)\exp \bigg [ \sum _{j=\ell +1}^{m}u_{j} \bigg ] \textrm{Q}(\alpha ,t_{\ell }x), \end{aligned}$$

(1.5)

$$\begin{aligned} {\mathcal {G}}_{\alpha }(x;\vec {t},\vec {u})&:= \frac{1}{{\mathcal {H}}_{\alpha }(x;\vec {t},\vec {u})} \frac{x^{\alpha -1}}{\Gamma (\alpha )} \sum _{\ell =1}^{m} (e^{u_{\ell }}-1)\exp \bigg [ \sum _{j=\ell +1}^{m}u_{j} \bigg ] t_{\ell }^{\alpha }e^{-t_{\ell }x}\frac{1-\alpha -t_{\ell }x}{2}, \end{aligned}$$

(1.6)

where $x\in (0,1]$, $\vec {u}=(u_{1},\ldots ,u_{m})\in {\mathbb {C}}^{m}$, $\vec {t}=(t_{1},\ldots ,t_{m})$ is such that $t_{1}>\ldots >t_{m} \ge 0$, $\Gamma (a):=\int _{0}^{+\infty } s^{a-1}e^{-s}ds$ is the Gamma function, and $\textrm{Q}$ is the normalized incomplete Gamma function:

$$\begin{aligned} \textrm{Q}(a,x) := \frac{\Gamma (a,x)}{\Gamma (a)}, \qquad \Gamma (a,x) := \int _{x}^{+\infty } s^{a-1}e^{-s}ds. \end{aligned}$$

(1.7)

Note that ${\mathcal {H}}_{\alpha }$ is also well-defined at $x=0$, while ${\mathcal {G}}_{\alpha }$ is well-defined at $x=0$ only for $\alpha \ge 1$.

The statement of our main theorem involves $\ln {\mathcal {H}}_{\alpha }$, and the function ${\mathcal {H}}_{\alpha }$ also appears in the denominator of (1.6). The following lemma implies that $\ln {\mathcal {H}}_{\alpha }$ and ${\mathcal {G}}_{\alpha }$ are well-defined and real-valued for $x \in (0,1]$, $\vec {u}=(u_{1},\ldots ,u_{m}) \in {\mathbb {R}}^{m}$, and $t_{1}>\ldots >t_{m} \ge 0$. In this paper, $\ln$ always denotes the principal branch of the logarithm.

Lemma 1.1

${\mathcal {H}}_{\alpha }(x;\vec {t},\vec {u})>0$ for all $x \in (0,1]$, $\vec {u}=(u_{1},\ldots ,u_{m}) \in {\mathbb {R}}^{m}$, $t_{1}>\ldots >t_{m} \ge 0$.

Proof

Since

$$\begin{aligned} \partial _{u_{1}}{\mathcal {H}}_{\alpha }(x;\vec {t},\vec {u}) = e^{u_{1}+\ldots +u_{m}} \textrm{Q}(\alpha ,t_{1}x)>0, \end{aligned}$$

it only remains to verify that ${\mathcal {H}}_{\alpha }|_{u_{1}=-\infty }\ge 0$. Setting $u_{1}=-\infty$ in (1.5) and rearranging the terms, we find

$$\begin{aligned} {\mathcal {H}}_{\alpha }(x;\vec {t},\vec {u})|_{u_{1}=-\infty } = \big [ 1-\textrm{Q}(\alpha ,t_{m}x) \big ] + \sum _{\ell =2}^{m} e^{u_{\ell }+\ldots +u_{m}}[\textrm{Q}(\alpha ,t_{\ell }x)-\textrm{Q}(\alpha ,t_{\ell -1}x)]. \end{aligned}$$

Recall that $t_{1}>\ldots >t_{m} \ge 0$ and $x\in (0,1]$. Hence, since ${\mathbb {R}}\ni s \mapsto \textrm{Q}(\alpha ,s)$ decreases from 1 to 0, the m terms in the above right-hand side are all $\ge 0$, which proves ${\mathcal {H}}_{\alpha }|_{u_{1}=-\infty }\ge 0$. $\square$

Theorem 1.2

Let $m \in {\mathbb {N}}_{>0}$, $\alpha >0$ and $t_{1}>\dots >t_{m} \ge 0$ be fixed parameters. For $n \in {\mathbb {N}}_{>0}$, define

$$\begin{aligned}&r_{\ell } = \Big ( 1-\frac{t_{\ell }}{n} \Big )^{1/2}, \qquad \ell =1,\dots ,m. \end{aligned}$$

(1.8)

Let $\textrm{N}(r):=\#\{z_{j}: |z_{j}| < r\} \in \{0,1,\ldots ,n\}$ be the random variable that counts the number of points of (1.1) in the disk centered at 0 of radius r. For any fixed $x_{1},\dots ,x_{m} \in {\mathbb {R}}$, there exists $\delta > 0$ such that

$$\begin{aligned} {\mathbb {E}}\bigg [ \prod _{j=1}^{m} e^{u_{j}\textrm{N}(r_{j})} \bigg ] = \exp \bigg ( C_{1} n + C_{2} + \mathcal{O}(n^{-\frac{2{\hat{\alpha }}+\alpha }{2+\alpha }} {+ \tfrac{{\textbf{1}}_{\alpha =1} \ln n}{n}}) \bigg ), \qquad \text{ as } n \rightarrow + \infty \end{aligned}$$

(1.9)

uniformly for $u_{1} \in \{z \in {\mathbb {C}}: |z-x_{1}|\le \delta \},\dots ,u_{m} \in \{z \in {\mathbb {C}}: |z-x_{m}|\le \delta \}$, where ${\hat{\alpha }}:= \min \{\alpha ,1\}$, ${\textbf{1}}_{\alpha =1}=1$ if $\alpha =1$ and ${\textbf{1}}_{\alpha =1}=0$ otherwise, and

$$\begin{aligned} C_{1}&= \int _{0}^{1}\ln {\mathcal {H}}_{\alpha }(x;\vec {t},\vec {u}) \, dx, \nonumber \\ C_{2}&= \int _{0}^{1} {\mathcal {G}}_{\alpha }(x;\vec {t},\vec {u}) \, dx + \frac{\ln {\mathcal {H}}_{\alpha }(1;\vec {t},\vec {u}) - \sum _{j=1}^{m}u_{j}}{2}. \end{aligned}$$

(1.10)

In particular, since ${\mathbb {E}}\big [ \prod _{j=1}^{m} e^{u_{j}\textrm{N}(r_{j})} \big ]$ is analytic in $u_{1},\dots ,u_{m} \in {\mathbb {C}}$ and is positive for $u_{1},\dots ,u_{m} \in {\mathbb {R}}$, the asymptotic formula (1.9) combined with Cauchy’s formula implies that

$$\begin{aligned} \partial _{u_{1}}^{k_{1}}\dots \partial _{u_{m}}^{k_{m}} \bigg \{ \ln {\mathbb {E}}\bigg [ \prod _{j=1}^{m} e^{u_{j}\textrm{N}(r_{j})} \bigg ] - \Big ( C_{1} n + C_{2} \Big ) \bigg \} = \mathcal{O}(n^{-\frac{2{\hat{\alpha }}+\alpha }{2+\alpha }}{+ \tfrac{{\textbf{1}}_{\alpha =1} \ln n}{n}}), \qquad \text{ as } n \rightarrow + \infty , \end{aligned}$$

(1.11)

for any $k_{1},\dots ,k_{m}\in {\mathbb {N}}$, and $u_{1},\dots ,u_{m}\in {\mathbb {R}}$.

Let $({\mathbb {N}}^{m})_{>0}:= \{\vec {j}=(j_{1},\dots ,j_{m}) \in {\mathbb {N}}^{m}: j_{1}+\dots +j_{m}\ge 1\}$. For $\vec {j} \in ({\mathbb {N}}^{m})_{>0}$, the joint cumulant $\kappa _{\vec {j}}=\kappa _{\vec {j}}(r_{1},\dots ,r_{m};n,\alpha )$ of $\textrm{N}(r_{1}), \dots , \textrm{N}(r_{m})$ is defined by

$$\begin{aligned} \kappa _{\vec {j}}=\kappa _{j_{1},\dots ,j_{m}}:=\partial _{\vec {u}}^{\vec {j}} \ln {\mathbb {E}}[e^{u_{1}\textrm{N}(r_{1})+\dots + u_{m}\textrm{N}(r_{m})}] \Big |_{\vec {u}=\vec {0}}, \end{aligned}$$

(1.12)

where $\partial _{\vec {u}}^{\vec {j}}:=\partial _{u_{1}}^{j_{1}}\dots \partial _{u_{m}}^{j_{m}}$ and $\vec {0}:=(0,\ldots ,0)$. For instance, we have

$$\begin{aligned}&{\mathbb {E}}[\textrm{N}(r)] = \kappa _{1}(r), \qquad \text{ Var }[\textrm{N}(r)] = \kappa _{2}(r) =\kappa _{(1,1)}(r,r), \qquad \\&\text{ Cov }[\textrm{N}(r_{1}),\textrm{N}(r_{2})] = \kappa _{(1,1)}(r_{1},r_{2}). \end{aligned}$$

Corollary 1.3

Let $m \in {\mathbb {N}}_{>0}$, $\vec {j} \in ({\mathbb {N}}^{m})_{>0}$, $\alpha > 0$, and $t_{1}>\dots >t_{m} \ge 0$ be fixed. For $n \in {\mathbb {N}}_{>0}$, define $\{r_\ell \}_{\ell =1}^m$ by (1.8).

• (a) The joint cumulant $\kappa _{\vec {j}}$ satisfies

  $$\begin{aligned} \kappa _{\vec {j}} = \partial _{\vec {u}}^{\vec {j}}C_{1}\big |_{\vec {u}=\vec {0}} \; n + \partial _{\vec {u}}^{\vec {j}}C_{2}\big |_{\vec {u}=\vec {0}} + \mathcal{O}\big (n^{-\frac{2{\hat{\alpha }}+\alpha }{2+\alpha }}{+ \tfrac{{\textbf{1}}_{\alpha =1} \ln n}{n}}\big ), \qquad n \rightarrow +\infty , \end{aligned}$$

  (1.13)

  where $C_{1},C_{2}$ are as in Theorem 1.2 and ${\hat{\alpha }}:= \min \{\alpha ,1\}$. In particular, for any $1 \le \ell < k \le m$,

  $$\begin{aligned} {\mathbb {E}}[\textrm{N}(r_{\ell })]&= b_1(t_\ell ) n + c_1(t_\ell ) + \mathcal{O}\big (n^{-\frac{2{\hat{\alpha }}+\alpha }{2+\alpha }}{+ \tfrac{{\textbf{1}}_{\alpha =1} \ln n}{n}}\big ), \\ \textrm{Var}[\textrm{N}(r_{\ell })]&= b_{(1,1)}(t_{\ell },t_{\ell })n + c_{(1,1)}(t_{\ell },t_{\ell }) + \mathcal{O}\big (n^{-\frac{2{\hat{\alpha }}+\alpha }{2+\alpha }}{+ \tfrac{{\textbf{1}}_{\alpha =1} \ln n}{n}}\big ), \\ \textrm{Cov}(\textrm{N}(r_{\ell }),\textrm{N}(r_{k}))&= b_{(1,1)}(t_{\ell },t_{k})n + c_{(1,1)}(t_{\ell },t_{k}) + \mathcal{O}\big (n^{-\frac{2{\hat{\alpha }}+\alpha }{2+\alpha }}{+ \tfrac{{\textbf{1}}_{\alpha =1} \ln n}{n}}\big ) \end{aligned}$$

  as $n \rightarrow + \infty$, where

  $$\begin{aligned} b_1(t_\ell )&=\; \int _{0}^{1} \textrm{Q}(\alpha ,t_{\ell }x)dx = \textrm{Q}(\alpha ,t_{\ell }) + \alpha \frac{1-\textrm{Q}(\alpha +1,t_{\ell })}{t_{\ell }}, \nonumber \\ c_1(t_\ell )&= \frac{t_{\ell }^{\alpha }}{\Gamma (\alpha )} \int _{0}^{1} x^{\alpha -1}e^{-t_{\ell }x}\frac{1-\alpha -t_{\ell }x}{2}dx + \frac{\textrm{Q}(\alpha ,t_{\ell })-1}{2}, \end{aligned}$$

  (1.14)

  and, for $\ell \le k$,

  $$\begin{aligned} b_{(1,1)}(t_{\ell },t_{k})&= \; \int _{0}^{1} \textrm{Q}(\alpha ,t_{\ell }x)\big (1-\textrm{Q}(\alpha ,t_{k}x)\big )dx, \end{aligned}$$

  (1.15)
  $$\begin{aligned} c_{(1,1)}(t_{\ell },t_{k})&= \; \int _{0}^{1} \bigg \{ (\alpha -1+t_{k}x)t_{k}^{\alpha }e^{-t_{k}x}\textrm{Q}(\alpha ,t_{\ell }x)\nonumber \\&\quad - (\alpha -1+t_{\ell }x)t_{\ell }^{\alpha }e^{-t_{\ell }x} \big (1-\textrm{Q}(\alpha ,t_{k}x)\big ) \bigg \}\frac{x^{\alpha -1}dx}{2\, \Gamma (\alpha )} \nonumber \\&\quad + \frac{1}{2}\textrm{Q}(\alpha ,t_{\ell })\big (1-\textrm{Q}(\alpha ,t_{k})\big ). \end{aligned}$$

  (1.16)

• (b) Assume furthermore that $t_{m}>0$. As $n \rightarrow + \infty$, the random variable $({\mathcal {N}}_{1},\dots ,{\mathcal {N}}_{m})$, where

  $$\begin{aligned}&{\mathcal {N}}_{\ell } := \frac{\textrm{N}(r_{\ell })-b_1(t_\ell ) n}{\sqrt{b_{(1,1)}(t_\ell ,t_\ell ) n}}, \qquad \ell =1,\dots ,m, \end{aligned}$$

  (1.17)

  convergences in distribution to a multivariate normal random variable of mean $(0,\dots ,0)$ whose covariance matrix $\Sigma$ is given by

  $$\begin{aligned} \Sigma _{\ell ,k} = \Sigma _{k, \ell } = \frac{b_{(1,1)}(t_{\ell },t_{k})}{\sqrt{b_{(1,1)}(t_{\ell },t_{\ell })b_{(1,1)}(t_{k},t_{k})}}, \qquad 1 \le \ell \le k \le m. \end{aligned}$$

Remark 1.4

If $t_{m}=0$, then $b_{1}(t_{m})={1}$ and $c_{1}(t_{m})=b_{(1,1)}(t_{m},t_{m})=c_{(1,1)}(t_{m},t_{m})=0$, which is consistent with the fact that $\textrm{N}(r_{m})=n$ with probability 1. This is the reason why we required $t_{m}>0$ in Corollary 1.3 (b). The graphs of $t \mapsto b_{1}(t)$ and $t \mapsto b_{(1,1)}(t,t)$ are shown in Fig. 3 for several values of $\alpha$.

Fig. 3

The coefficients $t \mapsto b_{1}(t)$ (left) and $t \mapsto b_{(1,1)}(t,t)$ (right) for the indicated values of $\alpha$. (Recall from Corollary 1.3 that $b_{1}(t)n$ and $b_{(1,1)}(t,t)n$ are the leading terms in the large n asymptotics of ${\mathbb {E}}[\textrm{N}(( 1-\frac{t}{n} )^{1/2})]$ and $\textrm{Var}[\textrm{N}(( 1-\frac{t}{n} )^{1/2})]$, respectively)

Proof of Corollary 1.3

Assertion (a) (except for the second equality in (1.14)) is a direct consequence of (1.11) and (1.12). The second equality in (1.14) is obtained using (1.7), Fubini’s theorem, and $\Gamma (\alpha +1)=\alpha \, \Gamma (\alpha )$:

$$\begin{aligned} \int _{0}^{1} \textrm{Q}(\alpha ,t_{\ell }x)dx&= \int _{0}^{1}dx \int _{t_{\ell }x}^{+\infty } dy \frac{e^{-y}y^{\alpha -1}}{\Gamma (\alpha )} \\&= \bigg ( \int _{0}^{t_{\ell }}dy \int _{0}^{\frac{y}{t_{\ell }}} dx + \int _{t_{\ell }}^{+\infty } dy \int _{0}^{1} dx \bigg )\frac{e^{-y}y^{\alpha -1}}{\Gamma (\alpha )} \\&= \frac{\alpha }{t_{\ell }} \int _{0}^{t_{\ell }} \frac{e^{-y}y^{\alpha }}{\Gamma (\alpha +1)}dy + \int _{t_{\ell }}^{+\infty }\frac{e^{-y}y^{\alpha -1}}{\Gamma (\alpha )}dy\\&= \alpha \frac{1-\textrm{Q}(\alpha +1,t_{\ell })}{t_{\ell }} + \textrm{Q}(\alpha ,t_{\ell }). \end{aligned}$$

We now turn to the proof of (b). Using (1.9) with $u_\ell = \frac{i v_\ell }{\sqrt{b_{(1,1)}(t_\ell ,t_\ell ) n}}$ and $v_\ell \in {\mathbb {R}}$ fixed, we get

$$\begin{aligned} {\mathbb {E}}[e^{i \sum _{\ell = 1}^m v_\ell {\mathcal {N}}_\ell }]&= {\mathbb {E}}[e^{\sum _{\ell = 1}^m u_\ell \textrm{N}(r_{\ell })}] e^{- \sum _{\ell = 1}^m u_\ell b_1(t_\ell ) n} \\&= e^{C_{1}(\vec {u}) n + C_{2}(\vec {u}) + \mathcal{O}(n^{-\frac{2{\hat{\alpha }}+\alpha }{2+\alpha }})} e^{- \sum _{\ell = 1}^m u_\ell \partial _{u_\ell } C_1|_{\vec {u}=\vec {0}} n } \end{aligned}$$

as $n \rightarrow +\infty$, where the dependence of $C_{1}$ and $C_{2}$ in $\vec {u}$ has been made explicit. Since $C_j|_{\vec {u}=\vec {0}} = 0$ for $j = 1,2$ and $u_\ell = \mathcal{O}(n^{-1/2})$, we thus have

$$\begin{aligned} {\mathbb {E}}[e^{i \sum _{\ell = 1}^m v_\ell {\mathcal {N}}_\ell }]&= e^{\frac{1}{2}\sum _{\ell ,k= 1}^m u_\ell u_k \partial _{u_\ell }\partial _{u_k} C_1|_{\vec {u}=\vec {0}} n + \mathcal{O}(|\vec {u}|^3 n + |\vec {u}| + n^{-\frac{2{\hat{\alpha }}+\alpha }{2+\alpha }})} \\&= e^{\frac{1}{2}\sum _{\ell ,k = 1}^m \frac{iv_\ell }{\sqrt{b_{(1,1)}(t_\ell ,t_\ell )}} \frac{iv_k}{\sqrt{b_{(1,1)}(t_k,t_k)}} b_{(1,1)}(t_{\min (\ell ,k)}, t_{\max (\ell ,k)}) + o( 1)} \\&\quad \rightarrow e^{-\frac{1}{2}\sum _{\ell , k=1}^m v_\ell \Sigma _{\ell ,k} v_k} \end{aligned}$$

as $n \rightarrow +\infty$. In other words, ${\mathbb {E}}[e^{i \sum _{\ell = 1}^m v_\ell {\mathcal {N}}_\ell }]$ converges pointwise to $e^{-\frac{1}{2}\sum _{\ell , k=1}^m v_\ell \Sigma _{\ell ,k} v_k}$ as $n\rightarrow + \infty$, which implies Assertion (b) by Lévy’s continuity theorem. $\square$

Comparison with other works on counting statistics. There has been a lot of interest recently on counting statistics of two-dimensional point processes. We will not attempt to survey this literature here, but refer the interested reader to [5] and the introduction of [1]. Our main goal in this subsection is to compare Theorem 1.2 with the works [3, 8].

In [8], the following Mittag-Leffler ensemble is considered:

$$\begin{aligned} \frac{1}{n!{\hat{Z}}_{n}} \prod _{1 \le j < k \le n} |z_{k} -z_{j}|^{2} \prod _{j=1}^{n}|z_{j}|^{2a}e^{-n |z_{j}|^{2b}}d^{2}z_{j}, \qquad z_{1},\ldots ,z_{n} \in {\mathbb {C}}, \end{aligned}$$

(1.18)

where $b>0$ and $a>-1$ are parameters of the model. The associated equilibrium measure $\mu ^{\textrm{ML}}$ is supported on the disk $\{|z| \le b^{-\frac{1}{2b}}\}$ and given by $\mu ^{\textrm{ML}}(d^{2}z) = \frac{b^{2}}{\pi }|z|^{2b-2}d^{2}z$. Note that $\mu ^{\textrm{ML}}$ is absolutely continuous with respect to the Lebesgue measure $d^{2}z$ (this contrasts with the equilibrium measure $\mu$ of (1.1), which is purely singular). Let $m \in {\mathbb {N}}_{>0}$, $r \in (0,b^{-\frac{1}{2b}})$, ${\mathfrak {s}}_{1},\ldots ,{\mathfrak {s}}_{m} \in {\mathbb {R}}$, $a > -1$ and $b>0$ be fixed parameters such that ${\mathfrak {s}}_{1}<\ldots <{\mathfrak {s}}_{m}$. The main result of [8] is the large n asymptotics of the m-point moment generating function of the disk counting statistics of (1.18) when the radii are merging either in the bulk, i.e. $r_{\ell } = r \big ( 1+\frac{\sqrt{2}\, {\mathfrak {s}}_{\ell }}{r^{b}\sqrt{n}} \big )^{\frac{1}{2b}}$ for all $\ell \in \{1,\ldots ,m\}$, or at the soft edge, i.e. $r_{\ell } = b^{-\frac{1}{2b}} \big ( 1+\sqrt{2b}\frac{{\mathfrak {s}}_{\ell }}{\sqrt{n}} \big )^{\frac{1}{2b}}$ for all $\ell \in \{1,\ldots ,m\}$. In both cases, it is shown in [8] that

$$\begin{aligned} {\mathbb {E}}^{\textrm{ML}}\bigg [ \prod _{j=1}^{m} e^{u_{j}\textrm{N}(r_{j})} \bigg ] = \exp \bigg ( D_{1} n + D_{2} \sqrt{n} + D_{3} + \frac{D_{4}}{\sqrt{n}} + \mathcal{O}\bigg (\frac{(\ln n)^{2}}{n}\bigg )\bigg ), \qquad \text{ as } n \rightarrow + \infty , \end{aligned}$$

and the constants $D_{1},\ldots ,D_{4}$ are determined explicitly. The constant $D_{1}$ is particularly simple; for example, in the bulk regime it is given by $D_{1} = \int _{|z|\le r} \mu ^{\textrm{ML}}(d^{2}z) \sum _{j=1}^{m}u_{j} = b r^{2b} \sum _{j=1}^{m}u_{j}$. The constant $D_{2}$ is more complicated and given by

$$\begin{aligned} D_{2} = {\left\{ \begin{array}{ll} \displaystyle \sqrt{2}\, b r^{b} \int _{-\infty }^{+\infty } \bigg ( \ln {\mathcal {H}}^{\textrm{ML}}(x; \vec {{\mathfrak {s}}},\vec {u}) - \chi _{(-\infty ,0)}(x) \sum _{j=1}^{m}u_{j}\bigg ) dx, &{} \text{ for } \text{ the } \text{ bulk } \text{ regime }, \\ \displaystyle \sqrt{2b}\int _{-\infty }^{0} \bigg ( \ln {\mathcal {H}}^{\textrm{ML}}(x; \vec {{\mathfrak {s}}},\vec {u}) - \sum _{j=1}^{m}u_{j}\bigg ) dx, &{} \text{ for } \text{ the } \text{ soft } \text{ edge } \text{ regime }, \end{array}\right. } \end{aligned}$$

where $\chi _{(-\infty ,0)}(x)=1$ if $x<0$ and $\chi _{(-\infty ,0)}(x)=0$ otherwise, $\vec {{\mathfrak {s}}}:= ({\mathfrak {s}}_{1},\ldots ,{\mathfrak {s}}_{m})$, and

$$\begin{aligned} {\mathcal {H}}^{\textrm{ML}}(x; \vec {{\mathfrak {s}}},\vec {u}):= 1 + \sum _{\ell =1}^{m} (e^{u_{\ell }}-1)\exp \bigg [ \sum _{j=\ell +1}^{m}u_{j} \bigg ] \frac{\textrm{erfc}(x-{\mathfrak {s}}_{\ell })}{2}. \end{aligned}$$

We find it curious that the above function has the same structure as the function ${\mathcal {H}}_{\alpha }$ in (1.5); namely, they are both of the form

$$\begin{aligned} 1 + \sum _{\ell =1}^{m} (e^{u_{\ell }}-1)\exp \bigg [ \sum _{j=\ell +1}^{m}u_{j} \bigg ] X_{\ell }(x) \end{aligned}$$

(1.19)

where $X_{\ell }(x):= \textrm{Q}(\alpha ,t_{\ell }x)$ in the present paper and $X_{\ell }(x):= \textrm{erfc}(x-{\mathfrak {s}}_{\ell })/2$ in [8]. Note also that

• ${\mathcal {H}}_{\alpha }$ already appears in the leading constant $C_{1}$, while ${\mathcal {H}}^{\textrm{ML}}$ appears in $D_{2}$,

• $t_{1},\ldots ,t_{m}$ are dilation parameters of $X_{\ell }$, in the sense that they appear in the multiplicative form “$t_{\ell }x$” in $\textrm{Q}(\alpha ,t_{\ell }x)$, while ${\mathfrak {s}}_{1},\ldots ,{\mathfrak {s}}_{m}$ are translation parameters of $X_{\ell }$, in the sense that they appear in the additive form “$x-{\mathfrak {s}}_{\ell }$” in $\textrm{erfc}(x-{\mathfrak {s}}_{\ell })/2$.

Let $0< \rho < b^{-\frac{1}{2b}}$ be fixed. The following point process was considered in [3]:

$$\begin{aligned} \frac{1}{n!{\tilde{Z}}_{n}} \prod _{1 \le j < k \le n} |z_{k} -z_{j}|^{2} \prod _{j=1}^{n}|z_{j}|^{2\alpha }e^{-n |z_{j}|^{2b}}d^{2}z_{j}, \qquad |z_{j}|\le \rho . \end{aligned}$$

(1.20)

The only (but important) difference between the point processes (1.18) and (1.20) is that in (1.20) the points are constrained to lie in the disk $\{|z| \le \rho \}$. Because $\rho <b^{-\frac{1}{2b}}$, the circle $\{|z| = \rho \}$ is a hard wall of (1.20) and it is shown in [3] that the associated equilibrium measure $\mu _{h}^{\textrm{ML}}$ is given by

$$\begin{aligned} \mu _{h}^{\textrm{ML}}(d^{2}z)&= \mu _{\textrm{reg}}^{\textrm{ML}}(d^{2}z) + \mu _{\textrm{sing}}^{\textrm{ML}}(d^{2}z), \nonumber \\ \mu _{\textrm{reg}}^{\textrm{ML}}(d^{2}z)&:= 2b^{2}r^{2b-1}dr\frac{d\theta }{2\pi }, \quad \mu _{\textrm{sing}}^{\textrm{ML}}(d^{2}z) := c_{\rho } \delta _{\rho }(r) dr \frac{d\theta }{2\pi }, \end{aligned}$$

(1.21)

where $z=re^{i\theta }$, $r>0$, $\theta \in (-\pi ,\pi ]$ and $c_{\rho }:= \int _{|z| > \rho }\mu ^{\textrm{ML}}(d^{2}z) = \int _{\rho }^{b^{-\frac{1}{2b}}} 2b^{2}r^{2b-1}dr = 1-b\rho ^{2b}$. For the hard edge regime $r_{\ell } = \rho \big ( 1-\frac{t_{\ell }}{n} \big )^{\frac{1}{2b}}$ with $t_{1}>\dots >t_{m}\ge 0$, it is proved in [3] that

$$\begin{aligned} {\mathbb {E}}_{h}^{\textrm{ML}}\bigg [ \prod _{j=1}^{m} e^{u_{j}\textrm{N}(r_{j})} \bigg ] = \exp \bigg (E_{1}n + E_{2}\ln n + E_{3} + \frac{E_{4}}{\sqrt{n}} + \mathcal{O}(n^{-\frac{3}{5}})\bigg ), \qquad \text{ as } n \rightarrow + \infty , \end{aligned}$$

(1.22)

where $E_{1} = \int _{|z|\le \rho } \mu _{\textrm{reg}}^{\textrm{ML}}(d^{2}z) \times \sum _{j=1}^{m}u_{j} + \int _{b\rho ^{2b}}^{1} \ln {\mathcal {H}}_{h}^{\textrm{ML}} (x;\vec {t},\vec {u})dx$ with

$$\begin{aligned} {\mathcal {H}}_{h}^{\textrm{ML}} (x;\vec {t},\vec {u}) = 1 + \sum _{\ell =1}^{m} (e^{u_{\ell }}-1)\exp \bigg [ \sum _{j=\ell +1}^{m}u_{j} \bigg ] e^{-\frac{t_{\ell }}{b}(x-b\rho ^{2b})}. \end{aligned}$$

This function is also in the form (1.19), with $X_{\ell }(x) = e^{-\frac{t_{\ell }}{b}(x-b\rho ^{2b})} = \textrm{Q}(1,\frac{t_{\ell }}{b}(x-b\rho ^{2b}))$. It is also interesting to note the presence of the term $E_{2}\ln n$ in (1.22), while in (1.9) there is no term proportional to $\ln n$. We believe the reason for this is that $\mu _{h}^{\textrm{ML}}$ has a non-trivial component $\mu _{\textrm{reg}}^{\textrm{ML}}$ which is absolutely continuous with respect to $d^{2}z$, while the equilibrium measure $\mu$ of (1.1) is purely singular. This belief is supported by the following fact: when $\rho \rightarrow 0$, the measure $\mu _{h}^{\textrm{ML}}$ becomes purely singular (because $c_{\rho }\rightarrow 1$), and $E_{2}\rightarrow 0$ (as can be easily checked from [3, Theorem 1.3]).

A transition regime between the hard edge and the bulk was also considered in [3]. This regime is called “the semi-hard edge regime” and corresponds to the case when the radii are at a distance of order $1/\sqrt{n}$ from the hard edge. More precisely, for $r_{\ell } = \rho \big ( 1+\frac{\sqrt{2}\, {\mathfrak {s}}_{\ell }}{\rho ^{b}\sqrt{n}} \big )^{\frac{1}{2b}}$ with ${\mathfrak {s}}_{1}<\dots<{\mathfrak {s}}_{m}<0$, we have

$$\begin{aligned} {\mathbb {E}}_{h}^{\textrm{ML}}\bigg [ \prod _{j=1}^{m} e^{u_{j}\textrm{N}(r_{j})} \bigg ] = \exp \bigg (F_{1}n + F_{2}\sqrt{n} + F_{3} + \frac{F_{4}}{\sqrt{n}} + \mathcal{O}\bigg (\frac{(\ln n)^{4}}{n}\bigg )\bigg ), \end{aligned}$$

where $F_{1} = \int _{|z|\le \rho } \mu _{\textrm{reg}}^{\textrm{ML}}(d^{2}z) \sum _{j=1}^{m}u_{j} = b \rho ^{2b} \sum _{j=1}^{m}u_{j}$ and

$$\begin{aligned} F_{2} = \sqrt{2} \, b \rho ^{b} \int _{-\infty }^{+\infty } \Big ( \ln {\mathcal {H}}^{\textrm{ML}}_{\textrm{sh}}(x; \vec {{\mathfrak {s}}},\vec {u})-\chi _{(-\infty ,0)}(x) \sum _{j=1}^{m}u_{j} \Big )dx, \end{aligned}$$

with

$$\begin{aligned} {\mathcal {H}}^{\textrm{ML}}_{\textrm{sh}}(x; \vec {{\mathfrak {s}}},\vec {u}) = 1+\sum _{\ell =1}^{m} (e^{u_{\ell }}-1)\exp \bigg [ \sum _{j=\ell +1}^{m}u_{j} \bigg ] \frac{\textrm{erfc}(x-{\mathfrak {s}}_{\ell })}{\textrm{erfc}(x)}. \end{aligned}$$

The function ${\mathcal {H}}^{\textrm{ML}}_{\textrm{sh}}$ is also in the form (1.19), with $X_{\ell }(x) = \frac{{\textrm{erfc}}(x-{\mathfrak {s}}_{\ell })}{{\textrm{erfc}}(x)}$. The above discussion is summarized in Table 1.

Table 1 Comparison of our main result with results from [3, 8]

2 Preliminaries

Let ${\mathcal {E}}_{n}:= {\mathbb {E}}\big [ \prod _{\ell =1}^{m} e^{u_{\ell }\textrm{N}(r_{\ell })} \big ]$, and define

$$\begin{aligned} w(z) = (1-|z|^{2})^{\alpha -1}\omega (|z|), \qquad \omega (x) := \prod _{\ell =1}^{m}{\left\{ \begin{array}{ll} e^{u_{\ell }}, &{} \text{ if } x<r_{\ell }, \\ 1, &{} \text{ if } x \ge r_{\ell }. \end{array}\right. } \end{aligned}$$

(2.1)

By rewriting $\prod _{1 \le j < k \le n} |z_{k} -z_{j}|^{2}$ as the product of two Vandermonde determinants, and then using standard algebraic manipulations, we get

$$\begin{aligned} {\mathcal {E}}_{n}&= \frac{1}{n!Z_{n}} \int _{{\mathbb {D}}}\dots \int _{{\mathbb {D}}} \prod _{1 \le j < k \le n} |z_{k} -z_{j}|^{2} \prod _{j=1}^{n} w(z_{j}) d^{2}z_{j} \nonumber \\&= \frac{1}{Z_{n}} \det \left( \int _{{\mathbb {D}}} z^{j} {\overline{z}}^{k} w(z) d^{2}z \right) _{j,k=0}^{n-1}. \end{aligned}$$

(2.2)

Since w is rotation-invariant, only the diagonal elements in (2.2) are non-zero. Indeed, after writing $z=xe^{i\theta }$, $x\ge 0, \theta \in [0,2\pi )$ and integrating over $\theta$, we find

$$\begin{aligned} {\mathcal {E}}_{n} = \frac{1}{Z_{n}}(2\pi )^{n}\prod _{j=1}^{n}\int _{0}^{1}{x}^{2j-1}w({x})d{x}. \end{aligned}$$

(2.3)

In the same way, we have $Z_{n}=(2\pi )^{n}\prod _{j=1}^{n}\int _{0}^{1}x^{2j-1}(1-x^{2})^{\alpha -1}dx$ (see also (2.14) below). Substituting this identity and (2.1) in (2.3), we then find

$$\begin{aligned} {\mathcal {E}}_{n}&= \prod _{j=1}^{n} \frac{\int _{0}^{1} x^{2j-1} (1-x^{2})^{\alpha -1} \omega (x) dx}{\int _{0}^{1} x^{2j-1} (1-x^{2})^{\alpha -1} dx}. \end{aligned}$$

(2.4)

It will be convenient for us to rewrite $\omega$ (defined in (2.1)) as follows:

$$\begin{aligned} \omega (x) = {1+} \sum _{\ell =1}^{{m}}\omega _{\ell } {\textbf{1}}_{[0,r_{\ell })}(x), \qquad \omega _{\ell } = {\left\{ \begin{array}{ll} e^{u_{\ell }+\dots +u_{m}}-e^{u_{\ell +1}+\dots +u_{m}}, &{} \text{ if } \ell < m, \\ e^{u_{m}}-1, &{} \text{ if } {\ell =m.} \end{array}\right. } \end{aligned}$$

(2.5)

Using (2.5) in (2.4) yields the following expression for $\ln {\mathcal {E}}_n$:

$$\begin{aligned} \ln {\mathcal {E}}_{n}&= \sum _{j=1}^{n} \ln \bigg (1 +\sum _{\ell =1}^{m} \omega _{\ell } F_{n,j,\ell } \bigg ), \end{aligned}$$

(2.6)

$$\begin{aligned} F_{n,j,\ell }&:= \frac{\int _{0}^{r_{\ell }} x^{2j-1} (1-x^{2})^{\alpha -1} dx}{\int _{0}^{1} x^{2j-1} (1-x^{2})^{\alpha -1} dx} = \frac{\textrm{B}(r_{\ell }^{2},j,\alpha )}{\textrm{B}(j,\alpha )}, \qquad j=1,\ldots ,n, \;\; \ell =1,\dots ,m, \end{aligned}$$

(2.7)

where $\textrm{B}(j,\alpha )$ is the Beta function

$$\begin{aligned} \textrm{B}(j,\alpha ) := \int _{0}^{1} y^{j-1}(1-y)^{\alpha -1}dy = \frac{\Gamma (j)\Gamma (\alpha )}{\Gamma (j+\alpha )}, \end{aligned}$$

(2.8)

and $\textrm{B}(v,j,\alpha )$ is the incomplete Beta function

$$\begin{aligned} \textrm{B}(v,j,\alpha ) := \int _{0}^{v} y^{j-1}(1-y)^{\alpha -1}dy. \end{aligned}$$

(2.9)

Many properties of these functions are stated e.g. in [15, Sections 5.12 and 8.17]. It is also convenient for us to consider the normalized incomplete Beta function, which is given by

$$\begin{aligned} I(v,j,\alpha ) := \frac{\textrm{B}(v,j,\alpha )}{\textrm{B}(j,\alpha )}, \end{aligned}$$

(2.10)

so that $F_{n,j,\ell } = I(r_{\ell }^{2},j,\alpha )$.

Hence, to analyze the right-hand side of (2.6), we need the asymptotics of $I(v,j,\alpha )$ when $(v - 1)\asymp n^{-1}$ and simultaneously $j\in \{1,\ldots ,n\}$ and $\alpha$ fixed. The large n behavior of $I(r_{\ell }^{2},j,\alpha )$ depends crucially on whether j remains bounded or not as $n\rightarrow + \infty$. We will therefore split the sum (2.6) in two parts as follows

$$\begin{aligned} \ln {\mathcal {E}}_{n}&= S_{0} + S_{1}, \qquad \text{ where } \quad S_{0} = \sum _{j=1}^{\frac{n}{M}-1} \ln \bigg (1 +\sum _{\ell =1}^{m} \omega _{\ell } F_{n,j,\ell } \bigg ), \qquad \\ S_{1}&= \sum _{j=\frac{n}{M}}^{n} \ln \bigg ( 1 + \sum _{\ell =1}^{m} \omega _{\ell } F_{n,j,\ell } \bigg ), \end{aligned}$$

and $M:=n (\lceil \frac{n}{n^{\frac{2}{2+\alpha }}} \rceil )^{-1} \asymp n^{\frac{2}{2+\alpha }}$ is a new parameter such that ${\mathbb {N}}\ni n/M \rightarrow + \infty$ as $n\rightarrow + \infty$. (A more naive choice for M would be $M = n/M'$ where $M'$ is large but fixed, but this choice does not yield a good control over certain error terms in the proof. The precise reason as to why we choose $M\asymp n^{\frac{2}{2+\alpha }}$ is technical and will become apparent at the end of Sect. 3.)

The following lemma establishes an exact identity that will be useful to handle the sum $S_{0}$, i.e. to obtain the large n asymptotics of $F_{n,j,\ell }$ when j is “not very large”.

Lemma 2.1

Let $j\in {\mathbb {N}}_{>0}$, $\alpha >0$ and $v\in [0,1]$. Then we have the exact identity

$$\begin{aligned} I(v,j,\alpha ) = 1 - \frac{(1-v)^{\alpha }}{\textrm{B}(j,\alpha )} \sum _{p=0}^{j-1} (-1)^{p} \left( {\begin{array}{c}j-1\\ p\end{array}}\right) \frac{(1-v)^{p}}{\alpha +p}. \end{aligned}$$

Proof

The statement follows from [15, eqs 8.17.4 and 8.17.7]. We also provide a short proof here for convenience. Substituting $x^{j-1} = \sum _{p=0}^{j-1} (-1)^{p}\left( {\begin{array}{c}j-1\\ p\end{array}}\right) (1-x)^{p}$ in (2.10) yields

$$\begin{aligned} I(v,j,\alpha )&= \frac{1}{\textrm{B}(j,\alpha )}\sum _{p=0}^{j-1} (-1)^{p} \left( {\begin{array}{c}j-1\\ p\end{array}}\right) \int _{0}^{v}(1-x)^{\alpha +p-1}dx \\&= \frac{1}{\textrm{B}(j,\alpha )} \left( \sum _{p=0}^{j-1} \left( {\begin{array}{c}j-1\\ p\end{array}}\right) \frac{(-1)^{p}}{\alpha +p} - (1-v)^{\alpha } \sum _{p=0}^{j-1} (-1)^{p} \left( {\begin{array}{c}j-1\\ p\end{array}}\right) \frac{(1-v)^{p}}{\alpha +p} \right) . \end{aligned}$$

Replacing v by 1 above yields $1=\frac{1}{\textrm{B}(j,\alpha )} \sum _{p=0}^{j-1} \left( {\begin{array}{c}j-1\\ p\end{array}}\right) \frac{(-1)^{p}}{\alpha +p}$, and the claim follows. $\square$

To analyze $S_{1}$, we will use the uniform asymptotics of the incomplete Beta function (this is the main novelty of the proof, as earlier works such as [3, 8] on the Mittag-Leffler ensemble rely instead on the uniform asymptotics of the incomplete gamma function). The following lemma is due to Temme [18, Section 11.3.3.1] (this result can also be found in e.g. [15, Section 8.18(ii)]).

Lemma 2.2

(Temme [18]) Let $N\in {\mathbb {N}}_{>0}$. As $j\rightarrow +\infty$ with $\alpha >0$ fixed,

$$\begin{aligned} I(v,j,\alpha ) = \frac{\Gamma (j+\alpha )}{\Gamma (j)}d_{0} F_{0} \bigg ( 1 + \sum _{k=1}^{N-1} \frac{d_{k}F_{k}}{d_{0}F_{0}} + \mathcal{O}(j^{-N}) \bigg ) \end{aligned}$$

uniformly for v in compact subsets of (0, 1]. The coefficients $F_{k}=F_{k}(v,j,\alpha )$ are defined by

$$\begin{aligned} F_{k} = \frac{k-1+\alpha -j \ln (v^{-1})}{j}F_{k-1} + \frac{(k-1)\ln (v^{-1})}{j}F_{k-2}, \qquad k\ge 2, \end{aligned}$$

(2.11)

with the initial assignments

$$\begin{aligned} F_{0} = j^{-\alpha }\textrm{Q}(\alpha ,j \ln (v^{-1})), \qquad F_{1} = \frac{\alpha -j \ln (v^{-1})}{j}F_{0} + \frac{(\ln (v^{-1}))^{\alpha }v^{j}}{j \Gamma (\alpha )}, \end{aligned}$$

(2.12)

where $\textrm{Q}$ is defined in (1.7) and the coefficients $d_{k}=d_{k}(v,\alpha )$ are defined through the generating function

$$\begin{aligned} \bigg ( \frac{1-e^{-t}}{t} \bigg )^{\alpha -1} = \sum _{k=0}^{\infty } d_{k}(t-\ln (v^{-1}))^{k}. \end{aligned}$$

(2.13)

In particular,

$$\begin{aligned} d_{0} = \bigg ( \frac{1-v}{\ln (v^{-1})} \bigg )^{\alpha -1}, \qquad d_{1} = \frac{(\alpha -1)(v-1+v\ln (v^{-1}))}{(v-1)^{2}} \bigg ( \frac{1-v}{\ln (v^{-1})} \bigg )^{\alpha }. \end{aligned}$$

Remark 2.3

(Determinants with circular root-type singularities) Note from (2.2) that ${\mathcal {E}}_{n}$ can be seen as a ratio of two determinants. The determinant on the numerator involves w, and this weight has a root-type singularity along the unit circle (i.e. along the hard edge). Other determinants with circular root-type singularities have been considered in [4]; however, the singularities in [4] lie in the bulk, and the asymptotics of the corresponding determinants involve the so-called associated Hermite polynomials (this contrasts drastically with the asymptotics of ${\mathcal {E}}_{n}$, which are given in Theorem 1.2).

Remark 2.4

(Partition function) Asymptotic expansions of partition functions of two-dimensional point processes are a classical topic of interest, see e.g. [5, Section 5.3]. For rotation-invariant (and determinantal) ensembles with soft edges, precise formulas up to and including the term of order 1 have been obtained in the recent work [6]. The class of ensembles considered in [6] includes (1.1) when $\alpha$ is proportional to n, see [6, Section 4.2]. As mentioned earlier, for $\alpha$ fixed, the ensemble (1.1) has a hard edge and is therefore not considered in [6]. As a minor aside, we compute here the partition function of (1.1) with $\alpha$ fixed using a similar formula as (2.3). As in (2.3) (but with w(u) replaced by $(1-|u|^{2})^{\alpha -1}$), we get

$$\begin{aligned} Z_{n}&= (2\pi )^{n}\prod _{j=0}^{n-1}\int _{0}^{1}u^{2j+1}(1-u^{2})^{\alpha -1}du = \pi ^{n} \prod _{j=1}^{n} \textrm{B}(j,\alpha ) \nonumber \\&= \pi ^{n}\Gamma (\alpha )^{n} \frac{G(n+1)G(1+\alpha )}{G(n+1+\alpha )}, \end{aligned}$$

(2.14)

where for the last identity we have used the functional equation for the Barnes G-function to write

$$\begin{aligned} \prod _{j=1}^{n} \Gamma (j+\alpha ) = \frac{G(n+\alpha +1)}{G(1+\alpha )}. \end{aligned}$$

(2.15)

Using the expansions (see [15, Eqs. 5.17.5 and 5.11.8])

$$\begin{aligned} \ln G(z+1)&= \frac{z^{2}}{4}+z \ln \Gamma (z+1)-\bigg ( \frac{z(z+1)}{2}+\frac{1}{12} \bigg )\ln z + \zeta '(-1)-\frac{1}{12} + \mathcal{O}(z^{-2}), \nonumber \\ \ln \Gamma (z+h)&= (z+h-\tfrac{1}{2})\ln z - z + \tfrac{1}{2} \ln (2\pi ) + \frac{1-6h+6h^{2}}{12z} + \mathcal{O}(z^{-2}), \end{aligned}$$

(2.16)

as $z\rightarrow +\infty$ for any fixed $h\in {\mathbb {C}}$, we then get

$$\begin{aligned} Z_{n}&= \exp \bigg ( \hspace{-0.1cm} -\alpha \, n \ln n + \big ( \alpha + \ln (\pi \Gamma (\alpha )\big )n - \frac{\alpha ^{2}}{2}\ln n \\&\quad + \ln G(1+\alpha ) - \frac{\alpha }{2} \ln (2\pi ) + \mathcal{O}(n^{-1}) \bigg ), \quad \text{ as } n \rightarrow + \infty . \end{aligned}$$

3 Proof of Theorem 1.2

As mentioned in Sect. 2, it is convenient to split the sum (2.6) into two parts:

$$\begin{aligned} \ln {\mathcal {E}}_{n} = S_{0} + S_{1}, \end{aligned}$$

(3.1)

where

$$\begin{aligned}&S_{0} = \sum _{j=1}^{\frac{n}{M}-1} \ln \bigg (1 +\sum _{\ell =1}^{m} \omega _{\ell } F_{n,j,\ell } \bigg ),{} & {} S_{1} = \sum _{j=\frac{n}{M}}^{n} \ln \bigg ( 1 + \sum _{\ell =1}^{m} \omega _{\ell } F_{n,j,\ell } \bigg ), \end{aligned}$$

(3.2)

and $M:=n (\lceil \frac{n}{n^{\frac{2}{2+\alpha }}} \rceil )^{-1} \asymp n^{\frac{2}{2+\alpha }}$. Define also $\Omega := e^{u_{1}+\dots +u_{m}}$. We first obtain the large n asymptotics of $S_{0}$ using Lemma 2.1. Let ${\textsf {T}}_{0}:= \sum _{\ell =1}^{m} \omega _{\ell }t_{\ell }^{\alpha }$.

Lemma 3.1

Let $x_{1},\dots ,x_{m} \in {\mathbb {R}}$ be fixed. There exists $\delta > 0$ such that

$$\begin{aligned} S_{0}&= \Big (\frac{n}{M}-1\Big ) \ln \Omega - \frac{{{\textsf {T} }_{0}}}{\Omega \, \Gamma (2+\alpha )} \frac{n}{M^{1+\alpha }} - \frac{{{\textsf {T} }_{0}}}{\Omega \, \Gamma (1+\alpha )} \frac{\alpha -2}{2}\frac{1}{M^{\alpha }} \\&\quad + \mathcal{O}\bigg ( \frac{n}{M^{2+\alpha }} + \frac{n}{M^{1+2\alpha }} + \frac{M}{n \, M^{\alpha }} \bigg ), \end{aligned}$$

as $n\rightarrow + \infty$, uniformly for $u_{1} \in \{z \in {\mathbb {C}}: |z-x_{1}|\le \delta \},\dots ,u_{m} \in \{z \in {\mathbb {C}}: |z-x_{m}|\le \delta \}$.

Proof

Let $K:=n/M-1$. Recalling that $F_{n,j,\ell } = I(r_{\ell }^{2},j,\alpha )$ and $r_{\ell } = (1-\frac{t_{\ell }}{n})^{1/2}$, and using Lemma 2.1, we infer that

$$\begin{aligned} F_{n,j,\ell } = 1 - \frac{t_{\ell }^{\alpha }}{n^{\alpha }\textrm{B}(j,\alpha )} \sum _{p=0}^{j-1} (-1)^{p} \left( {\begin{array}{c}j-1\\ p\end{array}}\right) \frac{t_{\ell }^{p}}{(\alpha +p)n^{p}} = 1-\frac{t_{\ell }^{\alpha }}{\alpha \, n^{\alpha }\textrm{B}(j,\alpha )}+\mathcal{O}\bigg (\frac{n^{-\alpha -1}j}{\textrm{B}(j,\alpha )}\bigg ), \end{aligned}$$

(3.3)

as $n \rightarrow + \infty$ uniformly for $j \in \{1,\dots ,K\}$ and $\ell \in \{1,\dots ,m\}$. Using (2.16), we infer that $\textrm{B}(j,\alpha ) = \mathcal{O}(j^{-\alpha })$ as $j\rightarrow +\infty$ with $\alpha$ fixed, so that the error term in (3.3) can be replaced by $\mathcal{O}((j/n)^{\alpha +1})$. Hence, since $1+\sum _{\ell =1}^{m} \omega _{\ell } = e^{u_{1}+\dots +u_{m}} = \Omega$,

$$\begin{aligned} S_{0}&= \sum _{j=1}^{K} \ln \bigg ( 1 + \sum _{\ell =1}^{m} \omega _{\ell } \bigg [1 - \frac{t_{\ell }^{\alpha }}{\alpha \, n^{\alpha }\textrm{B}(j,\alpha )} + \mathcal{O}\bigg (\hspace{-0.05cm}\Big (\frac{j}{n}\Big )^{1+\alpha }\hspace{-0.05cm}\bigg ) \bigg ] \bigg )\\&= \sum _{j=1}^{K} \ln \bigg ( \Omega - \frac{{{\textsf {T} }_{0}}}{\alpha \, n^{\alpha }\textrm{B}(j,\alpha )} + \mathcal{O}\bigg (\hspace{-0.05cm}\Big (\frac{j}{n}\Big )^{1+\alpha } \hspace{-0.05cm} \bigg ) \hspace{-0.05cm} \bigg ). \end{aligned}$$

The $\mathcal{O}$-term after the first equality is clearly independent of $u_{1},\dots ,u_{m}$, and therefore the $\mathcal{O}$-term after the second equality is uniform for $u_{1} \in \{z \in {\mathbb {C}}: |z-x_{1}|\le \delta \},\dots ,u_{m} \in \{z \in {\mathbb {C}}: |z-x_{m}|\le \delta \}$, for any fixed $\delta >0$. We can (and do) choose $\delta >0$ sufficiently small such that $\Omega$ remains bounded away from $(-\infty ,0]$ for $u_{1} \in \{z \in {\mathbb {C}}: |z-x_{1}|\le \delta \},\dots ,u_{m} \in \{z \in {\mathbb {C}}: |z-x_{m}|\le \delta \}$, so that

$$\begin{aligned} S_{0}&= \sum _{j=1}^{K} \bigg ( \ln \Omega - \frac{{{\textsf {T} }_{0}}}{\alpha \, \Omega \, \textrm{B}(j,\alpha ) \; n^{\alpha }} + \mathcal{O}\bigg ( \Big (\frac{j}{n}\Big )^{1+\alpha } + \Big (\frac{j}{n}\Big )^{2\alpha } \bigg ) \bigg ). \end{aligned}$$

Furthermore,

$$\begin{aligned} \sum _{j=1}^{K} \bigg ( \Big (\frac{j}{n}\Big )^{1+\alpha } + \Big (\frac{j}{n}\Big )^{2\alpha } \bigg ) = \mathcal{O}\bigg ( K\Big (\frac{K}{n}\Big )^{1+\alpha } + K\Big (\frac{K}{n}\Big )^{2\alpha } \bigg ), \qquad \text{ as } n \rightarrow + \infty . \end{aligned}$$

The above $\mathcal{O}$-term can also be written as $\mathcal{O}(\frac{n}{M^{2+\alpha }} + \frac{n}{M^{1+2\alpha }})$, and thus

$$\begin{aligned} S_{0} = \Big (\frac{n}{M}-1\Big ) \ln \Omega - \frac{{{\textsf {T} }_{0}}}{\alpha \, \Omega \; n^{\alpha }} \sum _{j=1}^{K}\frac{1}{\textrm{B}(j,\alpha )} + \mathcal{O}\bigg ( \frac{n}{M^{2+\alpha }} + \frac{n}{M^{1+2\alpha }} \bigg ), \qquad \text{ as } n \rightarrow + \infty . \end{aligned}$$

(3.4)

By (2.8) and the functional relation $\Gamma (z+1)=z\Gamma (z)$,

$$\begin{aligned} \sum _{j=1}^{K}\frac{1}{\textrm{B}(j,\alpha )} = \sum _{j=1}^{K}\frac{\Gamma (j+\alpha )}{\Gamma (j)\Gamma (\alpha )} {= \alpha \sum _{j=1}^{K} \left( {\begin{array}{c}j+\alpha -1\\ j-1\end{array}}\right) .} \end{aligned}$$

(3.5)

We now use the so-called “parallel summation formula” $\sum _{j=0}^{K-1}\left( {\begin{array}{c}j+\alpha \\ j\end{array}}\right) = \left( {\begin{array}{c}K+\alpha \\ K-1\end{array}}\right)$ to find

$$\begin{aligned} \sum _{j=1}^{K}\frac{1}{\textrm{B}(j,\alpha )} = \frac{K \, \Gamma (1+K+\alpha )}{\Gamma (1+K)\Gamma (\alpha )} \frac{1}{1+\alpha }. \end{aligned}$$

This formula can easily be expanded as $K=\frac{n}{M}-1\rightarrow +\infty$ using (2.16):

$$\begin{aligned} \frac{1}{n^{\alpha }}\sum _{j=1}^{K}\frac{1}{\textrm{B}(j,\alpha )} = \frac{1}{M^{\alpha }}\frac{1}{(1+\alpha )\Gamma (\alpha )} \bigg \{ \frac{n}{M} + \frac{(1+\alpha )(\alpha -2)}{2} + \mathcal{O}\Big ( \frac{M}{n} \Big ) \bigg \}. \end{aligned}$$

(3.6)

Substituting (3.6) in (3.4) yields the claim. $\square$

We now turn to the analysis of $S_{1}$. We will rely on Lemma 2.2, as well as on the following Riemann sum approximation lemma (whose proof is omitted).

Lemma 3.2

Let $A=A(n)$, $B=B(n)$ be bounded functions of $n \in \{1,2,\dots \}$, such that

$$\begin{aligned}&a_{n} := An \qquad \text{ and } \qquad b_{n} := Bn \end{aligned}$$

are integers. Assume also that $B-A$ is positive and remains bounded away from 0 as $n\rightarrow + \infty$. Let f be a function independent of n, which is $C^{2}([A,B])$ for all $n\in \{1,2,\dots \}$. Then as $n \rightarrow + \infty$, we have

$$\begin{aligned} \sum _{j=a_{n}}^{b_{n}}f(\tfrac{j}{n}) = n \int _{A}^{B}f(x)dx + \frac{f(A)+f(B)}{2} + \mathcal{O}\bigg ( \frac{f'(A)+f'(B)}{n} + \sum _{j=a_{n}}^{b_{n}-1} \frac{{\mathfrak {m}}_{j,n}(f'')}{n^{2}} \bigg ), \end{aligned}$$

(3.7)

where, for a given function g continuous on [A, B] and $j \in \{a_{n},\dots ,b_{n}-1\}$, ${\mathfrak {m}}_{j,n}(g):= \max _{x \in [\frac{j}{n},\frac{j+1}{n}]}|g(x)|$.

Lemma 3.3

For any fixed $x_{1},\dots ,x_{m} \in {\mathbb {R}}$, there exists $\delta > 0$ such that

$$\begin{aligned} S_{1}&= n \bigg \{ \int _{0}^{1}f_{0}(x)dx - \frac{1}{M} \ln \Omega + \frac{{\textsf {T} }_{0}}{\Omega \, \Gamma (\alpha + 2)} \frac{1}{M^{\alpha +1}} \bigg \} + \int _{0}^{1} f_{1}(x)dx + \frac{f_{0}(1) + \ln \Omega }{2} \\&\quad - \frac{(2-\alpha ){\textsf {T} }_{0}}{2\Omega \, \Gamma (\alpha +1)} \frac{1}{M^{\alpha }} + \mathcal{O}\bigg ( \frac{n}{M^{1+2\alpha }}+\frac{n}{M^{2+\alpha }} + \frac{1+M^{1-\alpha }{+ {\textbf{1}}_{\alpha =1} \ln M}}{n} \bigg ), \end{aligned}$$

as $n \rightarrow +\infty$ uniformly for $u_{1} \in \{z \in {\mathbb {C}}: |z-x_{1}|\le \delta \},\dots ,u_{m} \in \{z \in {\mathbb {C}}: |z-x_{m}|\le \delta \}$, where ${\textbf{1}}_{\alpha =1}=1$ if $\alpha =1$ and ${\textbf{1}}_{\alpha =1}=0$ otherwise, and

$$\begin{aligned} f_{0}(x)&:= \ln (1+\Sigma _{0}(x)),{} & {} f_{1}(x) := \frac{\Sigma _{1}(x)}{1+\Sigma _{0}(x)}, \end{aligned}$$

(3.8)

$$\begin{aligned} \Sigma _{0}(x)&:= \sum _{\ell =1}^{m} \omega _{\ell } \textrm{Q}(\alpha ,t_{\ell } x),{} & {} \Sigma _{1}(x) := \frac{x^{\alpha }}{x} \sum _{\ell =1}^{m} \omega _{\ell } \frac{e^{-t_{\ell }x}t_{\ell }^{\alpha }}{\Gamma (\alpha )} \frac{1-\alpha -t_{\ell }x}{2}. \end{aligned}$$

(3.9)

Proof

By Lemma 2.2, since $n/M\rightarrow +\infty$, we have

$$\begin{aligned} F_{n,j,\ell } = \frac{\Gamma (j+\alpha )}{\Gamma (j)}d_{0}(r_{\ell }^{2},\alpha )F_{0}(r_{\ell }^{2},j,\alpha ) \bigg ( 1 + \sum _{k=1}^{3} \frac{d_{k}(r_{\ell }^{2},\alpha )F_{k}(r_{\ell }^{2},j,\alpha )}{d_{0}(r_{\ell }^{2},\alpha )F_{0}(r_{\ell }^{2},j,\alpha )} + \mathcal{O}(j^{-4}) \bigg ) \end{aligned}$$

as $n\rightarrow + \infty$ uniformly for $\ell \in \{1,\ldots ,m\}$ and $j \in \{\frac{n}{M},\ldots ,n\}$. Moreover, using (2.11), (2.12), (2.13) and (2.16), we get

$$\begin{aligned} F_{n,j,\ell } = \textrm{Q}(\alpha , t_{\ell } j/n) + \frac{(j/n)^{\alpha }}{j} \frac{e^{-t_{\ell }j/n}t_{\ell }^{\alpha }}{\Gamma (\alpha )} \frac{1-\alpha - t_{\ell }j/n}{2} + \mathcal{O}\Big (\frac{1}{n^{2}}\frac{(j/n)^{\alpha }}{(j/n)^{2}}\Big ), \qquad \text{ as } n \rightarrow + \infty , \end{aligned}$$

uniformly for $\ell \in \{1,\ldots ,m\}$ and $j \in \{\frac{n}{M},\ldots ,n\}$. Hence, for small enough $\delta >0$,

$$\begin{aligned} \ln \bigg ( 1+\sum _{\ell =1}^{m} \omega _{\ell } F_{n,j,\ell } \bigg ) = f_{0}(j/n) + \frac{f_{1}(j/n)}{n} + \mathcal{O}\Big (\frac{1}{n^{2}}\frac{(j/n)^{\alpha }}{(j/n)^{2}}\Big ), \qquad \text{ as } n \rightarrow + \infty , \end{aligned}$$

(3.10)

uniformly for $j \in \{\frac{n}{M},\ldots ,n\}$ and $u_{1} \in \{z \in {\mathbb {C}}: |z-x_{1}|\le \delta \},\dots ,u_{m} \in \{z \in {\mathbb {C}}: |z-x_{m}|\le \delta \}$. Note that

$$\begin{aligned} \frac{1}{n^{2}} \sum _{j=\frac{n}{M}}^{n} \frac{(j/n)^{\alpha }}{(j/n)^{2}} = \mathcal{O}\bigg ( \frac{1+M^{1-\alpha } {+ {\textbf{1}}_{\alpha =1} \ln M}}{n} \bigg ). \end{aligned}$$

Furthermore, by Lemma 3.2 with $A=\frac{1}{M}$, $B=1$,

$$\begin{aligned} \sum _{j=\frac{n}{M}}^{n} f_{0}(j/n)&= n \int _{M^{-1}}^{1}f_{0}(x)dx + \frac{f_{0}(M^{-1})+f_{0}(1)}{2} + \mathcal{O}\bigg ( \frac{M^{1-\alpha }+1}{n} \bigg ), \end{aligned}$$

(3.11)

$$\begin{aligned} \frac{1}{n} \sum _{j=\frac{n}{M}}^{n} f_{1}(j/n)&= \int _{M^{-1}}^{1}f_{1}(x)dx + \mathcal{O}\bigg ( \frac{M^{1-\alpha }+1}{n} \bigg ), \end{aligned}$$

(3.12)

where, to estimate the $\mathcal{O}$-terms, we have used $n^{-1}f_{0}'(A) \lesssim n^{-1}A^{\alpha -1} = \mathcal{O}(\frac{M^{1-\alpha }}{n})$, $n^{-1}f_{0}'(B)=\mathcal{O}(n^{-1})$, $n^{-1}f_{1}(A) \lesssim n^{-1}A^{\alpha -1} = \mathcal{O}(\frac{M^{1-\alpha }}{n})$, and $n^{-1}f_{1}(B)=\mathcal{O}(n^{-1})$. Also, using (3.8)–(3.9), as $n\rightarrow \infty$ we get

$$\begin{aligned} n \int _{M^{-1}}^{1}f_{0}(x)dx&= n \int _{0}^{1}f_{0}(x)dx - \frac{n}{M} \ln \Omega + \frac{{\textsf {T} }_{0}}{\Omega \, \Gamma (\alpha +2)}\frac{n}{M^{1+\alpha }} + \mathcal{O}\Big ( \frac{n}{M^{1+2\alpha }}+\frac{n}{M^{2+\alpha }} \Big ), \\ f_{0}(M^{-1})&= \ln \Omega - \frac{{\textsf {T} }_{0}}{\Omega \, \Gamma (\alpha +1)}\frac{1}{M^{\alpha }} + \mathcal{O}\Big ( \frac{1}{M^{1+\alpha }}+\frac{1}{M^{2\alpha }} \Big ), \\ \int _{M^{-1}}^{1}f_{1}(x)dx&= \int _{0}^{1}f_{1}(x)dx - \frac{{\textsf {T} }_{0}(1-\alpha )}{2\Omega \, \Gamma (\alpha +1)} \frac{1}{M^{\alpha }} + \mathcal{O}\Big ( \frac{1}{M^{1+\alpha }}+\frac{1}{M^{2\alpha }} \Big ). \end{aligned}$$

Substituting the above in (3.11)–(3.12) and then in (3.10) yields

$$\begin{aligned} S_{1}&= \sum _{j=\frac{n}{M}}^{n} f_{0}(j/n) + \sum _{j=\frac{n}{M}}^{n} \frac{f_{1}(j/n)}{n} + \mathcal{O}\bigg ( \frac{1+M^{1-\alpha }{+ {\textbf{1}}_{\alpha =1} \ln M}}{n} \bigg ) \\&= n \bigg \{ \int _{0}^{1}f_{0}(x)dx - \frac{1}{M} \ln \Omega + \frac{{\textsf {T} }_{0}}{\Omega \, \Gamma (\alpha + 2)} \frac{1}{M^{\alpha +1}} \bigg \} + \int _{0}^{1} f_{1}(x)dx + \frac{f_{0}(1) + \ln \Omega }{2} \\&\quad - \frac{(2-\alpha ){\textsf {T} }_{0}}{2\Omega \, \Gamma (\alpha +1)} \frac{1}{M^{\alpha }} + \mathcal{O}\bigg ( \frac{n}{M^{1+2\alpha }}+\frac{n}{M^{2+\alpha }} + \frac{1+M^{1-\alpha }{+ {\textbf{1}}_{\alpha =1} \ln M}}{n} \bigg ) \end{aligned}$$

$\square$

Proof of Theorem 1.2

Combining Lemmas 3.1 and 3.3 yields

$$\begin{aligned} \ln {\mathcal {E}}_{n}&= n \int _{0}^{1}f_{0}(x)dx + \int _{0}^{1}f_{1}(x)dx + \frac{f_{0}(1) - \ln \Omega }{2} \\&\quad + \mathcal{O}\bigg ( \frac{n}{M^{1+2\alpha }}+\frac{n}{M^{2+\alpha }} + \frac{1+M^{1-\alpha }{+ {\textbf{1}}_{\alpha =1} \ln M}}{n} \bigg ). \end{aligned}$$

The above $\mathcal{O}$-term can be rewritten as

$$\begin{aligned} \mathcal{O}\bigg ( \frac{n}{M^{1+\alpha +{\hat{\alpha }}}} + \frac{M^{1-{\hat{\alpha }}}{+ {\textbf{1}}_{\alpha =1} \ln M}}{n} \bigg ), \end{aligned}$$

where ${\hat{\alpha }} = \min \{\alpha ,1\}$. Since $M \asymp n^{\frac{2}{2+\alpha }}$, we have

$$\begin{aligned} \frac{n}{M^{1+\alpha +{\hat{\alpha }}}} \asymp \frac{M^{1-{\hat{\alpha }}}}{n} \asymp n^{-\frac{2{\hat{\alpha }}+\alpha }{2+\alpha }}, \end{aligned}$$

which finishes the proof of Theorem 1.2. $\square$