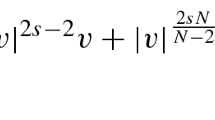Abstract
We study the existence of different types of positive solutions to problem
where \({\lambda_1, \lambda_2 \in (0, \Lambda_N)}\) , \({\Lambda_N := \frac{(N-2)^2}{4}}\) , and \({2* = \frac{2N}{N-2}}\) is the critical Sobolev exponent. A careful analysis of the behavior of Palais-Smale sequences is performed to recover compactness for some ranges of energy levels and to prove the existence of ground state solutions and mountain pass critical points of the associated functional on the Nehari manifold. A variational perturbative method is also used to study the existence of a non trivial manifold of positive solutions which bifurcates from the manifold of solutions to the uncoupled system corresponding to the unperturbed problem obtained for ν = 0.
Similar content being viewed by others
References
Abdellaoui, B., Felli, V., Peral, I.: Existence and multiplicity for perturbations of an equation involving a Hardy inequality and the critical Sobolev exponent in the whole of \({\mathbb{R}^N}\) . Adv. Differ. Equat. 9(5–6), 481–508 (2004)
Akhmediev, N., Ankiewicz, A.: Partially coherent solitons on a finite background. Phys. Rev. Lett. 82, 2661–2664 (1999)
Ambrosetti, A., Badiale, M.: Variational perturbative methods and bifurcation of bound states from the essential spectrum. Proc. Roy. Soc. Edinburgh Sect. A 128(6), 1131–1161 (1998)
Ambrosetti, A., Badiale, M.: Homoclinics: Poincaré–Melnikov type results via a variational approach. Ann. Inst. H. Poincaré Anal. Non Linéaire 15(2), 233–252 (1998)
Ambrosetti, A., Rabinowitz, P.H.: Dual variational methods in critical point theory and applications. J. Funct. Anal. 14, 349–381 (1973)
Ambrosetti, A., Colorado, E.: Bound and ground states of coupled nonlinear Schrödinger equations. C. R. Math. Acad. Sci. Paris 342(7), 453–458 (2006)
Ambrosetti, A., Colorado, E., Ruiz, D.: Multi-bump solitons to linearly coupled systems of nonlinear Schrödinger equations. Calc. Var. Partial Differ.l Equat. 30(1), 85–112 (2007)
Ambrosetti, A., Malchiodi, A.: Perturbation methods and semilinear elliptic problems on \({\mathbb{R}^N}\) , Progress in Mathematics, 240. Birkhäuser Verlag, Basel (2006)
Ambrosetti, A., Garcia Azorero, J., Peral, I.: Elliptic variational problems in \({\mathbb{R}^N}\) with critical growth, Special issue in celebration of Jack K. Hale’s 70th birthday, Part 1 (Atlanta, GA/Lisbon, 1998). J. Differ. Equat. 168(1), 10–32 (2000)
Bidaut-Veron, M.F., Grillot, P.: Singularities in elliptic systems with absorption terms. Ann. Scuola Norm. Sup. Pisa Cl. Sci. (4) 28(4), 229–271 (1999)
De Figueiredo, D.G., Peral, I., Rossi, J.: The critical hyperbola for a hamiltonian elliptic system with weights. Annali di Matematica Pura ed Applicata online, doi:10.1007/s10231-007-0054-1
Felli, V., Pistoia, A.: Existence of blowing-up solutions for a nonlinear elliptic equation with Hardy potential and critical growth. Commun. Partial Differ. Equat. 31(1-3), 21–56 (2006)
Felli, V., Schneider, M.: Perturbation results of critical elliptic equations of Caffarelli-Kohn-Nirenberg type. J. Differ. Equat. 191, 121–142 (2003)
Felli, V., Schneider, M.: A note on regularity of solutions to degenerate elliptic equations of Caffarelli-Kohn-Nirenberg type. Adv. Nonlinear Stud. 3, 431–443 (2003)
Felli, V., Terracini, S.: Fountain-like solutions for nonlinear elliptic equations with critical growth and Hardy potential. Commun. Contemp. Math. 7(6), 867–904 (2005)
Kaminow, I.P.: Polarization in optical fibers. IEEE J. Quantum Electron. 17, 15–22 (1981)
Lions, P.L.: The concentration-compactness principle in the calculus of variations. The limit case, part 1. Rev. Matemática Iberoamericana 1(1), 145–201 (1985)
Lions, P.L.: The concentration-compactness principle in the calculus of variations. The limit case, part 2. Rev. Matemática Iberoamericana 1(2), 45–121 (1985)
Lin, T.-C., Wei, J.: Ground state of N coupled nonlinear Schrödinger equations in \({\mathbb{R}^N}\) , n ≤ 3. Commun. Math. Phys. 255(3), 629–653 (2005)
Maia, L.A., Montefusco, E., Pellacci, B.: Positive solutions for a weakly coupled nonlinear Schrödinger system. J. Differ. Equat. 229(2), 743–767 (2006)
Menyuk, C.R.: Nonlinear pulse propagation in birefringence optical fiber. IEEE J. Quantum Electron. 23, 174–176 (1987)
Menyuk, C.R.: Pulse propagation in an elliptically birefringent Kerr medium. IEEE J. Quantum Electron. 25, 2674–2682 (1989)
Montefusco, E., Pellacci, B., Squassina, M.: Semiclassical states for weakly coupled nonlinear Schrödinger system. J. E. M. S. 10(1), 47–71 (2008)
Pomponio, A.: Coupled nonlinear Schrödinger systems with potentials. J. Differ. Equat. 227(1), 258–281 (2006)
Sirakov, B.: Least Energy Solitary Waves for a System of Nonlinear Schrödinger Equations in \({\mathbb{R}^N}\) . Commun. Math. Phys. 271(1), 199–221 (2007)
Smets, D.: Nonlinear Schrödinger equations with Hardy potential and critical nonlinearities. Trans. AMS 357, 2909–2938 (2005)
Struwe, M.: A global compactness result for elliptic boundary value problems involving limiting nonlinearities. Math. Z. 187, 511–517 (1984)
Terracini, S.: On positive entire solutions to a class of equations with singular coefficient and critical exponent. Adv. Differ. Equat. 1(2), 241–264 (1996)
Author information
Authors and Affiliations
Corresponding author
Additional information
B. Abdellaoui and I. Peral supported by projects MTM2007-65018, MEC and CCG06-UAM/ESP-0340, Spain. V. Felli supported by Italy MIUR, national project Variational Methods and Nonlinear Differential Equations.
Rights and permissions
About this article
Cite this article
Abdellaoui, B., Felli, V. & Peral, I. Some remarks on systems of elliptic equations doubly critical in the whole \({\mathbb{R}^N}\) . Calc. Var. 34, 97–137 (2009). https://doi.org/10.1007/s00526-008-0177-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00526-008-0177-2
Keywords
- Systems of elliptic equations
- Compactness principles
- Critical Sobolev exponent
- Hardy potential
- Doubly critical problems
- Variational methods
- Perturbation methods