Hybrid differential evolution and Nelder–Mead algorithm with re-optimization

Abstract

Nonlinear optimization algorithms could be divided into local exploitation methods such as Nelder–Mead (NM) algorithm and global exploration ones, such as differential evolution (DE). The former searches fast yet could be easily trapped by local optimum, whereas the latter possesses better convergence quality. This paper proposes hybrid differential evolution and NM algorithm with re-optimization, called as DE-NMR. At first a modified NM, called NMR is presented. It re-optimizes from the optimum point at the first time and thus being able to jump out of local optimum, exhibits better properties than NM. Then, NMR is combined with DE. To deal with equal constraints, adaptive penalty function method is adopted in DE-NMR, which relaxes equal constraints into unequal constrained functions with an adaptive relaxation parameter that varies with iteration. Benchmark optimization problems as well as engineering design problems are used to experiment the performance of DE-NMR, with the number of function evaluation times being employed as the main index of measuring convergence speed, and objective function values as the main index of optimum’s quality. Non-parametric tests are employed in comparing results with other global optimization algorithms. Results illustrate the fast convergence speed of DE-NMR.

Appendix

• 1. Weld beam design problem

  

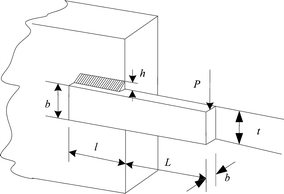  $$ \begin{aligned} {\text{Minimize}}\;& f\left( x \right) = 1.10471x_{1}^{2} x_{2} + 0.04811x_{3} x_{4} \left( {14 + x_{2} } \right) \\ {\text{subject}}\;to\;& g_{1} \left( x \right) = \tau \left( x \right) - 13,600 \le 0,\quad g_{2} \left( x \right) = \sigma \left( x \right) - 30,000 \le 0 \\ & g_{3} \left( x \right) = x_{1} - x_{4} \le 0,\quad g_{4} \left( x \right) = 0.1047x_{1}^{2} + 0.04811x_{3} x_{4} \left( {14.0 + x_{2} } \right) - 5.0 \le 0 \\ & g_{5} \left( x \right) = 0.125 - x_{1} \le 0,\quad g_{6} \left( x \right) = \delta \left( x \right) - 0.25 \le 0 \\ & g_{7} \left( x \right) = P - P_{c} \left( x \right) \le 0,\quad 0.1 \le x_{1} ,x_{4} \le 2 \\ & 0.1 \le x_{2} ,x_{3} \le 10 \\ \end{aligned} $$
  $$ \begin{gathered} \tau \left( x \right) = \sqrt {\left( {\tau^{\prime}} \right)^{2} + 2\tau^{\prime}\tau^{\prime\prime}{\frac{{x_{2} }}{{2{\text{R}}}}} + \left( {\tau^{\prime\prime}} \right)^{2} } ,\tau^{\prime} = {\frac{P}{{\sqrt 2 x_{1} x_{2} }}},\tau^{\prime\prime} = {\frac{QR}{J}},Q = P\left( {L + {\frac{{x_{2} }}{2}}} \right),R = \sqrt {{\frac{{x_{2}^{2} }}{4}} + \left( {{\frac{{x_{1} + x_{3} }}{2}}} \right)^{2} } \hfill \\ J = 2\left\{ {\sqrt 2 x_{1} x_{2} \left[ {{\frac{{x_{2}^{2} }}{12}} + \left( {{\frac{{x_{1} + x_{3} }}{2}}} \right)^{2} } \right]} \right\},\sigma \left( x \right) = {\frac{6PL}{{x_{4} x_{3}^{2} }}},\delta \left( x \right) = {\frac{{4PL^{3} }}{{Ex_{3}^{3} x_{4} }}},P_{c} \left( x \right) = {\frac{{4.013E\sqrt {x_{3}^{2} x_{4}^{6} } }}{{L^{2} }}}\left( {1 - {\frac{{x_{3} }}{2L}}\sqrt {{\frac{E}{4G}}} } \right) \hfill \\ P = 6,000,L = 14,E = 3 \times 10^{7} ,\quad G = 1.2 \times 10^{6} \hfill \\ \end{gathered} $$

• 2. Pressure vessel design problem

  

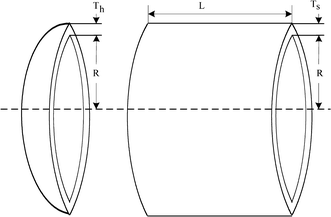  $$ \begin{aligned} \min \;f &= 0.6224x_{1} x_{3} x_{4} + 1.7781x_{2} x_{3}^{2} + 3.1661x_{1}^{2} x_{4} + 19.84x_{1}^{2} x_{3} \\ {\text{s.t.}}\quad & g_{1} \left( x \right) = - x_{1} + 0.193x_{3} \le 0 \\ & g_{2} \left( x \right) = - x_{2} + 0.00954 \le 0 \\& g_{3} \left( x \right) = - \pi x_{3}^{2} x_{4} - {\frac{4}{3}}\pi x_{3}^{3} + 1,296,000 \le 0 \\ & 0 \le x_{1} ,x_{2} \le 100,10 \le x_{3} ,x_{4} \le 200 \\ \end{aligned} $$

• 3. Spring design problem

  $$ \begin{gathered} \min \;f = x_{1}^{2} x_{2} \left( {x_{3} + 2} \right) \hfill \\ {\text{s.t.}}\quad g_{1} \left( x \right) = 1 - {\frac{{x_{2}^{3} x_{3} }}{{71,785x_{1}^{4} }}} \le 0 \hfill \\ g_{2} \left( x \right) = {\frac{{4x_{2}^{2} - x_{1} x_{2} }}{{12,566\left( {x_{2} x_{1}^{3} - x_{1}^{4} } \right)}}} + {\frac{1}{{5,108x_{1}^{2} }}} - 1 \le 0 \hfill \\ g_{3} \left( x \right) = 1 - {\frac{{140.45x_{1} }}{{x_{2}^{2} x_{3} }}} \le 0 \hfill \\ g_{4} \left( x \right){\frac{{x_{1} + x_{2} }}{1.5}} - 1 \le 0 \hfill \\ 0.05 \le x_{1} \le 2,0.25 \le x_{2} \le 1.3,2 \le x_{3} \le 15 \hfill \\ \end{gathered} $$

• 4. Speed reducer design (gear train)

  $$ \begin{aligned} \min \;&f = 0.7854x_{1} x_{2}^{2} \left( {3.3333x_{3}^{2} + 14.9334x_{3} - 43.0934} \right) - 1.508x_{1} \left( {x_{6}^{2} + x_{7}^{2} } \right) \\ & \quad + 7.477\left( {x_{6}^{3} + x_{7}^{3} } \right) + 0.7854\left( {x_{4} x_{6}^{2} + x_{5} x_{7}^{2} } \right) \\ {\text{s.t.}}\quad & g_{1} \left( x \right) = {\frac{27}{{x_{1} x_{2}^{2} x_{3} }}} - 1 \le 0,\quad g_{2} \left( x \right) = {\frac{397.5}{{x_{1} x_{2}^{2} x_{3}^{2} }}} - 1 \le 0,\quad g_{3} \left( x \right) = {\frac{{1.93x_{4}^{3} }}{{x_{2} x_{3} x_{6}^{4} }}} - 1 \le 0, \\ & g_{4} \left( x \right) = {\frac{{1.93x_{5}^{3} }}{{x_{2} x_{3} x_{7}^{4} }}} - 1 \le 0 \\& g_{5} \left( x \right) = {\frac{{\sqrt {\left( {{\frac{{745x_{4} }}{{x_{2} x_{3} }}}} \right)^{2} + 16.9 \times 10^{6} } }}{{110x_{6}^{3} }}} - 1 \le 0, \\ & g_{6} \left( x \right) = {\frac{{\sqrt {\left( {{\frac{{745x_{5} }}{{x_{2} x_{3} }}}} \right)^{2} + 157.5 \times 10^{6} } }}{{85x_{7}^{3} }}} - 1 \le 0,\quad g_{7} \left( x \right) = {\frac{{x_{2} x_{3} }}{40}} - 1 \le 0,\; \\ & g_{8} \left( x \right) = {\frac{{5x_{2} }}{{x_{1} }}} - 1 \le 0,\quad g_{9} \left( x \right) = {\frac{{x_{1} }}{{12x_{2} }}} - 1 \le 0,\quad g_{10} \left( x \right) = {\frac{{1.5x_{6} + 1.9}}{{x_{4} }}} - 1 \le 0, \\ & g_{11} \left( x \right) = {\frac{{1.1x_{7} + 1.9}}{{x_{5} }}} - 1 \le 0 \\ & 2.6 \le x_{1} \le 3.6,\quad 0.7 \le x_{2} \le 0.8,\quad 17 \le x_{3} \le 28,\quad 7.3 \le x_{4} \le 8.3, \\ & 7.3 \le x_{5} \le 8.3,\quad 2.9 \le x_{6} \le 3.9,\quad 5.0 \le x_{7} \le 5.5 \\ \end{aligned} $$