Dirichlet absorbing boundary conditions for classical and peridynamic diffusion-type models

Abstract

Diffusion-type problems in (nearly) unbounded domains play important roles in various fields of fluid dynamics, biology, and materials science. The aim of this paper is to construct accurate absorbing boundary conditions (ABCs) suitable for classical (local) as well as nonlocal peridynamic (PD) diffusion models. The main focus of the present study is on the PD diffusion formulation. The majority of the PD diffusion models proposed so far are applied to bounded domains only. In this study, we propose an effective way to handle unbounded domains both with PD and classical diffusion models. For the former, we employ a meshfree discretization, whereas for the latter the finite element method (FEM) is employed. The proposed ABCs are time-dependent and Dirichlet-type, making the approach easy to implement in the available models. The performance of the approach, in terms of accuracy and stability, is illustrated by numerical examples in 1D, 2D, and 3D.

1 Introduction

Peridynamics (PD) is a recent nonlocal theory that has received a widespread attention in computational mechanics. It has been widely exploited to solve various problems in mechanics and physics. The theory was originally introduced by Silling [56] and Silling et al. [58] to handle material failure in solid structures, which is not an easy task for the classical continuum mechanics (CCM) theory. In fact, the original formulation of PD introduces an equation of motion in solid mechanics based on integro-differential equations rather than on partial differential equations (PDEs) which are undefined at discontinuities. Therefore, PD models are effective tools in modelling material discontinuities, and they consider fracture and damage as natural parts of the solution. To this respect, many PD models have so far been proposed and applied to a broad range of problems in solids including fracture and crack propagation; to mention a few, see [7, 16, 40, 52, 57, 59, 66] and for a comprehensive review one may refer to [11, 17].

In nonlocal continuum theories, the value of a physical quantity at a given material point is influenced by quantities within a finite neighborhood around that point; we refer to such influences as nonlocal effects. PD models make use of a characteristic length scale called horizon that determines the region of the nonlocal interactions. Each material point establishes direct interactions with other points within its neighborhood. The interactions are governed by a response function that includes all the material constitutive information. As the horizon shrinks and asymptotically approaches zero, the interactions become local and the formulation reduces to that of the classical local theory when suitable regularity assumptions hold [19].

The focus of the present study is on diffusion-type problems. In fact, the solution of diffusion problems is of great importance for engineering and physics applications concerning heat and mass transfer. The mathematical description of many phenomena from areas such as fluid dynamics, chemistry, biology, information, environmental and materials sciences is governed by diffusion-type equations. In this regard, numerous numerical methods (based on the classical local diffusion) have so far been employed, for example the finite element method (FEM), the finite difference method (FDM), the boundary element method (BEM), and meshfree methods (see, e.g., [4, 6, 25, 31]). At the macroscale, most diffusion processes can be described well by local models based on Fourier’s law (heat conduction) as well as Fick’s law (mass transport). However, at this scale, nonlocal effects may play a crucial role; for instance, in the case of heat conduction with steep temperature gradients, stochastic jump processes and anomalous diffusion are observed in heterogeneous environments [21, 35, 36, 73]. Therefore, nonlocal diffusion equations as well as related numerical methods have received a considerable attention in the literature [29, 35, 42]. Recently, miniaturization of devices has provided more cases where the application of nonlocal models rather than local ones is more appropriate [61, 67].

Unfortunately, many of the nonlocal models are inapplicable for problems in which discontinuities (whether strong or weak) in the system emerge, interact, and evolve. Thermal cracking [5, 33, 65], hydraulic fracturing [43], and pitting corrosion [28] are just a few examples, where part of the solution is governed by diffusion, and, at the same time, they are subjected to the emergence of spontaneous discontinuities.

To address also such problems, PD is a promising approach. The first PD diffusion model was developed by Gerstle et al. [24] for electromigration that accounts for heat conduction in a 1D body. Bobaru and Duangpanya proposed a 1D PD heat conduction model in [9], and an extension of their work to 2D bodies with evolving discontinuities is presented in [10]. In these cases, the interaction between material points is prescribed by a thermal response function, and the spatial derivatives of temperature, involved in classical diffusion equations, are replaced by spatial integrals of the thermal response function. Zhao et al. [72] introduced a PD model for transient advection-diffusion problems. The majority of these models utilize the bond-based version of PD. For a mathematical investigation into the generic forms of PD diffusion models one can refer to the studies conducted in [18, 60]; moreover, the first attempts to derive the state-based formulation for thermal diffusion can be found in [42, 46]. There is still ongoing research on PD diffusion models [14, 64].

More recently, the application of PD to corrosion problems has received a considerable attention [15, 28, 29, 44]. Corrosion problems mainly involve a diffusion process in an electrolyte/solid system coupled with a phase-change mechanism; this results in a moving interface problem. Treatment of moving interfaces by local models is challenging since the accurate position of the interface, where the flux continuity conditions (Stefan conditions) are satisfied, must be traced over time [15, 22]. The situation gets worse for corrosion problems as the interfaces evolve and increase in number in time. PD models are effective tools for treating these problems since they simulate the evolution of the corrosion damage and material disintegration in a mathematically consistent manner. Moreover, the Stefan conditions are naturally satisfied by the PD solution [13]. PD modelling of such problems only requires modifying the nonlocal interactions between material points near the interfaces [13], and the autonomous evolution of moving interfaces is a natural part of the PD models.

All the aforementioned studies focus on the solution of bounded-domain problems. In contrast, the solution of diffusion-type problems in an infinite domain via both nonlocal and local models is the main concern of the present study. The application of unbounded-domain problems can be found abundantly in different fields, including fluid dynamics, heat conduction, biology, and finance [27, 32]. Modelling diffusion in unbounded domains finds application in many practical problems regarding corrosion [12]. The main challenge in modelling diffusion-type problems in unbounded domains lies in the infinity of the medium; however, the standard numerical methods, such as the FEM, are developed for bounded-problem domains.

Artificial boundary methods (ABMs) are the most common way of coping with unbounded domains numerically [53, 71]. The idea in ABMs is first to truncate the unbounded domain at an artificial boundary (or absorbing boundary) at a certain distance from the region of interest. Then, by constructing appropriate absorbing boundary conditions (ABCs), applied to the artificial boundary, one can convert the original problem into a bounded one. The exterior domain and the region of interest are referred to as far field and near field, respectively. One has to place the artificial boundary so that the near field includes all the sources. The numerical accuracy and stability strongly depend on the design of the ABCs. The reduced problem domain can reproduce the original solution (within the interior region) provided that accurate and reliable boundary conditions are imposed on the artificial boundary. In the last three decades, the derivation of ABCs, for local wave- and diffusion-type problems, has been the subject of numerous studies, yielding, e.g., the high-order ABCs [26, 69] and the perfectly matched layer (PML) method [3, 8]. However, the solution of nonlocal problems in unbounded domains has received little attention, and it is still an open subject of research [71]. In fact, construction of nonlocal ABCs is challenging since the interactions are nonlocal; in addition, the nonlocal operators are generally associated with volume constrained boundary conditions [2, 18, 46]. Some recent works in the literature regarding new techniques for enabling PD models to face unbounded domains can be found in [20, 51, 63, 68] for 1D and 2D wave and in [71] for 1D diffusion problems.

Herein, we propose a new strategy for constructing ABCs, explicitly in the time domain for both the classical local and the PD diffusion formulation. First, we construct the ABCs for the classical local diffusion equation. Then, the approach is extended and applied to a PD diffusion model. The present study is inspired by two recent works conducted in [38, 53] about a new type of ABCs for scalar and elastic wave propagation problems (hyperbolic PDEs) within the classical continuum framework. Here, similar to many other techniques, we truncate the unbounded domain at an artificial boundary and restrict the computational domain. The solution of the interior domain is computed by a standard FEM solver in the case of local diffusion and by a meshfree PD solver in the case of nonlocal diffusion; moreover, for marching in time, we make use of an explicit scheme. The ABCs are derived from a simple collocation approach that is local in time. The collocation employs a least-squares scheme over a subdomain centred at nodes to which the ABCs must be prescribed. The subdomain is referred to as cloud in the terminology of meshless methods. The collocation approach is simple and shares similarities with that of the meshless finite point method (FPM) [37, 41, 49, 50, 54]. We approximate the far field solution by a series of exponential basis functions (EBFs) which satisfy the governing equation of diffusion. EBFs are obtained as time-dependent fundamental solutions (modes) based on which a semi-analytical solution of the far field can be achieved. For this purpose, EBFs are adjusted so that they can play the role of vanishing modes capable of satisfying the corresponding conditions at infinity. The modes align the flux towards the exterior domain and prevent any unphysical reflection from the absorbing boundary. The unknown coefficients of the series can be found in terms of the nodal collocation values. In this way, the approximate solution provides Dirichlet ABCs for the corresponding nodes. In the case of the FEM, the corresponding nodes are located on the absorbing boundary, while in a PD model the corresponding nodes are located within a layer adjacent to the absorbing boundary. This will be explained in detail later.

The proposed approach offers several appealing features. First, the method does not interfere with the discretization scheme of the near field, and it is simple to implement. Second, as the method is local in time, it is free from Fourier and Laplace transform procedures; this feature is especially important for PD as, in this case, the calculation of the kernel function from the Laplace transform is complicated (due to the nonlocality) [71]. Third, the proposed ABCs are Dirichlet-type, so they can be simply prescribed at the corresponding nodes. Fourth, the method neither requires any spatial differentiation of the field variable nor any auxiliary variables involved in many high-order ABCs methods [69]. In the nonlocal diffusion case, the modes are dependent on the horizon. We shall show that they converge to the local modes in the limit when the horizon approaches zero. The extension of the presented approach to 3D problems is straightforward. To the best of our knowledge, our contribution addresses for the first time a PD model solved in an unbounded domain in 3D. In the section of numerical examples, we shall show that the method has a proper level of accuracy and performs well in the case of long-term calculations.

A brief outline of the rest of this paper is as follows. Section 2 describes the governing equations and physics of the problem, and it gives a brief overview of the PD formulation for diffusion-type problems. In Sect. 3 the way of deriving the fundamental solutions necessary for the far field solution is explained. The solution strategy of the method is thoroughly described in Sect. 4. The performance of the method, in terms of accuracy and stability, is investigated in Sect. 5. The final conclusions made throughout the paper are summarized in Sect. 6

2 Problem description

For simplicity, hereinafter we describe the problem for 2D cases, although the explanations are extensible to 1D and 3D.

Fig. 1

a A generic unbounded domain, b truncation of the exterior domain and representation of the computational domain

Let us consider a generic 2D unbounded domain $\Omega \subset \mathbb {R}^2$ of diffusion as shown in Fig. 1a. The medium is assumed to be isotropic, and it surrounds some physical objects (including baffles and sources). The governing diffusion equation, according to the classical local theory, for any point in the unbounded domain is:

$$\begin{aligned} {\dot{u}}({\mathbf {x}},t)-{\chi }^{2}{\nabla }^{2}u({\mathbf {x}},t)=s({\mathbf {x}},t), \quad {\mathbf {x}} \in \Omega , \quad t > 0, \end{aligned}$$

(1)

where $u({\mathbf {x}},t)$ is the concentration (the main field variable) of the diffusing material at point ${\mathbf {x}}$ with coordinates $\mathbf{x} = \langle x,y \rangle$ and at time t, $\chi ^{2}$ is referred to as the diffusion coefficient, $s({\mathbf {x}},t)$ is a given source function (for instance a heat source), and $\nabla ^{2}$ is the well-known Laplacian operator. Meanwhile, ${\dot{u}}={\partial u}/{\partial t}$ is the first time derivative of u. In fact, u is the diffusive concentration that can represent different physical quantities. For instance, u can represent the temperature in heat conduction or the mass concentration in mass transport such as the metal concentration in a corrosion problem. The surface of baffles are governed by either Dirichlet or Neumann boundary conditions as follows:

$$\begin{aligned} \begin{aligned} u = u^*({\mathbf {x}},t), \quad {\mathbf {x}} \in \Gamma _D, \\ {\mathbf {n}} \cdot \chi ^{2}\nabla u = q^*({\mathbf {x}},t), \quad {\mathbf {x}} \in \Gamma _N, \end{aligned} \end{aligned}$$

(2)

in which $u^*$ is a function that gives the concentration values prescribed at the Dirichlet boundary $\Gamma _D$, ${\mathbf {n}}=\left\langle n_x,n_y\right\rangle$ is an outward unit vector normal to the surface, and $q^*$ is a function that gives the values of the flux (the amount of concentration entering through the surface per unit area during a unit time interval) at the Neumann boundary $\Gamma _N$. The domain can be excited by an initial condition as follows:

$$\begin{aligned} u({\mathbf {x}},0)=u_{0}({\mathbf {x}}), \end{aligned}$$

(3)

where $u_{0}$ is a given function. In fact, $u_0$ in (3) and s in (1) are both compactly supported. Likewise, since the medium is unbounded, the following condition holds:

$$\begin{aligned} \lim \limits _{\Vert {\mathbf {x}}\Vert \rightarrow \infty } u({\mathbf {x}},t) = 0, \quad t > 0, \end{aligned}$$

(4)

which indicates that the concentration vanishes at infinity.

The main difficulty that arises out of the solution of (1) is the infinity of the medium. One way of applying the standard numerical methods, such as the FEM, is to discretize a very large portion of the unbounded domain $\Omega$. However, this strategy renders the approach inefficient and computationally expensive. A remedy is to bound the domain and restrict the computations to the region of interest. In this way, the exterior domain is truncated by an artificial boundary $\Gamma _{\infty }$, so-called absorbing boundary, as shown in Fig. 1b. Therefore, $\Omega$ is divided into a bounded domain $\Omega _{N}$ (near field or computational domain) and an exterior domain $\Omega _{F}=\Omega /\Omega _{N}$ (far field). $\Omega _{N}$ is the region that includes all the physical objects. $\Gamma _{\infty }$ is placed so that the entire support of the sources in (1) is contained in $\Omega _N$. Accordingly, one may conclude that the homogeneous counterpart of (1) for the exterior domain is:

$$\begin{aligned} {\dot{u}}({\mathbf {x}},t)-{\chi }^{2}{\nabla }^{2}u({\mathbf {x}},t)=0, \quad {\mathbf {x}} \in \Omega _{F}, \quad t>0, \end{aligned}$$

(5)

and the medium is initially at rest.

Consequently, obtaining a well-posed problem in $\Omega _N$ requires imposing the so-called absorbing boundary conditions (ABCs) on $\Gamma _{\infty }$, so that the effects of the far field are captured and the bounded domain reproduces the solution of the original problem. In this sense, the concentration (the diffusive quantity in $\Omega _{N}$) must be absorbed perfectly on $\Gamma _{\infty }$ and have a flux direction towards the exterior domain (no unphysical flux back to the near field is permitted). In view of (4), the flux should have a vanishing behaviour so that at infinity the concentration reaches a zero state. In the present work, we shall introduce a way, inspired by the study in [53], to construct time-dependent ABCs fulfilling the aforementioned requirements. The proposed method makes use of fundamental solutions (modes) that satisfy the governing equation of the exterior domain, expressed in (5), upon which Dirichlet ABCs are constructed. The way to construct the modes, for both classical and PD diffusion, is explained in Sect. 3, and the way of applying them to the far field solution is described in Sect. 4.2. Before that, in the following subsection we review the PD diffusion formulation.

2.1 Overview of the peridynamic diffusion formulation

In this section, the nonlocal formulation of PD for diffusion-type problems is briefly explained. One may refer to [9, 10] for a comprehensive study on the derivation of the formulation as well as the physical descriptions.

Fig. 2

A generic unbounded domain of diffusion in PD; a schematic representation of neighborhoods and the absorbing boundary layer

To construct the PD model, a region $H_{{\mathbf {x}}}$ (see Fig. 2) around each point ${\mathbf {x}}$ of the domain is considered. $H_{{\mathbf {x}}}$ is referred to as the neighborhood of $\mathbf{x}$ and is usually taken as a disk in 2D (a ball in 3D) centred at ${\mathbf {x}}$. A concentration value $u({\mathbf {x}},t)$ is associated to the point $\mathbf{x}$ at time t. The neighborhood specifies the region of points ${\mathbf {x}}'$ with which the point $\mathbf{x}$ establishes nonlocal interactions. In this way, each point is connected to its neighboring points through pipe-like conductors, diffusion bonds, which transfer the concentration among the points (buckets). In the bond-based PD formulation, the transport in $\varvec{\xi }:={\mathbf {x}}'-{\mathbf {x}}$, the bond connecting ${\mathbf {x}}$ and ${\mathbf {x}}'$, is independent of the transport in other bonds. In the present study, we follow the bond-based PD formulation.

The governing equation of diffusion in PD, the nonlocal counterpart of (1), is given by [9, 10]

$$\begin{aligned} {\dot{u}}({\mathbf {x}},t)-\int _{H_{\mathbf {x}}}J_{p}({\mathbf {x}}',{\mathbf {x}},t)\mathrm {d}V_{{\mathbf {x}}'}=s({\mathbf {x}},t), \quad {\mathbf {x}} \in \Omega , \quad t>0,\nonumber \\ \end{aligned}$$

(6)

where $J_{p}$ is the kernel of the integral operator or the concentration flow density that takes the following form [72]:

$$\begin{aligned} J_{p}({\mathbf {x}}',{\mathbf {x}},t)=\left\{ \begin{array}{cc} \begin{array}{cc} c(\varvec{\xi })\frac{u({\mathbf {x}} + \varvec{\xi },t)-u({\mathbf {x}},t)}{\Vert \varvec{\xi }\Vert ^{p}} \quad &{} \Vert \varvec{\xi }\Vert \le \delta , \\ 0 \quad &{} \Vert \varvec{\xi }\Vert > \delta , \end{array} \end{array}\right. \end{aligned}$$

(7)

where $\delta$ is the horizon (radius of the disk), p is an integer that influences the shape of the kernel, usually taken equal to 0, 1, or 2 (the reader may refer to [14] for more details), and c is known as the micro-diffusivity in PD. c can take different forms and two popular ones are constant and linear [72]. The constant micro-diffusivity is given by

$$\begin{aligned} c(\varvec{\xi })=\left\{ \begin{array}{cc} c_{0} \quad &{} \Vert \varvec{\xi }\Vert \le \delta , \\ 0 \quad &{} \Vert \varvec{\xi }\Vert > \delta , \end{array}\right. \end{aligned}$$

(8)

which is independent of the bond length. In contrast, in the linear form, the micro-diffusivity is linearly dependent on the bond length and given by

$$\begin{aligned} c(\varvec{\xi })=\left\{ \begin{array}{cc} c_{1}\left( 1-\frac{\Vert \varvec{\xi }\Vert }{\delta }\right) \quad &{} \Vert \varvec{\xi }\Vert \le \delta , \\ 0 \quad &{} \Vert \varvec{\xi }\Vert > \delta . \end{array}\right. \end{aligned}$$

(9)

The constants $c_0$ and $c_1$ can be related to the diffusion coefficient, $\chi ^2$. A way of correlating c with $\chi ^{2}$ is by matching the PD flux to that of the local diffusion as studied in [9]; we shall explain an alternative approach that ends up with similar results in the subsequent section. These relations are provided for different values of p in Table 1. Moreover, other forms for the micro-diffusivity are possible when considering more general influence functions in PD [48]. It is worthwhile to mention that (6) does not contain any spatial derivatives of the field variable (see (7)). As a consequence, the PD diffusion equation is valid in the whole domain including discontinuous regions.

Similar to the explanation given for (5), the governing equation of the far field in PD takes the following form:

$$\begin{aligned} {\dot{u}}({\mathbf {x}},t)-\int _{H_{\mathbf {x}}}J_{p}({\mathbf {x}}',{\mathbf {x}},t)\mathrm {d}V_{{\mathbf {x}}'}=0, \quad {\mathbf {x}} \in \Omega _{F}, \quad t>0.\nonumber \\ \end{aligned}$$

(10)

In PD models, the boundary conditions are usually imposed in volumetric regions rather than on surfaces which is the case for the local diffusion model (see Fig. 2). This is due to the nonlocality of the kernel and the associated neighborhood to each point. The common way of imposing Dirichlet boundary conditions is by prescribing the value of the corresponding boundary points [14]. However, for the Neumann boundary condition, the rate of concentration flow, denoted by ${\dot{Q}}$, entering through the boundary surface should be first calculated as follows:

$$\begin{aligned} \dot{Q}(t) = \int _{\Gamma _{N}}{q^{*}({\mathbf {x}},t)}\mathrm {d}\Gamma _\mathbf{x}, \end{aligned}$$

(11)

where $\Gamma _{N}$ is the surface to which the flux is applied. Then, $\dot{Q}$ must be appropriately distributed over the points in the boundary region and appears as part of the source term $s(\mathbf{x},t)$ in (6). In fact, the effective way of imposing Neumann boundary conditions requires a separate and comprehensive discussion; for brevity, we refer the reader to the studies in [14, 42, 62].

It should be remarked here that for a comprehensive investigation into the rate of convergence of the nonlocal solution to that of the classical solution, taking different forms of micro-diffusivity and kernel functions, the reader may refer to [14]. This topic is beyond the scope of the present study.

Fig. 3

A schematic representation of the neighborhood associated to node ${\mathbf {x}}_{i}$ in the discretized form

There are different ways to discretize a PD model [23]. In the present study, we pursue a common way of PD discretization given by a meshfree scheme introduced in [57]. This scheme is easy to implement and frequently used by researchers. In this meshfree approach, the domain is discretized using a uniform grid with grid spacing $\Delta x$ as shown in Fig. 3. The domain is represented by cells centred at the nodes and hence a volume is associated to each node (length $\Delta x$ in 1D, area $({\Delta x})^2$ in 2D, and volume $({\Delta x})^3$ in 3D). In Fig. 3, the node ${\mathbf {x}}_{i}$ interacts with all its family nodes ${\mathbf {x}}_{j}$ within its neighborhood $H_{{\mathbf {x}}_{i}}$. Moreover, the horizon is expressed as $\delta = m \Delta x$, so that the value of m determines the number of family nodes. Likewise, to compute the integral over each neighborhood, we apply a one-point quadrature with quadrature points given by the nodes and quadrature weights given by the volumes of the intersections between the neighborhood and the cells. The discertized form of the governing equation in (6) can be then written as

$$\begin{aligned} {\dot{u}}({\mathbf {x}}_{i},t) - \sum _{ j \in {\mathcal {F}}_i}J_{p}({\mathbf {x}}_{j},{\mathbf {x}}_{i},t)\beta (\varvec{\xi }_{ij})V_{j} = s({\mathbf {x}}_i,t), \end{aligned}$$

(12)

where ${\mathcal {F}}_i$ is the set of family nodes of ${\mathbf {x}}_{i}$; moreover, $\varvec{\xi }_{ij} :={\mathbf {x}}_{j}-{\mathbf {x}}_{i}$, $V_j$ is the associated volume to node ${\mathbf {x}}_{j}$, and $\beta$ plays the role of a correction function through which the actual volume of ${\mathbf {x}}_j$ covered by the neighborhood of ${\mathbf {x}}_{i}$ can be determined. In the present study, we take $\beta$ as recommended in [70]. Related works employing corrections known as partial volumes, which approximate the intersections between neighbor cells and the neighborhood of a given point to use as quadrature weights, have been presented in [45, 47].

3 Fundamental solutions (modes)

The main purpose of this section is to find fundamental solutions (modes) using exponential basis functions (EBFs) for the governing equations of diffusion in the far field. First, we attempt to find the modes for the local diffusion equation. Let us consider $\psi ({\mathbf {x}},t)$ as a mode that satisfies the governing Eq. (5). A general form of $\psi$ can be written as

$$\begin{aligned} \psi ({\mathbf {x}},t) = \exp (\varvec{\alpha }\cdot {\mathbf {x}} + \omega t), \quad \varvec{\alpha } = \left<\alpha _{x},\alpha _{y}\right>, \end{aligned}$$

(13)

where $(\alpha _{x},\alpha _{y},\omega ) \in \mathbb {R}^{3}$ are three given parameters. To take control over the direction of the diffusion flux, without loss of generality, we make the following assumption:

$$\begin{aligned} \left<\alpha _{x},\alpha _{y}\right> = \kappa \left<\cos \phi ,\sin \phi \right>, \quad \kappa \in \mathbb {R}, \quad 0\le \phi <{2}\pi , \end{aligned}$$

(14)

where $\kappa$ affects the magnitude of the flux, while $\phi$ determines the flux direction and, for the time being, we assume that the flux direction may be oriented towards any angle of the unit circle. We shall discuss the proper selection of the parameters later. Let us substitute $\psi$ from (13) for u in (5); then we have

$$\begin{aligned} \left[ \omega -{\chi }^{2}{\kappa }^{2}(\cos ^{2}\phi + \sin ^{2}\phi )\right] \exp (\varvec{\alpha }\cdot {\mathbf {x}} + \omega t) = 0. \end{aligned}$$

(15)

To reach a non-trivial solution, the expression in square brackets must vanish (since $\exp (\varvec{\alpha }\cdot {\mathbf {x}} + \omega t) \ne 0$), i.e.,

$$\begin{aligned} \omega - \chi ^{2}\kappa ^{2}(\cos ^{2}\phi + \sin ^{2}\phi ) = 0, \end{aligned}$$

(16)

which reduces to:

$$\begin{aligned} \omega = \chi ^{2}\kappa ^{2}. \end{aligned}$$

(17)

This equation is referred to as the characteristic equation. Replacing (17) into (13) leads to modes capable of constructing semi-analytical solutions for the local diffusion as follows:

$$\begin{aligned} \psi ({\mathbf {x}},t)=\exp \left( \varvec{\alpha }\cdot {\mathbf {x}} + \chi ^{2}\kappa ^{2}t\right) . \end{aligned}$$

(18)

A similar procedure is performed for PD. We again consider a generic mode as in (13) to construct fundamental solutions for the nonlocal diffusion equation. Let us assume $p=1$ in (7) and consider a constant micro-diffusivity. Then, insertion of $\psi$ into (10) leads to

$$\begin{aligned} {\dot{\psi }}({\mathbf {x}},t)-\int _{H_{{\mathbf {x}}}}c_{0}\frac{\psi ({\mathbf {x}}',t)-\psi ({\mathbf {x}},t)}{\Vert {\mathbf {x}}'-{\mathbf {x}}\Vert }\mathrm {d}V_{{\mathbf {x}}'}=0 \end{aligned}$$

(19)

and in view of (13) using the change of variables $\varvec{\xi } = \mathbf{x}^\prime - \mathbf{x}$, it can be rewritten as

$$\begin{aligned} \left( \omega - c_{0}\int _{H}\frac{\exp (\varvec{\alpha }\cdot \varvec{\xi })-1}{\Vert \varvec{\xi }\Vert }\mathrm {d}V_{\varvec{\xi }}\right) \exp (\varvec{\alpha }\cdot {\mathbf {x}} + \omega t)=0,\nonumber \\ \end{aligned}$$

(20)

where H is the neighbohood around the origin. To obtain a non-trivial solution, the expression inside the parentheses must vanish. Therefore, the characteristic equation of PD (the counterpart of (17)) can be obtained in the polar coordinate system, $\varvec{\xi }=r(\cos \theta ,\sin \theta )$, as follows:

$$\begin{aligned} \omega =c_{0}\int _{0}^{2\pi }\int _{0}^{\delta }\left[ \exp (r\eta )-1\right] \mathrm {d}r\mathrm {d} \theta , \end{aligned}$$

(21)

where $\eta = \varvec{\alpha }\cdot \left<\cos \theta ,\sin \theta \right>$. By replacing $\omega$ from (21) into (13), the PD mode can be obtained. However, to make the expression simpler and find the connection to the local modes, we rewrite the expression in (21) taking a Taylor expansion of the integrand with respect to $r \eta$ and about 0, as follows:

$$\begin{aligned} \omega =c_{0}\int _{0}^{2\pi }\int _{0}^{\delta }\left( \frac{r\eta }{1!} + \frac{r^2\eta ^{2}}{2!} + \frac{r^3\eta ^{3}}{3!} + \frac{r^4\eta ^{4}}{4!}+\ldots \right) \mathrm {d}r\mathrm {d}\theta ,\nonumber \\ \end{aligned}$$

(22)

which concludes:

$$\begin{aligned} \begin{aligned} \omega&=\frac{\kappa ^{2}(\cos ^{2}\phi +\sin ^{2}\phi )}{6}c_{0}\pi \delta ^{3} \\&+ \frac{\kappa ^{4}(\cos ^{2}\phi +\sin ^{2}\phi )^{2}}{160}c_{0}\pi \delta ^{5} \\&+ \frac{\kappa ^{6}(\cos ^{2}\phi +\sin ^{2}\phi )^{3}}{8064}c_{0}\pi \delta ^{7}+ \dots \\&=c_{0}\pi \left( \frac{\kappa ^{2} \delta ^{3}}{6}+\frac{\kappa ^{4} \delta ^{5}}{160}+\frac{\kappa ^{6}\delta ^{7}}{8064} \dots \right) , \end{aligned} \end{aligned}$$

(23)

and thus the nonlocal PD mode can be written as

$$\begin{aligned} \psi ({\mathbf {x}},t) = \exp \left[ \varvec{\alpha }\cdot {\mathbf {x}} + c_{0}\pi \left( \frac{\kappa ^{2} \delta ^{3}}{6}+\frac{\kappa ^{4} \delta ^{5}}{160}+ \dots \right) t\right] .\nonumber \\ \end{aligned}$$

(24)

A glance at the obtained modes in (18) and (24) reveals that the difference is in the temporal parts. By replacing

$$\begin{aligned} c_{0}=\frac{6\chi ^{2}}{\pi \delta ^{3}} \end{aligned}$$

(25)

in (23), we have

$$\begin{aligned} \omega =\chi ^{2}\kappa ^{2}\left( 1+\frac{3}{80}(\kappa \delta )^2+\frac{1}{1344}(\kappa \delta )^{4}+\dots \right) . \end{aligned}$$

(26)

In the limit as $\kappa \delta \rightarrow 0$, we obtain

$$\begin{aligned} \omega \rightarrow \chi ^{2}\kappa ^{2}, \end{aligned}$$

(27)

which indicates that the nonlocal mode recovers the local one provided that the micro-diffusivity is chosen appropriately in terms of the diffusion coefficient $\chi ^{2}$ and horizon $\delta$.

In Table  1 the expressions of the micro-diffusivity constants, in terms of the diffusion coefficient of the local diffusion and the horizon, are presented for various kernels in 1D, 2D, and 3D. The way of finding the 3D modes is explained in Appendix A.

Table 1 The expressions for the constants $c_0$ in (8) and $c_1$ in (9), in terms of $\chi ^{2}$ and $\delta$, for different choices of p for $J_p$ in (7) in 1D, 2D, and 3D

Remark 1

The modes are found so that the flux direction can be adjusted easily. We shall benefit from this feature to construct semi-analytical solutions for the far field (see Sect. 4.2). From (24) it can be inferred that by taking higher-order terms (inside the parentheses), i.e., keeping more terms from the Taylor expansion in (22), the semi-analytical solution should converge to the nonlocal solution and take more nonlocal effects into account. However, since the absorbing boundary is set far from the physical objects where the nonlocal effects can play an important role, for example, at the tip of a crack, even keeping only a few terms from the Taylor expansion, e.g., making use of the local modes, can still result in a proper approximation of the far field.

Fig. 4

a A generic cloud embedded in an unbounded domain; b the valid regions of $\phi$ in the unit circle to satisfy the infinity condition at angle $\theta ^{*}$ towards the first quadrant of the local coordinate system; and c the rotated valid regions of $\phi$ due to the change of $\theta ^{*}$

Now, let us consider a circular region, so-called cloud, centred at a generic point ${\mathbf {x}}$ as shown in Fig. 4a. The cloud is surrounded by an unbounded domain; moreover, a local coordinate system is centred at the point $\mathbf{x}$. In Sect. 4.2, we approximate the far field solution through a series of modes with a general form as in (18). In fact, the approximate solution must be obtained in terms of the values of the nodes within the cloud of the node ${\mathbf {x}}$. From (18), it can be inferred that a mode consists of a temporal part and a spatial part. One may rewrite it in polar coordinates as follows:

$$\begin{aligned} \psi (r,\theta ,t)= & {} \exp \left[ \kappa r \left( \cos \theta \cos \phi + \sin \theta \sin \phi \right) \right] \nonumber \\&\times \exp \left( \chi ^{2}\kappa ^{2}t\right) \nonumber \\= & {} \exp \left[ \kappa r \cos (\theta -\phi )\right] \exp \left( \chi ^{2}\kappa ^{2}t\right) . \end{aligned}$$

(28)

To enforce the infinity condition in the direction $\theta ^{*}$, we substitute $\psi$ for u in (4) and set $\theta = \theta ^{*}$, to obtain

$$\begin{aligned} \lim \limits _{r\rightarrow \infty } \psi (r, \theta ^*, t)= & {} \lim \limits _{r\rightarrow \infty } \exp \left[ \kappa r \cos (\theta ^{*}-\phi )\right] \nonumber \\&\times \exp \left( \chi ^{2}\kappa ^{2}t\right) = 0. \end{aligned}$$

(29)

At a given time $t>0$, provided that $\chi ^{2}\kappa ^{2}t<\infty$, the infinity condition is satisfied as long as the following condition is met:

$$\begin{aligned} \kappa \cos (\theta ^{*}-\phi )<0. \end{aligned}$$

(30)

The condition (30) reduces to two different conditions depending on the sign of $\kappa$ and the value of $\theta ^{*}$ towards which the infinity condition is of concern. For instance, for the first quadrant of the local coordinate system, i.e., $\theta ^{*}\in [0,\pi /2)$, the following conditions must be met so that the mode can satisfy the condition (30) at the angle $\theta ^{*}$:

$$\begin{aligned}&\kappa > 0: \quad \frac{\pi }{2}+\theta ^{*}<\phi<\frac{3\pi }{2}+\theta ^{*}, \nonumber \\&\kappa< 0: \quad \frac{3\pi }{2}+\theta ^{*}<\phi<2\pi + \theta ^* \quad \cup \quad \theta ^*\le \phi < \frac{\pi }{2} + \theta ^{*},\nonumber \\ \end{aligned}$$

(31)

which indicates two halves of the unit circle as shown in Fig. 4b. In other words, the semicircular regions illustrate the permitted range of flux direction $\phi$ (based on the sign of $\kappa$) through which the infinity condition at $\theta ^{*}$ is satisfied. The interface between the two semicircles is perpendicular to the direction of $\theta ^{*}$, and it rotates accordingly by changing the value of $\theta ^{*}$ (see Fig. 4c).

Fig. 5

A portion of a generic solution domain, close to the absorbing boundary, for a a PD model with a meshfree discretization, and b a FEM model using quadrilateral elements. (Color figure online)

Now let us assume that the infinity condition is always taking place in the first quadrant of the local coordinate system, i.e., $\theta ^{*}\in [0,\pi /2)$. Let us consider $\mathfrak {R}_{1}$ and $\mathfrak {R}_{2}$ as two valid regions of $\phi$ in the unit circle corresponding to $\theta ^{*} = 0$ and $\theta ^{*} = \pi /2$, respectively. Consequently, to satisfy the condition at any angle in the first quadrant of the coordinate system, $\phi$ must be chosen from the intersection of the regions, which is:

$$\begin{aligned} \mathfrak {R}_{1}\cap \mathfrak {R}_{2} = \left\{ \begin{array}{cc} \pi \le \phi \le 3\pi /2 &{} \quad \kappa >0, \\ 0\le \phi \le \pi /2 &{} \quad \kappa <0. \end{array} \right. \end{aligned}$$

(32)

With respect to the obtained regions in (32), in Sect. 4.2 we shall explain the proper application of the modes, the suitable orientation of the local coordinate system, and the way of patching the far field solution to that of the near field in a discretized PD or FEM model.

4 The solution strategy

The first part of the solution strategy concerns the near field approximation; in other words, employing a PD model discretized with a meshfree method or a local governing equation discretized by the FEM in space and proceeding in time with an explicit time marching algorithm. The second part, the main focus of the present study, corresponds to the approximation of the far field and construction of the ABCs. We assume that the absorbing boundary $\Gamma _{\infty }$ is a circle (or a sphere in 3D) surrounding the domain of interest. The details are explained in the following subsections.

4.1 Near field

Let us discretize a generic domain with a PD grid or a FEM mesh as shown in Fig. 5. The figure illustrates only a portion of the discretized domain close to the absorbing boundary. The nodes of the near field are indicated by black circles, while the absorbing nodes are indicated by blue circles. As can be seen in the figure, in the PD case the absorbing nodes are distributed within a certain distance of the absorbing boundary $\Gamma _{\infty }$; in contrast, in the FEM case only absorbing nodes along that boundary are required. In both cases, the domain is represented by a set of nodes ${\mathbf {x}}_{i}$, $i=1,2,\dots$, where ${\mathbf {x}}_{i}=\left<x_{i},y_{i}\right>$ contains the Cartesian coordinates of the node with respect to the global coordinate system. The time is discretized into instants, as $t^{0},t^{1},\dots ,t^{n},t^{n+1},\dots$. In the present study, we take a constant time step $\Delta t = t^{n+1}-t^{n}$ for any $n = 0,1,\dots$. Moreover, $u^{n}_{i}:=u({\mathbf {x}}_{i},t^{n})$ denotes the concentration value at the node ${\mathbf {x}}_{i}$ at time instant $t^{n}=t^{0} + n \Delta t$. The time marching is performed by means of an explicit forward Euler time integration scheme. Having known the nodal values of ${\mathbf {x}}_{i}$ at time instant $t^{n}$, i.e., $u^{n}_{i}$ and its first time derivative ${\dot{u}}^{n}_{i}$, the solver can proceed to the next time instant as follows:

$$\begin{aligned} {u}^{n+1}_{i}=u^{n}_{i}+\Delta t{\dot{u}}^{n}_{i} \end{aligned}$$

(33)

in which $\Delta t$ must be less than a critical value $\Delta t_{c}$ obtained as

$$\begin{aligned} \Delta t_{c} = {\text {CFL}}\left( \frac{\Delta _{\mathrm {min}}}{\chi }\right) ^{2}, \end{aligned}$$

(34)

where $\Delta _\mathrm {min}$ is the minimum PD grid spacing or the minimum element size in FEM in the spatial discretization, and $\text {CFL}$ stands for the well-known Courant-Friedrichs-Lewy condition (CFL is equal to 1/2, 1/4, and 1/8, respectively, for 1D, 2D, and 3D uniform discretizations). The value of ${\dot{u}}^{n+1}_{i}$ is calculated directly from the discretized form of the governing equation. The values of the absorbing nodes must be updated at each time step by a strategy thoroughly described in the subsequent section.

4.2 Far field

Inspired by the study in [53], an efficient updating technique is devised for the absorbing nodes. In this way, at each time instant, the far field solution (within a cloud around each absorbing node) must be first constructed using the modes introduced in Sect. 3 as the bases of the approximation. Then, the approximate solution provides the value of the corresponding absorbing node for the next time instant, and it can be conveniently imposed to the node as a Dirichlet boundary condition.

Figure 6 illustrates two generic clouds with two differently oriented local coordinate systems. In the figure, ${\mathbf {x}}_{i}$ represents an absorbing node to which a cloud denoted by $\Omega _{i}^{\infty }$ is associated, and ${\mathbf {x}}_{j}$ represents a neighboring node of the node ${\mathbf {x}}_{i}$. From the figure, it can be inferred that the local coordinate system is rotated by an angle $\tau$ (with respect to the global system) so that the first quadrant of the local coordinate system falls within the exterior domain and the bisection line of the $90^{\circ }$ between the axes is normal to the absorbing boundary. Within each cloud, we approximate the solution by $u_{\infty }({\mathbf {x}},t)$ using a series of modes with a form obtained in (18) as follows:

$$\begin{aligned} \begin{aligned}&u_{\infty }({\mathbf {x}},t) = \\&\sum _{k}\sum _{l}a_{k,l}\exp \left[ \kappa _{l}\left( x\cos \phi _{k} + y\sin \phi _{k}\right) + \chi ^{2}\kappa _{l}^{2}t\right] , \end{aligned} \end{aligned}$$

(35)

Fig. 6

Two generic clouds with rotated local coordinate systems for the far field approximation

where $a_{k,l}$ are unknown coefficients of the approximation. According to (32) as well as the orientation chosen for the local coordinate system of the cloud, we choose $\phi _{k}$ from a set of equally spaced angles within the following interval:

$$\begin{aligned} \phi _{k} \in \left[ 0,\frac{\pi }{2}\right] \end{aligned}$$

(36)

and we take $\kappa _{l}$ from a set of equally spaced numbers with negative values, within the following interval:

$$\begin{aligned} \kappa _{l} \in \Delta \kappa \left[ -1,0\right) , \quad \Delta \kappa > 0. \end{aligned}$$

(37)

A logical way of choosing $\Delta \kappa$ will be discussed in Sect. 4.3. Now the challenge is to find the unknown coefficients of the approximation in (35) in terms of the nodal values of the cloud. It should be pointed out that when the solver is at the beginning of the nth time step, i.e., the time interval between $t^{n}$ and $t^{n+1}$, we reset the time and assume that the approximation is valid for the local time interval $\left[ 0,\Delta t \right]$. This assumption is valid since here the approximation is local in time. To this end, in view of (35), we approximate the solution at the time interval between $t^n$ and $t^{n+1}$ as follows:

$$\begin{aligned} u^{n}_{\infty }({\mathbf {x}},{\bar{t}}) = \sum _{b=1}^{n_{b}}q^{n}_{b}\psi _{b}({\mathbf {x}},{\bar{t}}) = {\varvec{\psi }}({\mathbf {x}},{\bar{t}}){\mathbf {q}}^{n} \end{aligned}$$

(38)

in which the series run over $n_{b}$ modes and $q_{b}$ are the corresponding unknown coefficients; moreover, ${\varvec{\psi }}$ and ${\mathbf {q}}^{n}$ are:

$$\begin{aligned} \begin{aligned}&{\varvec{\psi }}({\mathbf {x}}, t) = \left( \psi _{1}({\mathbf {x}}, t) , \psi _{2}({\mathbf {x}}, t) , \ldots , \psi _{n_{b}}({\mathbf {x}}, t)\right) , \\&{\mathbf {q}}^{n} = \left( q^{n}_{1} , q^{n}_{2} , \ldots , q^{n}_{n_{b}}\right) ^{\mathrm {T}}. \end{aligned} \end{aligned}$$

(39)

At the beginning of the nth time step the nodal values of the cloud $\Omega ^{\infty }_{i}$, associated to node ${\mathbf {x}}_{i}$ as shown in Fig. 6 and according to (38), can be collected in a vector as (recalling that at the beginning of each step we set ${\bar{t}}=0$):

(40)

where ${\mathbf {M}}$ stands for the moment matrix of the local collocation procedure, ${\mathbf {x}}_{ij}$ denotes the local coordinates of ${\mathbf {x}}_{j}$, and ${\mathbf {R}}$ is a rotation matrix defined as

$$\begin{aligned} {\mathbf {R}}(\tau ) :=\left[ \begin{matrix} \cos {\tau } &{} \sin {\tau } \\ -\sin {\tau } &{} \cos {\tau } \end{matrix} \right] \end{aligned}$$

(41)

for transformation from the global coordinate system to the local one. By assuming that the number of nodes in the cloud are less than the number of modes $n_{b}$, one can find the unknown coefficients of the approximation ${\mathbf {q}}^{n}$ in terms of the nodal values of the cloud ${\mathbf {U}}^{n}$ as follows:

$$\begin{aligned} {\mathbf {q}}^{n} = {\mathbf {M}}^{+}{\mathbf {U}}^{n} \end{aligned}$$

(42)

in which the superscript “+” denotes the Moore-Penrose generalized inverse. By replacing ${\mathbf {q}}^{n}$ in (38) by the expression given in (42), one can write

$$\begin{aligned} u^{n}_{\infty }({\mathbf {x}},{\bar{t}})={\varvec{\psi }}({\mathbf {x}},{\bar{t}}){\mathbf {M}}^{+}{\mathbf {U}}^{n}={\mathbf {N}}({\mathbf {x}},{\bar{t}}){\mathbf {U}}^{n}, \end{aligned}$$

(43)

where ${\mathbf {N}}$ is a vector that contains the shape functions of the approximation and its size is equal to the number of nodes in the cloud. Equation (43) gives an approximation of the solution of the cloud explicitly in time taking the effects of the exterior domain to the near field into account.

According to (43), one can simply update the nodal value of the absorbing node at the nth time step and proceed to the time instant $t^{n+1}$ as follows:

$$\begin{aligned} u^{n+1}_{i}={\mathbf {N}}({\mathbf {0}},\Delta t){\mathbf {U}}^{n}={\mathbf {V}}{\mathbf {U}}^{n} \end{aligned}$$

(44)

in which ${\mathbf {V}}$ is referred to as the updating vector of the absorbing node; it should be recalled that the right-hand side of (44) is known since the solver is using an explicit time marching algorithm. In other words, (44) provides a Dirichlet ABC for the absorbing node in terms of the nodal values of its cloud.

Remark 2

Since a constant value for $\Delta t$ is assumed and the local time is reset at each time step, the updating vectors ${\mathbf {V}}$ of the absorbing nodes consist of constant values and thus they can be calculated once at the beginning of the simulation. This leads to a substantial reduction in the computational cost of the approach.

Remark 3

In 3D problems, $\Gamma _{\infty }$ is the surface of a truncating sphere in space. In this case, based on the discussion in Appendix A, we assume that the first octant of the local coordinate system falls within the exterior domain. In order to achieve that, we rotate the local coordinate system so that the unit vector $1/\sqrt{3}\left<1,1,1\right>$ becomes normal to the absorbing boundary and points toward the exterior domain.

Remark 4

In the present study, as shown in Fig. 5a, the thickness of the absorbing layer in the PD model is taken so that the neighborhoods of points in the near field have a full circular shape in 2D (spherical shape in 3D). Taking a narrower absorbing layer contributes to a well-known source of error in PD models, referred to as skin- or surface-effect [34, 55], that may deteriorate the accuracy of the near field solution (which is the main concern for the analyst). We shall show this issue in the numerical examples.

In the subsequent section, some implementation aspects of the present study are discussed.

4.3 Implementation

Since the proposed method is devised preserving the discretization scheme of the near field, it has a simple and straightforward implementation. The main steps are discretizing the computational domain using a grid of nodes (in PD) or a mesh of elements (in the FEM); specifying the absorbing nodes; constructing the neighborhoods (only in PD) as well as the clouds of the absorbing nodes; forming the final system of equations; calculating the updating vectors of the clouds; and finally marching in time with the explicit algorithm described earlier.

For both the PD and FEM cases, it is possible to construct a final system of equations, based on their discretization schemes, as follows:

$$\begin{aligned} \tilde{{\mathbf {M}}}\dot{{\mathbf {U}}}_{T} + \tilde{{\mathbf {K}}}{\mathbf {U}}_{T}=\tilde{{\mathbf {F}}}, \end{aligned}$$

(45)

where $\tilde{{\mathbf {M}}}$ and $\tilde{{\mathbf {K}}}$ are the lumped mass and stiffness matrices of the global system of equations, respectively, ${\mathbf {U}}_{T}$ and $\dot{{\mathbf {U}}}_{T}$ are two vectors collecting the nodal values and their first time derivative in the global system, and $\tilde{{\mathbf {F}}}$ is a vector of known values. In the present study, the system of equations for both the bounded-domain problem and the unbounded-domain with ABCs problem is identical. However, for the unbounded-domain problem an extra procedure to update the nodal values of the absorbing nodes is required. One may refer to Algorithm 1 to get more insight into the step-by-step solution procedure of the present study. In the algorithm, $d_{\infty }$ refers to the radius of the clouds centred at the absorbing nodes and $t_{f}$ is the final time instant of the solution.

As discussed earlier, we construct the modes taking $\phi$ and $\kappa$ from the intervals expressed in (36) and (37), respectively. In fact, $\Delta \kappa$ is an influential parameter for the stability of the numerical solution. This is due to the fact that it directly influences the magnitude of the temporal part of the modes. According to (29), the temporal part should be bounded so that the satisfaction of the infinity condition can be guaranteed. Moreover, taking a large value for $\Delta \kappa$ may give rise to exponentially big numbers for the moment matrix ${\mathbf {M}}$ in (40) and contribute to significant numerical errors. To confine the magnitude of the temporal part, we select $\Delta \kappa$ so that the following condition is met (recalling that, at each time step, ${\bar{t}}=\Delta t$ is plugged into (43)):

$$\begin{aligned} 0<\chi ^{2}\Delta \kappa ^{2}\Delta t < 1. \end{aligned}$$

(46)

In view of (34), the following suitable range for $\Delta \kappa$ is obtained:

$$\begin{aligned} 0<\Delta \kappa < \frac{1}{\sqrt{\mathrm {CFL}}\Delta _{\mathrm {min}}}. \end{aligned}$$

(47)

We note that the collocation in each cloud must be taken over a sufficiently large number of neighbouring nodes to ensure a proper approximation of the far field solution. Based on our experience the radius $d_{\infty }$ must be large enough so that the cloud of each absorbing node in 1D, 2D, and 3D includes at least 3, 5, and 7 neighbouring nodes, respectively. It should be pointed out that $d_{\infty }$ determines solely the region of the least-squares approximation and does not convey the range of nonlocal interaction as done by $\delta$.

In this study, for the sake of computer implementation we have used the C++ programming language. To increase the performance of the developed code, the major parts have been parallelized using OpenMP directives. The library libkdtree has been employed for constructing the neighborhoods and the clouds in a high-performance way; the reader may refer to [39] for more details. In order to perform the Moore-Penrose generalized inverse in (42), we have exploited the well-known library LAPACK [1].

5 Numerical examples

In this section the performance of the proposed method in the solution of some problems is investigated. In the last two examples, we apply the proposed method to a PD corrosion problem. In this way, we demonstrate one of the appealing applications of the method. The way of tackling corrosion with PD corresponds to the near field solution. To this respect, we employ the PD model proposed in [29] for the near field solution. One may refer to [13] for more details about the parameters and the algorithms required to treat corrosion in PD.

To scrutinize the performance of the method, in terms of accuracy and stability, we define the energy of the solution $\Pi$ at time t as follows:

$$\begin{aligned} \Pi (t) :=\int _{\Omega _{N}}u^{2}({\mathbf {x}},t)\mathrm {d}V_\mathbf{x}, \quad t\ge 0, \end{aligned}$$

(48)

where $\Omega _{N}$ is the near field. In fact, $\Pi$ provides a quantity to study the behaviour of the solution. In this sense, the energy must be a non-increasing function of time. It should be pointed out that in the first two examples, we take the solution of an extremely large bounded domain with homogeneous Neumann boundary conditions as the reference solution. The extended-domain solution can play the role of a reference solution as long as the boundary region of the extended domain is not perturbed and it remains at a zero state of concentration. In all the examples, for the PD model, we take $p=1$ in the kernel of the integral operator (7) and the micro-diffusivity c is assumed to be constant as in (8).

It should be pointed out that all the examples are set up in a dimensionless system; moreover, the chosen values for the geometrical and physical parameters of the problems are not motivated by any real physical application.

5.1 Example 1

The main goal of this example is to show the performance of the proposed method in the case of a 1D unbounded problem domain $\left( -\infty ,\infty \right)$. The diffusion parameter of the medium is $\chi ^{2}=1$. We consider the region $(-30,30)$ as the computational domain $\Omega _{N}$. To validate the obtained results, the solution of an extended domain within $\Omega _{N}$ is taken as the reference solution. The extended domain is $(-150,150)$. The problem domain is excited by an initial concentration as follows:

$$\begin{aligned} u_{0}(x) =\exp (-4x^2). \end{aligned}$$

(49)

We begin with the solution given by a FEM model using linear 1D elements; then, we look into the solution of a PD model. For both models we take an identical discretization resolution in space and time. For the spatial discretization, we take $\Delta x = 0.125$ which results in 2401 and 481 nodes, respectively, for the extended domain and the truncated domain (or computational domain). The solution for a time duration $t_{f} =250$ is of concern; this duration is set so that the concentration close to the boundaries of the extended domain remains almost zero. The time step $\Delta t$ is set to be 0.001 and thus the calculations are performed over 250,000 time steps. In the FEM model, the ABCs are constructed by placing only two clouds on the nodes positioned at $x=-30$ and $x=30$. The local coordinate system of the cloud at $x=-30$ is oriented so that its axis points towards the left direction, whereas the one at $x=30$ points towards the right direction (similar to that of the global coordinate system). The construction of the far field solution is carried out using $n_{b}=20$ modes.

Fig. 7

The concentration field obtained for the truncated domain and the extended domain in Example 1, using the FEM solver

Figure 7 illustrates the concentration field obtained at different time instants for the truncated domain and the extended domain using the FEM solver. For a better comparison between the solutions, only the part of the reference solution coinciding with the truncated domain is shown in the figure. It can be inferred that the solution obtained by the proposed method conforms to the reference solution very well. Meanwhile, the solution of the truncated domain is continued further up to $t_{f}=4$,000 and, as expected, the concentration reaches a zero state. To get more insight into the performance of the proposed method, the variation of energy over time for the truncated domain with ABCs as well as the extended domain is reported in Fig. 8. The energy is calculated within the near field in both cases. The energy is normalized with respect to the energy of the system at the first time instant. Moreover, the normalized energy difference between the solutions is defined as follows:

$$\begin{aligned} \Delta \Pi /\Pi _{0}(t) = \frac{|\Pi (t) - \Pi _{\mathrm {ref}}(t)|}{\Pi _{\mathrm {ref}}(0)}, \end{aligned}$$

(50)

where $\Pi _{\mathrm{ref}}(t)$ is the energy of the reference solution at time t. The results are reported in Fig. 9. In the same figure, for the sake of comparison, we report the error when the truncated domain is not equipped with the ABCs, but instead homogeneous Neumann boundary conditions are imposed. The results in Fig. 8 indicate that the energy dissipates from the near field monotonically ($\mathrm {d}\Pi <0$) having an excellent match with the reference solution. As can be seen in Fig. 9, the difference is very small as long as the truncated domain is equipped with the ABCs, while this is not the case when the homogeneous Neumann boundary conditions are employed in which case the difference rapidly grows in time. It can be concluded that the proposed ABCs are performing well and no accountable spurious flux reflecting back to the near field from the boundaries can be observed. As shown in Fig. 8, in order to check the stability of the present approach, the energy is calculated up to $t_{f}=4$,000 which results in $4\times 10^{6}$ time steps. It can be inferred that the method performs stably in time and no instability due to long-term calculations takes place.

Fig. 8

The variation of energy in Example 1, using the FEM solver

Fig. 9

The normalized energy difference $\Delta \Pi /\Pi _{0}$ in Example 1, using the FEM solver with and without ABCs

Fig. 10

The concentration field obtained for the truncated domain and the extended domain in Example 1, using the PD solver

Fig. 11

The variation of energy in Example 1, using the PD solver

Fig. 12

The concentration field obtained for the truncated domain and the extended domain at $t=250$ in Example 1, using the PD solver with different sizes of the absorbing layer

In the second part of this example, we redone the procedure with a PD solver. The horizon is taken as $\delta = 4\Delta x$ and to the absorbing nodes a cloud with $d_{\infty } = \delta /2$ is associated. Based on the discussion in Remark 4, the absorbing layer thickness is taken as $\delta _{L}=\delta$; the layer is wide enough so that each neighborhood in the near field has a full integration domain.

The concentration field obtained for the truncated domain and the extended domain using the PD solver at different time instants is depicted in Fig. 10. Moreover, the variation of energy versus the time step number, for both the truncated domain and the extended domain, is reported in Fig. 11. Similar to the FEM case, applying the proposed ABCs to the PD solver culminates in accurate results with a very good agreement, even at the energy level, with those of the reference solution.

To investigate the effects of the absorbing layer thickness $\delta _{L}$ on the accuracy of the truncated-domain solution, we redo the simulation with the PD solver taking different layer thicknesses equal to $3\Delta x$, $2 \Delta x$, and $\Delta x$. Figure 12 illustrates the concentration field at $t=250$ taking different values for $\delta _{L}$. The results indicate that taking a smaller value for $\delta _{L}$, and consequently increasing the surface effect, results in a lower accuracy of the solution. It can be observed that the mismatch between the numerical solution and the reference solution is more pronounced near the boundaries, which is consistent with the discussion in Remark 4. In Fig. 13, the normalize energy difference between the solutions of the truncated domain, using different sizes of the absorbing layer, and the reference solution is reported. As can be seen, the method exhibits results with an appropriate level of accuracy provided that the absorbing layer is taken wide enough, i.e., $\delta _{L}\ge 3\Delta x$.

Fig. 13

The normalized energy difference $\Delta \Pi /\Pi _{0}$ in Example 1, using the PD solver and taking different sizes of the absorbing layer

Fig. 14

The initial concentration field in Example 2

Fig. 15

The concentration field at different time instants in Example 2 for the reference solution (left column) and the solution of the truncated domain (right column)

Fig. 16

The gradient field of concentration obtained by the present method at different time instants in Example 2

5.2 Example 2

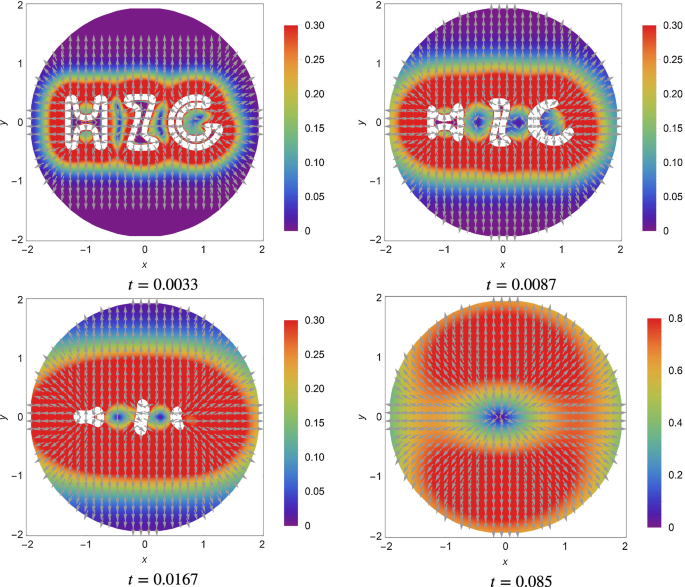
The purpose of this example is to scrutinize the performance of the proposed method in the solution of a 2D corrosion problem in an unbounded domain. This problem concerns the corrosion of a metallic specimen (shown in Fig. 14) surrounded by an unbounded electrolyte that leads to reduction of the solid material due to dissolution into the liquid medium. In this example, the intact metal (the “HZG”¹ letters with initial concentration value $u_{0}=2$) is the initial solid phase and the surrounding electrolyte (with initial concentration value $u_{0}=0$) is the initial liquid phase of the problem domain. During the corrosion process, due to the so-called dissolution flux, the solid phase reduces and, consequently, the dissolved material diffuses out into the electrolyte. The whole process can be modelled by a PD diffusion solver. It should be pointed out that the solution of such a problem by the standard classical models is cumbersome since the interfacial dissolution flux (between the phases) cannot be defined easily in the framework of local diffusion [28]. This roots from the fact that the concentration field is not smooth at the corrosion front; therefore, capturing the existing jumps (strong discontinuities) is not an easy task for the local models. Furthermore, in this example the solid phase consists of sharp corners (weak discontinuities) which make the application of the local models more complicated.

For the PD model, it is required to associate two micro-diffusivity parameters $c_{\mathrm {liq}}$ and $c_{\mathrm {int}}$. The latter is referred to as the micro-dissolvability [30] and corresponds to the bonds with one end in the solid phase and one end in the liquid phase (interfacial bonds). The former corresponds to the bonds whose endings are in the liquid phase. It is assumed that no flux between two points in the solid phase occurs. It is also necessary to define a threshold concentration $u_{\mathrm {sat}}$ that stands for the minimum concentration of the solid phase during the dissolution. Once the dissolution process (diffusion through the interfacial bonds) drops the concentration of a solid point below $u_{\mathrm {sat}}$, the point is regarded as a liquid point afterwards. This phase-change results in autonomous propagation of the dissolution front.

In this example it is assumed that $\delta =0.04$, $u_{\mathrm {sat}}=0.8$, $c_{\mathrm {liq}} = 7957.70$, and $c_{\mathrm {int}}=795.77$. As shown in Fig. 14, a circular domain with a radius equal to 2 is considered for the truncated domain. The domain is surrounded by an absorbing layer with a thickness equal to the horizon $\delta$. To each absorbing node a cloud with a radius $d_{\infty }=\delta /2$ is associated. In each cloud, the far field is approximated by $n_{b}=55$ modes. For the sake of verification, the solution of an extended circular domain with a radius equal to 10 is taken as the reference solution. Homogeneous Neumann boundary conditions are imposed on the boundary of the extended domain. Both domains are discretized with the same grid spacing, $\Delta x = 0.02$; therefore, the calculations runs over $31,417$ nodes for the truncated domain (including 2500 absorbing nodes), while they run over $785,349$ nodes for the extended domain. To proceed in time, in both models an incremental time step $\Delta t=3.3\times 10^{-7}$ is applied.

In Fig. 15, the concentration level of metal captured by the truncated domain using ABCs and the extended domain at different time instants is presented. The regions with the concentration level higher than 0.8 represent the solid phase of the solution domain. The obtained results demonstrate that the solution of the truncated domain resembles that of the extended domain The metal concentration begins to diffuse out and crosses the truncating boundary with a pattern very similar to that of the reference solution. By $t=0.085$ the concentration level of the near field reaches almost a zero state, which indicates that the ABCs are performing properly.

Another way to demonstrate that the applied ABCs are performing appropriately is to check the gradient field of concentration. Contour plots of the gradient field of concentration at different time instants are presented in Fig. 16. The arrows show the direction of gradient vectors while the contours indicate the magnitude. It should be pointed out that the gradient values are calculated by using a simple finite difference approach. Since close to the truncating boundary all the arrows are towards the exterior domain, it can be concluded that the applied boundary conditions are performing suitably in time.

To get a better understanding of the accuracy of the solution, the difference between the solution obtained for the truncated domain and the extended domain, on the basis of (50), is reported in Fig. 17. For comparison, in the same plot, the results of the truncated domain with homogeneous Neumann boundary conditions (when the domain is not equipped with the absorbing layer) is shown. It can be concluded that the difference between the solution of the truncated domain and the extended domain is relatively small as long as the absorbing layer is applied, while the solution of the truncated domain diverges from the reference solution when the absorbing layer is removed. To check the stability of the solution, the variation of energy obtained by the truncated domain and the extended domain is reported in Fig. 18. For the truncated domain the calculations are run up to almost $7\times 10^{6}$ time steps. It can be inferred that the absorbing boundary layer is performing with a stable behaviour in time and the energy dissipates monotonically from the computational domain in a very good agreement with the reference solution.

Fig. 17

The normalized energy difference $\Delta \Pi /\Pi _{0}$ in Example 2 for the truncated domain with and without ABCs

Fig. 18

The variation of energy in Example 2

Fig. 19

The initial concentration field in Example 3

Fig. 20

The concentration field (left column) and the gradient field (right column) within the first octant of the global coordinate system in Example 3

5.3 Example 3

The goal of this example is to demonstrate that the proposed method is applicable to 3D problems. For this purpose, we simulate the dissolution process of a spherical metallic specimen (with an initial concentration value $u_{0}=1$) in an unbounded domain occupied by an electrolyte (with an initial concentration value $u_{0}=0$).

As shown in Fig. 19, the initial solid phase has a radius equal to 3.33 and the domain is truncated by a spherical domain with a radius equal to 5. The required parameters of the PD corrosion model are taken as $\delta =0.2$, $u_{\mathrm {sat}}=0.8$, $c_{\mathrm {int}}=795.77$, and $c_{\mathrm {liq}}=7,957.7$. Similar to previous examples, the thickness of the absorbing layer is equal to the horizon $\delta$ and to each absorbing node a cloud with a radius $d_{\infty }=\delta /2$ is assigned. In each cloud, the far field is approximated by $n_{b}=605$ modes. The domain is discretized with a grid spacing $\Delta x = \delta /2$, which results in 523,155 nodes for the computational domain (including 60,374 absorbing nodes). For marching in time, an incremental time step $\Delta t= 3.33\times 10^{-8}$ is used. Since construction of a reference solution for this example requires an extremely large computational domain, the solution is validated qualitatively.

Figure 20 illustrates the metal concentration level as well as the gradient field of the solution at three different time instants. Due to symmetry, we only show a portion of the solution domain in the first octant of the global coordinate system. From the concentration plots, it is clear that the solid phase is gradually reducing in time and the corrosion front is moving towards the centre of the sphere. Moreover, the results obtained for the gradient field indicates that the solid concentration is diffusing out of the domain with a flux perpendicular to the truncating surface and towards the exterior domain. It can be concluded that the absorbing layer is performing properly. For further investigation, the variation of energy in time is reported in Fig. 21. It can be inferred that the energy is dissipating monotonically in time. The calculations were done up to more than $2 \times 10^{6}$ time steps. No indication of instability was observed.

Fig. 21

The variation of energy in Example 3

6 Conclusions

This paper proposes a new strategy for constructing absorbing boundary conditions (ABCs) suitable for diffusion-type problems in unbounded domains. A particular attention is paid to develop the ABCs for a peridynamic (PD) diffusion model. We develop the ABCs for both local and nonlocal diffusion at the continuum level and we devise an appropriate implementation of the method at the discrete level. The method is applicable to available meshfree PD discretizations for the nonlocal diffusion as well as the standard finite element method (FEM) for the local diffusion equation. The proposed ABCs are derived from exponential basis functions (EBFs) which play the role of vanishing modes capable of constructing semi-analytical solutions for the exterior domain. The way of adjusting the EBFs for proper satisfaction of the infinity condition is thoroughly discussed in the paper. Following that, the far field solution is patched to the near field one by prescribing accurate Dirichlet ABCs obtained from the semi-analytical solution. Since the ABCs are Dirichlet-type, the method is simple to implement and free from any approximating differential operator. The ABCs are developed explicitly in the time domain and thus the method is free from any Fourier and Laplace transform procedures. In fact, this feature is especially appealing for the PD nonlocal diffusion equation, since the calculation of the kernel function (involved in the corresponding nonlocal operators) from the Laplace transform is cumbersome. The performance of the method is studied through some examples, including a 3D corrosion problem. Our investigations demonstrate that the method produces accurate results and exhibits a stable behavior even in the case of long-term computations.

Appendix A Computation of modes in 3D

We discuss the way of finding the modes in 3D problems. Let us take $\psi$ as a generic 3D mode of the following form:

$$\begin{aligned} \psi ({\mathbf {x}},t) = \exp (\varvec{\alpha }\cdot {\mathbf {x}} + \omega t), \quad \varvec{\alpha } = (\alpha _{x},\alpha _{y},\alpha _{z}), \end{aligned}$$

(51)

where $(\alpha _{x},\alpha _{y}, \alpha _{z},\omega ) \in \mathbb {R}^{4}$ and ${\mathbf {x}} = (x,y,z)$ in the Cartesian coordinate system. Similar to (14), without loss of generality, we make the following assumption, to consider all possible flux directions (here within a unit sphere):

$$\begin{aligned} \begin{aligned}&(\alpha _{x},\alpha _{y},\alpha _{z}) = \kappa \left( \cos \phi _{1}\sin \phi _{2},\sin \phi _{1}\sin \phi _{2},\cos {\phi _{2}}\right) , \\&\kappa \in \mathbb {R}, \quad 0\le \phi _{1}< 2\pi , \quad 0\le \phi _{2}<\pi . \end{aligned} \end{aligned}$$

(52)

Similar to the procedure in 2D, by replacing the above equation for $\varvec{\alpha }$ in (51) and plugging $\psi$ into the governing equation of the local diffusion (with 0 right-hand side) as well as taking the trivial solution aside, one can reach to the following characteristic equation in 3D:

$$\begin{aligned} \begin{aligned}&\omega = \chi ^{2}\kappa ^{2}\left[ \cos ^{2}\phi _{2} + \sin ^{2}\phi _{2} \left( \cos ^{2}\phi _{1} + \sin ^{2}\phi _{1} \right) \right] \\&\quad = \chi ^{2}\kappa ^{2}, \end{aligned} \end{aligned}$$

(53)

which is the exact analogue of that in 2D in (17). Thus, according to (51), $\psi$ is given by

$$\begin{aligned} \psi ({\mathbf {x}},t) = \exp \left( \varvec{\alpha } \cdot {\mathbf {x}} + \chi ^{2}\kappa ^{2}t\right) . \end{aligned}$$

(54)

To find the PD mode in 3D, for example by taking $p=1$ for the kernel function in (7) and assuming a constant micro-diffusivity c, one can proceed with a similar procedure to that from (18) to (20) assuming a spherical shape for the neighborhood. The characteristic equation of the nonlocal diffusion, counterpart of (21) for 3D cases, in the spherical coordinate system using $\varvec{\xi } = r (\cos \theta \sin \varphi ,\sin \theta \sin \varphi ,\cos \varphi )$, can be written as follows:

$$\begin{aligned} \omega =c_{0}\int _{0}^{\pi }\int _{0}^{2\pi }\int _{0}^{\delta }\left[ \exp (r\eta )-1\right] r \sin \varphi \mathrm {d}r\mathrm {d} \theta \mathrm {d}\varphi , \end{aligned}$$

(55)

where $\eta = \varvec{\alpha }\cdot \left( \cos {\theta }\sin {\varphi },\sin {\theta }\sin {\varphi },\cos {\varphi }\right)$. Now, similar to the procedure for (22), rewriting the integrand of (55) by taking a Taylor expansion with respect to $r \eta$ and about 0 concludes:

$$\begin{aligned} \omega = c_{0}\pi \left( \frac{\kappa ^2\delta ^{4}}{6} + \frac{\kappa ^4\delta ^{6}}{180} + \frac{\kappa ^6\delta ^{8}}{10080} + \ldots \right) , \end{aligned}$$

(56)

and thus, by replacing $\omega$ from the above equation in (51), the PD mode takes the following form:

$$\begin{aligned} \psi ({\mathbf {x}},t) = \exp \left( \varvec{\alpha } \cdot {\mathbf {x}} + c_{0}\pi \left( \frac{\kappa ^2\delta ^{4}}{6} + \frac{\kappa ^4\delta ^{6}}{180} + \ldots \right) t\right) . \end{aligned}$$

(57)

Similar to the procedure given in (25)–(27), assuming that in the limit $\kappa \delta \rightarrow 0$ the nonlocal mode recovers the local one, the appropriate value for $c_{0}$ can be found as:

$$\begin{aligned} c_{0} = \frac{6 \chi ^{2}}{\pi \delta ^{4}}. \end{aligned}$$

(58)