1 Introduction

With the advent of micro-fabrication technologies [1], the demand for miniature devices utilizing heterogeneous materials is steadily increasing. These devices encompass a variety of applications, ranging from electronic machinery [2, 3] to a special class of engineered materials called thermal meta-materials [4] which can be used to harvest thermal energy [5,6,7], manipulate heat flux [8, 9], as well as to perform thermal cloaking [10,11,12]. In order to design these components, it is important to correctly simulate and capture the underlying physics. Usually, an energy balance equation is solved to capture the heat transfer using a numerical method such as finite elements [13]. However, a high contrast in material properties, a complex topology and time varying thermal loads render the coefficients in the energy balance equation highly oscillatory, which an excessively a very fine discretization in both space and time. Consequently, simulations become computationally intractable.

The homogenization of heterogeneous medium [14,15,16,17,18] introduces the concept of an equivalent homogeneous macroscopic medium, representing an effective behavior of the microscopic medium with highly variable coefficients. Homogenization enables reduction of the computational cost, since an approximate response can be captured with a coarser discretization. It is achieved by solving a two-scale problem in a coupled manner, which requires the solution of the energy balance equation at the microscale, usually using a representative volume element (RVE), associated to each macroscopic material point, followed by an averaging procedure to extract homogenized effective macroscopic quantities that are used in the energy balance equation at the macroscale. To include transient terms in the energy balance equation, certain conditions on the material properties and loading should hold [19,20,21,22], which requires a proper definition of the separation of scales. For heat conduction problems, separation of scales is defined based on the characteristic diffusion times \(t_k\) associated to each k-th material constituent and the characteristic loading time T.

For the homogenization of transient diffusion problems, the ratios between the different characteristic diffusion times and the loading time determines if the microscale and the macroscale are separated or not. A full separation of scales indicates that the characteristic macroscopic loading time scale is much larger than all the microscopic characteristic diffusion times, independently of the ratios between the characteristic diffusion times of the different microstructural constituents. In such regimes, transient effects are negligible at the microscale and it is appropriate to use a steady-state energy balance equation at the microscale. This assumption has been widely used in the literature, see for example [19, 22,23,24,25,26,27]. The macroscopic thermal gradient is then the only conjugate quantity for the macroscopic heat flux and the macroscopic heat capacity can be calculated using the rule of mixtures. For a linear material model, in the regime of full separation of scales, the microscopic analysis and averaging performed only once to recover the (constant) effective macroscopic quantities.

However, when the microscopic characteristic diffusion times are of the same order of magnitude as the characteristic macroscopic loading time scale, the assumption of full separation of scales is no longer valid and the macro and microscale phenomena are coupled. In such regimes, significant transient effects are present at the microscale, in some or all microstructural constituents, which must be taken into account when homogenization is performed. If steady-state is assumed in such regimes, the microscopic transient effects, due to so-called microscale thermal inertia [28], will not be captured in the homogenized macroscopic description. Taking into account the transient microscale effects, the energy balance equation with the transient term should be solved at both scales. Homogenization in such transient regimes for thermal diffusional [28,29,30,31] and mechanical vibration [32,33,34,35] problems have already been developed. Since, the microscopic problem has to be solved at each macroscopic material point in time, the homogenization in transient regimes comes with a substantially higher computational cost. The present work aims at reducing the computational cost for homogenization in such transient regimes.

A reduced order model based on sub-structuring technique such as Craig–Bampton mode synthesis [36] was proposed for the homogenization of mechanical acoustic meta-materials [37]. It makes use of material linearity and the relaxed separation of scales. Substructuring of a mechanical system involves the division of the whole structure into smaller sub-structures with connected boundaries. Each substructure boundary is assumed to experience a rigid body motion and the dynamic effects only exist internally. If the boundary of the substructure is also dynamic then the substructuring provides a stiffer approximation [37]. For the homogenization of transient mechanical problems, the relaxed separation of scales implies that the matrix remains quasi-static under transient loading conditions and only the inclusions experience dynamic effects [32]. In the context of computational homogenization, when relaxed separation of scales is satisfied, each microscopic domain attached to a macroscopic material point is assumed to be a substructure attached to the macroscopic domain.

Similarly, in transient heat conduction problems, the relaxed separation of scales constitutes a thermal diffusion phenomenon in which the matrix remains in steady-state under transient thermal loads and only the inclusions exhibit transient heat diffusion. Assuming linear material properties and relaxed separation of scales, an additive decomposition is performed to compute the microscopic steady-state and transient response, separately. The reduced basis is obtained using a static condensation for the steady-state part and an eigenvalue problem is solved for the transient part. To benefit from the model reduction, the microscopic problem is projected on the reduced basis subspace, which yields an evolution equation for the microscale thermal inertia in terms of the coefficients of the reduced basis. These evolution equations for the amplitudes of the reduced variables, together with the macroscopic energy balance and the effective homogenized constitutive equations give rise to an enriched continuum description at the macroscale. This article deals with the model reduction at the microscale and compares the proposed formulation with a conventional transient computational homogenization scheme [28, 29]. The solution of the macroscale enriched continuum, emerging from the model reduction at the microscale, and the comparison to direct numerical simulations are beyond the scope of this contribution and will be addressed in the future work.

A related paper has been published in [38], which focuses primarily on the error analysis for the model reduction in transient computational homogenization. However, in that work no discussion is made on the separation of scales and the limitations it imposes on reduced order computational homogenization. To the best of authors’ knowledge the novel aspects of the current work, in the context of computational homogenization for transient heat conduction problems, are:

  • Introduction of the relaxed separation of scales.

  • A model reduction technique for the microscale which leads to an enriched continuum formulation at the macroscale.

1.1 Outline

In this article, the homogenization framework is derived in Sect. 2; the notion of the separation of scales is here defined, the generalized Hill–Mandel condition, upscaling, and downscaling relations are presented. In Sect. 3, a computational method combined with model reduction is developed. Section 4 presents the proof-of-principle numerical examples. The paper ends with concluding remarks and future perspectives.

1.2 Symbols and notations

Macroscopic quantities are represented with a bar on top: for example a scalar, a vector and a second-order tensorial macroscopic quantity are written as \(\overline{a}, \ \overline{\varvec{a}}, \text { and } \overline{\varvec{A}}\), respectively. Microscopic quantities are represented without a bar on top, a microscopic scalar, vector and second-order tensorial quantity are written as \(a, \ \varvec{a}\text { and } \varvec{A}\). The same cartesian basis is adopted at the macro and micro scales. The dot product between two vectors and between a second-order tensor and a vector is represented as \(\varvec{a}\cdot \varvec{b}:= a_i b_i\) and \(\varvec{A}\cdot \varvec{a}:= A_{ij} a_j \varvec{e}_i\), respectively. A tensorial dyadic product is denoted with \(\varvec{a}\otimes \varvec{b}:= a_i b_j \varvec{e}_i \otimes \varvec{e}_j\) and \(\varvec{A}\otimes \varvec{a}:= A_{ij} a_k \varvec{e}_i \otimes \varvec{e}_j \otimes \varvec{e}_k\). The gradient of a scalar and a vector is defined as \(\varvec{\nabla }a := {\partial a}/{\partial x_i} \varvec{e}_i\) and \(\varvec{\nabla }\varvec{a}:= {\partial a_i}/{\partial x_j} \varvec{e}_i \otimes \varvec{e}_j\). Similarly, the divergence operates as \(\varvec{\nabla }\cdot \varvec{a}:= {\partial a_i}/{\partial x_i}\) and \(\varvec{\nabla }\cdot \varvec{A}:= {\partial A_{ij}}/{\partial x_i} \varvec{e}_j\). For linear algebra operations, columns are represented with a tilde underneath a lowercase letter e.g. and matrices are represented with a bar underneath an uppercase letter e.g. \(\underline{A}\). A tensorial product between two column arrays of vectors is defined as , where

$$\begin{aligned} \underline{\otimes } := \left[ \begin{matrix} \otimes &{}\quad 0&{}\quad \cdots &{}\quad 0 \\ 0&{}\quad \otimes &{}\quad &{}\quad \vdots \\ \vdots &{}\quad &{}\quad \ddots &{} \\ 0&{}\quad 0&{}\quad \cdots &{}\quad \otimes \end{matrix} \right] . \end{aligned}$$
(1)

The microscopic domain and its boundary are represented by \(\Omega \) and \(\partial \Omega \), respectively. The volume average of a microscopic quantity \(\bullet \) is defined as

$$\begin{aligned} \left\langle \bullet \right\rangle := \frac{1}{V} \int _{\Omega } \bullet \,\text {d}\Omega , \end{aligned}$$
(2)

where \(V = \int _{\Omega }\,\text {d}\Omega \) is the volume of the microscopic domain \(\Omega \). Acronyms RTH, CTH  and SSH are used for reduced transient computational homogenization (present contribution), conventional transient homogenization (i.e. without model reduction) and steady-state computational homogenization, respectively. The material with the lowest characteristic diffusion time is called “fast” and the material with large characteristic diffusion time is called “slow”.

2 Homogenization framework

In this section, the relaxed separation of scales is defined for heat conduction problems. The energy balance equations at the micro and macroscales are presented and finally, the downscaling and upscaling relations are derived.

2.1 Separation of scales

The separation of scales in homogenization of transient diffusion problems is defined in terms of the characteristic diffusion times that are linked to the loading conditions, material properties and characteristic length scales. In this work, a two-phase periodic medium is considered in which the connected phase is the matrix and the embedded particulates are the inclusions. The characteristic diffusion times for the matrix \( t_m \) and inclusions \( t_i \) are defined as

$$\begin{aligned} t_m := \frac{l_m^2}{\mathcal {D}_m}, \quad \text {and} \quad t_i := \frac{d^2}{\mathcal {D}_i}, \end{aligned}$$
(3)

where \(l_m\) and d are the characteristic lengths, e.g. the spacing between the inclusions and the inclusion diameter, respectively, and \(\mathcal {D}_m\) and \(\mathcal {D}_i\) are the thermal diffusivity coefficients of the matrix and inclusions, respectively. The characteristic loading time T is the inverse of the ratio of the rate of change of the macroscopic temperature field \( \dot{\bar{\theta }} \) with respect to the macroscopic temperature \( \bar{\theta }\)

$$\begin{aligned} T \sim \frac{1}{\omega } := \left( \frac{\dot{\bar{\theta }}}{\bar{\theta }} \right) ^{-1}, \end{aligned}$$
(4)

where \(\omega \) is the (angular) loading frequency. Different relations between \( t_m, \ t_i \) and T define different separation of scales regimes. For the development of the reduced computational homogenization and comparison to conventional methods a few separation of scales regimes are defined here.

Full separation of scales: In a full separation of scales regime the characteristic diffusion times at the microscale are much smaller than the characteristic loading time T, i.e. the material constituents reach steady-state instantly

$$\begin{aligned} T \gg (t_m \sim t_i), \text { or } \quad T \gg (t_m < t_i), \text { or } \quad T \gg (t_m > t_i). \end{aligned}$$
(5)

The ratio between the characteristic diffusion times of different constituents does not matter in this case. Under these conditions, the classical steady-state homogenization is sufficient to capture the heat diffusion phenomena in a heterogeneous medium. For example, the homogenization procedure adopted in [24] assumes a steady-state microscale model for the simulation of refractory bricks used in a furnace lining. The macroscopic heat flux is obtained through the computational homogenization and the heat storage capacity is obtained by using the rule of mixtures.

Non-separating scales: In these regimes, the microscopic diffusion times of the matrix, the inclusions or both are of the same order of magnitude as the macroscopic loading time. As a consequence, transient phenomena are active at the microscale. Some of these regimes can be represented as

$$\begin{aligned}&T \sim t_m \sim t_i \,, \end{aligned}$$
(6a)
$$\begin{aligned}&(T \sim t_m) > t_i \,, \end{aligned}$$
(6b)
$$\begin{aligned}&(T \sim t_i) > t_m \,. \end{aligned}$$
(6c)

In (6a) both the matrix and the inclusions are transient, in (6b) the matrix is more transient than the inclusion and (6c) shows the regime in which the inclusions experience more transient effects than the matrix. The energy balance equation with the transient terms has to be used at the microscale to capture thermal inertia accurately. For example in [28], a sintering problem is solved using transient computational homogenization, the material properties and the loading conditions were such that they are adequately represented by the separation of scales regime of Eq. (6c). Therefore, both the macroscopic heat flux and the rate of change of the macroscopic internal energy are calculated by computational homogenization; if the rule of mixture would have been used instead, it would entail significant errors.

Relaxed separation of scales: This intermediate regime is characterized by specific material properties: a fast matrix, i.e. it attains the steady state almost instantaneously, and slow inclusions. It can be defined as

$$\begin{aligned} (T \sim t_i)\,\gg \, t_m. \end{aligned}$$
(7)

This is a limiting case of the regime given by Eq. (6c) and represents no or negligible transient effects in the matrix. Heterogeneous materials operating in this regime are characterized by a high conductivity and low heat storage capacity in the matrix and low conductivity and high heat storage capacity in the inclusions. Since the evolution of the temperature field in the matrix is different from that in the inclusions, the microscopic temperature field can be decomposed into steady-state and transient parts. To capture the micro inertia effects, the transient balance of energy has to be solved at the microscale and both, the macroscopic heat flux and rate of change of macroscopic internal energy, must be computed/upscaled using computational homogenization.

2.2 Energy balance equation at the macro and microscales

To model the transient heat conduction at the macroscale, the energy balance equation with the transient term is used

$$\begin{aligned} \overline{\varvec{\nabla }}\cdot \overline{\varvec{q}}+ \dot{\overline{\epsilon }} = 0, \end{aligned}$$
(8)

where \(\overline{\varvec{q}}\) and \(\dot{\overline{\epsilon }}\) are the macroscopic heat flux and the rate of change of macroscopic internal energy. The constitutive forms for \(\overline{\varvec{q}}\) and \(\dot{\overline{\epsilon }}\) are yet unknown, and in the computational homogenization are obtained through an upscaling procedure. The macroscale problem is complemented by boundary and initial conditions as given by the particular problem at hand. To capture the thermal inertia effects, the transient energy balance equation is considered at the microscale as well

$$\begin{aligned} \varvec{\nabla }\cdot \varvec{q}+ \dot{\epsilon } = 0, \end{aligned}$$
(9)

where \(\varvec{q}\) and \(\dot{\epsilon }\) are the microscopic heat flux and the rate of change of the microscopic internal energy. The constitutive relations, for each microscale constituent, are assumed to be known and may in general be non-linear. In the present work only linear micro-constituent materials will be considered to facilitate the application of the model reduction. For the microscopic heat flux, Fourier’s law \(\varvec{q}= -\lambda \varvec{\nabla }\theta \) is used and for the internal energy \(\epsilon \) the constitutive relation \(\epsilon = \rho c \theta \) applied. In this work, an isotropic material behavior is assumed for simplicity, even though the methodology would be directly applicable to general anisotropic materials as well. To ensure consistent scale transition in computational homogenization, specific types of boundary conditions are required at the microscale, which will be defined through the downscaling procedure.

2.3 Downscaling

The microscopic temperature field is defined as a first order Taylor’s approximation around a macroscopic point \(\overline{\varvec{x}}\)

$$\begin{aligned} \theta (\overline{\varvec{x}}, \varvec{x}, t) := \bar{\theta }(\overline{\varvec{x}}, t) + \overline{\varvec{\nabla }}\bar{\theta }(\overline{\varvec{x}}, t) \cdot (\varvec{x}- \overline{\varvec{x}}) + \tilde{\theta }(\overline{\varvec{x}}, \varvec{x}, t), \end{aligned}$$
(10)

where \(\varvec{x}\) denotes the position vector at the microscale and \(\tilde{\theta }\) represents the higher order term in the expansion which are the fluctuations in the temperature field at the microscale. These fluctuations arise due to the difference in material properties between the constituents subjected to transient loading conditions. The microscale is positioned relative to the macroscopic point such that \(\langle \varvec{x}- \overline{\varvec{x}}\rangle = \varvec{0}\).

Downscaling is a procedure to transfer information from the macroscale to the microscale. In the first-order computational homogenization, both the macroscopic temperature and its gradient are transferred to the microscale and assumed to be constant over the considered microstructure domain. The downscaling relations in transient computational homogenization provide two constraints to be satisfied:

  1. 1.

    The average of the microscopic temperature field should be equal to the macroscopic temperature field at the macroscopic point \( \overline{\varvec{x}}\)

    $$\begin{aligned} \bar{\theta }(\overline{\varvec{x}}, t) = \left\langle \theta (\overline{\varvec{x}}, \varvec{x}, t) \right\rangle , \end{aligned}$$
    (11)

    which by using Eq. (10) and \( \langle \varvec{x}- \overline{\varvec{x}}\rangle = 0 \), requires the average of the fluctuation field at the microscale vanish

    $$\begin{aligned} \langle \tilde{\theta }\rangle = 0. \end{aligned}$$
    (12)
  2. 2.

    The average of the microscopic temperature gradient field should be equal to the macroscopic temperature field

    $$\begin{aligned} \overline{\varvec{\nabla }}\bar{\theta }(\overline{\varvec{x}}, t) = \left\langle \varvec{\nabla }\theta (\overline{\varvec{x}}, \varvec{x}, t) \right\rangle . \end{aligned}$$
    (13)

    It is obtained by taking the gradient of the microscopic temperature field, in Eq. (10), and averaging it over the microscopic domain

    $$\begin{aligned} \left\langle \varvec{\nabla }\theta \right\rangle = \overline{\varvec{\nabla }}\bar{\theta }+ \left\langle \varvec{\nabla }\tilde{\theta }\right\rangle , \end{aligned}$$
    (14)

    where the identity \( \varvec{\nabla }(\varvec{x}- \overline{\varvec{x}}) = \varvec{I}\) is used. To fulfill the condition in Eq. (14), the average of the gradient of the fluctuation field has to be zero \( \langle \varvec{\nabla }\tilde{\theta }\rangle = \varvec{0} \), which after applying Gauss’s divergence theorem, is written as

    $$\begin{aligned} \int _{\partial \Omega } \tilde{\theta }\varvec{n}\text { d} a = \varvec{0}, \end{aligned}$$
    (15)

    where \( \varvec{n}\) is the unit-normal outward vector on the microscopic boundary \( \partial \Omega \) with infinitesimal surface area \( \text {d}a \).

Constraint (12) enforces the macroscopic temperature \( \bar{\theta }(\overline{\varvec{x}}, t) \) to be the reference temperature in the microscopic domain and constraint (15) requires specific types of boundary conditions to be used at the microscale. Typical choices for these boundary conditions adopted in the literature are (i) zero fluctuation boundary conditions or (ii) periodic fluctuation boundary conditions. Now that, the microscopic temperature field and the downscaling relations are defined, the upscaling relations are established next.

2.4 Upscaling

Upscaling is performed to transfer information from the microscale to the macroscale through an averaging procedure. For transient computational homogenization, a generalized Hill–Mandel condition is used [28, 29], which states that the volume average of the virtual power at the microscale is equal to the virtual power (per unit of volume) at the associated macroscopic point \( \overline{\varvec{x}}\)

$$\begin{aligned} - \overline{\varvec{\nabla }}\delta \bar{\theta }\cdot \overline{\varvec{q}}+ \delta \bar{\theta }\dot{\overline{\epsilon }} = \left\langle - \varvec{\nabla }\delta \theta \cdot \varvec{q}+ \delta \theta \dot{\epsilon } \right\rangle . \end{aligned}$$
(16)

Substitution of the perturbation of the microscopic temperature field (10) and its gradient in the right hand side of Eq. (16) provides

$$\begin{aligned} - \overline{\varvec{\nabla }}\delta \bar{\theta }\cdot \overline{\varvec{q}}+ \delta \bar{\theta }\dot{\overline{\epsilon }}= & {} \left\langle - \left( \overline{\varvec{\nabla }}\delta \bar{\theta }+ \varvec{\nabla }\delta \tilde{\theta }\right) \cdot \varvec{q}\right. \nonumber \\&\left. + \left( \delta \bar{\theta }+ \overline{\varvec{\nabla }}\delta \bar{\theta }\cdot (\varvec{x}- \overline{\varvec{x}}) + \delta \tilde{\theta }\right) \dot{\epsilon } \right\rangle . \nonumber \\ \end{aligned}$$
(17)

Expanding and rearranging the above expression for \(\delta \bar{\theta }\) and \(\delta \tilde{\theta }\) gives

$$\begin{aligned} - \overline{\varvec{\nabla }}\delta \bar{\theta }\cdot \overline{\varvec{q}}- \delta \bar{\theta }\dot{\overline{\epsilon }}= & {} \left\langle \left[ - \overline{\varvec{\nabla }}\delta \bar{\theta }\cdot \left( \varvec{q}+ (\varvec{x}- \overline{\varvec{x}}) \dot{\epsilon } \right) + \delta \bar{\theta }\dot{\epsilon } \right] \right. \nonumber \\&\left. + \left[ - \varvec{\nabla }\delta \tilde{\theta }\cdot \varvec{q}+ \delta \tilde{\theta }\dot{\epsilon } \right] \right\rangle . \end{aligned}$$
(18)

The last term in Eq. (18) is the weak form of the microscopic balance of energy with admissible temperature fluctuation field \( \delta \tilde{\theta }\), which by using integration by parts and the divergence theorem can be written as

$$\begin{aligned} \left\langle -\varvec{\nabla }\delta \tilde{\theta }\cdot \varvec{q}+ \delta \tilde{\theta }\dot{\varepsilon } \right\rangle = \left\langle \delta \tilde{\theta }\left( \varvec{\nabla }\cdot \varvec{q}+ \dot{\epsilon } \right) \right\rangle - \int _{\partial \Omega } \delta \tilde{\theta }\varvec{q}\cdot \varvec{n}\text { d}a. \end{aligned}$$
(19)

The first term in the right hand side of the above equation is the balance of energy at the microscale (9) which is satisfied by the microscale solution and therefore equals zero. The second term is also zero when appropriate boundary conditions are used, as discussed at the end of the previous section, for more details see [24]. Finally, Eq. (18) reduces to

$$\begin{aligned} - \overline{\varvec{\nabla }}\delta \bar{\theta }\cdot \overline{\varvec{q}}+ \delta \bar{\theta }\dot{\overline{\epsilon }} = - \overline{\varvec{\nabla }}\delta \bar{\theta }\cdot \left\langle \varvec{q}- (\varvec{x}- \overline{\varvec{x}}) \dot{\epsilon } \right\rangle + \delta \bar{\theta }\left\langle \dot{\epsilon } \right\rangle , \end{aligned}$$
(20)

from where the macroscopic heat flux is recognized as

$$\begin{aligned} \overline{\varvec{q}}= \left\langle \varvec{q}- (\varvec{x}- \overline{\varvec{x}}) \dot{\epsilon } \right\rangle , \end{aligned}$$
(21)

and the rate of change of the macroscopic internal energy as

$$\begin{aligned} \dot{\overline{\epsilon }} = \left\langle \dot{\epsilon } \right\rangle . \end{aligned}$$
(22)

The second term in Eq. (21) is the moment of the rate of change of the microscopic internal energy, which is responsible for transferring the microscale thermal inertia to the macroscale. It also carries the information about the size of the microscale, which makes transient computational homogenization sensitive to the microscale size. In the limit, when the RVE size is vanishingly small, the transient effects disappear and a classical SSH result \(\overline{\varvec{q}}= \langle \varvec{q}\rangle \) is obtained.

Substituting the definition of the microscopic temperature field (10) into the constitutive Eq. (22) reveals that it is also a function of the macroscopic temperature gradient i.e. , \( \overline{\epsilon } = \overline{\epsilon } (\bar{\theta }, \overline{\varvec{\nabla }}\bar{\theta }) \). This non-local dependence is not present in classical irreversible thermodynamics and requires a non-local thermodynamic description at the macroscale. In the gradient enriched thermodynamics, an additional dissipation term is added in the entropy inequality at the macroscale, upon averaging the (classical) dissipation at the microscale and applying proper boundary conditions, which can be recognized as the second term in the expression of macroscopic flux in Eq. (21). For a more detailed analysis of the emerging macroscopic thermodynamics in computational homogenization of transient dissipative phenomena the reader is directed to the recent articles on the topic [39, 40]. Also in [41], a thermodynamical model including temperature gradients is developed and rationalized using homogenization of heterogeneous media. However a steady-state assumption was made in that case. For a general analysis of extended thermodynamic theories the reader is directed to the review article [42].

Converting the volume integrals of Eqs. (21) and (22) into boundary integrals using the divergence theorem and the microscopic energy balance (9), allows to write the macroscopic heat flux as

$$\begin{aligned} \overline{\varvec{q}}= \frac{1}{V} \int _{\partial \Omega } q_n (\varvec{x}-\overline{\varvec{x}}) \text { d}a, \end{aligned}$$
(23)

and the rate of change of macroscopic internal energy as

$$\begin{aligned} \dot{\overline{\epsilon }}= - \frac{1}{V} \int _{\partial \Omega } q_n \text { d}a, \end{aligned}$$
(24)

where \(q_n = \varvec{q}\cdot \varvec{n}\) is the normal outward heat flux at the boundary of the microscopic domain. Once \( q_n \) is known, the macroscopic quantities are obtained. Next, the solution procedure will be discussed, along with the model reduction to obtain \( q_n \).

3 Model order reduction

In this section, first the balance of energy at the microscale, Eq. (9), is written in a discrete form using the finite element formulation. Next, the reduced basis is obtained for the steady-state and transient parts of the microscopic response. The macroscopic constitutive equations and the microscopic balance of energy are then written in terms of the coefficients of the reduced variables leading to a thermal enriched continuum resulting from the model reduction. Finally, the guidelines to identify the transient reduced basis are discussed.

Fig. 1
figure 1

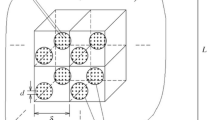
Discretized microscopic domain. The total set of DOFs are first divided into tied (dependent) and retained (independent) parts and then the retained DOFs are further subdivided into the prescribed and free parts (this figure is for illustrative purpose only; calculations were performed on a material and geometry conforming mesh)

Full size image

3.1 Microscale discrete problem

The semi-discrete form of the balance of energy at the microscale reads

(25)

where \(\underline{K}\) and \(\underline{C}\) are thermal conductivity and capacity matrices, respectively, is the column of nodal temperature values and is the incoming heat flux. The constraints following from Eqs. (12) and (15) are applied using the master-slave approach [43]. The periodic boundary conditions are applied by setting the fluctuation fields on opposite sides of the microscopic domain to be equal i.e. \(\tilde{\theta }^R = \tilde{\theta }^L\) and \(\tilde{\theta }^T = \tilde{\theta }^B\), where R denotes right, L—left, T—top and B—bottom boundary of the unit cell as shown in Fig. 1. Inserting \(\tilde{\theta }^R = \tilde{\theta }^L\) and \(\tilde{\theta }^T = \tilde{\theta }^B\) in Eq. (10) provides the constraint equations

$$\begin{aligned} \begin{aligned} \theta ^L - \theta ^R&= \overline{\varvec{\nabla }}\bar{\theta }\cdot (\varvec{x}^L-\varvec{x}^R), \\ \theta ^B - \theta ^T&= \overline{\varvec{\nabla }}\bar{\theta }\cdot (\varvec{x}^B-\varvec{x}^T). \end{aligned} \end{aligned}$$
(26)

For temperature independent material properties, constraint (12) can be applied by prescribing the microscopic temperature \(\theta (\overline{\varvec{x}}, \varvec{x}, t)\) at a point in the microscopic domain to be equal to the macroscopic temperature \(\bar{\theta }(\overline{\varvec{x}}, t)\). Here, this point is chosen arbitrarily to be node 1 at position \(\varvec{x}^1\). Then by applying (26) to the corner nodes 1, 2, 3 and 4, the temperature at these nodes is fully prescribed and given by

(27)

where \( p = \{ 1, 2, 3, 4 \} \) and is a column of ones with dimension \((p\times 1)\). The set of the corner nodes thus will be called “prescribed”. The constraint Eq. (26) can then also be written in a discrete setting in terms of the prescribed corner nodes as

(28)

where is a column of ones. In Eq. (28), the temperature fields on the left hand side are dependent on the temperature fields on the right hand side. To apply these boundary conditions, the microscopic degrees of freedom (DOF) are first split into tied (dependent) t and retained (independent) r DOFs. The retained DOFs are then further subdivided into prescribed p (nodes 1, 2, 3, 4) and free f parts as shown in Fig. 1. Following the master-slave implementation procedure, a matrix of tying relations \(\underline{M}\) is created from the constraint Eq. (28), which eliminates the tied DOFs by mapping the complete set of DOFs to the retained DOFs only

(29)

where are the temperature values of the tied DOFs and are the temperature values of the retained DOFs. The constraints are applied by substituting the expression of from (29) into (25), and pre-multiplying it with \( \underline{M}^T \), giving

(30)

which reduces the dimensionality of the problem to the retained DOFs only

(31)

where \(\overset{*}{\underline{K}}, \text { and } \overset{*}{\underline{C}}\) are the reduced thermal conductivity and capacity matrices, respectively, and is the column of the incoming reaction heat fluxes at the retained DOFs. In the subsequent text the superscript ‘r’ will be dropped from for brevity.

3.2 Microscale model reduction

To calculate the macroscopic quantities \( \overline{\varvec{q}}\) and \( \dot{\overline{\epsilon }} \), the expressions given in (23) and (24) are used. These expressions contain the incoming heat flux \( q_n \). In a discrete setting, the incoming (reaction) heat flux at the prescribed nodes can be post-processed once the solution of the microscale problem is available. After further partitioning the system of Eq. (31) into the prescribed and free parts, it reads as

(32)

Solving this system for each macroscopic point \( \overline{\varvec{x}}\) in time is a computationally expensive task, especially for a large macroscopic problem with a complex microstructural topology that usually requires a fine discretization in space and time. Therefore, a reduced model is sought which approximates the solution with a fewer DOFs only. The incoming heat flux can then be written in terms of the coefficients of the reduced basis, making the homogenization process computationally efficient. To perform the model reduction at the microscale, the microscopic temperature field \(\theta \) is decomposed into its steady-state \(\theta _{ss}\) and transient \(\theta _{tr}\) parts

$$\begin{aligned} \theta = \theta _{ss} + \theta _{tr}. \end{aligned}$$
(33)

This additive split is always warranted for linear problems in the relaxed separation of scales regime, where the transient temperature field in the inclusions evolves independently of the temperature field in the matrix. This decomposition is also advantageous because the reduced global bases for the steady-state and transient parts are calculated separately, and later a linear superposition is performed to reconstruct the total microscopic temperature field.

3.2.1 Steady-state contribution

The steady-state part of the microscale solution \( \theta _{ss} \) represents very slow time variations, where the microscale still follows the macroscale instantaneously. In the physical sense, this is a microscale that reaches steady-state very quickly. To obtain the steady-state response, the discrete system (32) is written in terms of \( \theta _{ss} \) only

(34)
(35)

Equation (34) provides the steady-state reaction fluxes at the prescribed DOFs and (35) is the evolution equation for the steady-state part of the microscopic temperature field at the free DOFs. Imposing the steady-state assumption on (35) requires to fulfill the following constraint

(36)

which provides the steady-state response \( \theta _{ss} \) in terms of the prescribed temperature field as

(37)

where and \(\underline{I}^{pp}\) is the unit diagonal matrix with dimension \((p \times p)\). The columns of \( \underline{S} \) can be interpreted as the steady-state reduced basis for each \( \theta \) in . To obtain the steady-state reaction fluxes in terms of the temperature at the prescribed DOFs, the constraint (36) is projected on the prescribed DOFs by premultiplying it with \( \underline{S}^T \) and the taking transpose of the expression i.e.

(38)

and then added to Eq. (34) which yields

(39)

where the steady-state conductivity and capacity matrices are defined as

(40)

The steady-state contribution does not capture the thermal inertia and microscale size effects. The transient contribution will therefore be added next.

3.2.2 Transient contribution

The transient part of the microscopic solution is described through the reduced basis vector and the corresponding reduced degrees of freedom \(\eta ^k\), where \(k = 1, 2, \ldots , N_q\) and \(N_q \ll N\), with \( N_q \) as the number of the reduced degrees of freedom and N the total number of the degrees of freedom of the original problem. The transient part of the microscopic solution can then be written as

(41)

where \(\underline{0}^{pq}\) is a \((N_p \times N_q)\) matrix of zeros, \(\overset{*}{\underline{\Phi }}\) is the matrix combining all the reduced basis vectors and is the column of the coefficients of the reduced basis. The energy balance Eq. (9) is a parabolic partial differential equation, which has a natural solution that decays exponentially in time i.e. , substituting this expression in the free part of (32)

(42)

provides

(43)

Since the transient heat problem at the microscale is linear, Eq. (43) can be solved as a classical eigenvalue problem leading to the eigenvalues \( \alpha _k \) and eigenvectors . It is a standard procedure used in model reduction and stability analyses of time integration schemes for transient diffusion problems see i.e.  [13, 44, 45]. Provided that is semi-positive definite and is positive definite, the eigenvectors are orthogonal and the corresponding eigenvalues \(\alpha ^k\) are real and can be arranged in a diagonal matrix \(\underline{\alpha }\)

$$\begin{aligned} \underline{\alpha } = \begin{bmatrix} \alpha ^1&\quad 0&\quad 0 \\ 0&\quad \ddots&\quad 0 \\ 0&\quad 0&\quad \alpha ^{N_q} \end{bmatrix}. \end{aligned}$$
(44)

When the eigenvalue problem (43) is solved, the number of eigenvectors is the same as the number of DOFs in the original discrete system of equations and at this point no reduction has been performed. The reduction from the full transient basis \( \underline{\Phi } \) to the reduced basis \( \overset{*}{\underline{\Phi }} \) is performed by selecting a limited set of eigenvectors, based on criteria proposed at the end of this section. In heat conduction problems, the eigenvectors are the temperature distributions inside the domain and the corresponding eigenvalues are the inverse of decay/rise times i.e. \(\tau ^k = {2\pi }/{\alpha ^k}\) [44]. Normalizing the eigenvectors with respect to the capacity matrix,

(45)

yields the eigenvalues as

(46)

Now that the the transient reduced basis \( \underline{\overset{*}{\Phi }}\) is identified through the eigenproblem analysis, it can be used for model reduction of the free part of the discrete system of Eq. (32). Substituting Eq. (41) in (32) yields

(47)

providing a set of decoupled ordinary differential equations (ODE). Using the normalization conditions (45) and (46) Eq. (47) takes the form

(48)

Equation (48) represents the transient evolution of the microscopic solution in terms of the variables , which in this form it is not influenced by the macroscale excitation. Next, the microscale steady-state and transient responses will be coupled through linear superposition.

3.2.3 Linear superposition

The microscopic steady-state and transient temperature fields, given by Eqs. (37) and (41) are superposed to obtain the total response

(49)

The right-hand side of this expression resembles the Craig–Bampton reduction matrix as originally proposed in [36] in the context of structural dynamics. Substituting (49) into (32) yields a set of coupled equations

(50)
(51)

Equation (50) relates the incoming heat flux at the prescribed nodes to the temperature at the prescribed nodes and the coefficients (i.e. macroscale variables) of the transient reduced basis. Equation (51) is the microscale evolution equation for in terms of . Premultiplying Eq. (47) with \( \underline{S}^T \) and using the expression for the steady-state reduced basis provides the expression for the first term in Eq. (50) as . Adding the constraint (38) to (51) and then rearranging for , and , allows to write the heat fluxes at the prescribed nodes as

(52)

where the matrix \( \underline{\varrho }\) is defined as

(53)

\(\underline{\varrho }\) provides the coupling between microscopic transient effects and the macroscopic quantities through . Equation (51) is projected onto the orthogonal basis by premultiplying it with \(\underline{\Phi }^T\)

(54)

Using cancels out the third and the fourth terms in the above equation and finally using the normalization conditions (45) and (46) leads to

(55)

Unlike Eq. (48), the above equation is coupled to the macroscale through , which is the forcing term for this ordinary differential equation and that serves as the input from the macroscale in terms of the prescribed temperature field . Next, the expression for given by Eq. (52) is used to express the homogenized macroscopic constitutive Eqs. (23) and (24) in terms of the coefficients of the steady state and transient reduced bases i.e. and .

3.3 Macroscopic quantities

In the discrete form, the boundary integral of the macroscopic heat flux (23) reads,

(56)

where , and the discrete form of the rate of change of the macroscopic internal energy (24) is written as

(57)

Substituting the expression for the reaction heat flux at the prescribed part of the boundary from Eq. (52) in Eq. (56) and using the discrete form of the prescribed temperature field, given by Eq. (27), the macroscopic heat flux \( \overline{\varvec{q}}\) is written as

(58)

where

(59)

Similarly, substituting the expression for the reaction heat flux from Eq. (52) in (57) and using the discrete form of the prescribed temperature field, given by Eq. (27), leads to the expression for the rate of change of the macroscopic internal energy

(60)

where

(61)

The evolution of the microscopic (modal) DOFs can also be expressed in terms of \(\bar{\theta }\) and \(\overline{\varvec{\nabla }}\bar{\theta }\) using Eq. (55) in conjunction with Eq. (27)

(62)

For the selected microscopic RVE, with known (constant) material properties, the calculation of, the steady-state basis, the eigenvectors , decay times \(\tau ^k\) and the coefficients in Eqs. (59) and (61) are performed in an off-line stage once and for all. The online stage consists of the solution of only the macroscopic enriched continuum equations which are specialized in the following subsection.

3.4 Thermal enriched continuum at macroscale

Together, the energy balance equation at the macroscale (8), the constitutive equation for the macroscopic heat flux (58), the constitutive equation for the rate of change of macroscopic internal energy (60) and the evolution equation for (62) constitute an enriched continuum model at the macroscale

(63)

The modal amplitudes , can be considered at the macroscopic description as internal variables which are responsible for the representation of the lagging behavior due to thermal inertia. To solve the system of Eq. (63) different solution schemes can be adopted. For example, can be condensed out at the macroscopic integration points leading to a single field (macroscopic temperature \( \bar{\theta }\)) solution scheme, or both and \( \bar{\theta }\) can be solved as macroscopic degrees of freedom, which leads to a multi-field solution scheme. The solution of the enriched macroscale continuum is not the scope of the present paper, but will be provided in future work instead.

3.5 Identification of transient reduced basis

Here, we discuss the selection of the transient reduced basis \(\overset{*}{\underline{\Phi }}\) from the complete basis \( \underline{\Phi } \) obtained by solving the eigenvalue problem (43). Since the right-hand side of Eq. (62) acts as the forcing term for each k-th equation, the variable \( \eta ^k \) corresponding to a higher value of the coupling term \( d^k \) or \( a_i^k \) will have a higher amplitude. This information is exploited to identify the eigenvectors with a significant contribution to the thermal inertia at the macroscale, whereas the other eigenvectors can be neglected in the analysis. The eigenvectors associated to \(d^k\) with relatively high contribution are identified using

$$\begin{aligned} E_{d^k} = {| d^k |}/{\max |d^k| }, \end{aligned}$$
(64)

and the eigenvectors associated to \(a_i^k\) with relatively high contribution are identified by,

$$\begin{aligned} E_{a_i^k} = {|| \varvec{a}^k ||}/{\max |a_i^k| }, \end{aligned}$$
(65)

Then, a reduced transient eigenbasis \(\overset{*}{\underline{\Phi }}\) can be obtained by requiring a minimum threshold \( \varepsilon \)

(66a)
(66b)
(66c)

4 Numerical examples

In this section, numerical examples are presented for a microstructure with randomly distributed circular inclusions. First, the steady-state and the transient reduced basis are identified, then the identification criteria for the transient reduced basis are assessed by analyzing the \( \eta ^k \) evolution and the error norms. The temperature profile and the macroscopic quantities computed with the proposed reduced order homogenization method are compared with the conventional steady-state and transient computational homogenization. Finally, an analysis is performed for different separation of scales regimes and microscale domain sizes, which explores the range of validity of the proposed reduced order homogenization.

Fig. 2
figure 2

A microscopic domain (RVE) with monodispersed circular inclusions; l is the characteristic size of the RVE and d the diameter of the inclusion

Full size image
Table 1 Default parameters used in the simulation
Full size table

4.1 Problem settings

A microscopic domain, shown in Fig. 2, with monodispersed circular inclusions is generated using a level set based random sequential adsorption method [46]. The inclusions are allowed to cross the RVE boundary under the applied periodicity constraint. The RVE is discretized with a periodic finite mesh, which ensures that opposite sides of the domain have corresponding nodes to match periodicity. The default parameters used in the numerical examples are provided in Table 1. A high contrast two phase material is considered in the simulations, such that the ratio between the diffusivity of the matrix and the inclusion is \( {\mathcal {D}_m}/{\mathcal {D}_i} = 10^{5} \). The microscopic domain is excited by the macroscopic temperature \( \bar{\theta }\) and its gradient \( \overline{\varvec{\nabla }}\bar{\theta }\) oscillating in time as

$$\begin{aligned} \bar{\theta }(\overline{\varvec{x}}, t)&= \bar{\theta }_{\max } \sin (\omega t) \nonumber \\ \overline{\varvec{\nabla }}\bar{\theta }(\overline{\varvec{x}}, t)&= (\overline{\varvec{\nabla }}\bar{\theta })_{\max } \sin (\omega t) \end{aligned}$$
(67)

where \( \omega = {2\pi }/{T} \) is the angular frequency and T is the total loading time. In the simulations, one period of the loading cycle has been considered. Note, that the default material parameters, microscopic length scales and the characteristic loading time satisfy the relaxed separation of scales as presented in Sect. 2. The RVE is discretized with three-node linear triangular finite elements with a finer mesh inside the inclusion. The time integration is performed using a backward-Euler scheme with a time step size of \( \Delta t = 10^{-3} T \). Finally, a non-dimensional problem is solved, in which the total time is normalized with respect to the characteristic diffusion time of the inclusion i.e. \( \hat{t} = {t}/{t_i} \), the lengths are normalized with respect to the characteristic length of the RVE i.e. \( \hat{l} = {x}/{l} \), and the temperature is normalized with the maximum attainable temperature in the microscopic domain i.e. \( \hat{\theta }={\theta }/{\theta _{\max }} \), where \( \theta _{\max } = \bar{\theta }_{\max } + \overline{\varvec{\nabla }}\bar{\theta }_{\max }\cdot \varvec{x}_{\max } \) and \( \varvec{x}_{\max } = [l,\ l] \). Next, we identify the steady-state and transient reduced basis.

4.2 Reduced basis identification

The reduced bases are computed during an off-line stage, which consists in performing the static condensation, solving an eigenvalue problem and computing the coefficients given in Eqs. (59) and (61).

Fig. 3
figure 3

The steady-state part of the temperature field \( \theta _{ss} \) decomposed into its reduced basis \( \underline{S} \) and corresponding coefficients \( \theta ^p \)

Full size image
Fig. 4
figure 4

The transient part of the temperature field \( \theta _{tr} \) decomposed into its reduced basis \( \underline{\Phi } \) and corresponding coefficients \(\eta \)

Full size image

4.2.1 Steady-state basis

The steady-state part of the microscopic temperature field \( \theta _{ss} \) is given by Eq. (37), where each column of \( \underline{S} \) is a load case constituting the steady-state global basis. The corresponding prescribed temperature degrees of freedom in are the coefficients. The size of the steady-state reduced basis is dependent on the type of boundary conditions used at the microscale. If, for example, zero fluctuations boundary condition is applied to all nodes on the boundary to fulfill the scale transition relations then the size of the steady-state reduced basis will be equal to the number of nodes on the RVE boundary and the corresponding coefficients will be the prescribed temperature degrees of freedom at all the nodes of the RVE boundary. For the periodic boundary conditions, as used in this work, includes the temperature values of the three prescribed nodes, i.e. which are defined at nodes 1, 2 and 4 and the size of the steady state reduced basis consequently equals three corresponding to the three load cases to be solved. For the considered microstructural model, the steady-state response is decomposed into its reduced basis and corresponding coefficients as shown in Fig. 3.

4.2.2 Transient basis

To identify the transient basis, an eigenvalue problem is solved for the first 200 eigenvectors \( \underline{\Phi } \), through which the transient reduced basis \(\overset{*}{\underline{\Phi }}\) is identified. The size of the transient reduced basis depends on the micro-structure topology and material contrast between the matrix and the inclusions. It is selected by the criteria provided in Eq. (66) based on the relative contribution of the coupling terms and . The transient response \( \theta _{tr} \) is decomposed into its reduced basis, and corresponding coefficients, as shown in Fig. 4. Since the relaxed separation of scales is satisfied, the eigenvectors have non-negligible contributions only inside the inclusions. In general, when using a reduced basis description for the transient analysis of a heat conduction problem, only the first or first few consecutive eigenvectors with the lowest eigenvalues are commonly used [13]. This is different in the current analysis, where based on the coupling terms and , eigenvectors , with high eigenvalues have also been selected, which are significantly important for capturing the effect of the microscale thermal inertia at the macroscale. This will be verified in the following by assessing the evolution of the \( \eta ^k \) fields, and comparing the error norms with respect to the reference CTH solution.

The evolution of is obtained by time integration of Eq. (55) for the given \( \bar{\theta }\) and \( \overline{\varvec{\nabla }}\bar{\theta }\). Seven \( \eta ^k \) with the highest amplitude are shown in Fig. 5. These \( \eta ^k \) values correspond to the reduced transient basis shown in Fig. 4, selected by the criteria (66). The selected eigenvectors, even these with higher eigenvalues, are important for an adequate approximation of the macroscopic quantities \( \overline{\varvec{q}}\) and \( \dot{\overline{\epsilon }} \). Next, we perform an error analysis to verify this assertion.

Fig. 5
figure 5

The time evolution of the \( \eta ^k \) coefficients acting on the transient reduced basis \( \overset{*}{\underline{\Phi }} \)

Full size image
Fig. 6
figure 6

a Time averaged \( L_2 \) error norm for the microscopic temperature field. b \( L_2 \) error norm for the rate of change of macroscopic internal energy \( \dot{\overline{\epsilon }} \). The error is computed relative to the reference CTH solution for the sequential enrichment of the microscopic transient basis by addition of extra eigenvectors

Full size image

Considering the computational transient homogeniztaion (CTH) solution as the reference one, the selection criteria for the reduced transient basis \( \overset{*}{\underline{\Phi }} \) can be verified using a-posteriori error measures. To evaluate the effect of the addition of each new eigenvector on the accuracy of the microscopic temperature field \( \theta ^{\textsf {RTH}} \) calculated with the reduced transient homogenization (RTH), it is enriched sequentially with \( N_q \) eigenvectors i.e. ,

(68)

A time averaged \( L_2 \) error norm with respect to the reference CTH solution can be written as

$$\begin{aligned} \varepsilon ^\theta _{N_q} = \frac{1}{T} \int _T \frac{|| \theta ^{\textsf {CTH}}(t) - \theta ^{\textsf {RTH}}_{N_q} (t) ||_{L_2} }{|| \theta ^{\textsf {CTH}} (t) ||_{L_2}} \text {dt}, \quad N_q = 1,2,3, \ldots ,200. \end{aligned}$$
(69)

Figure 6a shows that the decrease in the error \( \varepsilon ^\theta _{N_q} \) only occurs with the addition of particular eigenvectors, which are exactly the ones identified by criterion (66) and shown in Fig. 4. Similarly, an error measure is formulated for the macroscopic quantities, in this case for the rate of change of macroscopic internal energy as

$$\begin{aligned} \varepsilon _{N_q}^{\dot{\overline{\epsilon }}} = \frac{|| \dot{\overline{\epsilon }}^\textsf {CTH}- \dot{\overline{\epsilon }}_{N_q}^\textsf {RTH}||_{L_2}}{|| \dot{\overline{\epsilon }}^\textsf {CTH}||_{L_2}}, \quad N_q = 1,2,3, \ldots ,200. \end{aligned}$$
(70)

The accuracy of the macroscopic quantity \( \dot{\overline{\epsilon }} \) also increases only with the addition the dominant eigenvectors indicated by the criteria in Eq. (66). This a-posteriori analysis is carried out for validation purposes only. Because of its associated computational costs, it is not recommended to be used in an actual multi-scale analysis.

4.3 Homogenization results

Next, we compare the microscopic temperature field and the macroscopic quantities computed with the proposed reduced transient homogenization (RTH), method the conventional steady-state (SSH) and the transient computational homogenization (CTH) methods.

Fig. 7
figure 7

Non-dimensional temperature fields computed with the SSH (left), RTH (center) and CTH (right) at time step \( t = 156\Delta t\)

Full size image

4.3.1 Microscopic temperature field

In this article, conventional transient homogenization (CTH) is considered as the reference solution, which is proven against DNS in the literature, for example see [28, 29]. Therefore, we chose not to repeat the validation of CTH against DNS. In general, homogenization methods require the solution of the primary variable at the microscale and then averaging is performed to obtain macroscopic quantities. To calculate the temperature fields in SSH and CTH  standard finite element computations (with periodic boundary conditions) on the microstructural domain (RVE) are performed. For computing the temperature field in RTH, first the variables are solved using Eq. (62), then the total microscopic response is obtained by substituting and into Eq. (49). Figure 7 shows the temperature profiles at time step \( t = 156 \times \Delta t\)[s] for RTH in the center, SSH on the left and CTH on the right. The RTH response is further decomposed into its steady-state \( \theta _{ss} \) and transient \( \theta _{tr} \) parts. The steady-state RTH part is equal to the SSH full microscopic response \( \theta ^{\textsf {SSH}} \) (i.e. computed using steady-state assumption at the microscale). The steady-state approximation is not able to capture the transient effects and be used in the transient regimes represented by Eqs. (6) and (7). The RTH properly accounts for the transient and inertial effects and the resulting solution field is approximately equal to the reference, but computationally expensive, CTH response. Next, we compare the effective macroscopic quantities calculated with the different homogenization methods.

4.3.2 Effective macroscopic quantities

The effective macroscopic quantities are post-processed from the microscopic temperature field. The procedure for the evaluation of the effective quantities differ for the different homogenization schemes. In the SSH and CTH schemes, the computation of and post-processing to obtain follows from the solution of the finite element system of equations and (32), respectively. For calculating the macroscopic heat flux \( \overline{\varvec{q}}\), in both SSH and CTH, Eq. (56) is used. For calculating the rate of change of the macroscopic energy \( \dot{\overline{\epsilon }}\) for CTH, expression (57) is utilized. Since in SSH transient inertia effects are disregarded, following the work of [24], the rule of mixtures for the effective thermal capacity is used. In RTH, once the coefficients terms in (59) and (61) are calculated, the macroscopic heat flux \( \overline{\varvec{q}}\) and the rate of change of the macroscopic internal energy \( \dot{\overline{\epsilon }}\) are computed directly using (58) and (60), respectively. The expressions for the macroscopic quantities used in different homogenization schemes are summarized in Table 2. As shown in Fig. 8, the effective macroscopic quantities calculated with the proposed RTH method approximate very well the reference solution calculated with the CTH method. This indicates that the RTH method adequately captures the macroscopic phenomena. The macroscopic heat flux calculated with SSH is nearly equal to the one calculated with the transient homogenization methods, which implies that for the considered example, the difference \( \langle \dot{\epsilon }(\varvec{x}- \overline{\varvec{x}}) \rangle \) is negligible compared to \( \langle \varvec{q}\rangle \). Indeed, due to the “fast” connected matrix, the heat flux reaches a steady-state almost instantaneously when the temperature changes at the prescribed part of the boundary. When some transient phenomena in the matrix are not negligible, for example in the regime given by Eq. (6c), the difference \( \langle \dot{\epsilon } (\varvec{x}-\overline{\varvec{x}}) \rangle \) becomes significant. However, such regimes are outside the limits of applicability of RTH; this limitation is further examined in Sect. 4.4. In SSH, the rate of change of the macroscopic internal energy \( \dot{\overline{\epsilon }} \) is overestimated due to the use of the rule of mixtures. The thermal inertia, due to the slow transient inclusions, results in a lagging behavior which is well captured by CTH and the proposed RTH method.

Table 2 Expressions for the effective macroscopic quantities in different homogenization schemes
Full size table
Fig. 8
figure 8

Comparison of a effective macroscopic heat flux \( \overline{\varvec{q}}\) and b effective rate of change of macroscopic internal energy \( \dot{\overline{\epsilon }} \) computed with the CTH, RTH and SSH method

Full size image

4.3.3 Computational costs

In RTH, the solution of the microscale problem is obtained in two steps; an off-line step and an on-line step. In the off-line step, the eigenvalue problem is solved and the coefficients (59) and (61) are calculated and stored. In the on-line step, evolution of the modal coefficients is obtained by solving (62) and subsequently used to extract the effective quantities. In CTH, the solution to the microscale problem is obtained by an on-line step, only involving the solution of the system of Eq. (32). Comparison between the computational times for CTH and RTH, should be made only for the on-line solution stage corresponding to the costs of computing the effective quantities for a macroscopic point, since the RTH off-line stage and storage of the coefficients is done once and for all on beforehand. Figure 9 shows the computational times, as a function of the number of the underlying microscopic problems (in a two-scale macroscopic simulation this corresponds to an increasing number of elements at the macroscale). The simulations were performed on a computer with a core-i5@3.2 GHz processor and 8 Gb RAM using Matlab 2018b. The computational gain with RTH is significant. The ratio between the simulation times using CTH and RTH was approximately \( 2.5\times 10^7 \) in all cases. Considering the resulting high accuracy, as shown in Fig. 6, and the computational gain observed here, RTH is qualified for replacing CTH in the regimes where it is applicable. To properly assess the limits of applicability of RTH the separation of scales due to changes in material properties and the size of microscopic domain are scrutinized next.

Fig. 9
figure 9

CPU time as a function of the number of microscopic problems solved with with computational expensive CTH and the proposed reduced order RTH method

Full size image
Fig. 10
figure 10

Comparison of the time evolution of the macroscopic quantities, effective heat flux—first row and the rate of change of internal energy—second row, calculated using RTH and CTH with different material properties leading to different separation of scales regimes as shown in Table 3

Full size image
Fig. 11
figure 11

Effect of RVE size \( \hat{l} \) on the time averaged a macroscopic heat flux and b the rate of change of macroscopic internal energy calculated with the SSH, CTH and RTH methods

Full size image

4.4 Applicability limits of RTH

Performing RTH for mechanical problems [37] is equivalent to substructuring in structural dynamics systems [36], in which the boundary of each substructure is assumed to accommodate a rigid body motion with respect to the loading conditions, for which neglecting the dynamic effects of the boundary may lead to a too stiff mechanical response. Similar phenomena are observed here for heat conduction problems, i.e. when the combination of material properties of the microscale constituents and the loading conditions do not satisfy the relaxed separation of scale, pushing RTH outside its applicability limits, as illustrated in the following.

Table 3 Material properties used to achieve different scale separation regimes
Full size table

4.4.1 Scale separation regimes

To perform this analysis, only the material properties are varied to achieve different scale separation regimes in Eq. (6). These material properties are given in the Table 3.

When significant transient phenomena exist in the matrix, represented by Eqs. (6a) and (6b), the results are shown in Fig. 10a, b. In this case, the proposed RTH method over- or underestimates the macroscopic quantities as compared to CTH. However, when the matrix is comparatively less transient, as in Eq. (6c), RTH approximation becomes better again.

4.4.2 Size effect

To obtain non-zero time averaged macroscopic quantities, the normalized loading frequency is changed to \( \omega = 0.25 \). The effect of the non-dimensional microscopic length \( \hat{l} \) on the time-averaged macroscopic quantities can be seen in Fig. 11. As discussed earlier, the SSH method relies on the steady-state assumption at the microscale and is therefore unable to capture the size effects; the SSH response remains constant as the RVE size increases. Both CTH and RTH methods capture the size effect, however as the RVE size increases the characteristic diffusion time of the matrix also increases, which leads to a “stiff” response and RTH becomes slightly less accurate compared to the reference CTH solution.

5 Conclusions and perspectives

A reduced model for the homogenization of transient heat conduction problems was developed. It is based on the relaxed separation of scales, under material linearity, in which the matrix always remains in steady-state and only inclusions experience transient effects. The effective macroscopic quantities for transient homogenization were obtained using the extended Hill–Mandel condition adopted for the transient thermal problems. The main contribution of this work is the development of a model reduction approach at the microscale, where the microscopic solution and the macroscopic quantities are represented in terms of the steady-sate and transient reduced bases along with their corresponding coefficients. This reduced homogenization technique adequately captures microscopic transient effects in its target regime of scale separation. Significant computational gain was observed as compared to the conventional transient homogenization scheme. In future work, the enriched continuum formulation resulting from the reduced transient homogenization procedure will be used to solve macroscopic boundary value problems. A reduced model for coupled thermo-mechanical problems can also be formulated in which both the thermal and mechanical problems can be solved with a similar reduced approach.