Structural topology optimization involving bi-modulus materials with asymmetric properties in tension and compression

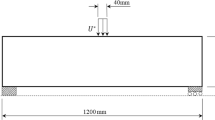
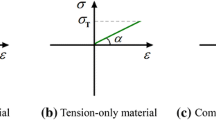
Abstract

Many materials show asymmetric performance under tension and compression and their mechanical property can be well simulated by a so-called bi-modulus type constitutive relation. The underlying non-smoothness nature associated with this kind of constitutive behavior, however, makes it extremely difficult to investigate structural topology optimization problems involving bi-modulus materials. In the present paper, rigorous sensitivity results and efficient solution procedure for topology optimization problems involving a single-phase bi-modulus material are established and generalized to two-phase bi-modulus materials case. The validity and effectiveness of the proposed approach are verified by analytical solutions and numerical results. It is also found that the optimal structural topologies may be highly dependent on the tension to compression modulus ratios and quite different from the one obtained under the assumption of linear elasticity. Besides, the present results can be successfully used for engineering applications such as design of no-tension/no-compression structures and strut-and-tie models.

Appendix: Proof of the lemma for sensitivity analysis in Sect. 3.1

Proof

For a general conservative non-linear elastic system, the displacement field in equilibrium state can be determined according to the minimum potential energy principle as:

$$\begin{aligned} {\varvec{u}}\in \hbox {Arg }\mathop {\min }\limits _{v\in \mathcal{U}_{ad} } \left( {{\Pi }\left( {\varvec{v}} \right) } \right) , \end{aligned}$$

(A1)

where ${\varvec{v}}$ is the feasible displacement filed; ${\Pi }\left( {\varvec{v}} \right)$ denotes the total potential energy, i.e.,

$$\begin{aligned} {\Pi }\left( {\varvec{v}} \right)= & {} \mathop \int \nolimits _0^t \mathop \int \nolimits _{\Omega } {\mathbb {C}}\left( {\varvec{v}} \right) :{{\varvec{\upvarepsilon }}}\left( {\varvec{v}} \right) :{ {\dot{{\varvec{\upvarepsilon }}}}}({\varvec{v}})\hbox {dV } \hbox {dt}\nonumber \\&-\mathop {\int }\nolimits _{\Omega } {\varvec{f}}\cdot {\varvec{v}} \hbox {dV}- \mathop {\int }\nolimits _{\mathrm{S}_{\mathrm{t}}} \bar{\varvec{t}} \cdot {\varvec{v}}\hbox {d}S. \end{aligned}$$

(A2)

According to Eqs. (21) and (22), we have:

$$\begin{aligned} {\Pi }\left( {\varvec{u}} \right)= & {} U\left( {\varvec{u}} \right) -\mathop \int \nolimits _{\Omega } {\varvec{f}}\cdot {\varvec{u}}\hbox {dV}-\mathop \int \nolimits _{{\mathrm{S}}_{\mathrm{t}} } {\bar{{\varvec{t}}}}\cdot {\varvec{u}}\hbox {dS}\nonumber \\= & {} \left( {\alpha -1} \right) \left( \mathop \int \nolimits _{\Omega } {\varvec{f}}\cdot {\varvec{u}}\hbox {dV}+\mathop \int \nolimits _{\mathrm{S}_{\mathrm{t}} } {\bar{{\varvec{t}}}}\cdot {\varvec{u}}\hbox {dS}\right) , \end{aligned}$$

(A3)

and

$$\begin{aligned} c\left( {\varvec{u}} \right)= & {} \mathop \int \nolimits _{\Omega } {\varvec{f}}\cdot {\varvec{u}}\hbox {dV}+\mathop \int \nolimits _{\mathrm{S}_{\mathrm{t}} } {\bar{{\varvec{t}}}} \cdot {\varvec{u}}\hbox {dS}=\frac{1}{\alpha -1}{\Pi }\left( {\varvec{u}} \right) \nonumber \\= & {} \frac{1}{\alpha -1}\mathop {\min }\limits _{{\varvec{v}}\in \mathcal{U}_{ad} } \left( {{\Pi }\left( {\varvec{v}} \right) } \right) . \end{aligned}$$

(A4)

Hence, the objective function can be expressed as:

$$\begin{aligned} c= & {} c\left( {{\varvec{u}}\left( {\rho \left( {\varvec{x}} \right) } \right) ,\rho \left( {\varvec{x}} \right) } \right) =\frac{1}{\alpha -1}{\Pi }\left( {{\varvec{u}}\left( {\rho \left( {\varvec{x}} \right) } \right) ,\rho \left( {\varvec{x}} \right) } \right) .\nonumber \\ \end{aligned}$$

(A5)

On the other hand, the first order variation of mean compliance with respect to density field is:

$$\begin{aligned} \delta c\left( {\rho ;\Delta \rho } \right)= & {} \mathop {\lim }\limits _{s\rightarrow 0} \frac{c\left( {{\varvec{u}}\left( {\rho +s\Delta \rho } \right) ,\rho +s\Delta \rho } \right) -c\left( {{\varvec{u}}\left( \rho \right) ,\rho } \right) }{s}\nonumber \\= & {} \mathop {\lim }\limits _{s\rightarrow 0} \frac{c\left( {{\varvec{u}}\left( {\rho +s\Delta \rho } \right) ,\rho +s\Delta \rho } \right) -c\left( {{\varvec{u}}\left( \rho \right) ,\rho +s\Delta \rho } \right) }{s}\nonumber \\&+\mathop {\lim }\limits _{s\rightarrow 0} \frac{c\left( {{\varvec{u}}\left( \rho \right) ,\rho +s\Delta \rho } \right) -c\left( {{\varvec{u}}\left( \rho \right) ,\rho } \right) }{s}\nonumber \\= & {} \frac{\partial c\left( {{\varvec{u}},\rho } \right) }{\partial {\varvec{u}}}\cdot \delta {\varvec{u}}\left( {\rho ;\Delta \rho } \right) +\frac{\partial c\left( {{\varvec{u}},\rho } \right) }{\partial \rho }\cdot \Delta \rho . \end{aligned}$$

(A6)

In the above equation, the first order differentiability of $c\left( {{\varvec{u}},\rho } \right)$ with respect to arbitrary $\rho$ and ${\varvec{u}}$ is used.

With use of Eq. (A5), the first term in Eq. (A6) can be simplified as:

$$\begin{aligned} \frac{\partial c\left( {{\varvec{u}},\rho } \right) }{\partial {\varvec{u}}}= & {} \frac{\partial }{\partial {\varvec{u}}}\left( {\frac{1}{\alpha -1}{\Pi }\left( {{\varvec{u}},\rho } \right) } \right) \nonumber \\= & {} \frac{1}{\alpha -1}\frac{\partial {\Pi }\left( {{\varvec{u}},\rho } \right) }{\partial {\varvec{u}}}=\frac{1}{\alpha -1}\left. {\frac{\partial {\Pi }\left( {\varvec{v},\rho } \right) }{\partial \varvec{v}}} \right| _{{\varvec{v}}={\varvec{u}}} =0,\nonumber \\ \end{aligned}$$

(A7)

where the fact of Eq. (A1) is used. Then Eq. (A6) becomes

$$\begin{aligned} \delta c\left( {\rho ;\Delta \rho } \right) =\frac{1}{\alpha -1}\frac{\partial {\Pi }\left( {{\varvec{u}},\rho } \right) }{\partial \rho }\cdot \Delta {\rho }, \end{aligned}$$

(A8)

Furthermore, if finite element method is adopted to discretize the corresponding continuum topology optimization problem, we have:

$$\begin{aligned} {\Pi }\left( {{\varvec{u}},{\varvec{\rho }} } \right) =\alpha {\varvec{u}}^{\top }{} \mathbf{K}\left( {{\varvec{\rho }} ,{\varvec{u}}} \right) {\varvec{u}}-{\varvec{F}}^{\top }{\varvec{u}}, \end{aligned}$$

(A9)

and Eq. (A8) has the following form:

$$\begin{aligned} \delta c\left( {{\varvec{\rho }} ;\Delta {{\rho }}_i } \right) =\left( {\frac{\alpha }{\alpha -1}} \right) {\varvec{u}}^{\top }\cdot \frac{\partial \mathbf{K}\left( {{\varvec{\rho }}, {\varvec{u}}} \right) }{\partial \rho _i }\cdot {\varvec{u}}\cdot \Delta \rho _i , \end{aligned}$$

(A10)

or

$$\begin{aligned} \frac{\partial c}{\partial \rho _i }=\frac{\alpha }{1-\alpha }{\varvec{u}}^{\top }\frac{\partial \mathbf{K}({\varvec{\rho }}, {\varvec{u}})}{\partial \rho _i }{\varvec{u}}, \end{aligned}$$

(A11)

where $\rho _i$ denotes the density of the ith element.

Finally, it should be pointed out that the non-smooth property of the bi-modulus constitutive relation results in the non-differentiability of the second order of the strain energy density, however, the first order partial derivatives of the strain energy density or the mean compliance are still continuous, i.e., $w\left( {\varvec{u}} \right) \in H^{1}\left( {\varvec{u}} \right)$, $c\left( {\varvec{u}} \right) \in H^{1}\left( {\varvec{u}} \right)$. Specifically, in one dimensional case,

$$\begin{aligned} \left. {\frac{\partial w}{\partial \varepsilon }} \right| _{\sigma \rightarrow 0^{+}} =\left. \sigma \right| _{\sigma \rightarrow 0^{+}} =\left. {\frac{\partial w}{\partial \varepsilon }} \right| _{\sigma \rightarrow 0^{-}} =\left. \sigma \right| _{\sigma \rightarrow 0^{-}} =0,\nonumber \\ \end{aligned}$$

(A12)

and

$$\begin{aligned} \left\{ {{\begin{array}{l} {\left. {\frac{\partial ^{2}w}{\partial \varepsilon ^{2}}} \right| _{\sigma \rightarrow 0^{+}} =E^{+},} \\ {\left. {\frac{\partial ^{2}w}{\partial \varepsilon ^{2}}} \right| _{\sigma \rightarrow 0^{-}} =E^{-}.} \\ \end{array} }} \right. \end{aligned}$$

(A13)

$\square$